Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2004 Feb;13(2):400–411. doi: 10.1110/ps.03348304

An accurate, residue-level, pair potential of mean force for folding and binding based on the distance-scaled, ideal-gas reference state

Chi Zhang 1,1, Song Liu 1,1, Hongyi Zhou 1, Yaoqi Zhou 1
PMCID: PMC2286718  PMID: 14739325

Abstract

Structure prediction on a genomic scale requires a simplified energy function that can efficiently sample the conformational space of polypeptide chains. A good energy function at minimum should discriminate native structures against decoys. Here, we show that a recently developed, residue-specific, all-atom knowledge-based potential (167 atomic types) based on distance-scaled, finite ideal-gas reference state (DFIRE-all-atom) can be substantially simplified to 20 residue types located at side-chain center of mass (DFIRE-SCM) without a significant change in its capability of structure discrimination. Using 96 standard multiple decoy sets, we show that there is only a small reduction (from 80% to 78%) in success rate of ranking native structures as the top 1. The success rate is higher than two previously developed, all-atom distance-dependent statistical pair potentials. Applied to structure selections of 21 docking decoys without modification, the DFIRE-SCM potential is 29% more successful in recognizing native complex structures than an all-atom statistical potential trained by a database of dimeric interfaces. The potential also achieves 92% accuracy in distinguishing true dimeric interfaces from artificial crystal interfaces. In addition, the DFIRE potential with the Cα positions as the interaction centers recognizes 123 native structures out of a comprehensive 125-protein TOUCHSTONE decoy set in which each protein has 24,000 decoys with only Cα positions. Furthermore, the performance by DFIRE-SCM on newly established 25 monomeric and 31 docking Rosetta-decoy sets is comparable to (or better than in the case of monomeric decoy sets) that of a recently developed, all-atom Rosetta energy function enhanced with an orientation-dependent hydrogen bonding potential.

Keywords: Knowledge-based potential, decoy sets, ideal-gas reference state, residue-level potential

One of the bottlenecks for accurate prediction of protein structures and the structures of binding complexes is the immense number of possible conformations accessible to polypeptide chains (Dill and Chan 1997; Dobson et al. 1998; Honig 1999). One way to increase the computational efficiency of sampling the conformational space is to use a reduced, residue-level rather than atom-level representation of proteins (Levitt 1976; Eyrich et al. 1999; Kihara et al. 2001, 2002; Simons et al. 2001; Bonneau et al. 2002; Gray et al. 2003; Nanias et al. 2003; Zacharias 2003). Except for a few semi-physical/empirical energy functions (Lazaridis and Karplus 2000; Kihara et al. 2001; Pillardy et al. 2001), most existing residue-based energy functions (Miyazawa and Jernigan 1985; Hendlich et al. 1990; Sippl 1990; Jones et al. 1992; Panchenko et al. 2000; Vijayakumar and Zhou 2000; Melo et al. 2002) are knowledge-based potentials which are obtained from statistical analysis of known protein structures (Tanaka and Scheraga 1976; Bowie and Eisenberg 1994) and/or optimization of the bias of native structures against their decoys (Tobi and Elber 2000; Vendruscolo et al. 2000; Chhajer and Crippen 2002). Knowledge-based potentials are attractive because they are simple to construct and easy to use. Basic physical principles, however, are often violated (or ignored) in this procedure, because proteins are an inhomogeneous mixture of amino-acid residues, and the composition of amino-acid residues determines the statistical outcome. For example, the higher population of hydrophobic residues compared to that of hydrophilic residues at the core of proteins leads to unphysical long-range repulsion between hydrophobic residues (Thomas and Dill 1996) for the distance-dependent pair potential based on the commonly used Sippl approximation (Sippl 1990). The significantly different compositions at the surface, core, and interface of proteins (Glaser et al. 2001; Lu et al. 2003; Ofran and Rost 2003) yield quantitatively different distance-dependent pair potentials for folding and binding studies (Moont et al. 1999; Lu et al. 2003), despite the fact that folding and binding involve the same physical interaction, that is, water-mediated interaction between amino-acid residues. These unphysical characteristics of statistical potentials have limited their accuracy.

A residue-specific, all-atom, distance-dependent potential of mean-force was recently extracted from the structures of single-chain proteins by using a physical state of uniformly distributed points in finite spheres (distance-scaled, finite, ideal-gas reference [DFIRE] state) as the zero-interaction reference state (Zhou and Zhou 2002). Remarkably, the physical reference state yields a potential of mean-force that no longer possesses some unphysical characteristics associated with other statistical potentials. It was shown that the accuracy of DFIRE-based potential is insensitive to the partitioning of hydrophobic and hydrophilic residues within a protein (Zhou and Zhou 2002). More importantly, the new structure-derived potential can quantitatively reproduce the likelihood of a residue to be buried (i.e., the composition difference of amino-acid residues between core and surface; Zhou and Zhou 2004). The potential also produces a stability scale of amino-acid residues in quantitative agreement with that independently extracted from mutation experimental data (Zhou and Zhou 2004). Moreover, the “monomer” potential (derived from single-chain proteins) is found to be equally successful in discriminating against docking decoys, distinguishing true dimeric interface from crystal interfaces, and predicting binding free energy of protein-protein and protein-peptide complexes (Liu et al. 2004). The independence of the performance on amino-acid compositions suggests that the DFIRE-based potential captures the essence of the common physical interaction masked under different compositions of amino-acid residues on the surface, at the core, and at the interface of proteins.

The DFIRE-based potential was an all-atom potential. An initial study of the potential at the level of Cβ atoms plus backbone atoms indicated that the accuracy of the potential reduces somewhat but remains reasonable (Zhou and Zhou 2002). In the present study, we further reduced the number of atoms for representing a residue to a single united center such as Cα (Melo et al. 2002), Cβ (Hendlich et al. 1990), or side-chain center of mass (SCM, geometry; Bryant and Lawrence 1993; Kocher et al. 1994; Thomas and Dill 1996; Zhang and Kim 2000). The united-residue potential of mean force was tested by the multiple decoy sets of single-chain proteins as well as by docking decoys. We show that the DFIRE-SCM potential of mean force is even more successful than the all-atom potentials of mean force based on statistically average reference states (RAPDF; Samudrala and Moult 1998) and atomic Knowledge-Based Potential (KBP; Lu and Skolnick 2001) in recognizing native structures from 96 multiple decoy sets and 21 docking decoy sets. It is also more successful than a sophisticated semiphysical energy function enhanced with hydrogen-bonding interactions (Kortemme-Morozov-Baker [KMB] potential; Kortemme et al. 2003) in structure discrimination using a new Rosetta monomeric decoy set, and it is comparably successful in the Rosetta docking decoy set. Results suggest that the DFIRE-SCM potential is one of the most accurate coarse-grained potentials that should be useful in assisting structure prediction on a genomic scale (Baker and Sali 2001; Schonbrun et al. 2002; Vajda et al. 2002; Janin and Seraphin 2003).

Results

Structure selections from 96 standard multiple decoy sets

We compiled 96 standard multiple decoy sets available from the literature to test simplified potentials of mean force (Table 1). They include the 4state_reduced set (Park and Levitt 1996), lmds set (through conformational enumeration of loop region; Keasar and Levitt 2003), fisa set (Simons et al. 1997), fisa_casp3 set (Simons et al. 1997), Rosetta (Simons et al. 1999; through Rosetta method, Simons et al. 1997), lattice_ssfit (Samudrala et al. 1999; through conformational enumeration on whole protein), and CASP4 decoy sets (rebuilt by Feig and Brooks 2002). No decoy structures in the original decoy sets were omitted in this study. The diverse and comprehensive decoy sets ensure the fair evaluation of the overall quality of a potential.

Table 1.

The standard 96 multiple decoy sets

Source Decoy number Target (PDB ID)
4statea 630–687 1ctf, 1r69, 1sn3, 2cro, 3icb, 4pti, 4rxng
lattice_ssfitb 2000 1beo, 1ctf, 1dkt-A, 1fca, 1nkl, 1pgb, 1trl-A, 4icb
lmdsc 343–500 1b0n-Bg,h,i, 1bbag,h,i, 1ctf, 1dtkg,i, 1fc2g,h, 1igdg, 1shf-A, 2cro, 2ovog, 4ptig
fisad 500–1200 1fc2g,h, 1hdd-C, 2cro, 4icb
fisa_casp3e 500–1200 1bg8-A, 1bl0, 1jwe
CASP4f 42–112 t0086(1fw9), t0087(1i74), t0091(1j8b)g,h,i, t0092(1im8), t0096(1e2x), t0098(1fc3), t0100(1qjv), t0103(1ga6), t0104(1fl9), t0106(1ijx)g, t0107(1i8u), t0108(1j83), t0111(1e9i), t0112(1e3j), t0113(1e3w), t0115(1fwk), t0117(1j90), t0118(1fzr)g,h, t0121(1g29), t0123(1exs)g,h, t0125(1ghk), t0126(1f35), t0127(1g8p)
Rosettae 1000 1aa2, 1acf, 1ahog,i 1ail, 1ajjg,h,i, 1bdo, 1cc5, 1csp, 1ctf, 1eca, 1erv, 1gvp, 1hlb, 1kte, 1lfbg,i, 1lis, 1lzl, 1mbd, 1msi, 1mzm, 1nxbg,h,i, 1orc, 1pal, 1pdo, 1pgx, 1ptqg,i 1r69, 1ris, 1tul, 1utgg, 1vls, 1who, 2acy, 2erl, 2fdn, 2fha, 2gdm, 2sn3, 4fgf, 5icb, 5ptig,i
Open in a new tab

a (Park and Levitt 1996).

b (Xia et al. 2000).

c (Keasar and Levitt 2003).

d (Simons et al. 1997).

e (Simons et al. 1999).

f (Feig and Brooks 2002).

g Missed by DFIRE SCM potential in native rank.

h Missed by DFIRE SCM potential in top 5 rank.

i Targets which do not have a corresponding X-ray crystal structure, have >10% difference in the number of atoms between target and decoy structures, or contain constitutive ligands (e.g., heme groups or iron-sulfur clusters).

We first tested which representation of force centroids (Cα, Cβ, and SCM) yields the most accurate distance-dependent pair potential. The three representations have different characteristics: The Cα-Cα distance reflects the proximity of backbone atoms, the Cβ-Cβ potential is sensitive to the direction of the side chains, and the center of mass, on the other hand, takes into account the average side-chain conformations (Kocher et al. 1994). Figure 1 ▶ compares the performance of different force centroids in recognizing native structures from decoys. For all three statistical potentials of mean force (KBP, Lu and Skolnick 2001; RAPDF, Samudrala and Moult 1998; DFIRE, Zhou and Zhou 2002), the potential based on the side-chain center of mass (or center of geometry) is the most accurate one. For example, the success rate of the DFIRE potential (the percent of native structures that are ranked by their energy scores as number one in 96 decoy sets) increases dramatically from 35%, 50%, to 78% as the interaction center moves from Cα, Cβ, to SCM. For each type of interaction center, the DFIRE-based potential outperforms the other two methods by a significant 9% to 22%. More importantly, the average Z-score increases significantly from 3.26 for RAPDF-SCM (or 3.99 for KBP-SCM) to 4.30 for DFIRE-SCM. This suggests that DFIRE-SCM provides a stronger bias against decoys than the other two methods. Because the potential based on SCM performs the best, as found earlier (Kocher et al. 1994), hereafter we shall report the results from SCM-based potentials only, unless indicated otherwise.

Figure 1.

Figure 1.

Open in a new tab

The number of correctly identified native structures (top) and the average Z-score (bottom) in the 96 standard multiple decoy sets by three potentials using Cα, Cβ, SCM, and all-atoms as the interaction centers.

The performances of the three SCM-based potentials are compared in more detail in Table 2. The results are presented in terms of the average Z-score and the number of first-ranked native structures within the decoy sets. Among the three potentials, DFIRE-SCM has the highest number of rank-1 native structures and the highest average Z-score in 4state, lattice_ssfit, and Rosetta decoy sets. For the fisa_casp3 and fisa decoy sets, DFIRE-SCM has the same number of rank-1 native structures as KBP-SCM, but the former has a higher Z-score. In the CASP4 decoy set, DFIRE-SCM has a somewhat lower Z-score (3.15) than KBP-SCM (3.83), but the former recognizes more native proteins (19/23) than the latter (17/23). Thus, DFIRE-SCM improves over the other two types of statistical potentials in essentially every single decoy set. This suggests that the improvement is real and robust. If a success is defined by ranking the native structure as one of the five lowest-energy conformations (top 5 rank), the success rate of DFIRE-SCM increases to 88.5%. This is remarkable considering that each residue is represented by a single interaction center.

Table 2.

The success rate and the average Z-score of different SCM potentials using the 96 standard decoy sets

Source RAPDF-SCM KBP-SCM DFIRE-SCM
4state 5/7 (3.21)a 4/7 (3.91) 6/7 (3.94)
lattice_ssfit 6/8 (5.36) 6/8 (5.11) 8/8 (6.19)
lmds 2/10 (1.78) 4/10 (2.59) 3/10 (2.56)
fisa 1/4 (2.51) 3/4 (3.99) 3/4 (4.70)
fisa_casp3 2/3 (3.70) 3/3 (4.96) 3/3 (6.05)
CASP4 19/23 (2.74) 17/23 (3.83) 19/23 (3.15)
Rosetta 27/41 (3.55) 29/41 (4.16) 33/41 (4.90)
Summary 62/96 (3.26 ± 1.87) 66/96 (3.99 ± 2.13) 75/96 (4.30 ± 2.22)
75/96 (top5)b 77/96 (top5) 85/96 (top5)
Open in a new tab

a The first number is the number of native structures ranked number one; the second number is total number of proteins in the decoy set. The numbers in parentheses are the average Z-scores.

b The first number is the number of native structures that are within the rank of top 5.

A close examination of the decoy sets in which DFIRE-SCM failed indicates that many of those decoy sets belong to the proteins that do not have an X-ray native structure, or have more than 10% difference in the number of atoms between target and decoy structures, or contain constitutive ligands such as heme groups and iron-sulfur clusters (see Table 1). If these proteins are removed from the decoy sets (as in McConkey et al. 2002), the success rate of DFIRE-SCM (defined as native-rank as top 1 rank) increases further to 89%.

It is of interest to know the loss in accuracy after reducing all-atom representation to single-interaction center. Table 3 compares the performance of DFIRE-SCM with those of all-atom versions of RAPDF, atomic KBP, and DFIRE (see also Fig. 1 ▶). Remarkably, DFIRE-SCM is more accurate than the all-atom version of RAPDF and atomic KBP in native structure selections in all decoy sets except 4state the CASP4 and lattice_ssfit decoy sets. For CASP4 decoy sets, the number of native structures as rank-1 is 19 for DFIRE-SCM and 20 for KBP-all-atom and RAPDF-all-atom. However, the average Z-score from DFIRE-SCM (3.15) is higher than that from either KBP-all-atom (2.93) or RAPDF-all-atom (2.17). For lattice_ssfit, only the average Z-score from DFIRE-SCM (6.19) is lower than that from either KBP-all-atom (6.61) or RAPDF-all-atom (7.18). For all of the 96 multiple decoy sets, however, the success rate of DFIRE-SCM is 10% higher than that of RAPDF-all-atom (or 15% in the case of atomic KBP). The average Z-score given by DFIRE-SCM is also higher than those given by both RAPDF-all-atom and KBP-all-atom. The change in accuracy after reducing all-atom representation to single-interaction center for DFIRE is small except for lmds decoy sets, where the number of rank-1 native structures is seven for the all-atom DFIRE potential, compared to three for the DFIRE-SCM potential. (The number of native structures in the lmds set within top 5 is also seven for DFIRE-SCM, however.) The overall reduction in success rate based on top 1 ranking for all 96 decoy sets is only 2%. However, both potentials have nearly the same success rate based on the top 5 ranking (~89%). Thus, the abilities of DFIRE-all-atom and DFIRE-SCM to distinguish native structures from decoys are comparable for this 96 decoy sets. We also observed similar behavior for the RAPDF and KBP potentials.

Table 3.

The success rate and the average Z-score of different all-atom potentials compared to that of the DFIRE-SCM potential

Source RAPDF-all-atom KBP-all-atom DFIRE-all-atom DFIRE-SCM
4state 7/7 (3.01)a 7/7 (3.24) 6/7 (3.49) 6/7 (3.94)
lattice_ssfit 8/8 (7.18) 8/8 (6.61) 8/8 (9.47) 8/8 (6.19)
lmds 3/10 (−0.52) 3/10 (0.53) 7/10 (0.90) 3/10 (2.56)
fisa 1/4 (1.27) 0/4 (1.21) 3/4 (4.80) 3/4 (4.70)
fisa_casp3 3/3 (4.09) 0/3 (2.08) 3/3 (5.40) 3/3 (6.05)
CASP4 20/23 (2.17) 20/23 (2.93) 19/23 (2.61) 19/23 (3.15)
Rosetta 24/41 (3.18) 23/41 (3.17) 31/41 (3.91) 33/41 (4.90)
Summary 66/96 (2.82 ± 2.87) 61/96 (3.01 ± 2.46) 77/96 (3.80 ± 3.31) 75/96 (4.30 ± 2.22)
75/96 (top5)b 70/96 (top5) 84/96 (top5) 85/96 (top5)
Open in a new tab

a The first number is the number of native structures ranked number one; the second number is total number of proteins in the decoy set. The numbers in parentheses are the average Z-scores.

b The first number is the number of native structures that are with top 5 rank.

Structure selections from 21 docking decoy sets

The docking decoy set consists of 16 and 5 decoy sets downloaded from the Sternberg group’s Web site (http://www.bmm.icnet.uk) and the Vakser group’s Web site (http://reco3.ams.sunysb.edu/data/decoy/database.html), respectively. The 21 decoy sets contain 15 dimers and 6 trimers. Each decoy set has one native complex structure and 99 decoys.

Table 4 compares the results of the DFIRE-SCM potential with those of the all-atom knowledge-based Lu-Lu-Skolnick (LLS) potential (Lu et al. 2003). The LLS potential is the KBP trained with interfacial structures of dimers. The performance of the all-atom LLS potential is worse than the DFIRE-SCM potential, although the latter was not trained with any interfacial information. The success rates of the all-atom LLS potential based on top 1 ranking are 10/15 (67%) for dimers and 1/6 (17%) for trimers. The corresponding rates for DFIRE-SCM are 13/15 (87%) and 4/6 (67%), respectively. It is of interest to note that there is also a residue-level LLS potential whose success rates are significantly lower than its all-atom counterpart (20% for dimers and 0% for trimers). The DFIRE-all-atom potential, on the other hand, achieved 100% success rates for both dimers and trimers (Liu et al. 2004).

Table 4.

The ranking of the native structures and the Z-scores for the 21 docking decoy sets

PDB IDa 1chg/1hpt 1sup/2ci2 2ptn/4pti 5cha/2ovo 1a2p/1a19 lavz 1bgs 1brc
LLSb 3 2 1 1 4 2 1 1
DFIRE-SCMc 1/4.79 1/2.13 1/2.84 1/1.96 1/2.06 4/1.66 1/2.36 1/2.18
1fss 1ugh 1wql 2pcc 2sic 1cgi 1dfj %Successd
1 1 1 1 1 1 4 10/15 (67%)
1/1.97 1/3.53 1/2.66 4/2.09 1/2.33 1/2.71 1/2.51 13/15 (87%)
PDB IDe 1ahw 1bvk 1dqj 1mlc 1wej 2kai %Successd
LLSb 3 4 4 3 1 14 1/6 (17%)
DFIRE-SCMc 1/2.05 1/1.85 1/1.68 1/1.95 2/1.84 2/1.81 4/6 (67%)
Open in a new tab

a Dimers.

b The all-atom knowledge-based potential due to Lu, Lu and Skolnick derived from the interfacial structures of a dimer database (Lu et al. 2003). The number in each cell indicates the rank of the native structure. (The Z-score was not reported in Lu et al. (2003)).

c The DFIRE-based potential derived from a monomer database (Zhou and Zhou 2002). The two numbers in each cell represent the rank of native structure and the Z-score, respectively.

d The overall success rate based on the first rank.

e Trimers.

Interface selections

The simplified DFIRE-based potential is used to distinguish the true interfaces from artificial interfaces in crystalline state. The data set of 171 interfaces was established by Ponstingl et al. (2000). In Figure 2 ▶, the distributions of energies of both true and false complexes calculated with the DFIRE-SCM potential are shown. In general, true interfaces have lower energies than those of artificial interfaces. If one uses an energy score of −15 as a cutoff value to distinguish the true from the false interfaces, 92% of the dimers or monomers are assigned correctly. In contrast, the success rate of the residue-level LLS potential is only 59% for the potential trained by monomer structures and 86% for the same potential trained by the interfacial regions of dimers (Lu et al. 2003). The success rate of DFIRE-SCM is slightly less than 95% by the all-atom LLS potential (Lu et al. 2003) and 93% obtained by a method of atomic contact vectors (Mintseris and Weng 2003), but is superior to the rate of 86% obtained by a sequence-based method (Elock and McCammon 2001), the rate of 85%–88% by a solvent accessible surface area and a pair scoring function (Ponstingl et al. 2000). Note that the DFIRE-all-atom potential has a success rate of 93% (Liu et al. 2004).

Figure 2.

Figure 2.

Open in a new tab

The distribution of energy scores of the artificial (open bars) and true (filled bars) dimeric interfaces.

Structure selections from new Rosetta single-chain and docking decoy sets

To further test the DFIRE-SCM potential, we used the new Rosetta monomeric and docking decoy sets that were designed for testing energy functions (Tsai et al. 2003). The monomeric decoy sets contain 25 proteins, each of which has about 2000 decoys. The docking decoy set contains 18 complexes of antibody-antigen and 13 other complexes. There are 400 decoys for each docking structure. For comparison, we used the same definition for a successful discrimination as Kortemme et al. (2003); that is, a discrimination is successful if a Z-score is greater than 1.0.

Table 5 compares the Z-scores from DFIRE-SCM and those from KMB potential (Kortemme et al. 2003) for both monomer and docking decoy sets. The Z-score of the KMB potential ranges from −1.53 to 8.22 for the monomeric decoy sets and from −1.03 to 14.06 for the docking decoy sets. These strongly fluctuating Z-score values suggest that the KMB potential is suitable for discriminating some proteins but not others. On the other hand, the Z-score of the DFIRE-SCM potential is relatively stable, with a much narrower range. The Z-score range is between 0.48 and 5.21 for the monomeric decoy sets and between −0.45 and 3.36 for docking decoys. The overall success rate for KMB is 22/25 (88%) and 23/31 (74%) for monomeric and docking decoys, respectively. The corresponding numbers for DFIRE-SCM are 24/25 (96%) and 23/31 (74%), respectively. Thus, the DFIRE-SCM is more successful in discriminating against decoys than KMB for monomeric proteins and is comparably successful for docking decoys. This is remarkable considering the fact that the KMB potential is an all-atom potential with sophisticated, weight-optimized, energetic terms for van der Waals, solvation, hydrogen-bond interactions, and rotamer probabilities.

Table 5.

The Z-scores for 25 monomeric and 31 docking Rosetta decoy sets

Monomeric decoys Docking decoys
PDB ID KMBa DFIRE-SCMb PDB ID KMBa DFIRE-SCMb
1a32 4.59 1.92 1a2yc 2.47 0.97
1ail 8.22 2.17 1qfuc 0.01 2.14
1am3 2.39 2.14 1cz8c 6.04 1.45
1bq9 6.37 3.07 1wejc 0.79 −0.45
1cc5 −1.53 1.46 1dqjc 5.80 1.65
1cei 5.80 4.38 1e6jc 5.28 1.96
1csp 2.43 4.57 1egjc 0.72 1.04
1ctf 6.01 4.11 1eo8c 0.96 0.82
1dol 0.57 3.34 1fdlc 2.66 1.13
1hyp 3.30 5.21 1fj1c 1.51 2.01
1lfb 0.45 1.90 1g7hc 3.38 1.13
1msi 3.82 2.28 1ic4c 5.29 1.82
1mzm 2.79 2.07 1jhlc 2.31 0.72
1orc 3.57 2.83 1jrhc 8.56 1.35
1pgx 4.47 3.17 1mlcc 2.33 1.20
1ptq 3.18 0.48 1ncac 0.50 2.23
1r69 3.36 4.52 1nsnc −0.36 0.25
1tif 7.09 2.56 1ospc 7.82 1.61
1tuc 4.38 2.10 1acb 11.33 1.84
1utg 4.80 1.25 1avz 1.05 0.73
1vcc 5.50 2.73 1brs 3.43 1.44
1vif 4.47 2.27 1cho 12.06 2.51
2fxb 2.48 3.86 1ugh 2.34 2.52
5icb 5.61 3.95 2btf 4.18 1.73
5pti 6.62 1.92 1mda −1.03 0.52
1ppf 8.77 1.95
1spb 14.06 3.36
2ptc 6.18 1.69
1cse 9.16 1.91
2pcc −0.87 0.59
1fin 3.65 3.08
Average 4.03 ± 2.18 2.81 ± 1.16 4.21 ± 3.91 1.51 ± 0.80
%successd 88% 96% 74% 74%
Open in a new tab

a The Kortemme-Morozov-Baker empirical free-energy function enhanced by orientation-dependent hydrogen bonding potential (Kortemme et al. 2003).

b This work.

c Antibody antigen complex.

d The success rate based on the number of decoy sets with Z-score >1 as in Ref. (Kortemme et al. 2003).

TOUCHSTONE decoy set

The TOUCHSTONE decoy set was generated by the TOUCHSTONE II structure-prediction program (Zhang et al. 2003). The decoy set contains a comprehensive 125 proteins, each of which contains 24,000 decoys. As each decoy has only Cα positions, only the performances of RAPDF-Cα, KBP-Cα, and DFIRE-Cα are compared in Table 6. DFIRE-Cα is able to identify 123 native structures out of 125 decoy sets (98%). This is in sharp contrast to 79 native structure by RAPDF-Cα (63%) and 45 native structures by KBP-Cα (36%). The average Z-score given by DFIRE-Cα (7.96) is also significantly higher than any of those given by either RAPDF-Cα (4.59) or KBP-Cα (3.01).

Table 6.

The success rate and the average Z-score of Cα-based potentials on the TOUCHSTONE decoy set

Method RAPDF-Cα KBP-Cα DFIRE-Cα
# Correct/Total 79/125 45/125 123/125
〈Z score〉 4.59 ± 2.20 3.01 ± 2.37 7.96 ± 3.24
Open in a new tab

Comparison with other residue-level potentials

It is of interest to compare the DFIRE-based method with other well established residue-level energy functions. Tobi and Elber (2000) compared several residue-based energy functions with their TE-13 potential generated from a linear programming method. The TE-13 potential is also a distance-dependent pair potential based on side-chain center of mass (geometry). Table 7 compares the results of DFIRE-SCM with those listed by Tobi and Elber (2000) as well as the methods of Errat (Colovos and Yeates 1993), ProsaII (Sippl 1993), and VERIFY-3D (Eisenberg et al. 1997). (The results of Errat, ProsaII, and VERIFY-3D were obtained from http://www.sbc.su.se/~bjorn/ProQ/.) The success rate of the DFIRE-SCM potential is at least 15% more than those of the other 10 energy functions examined. The DFIRE-SCM potential also has the highest Z-score among 11 energy functions. For a further comparison with other residue-based potentials, the distance dependences of the DFIRE-SCM potential for two representative residue pairs are shown in Figure 3 ▶. We found that the distance dependence of the DFIRE-SCM potential between hydrophobic residues Phe and Val is qualitatively similar to those of the TE-13 and Bahar-Jernigan (BJ) potentials (shown in Fig. 1E ▶ of Tobi and Elber 2000). All three have a double well, although the exact locations are somewhat different. On the other hand, the distance dependence of the DFIRE-SCM potential between hydrophobic Met and hydrophilic Arg is qualitatively different from the TE-13 or the BJ potential (Fig. 2C ▶ of Tobi and Elber 2000). The interaction between Met and Arg given by the DFIRE-SCM potential is essentially unfavorable at any distance, whereas it is favorable at most distances for TE-13. For the BJ potential, a long-range attraction between Met and Arg is observed.

Table 7.

The success rate and the average Z-score of different potentials using a subset of the Levitt’s multiple decoy sets

Methoda TE-13 MJ GKS BT HL BJ
# Correct/Totalb 13/15 11/25 9/25 9/25 8/25 15/25
〈Z score〉 3.53 ± 1.14 2.82 ± 2.27 2.36 ± 2.53 2.65 ± 2.37 2.67 ± 2.02 2.75 ± 2.10
Method XCJ Errat ProsaII Verify3D DFIRE-SCM
Correct/Total 11/19 11/25 15/25 10/25 19/25
〈Z score〉 2.72 ± 1.82 4.04 ± 2.45 3.05 ± 1.63 2.40 ± 1.74 4.52 ± 1.75
Open in a new tab

a Energy functions listed: Tobi and Elber (TE-13) (Tobi and Elber 2000), Miyazawa and Jernigan (MJ) (Miyazawa and Jernigan 1999), Godzik, Koliniski, and Skolnick (GKS) (Godzik et al. 1995), Betancourt and Thirumalai (BT) (Betancourt and Thirumalai 1999), Hinds and Levitt (HL) (Hinds and Levitt 1992), Bahar and Jernigan (BJ) (Bahar and Jernigan 1997), Xiang, Chang and Jie (XCJ) (Li et al. 2003), Colovos and Yeates (Errat) (Colovos and Yeates 1993), Sippl(ProsaII) (Sippl, 1993), Eisenberg, Luthy, and Bowie (VERIFY-3D) (Eisenberg et al. 1997), and DFIRE-SCM (this work).

b The number of correctly ranked as number one in the total of 25 multiple decoys used in Tobi and Elber (2000). The decoy sets include 4state_reduced (1ctf,1r69,1sn3,2cro,4pti,4rxn), fisa (1fc2,1hdd-C,2cro), fisa_casp3 (1bg8-A,1bl0,1jwe), lattice_ssfit (1etf,1dkt-A, 1fca,1nkl,1pgb,1trl-A) and lmds (1ctf,1dtk,1fc2-C,ligd,1shf-A,2cro,2ovo).

Figure 3.

Figure 3.

Figure 3.

Open in a new tab

Distance dependence of the DFIRE-SCM potential between hydrophobic residues Phe and Val (left) and between hydrophobic Met and hydrophilic Arg (right).

Discussion

In this paper, a newly developed all-atom knowledge-based potential has been simplified to a residue-level energy function. The application of this reduced energy function indicates that the reduction from a full atomic representation to the residue-level representation leads to only a small change in its success rate for native-structure discrimination. More significantly, its success rate for native discrimination is higher than those of the all-atom knowledge-based potentials (RAPDF and KBP) and the all-atom semiphysical KMB potential. The discriminative ability of this reduced potential is also comparable to a recently developed atom-atom contact scoring function (McConkey et al. 2002), which achieved a success rate of 7/7 for 4state, 8/8 for lattice_ssfit, 6/8 for lmds, 19/23 for Rosetta, and 19/23 for CASP4. The corresponding rates for DFIRE-SCM are 6/7, 8/8, 3/8, 20/23, and 19/23. (This comparison is based on the same reduced decoy sets used in McConkey et al. 2002.) This suggests that the new energy function is likely to be useful as a screening tool for genomic-scale structure prediction. Unlike previously developed statistical potentials, the new potential, similar to its all-atom counterpart, can be used directly and is equally successfully in selecting native structures from docking decoys. It should be stressed that it is impossible to make an exhaustive comparison with all existing residue-level potentials. It is possible that other published residue-level potentials may exist that outperform the DFIRE-SCM potential.

The ability to successfully select native structures from decoys is the minimum requirement for an energy function. A stricter requirement for an energy function is its ability to discriminate near-native conformations in the absence of the native conformation. Although this stricter requirement is usually reserved for more refined energy functions at an all-atom level, it is of interest to know the performance of DFIRE-SCM in this aspect. One way to characterize the ability of detecting near-native conformations is the near-native Z-score, that is, the score difference between the high-rmsd decoys and the low-rmsd decoys normalized by the score fluctuation of the high-rmsd decoys (Kortemme et al. 2003). A decoy is considered a low-rmsd decoy if it is in the lowest 5% of rmsd distribution (Kortemme et al. 2003). For a separate 23 monomeric Rosetta decoy sets (Kortemme et al. 2003), there are only four proteins whose near-native Z-scores are greater than 1 for the KMB energy function. The corresponding number is four for DFIRE-all-atom and two for DFIRE-SCM. For 31 Rosetta docking decoys, there are 22, 22, and 14 proteins with a Z-score (near-native) > 1 for the KMB, DFIRE-all-atom, and DFIRE-SCM, respectively. Another way to characterize the ability to detect near-native conformations is the correlation between energy score and rmsd when the rmsd is smaller than about 3 Å (Kortemme et al. 2003). In the docking decoy set, the number of proteins whose correlation coefficients are equal to or greater than 0.5 is 18 for KMB, 23 for DFIRE-all-atom, and 15 for DFIRE-SCM. Examples are given in Figs. 4 ▶–6 ▶, where the rmsd values of decoys are plotted against their energy scores for some selected monomeric proteins, antibody/antigen, and non-antibody complexes. It is clear that DFIRE-SCM is not as good as DFIRE-all-atom or KMB in detecting near-native conformations, whereas DFIRE-all-atom and KMB have comparable ability in detecting near-native structures based on this Rosetta decoy set. However, as a common practice, the above results were obtained by DFIRE-all-atom and DFIRE-SCM without performing any minimization on either native structures or decoys due to discretization of knowledge-based potentials. We are currently developing techniques for minimization. Preliminary results suggest that minimization can further improve the detection of near-native conformations by DFIRE-all-atom and DFIRE-SCM. The details will be reported elsewhere.

Figure 4.

Figure 4.

Figure 4.

Figure 4.

Figure 4.

Open in a new tab

Scatter plots of the DFIRE-SCM score (left) and DFIRE-all-atom score (right) vs. rmsd of decoy from the native structure (based on Cα atoms). Results of two proteins (1r69 at top and 1vif at bottom) from the 23 monomeric single-domain Rosetta decoys sets are shown.

Figure 6.

Figure 6.

Figure 6.

Figure 6.

Figure 6.

Figure 6.

Figure 6.

Open in a new tab

As in Figure 4 ▶ but for 1fin (top), 1spb (middle), and 1ugh (bottom) in the non-antibody docking decoy sets.

Materials and methods

DFIRE-based potential

The derivation of equations, and the method for extracting the DFIRE-based potential using a structure database as well as the resulting potential have been described or obtained previously (Zhou and Zhou 2002). Here, we give a brief summary for completeness.

The DFIRE potential of mean force u(i, j, r) between atom (or residue) types i and j that are distance r apart is given by (Zhou and Zhou 2002):

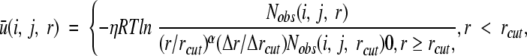graphic file with name M1.gif (1)

where η (= 0.0157) is a scaling constant, R is the gas constant, T = 300K, α = 1.61, Nobs(i, j, r) is the number of (i, j) pairs within the distance shell r observed in a given structure database, rcut = 14.5 Å, and Δr(Δrcut) is the bin width at r(rcut). (Δr = 2 Å, for r < 2 Å; Δr = 0.5 Å for 2 Å < r <8 Å; Δr = 1 Å for 8 Å < r <15 Å.) The exponent α for the distance dependence was obtained from the distance dependence of the pair distribution function for uniformly distributed points in finite spheres (finite ideal-gas reference state). The number of observed atomic (force centroids) pair (i, j) with the distance shell r [Nobs(i, j, r)] was obtained from a structural database of 1011 nonhomologous (< 30% homology) proteins with resolution <2 Å, which was collected by Hobohm et al. (1992), http://chaos.fccc.edu/research/labs/dunbrack/culledpdb.html. The potential u(i, j, r) is set to 2η if Nobs(i, j, r) = 0.

Residue-specific atomic types were used (167 atomic types; Samudrala and Moult 1998; Lu and Skolnick 2001). For a residue-based potential, all atoms in a residue are replaced by a united interaction site located at Cα, Cβ, and SCM, respectively. The numbers of types of force centroids for all three reduced potentials are 20. We use the same equation (1), same parameters, and same bin procedures to generate DFIRE-Cα, DFIRE-Cβ, and DFIRE-SCM that denote Cα-based, Cβ-based, and SCM residue-level potentials, respectively. This is reasonable because residue-specific atomic types were used in generating the all-atom DFIRE potential.

The RAPDF and KBP potentials

In order to compare the DFIRE-based potentials with the RAPDF (Samudrala and Moult 1998) and KBP (Lu and Skolnick 2001) potentials, we regenerated the two potentials using the same procedures described in their original papers. For RAPDF (Samudrala and Moult 1998), the first bin covers 0–3.0 Å, and the distance between 3.0–20 Å is binned every 1 Å. The total number of bins is 18. All 18 bins with a cutoff distance of 20 Å are used for scoring. For KBP (Lu and Skolnick 2001), the distance between 1.5 Å to 14.5 Å, is binned every 1 Å and the last bin is from 14.5 Å to infinite. The total number of bins is 14. The first and second sequence neighbors are excluded whereas backbone atoms are included in counting contacts. When used in scoring, only the bins covering 3.5–6.5 Å are used. In all cases, contacts between atoms within a single residue are excluded from the counts and scoring. In case of zero pairs, both potentials are set to be 2η kcal/mole. The structural database is the 1011 structures described above for the DFIRE-based potentials rather than the 265 proteins used in RAPDF and 1291 proteins used in atomic KBP in their respective original publications. It was shown that the change of database has little effect on the overall accuracy of the RAPDF and atomic KBP potentials (Zhou and Zhou 2002). For RAPDF and KBP residue-based potentials, we used the force centroids as for DFIRE. We used the same equation, same parameters, and same bin procedures to generate RAPDF-Cα (KBP-Cα), RAPDF-Cβ (KBP-Cβ), and RAPDF-SCM (KBP-SCM) denoting Cα-based, Cβ-based, and SCM residue-level potentials, respectively. No attempts were made to optimize the parameters and/or procedures presented in the original papers for possibly better performance.

Structure selections from decoys

For a given 3-D structures of a protein, the total residue–residue potential of mean force, G, is

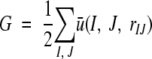graphic file with name M2.gif (2)

where the summation is over all pairs of residues. In structure selections from decoy sets, the total potential G is calculated for each structure, including native state and decoys. The native state is correctly identified if its structure has the lowest value of G. Z-score is defined as

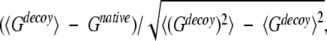graphic file with name M3.gif

where 〈〉 denotes the average over all decoy structures of a given native protein, and Gnative is the total residue-residue potential of the native structure. Z-score is a measure of the bias toward the native structure. To characterize the ability of detecting near-native conformations, the near-native Z-score, which is the score difference between the high-rmsd decoys and the low-rmsd decoys normalized by the score fluctuation of the high-rmsd decoys, was used (Kortemme et al. 2003). The near-native Z-score is expressed as (Kortemme et al. 2003)

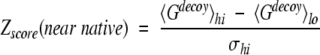graphic file with name M4.gif (3)

where 〈Gdecoy〉lo(〈Gdecoy〉hi) is the average energy score of the low (high)-rmsd decoys, and σhi is the standard deviation of the energy score of the high-rmsd decoys. A decoy is considered a low-rmsd decoy if it is in the lowest 5% of rmsd distribution (Kortemme et al. 2003). The low-rmsd decoys represent the near-native structures.

Structure selections from docking decoys/artificial interfaces

The binding free energy of a dimer AB is obtained as follows:

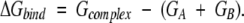graphic file with name M5.gif (4)

Because the structures of monomers are approximated as rigid bodies and the residues at the interface contribute most to ΔGbind, equation 4 can be further simplified to

graphic file with name M6.gif (5)

where the summation is over any two atoms belonging to an “interacting” residue pair from different chains at the interface. We follow the definition, due to Lu et al. (2003), in which an interacting residue pair is a pair of residues from different chains that have at least one pair of heavy atoms within 4.5 Å of each other. Equation 5 can also be used for complexes with more than two partners. The binding free energy 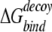Inline graphicis calculated for each docking decoy (or artificial interface). The native state is correctly identified if Δ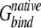Inline graphic is the lowest value among all 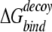Inline graphic values (the first rank). A Z-score is defined as

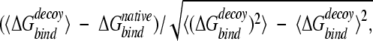graphic file with name M10.gif

where 〈〉 denotes the average over all decoy structures of a given protein. The Z-score is a measure of the free-energy bias toward the native complex structure. For docking decoys, we used the same definition of near-native Z-score to evaluate the ability of recognizing near-native structures for a potential, except that the energy for monomer decoys is replaced by binding free energy 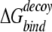Inline graphic.

Figure 5.

Figure 5.

Figure 5.

Figure 5.

Figure 5.

Figure 5.

Figure 5.

Open in a new tab

As in Figure 4 ▶ but for 1e6j (top), 1nca (middle), and 1qfu (bottom) in the antibody/antigen docking decoy sets.

Acknowledgments

We thank Profs. Charles L. Brooks and Michael Feig for the CASP4 decoy sets; Prof. David Baker and Dr. Alex Morozov for providing us the new Rosetta decoy sets; Dr. Hannes Ponstingl for the list of hypothetical dimers’ structure; and Profs. Jeffrey Skolnick and Yang Zhang for the TOUCHSTONE decoy set. This work was supported by NIH (R01 GM 966049 and R01 GM 068530), a grant from HHMI to SUNY Buffalo, and by the Center for Computational Research and the Keck Center for Computational Biology at SUNY Buffalo.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.03348304.

References

  1. Bahar, I. and Jernigan, R. 1997. Inter-residue potentials in globular proteins and the dominance of highly specific hydrophilic interactions at close separation. J. Mol. Biol. 266 195–214. [DOI] [PubMed] [Google Scholar]
  2. Baker, D. and Sali, A. 2001. Protein structure prediction and structural genomics. Science 294 93–96. [DOI] [PubMed] [Google Scholar]
  3. Betancourt, M.R. and Thirumalai, D. 1999. Pair potentials for protein folding: Choice of reference states and sensitivity of predicted native states to variations in the interaction schemes. Protein Sci. 8 361–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bonneau, R., Strauss, C., Rohl, C., Chivian, D., Bradley, P., Malmstrom, L., Robertson, T., and Baker, D. 2002. De novo prediction of three-dimensional structures for major protein families. J. Mol. Biol. 322 65–78. [DOI] [PubMed] [Google Scholar]
  5. Bowie, J.U. and Eisenberg, D. 1994. An evolutionary approach to folding small α-helical proteins that uses sequence information and an empirical guiding fitness function. Proc. Natl. Acad. Sci. 91 4436–4440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bryant, S.H. and Lawrence, C.E. 1993. An empirical energy function for threading protein sequence through the folding motif. Proteins 16 92–112. [DOI] [PubMed] [Google Scholar]
  7. Chhajer, M. and Crippen, G.M. 2002. A protein folding potential that places the native states of a large number of proteins near a local minimum. BMC Struct. Biol. 2 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Colovos, C. and Yeates, T.O. 1993. Verification of protein structures: Patterns of nonbonded atomic interaction. Protein Sci. 2 1511–1519. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dill, K.A. and Chan, H.S. 1997. From Levinthal to pathways to funnels. Nat. Struct. Biol. 4 10–19. [DOI] [PubMed] [Google Scholar]
  10. Dobson, C.M., Sali, A., and Karplus, M. 1998. Protein folding: A perspective from theory and experiment. Angew. Chem. Int. Ed. Engl. 198 868–893. [DOI] [PubMed] [Google Scholar]
  11. Eisenberg, D., Lüthy, R., and Bowie, J.U. 1997. VERIFY3D: Assessment of protein models with three-dimensional profile. Methods Enzymol. 277 396–404. [DOI] [PubMed] [Google Scholar]
  12. Elock, A. and McCammon, J. 2001. Identification of protein oligomerization states by analysis of interface conservation. Proc. Nat. Acad. Sci. 98 2990–2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Eyrich, V.A., Standley, D.M., and Friesner, R.A. 1999. Prediction of protein tertiary to low resolution: Performance for a large and structurally diverse test set. J. Mol. Biol. 288 725–742. [DOI] [PubMed] [Google Scholar]
  14. Feig, M. and Brooks III, C.L. 2002. Evaluating CASP4 predictions with physical energy functions. Proteins 49 232–245. [DOI] [PubMed] [Google Scholar]
  15. Glaser, F., Sternberg, D., Vakser, I., and Ben-Tal, N. 2001. Residue frequencies and pairing preferences at protein–protein interfaces. Proteins 43 89–102. [PubMed] [Google Scholar]
  16. Godzik, A., Kolinski, A., and Skolnick, J. 1995. Are proteins ideal mixtures of amino acids? Analysis of energy parameter sets. Protein Sci. 4 2107–2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gray, J., Moughon, S., Kortemme, T., Furman, O., Misura, K., Morozov, A., and Baker, D. 2003. Protein–protein docking predictions for the CAPRI experiment. Proteins 52 118–122. [DOI] [PubMed] [Google Scholar]
  18. Hendlich, M., Lackner, P., Weitckus, S., Floeckner, H., Froschauer, R., Gottsbacher, K., Casari, G., and Sippl, M.J. 1990. Identification of native protein folds amongst a large number of incorrect models. The calculation of low energy conformations from potentials of mean force. J. Mol. Biol. 216 167–180. [DOI] [PubMed] [Google Scholar]
  19. Hinds, D. and Levitt, M. 1992. A lattice model for protein structure prediction at low resolution. Proc. Nat. Acad. Sci. 89 2536–2540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hobohm, U., Scharf, M., Schneider, R., and Sander, C. 1992. Selection of representative protein data sets. Protein Sci. 1 409–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Honig, B. 1999. Protein folding: From the Levinthal paradox to structure prediction. J. Mol. Biol. 293 283–293. [DOI] [PubMed] [Google Scholar]
  22. Janin, J. and Seraphin, B. 2003. Genome-wide studies of protein–protein interaction. Curr. Opin. Struct. Biol. 13 383–388. [DOI] [PubMed] [Google Scholar]
  23. Jones, D.T., Taylor, W.R., and Thornton, J.M. 1992. A new approach to protein fold recognition. Nature 358 86–89. [DOI] [PubMed] [Google Scholar]
  24. Keasar, C. and Levitt, M. 2003. A novel approach to decoy set generation: Designing a physical energy function having local minima with native structure characteristics. J. Mol. Biol. 329 159–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kihara, D., Lu, H., Kolinski, A., and Skolnick, J. 2001. TOUCHSTONE: An ab initio protein structure prediction method that uses threading-based tertiary restraints. Proc. Nat. Acad. Sci. 98 10125–10130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kihara, D., Zhang, Y., Lu, H., Kolinski, A., and Skolnick, J. 2002. Ab initio protein structure prediction on a genomic scale: Application to the mycoplasma genitalium genome. Proc. Nat. Acad. Sci. 99 5993–5998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kocher, J.-P.A., Rooman, M., and Wodak, S. 1994. Factors influencing the ability of knowledge-based potentials to identify native sequence-structure matches. J. Mol. Biol. 235 1598–1613. [DOI] [PubMed] [Google Scholar]
  28. Kortemme, T., Morozov, A., and Baker, D. 2003. An orientation-dependent hydrogen bonding potential improves prediction of specificity and structure for proteins and protein–protein complexes. J. Mol. Biol. 326 1239–1259. [DOI] [PubMed] [Google Scholar]
  29. Lazaridis, T. and Karplus, M. 2000. Effective energy function for protein structure prediction. Curr. Opin. Struct. Biol. 10 139–145. [DOI] [PubMed] [Google Scholar]
  30. Levitt, M. 1976. A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol. 104 59–107. [DOI] [PubMed] [Google Scholar]
  31. Li, X., Hu, C., and Liang, J. 2003. Simplicial edge representation of protein structures and α contact potential with confidence measure. Proteins 53 792–805. [DOI] [PubMed] [Google Scholar]
  32. Liu, S., Zhang, C., Zhou, H., and Zhou, Y. 2004. A physical reference state unifies the structure-derived potential of mean force for protein folding and binding. Proteins (in press) [DOI] [PubMed]
  33. Lu, H. and Skolnick, J. 2001. A distance-dependent atomic knowledge-based potential for improved protein structure selection. Proteins 44 223–232. [DOI] [PubMed] [Google Scholar]
  34. Lu, H., Lu, L., and Skolnick, J. 2003. Development of unified statistical potentials describing protein–protein interactions. Biophys. J. 84 1895–1901. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. McConkey, B.J., Sobolev, V., and Edelman, M. 2002. Discrimination of native protein structures using atom–atom contact scoring. Proc. Natl. Acad. Sci. 100 3215–3220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Melo, F., Sanchez, R., and Sali, A. 2002. Statistical potentials for fold assessment. Protein Sci. 430 430–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Mintseris, J. and Weng, Z. 2003. Atomic contact vectors in protein–protein recognition. Proteins 53 629–639. [DOI] [PubMed] [Google Scholar]
  38. Miyazawa, S. and Jernigan, R.L. 1985. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 18 534–552. [Google Scholar]
  39. ———. 1999. An empirical energy potential with a reference state for protein fold and sequence recognition. Proteins 36 357–369. [PubMed] [Google Scholar]
  40. Moont, G., Gabb, H., and Sternberg, M. 1999. Use of pair potentials across protein interfaces in screening predicted docked complexes. Proteins 35 364–373. [PubMed] [Google Scholar]
  41. Nanias, M., Chinchio, M., Pillardy, J., Ripoll, D., and Scheraga, H. 2003. Packing helices in proteins by global optimization of a potential energy function. Proc. Nat. Acad. Sci. 100 1706–1710. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Ofran, Y. and Rost, B. 2003. Analyzing six types of protein–protein complexes. J. Mol. Biol. 325377–387. [DOI] [PubMed] [Google Scholar]
  43. Panchenko, A.R., Marchler-Bauer, A., and Bryant, S.H. 2000. Combination of threading potentials and sequence profiles improves fold recognition. J. Mol. Biol. 296 1319–1331. [DOI] [PubMed] [Google Scholar]
  44. Park, B. and Levitt, M. 1996. Energy functions that discriminate X-ray and near native folds from well-constructed decoys. J. Mol. Biol. 258 367–392. [DOI] [PubMed] [Google Scholar]
  45. Pillardy, J., Czaplewski, C., Liwo, A., Lee, J., Ripoll, D.R., Kamierkiewicz, R., Oldziej, S., Wedemeyer, W.J., Gibson, K.D., Arnautova, Y.A., et al. 2001. Recent improvements in prediction of protein structure by global optimization of a potential energy function. Proc. Natl. Acad. Sci. 98 2329–2333. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Ponstingl, H., Henrick, K., and Thornton, J. 2000. Discriminating between homodimeric and monomeric proteins in the crystalline state. Proteins 41 47–57. [DOI] [PubMed] [Google Scholar]
  47. Samudrala, R. and Moult, J. 1998. An all-atom distance-dependent conditional probability discriminatory function for protein structure prediction. J. Mol. Biol. 275 895–916. [DOI] [PubMed] [Google Scholar]
  48. Samudrala, R., Xia, Y., Levitt, M., and Huang, E. 1999. A combined approach for ab initio construction of low resolution protein tertiary structures from sequence. Pac. Symp. Biocomput. 4 505–506. [DOI] [PubMed] [Google Scholar]
  49. Schonbrun, J., Wedemeyer, W., and Baker, D. 2002. Protein structure prediction in 2002. Curr. Opin. Struct. Biol. 12 348–354. [DOI] [PubMed] [Google Scholar]
  50. Simons, K.T., Kooperberg, C., Huang, E., and Baker, D. 1997. Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J. Mol. Biol. 268 209–225. [DOI] [PubMed] [Google Scholar]
  51. Simons, K., Bonneau, R., Ruczinski, I., and Baker, D. 1999. Ab initio protein structure prediction of CASP III targets using ROSETTA. Proteins 37(S3) 171–176. [DOI] [PubMed] [Google Scholar]
  52. Simons, K., Strauss, C., and Baker, D. 2001. Prospects for ab initio protein structural genomics. J. Mol. Biol. 306 1191–1199. [DOI] [PubMed] [Google Scholar]
  53. Sippl, M.J. 1990. Calculation of conformational ensembles from potentials of mean force. An approach to the knowledge-based prediction of local structures in globular proteins. J. Mol. Biol. 213 859–883. [DOI] [PubMed] [Google Scholar]
  54. ———. 1993. Recognition of errors in three-dimensional structures of proteins. Proteins 17 355–362. [DOI] [PubMed] [Google Scholar]
  55. Tanaka, S. and Scheraga, H.A. 1976. Medium- and long-range interaction parameters between amino acids for predicting three-dimensional structures of proteins. Macromolecules 9 945–950. [DOI] [PubMed] [Google Scholar]
  56. Thomas, P.D. and Dill, K.A. 1996. Statistical potentials extracted from protein structures: How accurate are they? J. Mol. Biol. 257 457–469. [DOI] [PubMed] [Google Scholar]
  57. Tobi, D. and Elber, R. 2000. Distance-dependent, pair potential for protein folding: Results from linear optimization. Proteins 41 40–46. [PubMed] [Google Scholar]
  58. Tsai, J., Bonneau, R., Morozov, A.V., Kuhlman, B., Rohl, C.A., and Baker, D. 2003. An improved protein decoy set for testing energy functions for protein structure prediction. Proteins 53 76–87. [DOI] [PubMed] [Google Scholar]
  59. Vajda, S., Vakser, I., Sternberg, M., and Janin, J. 2002. Modeling of protein interactions in genomes. Proteins 47 444–446. [DOI] [PubMed] [Google Scholar]
  60. Vendruscolo, M., Mirny, L., Shakhnoich, E.I., and Domany, E. 2000. Comparison of two optimization methods to derive energy parameters for protein folding: Perception and Z score. Proteins 41 192–201. [PubMed] [Google Scholar]
  61. Vijayakumar, M. and Zhou, H.-X. 2000. Prediction of residue–residue pair frequencies in proteins. J. Phys. Chem. B 104 9755–9764. [Google Scholar]
  62. Xia, Y., Huang, E.S., Levitt, M., and Samudrala, R. 2000. Ab initio construction of protein tertiary structures using a hierarchical approach. J. Mol. Biol. 300 171–185. [DOI] [PubMed] [Google Scholar]
  63. Zacharias, M. 2003. Protein–protein docking with a reduced protein model accounting for side-chain flexibility. Protein Sci. 12 1271–1282. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Zhang, C. and Kim, S. 2000. Environment-dependent residue contact energies for proteins. Proc. Natl. Acad. Sci. 97 2550–2555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Zhang, Y., Kolinski, A., and Skolnick, J. 2003. TOUCHSTONE II: A new approach to ab initio structure prediction. Biophys. J. 85 1145–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Zhou, H. and Zhou, Y. 2002. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 11 2714–2726. Corrections 12: 2121 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. ———. 2004. Quantifying the effect of burial of amino acid residues on protein stability. Proteins (in press) [DOI] [PubMed]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES