Abstract
The accuracy of protein synthesis relies on the ability of aminoacyl-tRNA synthetases (aaRSs) to discriminate among true and near cognate substrates. To date, analysis of aaRSs function, including identification of residues of aaRS participating in amino acid and tRNA discrimination, has largely relied on the steady state kinetic pyrophosphate exchange and aminoacylation assays. Pre-steady state kinetic studies investigating a more limited set of aaRS systems have also been undertaken to assess the energetic contributions of individual enzyme-substrate interactions, particularly in the adenylation half reaction. More recently, a renewed interest in the use of rapid kinetics approaches for aaRSs has led to their application to several new aaRS systems, resulting in the identification of mechanistic differences that distinguish the two structurally distinct aaRS classes. Here, we review the techniques for thermodynamic and kinetic analysis of aaRS function. Following a brief survey of methods for the preparation of materials and for steady state kinetic analysis, this review will describe pre-steady state kinetic methods employing rapid quench and stopped-flow fluorescence for analysis of the activation and aminoacyl transfer reactions. Application of these methods to any aaRS system allows the investigator to derive detailed kinetic mechanisms for the activation and aminoacyl transfer reactions, permitting issues of substrate specificity, stereochemical mechanism, and inhibitor interaction to be addressed in a rigorous and quantitative fashion.
Keywords: aminoacylation, aminoacyl-tRNA synthetases
1. Introduction
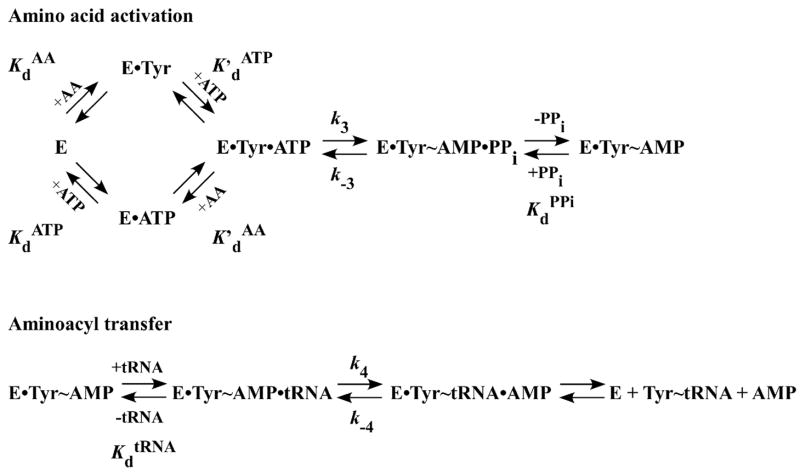
Aminoacyl-tRNA synthetases (aaRSs)1 catalyze the fundamental two-step reaction that provides aminoacyl-tRNA for protein synthesis [1–3]:
| (1) |
| (2) |
The first reaction involves the condensation of amino acid (AA) and ATP to form the enzyme-bound aminoacyl adenylate intermediate (E•AA~AMP), with pyrophosphate as product. Next, the 2′ or 3′-terminal OH group of tRNA attacks the aminoacyl adenylate intermediate to form the cognate aminoacyl-tRNA (AA-tRNAAA). Aminoacyl-tRNA is subsequently delivered by an elongation factor to the ribosome for decoding and translation.
The aaRSs are divided into two distinct evolutionarily unrelated classes that differ on the basis of their catalytic fold, signature sequences, regiochemistry, and interactions with tRNAs [4–6]. With the notable exceptions of the enzymes GlnRS, GluRS, ArgRS, and Class I LysRS, all aaRSs catalyze formation of the aminoacyl adenylate intermediate in the absence of tRNA. In some taxa, there is an aaRS corresponding to each of the 20 standard amino acids. However, only 17 canonical aaRS are conserved in all organisms: for asparagine, glutamine, and cysteine, indirect pathways exist by which the AA-tRNAAA is synthesized on the tRNA, after initial aminoacylation by a noncognate or noncanonical aaRS [7, 8]. Each aaRS obligatorily interacts with three distinct substrates: ATP, amino acid and tRNA. While ATP universally serves to activate the amino acid for all aaRSs, the other substrates have distinct structural and chemical features that provide a basis for discrimination. The need for individualized active sites to accommodate the distinctive chemical features of each amino acid serves to divide the aaRSs into 20 families, each of which is specific for its cognate amino acid. A goal of much of the work on the aaRSs is to determine how discrimination occurs with the fidelity and efficiency necessary to support physiological rates of accurate protein synthesis.
Most published kinetic analyses of the aaRSs have relied on steady state kinetics. The advantages of this approach are that (i) it does not require large amounts of materials; (ii) the assays are generally fast and involve minimal workup; and (iii) data from a large number of enzyme and tRNA variants can be rapidly obtained and compared by determining the ratio of (kcat/Km)cognate/(kcat/Km)non-cognate [9]. Although steady state kinetic assays do not allow elementary steps to be characterized, initial velocity and product inhibition patterns can provide information on the orders of substrate binding and product release [10]. The most important steady state kinetic assays for the aminoacyl-tRNA synthetases are the pyrophosphate exchange assay, which measures the rate of exchange of [32P]-PPi into ATP, and the aminoacylation assay, which measures the rate of AA-tRNAAA formation. Both are described below.
While steady state kinetics is advantageous for the initial characterization of an enzyme, pre-steady state kinetics is required to investigate mechanistic questions in detail, including the contribution of individual protein residues and tRNA nucleotides to the rates of specific elementary steps. While less broadly applied, pre-steady state experiments have provided valuable insights into catalytic mechanisms in many aaRS systems (summarized in Table 1), often allowing the determination of the thermodynamic and kinetic contributions of particular enzyme-substrate interactions to specific steps and energetic barriers along a reaction path [11]. The most common pre-steady state kinetic approaches for the aaRSs are rapid chemical quench assays, which follow rates of product formation, and stopped-flow fluorimetry, which takes advantage of changes in the intrinsic tryptophan fluorescence that are correlated with the reaction chemistry. Here, we review the methods, including both steady state and pre-steady state kinetics, that can be used to characterize the thermodynamic and kinetic parameters of the aminoacylation reaction. Although specific procedures are discussed with reference to a relatively limited number of systems, the methods are broadly applicable to all twenty aaRSs. This review will not cover in vivo approaches for characterizing aaRS function, such as amber suppression of reporter proteins, or methods for assessing tRNA aminoacylation in vivo under different conditions.
Table 1.
Rapid Kinetics Studies on Aminoacyl-tRNA Synthetases
| Class I aaRS Families | Class II aaRS Families | Site of Aminoacylation on A76 | Selected References for Stopped-flow kinetic Analysis |
|---|---|---|---|
| MetRS | 2′OH | [87] | |
| IleRS | 2′OH | [74] | |
| ValRS | 2′OH | [63, 88] | |
| LeuRS | 2′OH | ||
| CyRS | 2′OH, 3′OH | [63] | |
| GluRS | 2′OH | ||
| GlnRS | 2′OH | [40, 59] | |
| ArgRS | 2′OH | [89] | |
| TyrRS | 2′OH | [41, 60, 86, 90–93] | |
| TrpRS | 2′OH | [94, 95] | |
| LysRS | 2′OH | ||
|
| |||
| SerRS | 3′OH | [96, 97] | |
| ThrRS | 3′OH | [43] | |
| ProRS | 3′OH | [63] | |
| HisRS | 3′OH | [62, 66] | |
| AlaRS | 3′OH | [63] | |
| GlyRS | 3′OH | ||
| PheRS | 2′OH | [98] | |
| AspRS | 3′OH | ||
| AsnRS | 3′OH | ||
| LysRS | 3′OH | [99] | |
2. Description of Methods
2.1. Preparation of tRNA for kinetic studies
The tRNAs employed for kinetic studies are typically prepared by one of three different methods: 1) purification from cells harboring a tRNA expression plasmid; 2) enzymatic synthesis by in vitro transcription using T7 RNA polymerase; or 3) chemical synthesis of tRNA half molecules that can be ligated by T4 RNA ligase. Each approach has its own characteristic set of strengths and weaknesses. The basic approach for preparing tRNA from overexpressing strains involves insertion of the appropriate tRNA gene into a plasmid with a highly transcribed promoter, purifying the tRNA from intact cells by phenol extraction, fractionation by native polyacrylamide gel electrophoresis (PAGE) and, when necessary, further purification by additional chromatographic steps [12–15]. Recently, such methods have been refined to allow the separation of tRNAs based on their ability to hybridize to complementary DNA sequences [16].
The principal advantage to purifying tRNA directly from over-expressing cells is that the tRNA obtained contains the base modifications characteristic of natural tRNAs. In some systems (e.g. Glu and Thr) these are essential for efficient recognition by the aaRS, and there is evidence that modifications contribute a stabilizing influence on the tRNA structure [17, 18]. The chief disadvantage of purifying tRNA from in vivo sources is that it can be difficult to obtain homogenous preparations, owing to difficulties in separating the various isoacceptors of a given tRNA family, and because varying degrees of nucleobase modification will arise when tRNA levels exceed the capacity of the modification enzymes. In the E. coli GlnRS system, comparison of enzyme co-crystal structures bound to tRNAs prepared by in vivo or in vitro approaches explicitly demonstrated that 4-thiouracil at position 8 and pseudouridines at positions 38 and 39 are underrepresented in the overproduced tRNAGln purified from cells [19]. In addition, some tRNA sequences are not readily over-expressed in vivo, perhaps due to inefficient synthesis, folding, or processing. Care should be taken when attempting to obtain multimilligram quantities of purified tRNA by this procedure, as some of the reagents (i.e., phenol) are toxic. Generally, the successful purification of in vivo produced tRNA is dependent on the degree of enrichment of the tRNA of interest in the crude tRNA pool. If this value is high (> 500 pmol amino acid acceptance/A260 unit), then the standard methods yield tRNA preparations of reasonably high specific activity (~ 1200–1400 pmol amino acid acceptance/A260 unit). If the degree of enrichment is substantially less, then obtaining homogenous material is more difficult.
The most generally useful method for preparing large quantities of tRNA for kinetic and thermodynamic analysis is by in vitro synthesis of tRNA transcripts using T7 RNA polymerase [17, 20, 21]. The most powerful feature of the method is that tRNAs of virtually any sequence can be prepared, with the caveat that transcription yields are considerably diminished for transcripts initiating with nucleotides other than G. This limitation has recently been overcome through the development of a variant T7 RNA polymerase with reduced specificity for the first nucleotide [22]. Most commonly, the tRNA gene of interest is inserted into the multiple cloning site of an expression plasmid, downstream from the T7 RNA promoter. The tRNA gene typically terminates with a Fok I or Bst N1 restriction site, such that run-off transcription of the linearized plasmid produces a tRNA transcript with the correct CCA end. Reaction conditions for different tRNA sequences can be optimized by fine-tuning of dNTP concentrations, temperature, T7 RNAP concentration, and other variables [21, 23, 24]. Transcript purification is performed by fractionation on 8M urea/12% polyacrylamide gels, or by reverse phase chromatography on a preparative C4 column.
The biggest limitation to preparing tRNA by in vitro transcription is that the products frequently possess 3′ and/or 5′ sequence heterogeneities [20, 25, 26]. These must be eliminated by either tedious purification at reduced yields, or by use of ribozyme sequences to excise the full-length tRNA from flanking regions [27, 28]. Alternatively, 3′ heterogeneity may be reduced by employing synthetic DNA templates rather than linearized plasmids (Figure 1). The synthetic DNA is modified at the penultimate or the last two nucleotides at the 5′-terminus, using either DNA base analogs [29] or 2′-O-methyl substitutions [30]. These significantly reduce the proportion of runover transcripts and, in some cases, also increase yield [30]. A preparative scale application of the synthetic-template approach to in vitro tRNA synthesis is described in Sherlin et al. [31]. The use of Klenow fragment polymerase for partial synthesis from shorter overlapped oligonucleotides substantially increases the yield of DNA over complete chemical synthesis of the duplex, and substantially increases the size of RNA molecules that may be synthesized on a multimilligram scale without the need for preparation of plasmid templates. In the case of E. coli tRNA2Gln transcription, levels of correctly-terminated 3′-CCA tRNAs are typically in the 60%–80% range, and sometimes exceed 90%, as compared with 15%–20% correct synthesis from runoff plasmid templates [31].
Figure 1.

Schematic of synthetic template transcription. Overlapping synthetic nucleotides are used as a template for Klenow fragment extension by annealing and extension cycles. The template strand contains 2′-O-methyl modifications on the two terminal 5′ residues (inset). The double-stranded fragment then acts as a template for T7 RNA polymerase. The DNA modifications are thought to cause the polymerase to dissociate from the template before adding nontemplated residues, thereby increasing product homogeneity [30]. From Sherlin et al., 2001 [31].
The final method for preparing tRNA is through the chemical synthesis of half-molecules with a break in the anticodon loop, followed by enzymatic ligation [32]. This is valuable when a homogeneous 5′-end is required, but the tRNA begins with nucleotides unfavorable for efficient transcription initiation by T7 RNA polymerase. In addition, chemically modified nucleotides for structure-function studies of aminoacylation, tRNA modification, and ribosomal translation may be incorporated site-specifically. The approach involves annealing 35- to 40-mer oligoribonucleotides purchased from Dharmacon (Lafayette, CO) via custom synthesis to generate a tRNA that is nicked in the anticodon loop; this is subsequently ligated by T4 RNA ligase [31, 32]. The full-length RNA is then purified by repeated phenol/chloroform/isoamyl alcohol extraction, ethanol precipitation, and purification on polyacrylamide gels. For the E. coli tRNA2Gln system, 70% ligation efficiencies are obtained in experiments in which the break in the anticodon loop is present either between nucleotides 37 and 38, or between nucleotides 38 and 39. Ligation efficiencies will generally vary for different tRNAs, so the ideal position at which to locate the break should be explored when adapting this approach to any new system. Alternatively, modifications at the 3′-CCA end (including base changes and substitution by deoxyribonucleotides) are readily obtained by use of the tRNA nucleotidyltransferase, also referred to as the CCA-adding enzyme [33]. Scaling up reactions with this enzyme readily allow 3′-end modified tRNAs to be produced in sufficient quantities for rapid kinetics.
2.2. Preparation of aminoacyl-tRNA synthetases from over-producer strains
Aminoacyl-tRNA synthetases are routinely purified from overexpression strains where the gene for the appropriate aaRS is placed under control of a strong promoter (tac, T7, etc.) The over-expression plasmids typically encode an N-terminal or C-terminal His6 tag to aid in purification, although for some applications the absence of a purification tag may be desirable. The His6 tag is particularly useful in the purification of E. coli tRNA synthetase mutants from E. coli strains harboring expression plasmids, because it enables separation from the wild-type background enzyme without the use of deletion strains. Typical purification protocols involve initial purification over a Ni-NTA column (Qiagen), followed by anion exchange chromatography to remove contaminating proteins. Detailed protocols for purification of aaRS from over expression strains have been published previously [23, 34–36]. Removal of the His6 tag by incorporating a specific protease site (e.g. enteropeptidase) has also been reported [37]. Depending on sequence context, this can be problematic for some constructs. For aaRS that lack a His6 tag, chromatography over multiple columns is required. A sequence that is generally useful for Class II aaRSs is Q Sepharose, hydroxyapatite, and Superose 6 size exclusion chromatography. The selection of specific chromatographic methods is typically highly system dependent, but ion-exchange chromatography is invariably an effective first step.
2.3. Determining the concentration of active enzyme
The active concentration of functional enzyme is most readily determined by the active site titration assay [38]. This assay can be performed either by monitoring the formation of the enzyme-bound aminoacyl-adenylate intermediate using [14C]-labeled amino acid, or by monitoring the initial burst of ATP consumption, which corresponds to the first catalytic turnover and represents the concentration of active sites that are competent for catalysis. Both assays rely on the observation that in the amino acid activation reaction, the reaction chemistry is fast relative to the rate of product release. Use of the first method assumes that the enzyme-bound aminoacyl adenylate intermediate is stable over the course of the assay (i.e. the aminoacyl adenylate product is not released), that tRNA is not required for formation of this intermediate, and that [14C]-labeled amino acid is commercially available. In contrast, the second method assumes only that product release is slow relative to formation of the enzyme-bound aminoacyl adenylate intermediate. The second method can be used with all aminoacyl-tRNA synthetases regardless of whether they require tRNA for the amino acid activation step.
2.3.1 Active site titration assay I - monitoring the formation of the E•AA~AMP intermediate
In this assay, the aminoacyl-tRNA synthetase is incubated with [14C]-labeled amino acid, ATP, and inorganic pyrophosphatase to form the E•AA~AMP intermediate. The assay takes advantage of the observation that the E•AA~AMP intermediate binds to nitrocellulose filters, while the free amino acid passes through the filter. For tyrosyl-tRNA synthetase, a typical assay mix consists of the aminoacyl-tRNA synthetase (estimated concentration = 1–10 μM), 10 μM [14C] tyrosine (final specific activity = 5 μCi/mL), 2 mM Mg·ATP, 144 mM Tris-HCl (pH 7.78), 10 mM MgCl2, inorganic pyrophosphatase (1 U/mL), and 5 mM β-mercaptoethanol. The ATP stock solution is prepared as the Mg2+ salt and its pH is adjusted to 7.78 prior to addition to the assay mix. The assay is generally performed at 25 °C and the reaction is initiated by the addition of enzyme. (The temperature referred to in this all and subsequent enzymatic protocols should be adjusted to take into account the source of the enzyme. While enzymes from mesophillic organisms can be conveniently studied in the range of 25–37 °C, assays for enzymes from thermophiles are typically performed at 65 °C or higher.) At time points of 2, 5, and 10 minutes, aliquots are removed and filtered through nitrocellulose filters (BA85 filters, Schleicher & Schuell) that have been presoaked in Tris buffer (144 mM Tris-HCl, pH 7.78). The nitrocellulose filters are then washed with cold Tris buffer and dried under a heat lamp prior to scintillation counting. An aliquot of assay mix is spotted directly onto a nitrocellulose filter and dried without washing to determine the specific activity of the assay mix. This specific activity is then used to calculate the amount of enzyme that contains bound aminoacyl adenylate. If the concentration of enzyme containing [14C]AA~AMP increases as the incubation time is increased, then the amino acid activation reaction has not gone to completion and either longer assay times or elevated temperatures must be used.
2.3.2 Active site titration assay II - monitoring the initial burst of ATP consumption
In this assay, the aminoacyl-tRNA synthetase is incubated with unlabelled amino acid, γ-[32P]ATP, inorganic pyrophosphatase and, in the case of GlnRS, GluRS, ArgRS, and Class I LysRS, tRNA. A representative 2X reaction mix is prepared composed of the following: 100 mM HEPES (pH 7.5), 20 mM MgCl2, 200 mM KCl, 2 mM DTT, 20 μM ATP, 5 mM amino acid, 0.4 U/mL PPiase, γ-[32P]-ATP (1000 CPM/μL final). The final reaction contains 50 μL of 2X mix, 40 μL ddH2O, and 10 μL of diluted enzyme solution (estimated to give a final concentration in the neighborhood of 1–2 μM) and is equilibrated to 37 °C before addition of enzyme. Aliquots of 10 μL are removed into 100 μL of 7% perchloric acid at varying time points (e.g., 0 seconds to 30 min.). Calculating the extent of conversion of ATP into AMP can be performed by either of two methods. The classical method features absorption of the ATP on activated charcoal. Each quenched reaction time point and controls (i.e., t=0 ) is mixed with 200 μL of activated charcoal solution (7.5% in charcoal, and 10 mM in cold sodium pyrophosphate), filtered over Whatmann GC glass fiber filters in a 12 port manifold filtration apparatus (Whatman), and then dried briefly before scintillation counting. The known concentration of ATP in the 2X reaction mixture is used to convert counts per minute to pmoles of ATP. More recently, a thin layer chromatography (TLC) method has been described for separation and quantitation of ATP and PPi [39, 40]. In this approach, aliquots of the quenched reaction are applied to polyethylenimine thin layer chromatography plates (Scientific Adsorbents, Inc., Atlanta) that have been pre-run in water. The chromatogram is developed in a mobile phase of 750 mm KH2PO4 (pH 3.5) and 4M urea, at a running temperature of 25 °C. The radioactive spots are detected and quantified by phosphorimaging. In either method, the decay of [ATP] over time is plotted to an exponential decay curve, with the loss of [ATP] being fit to the exponential decay curve:
| (3) |
where ‘A’ represents the burst amplitude related to formation of the enzyme-bound aminoacyl adenylate intermediate, ‘B’ represents the ‘steady state’ decay of on-enzyme aminoacyl adenylate, and ‘C’ represents the offset from the y-axis. The results from a typical active site titration experiment are shown in Figure 2.
Figure 2.
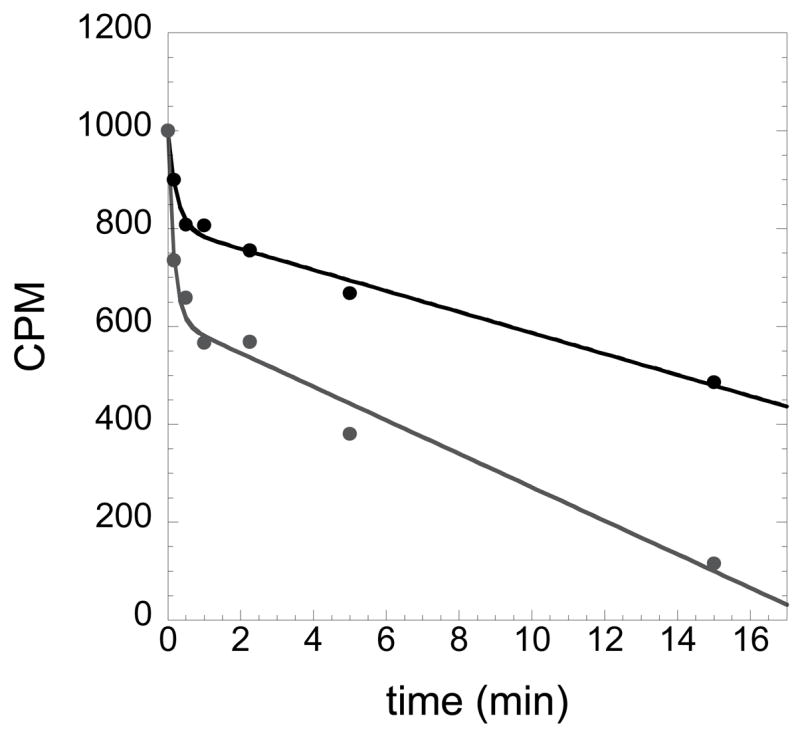
Active site titration to determine the concentration of HisRS. The disappearance of ATP is fit to an equation that is based on a first order exponential decay followed by a linear phase. The concentration of active enzyme is determined from the burst amplitude. The two plots shown represent two different concentrations of histidyl-tRNA synthetase, with the top plot representing a reaction performed using 2 μM HisRS, and the lower plot representing HisRS at 4 μM. Note that the steady state rate of ATP consumption in both cases is the same: the key difference is in the amplitude of the exponential.
2.4. Equilibrium dialysis assay for measuring amino acid binding affinities
A convenient method for measuring the affinity of amino acids for aaRS is equilibrium dialysis [41–43]. These experiments have traditionally been performed using a multi-cell microdialyzer apparatus (Spectrum Medical Industries, Los Angeles). Recently, disposable equilibrium dialysis chambers have become commercially available (The NEST Group, Inc., Southborough, MA) and offer a convenient alternative to the use of the multi-cell microdialyzer apparatus. Prior to the binding experiment, protein stocks are dialyzed in 50 mM Tris-HCl (pH 7.5), 50 mM NaCl, 10 mM MgCl2, and 1 mM β-mercaptoethanol. The experiment is performed by placing enzyme (25–50 μM) and amino acid (10–1000 μM, [3H]-labeled to 50–75 CPM/pmol) suspended in the buffer above in the two chambers that lie on either side of a semi-permeable membrane. The binding reactions are incubated overnight at 4 °C with continuous rotation. The radioactivity in both chambers is measured by scintillation counting after the system has come to equilibrium, allowing the calculation of free and (bound +free) amino acid at each ligand concentration. Dissociation constants and the number of independent binding sites per mole of enzyme are obtained by plotting bound vs. free concentrations, and fitting the data to the following equation using non-linear regression [44]:
| (4) |
For display purposes, a linear transform of the Scatchard plot is typically used to present the data:
| (5) |
To avoid artifacts associated with surface adsorption, the assays should be run at both initial conditions; i.e. starting enzyme and amino acid in different compartments on either side of the membrane, or by placing both in the same compartment. The binding constant for ATP cannot be reliably determined by equilibrium dialysis, owing to the tendency of nucleotide to adsorb to the surfaces of the chamber and the dialysis membrane and, in some cases (e.g. TyrRS), the low affinity with which ATP binds. Accurate determination of dissociation constants requires that the concentration of enzyme is approximately equal to the concentration of amino acid in the assay.
2.5. Measurement of Equilibrium Dissociation constants for tRNA: Filter Binding & Gel Mobility shift assays
In order to develop a thorough understanding of tRNA recognition, it is useful to be able to study the binding event independent of the overall aminoacylation reaction. In addition to fluorescence based approaches (described in section 2.11), other methods that have been used to determine the affinity of the aaRS:tRNA interaction include filter binding and gel mobility shift assays. Owing to the formal possibility that interactions of the aaRS:tRNA complex with the support (i.e. filter or gel matrix) alter the macromolecular equilibrium, both approaches do not, strictly speaking, provide true equilibrium binding measurements. The filter binding assay was used in early work on aaRSs to quantitate the tRNA dissociation constant under a variety of conditions [45]. The chief shortcoming of the assay is that the optimal pH for capture of complexes on nitrocellulose is 5.5, which is well below the optimal pH for the aminoacylation reaction, and thus physiological conditions. Provided that all measurements are made at this pH, it is possible to make comparisons between different tRNA substrates and aaRS variants, because specificity for tRNA is retained at the lower pH [46, 47]. Recently, this procedure was updated by Wong & Lohman [48], and later adapted for tRNA by Silvian & Steitz [49] into a 96-well format. Conditions for the filter binding assay are provided in the previous references, as well as in a report describing the recognition of tRNAHis by HisRS [47]. The updated method features a three layer membrane filter approach, each layer binding a different population of molecules. The top layer is a 0.45 μM polysulfone filter (HT-Tuffryn, Gelman Sciences) that captures large aggregates of protein and/or nucleic acids that interact non-specifically. The middle layer is nitrocellulose (BA-85, 0.45 μM Schleicher and Schull), and binds the specific aaRS complexes that comprise the “bound” fraction. The bottom, positively charged nylon (Hybond N+, Amersham) retains the remaining tRNA that is not bound by the aaRS to the nitrocellulose. A notable feature of the improved method is that both free and bound [32P]-labeled tRNAs can be directly quantitated by phosphorimaging analysis of all three filters.
A related approach to studying aaRS:tRNA interactions is gel mobility shift analysis. While this approach has been broadly applied to the study of protein:DNA complexes, it has proven somewhat less useful for studying the aaRS:tRNA interactions. The latter generally have lower affinity than protein:DNA interactions, so the complexes are less stable to the conditions of electrophoresis. In spite of these limitations, gel mobility shift analysis has been exploited to good effect, particularly in the seryl-tRNA synthetase system, where non-covalent aaRS:tRNA and covalently linked complexes have both been studied [50]. Unlike the filter binding assay, the gel mobility shift assay can be performed at pH values that are closer to the physiological pH of 7.5. A useful version of the gel mobility shift is a Ferguson plot analysis, where aaRS:tRNA complexes are fractionated on a series of polyacrylamide gels of increasing acrylamide/bisacrylamide concentration [51]. By comparing the retardation coefficient of a covalent aaRS:tRNA complex to a standard curve derived from plotting retardation coefficients of a set of standards against the log of their molecular mass (kDa), the molecular mass (and thus aaRS:tRNA stoichiometry) of the aaRS:tRNA complex can be determined.
2.6. Pyrophosphate exchange assay
The activation of amino acids by aaRSs has traditionally been studied by the pyrophosphate exchange reaction [52, 53]. Here, the aaRS is added to a reaction mixture of amino acid, MgATP, and [32P]-pyrophosphate in a suitable reaction buffer, and then aliquots are withdrawn over a short time course and quenched by transfer to 7% perchloric acid. The [32P]-ATP formed is then captured by adsorption onto activated charcoal, or quantified using thin layer chromatography on PEI plates, as described in Section 2.3. It should be kept in mind that PPi exchange is typically performed in the absence of tRNA, so the apparent kcat and Km parameters derived do not necessarily represent the true rate of amino acid activation in the presence of tRNA, nor the Km for amino acid in the overall aminoacylation reaction.
The standard pyrophosphate exchange assay is performed at 37 °C in a reaction containing 100 mM Tris-HCl (pH 8.0), 10 mM β-mercaptoethanol, 10 mM KF, 10 mM MgCl2, 2 mM [32P] NaPPi, 1–10 nM aaRS, amino acid in concentrations ranging from 0.2 – 10 times Km, and 10–5000 μM ATP. The reaction is pre-incubated for 5 minutes, and then initiated by the addition of concentrated enzyme, typically to a final concentration 1–5 nM. Aliquots (0.2 × total reaction volume) are removed at various time points to four volumes of 7% perchloric acid, and then processed as described above (Section 2.3) for the active site titration, employing either activated charcoal or thin layer chromatography. The progress curves at each concentration of substrate are fit to linear initial rates, providing the velocity in pmoles/min. The velocity data (converted to sec−1 by dividing against [E]0) is plotted against [AA] or [ATP], and then fit directly to the Michaelis-Menten equation by non-linear regression (Kaleidagraph, Synergy Software, Reading, PA). The pyrophosphate exchange assay described above technically measures the rate of isotopic exchange of 32P into ATP, and can provide information about the kinetic mechanism (i.e., whether substrate binding is random or ordered) [54]. As described in Section 2.9, the forward reaction alone may be measured directly by use of [α-32P]-labeled ATP, monitoring conversion of ATP to AMP using thin-layer chromatography [55]. The advantage of this approach is that it enables separate detection of AMP and aminoacyl~AMP on the TLC plates. This is of particular significance to measurements of pre-transfer editing in those aaRSs that perform this reaction.
2.7. The steady state aminoacylation reaction
The complete aminoacylation reaction is traditionally investigated by a discontinuous steady state assay that monitors the formation of [3H] or [14C] AA-tRNAAA over time. The reaction is run at 37 °C and is optimized for each system, depending on the optimal temperature and other properties of the native enzyme. A typical reaction mixture contains 50 mM Tris-HCl (or HEPES) pH 7.5, 20 mM KCl, 4 mM DTT, 10 mM MgCl2, 0.2 mg/mL bovine serum albumin, 1–5 nM aaRS, and a range of amino acid, ATP, and tRNA concentrations. For measurements of the Km for tRNA or for amino acid, 2 mM ATP generally suffices to ensure saturation, although this should be checked in each system. Attaining saturation for the amino acid in measurements of the Km for tRNA may be more difficult, because radiolabeled amino acids are not commercially available at high specific activities. Because Km values for the amino acid substrates are in the range of 100 μM, and because the amino acid Km often increases when the tRNA or enzyme is mutated, amino acid saturation may not be obtainable, thus compromising the reliability of the tRNA Km determination. Accurate measurements of the amino acid Km are obtainable up to a maximum level of 1–10 mM, depending on the system.
To perform the assay, aliquots are removed at varying time points (typically within the first 2–5 minutes), and then spotted on Whatmann 3MM paper filters pre-soaked with 10% trichloroacetic acid (TCA). Once the time course is complete, the filters are washed 3–4 times in a large volume excess of TCA, once with 95% ethanol, and then dried under a heat lamp prior to processing in a liquid scintillation counter. For amino acids (such as cysteine) with a pronounced tendency for non-specific adsorption to the filters and other surfaces, treatment with a chemical blocking agent (i.e., 0.24 M iodoacetic acetic/0.1 M sodium acetate/formamide, pH 5.0) is an essential part of the quench procedure. When characterizing a new enzyme or system, the enzyme concentrations and the length of the time course have to be adjusted in order to obtain a linear initial rate. In addition, care should be taken to preserve Michaelis-Menten conditions, such that the enzyme concentration employed should be no greater than 0.05 times the lowest concentration of tRNA. The initial rate data at each tRNA concentration is converted to velocity (sec−1), and then plotted against [tRNA]. The curve is fit to the Michaelis-Menten equation by non-linear regression.
An important limitation of the steady state aminoacylation assay is that amino acid concentrations are operationally limited to concentrations below 1 mM, owing to the relatively low specific activity of commercially available [3H] and [14C]-labeled amino acids. (If product is quantitated as radiolabeled AA-tRNAAA, those amino acids not available as radionuclides cannot, of course, be employed as substrates.) These limitations are overcome by a novel assay that employs 3′-[32P]-labeled tRNA together with unlabeled amino acid [56, 57]. The assay (described more fully in the contribution of Uhlenbeck, this volume) has been used to determine both steady-state and microscopic kinetic constants, and should be widely applicable to most if not all aminoacyl-tRNA synthetases. Briefly, tRNA is labeled with [32P] at the 3′-internucleotide linkage by the ATP-PPi exchange reaction catalyzed by the E. coli CCA enzyme. The aminoacylation reaction is then performed as described above, quenching the reaction time points in 0.1% SDS, 0.15 M sodium acetate (pH 5.2). The aminoacylated tRNA is digested with P1 nuclease, and then the radioactive products (i.e. as 3′-aminoacylated A76) are analyzed by thin layer chromatography. Since the amino acid is unlabeled, it may be used at any concentration consistent with solubility. This feature of the assay enables accurate measurement of aminoacylation kinetics on enzyme variants with elevated amino acid Km values, the quantitation of noncognate aminoacylation rates, and the aminoacylation of nonstandard amino acids that are not commercially available in radiolabeled form [40, 58, 59]. The assay is also adaptable to measure single-turnover kinetics, using molar excess of enzyme (see Section 2.8).
2.8. Rapid quench methods for studying the half reactions of aminoacylation: single turnover assay
Stopped-flow and quench flow methods both involve rapid mixing of the enzyme with substrate, followed by sampling of the reaction on the millisecond time scale. The former assay is continuous, while the latter is discontinuous. In addition, stopped-flow experiments typically rely on a fluorescence signal that indirectly reports on the progress of the reaction, whereas quench flow experiments invariably involve the direct measure of a radioactively-labeled reaction product.
There are two basic designs for rapid chemical quench experiments: single turnover, performed under conditions of enzyme excess (usually under conditions of [S] ≫ Km, so that substrate binding is not limiting), and multiple turnover, performed under conditions of substrate excess relative to enzyme. By judicious use of single turnover and multiple turnover experiments, the rate-limiting step of the overall aminoacylation reaction can be determined. For those aaRS that require tRNA to catalyze formation of the aminoacyl adenylate intermediate, the kinetics of the individual half reactions cannot be cleanly separated by rapid quench methods. Instead, comparing single-turnover and multiple turnover experiments provides information about the limiting rate up to the point of product release, and how this compares to the overall steady-state rate. Owing to their thermostability and increased temperature optimum, rapid kinetics experiments using thermophillic aaRSs can present more technical challenges than those performed using mesophillic enzymes.
An important consideration in the design of rapid quench experiments for aaRS is the concentration of amino acid to be used. If the experimental design invovles amino acid concentrations in an operational range below approximately 1 mM, than radiolabeled amino acid substrates can be used, and reaction progress can be monitored by trichloroacetic acid precipitation of the AA-tRNAAA product. Alternatively, if a non-cognate amino acid or substrate is used with a Kd in the range approximately above one millimolar (or radioactive amino acid is not available), then the Wolfson-Uhlenbeck method is more suitable. A final consideration is the specific chemical basis of the quench. For any useful quench, the rate at which the reaction is terminated must be at least an order of magnitude faster than the rate that is being measured. The quench must also preserve the chemical structure of the product (i.e. the aminoacyl ester bond) and irreversibly denature the enzyme. Operationally, this can be achieved by a second agent in the collection tubes, e.g. 1% SDS or chloroform prior to neutralization, which prevents enzyme from reinitiating catalysis.
Rapid chemical quench experiments are routinely performed in the KinTek RQF-3 (KinTek, College Park, PA), an instrument with three drive syringes, and two ports for injection of sample (Figure 4). In design, this instrument is similar to the original pulsed quench flow device described by Fersht [60]. By use of multiple internal sample loops of varying lengths, as well as the ability to program in specific pauses following the rapid mixing of the contents of the A and B syringes, the machine allows reaction time points to be programmed from as short as 5–10 milliseconds to tens of seconds, allowing reactions with rate constants of ~200 sec−1 to 10−3 sec−1 to be routinely studied. The theoretical parameters associated with the design of the quench apparatus are addressed in Johnson [61]. Before using any new system, a calibration protocol (provided by the manufacturer) must be carried out to determine the volume of the reaction lines.
Figure 4.
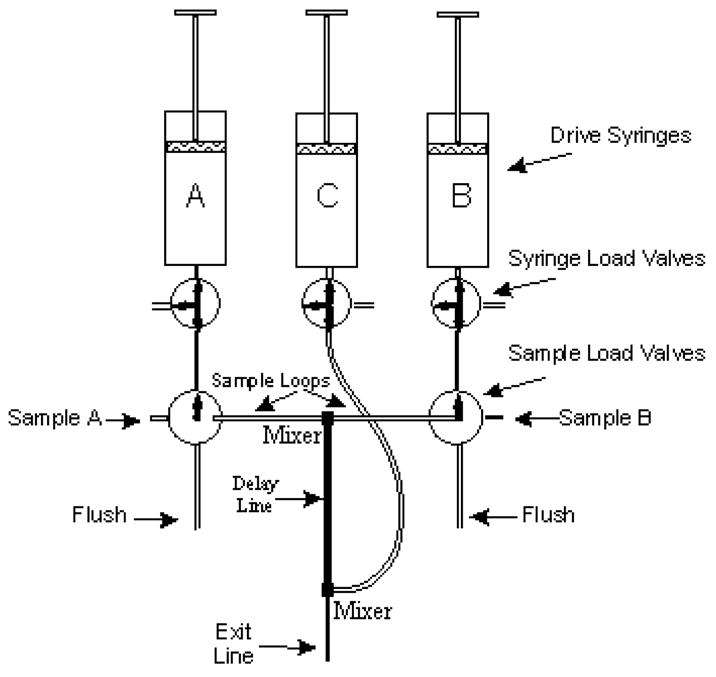
Valve system on the Kintek RQF-3, indicating the arrangement of the sample loops relative to the drive syringes and the central mixer. Figure courtesy of the Kin-Tek Corporation (http://www.kintek-corp.com/)
The methodology for the rapid quench method under single turnover conditions is described in earlier work by Fersht and co-workers [60], with additional recent modifications by the authors [40, 62, 63]. The approach will be slightly different for different enzymes, depending on whether or not the aaRS is capable of forming the aminoacyl adenylate intermediate in the absence of tRNA. An example of a system where formation of the aminoacyl adenylate intermediate is independent of tRNA is histidyl-tRNA synthetase (HisRS). The preparative HisRS aminoacyl adenylate formation reaction contains: 30 μM HisRS, 2.5 mM ATP, 80–100 μM [14C]- or [3H]-histidine, and 0.2 U/mL of inorganic pyrophosphatase in a standard adenylation buffer composed of 10 mM HEPES-KOH (pH 7.5), 100 mM KCl, 1 mM DTT, and 10 mM MgCl2. Following a half hour incubation at 37 °C, the enzyme-bound aminoacyl adenylate intermediate is purified by G-25 Sephadex spin chromatography (Roche) using a column pre-equilibrated in adenylation buffer. The column eluate is stored on ice, and aliquots are processed by scintillation counting to analyze the concentration of the enzyme-bound aminoacyl adenylate intermediate2. The purified enzyme:aminoacyl adenylate complex is then introduced into one syringe, while tRNA is placed in the second syringe. To ensure constant temperature during the reaction, the reaction chamber is connected to a water bath at 37 °C. Single turnover conditions and saturation of tRNA binding are ensured by use of tRNA concentrations that are less than that of the enzyme-bound aminoacyl adenylate intermediate, but at least 5 times greater than the KdtRNA. Each measurement of ktrans (the rate constant for the transfer of the aminoacyl moiety to tRNA) involves the creation of a time course that spans the range from 2 milliseconds to five seconds, with the former representing the dead time of the instrument, and the latter representing 10 half lives of the reaction. Each time point involves the mixing of 20 μL of the enzyme-bound aminoacyl adenylate intermediate mixture with 20 μL of tRNA. Following the desired interval, the reactions are terminated by rapid mixing into 3M NaOAc (pH 4.5), and then expelled into collection tubes containing 1% SDS. The quenched reactions are precipitated on 5% TCA soaked filter pads as for typical steady state kinetics, and then counted by liquid scintillation counting. The counts per minute are converted to pmoles of product based on the specific activity of the radioactive amino acid label, and then plotted against time (Figure 5A).
Figure 5.
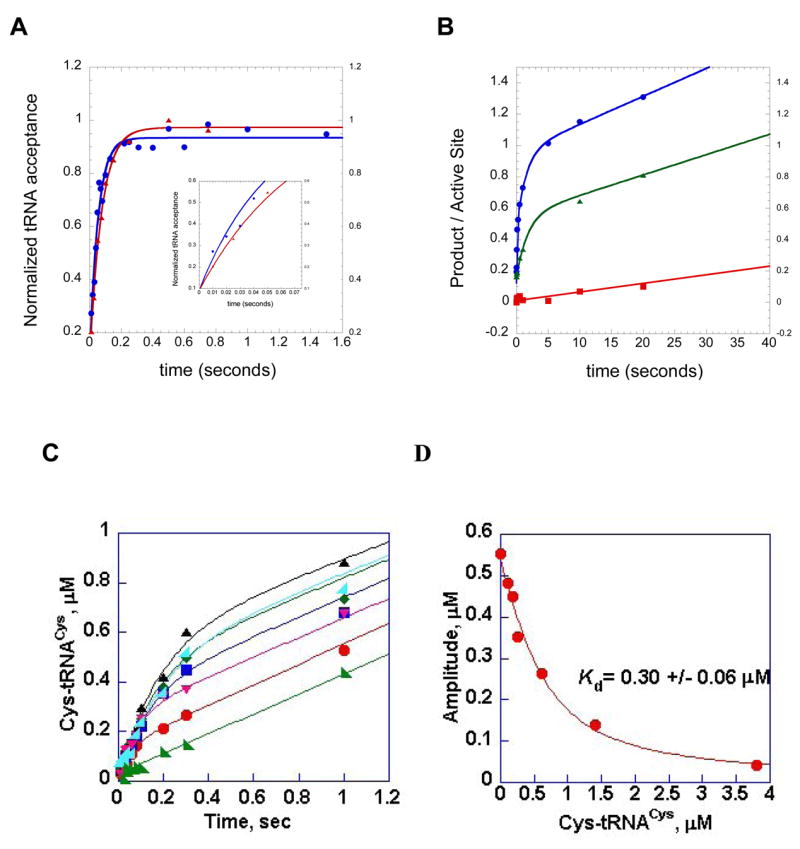
Representative single turnover and multiple turnover rapid chemical quench kinetic experiments performed in the HisRS and CysRS systems. (A) single turnover aminoacylation kinetics of wild type HisRS:wild type tRNA cognate interaction (blue circles), and the interaction of wild type HisRS with G34U tRNAHis (red triangles). The inset provides a close-up of the first 100 milliseconds of both reactions, illustrating the faster rate of wild type relative to the tRNAHis variant. (B) pre-steady kinetics of HisRS AMP and His-tRNAHis formation, for the identity-compromised C73U tRNAHis variant. Filled blue circles, AMP formation by wild type HisRS in the absence of tRNA. The progress curve is fit to a double exponential followed by a linear phase. Green triangles, AMP formation by wild type HisRS in the presence of C73U tRNAHis. The plot is fit to a single exponential followed by a linear phase. Red squares, His-tRNAHis formation by the C73U tRNAHis variant tRNA. This curve is fit to a linear equation. The difference in slope between the linear portions of the plots for AMP formation and His-tRNAHis formation by the C73U tRNAHis variant represents the stoichiometry of ATP consumption relative to aminoacylated tRNA product formation. The data to derive plots A and B were reported in [66]. (C) time course of synthesis of Cys-tRNACys under single turnover (enzyme concentration in excess) conditions. The concentration of tRNACys was held fixed at 0.5 μM, while that for CysRS was varied between 1 and 20 μM. (D) Re-plot of amplitudes from plot C against the concentration of Cys-tRNACys by hyperbolic fit to derive the Kd for tRNACys. Plots C and D are adapted from Zhang et al.[63].
The reaction monitors transformation of the bound enzyme•substrate (ES) complex to the enzyme•product complex (EP), such that the reaction is limited neither by the rate of substrate binding, nor by the rate of product release. (Note that the quenched product obtained represents the sum of both released product and product still bound that has not been released.) This choice of experimental conditions represents pseudo first order kinetics, which considerably simplifies the analysis. It should be noted in this mechanism that the observed first order rate constant ktrans should be considered as a “limiting rate”, meaning that it reflects the slowest first order rate constant (after all substrates are bound but before product release), rather than a single elementary chemical or conformational step. Under these conditions, the progress curves are well described by a simple first order exponential of the form:
| (6) |
where A is the scaling constant, C is the y intercept offset, kobs is the observed rate constant, and t is time in seconds. It is preferable to obtain the fit using nonlinear regression methods, as approaches using a logarithmic transformation of the data invariably compress the data at the start of the reaction, and depend on an accurate determination of the endpoint of the reaction. This leads to the least accurately determined data points being weighted the most heavily, as well as error bars whose magnitudes vary with substrate concentration [61, 64, 65].
The single turnover assay may also be performed without preliminary formation and separation of the enzyme-bound aminoacyl adenylate intermediate, a useful variation for those aminoacyl-tRNA synthetases (such as GlnRS) that either require tRNA for the adenylation reaction, or for which the aminoacyl adenylate intermediate has too short a half life (Y.-M.H. and C.F., unpublished observations). In these experiments, the aminoacyl adenylate intermediate is formed in situ under rapid mixing conditions, prior to aminoacyl transfer. In a representative experiment from the cysteine system, saturating concentrations of the three substrates (5 μM tRNACys, 500 μM [35S]-cysteine (275 Ci/mmol), and 6.25 mM ATP) in suitable reaction buffer are incubated in one syringe, while molar excess of CysRS over tRNA is incubated in the second syringe. These are rapidly mixed and a time course constructed as described above. Following quenching with sodium acetate and alkylation with 1.2 M iodoacetic acid, 0.5 M sodium acetate (pH 5.0), the samples are deposited on TCA-soaked filter pads and processed as above. Depending on the concentration of amino acid required, and the availability of radiolabeled substrate, it may desirable to monitor product formation with radiolabeled tRNA by use of the Wolfson-Uhlenbeck assay. This has been robustly implemented in the glutamine system, where it is not possible to trap the aminoacyl adenylate intermediate in the absence of tRNA [40]. When the concentrations of all three substrates are above saturation (so that binding steps are fast relative to aminoacyl transfer), and the enzyme is in excess, aminoacyl-tRNA formation is well described by a single exponential equation. For GlnRS, the kobs obtained represents a composite rate constant that is the limiting rate for all steps prior to product release. An additional feature of the single turnover rapid quench assay is that, provided substrate binding is in rapid equilibrium relative to the rate of transfer, the apparent dissociation constants (Kd ) for amino acid and tRNA can be determined [40, 63]. Another useful variation of the single turnover rapid quench assay employs varying concentrations of the aminoacyl-tRNA product as inhibitor of the forward aminoacylation reaction. For CysRS, a plot of the variation in amplitude of the first order exponential against the AA-tRNAAA concentration (Figure 5 panels C and D) can be used to extract the Kd for the aminoacyl-tRNA product [63].
2.9. Rapid quench methods for studying the half reactions of aminoacylation: pre-steady state assay
The rapid quench assay may also be performed under pre-steady state conditions, where substrates are in excess relative to enzyme. Under these conditions, the transition between the first and subsequent turnovers of the enzyme is visualized, providing useful information. Notably, a comparison of the pre-steady state kinetics of Class I and Class II aaRSs indicates that the former exhibit a burst of aminoacyl-tRNA in the first turnover, while the latter do not [40, 62, 63]. One interpretation of these data is that the overall aminoacylation catalyzed by Class I enzymes, but not Class II enzymes, is limited by the rate of product release. To perform these experiments, reactions are prepared featuring saturating amino acid, Mg·ATP, and tRNA, allowing the maximal rate of multiple turnover aminoacylation (equivalent to kcat) to be obtained from the linear phase of the progress curve. Representative conditions for different systems have been described in detail [40, 62, 63].
Depending on the choice of the radiolabel and concentrations of the various substrates, different kinetic parameters within the overall aminoacylation reaction can be obtained. The kinetics of the adenylation reaction can be followed under pre-steady state kinetic conditions by monitoring the conversion of [α-32P] ATP to [α-32P] AMP, making use of the thin layer chromatography separation approach described above. By constructing parallel reactions where one series employs labeled [14C]-amino acid, and a second set that employs [α-32P] ATP, one can experimentally measure the ratio of ATP consumption to production of AA-tRNAAA formed (Figure 5B). Such experiments have provided insight into the role that tRNA plays in the kinetics of adenylation reaction [66], and into mechanisms for pre-transfer editing [55].
For both Class I and Class II aminoacyl-tRNA synthetases, the pre-steady state kinetics of aminoacylation can be simplified using a two step irreversible mechanism:
| (7) |
For this mechanism, the time dependence of product formation is given by a single exponential followed by a linear phase:
| (8) |
In this form of the equation, [P] represents the concentration of product formed, and [E0] represents the concentration of enzyme in the reaction. The quotient [P]/[E0] is a useful way to express the moles of product formed per active site, and is thus independent of the amount of enzyme used in the experiment. This facilitates comparisons across systems. The amplitude term, A0, is defined by the expression [k2/(k2+k3)]2, while the rate constant is the sum of k2 and k3. The linear phase, kcat, is equal to k2k3/(k2+k3). Notably, all three terms of interest, the amplitude and rate of the exponential, and the linear rate, are functions of both k2, the rate of product formation, and k3, the rate of product release. To a first approximation, the kinetics of the Class I and Class II enzymes appear to represent the limiting cases where, respectively, k2>k3 and k2<k3. Inspection of the above equations indicates that when k2≫k3, the amplitude of the burst approaches unity, the rate constant for the exponential approaches the rate of transfer, and kcat≅k3, the rate constant for product release. By contrast, when product release is fast relative to rate of transfer, the amplitude of the burst approaches zero, and the steady state rate approaches k2. Notably, Class II aaRS that have been examined by pre-steady state kinetics do not exhibit a burst in aminoacyl-tRNA formation, and therefore appear not to be limited by product release.
The kinetics associated with a two step irreversible mechanism predict that when the k2 and k3 terms are on the same order of magnitude, the amplitude of the burst will decrease from unity, and kcat will become slower than either term. It should also be noted that the mechanism above assumes that, as a simplification, aminoacylation is irreversible. If this assumption is not valid, then the kinetics predict that the amplitude of the burst will diminish, and the rate of the burst will increase. If this is observed experimentally, then the assumption for irreversibility of the reaction must be challenged.
2.10 Fluorescence approaches to studying adenylation and aminoacylation: steady state measurements
For many aaRS systems, the binding of amino acid, ATP and or tRNA is accompanied by a change in the fluorescence of the protein. These can arise from changes in the intrinsic fluorescence of tryptophan or from extrinsic probes conjugated to the enzyme. This property has been exploited most broadly to follow the kinetics for formation of the enzyme-bound aminoacyl adenylate intermediate in a variety of class I and class II systems (Table 1). Alternatively, the aaRS can be chemically modified by derivatization with an extrinsic probe that is sensitive to local chemistry, thereby serving as a reporter of local changes in structure. The extrinsic probes employed include those that interact with the protein non-covalently, such as 5′,5′-bis(8-anilino-1-naphthalene sulfonate [67] and AF-tetrafluorophenylester [68], or those that can be covalently linked to exposed cysteines by maleimide chemistry [69]. Alternatively, if the labeling of the protein is not feasible, methods have been described for the extrinsic labeling of the 5′-terminus of the tRNA with a fluorophore [70, 71]. For both intrinsic and extrinsic probes to produce a useful fluorescence signal, the binding event must directly or indirectly alter the chemical environment of the probe.
The first step in any fluorescence-based steady state or kinetic analysis is the survey of the various potential binding or chemical reactions of the aaRS to establish which, if any, produce a change in fluorescence. Useful fluorescence changes must be of sufficient amplitude (typically at least 5% of the overall fluorescence signal), and occur with kinetics that can be captured in a transient kinetic experiment. The dead time of the instrument, the concentration of ligand, and the association rate constant of the ligand all act as constraints on these measurements, and fluorescence events that occur faster than 200 sec−1 present significant technical challenges with respect to signal to noise and data fitting. As a prelude to kinetic measurements, initial steady state measurements can be useful in developing thermodynamic parameters, such as dissociation constants for amino acid and tRNA. Unlike the approaches described in Section 2.5, the steady state measurements are true equilibrium methods, and are quite useful in interpreting amplitude information obtained from subsequent transient experiments. Intrinsic tryptophan fluorescence measurements typically rely on excitation at 290 ± 5 nm, and detection of emission at 330 nm, but it is useful to conduct wavelength scans to determine the optimal excitation and emission wavelengths. Once these are established, pilot experiments are performed using various concentrations of the cognate amino acid and ATP to correlate observed fluorescence signals with specific ligand binding and chemical events. The use of degassed buffers and samples, as well as the use of the highest purity water available, is highly recommended to minimize fluorescence changes due to oxidation. The presence of 1 mM DTT is also recommended to minimize oxidation and photobleaching. The values for protein concentration and slit width are generally chosen to provide a robust signal, against which transient kinetic changes can be observed. The instrument we routinely use for steady state measurements is a PTI QM-6 spectrofluorimeter (Photon Technology International, Monmouth Junction, NJ). As a first step, a mock titration with buffer is performed to correct for possible photobleaching effects. Once a steady base line signal has been obtained, titration experiments are performed by addition of small aliquots of a concentrated amino acid or ATP stock. The titration concentration range should span 0.2 to 5 × Kd for the ligand. Titration experiments can be performed using amino acid alone, ATP alone, and all possible mixing orders. Notably, titration of amino acid alone into ThrRS, TyrRS, and IleRS produces a fluorescence change, while titration of ATP alone does not produce a signal once the fluorescence spectrum is corrected for inner filter effects. Fluorescence changes associated with the reverse reaction can also be investigated by pre-forming the enzyme-bound aminoacyl adenylate intermediate and titrating with pyrophosphate. Measurements of tRNA binding can be performed by titrating tRNA at a fixed concentration of enzyme, or vice versa. Typical equilibrium dissociation constants for native complexes are in the range of 0.1 μM to 1.0 μM. In this range, a good approach is to employ a fixed concentration of enzyme (50 – 100 nM) and titrate tRNA concentrations from 100 nM to 10 μM [72].
The data from the steady state fluorescence experiments are corrected for dilution and for the inner filter effect arising from light absorption by the ligand (particularly when tRNA is the variable ligand), according to the following formula [73]:
| (9) |
where Fc is the corrected fluorescence; Fobs is the observed fluorescence intensity; vf is the volume of solution after each addition; v0 is the starting volume; Absex is the absorbance at 290 nm; and Absem is the absorbance of the enzyme substrate complex at 330 nm. Kd values can then be determined by fitting the data to a hyperbolic decay curve, or to the quadratic form of the binding isotherm if binding is very tight relative to enzyme concentration:
| (10) |
2.11.1 Monitoring tRNA aminoacylation by stopped-flow fluorescence
A. General Considerations
The goal of a transient kinetic experiment is to determine rate and dissociation constants for each step in the tRNA aminoacylation reaction. Like the rapid quench single turnover reaction, stopped-flow fluorescence events monitor a single turnover of the enzyme, allowing true rate and dissociation constants to be determined. While it is assumed that the change in the intrinsic fluorescence of the protein correlates with the rate-limiting step for the reaction (e.g. formation of the transition state), this assumption must be validated by comparing rate and dissociation constants obtained from the stopped-flow fluorescence experiments with those obtained by methods that directly monitor the progress of the chemical reaction (e.g. rapid quench flow methods, Section 2.8). Alternatively, substrate analogs that preserve binding determinants while eliminating functional groups necessary for aminoacylation chemistry can be employed [43].
As noted above, the use of initial steady state fluorescence assays is essential to distinguish between substrates that are invisible, and those that produce a kinetically useful signal. Once a substrate has been identified that produces a signal of useful amplitude, initial pilot studies are performed to obtain an estimate of the kinetics of binding. The dead time of most stopped-flow fluorimeters is typically on the order of 2 milliseconds, which means that events that occur on the order of 500 sec−1 or faster cannot be followed kinetically. However, the presence of fast binding events can be inferred by careful inspection of fluorescence amplitudes. Accordingly, carrying out control transient experiments by rapid mixing with buffer is essential to set the baseline for any transient observations.
In general, reaction rates are determined under pseudo-first order conditions. This means that the concentration of substrate that is varied should be either 1/10 or 10 times its dissociation constant (Kd). Under these conditions, ~91% of the enzyme will be either unliganded ([S]=1/10 Kd) or have substrate bound to it ([S]=10Kd). The substrate whose Kd is being determined should vary between 1/10 and 10 times the Kd, if possible. Typically, one syringe contains the enzyme and the invariant substrate. The other syringe contains the substrate whose Kd is being determined and the invariant substrate. If the amino acid activation reaction is being monitored, both syringes also contain inorganic pyrophosphatase to drive the reaction to completion. Equal volumes are injected into a mixing chamber, and changes in the intrinsic fluorescence of the protein are monitored by exciting the sample at 295 nm and collecting the fluorescence above 320 nm using a cut-off filter. In the case of tyrosyl-tRNA synthetase, for example, there is a decrease in the intrinsic fluorescence of the enzyme on formation of the E•Tyr~AMP intermediate (Figure 6, panel A). In contrast, addition of inorganic pyrophosphate (PPi) to the purified E•Tyr~AMP intermediate results in an increase in the intrinsic fluorescence that corresponds to the conversion of E•Tyr~AMP + PPi to the E•Tyr•ATP complex (Figure 6, panel B). An analogous increase in the intrinsic fluorescence of the enzyme is observed when tRNA is added to the purified E•Tyr~AMP intermediate.
Figure 6.
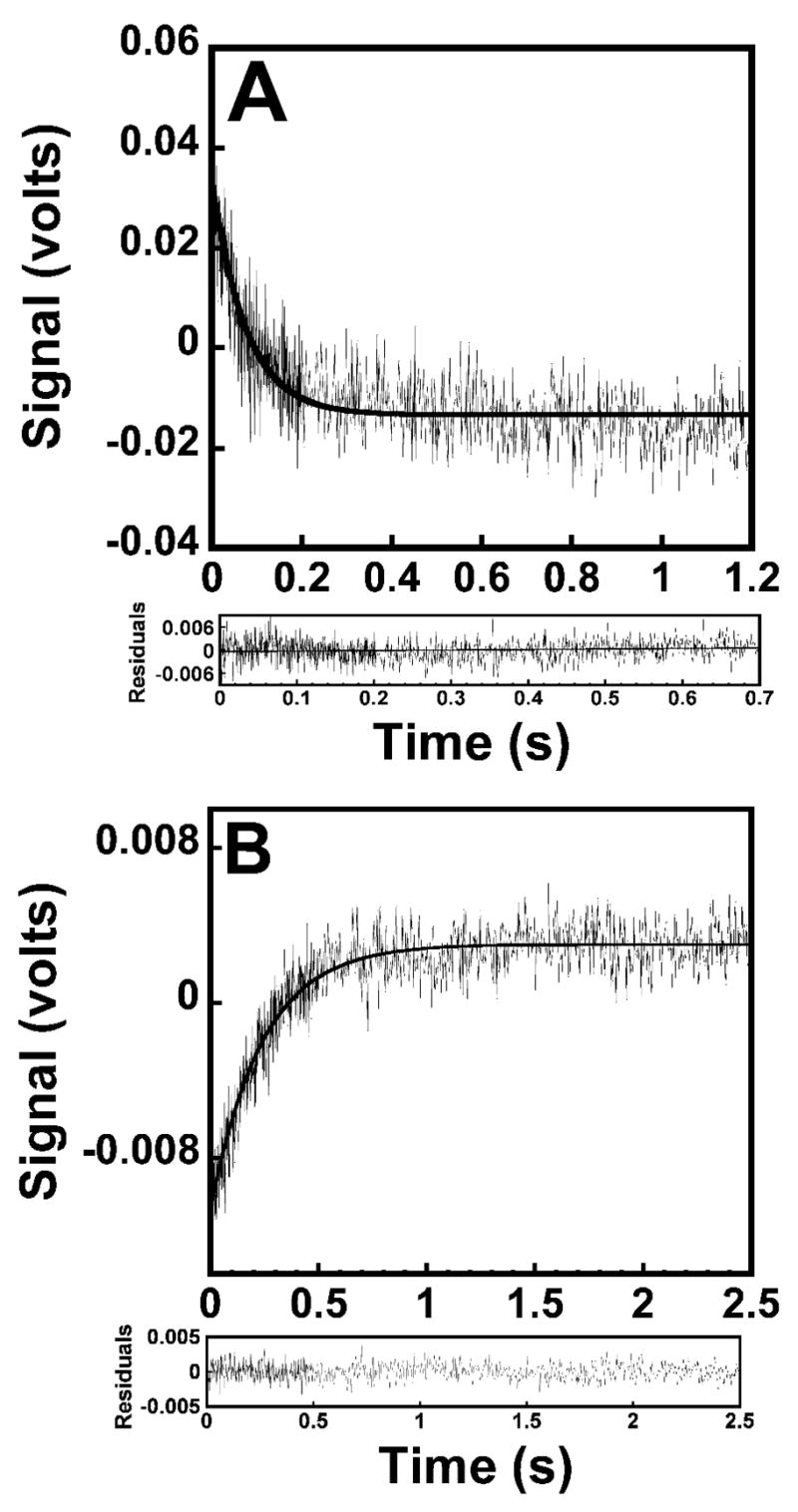
Stopped-flow fluorescence emission spectra for the formation and pyrophosphorylation of the TyrRS•Tyr~AMP complex. (A) reaction trace for the formation of the TyrRS•Tyr~AMP complex, as determined by monitoring the decrease in the fluorescence emission above 320 nm. Bacillus stearothermophilus tyrosyl-tRNA synthetase was preincubated in the presence of tyrosine and subsequently mixed with MgATP. (B), conversion of TyrRS•Tyr~AMP + pyrophosphate to TyrRS + Tyr + ATP, determined by monitoring the increase in the fluorescence emission above 320 nm. Data acquisition for both curves was split, with 500 data points measured during the initial 20% of each reaction trace and 500 data points measured during the remainder of the reaction trace. Residual values are shown beneath each reaction trace.
To improve the signal to noise ratio, it is customary to discard the first six injections of the series, and then average the reaction traces of the next 6–8 injections prior to data fitting. When fitting the reaction trace, it is often helpful to omit the initial time points, since they may contain artifacts arising from mixing. In addition, after an initial series of experiments has been performed and rates for fluorescence transients have been determined, it may be desirable to modify the data collection strategy to maximize the “density” of data points over the critical time intervals that define the shape of the transients. As a general rule of thumb data should be collected up to six half lives of the reaction, but no further.
The change in fluorescence with respect to time should be fit to a single exponential equation with a floating end point. For the fluorescence decrease observed in the amino acid activation reaction, this equation is:
| (11) |
where F is the relative fluorescence at time t, Fo is the initial relative fluorescence value, kobs is the observed rate constant, t is the time, and C is the offset of the curve from zero. For the fluorescence increase observed in either the reverse amino acid activation reaction (E•Tyr~AMP + PPi ⇌ E + Tyr + ATP) or the transfer of the tyrosyl moiety to tRNA (E•Tyr~AMP + tRNA ⇌ E + Tyr~tRNA + AMP), the following equation is used:
| (12) |
where F∞ is the final relative fluorescence value, and F, kobs, , t, and C are as defined above. When fitting the data to these equations, the residuals are plotted to ensure that they are randomly distributed. If the data do not fit one of the single exponential equations shown above, one must determine whether the kinetics actually fit to a higher exponential, or if the lack of goodness of fit is simply an artifact due to a problem with either the equipment or the sample. It should be noted that a double exponential equation will always fit the data better than a single exponential equation due to the increased number of variables. For this reason, when assessing the goodness of fit, it is essential that one looks at whether the residuals are randomly distributed, rather than directly comparing how the single and double exponentials fit the data (Figure 7).
Figure 7.
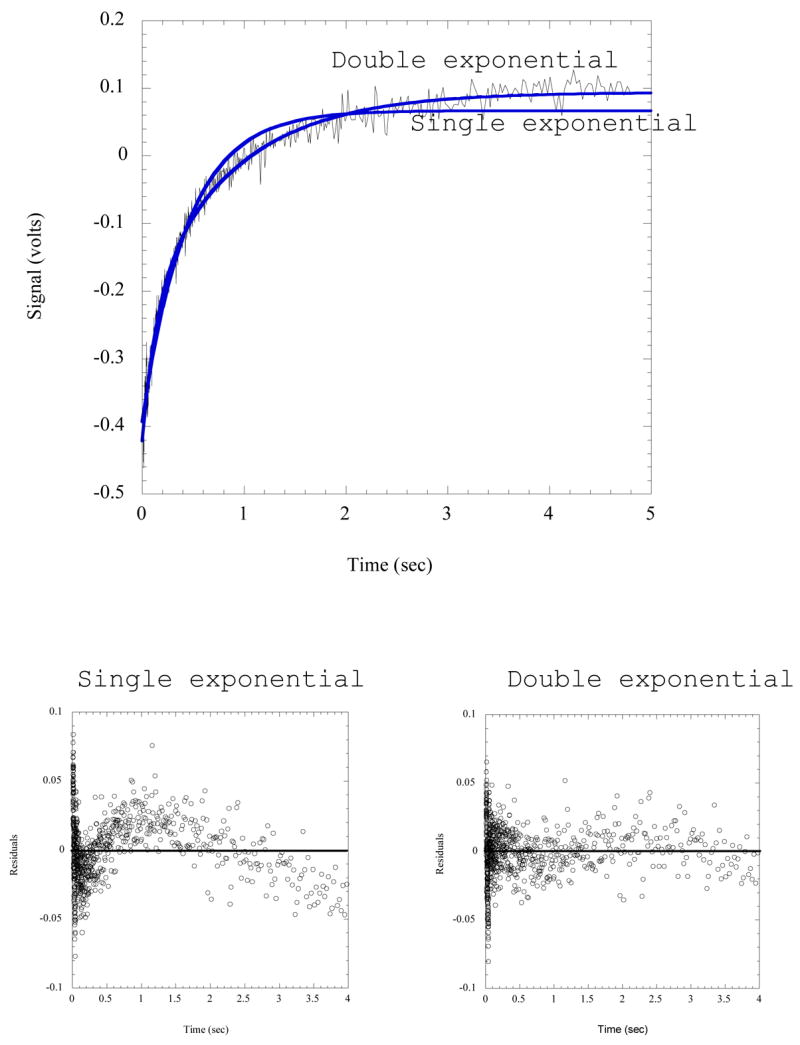
Comparison of single and double exponential fits to stopped flow fluorescence data. The reaction trace shown records the formation of His-tRNAHis by rapid mixing of HisRS·His~AMP with tRNAHis, employing MDCC-labeled HisRS. Fits to both a single and double exponential are shown on the plot; and the resulting residuals are plotted below. The wave-like pattern of the residuals relative to zero for the single exponential is indicative of a poorer fit.
2.11.2. Experimental Design
For simplicity, the following analysis is based on the TyrRS system; comparative analyses on the isoleucyl- and threonyl-tRNA synthetases have been reported [43, 74]. Rate and dissociation constants refer to the reaction mechanism shown in Figure 8. All experiments are performed at 25 °C in standard buffer (e.g. 20 mM Tris-HCl, pH 7.5, 150 mM KCl, and 10 mM MgCl2, and 1 mM dithiothreitol).
Figure 8.
Reaction mechanism for the aminoacylation of tRNA. The reaction mechanism for the amino acid activation and the aminoacyl transfer steps of the tRNA aminoacylation reaction are shown. In this mechanism, the amino acid (AA) and ATP are assumed to bind to the aminoacy-tRNA synthetase (E) in random order. “•” and “~” represent noncovalent and covalent bonds, respectively. Rate and dissociation constants are shown next to the steps to which they correspond.
Determination of KdAA
Typically, the equilibrium constant for the dissociation of the amino acid (AA) from the E•AA complex, KdAA, is determined by equilibrium dialysis (Section 2.4). It is also possible, however to determine KdAA using the stopped-flow fluorescence method. This is done by measuring the observed rate constant (kobs) under conditions where the concentration of ATP is less than 1/10 KdATP. This ensures that the amino acid initially binds to the free enzyme rather than to the E•ATP complex. Typical reaction conditions are as follows: Syringe 1 contains the aminoacyl-tRNA synthetase (0.25–0.5 μM) in standard buffer, while syringe 2 contains 2 – 200 μM amino acid in standard buffer. Both syringes contain MgATP (1/10 KdATP) and inorganic pyrophosphatase (1 U/μl).
Determination of KdATP
This procedure is analogous to that used to determine KdAA, except that the concentration of the amino acid is held constant at 1/10 KdAA and the MgATP concentration is varied.
Determination of k3 and K′dATP
This procedure is analogous to that used to determine KdATP, except that a saturating concentration of the amino acid (e.g. 10 KdAA) is used.
Determination of k−3 and KdPPi
The reverse rate constant and dissociation constant for pyrophosphate are determined by mixing the preformed E•AA~AMP intermediate with various concentrations of inorganic pyrophosphate. E•AA•AMP is preformed by incubating tyrosyl-tRNA synthetase with 2 mM MgATP, 100 μM amino acid, and inorganic pyrophosphatase (1 U/ml) at 25 °C in Tris buffer. The E•AA~AMP intermediate is then separated from the other reaction products by size exclusion chromatography on a Nap 25 column (Pfizer-Pharmacia). Syringe 1 contains the preformed E•AA~AMP intermediate in Tris buffer and syringe 2 contains varying amounts of pyrophosphate in Tris buffer. Tris buffer is identical to standard buffer except that, owing to the low solubility of magnesium pyrophosphate, it contains 2 mM MgCl2 instead of the 10 mM MgCl2 that is present in standard buffer.
Determination of k4 and KdtRNA
This procedure is analogous to that used to determine k−3 and KdPPi, except that the preformed E•AA~AMP intermediate is mixed with varying amounts of tRNA. Both the E•AA~AMP intermediate and tRNA are in standard buffer.
3.0 Data Analysis
3.1 Hyperbolic kinetics
In general, a plot of kobs vs. substrate concentration can be fit using a hyperbolic equation that is analogous to the Michaelis-Menten equation used for steady state kinetics:
| (13) |
where kn is the rate constant for the reaction, and [S]T and Kd are the total concentration and dissociation constant for the substrate of interest, respectively [75]. For example, under saturating amino acid concentrations, the forward rate constant for the amino acid activation reaction, k3, and the equilibrium constant for the dissociation of ATP from the E•AA•ATP complex can be determined from the following hyperbolic equation:
| (14) |
Similarly, the values of k−3, KdPPi, k4, and KdtRNA can be determined from equations (15) and (16).
| (15) |
| (16) |
It should be noted that when the nonvaried substrate is at subsaturating concentrations (i.e. when KdAA or KdATP is determined), then the rate constant, kn, is dependent on the concentration of the nonvaried substrate and is of little value. If it is not possible to use substrate concentrations that are 5 × Kd, then the rate and dissociation constants cannot be independently determined since the data cannot be accurately fit to a hyperbolic equation (e.g. equations 14–16). It is still possible, however, to determine the specificity constant (e.g. k3/K′dATP) from the slope of the linear part of the curve since Kd ≫ [S] under these conditions.
To determine the goodness of fit for the hyperbolic equation, an Eadie-Hoftsee transformation of the data is used [76, 77]:
| (17) |
The advantages of the Eadie-Hoftsee transformation are: (1) it gives a linear plot of the data making it easy to determine how well the data fit the transformation, (2) it does not preferentially weight the least precisely determined data points, and (3) the magnitudes of the error bars do not vary with substrate concentration. The latter two points are a particular concern when double reciprocal (e.g. Lineweaver-Burk) transformations are used [61, 64, 65].
Although rate and dissociation constants can be determined from a linear transformation, this should be avoided as the limitations of these transformations decrease the accuracy of the values that are determined. Instead, the data should be fit directly to the appropriate hyperbolic equation using the method of least squares analysis. A variety of curve fitting programs, such as Grafit (Erithacus Software) and Kaleidagraph (Synergy Software) are available for data analysis.
3.2 Sigmoidal kinetics
Although the aminoacyl-tRNA synthetases in subclasses Ia and Ib are functional monomers, the members of subclass Ic (TyrRS and TrpRS) and the class II aminoacyl-tRNA synthetases are all functional dimers. The presence of two active sites in these enzymes raises the possibility that there may be communication between the two sites that results in sigmoidal kinetics. In the event that sigmoidal kinetics are observed, the data can be fit to an Adair equation [78]:
| (18) |
where kobs is the observed rate constant for the reaction, k3 is the forward rate constant for the tyrosine activation reaction, [S]T is the total concentration of the substrate of interest, and α, β, and γ are fitting constants. If the k3 values for the mono- and bi-liganded species are assumed to be identical, then α corresponds to K1, β corresponds to K2, and γ corresponds to K1K3. To determine the extent of cooperativity, the data can be fit to the Hill equation [79]:
| (19) |
where kobs/(k3−kobs) is the fraction of substrate binding sites that are occupied, [S]T and Kd are the total concentration and dissociation constant for the substrate of interest, respectively, and nH is the Hill coefficient, which measures the extent of cooperativity between the binding sites.
3.3 Substrate Inhibition
In the case of tyrosyl-tRNA synthetase, kobs is observed to decrease at high ATP concentrations. This is an indication of substrate inhibition, which can be handled in a manner analogous to the analysis of substrate inhibition in steady state kinetics. For example, in the case of human tyrosyl-tRNA synthetase, an uncompetitive inhibition model has been used to fit the kinetic data to the following equation:
| (20) |
where k3 is the forward rate constant for the amino acid activation reaction, K′dATP is the equilibrium constant for the dissociation of ATP from the E•Tyr•ATP complex, and KiATP is the binding constant for ATP at the site of inhibition.
3.4. Calculation of Relative Standard Free Energies
The relative standard free energy values for each state along the amino acid activation reaction pathway can be calculated from the rate and dissociation constants using the following equations:
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
where ΔGo is the Gibbs free energy relative to that of the unliganded enzyme (i.e. GoE = 0), R is the universal gas constant, T is the absolute temperature, kB is the Bolzmann constant, h is Planck’s constant, and E•[AA~ATP]‡ is the transition state complex [80].
For the aminoacyl transfer reaction pathway, the relative standard free energies can be calculated relative to the standard free energy of the E•AA~AMP intermediate using the following equations:
| (26) |
| (27) |
The Gibbs activation energy for each reaction can be calculated by subtracting the standard free energy for the enzyme complex preceding the transition state from that of the transition state. All free energies are calculated assuming a standard state of 1 M ATP, 1 M amino acid, and 1 M pyrophosphate.
3.5. Free Energy Cycles
The role that a particular residue plays in catalysis can be determined through kinetic analysis of amino acid variants at that position. Free energy plots, such as the one shown in Figure 9, greatly facilitate this analysis, allowing the relative standard free energies of the wild type and variant enzymes to be directly compared at each step along the reaction pathway. Determining the precise role that the amino acid plays is complicated, however, by the observation that altering the (wild type) side chain disrupts not only potential interactions between the side chain and the substrate, but also any interactions that the side chain makes with its environment (e.g. other amino acids in the protein). This limitation can be overcome by using free energy cycles [81, 82].
Figure 9.
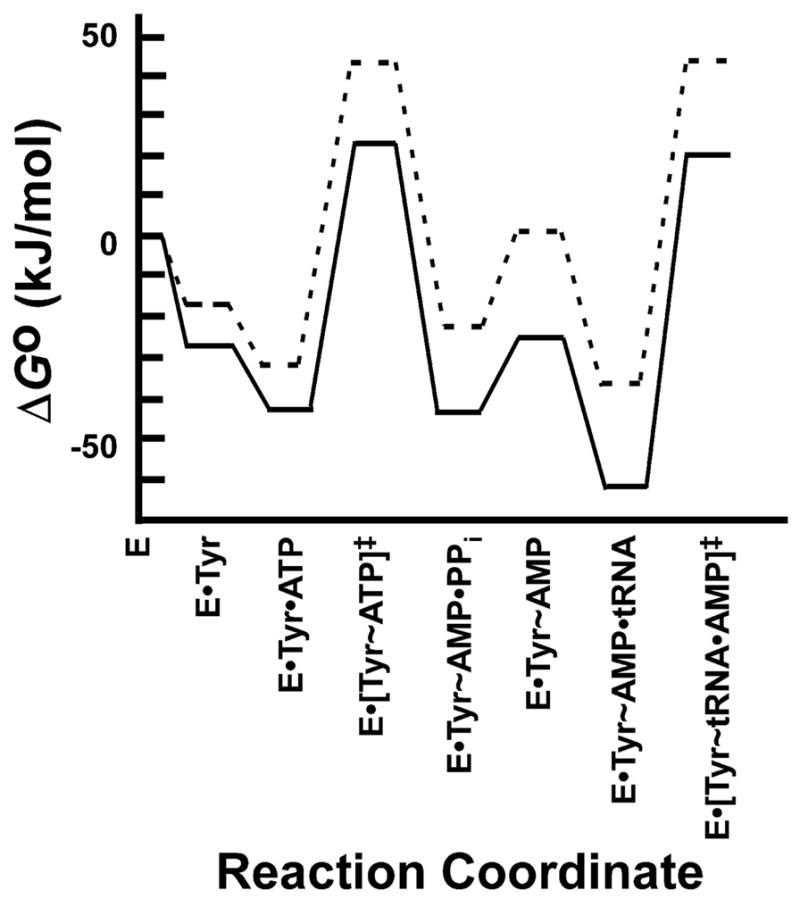
Standard free energy profile for the wild type and Q195A variants of Bacillus stearothermophilus tyrosyl-tRNA synthetase. Standard free energy values (ΔGo) are shown for each intermediate and transition state along the tRNA aminoacylation pathway for the wild type and Q195A variants of Bacillus stearothermophilus tyrosyl-tRNA synthetase. Standard free energies were calculated from rate and dissociation constants as described in the text. Values for the rate and dissociation constants are taken from [85] and [86].
Consider the free energy cycle shown in Figure 10. In this cycle, the double mutant (K230A/T234A) and wild type enzymes are shown in the upper left and lower right corners, respectively. ΔGoa corresponds to the standard free energy for converting the K230A/T234A variant to the K230/T234A variant, while ΔGod corresponds to the standard free energy for converting the K230A/T234 variant to the wild type enzyme (K230/T234). Note that in both cases, K230A is replaced by K230. In other words, the only difference between these two processes is the absence or presence of the T234 side chain. If there is no interaction (or “coupling”) between the K230 and T234 side chains, then ΔGoa and ΔGod will be identical (i.e. Δ ΔGoint = ΔGod − ΔGoa = 0). If, however, there is a synergistic (i.e. favorable) interaction between the K230 and T234 side chains, the Δ ΔGoint will be negative. If the interaction is antisynergistic (i.e. unfavorable) then Δ ΔGoint will be positive. Due to the cyclic nature of the process, Δ ΔGoint = ΔGod − ΔGoa = ΔGoc − ΔGob. In other words, if K230 interacts with T234, then T234 must interact with K230.
Figure 10.
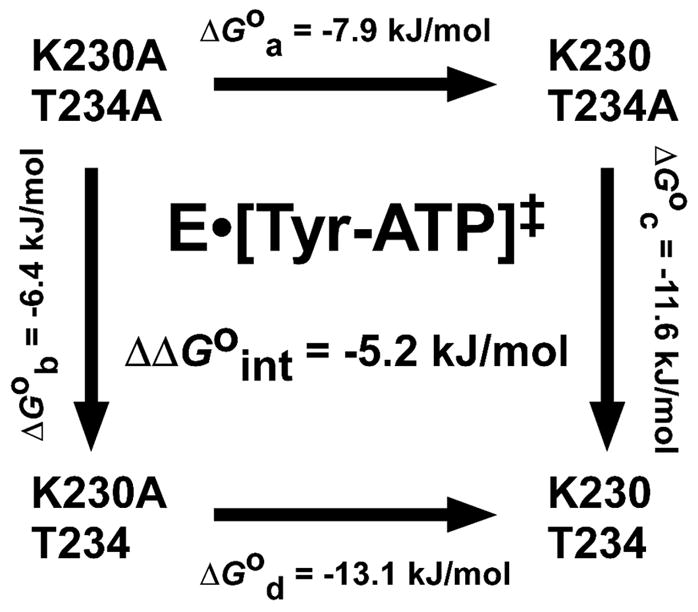
Quantifying the interaction between K230 and T234 in the transition state of Bacillus stearothermophilus tyrosyl-tRNA synthetase. The double mutant free energy cycle shown is used to determine the standard free energy of interaction (ΔΔGoint) for the interaction between the K230 and T234 side chains in the E•[Tyr~ATP]‡ transition state of Bacillus stearothermophilus tyrosyl-tRNA synthetase. Standard free energies for each variant are calculated using equation 23. Standard free energies corresponding to the addition of each side chain (ΔGa through ΔGd) are calculated by subtracting the standard free energies of each variant. For example, to calculate ΔGa, the standard free energy of the K230A/T234A variant is subtracted from that of the K230/T234A variant (ΔGoa = ΔGoK230/T234A − ΔGoK233A/T234A). The standard free energy of interaction is calculated by subtracting ΔGoa from ΔGod (ΔΔGoint = ΔGod − ΔGoa). Since free energy is a state function, the standard free energy of interaction can also be calculated by subtracting ΔGob from ΔGoc (ΔΔGoint = ΔGoc − ΔGob). Analogous double mutant free energy cycles can be used to calculate the free energy of interaction of the K230 and T234 side chains for each step along the reaction pathway. Rate and kinetic constants used to calculate the standard free energies of each variant are taken from [83].
Note that the sign of Δ ΔGoint is dependent on the configuration of the free energy cycle. In the literature, free energy cycles are often drawn with the wild type enzyme in the upper left corner. In this case, the interpretation of Δ ΔGoint is reversed, with Δ ΔGoint > 0 indicating a synergistic interaction. The advantage of using the configuration shown in Figure 9 is that the sign of Δ ΔGoint is consistent with the standard convention, where a negative free energy indicates that the process is thermodynamically favorable.
The standard free energy changes for each side of the free energy cycle are calculated from the relative standard free energies for each of the enzyme variants using equations 21–27. This results in a separate free energy cycle for each intermediate complex and the transition state, allowing changes in the interaction to be quantified throughout the reaction pathway. This enables one to determine the specific role(s) that the interaction plays in catalysis. It should be emphasized that this interaction is an energetic coupling and does not necessarily indicate a direct physical interaction. Since the coupling between two residues may occur over long distances, in the absence of structural information one cannot know whether Δ ΔGoint represents a direct physical interaction, or indirect coupling through other residues in the protein.
The above analysis can be extended in two ways. First, free energy cycles are not limited to analyzing interactions between amino acid side chains. For example, one can investigate whether an amino acid in the aminoacyl-tRNA synthetase and a nucleotide in its cognate tRNA interact during catalysis using a free energy cycle in which both the amino acid and nucleotide are mutated. Second, the free energy analysis can be extended to higher order couplings involving more than two side chains. For example, a triple mutant cube can be used to determine the effect that a third residue has on the coupling between two amino acids. For a detailed analysis of higher order couplings, see [83, 84].
4. Summary
The physiological production of correctly formed aminoacyl-tRNA for protein synthesis and other functions depends critically on the ability of aminoacyl-tRNA synthetases to select their cognate amino acid and tRNA substrates from disparate pools of chemically and structurally similar molecules, and to link them together at physiologically appropriate rates. While steady state kinetics provides a useful initial and fundamentally qualitative view into this process, the more rigorous thermodynamic and pre-steady state kinetic approaches described here are required for the determination of elementary binding and kinetic constants. Such parameters allow the investigator to construct a detailed free energy profile of the aminoacylation reaction, and thereby assess the significance of specific enzyme•substrate interactions. With the assistance of these experimental tools, long standing questions concerning structural and functional relationships among the disparate aaRS classes can be rigorously investigated, and novel engineered versions of aaRS:tRNA pairs can be characterized with an eye to analytically determining quantitative boundaries of specificity for unnatural amino acids. Other critical challenges in the field that will benefit from the application of the techniques described above include the correlation of binding and reaction chemical steps to specific structural changes that occur in the enzymes during the catalytic cycle. In spite of the more than four decades of research that has already been performed on these enzymes, many additional and important questions still remain, particularly with regard to the global integration of protein synthesis in the mammalian cell. Addressing this latter problem from a global system approach depends, in turn, on our ability to precisely model the rates of substrate disappearance and product appearance for each enzyme on its own. As the tools described here achieve broader use, this goal will become more feasible.
Figure 3.
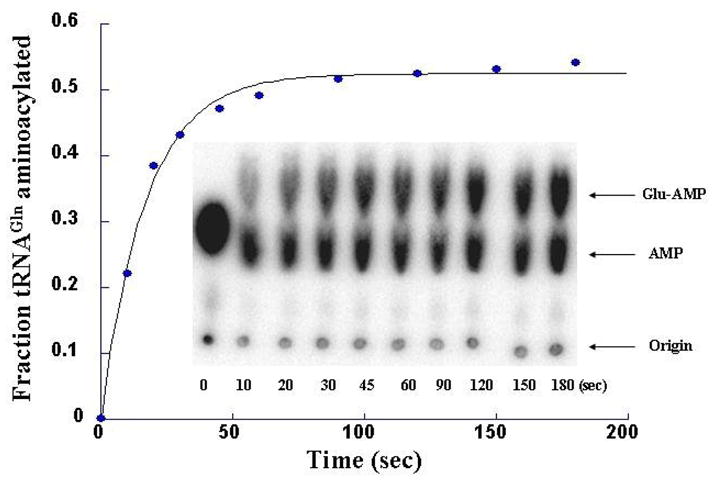
Example of a single-turnover noncognate glutamylation reaction by E. coli GlnRS. The reaction was conducted in a rapid chemical-quench instrument using 71 μM GlnRS, 33 μM [32P]-labeled tRNAGln, 2 M glutamate, and 10 mM ATP. The quenched time points of the reaction were analyzed according to Wolfson-Uhlenbeck method [56]. The ratio of Glu~AMP and AMP gives the fraction aminoacylated at each timepoint. kobs is determined by single-exponential fit of the data.
Acknowledgments
The authors thank Mr. Ethan Guth for providing the rapid quench data in Figure 5A,B, and Dr. Anita Sheoran for providing the stopped-flow fluorescence emission spectra shown in Figure 6. This work was supported by National Institutes of Health grants GM54899 (to C.F.), GM68070 (to E.F.), GM63713 (to J.P.), and GM56662 (to Y.-M.H.)
Abbreviations
Specific aminoacyl-tRNA synthetases are abbreviated by the standard three letter abbreviation for their cognate amino acid followed by the letters “RS” to indicate that it is the tRNA synthetase (e.g. histidyl-tRNA synthetase is abbreviated HisRS). Other abbreviations used in the text are as follows
- aaRS
aminoacyl-tRNA synthetase
- E
enzyme
- AA
amino acid
- PPi
inorganic pyrophosphate
- S
substrate
- ES
enzyme substrate complex
- EP
enzyme product complex
- E•AA~AMP
enzyme-bound aminoacyl adenylate intermediate
- DTT
dithiothreitol
- MDCC
7-diethylamino-3-((((2-maleimidyl)ethyl)amino)carbonyl)coumarin
- TCA
trichloroacetic acid
- TLC
and thin layer chromatography
Footnotes
For HisRS and ThrRS, formation of the aminoacyl adenylate intermediate uniformly occurs with a stoichiomety of one per dimer.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Covalent and noncovalent bonds are indicated by “~” and “•”
References
- 1.Schimmel PR, Soll D. Annu Rev Biochem. 1979;48:601–48. doi: 10.1146/annurev.bi.48.070179.003125. [DOI] [PubMed] [Google Scholar]
- 2.Carter CW., Jr Annu Rev Biochem. 1993;62:715–48. doi: 10.1146/annurev.bi.62.070193.003435. [DOI] [PubMed] [Google Scholar]
- 3.Ibba M, Soll D. Annu Rev Biochem. 2000;69:617–50. doi: 10.1146/annurev.biochem.69.1.617. [DOI] [PubMed] [Google Scholar]
- 4.Eriani G, Delarue M, Poch O, Gangloff J, Moras D. Nature. 1990;347:203–06. doi: 10.1038/347203a0. [DOI] [PubMed] [Google Scholar]
- 5.Cusack S. Curr Opin in Struct Biol. 1998;7:881–89. doi: 10.1016/s0959-440x(97)80161-3. [DOI] [PubMed] [Google Scholar]
- 6.Arnez JG, Moras D. Trends Biochem Sci. 1997;22:211–6. doi: 10.1016/s0968-0004(97)01052-9. [DOI] [PubMed] [Google Scholar]
- 7.Woese CR, Olsen GJ, Ibba M, Soll D. Microbiol Mol Biol Rev. 2000;64:202–36. doi: 10.1128/mmbr.64.1.202-236.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sauerwald A, Zhu W, Major TA, Roy H, Palioura S, Jahn D, Whitman WB, Yates JR, 3rd, Ibba M, Soll D. Science. 2005;307:1969–72. doi: 10.1126/science.1108329. [DOI] [PubMed] [Google Scholar]
- 9.Fersht AR. Structure and Mechanism in Protein Science. WH Freeman; New York: 1999. [Google Scholar]
- 10.Cleland WW. Biochim et Biophys Acta. 1963;67:188–96. doi: 10.1016/0006-3002(63)91816-x. [DOI] [PubMed] [Google Scholar]
- 11.Fersht AR, Shi JP, Knill-Jones J, Lowe DM, Wilkinson AJ, Blow DM, Brick P, Carter P, Waye MMY, Winter G. Nature. 1985;314:235–38. doi: 10.1038/314235a0. [DOI] [PubMed] [Google Scholar]
- 12.Perona JJ, Swanson R, Steitz TA, Söll D. J Mol Biol. 1988;202:121–26. doi: 10.1016/0022-2836(88)90524-4. [DOI] [PubMed] [Google Scholar]
- 13.Hou YM, Schimmel P. Nature. 1988;333:140–45. doi: 10.1038/333140a0. [DOI] [PubMed] [Google Scholar]
- 14.Eiler S, Boeglin M, Martin F, Eriani G, Gangloff J, Thierry JC, Moras D. J Mol Biol. 1992;224:1171–73. doi: 10.1016/0022-2836(92)90478-3. [DOI] [PubMed] [Google Scholar]
- 15.Martin F, Eriani G, Eiler S, Moras D, Dirheimer G, Gangloff J. J Mol Biol. 1993;234:965–74. doi: 10.1006/jmbi.1993.1651. [DOI] [PubMed] [Google Scholar]
- 16.Miyauchi K, Ohara T, Suzuki T. Nucleic Acids Res. 2007;35:e24. doi: 10.1093/nar/gkl1129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sampson JR, DiRenzo AB, Behlen LS, Uhlenbeck OC. Science. 1989;243:1363–6. doi: 10.1126/science.2646717. [DOI] [PubMed] [Google Scholar]
- 18.Sampson JR, DiRenzo AB, Behlen LS, Uhlenbeck OC. Biochemistry. 1990;29:2523–32. doi: 10.1021/bi00462a014. [DOI] [PubMed] [Google Scholar]
- 19.Arnez JG, Steitz TA. Biochemistry. 1994;33:7560–67. doi: 10.1021/bi00190a008. [DOI] [PubMed] [Google Scholar]
- 20.Milligan JF, Groebe DR, Witherell GW, Uhlenbeck OC. Nucl Acids Res. 1987;15:8783–98. doi: 10.1093/nar/15.21.8783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Milligan JF, Uhlenbeck OC. Methods Enzymol. 1989;180:51–62. doi: 10.1016/0076-6879(89)80091-6. [DOI] [PubMed] [Google Scholar]
- 22.Guillerez J, Lopez PJ, Proux F, Launay H, Dreyfus M. Proc Natl Acad Sci U S A. 2005;102:5958–63. doi: 10.1073/pnas.0407141102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yan W, Augustine J, Francklyn C. Biochemistry. 1996;35:6559–68. doi: 10.1021/bi952889f. [DOI] [PubMed] [Google Scholar]
- 24.Yin Y, Carter CW., Jr Nucleic Acids Res. 1996;24:1279–86. doi: 10.1093/nar/24.7.1279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Helm M, Brule H, Giege R, Florentz C. RNA. 1999;5:618–21. doi: 10.1017/s1355838299982328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pleiss JA, Derrick ML, Uhlenbeck OC. RNA. 1998;4:1313–7. doi: 10.1017/s135583829800106x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Price SR, Ito N, Oubridge C, Avis JM, Nagai K. J Mol Biol. 1995;249:398–408. doi: 10.1006/jmbi.1995.0305. [DOI] [PubMed] [Google Scholar]
- 28.Ferre-D’Amare AR, Doudna JA. Nucleic Acids Res. 1996;24:977–8. doi: 10.1093/nar/24.5.977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Moran S, Ren RX, Sheils CJ, Rumney St, Kool ET. Nucleic Acids Res. 1996;24:2044–52. doi: 10.1093/nar/24.11.2044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kao C, Zheng M, Rudisser S. RNA. 1999;5:1268–72. doi: 10.1017/s1355838299991033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sherlin LD, Bullock TL, Nissan TA, Perona JJ, Lariviere FJ, Uhlenbeck OC, Scaringe SA. RNA. 2001;7:1671–8. [PMC free article] [PubMed] [Google Scholar]
- 32.Pleiss JA, Wolfson AD, Uhlenbeck OC. Biochemistry. 2000;39:8250–8. doi: 10.1021/bi0001022. [DOI] [PubMed] [Google Scholar]
- 33.Cho HD, Verlinde CL, Weiner AM. Proc Natl Acad Sci USA. 2007;104:54–9. doi: 10.1073/pnas.0606961104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Francklyn C, Harris D, Moras D. J Mol Biol. 1994;241:275–7. doi: 10.1006/jmbi.1994.1498. [DOI] [PubMed] [Google Scholar]
- 35.Boeglin M, Dock-Bregeon A, Eriani G, Gangloff J, Ruff M, Poterszman A, Mitschler A, Thierry JC, Moras D. Acta Cryst D Biol Cryst. 1996;D52:211–14. doi: 10.1107/S090744499500727X. [DOI] [PubMed] [Google Scholar]
- 36.Kleeman TA, Wei D, Simpson KL, First EA. J Biol Chem. 1997;272:14420–5. doi: 10.1074/jbc.272.22.14420. [DOI] [PubMed] [Google Scholar]
- 37.Austin J, First EA. J Biol Chem. 2002;277:14812–20. doi: 10.1074/jbc.M103396200. [DOI] [PubMed] [Google Scholar]
- 38.Fersht AR. Biochemistry. 1975;14:5–12. doi: 10.1021/bi00672a002. [DOI] [PubMed] [Google Scholar]
- 39.Mursinna RS, Lincecum TL, Jr, Martinis SA. Biochemistry. 2001;40:5376–81. doi: 10.1021/bi002915w. [DOI] [PubMed] [Google Scholar]
- 40.Uter NT, Gruic-Sovulj I, Perona JJ. J Biol Chem. 2005;280:23966–77. doi: 10.1074/jbc.M414259200. [DOI] [PubMed] [Google Scholar]
- 41.Fersht AR, Mulvey RS, Koch GLE. Biochemistry. 1975;14:13–18. doi: 10.1021/bi00672a003. [DOI] [PubMed] [Google Scholar]
- 42.Austin J, First EA. J of Biol Chem. 2002;277:28394–9. doi: 10.1074/jbc.M204404200. [DOI] [PubMed] [Google Scholar]
- 43.Bovee ML, Pierce MA, Francklyn CS. Biochemistry. 2003;42:15102–13. doi: 10.1021/bi0355701. [DOI] [PubMed] [Google Scholar]
- 44.Scatchard G. Ann NY Acad Sci. 1948;51:660–72. [Google Scholar]
- 45.Yarus M, Berg P. Anal Biochem. 1970;35:450–65. doi: 10.1016/0003-2697(70)90207-1. [DOI] [PubMed] [Google Scholar]
- 46.Park SJ, Hou YM, Schimmel P. Biochemistry. 1989;28:2740–6. doi: 10.1021/bi00432a056. [DOI] [PubMed] [Google Scholar]
- 47.Bovee ML, Yan W, Sproat BS, Francklyn CS. Biochemistry. 1999;38:13725–35. doi: 10.1021/bi991182g. [DOI] [PubMed] [Google Scholar]
- 48.Wong I, Lohman TM. Proc Natl Acad Sci USA. 1993;90:5428–32. doi: 10.1073/pnas.90.12.5428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Silvian L. Molecular Biophysics and Biochemistry. Vol. 190. Yale University; 1997. [Google Scholar]
- 50.Gruic-Sovulj I, Landeka I, Soll D, Weygand-Durasevic I. Eur J Biochem. 2002;269:5271–9. doi: 10.1046/j.1432-1033.2002.03241.x. [DOI] [PubMed] [Google Scholar]
- 51.Orchard K, May GE. Nucleic Acids Res. 1993;21:3335–6. doi: 10.1093/nar/21.14.3335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Calendar R, Berg P. Biochemistry. 1966;5:1690–95. doi: 10.1021/bi00869a034. [DOI] [PubMed] [Google Scholar]
- 53.Fersht AR, Ashford JS, Bruton CJ, Jakes R, Koch GLE, Hartley BS. Biochemistry. 1975;14:1–4. doi: 10.1021/bi00672a001. [DOI] [PubMed] [Google Scholar]
- 54.Segel I. Enzyme Kinetics: behavior and analysis of rapid equilibrium and steady state kinetics. Wiley; New York: 1975. [Google Scholar]
- 55.Gruic-Sovulj I, Uter N, Bullock T, Perona JJ. J Biol Chem. 2005;280:23978–86. doi: 10.1074/jbc.M414260200. [DOI] [PubMed] [Google Scholar]
- 56.Wolfson AD, Pleiss JA, Uhlenbeck OC. RNA. 1998;4:1019–23. doi: 10.1017/s1355838298980700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wolfson AD, Uhlenbeck OC. Proc Natl Acad Sci USA. 2002;99:5965–70. doi: 10.1073/pnas.092152799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bullock TL, Uter N, Nissan TA. and J J Perona J Mol Biol. 2003;328:395–408. doi: 10.1016/s0022-2836(03)00305-x. [DOI] [PubMed] [Google Scholar]
- 59.Uter NT, Perona JJ. Proc Natl Acad Sci USA. 2004;101:14396–401. doi: 10.1073/pnas.0404017101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Fersht AR, Jakes R. Biochemistry. 1975;14:3350–56. doi: 10.1021/bi00686a010. [DOI] [PubMed] [Google Scholar]
- 61.Johnson KA. Methods Enzymol. 1995;249:38–61. doi: 10.1016/0076-6879(95)49030-2. [DOI] [PubMed] [Google Scholar]
- 62.Guth E, Connolly SH, Bovee M, Francklyn CS. Biochemistry. 2005;44:3785–94. doi: 10.1021/bi047923h. [DOI] [PubMed] [Google Scholar]
- 63.Zhang CM, Perona JJ, Ryu K, Francklyn C, Hou YM. J Mol Biol. 2006;361:300–11. doi: 10.1016/j.jmb.2006.06.015. [DOI] [PubMed] [Google Scholar]
- 64.Cornish-Bowden A. Methods. 2001;24:181–90. doi: 10.1006/meth.2001.1179. [DOI] [PubMed] [Google Scholar]
- 65.Leatherbarrow RJ. Trends Biochem Sci. 1990;15:455–8. doi: 10.1016/0968-0004(90)90295-m. [DOI] [PubMed] [Google Scholar]
- 66.Guth E, Francklyn CS. Molecular Cell. 2007;25:531–42. doi: 10.1016/j.molcel.2007.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Bhattacharyya T, Bhattacharyya A, Roy S. Eur J Biochem. 1991;200:739–45. doi: 10.1111/j.1432-1033.1991.tb16239.x. [DOI] [PubMed] [Google Scholar]
- 68.An S, Musier-Forsyth K. J Biol Chem. 2005;280:34465–72. doi: 10.1074/jbc.M507550200. [DOI] [PubMed] [Google Scholar]
- 69.Bhattacharyya T, Roy S. Biochemistry. 1993;32:9268–73. doi: 10.1021/bi00087a002. [DOI] [PubMed] [Google Scholar]
- 70.Chan B, Weidemaier K, Yip WT, Barbara PF, Musier-Forsyth K. Proc Natl Acad Sci USA. 1999;96:459–64. doi: 10.1073/pnas.96.2.459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Ghosh SS, Kao PM, McCue AW, Chappelle HL. Bioconj Chem. 1990;1:71–6. doi: 10.1021/bc00001a009. [DOI] [PubMed] [Google Scholar]
- 72.Liu C, Gamper H, Shtivelband S, Hauenstein S, Perona JJ. and Y M Hou J Mol Biol. 2007;367:1063–78. doi: 10.1016/j.jmb.2007.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Patel SS, Bandwar RP, Levin MK. In: Kinetic Analysis of Macromolecules. Johnson KA, editor. Oxford University Press; 2003. [Google Scholar]
- 74.Pope AJ, Lapointe J, Mensah L, Benson N, Brown MJ. and K J Moore J Biol Chem. 1998;273:31680–90. doi: 10.1074/jbc.273.48.31680. [DOI] [PubMed] [Google Scholar]
- 75.Engel P. Enzymology Labfax. Academic Press; New York: 1996. [Google Scholar]
- 76.Eadie GS. J Biol Chem. 1942;146:85–93. [Google Scholar]
- 77.Hofstee BH. Nature. 1959;184:1296–8. doi: 10.1038/1841296b0. [DOI] [PubMed] [Google Scholar]
- 78.Adair GS, Bock AV, Field HF. Jr J Biol Chem. 1925;63:529–45. [Google Scholar]
- 79.Hill AV. Journal of Physiology (London) 1910;40:4–7. [Google Scholar]
- 80.Wells TNC, Fersht AR. Biochemistry. 1986;25:1881–86. doi: 10.1021/bi00356a007. [DOI] [PubMed] [Google Scholar]
- 81.Carter PJ, Winter G, Wilkinson AJ, Fersht AR. Cell. 1984;38:835–40. doi: 10.1016/0092-8674(84)90278-2. [DOI] [PubMed] [Google Scholar]
- 82.Horovitz A. J Mol Biol. 1987;196:733–5. doi: 10.1016/0022-2836(87)90045-3. [DOI] [PubMed] [Google Scholar]
- 83.First EA, Fersht AR. Biochemistry. 1995;34:5030–43. doi: 10.1021/bi00015a014. [DOI] [PubMed] [Google Scholar]
- 84.Horovitz A, Fersht AR. J Mol Biol. 1992;224:733–40. doi: 10.1016/0022-2836(92)90557-z. [DOI] [PubMed] [Google Scholar]
- 85.Fersht AR. Biochemistry. 1988;27:1577–80. doi: 10.1021/bi00405a027. [DOI] [PubMed] [Google Scholar]
- 86.Xin Y, Li W, First EA. Biochemistry. 2000;39:340–7. doi: 10.1021/bi991675l. [DOI] [PubMed] [Google Scholar]
- 87.Hyafil F, Jacques Y, Fayat G, Fromant M, Dessen P. and S Blanque,t Biochemistry. 1976;15:3678–85. doi: 10.1021/bi00662a006. [DOI] [PubMed] [Google Scholar]
- 88.Fersht AR, Dingwall C. Biochemistry. 1979;18:2627–31. doi: 10.1021/bi00579a030. [DOI] [PubMed] [Google Scholar]
- 89.Fersht A, Gangloff J, Dirheimer G. Biochemistry. 1978;17:3740–46. doi: 10.1021/bi00611a011. [DOI] [PubMed] [Google Scholar]
- 90.Fersht AR, Kaethner MM. Biochemistry. 1976;15:818–23. doi: 10.1021/bi00649a014. [DOI] [PubMed] [Google Scholar]
- 91.Avis J, Fersht AR. Biochemistry. 1993;32:5321–26. doi: 10.1021/bi00071a006. [DOI] [PubMed] [Google Scholar]
- 92.Avis JM, Day AG, Garcia GA, Fersht AR. Biochemistry. 1993;32:5312–20. doi: 10.1021/bi00071a005. [DOI] [PubMed] [Google Scholar]
- 93.Xin Y, Li W, First EA. J Mol Biol. 2000;303:299–310. doi: 10.1006/jmbi.2000.4126. [DOI] [PubMed] [Google Scholar]
- 94.Trezeguet V, Merle M, Gandar JC, Labouesse B. Biochemistry. 1986;25:7125–36. doi: 10.1021/bi00370a055. [DOI] [PubMed] [Google Scholar]
- 95.Ibba M, Sever S, Praetorius-Ibba M, Soll D. Nucleic Acids Res. 1999;27:3631–7. doi: 10.1093/nar/27.18.3631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Dibbelt L, Pachmann U, Zachau HG. Nucleic Acids Res. 1980;8:4021–39. doi: 10.1093/nar/8.17.4021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Dibbelt L, Zachau HG. FEBS Lett. 1981;129:173–6. doi: 10.1016/0014-5793(81)80783-1. [DOI] [PubMed] [Google Scholar]
- 98.Krauss G, Riesner D, Maass G. Eur J Biochem. 1976;68:81–93. doi: 10.1111/j.1432-1033.1976.tb10766.x. [DOI] [PubMed] [Google Scholar]
- 99.Takita T, Akita E, Inouye K, Tonomura B. J Biochem (Tokyo) 1998;124:45–50. doi: 10.1093/oxfordjournals.jbchem.a022095. [DOI] [PubMed] [Google Scholar]