A neural network model of attention-modulated neurodynamics

Abstract

Visual attention appears to modulate cortical neurodynamics and synchronization through various cholinergic mechanisms. In order to study these mechanisms, we have developed a neural network model of visual cortex area V4, based on psychophysical, anatomical and physiological data. With this model, we want to link selective visual information processing to neural circuits within V4, bottom-up sensory input pathways, top-down attention input pathways, and to cholinergic modulation from the prefrontal lobe. We investigate cellular and network mechanisms underlying some recent analytical results from visual attention experimental data. Our model can reproduce the experimental findings that attention to a stimulus causes increased gamma-frequency synchronization in the superficial layers. Computer simulations and STA power analysis also demonstrate different effects of the different cholinergic attention modulation action mechanisms.

Introduction

Attention is known to play a key role in perception, including action selection, object recognition and memory (Hamker 2004a, b). The main effect of attentional selection appears to be a modulation of the underlying competitive interaction between the stimuli in the visual field. Studies of cortical areas V2 and V4 indicate that attention serves to modulate the suppressive interaction between two or more stimuli presented simultaneously within the receptive field (Corchs and Deco 2002). Intermodular competition and mutual biasing result from the interaction between modules corresponding to different visual areas (Deco and Rolls 2004). Analysis of in vivo visual attention experimental data has revealed that visual attention has several effects in modulating cortical oscillations, in terms of changes in firing rate (McAdams and Maunsell 1999), and gamma and beta coherence (Fries et al. 2001). In selective attention tasks, after the cue onset and before the stimulus onset, there is a delay period during which the monkey’s attention was directed to the place where the stimulus would appear (Fries et al. 2001). Data analysis showed that during the delay, the power spectra were dominated by frequencies around 17 Hz. With attention, this low-frequency synchronization was reduced. During the stimulus period, there were two distinct bands in the power spectrum, one below 10 Hz and another at 35–60 Hz. With attention, the reduction in low-frequency synchronization was maintained and, conversely, gamma-frequency synchronization was increased.

Visual attention is clearly associated with the visual cortex. This cortical structure is composed of a multi-scale network system and is apparently involved in many higher level information processing tasks, including cognition and consciousness. At a macro-scale, visual cortex is organized as a hierarchy of cortical areas. Cognitive tasks in a simple environment, or perception of novel unexpected stimuli, seems to involve a pure bottom-up processing, driven by external stimuli through a cascade from lower to higher areas. However, when the environment is cluttered, or there is internal expectancy, attention, or a behavioral goal, experimental evidence indicates a more complex interaction between top-down and bottom-up signals. Such top-down information from higher areas, driven by internal signals, and bottom-up signals from lower areas, driven by external stimuli, seems involved in complex cognition and conscious awareness tasks (Desimone and Duncan 1995; Hupé et al. 2001; Fries et al. 2001; Angelucci and Bullier 2003; Kranczioch et al. 2005). Results in Hupé et al. (2001) indicate that higher area top-down feedback acts on the earliest part of the response in lower areas, and can last throughout the whole duration of the stimulus response. Angelucci and Bullier (2003) suggest that top-down feedback projections from higher areas contact both pyramidal and inhibitory neurons in the lower area, and spread much further laterally than the local lateral connections within the lower area. At a meso-scale, each area of the visual cortex is conventionally divided into six layers, some of which can be further divided into several sub-layers, based on their detailed functional roles in visual information processing (such as orientation and retinotopic position).

According to the basic signal transferring and processing functions, the six layers can be roughly regarded as three layers: layer 2/3, layer 4 and layer 5/6. A major part of bottom-up inter-areal connections terminate in the granular layer (layer 4), another, smaller part of bottom-up inter-areal connections terminate in layer 6. Top-down inter-areal connections terminate in the supra- (layer 2/3) and infra-granular layers (layer 5/6). Using techniques of microinjections of D-3H-Asp and injections of horseradish peroxidase, very detailed intra-areal connections, including intra-laminar and lateral excitatory projections have been experimentally investigated (Fitzpatrick et al. 1985; Blasdel et al. 1985 and Kisvarday et al. 1989).

The inter-scale network interactions of various excitatory and inhibitory neurons in the visual cortex generate oscillatory signals with complex patterns of frequencies associated with particular states of the brain. Synchronous activity at an intermediate and lower-frequency range (theta, delta and alpha) between distant areas was observed during perception of stimuli with varying behavioral significance (von Stein et al. 2000; Siegel et al. 2000). Particularly, von Stein et al. (2000) found that intermediate (4–12 Hz, theta/alpha) frequency interactions were related to stimulus expectancy, and suggest that intermediate-frequency interaction might mediate top-down processes. Rhythms in the beta (12–30 Hz) and the gamma (30–80 Hz) ranges are also found in visual cortex, and are often associated with attention, perception, cognition and conscious awareness (Fries et al. 2001). Data suggest that gamma rhythms are associated with relatively local computations, whereas beta rhythms are associated with higher level interactions. Generally, it is believed that lower frequency bands are generated by global circuits, while higher frequency bands are derived from local connections.

Previously, Wright and Liley (1995) have developed a global scale model of electrocortical activity, using cortico-cortical and intracortical synaptic coupling densities and local field potentials. The simulated spectra of their model show realistic peaks of power occurring at theta, alpha, beta and gamma ranges. With increasing cortical activation parameter, there is a ‘shift to the right’ of spectral density, imitating the effect of increasing cortical arousal. Kopell and her colleagues have demonstrated, with a small network composed of two pyramidal neurons and two inhibitory Hodgkin–Huxley neurons, that oscillations may shift from gamma to beta, when increasing the strength of recurrent excitatory synapses and the amplitude of one or more slow K conductances (Kopell and Ermentrout 2000). They also developed a cortical local circuit model in which cholinergic modulation, acting on adaptation currents in principal cells, induces a transition between asynchronous spontaneous activity and a “background” gamma rhythm (Börgers et al. 2005). In earlier work of our own group, we have studied oscillations of this kind in olfactory information processing, using neural population models of the olfactory cortex (Liljenström 1991; Wu and Liljenström 1994; Liljenström and Hasselmo 1995; Basu and Liljenström 2001). For example, in Liljenström and Hasselmo (1995) we demonstrated cholinergic modulation shifts in olfactory network oscillations. Recently, we have developed neural network models with realistic anatomical circuits and physiological parameters of neocortex to simulate and analyze EEG-like signals and investigate how the dynamics are affected by the internal local and global connection topology, and different types of external stimuli and signals (Gu et al. 2004, 2006). In the present work, we further develop and generalize our experiences and ideas from previous neural network modeling for visual cortex. We construct a model of the visual cortex area V4, based on anatomical and physiological data. Using our model of the visual cortex, we simulate some data analysis results from selective visual attention tasks, carried out on macaque monkeys attended to behaviorally relevant stimuli and ignored distracters (Fries et al. 2001). We also discuss hypotheses about various cholinergic action mechanisms involved in top-down attention modulation.

Methods

Neuron types and equations describing the dynamics of neurons

Our model is composed of three functional layers including layer 2/3, layer 4 and layer 5/6. Each layer contains 20 × 20 excitatory neurons (pyramidal neurons in layer 2/3 and layer 5/6, and spiny stellate neurons in layer 4) in a quadratic lattice with lattice distance 0.2 mm, and 10 × 10 inhibitory neurons in a quadratic lattice with lattice distance 0.4 mm. Thus, there are 20% inhibitory neurons, which roughly corresponds to the cortical distribution. The pyramidal neurons in layer 2/3 and layer 5/6, and the spiny stellate neurons in layer 4 satisfy Hodgkin–Huxley equations of the following form (which are essentially the same as in Kopell et al. 2000):

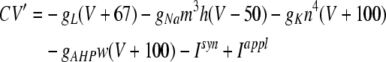1

where V is the membrane potential and C = 1μF is the membrane capacitance. g_L = 0.1 mS is the leak conductance, g_Na = 20 mS and g_K = 10 mS are the maximal sodium and potassium conductances, respectively, g_AHP the maximal slow potassium conductance of the afterhyperpolarization (AHP) current, which varies from 0 mS to 1.0 mS, depending on the attention state: in idle state, g_AHP = 1.0 mS, with attention, g_AHP ≤ 1.0 mS. The variables m, h, n and w satisfy

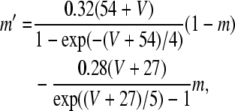2

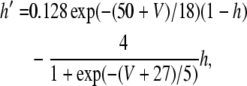3

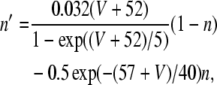4

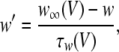5

where

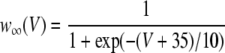6

and

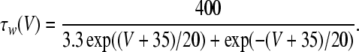7

The inhibitory neurons have identical equations, except there is no AHP current.

The synaptic input current I^syn and the applied current I^appl of pyramidal, stellate, and inhibitory neurons will be described in section "Network architecture and equations".

Network architecture and equations

Figure 1 shows the schematic diagram of the network topology, in which we take into account different types of spiking neurons and the detailed connection circuitry based on anatomical and physiological findings. Three different types of signal flows are included in our model: one type is the local interaction signals within each layer and between different layers; another type is the bottom-up input signals from the lower area; the other type is the top-down input signals from the higher area. The inhibitory neurons in each layer have interactions within their own layer only, while excitatory neurons have interactions within their own layer, as well as between layers and areas. The connections between excitatory and inhibitory neurons within each layer form a “Mexican hat” shape with an on-center and an off-surround lateral synaptic input for each neuron, as shown in Fig. 2 and described in detail below.

Fig. 1.

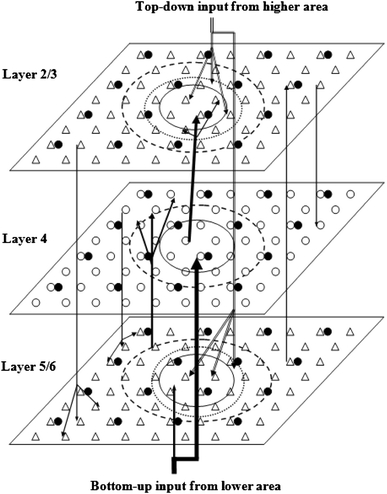
A schematic diagram of the model architecture. The small triangles in layer 2/3 and layer 5/6 represent pyramidal neurons, the small open circles in layer 4 are spiny stellate neurons, and the small solid circles in each layer are inhibitory neurons. The arrows show the connection patterns between different layers and the signal flows coming from the other areas. The large solid open circle in each layer represents the lateral excitatory connection radius, the large dashed open circle in each layer represents inhibitory connection radius. The dotted open circles in layer 2/3 and layer 5/6 denote the top-down attention modulation radius

Fig. 2.

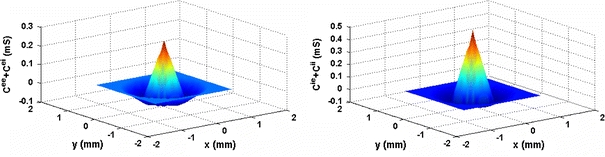
The lateral connection strength to an excitatory neuron (a) and that to an inhibitory neurons (b) as function of distance in each layer. In this graph, the parameter values of various synaptic strengths and various connection rediuses are: g^ee = 0.25 mS, g^ie = 0.5 mS, g^ei = 0.3 mS, gⁱⁱ = 0.3 mS, R^ee = 0.5 mm, R^ie = 0.5 mm, R^ei = 1.0 mm, Rⁱⁱ = 1.0 mm

The bottom-up sensory inputs from lower areas, which constitute the strongest signal flow in the network, activate the local area network via two routes. The major stream of the bottom-up signal inputs to spiny stellate neurons in layer 4. The minor stream of the bottom-up signal inputs to pyramidal neurons in layer 5/6. Layer 4 spiny stellate neurons excite the layer 2/3 pyramidal neurons with laterally spread connections, which constitute the strongest interactions between layers. Layer 5/6 pyramidal neurons activate the spiny stellate neurons in layer 4 with laterally spread connections, which constitute the second strongest connections between layers. Layer 2/3 pyramidal neurons send feedback signals to layer 6 pyramidal neurons with laterally distributed connections. Layer 4 spiny stellate neurons send descending signals to layer 5/6 pyramidal neurons with spread connections. Layer 5/6 pyramidal neurons send ascending small focus signals to layer 2/3 pyramidal neurons above. Layer 2/3 pyramidal neurons send descending focus signals to layer 4 stellate neurons below. Attention-activated cholinergic modulation signals from higher area pass down into layer 5/6 and layer 2/3. These signals spread laterally with a radius which is larger than the lateral excitatory connection radius, but smaller than the lateral inhibitory connection radius in these two layers. The reason for this top-down input structure is that the higher areas have larger receptive fields than the lower areas.

In each layer j (where j = 2/3, 4, and 4/6) of the local area network, there are four types of interactions: (1) lateral excitatory–excitatory, (2) excitatory–inhibitory, (3) inhibitory–excitatory, and (4) inhibitory–inhibitory, with corresponding connection strengths, C^ee_j,kl, C^ie_j,kl, C^ei_j,kl, and Cⁱⁱ_j,kl, which vary with distance between neurons k and l. We construct our lateral connections based on the experimental findings that the lateral interaction can be described by a Mexican hat shape, i.e. the total lateral synaptic inputs to a neuron are, in general, excitatory at a short distance, and inhibitory at a long distance.

The excitatory–excitatory connections apparently activate neighboring excitatory neurons, whereas the excitatory–inhibitory connections activate neighboring inhibitory neurons, which subsequently could inhibit distant excitatory neurons. Therefore, in our model, the lateral excitatory connection strength from neuron l to neuron k is strongest between close neighbors, and decreasing with distance as,

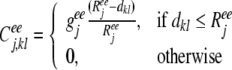8

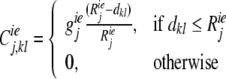9

The lateral inhibitory–inhibitory connections could inhibit distant inhibitory neurons, thus weakening the inhibitory effect of distant inhibitory neurons. Hence, in our model, the inhibitory connection strength is weakest for neighboring neurons, and increasing with distance. The lateral inhibitory connection strength reaches a maximal value when the distance between neurons is half of the inhibitory interaction radius, then decreases with distance between neurons. Inhibitory connection strength from neuron l to neuron k is described by

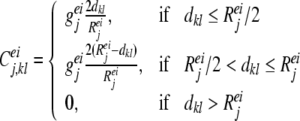10

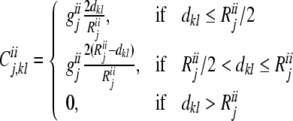11

where g^ee_j, g^ie_j, g^ei_j and gⁱⁱ_j are conductances, representing the maximum excitatory—excitatory, excitatory—inhibitory, inhibitory—excitatory, and inhibitory—inhibitory coupling strengths in layer j, respectively. R^ee_j, R^ie_j, R^ei_j and Rⁱⁱ_j are the corresponding lateral connection radiuses, and d_kl is the distance between neuron k and l.

From Eqs. (8) and (10), we can obtain that the total connection strength to an excitatory neuron, as a function of distance, has a Mexican hat shape, as shown in Fig. 2A. Similarly, Eqs. (9) and (11) give a Mexican hat shape for the total connection strength to an inhibitory neuron as a function of distance, as shown in Fig. 2B.

In our model, the connection strength from the excitatory neuron l in layer j to the excitatory neuron k in layer i is given by

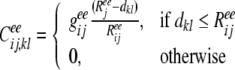12

where d_kl is the lateral distance between neuron l and k.

The synaptic input currents, I^syn, for each one of the excitatory (pyramidal) and inhibitory neurons are defined below.

The synaptic input current, I^syn_2/3p,k(t) of the kth pyramidal neuron in layer 2/3 at time t is composed of lateral excitatory inputs from neighboring pyramidal neurons and lateral inhibitory inputs from neighboring inhibitory neurons in layer 2/3, feedforward inputs from the stellate neurons in layer 4, and from the pyramidal neurons in layer 5/6:

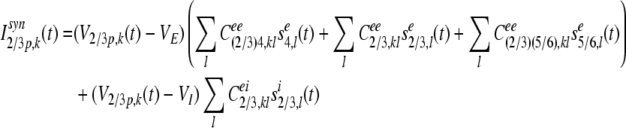13

where V_2/3p,k(t) is the membrane potential of pyramidal neuron k in layer 2/3 at time t. V_E = 0 mV is the reversal potential for excitatory synaptic currents, V_I = −80 mV is the reversal potential for inhibitory synaptic currents. s^x_j,l is the presynaptic output signal from neuron l in layer j, with x = e for excitatory, or x = i for inhibitory signals, respectively, and defined by Eqs. (19) and (20).

The synaptic input current,I^syn_2/3i,k of the kth inhibitory neuron in layer 2/3 is composed of the lateral excitatory inputs from neighboring pyramidal neurons, and lateral inhibitory inputs from neighboring inhibitory neurons:

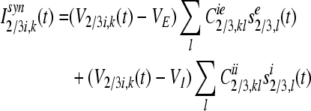14

The synaptic input current, I^syn_4s,k(t) of the kth stellate neuron in layer 4 at time t is composed of the ascending input from the pyramidal neurons in layer 6, descending input from the pyramidal neurons in layer 2/3, and lateral excitatory inputs from the on-center neighboring stellate neurons in layer 4, and lateral inhibitory inputs from the off-surround neighboring inhibitory neurons in the same layer:

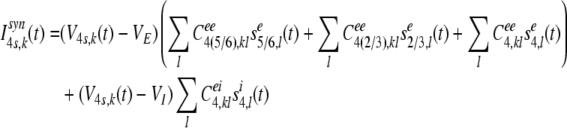15

The synaptic input current, I^syn_4i,k of the kth inhibitory neuron in layer 4 is composed of the lateral excitatory inputs from neighboring stellate neurons and lateral inhibitory inputs from neighboring inhibitory neurons:

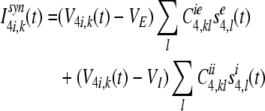16

The synaptic input current I^syn_5/6p,k(t) of the kth pyramidal neuron in layer 5/6 at time t is composed of the feedback inputs from pyramidal neurons in layer 2/3, descending inputs from stellate neurons in layer 4, and lateral excitatory inputs from neighboring pyramidal neurons and lateral inhibitory inputs from neighboring inhibitory neurons:

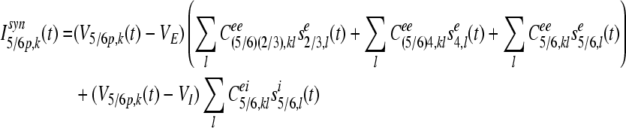17

Finally, the synaptic input current, I^syn_6i,k of the kth inhibitory neuron in layer 6 is composed of lateral excitatory inputs from neighboring pyramidal neurons and lateral inhibitory inputs from neighboring inhibitory neurons:

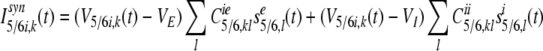18

The excitatory and inhibitory presynaptic outputs in Eqs. (13–18) satisfy first order Eqs. of (19) and (20), respectively:

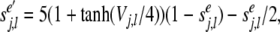19

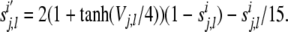20

where j refers to the layer, and l to the presynaptic neuron. V_j,l corresponds to the membrane potential of presynaptic neuron l in layer j.

Computer simulation, result analysis and comparison with experimental results

Computer simulations of the model are carried out in Visual C++ 6.0 environment. The values of network parameters in an idle state are given in Tables 1 and 2. In our simulations, the top-down modulation radius R_modu is taken as 0.6 mm, which is larger than the lateral excitatory connection radius of 0.5 mm, in each layer. In addition, each neuron of the network receives an internal background noise input current. The background current to each excitatory neuron is given by a random number between 0 and 10 (μA), and the corresponding background current to each inhibitory neuron is given by a random number between 0 and 3 (μA). The differential equations given in section "Methods" are solved by a forward Euler method, with time step 0.1 ms. In each case, the total simulation time is 1 s.

Table 1.

Parameters of network connection structure and strength in layers

	geej (mS)	giej (mS)	geij (mS)	giij (mS)	Reej (mm)	Riej (mm)	Reij (mm)	Riij (mm)
Layer 2/3	0.25	1.0	0.3	0.15	0.5	0.5	1.0	1.0
Layer 4	0.25	1.0	0.3	0.15	0.5	0.5	1.0	1.0
Layer 6	0.25	1.0	0.3	0.15	0.5	0.5	1.0	1.0

Table 2.

Parameters of feedforward and feedback connection strength between layers

	geeij (mS)	Ree j(mm)
Layer 4 to layer 2/3	0.3	0.5
Layer 5/6 to layer 2/3	0.15	0
Layer 2/3 to layer 4	0.15	0
Layer 5/6 to layer 4	0.2	0.5
Layer 2/3 to layer 5/6	0.15	0.5
Layer 4 to layer 5/6	0.15	0.5

To mimic the situation in the visual attention experiment in Fries et al. (2001), in each layer, we have groups of “attended-in” neurons (where attention is directed to a stimulus location inside the receptive field (RF) of these neurons) and groups of “attended-out” neurons (where attention is directed to a stimulus location outside the RF these neurons), as shown in Fig. 3. During a stimulus period, two identical stimuli are presented; one appears at a location inside the RF of the attended-in group and the other appears at a location inside the RF of the attended-out group.

Fig. 3.

A schematic diagram of the locations of ‘attended-in’ and ‘attended-out’ groups in each layer

To analyze the simulation results of spike trains, and compare with experimental results (Fries et al. 2001), we calculate power spectra of spike triggered averages (STAs) of the local field potential (LFP), representing the oscillatory synchronization between spikes and LFP. Since the initial stage for each simulation is unstable, the first 0.1 s of the simulation results are discarded before analysis. The analysis is performed in a Matlab 7.1 environment. The LFP for each excitatory neuron in the attended-in and attended-out groups is estimated as the sum of excitatory inputs to this neuron, including the inputs from neighboring neurons in the same layer, and from neurons in the other layers. The LFP is filtered by a Butterworth filter of order 2 with a cutoff at 200 Hz. The spike time of a neuron is calculated as the time when the membrane potential crosses −20 mV from below. STA of a neuron is computed as the sum of the 241 ms LFP centered in each spike time, divided by the number of spikes of that neuron. The STAs of the attended-in group or attended-out group are computed as the sum of the STAs of all the neurons in that group, divided by the number of neurons (in that group). The STAs are first detrended before the power spectra are computed. We investigate the dynamics and the effects of attention (cholinergic modulation) in an idle state, during a delay period, and during stimulation, as described in more detail in the following sub-sections.

Network dynamics in an idle state

The results of our model simulations in an idle state, only using background random inputs to the neurons, are shown in Fig. 4. In Fig. 4A, a raster graph shows the spiking activities of 5 × 5 pyramidal neurons (out of 20 × 20 total) in layer 2/3. Fig. 4B shows the corresponding STA power spectra of the attended-in and attended-out groups in the superficial layer 2/3 during the idle period, when no attention modulation is applied. Figure 4 implies that low frequencies in 16∼22 Hz of the beta band are the dominant frequencies of the network neurons. Fig. 4B indicates that the oscillatory synchronization in this band is also quite strong. These results agree with the experimental findings that power spectra are dominated by frequencies around 17 Hz in idle states (Fries et al. 2001).

Fig. 4.

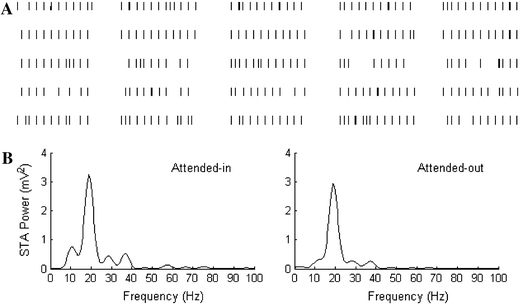
Raster graph of spikes of 25 pyramidal neurons (A) and STA power of attended-in and attended-out group measured in superficial layer during idle period (B)

Attention effects during a delay period

When attention is directed to a certain place, the prefrontal lobe sends top-down cholinergic input signals via top-down pathways to layers 2/3 and 5/6 of the visual cortex, as shown in Fig. 1. To test various experimental hypotheses about the mechanisms of attention modulation on individual neurons and network connections, we assume that the top-down signals may have three different effects on the pyramidal neurons and on the local and global network connections in our simulations. One effect is to facilitate extracortical top-down excitatory synaptic inputs to the pyramidal neurons (global connections). Another effect is to inhibit certain intracortical excitatory and inhibitory synaptic conductances (local connections), as discussed in Kuczewski et al. (2005) and in Korchounov et al. (2005). A third effect is to modulate the slow AHP current by decreasing the K conductance, g_AHP, thus increasing the excitability, as discussed by Börgers et al. (2005).

We simulated the cholinergic modulation effect of inhibiting the intracortical excitatory and inhibitory synaptic inputs, by decreasing the lateral excitatory and inhibitory conductances to zero (i.e. g^ee_j = 0 mS and g^ei_j = 0 mS) for the pyramidal neurons in the attended-in group, within 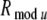in layers 2/3 and 5/6. The background random input currents to each excitatory and inhibitory neuron are the same as in section "Network dynamics in an idle state". The spikes of one pyramidal neuron in the attended-in group and of one pyramidal neuron in the attended-out group are shown in the second row of Fig. 5A. The computed LFP, STA and STA power of attended-in and attended-out neurons in layer 2/3 are also illustrated in Fig. 5A. Comparing Fig. 4B with the bottom panel of Fig. 5A, one can see that the dominant frequency of the oscillatory synchronization and its STA power in the attended-in group decreased by inhibition of the intracortical synaptic inputs. This result agrees qualitatively with experimental findings that low-frequency synchronization is reduced during attention.

Fig. 5.

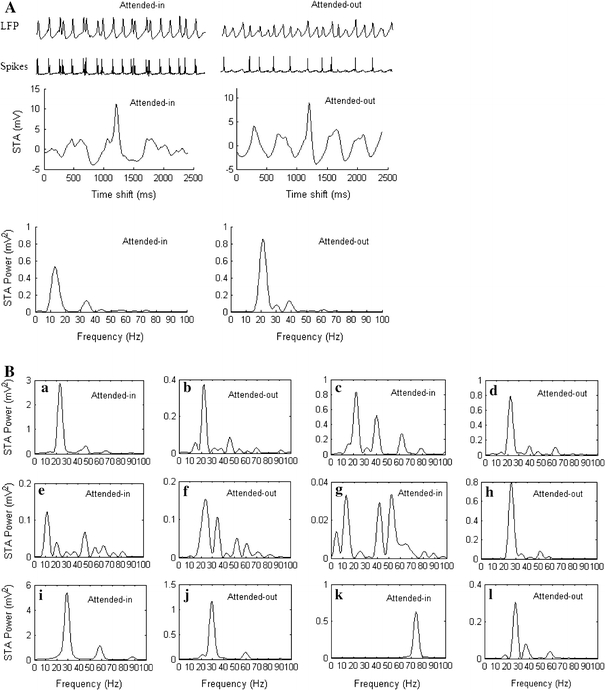
Cholinergic modulation effects during a delay period. (A) LFP, spikes, STA and STA power of attended-in and attended-out groups, calculated for the superficial layer, when the excitatory connections and inhibitory connections to each pyramidal neuron in the attended-in group within 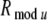in layer 2/3 and layer 5/6 are reduced to zero, g^ee_j = 0 mS   g^ei_j = 0 mS. (B) STA power spectra of attended-in and attended-out groups calculated for the superficial layer under different modulation conditions. Note the different scales in the y axes, and see text for further details

In Fig. 5B, we present simulation results of the cholinergic effect of facilitating the extracortical top-down excitatory synaptic inputs, and of decreasing the K conductance, g_AHP, as well as different combinations of these effects. The STA power spectra are calculated for attended-in and attended-out groups in the superficial layer 2/3. In all the frames (a) to (l) in Fig. 5B, the attention top-down modulations are applied to the pyramidal neurons, or to connections to the pyramidal neurons in the attended-in group and around this group within radius 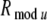in layers 2/3 and 5/6. In (a) and (b), a 5 μA top-down modulating input current is applied. In (c) and (d), the conductance, g_AHP = 0 mS. In (e) and (f), a 5 μA modulating input current is applied, while g^ee_j = 0 mS and g^ei_j = 0 mS. In (g) and (h), the conductances, g_AHP = 0.5 mS, g^ee_j = 0 mS, and g^ei_j = 0 mS. In (i) and (j), a 5 μA top-down modulating input current is applied, while g_AHP = 0 mS. In (k) and (l), a 5 μA modulating input current is applied, while g_AHP = 0.5 mS, g^ee_j = 0 mS, and g^ei_j = 0 mS.

The results shown in Fig. 5B demonstrate that the top-down cholinergic effects on individual neurons and on the local and global network connections are quite different. The cholinergic effect of facilitating global extracortical connections results in a slight shift of the dominant frequency in the STA power spectrum to higher beta, in both the attended-in and the attended-out groups. In particular, the higher beta synchronization of the attended-in group of frame (a) is much stronger than that of the attended-out group of frame (b). (Note the different scales along the y axis).

The cholinergic effect of decreasing the K conductance, g_AHP, of individual pyramidal neurons also leads to a slight shift of the dominant frequency in the STA power spectrum to higher beta, in both the attended-in and the attended-out groups. However, the beta synchronization of both attended-in and attended-out group is almost equally strong. What differs is that two peaks around 40 Hz and 60 Hz in the gamma band of the STA power spectrum of the attended-in group (frame (c)) are higher than those of the attended-out group (frame (d)).

The cholinergic effect of both facilitating extracortical connections and inhibiting intracortical connections results in that the beta synchronization around 19 Hz is reduced in the attended-in group (frame (e)), relative to the attended-out group (frame (f)), and a peak around 11 Hz (lower beta) appears in the attended-in group. In addition, some peaks of the STA power spectrum in the lower and higher gamma appear in both groups.

The cholinergic effect of inhibiting intracortical connections, while at the same time decreasing the K conductance, g_AHP, results in reducing the beta synchronization around 19 Hz in the attended-in group, relative to the attended-out group, and clear peaks of the STA power spectrum in the lower beta and the gamma bands appear in the attended-in group (frame (g)). In addition, the dominant frequency of the STA power spectrum in the attended-out group is slightly shifted to higher beta (frame (h)).

However, the cholinergic effect of facilitating extracortical connections and on decreasing the K conductance, g_AHP, leads to a shift of the dominant frequency in the STA power spectrum of both the attended-in and the attended-out groups to higher beta and lower gamma range, while enhancing the dominant STA power in the attended-in group (frame (i)), relative to the attended-out group (frame (j)).

Finally, the cholinergic effect of facilitating extracortical connections and of inhibiting intracortical connections in combination with decreasing the K conductance, g_AHP, results in the disappearance of the beta synchronization. At the same time, gamma synchronization around 70–80 Hz appears in the attended-in group (frame (k)), and the beta synchronization shifted to higher beta in the attended-out group (frame (l)).

Attention effects during a stimulus period

To simulate the dynamics during a stimulus period, (apart from the background random input currents to all neurons), we apply bottom-up sensory stimulation currents. The bottom-up sensory stimulation inputs are separated into one stronger current of 25 μA, and one weaker current of 5 μA. The stronger current is directly applied to layer 4 stellate neurons in both the attended-in and the attended-out groups. The weaker current is applied to layer 5/6 pyramidal neurons in both the attended-in and the attended-out groups. In addition, top-down attention modulation is applied to the system.

As in the delay period (see section "Attention effects during a delay period"), we first investigated the cholinergic modulation effect of inhibiting the intracortical excitatory and inhibitory synaptic inputs, by decreasing to zero the lateral excitatory and inhibitory connection strengths to the pyramidal neurons, g^ee_j = 0 mS and g^ei_j = 0 mS, in the attended-in group, within radius 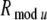in layers 2/3 and 5/6. Fig. 6A shows the simulated spikes of one pyramidal neuron in the attended-in group and of one pyramidal neuron in the attended-out group in layer 2/3, as well as the LFP, STA and STA power of the attended-in group and the attended-out group in the superficial layer 2/3. In comparison with Fig. 5A, the dominant frequency of the STA power spectrum of both the attended-in and the attended-out groups in Fig. 6A shifts to gamma band, due to the stimulation inputs. The STA power of the dominant frequency of the attended-in group is higher than that of the attended-out group. This result agrees with the experimental findings that gamma synchronization increases in the attended-in group during a stimulus period.

Fig. 6.

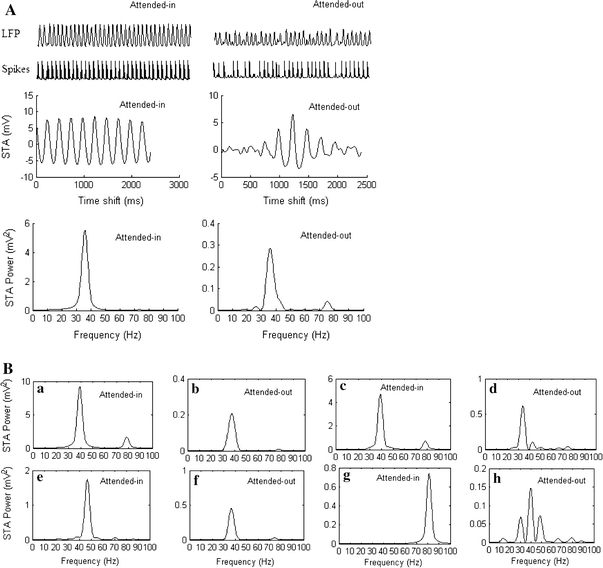
Cholinergic modulation effects during a stimulus period. (A) LFP, spikes, STA and STA power of attended-in and attended-out group calculated for the superficial layer, when the excitatory connections and inhibitory connections to each pyramidal neuron in the attended-in group within 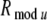in layer 2/3 and layer 5/6 are reduced to zero, g^ee_j = 0 mS   g^ei_j = 0 mS. (B) STA power spectra of attended-in and attended-out groups calculated for the superficial layer under different modulation conditions. Note the different scales in the y axes, and see text for further details

In order to study different top-down cholinergic effects during a stimulus period, we simulated the cholinergic effects of facilitating extracortical top-down excitatory synaptic inputs, and of decreasing the K conductance, g_AHP, as well as different combinations of these effects. The STA power spectra of attended-in and attended-out groups, calculated in the superficial layer, are shown in Fig. 6B. In all the frames of Fig. 6B, top-down modulations are applied to the pyramidal neurons or connections to the pyramidal neurons in the attended-in group, and around this group within radius 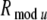in layers 2/3 and 5/6. In (a) and (b), g_AHP = 0 mS. In (c) and (d), a 5 μA top-down modulating input current is applied. In (e) and (f), a 5 μA modulating input current is applied, while g^ee_j = 0 mS and g^ei_j = 0 mS. In (g) and (h), a 5 μA modulating input current is applied, while g_AHP = 0.5 mS, g^ee_j = 0 mS, and g^ei_j = 0 mS.

The results shown in Fig. 6B demonstrate that the dominant frequencies shift to gamma band, and that gamma synchronization in the attended-in group is stronger than that in the attended-out group, in all cases. However, the exact dominant frequencies in the gamma range can be different and the relative strength of the STA power of the attended-in group and the attended-out group can also differ for different modulation situations. In particular, in frames (e), (f), (g), and (h) of Fig. 6B, the dominant frequencies of the STA power spectrum of the attended-in group shift to high gamma, while those in the attended-out group shift to low gamma. In all of the cases, the beta synchronization disappeared.

Discussion

In this paper, we have presented a three layer dynamical neural network model of the visual cortex V4 for investigating attention-modulated synchronization effects. The model includes bottom-up sensory input pathways, top-down cholinergic attention modulation pathways, local ascending and descending circuits between layers, as well as lateral connections within each layer. We base our network structure and connections on anatomical and physiological data. The neurons are modeled with Hodgkin–Huxley type equations, describing realistic spiking activities of various neuron types in different layers.

The simulation results of our model show (1) beta synchronization in an idle state, (2) reduced beta synchronization with attention during a delay period (under certain modulation situations), and (3) enhanced gamma synchronization, due to attention during a stimulus period. These results agree to a great extent with experimental findings (Fries et al. 2001). In particular, our simulation and analysis results demonstrate the effects of different cholinergic modulation mechanisms. However, the lower beta synchronization during a stimulus period, as described in Fries et al. (2001), disappears in our model simulations, where we only found gamma synchronization during such a period.

Our model simulations show that many factors play important roles in the network neurodynamics. These include (1) the interplay between ion channel dynamics and neuromodulation at a micro-scale, (2) the lateral connection patterns within each layer, (3) the feedforward and feedback connections between different layers at a meso-scale, and (4) the top-down and bottom-up circuitries at a macro-scale. The interaction between the top-down attention modulation, and the lateral short distance excitatory and long range inhibitory interactions, all contribute to the beta synchronization decrease during the delay period, and to the gamma synchronization enhancement during the stimulation period in the attended-in group. The top-down cholinergic modulation tends to enhance the excitability of the attended-in group neurons, whereas the Mexican hat shape lateral interactions mediate the competition between attended-in and attended-out groups.

The different cholinergic modulation mechanisms that we have investigated with our model suggest new experiments to test these mechanisms more precisely and quantitatively. The absence of beta synchronization during stimulation in our model simulations could be explained by the higher area networks, and that extracortical synaptic connections between higher area networks and the local V4 network are not included in our model. We have just used extracortical input currents to represent these interactions.

In conclusion, we consider this kind of computational approach as an essential complement to integrating various experimental findings and hypotheses in understanding the inter-relation between structure, dynamics and function of the brain and its cognitive and conscious activity. We hope the current paper can serve as a small step towards a more complete understanding that eventually will emerge from integrative neuroscience.