Dipole tensor-based atomic-resolution structure determination of a nanocrystalline protein by solid-state NMR

Abstract

Magic-angle spinning (MAS) solid-state NMR (SSNMR) techniques have emerged in recent years for solving complete structures of uniformly labeled proteins lacking macroscopic order. Strategies used thus far have relied primarily on semiquantitative distance restraints, analogous to the nuclear Overhauser effect (NOE) routinely used in solution NMR. Here, we present a complementary approach for using relative orientations of molecular fragments, determined from dipolar line shapes. Whereas SSNMR distance restraints typically have an uncertainty of ≈1 Å, the tensor-based experiments report on relative vector (pseudobond) angles with precision of a few degrees. By using 3D techniques of this type, vector angle (VEAN) restraints were determined for the majority of the 56-residue B1 immunoglobulin binding domain of protein G [protein GB1 (a total of 47 HN-HN, 49 HN-HC, and 12 HA-HB restraints)]. By using distance restraints alone in the structure calculations, the overall backbone root-mean-square deviation (bbRMSD) was 1.01 ± 0.13 Å (1.52 ± 0.12 Å for all heavy atoms), which improved to 0.49 ± 0.05 Å (1.19 ± 0.07 Å) on the addition of empirical chemical shift [torsion angle likelihood obtained from shift and sequence similarity (TALOS)] restraints. VEAN restraints further improved the ensemble to 0.31 ± 0.06 Å bbRMSD (1.06 ± 0.07 Å); relative to the structure with distances alone, most of the improvement remained (bbRMSD 0.64 ± 0.09 Å; 1.29 ± 0.07 Å) when TALOS restraints were removed before refinement. These results represent significant progress toward atomic-resolution protein structure determination by SSNMR, capabilities that can be applied to a large range of membrane proteins and fibrils, which are often not amenable to solution NMR or x-ray crystallography.

Structural studies of proteins by solid-state NMR (SSNMR) have progressed rapidly in recent years, with the introduction of multidimensional methods and uniform isotopic labeling for site-specific chemical shift assignments (1). Combined with distance estimation methods, these restraints have yielded 3D protein structures (2–4), albeit at relatively low resolution compared with x-ray crystallography and solution NMR. To leverage the unique potential of SSNMR to solve membrane protein and fibril structures (5–8) at atomic resolution therefore requires further advances in SSNMR structure methods. Over the past decade, improved structural resolution in solution NMR has come from the development of residual dipolar coupling (RDC) methodologies (9, 10). The RDC approach requires partial alignment of the protein, and has conceptual similarities to SSNMR techniques such as polarization inversion with spin exchange at the magic angle (PISEMA) (11), where lipid bilayer samples containing membrane proteins are fully macroscopically aligned. In both approaches, performing NMR experiments with sample alignment requires a compromise between the optimal spectral resolution observed in the isotropic limit and the rich structural information found in aligned samples. For RDC measurements, the degree of alignment is typically ≈0.1% to ≈1.0%, resulting in RDC values of a few hertz while retaining high-resolution spectra. In PISEMA experiments, nearly complete alignment is achieved, either mechanically or magnetically, yielding large-amplitude (kHz) dipolar couplings at the expense of broad linewidths because of the anisotropic chemical shift.

In magic-angle spinning (MAS) SSNMR, both the high-resolution isotropic chemical shifts and the complete tensor properties can be obtained under a single experimental condition. Correlations between these two types of interactions are derived from multiple-pulse recoupling methods, which have been of prime historical importance to SSNMR (12), and we have recently applied several of these classic methods to uniformly labeled proteins to measure relative orientation restraints (13–15). MAS SSNMR methods at high field (≈500 to 900 MHz ¹H frequencies) offer an attractive combination of site resolution and atomic-resolution structural information. This combined approach has been demonstrated on a tripeptide (16) and several dihedral angles have been measured in a study of the protein SH3 (17). Yet the systematic application of these methods in a protein to improve structure quality has remained an outstanding problem.

Here, we demonstrate the combination of vector angle (VEAN) angle restraints with internuclear distance estimations and empirical chemical shift restraints to solve the high-resolution structure of the B1 Ig binding domain of protein G (GB1). Spectra of nanocrystalline GB1 are sufficiently well resolved to yield correlated isotropic chemical shifts and dipolar line shapes throughout the majority of the protein, enabling a systematic analysis of the impact such restraints have on structure quality. The results bode well for efforts to determine structures of macroscopically disordered proteins with a resolution comparable to x-ray diffraction and high-resolution solution NMR methods.

Results

Determination of Global Structural Fold of Nanocrystalline GB1.

Chemical shift assignments were performed with GB1 samples uniformly ¹³C,¹⁵N- and ¹⁵N-labeled, respectively (samples A and B; Table 1) (15, 18). An initial set of distance restraints was obtained from 2D ¹³C- and ¹⁵N-resolved ¹H–¹H correlation spectra (3) of a third, isotopically diluted sample (sample C; supporting information (SI) Fig. 6). The dilution minimized intermolecular couplings and thereby enabled the determination of a first low-resolution fold from the SSNMR data alone (3, 19, 20). Sequential correlations (between residues i and i ± 1) were identified first, followed by unambiguous medium (between residues i and j, where | i − j | < 5) and long-range (| i − j | > 4) restraints. A total of 641 restraints (374 intraresidue, 182 sequential, 40 medium-range, and 45 long-range) were used in initial rounds of distance geometry and simulated annealing calculations with X-PLOR-NIH (21, 22), resulting in a low-resolution fold (≈2.0 Å bbRMSD). This family of 10 structures improved slightly (to ≈1.5 Å) on addition of TALOS (23) dihedral angle restraints. We used this ensemble to assign additional, previously ambiguous cross-peaks in the ¹H–¹H datasets and to identify correlations arising from intermolecular contacts, which were excluded from subsequent rounds of calculations. This logic was applied iteratively to arrive at a self-consistent solution, as with previously developed protocols applied to SSNMR proteins (2–4, 24).

Table 1.

Isotopic labeling of GB1 samples prepared for this study

Sample	Isotopic labeling condition
A	Uniform-13C, 15N-enriched*
B	Uniform 15N†
C	1:4 ratio of uniform-13C,15N-labeled in natural abundance‡
D	Prepared from 1,3-13C-glycerol and 15NH4Cl§
E	Prepared from 2-13C-glycerol and 15NH4Cl¶

*Expressed with ¹³C glucose and ¹⁵NH₄Cl.

^†Expressed with natural abundance glucose and ¹⁵NH₄Cl.

^‡One part uniformly ¹³C,¹⁵N-labeled GB1 was diluted in four parts natural abundance GB1 prior to precipitation by the standard protocol.

^§Expressed with 1,3-¹³C-glycerol and natural abundance Na₂CO₃ as the sole carbon sources in the growth medium and ¹⁵NH₄Cl.

^¶Expressed with 2-¹³C-glycerol and Na₂¹³CO₃ as the sole carbon sources and ¹⁵NH₄Cl.

Next, samples prepared with 1,3-¹³C- (sample D) or 2-¹³C-glycerol (sample E) (2) were examined at 750 MHz ¹H frequency. Two-dimensional ¹³C–¹³C dipolar-assisted rotational resonance (DARR) (25) spectra (Fig. 1 and SI Figs. 7, 8, and 9) provided a more complete set of homonuclear distance restraints. Spectra acquired with short mixing times (50 and 100 ms) served two purposes. First, peak positions were identified with high precision (±0.1 ppm or better). Although the chemical shift values agreed with our previous report (18), the improved digital resolution here necessitated confirming peak positions more precisely on each sample; for example, some small but systematic changes (0.05–0.20 ppm) arose from the reduction of near-rotational resonance broadening or shifts (26) in the glycerol-derived samples. Second, the short mixing-time spectra accurately reported on the relative ¹³C-labeling efficiency in the glycerol growth media. The labeling patterns closely resembled those reported (2), with relatively minor variations in the absolute intensity among amino acid types derived from the citric acid cycle. Insights into the labeling patterns simplified assignment of the longer mixing time datasets.

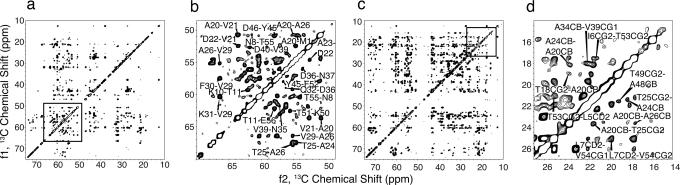
Fig. 1.

2D ¹³C–¹³C correlation spectra of sparsely ¹³C-labeled samples of GB1, 750 MHz ¹H frequency, 300 ms longitudinal DARR mixing, 12.5 kHz MAS rate. (a) Aliphatic region, sample E. (b) Expansion of the near-diagonal CA region (sample E), illustrating medium and long-range CA[i]-CA[j] correlations. (c) Aliphatic region, sample D. (d) Expansion of the methyl region (sample D). Detailed acquisition and processing parameters are described in SI Figs. 7–9. Peak intensities are interpreted semiempirically in terms of internuclear distances.

Several hundred unambiguous assignments were made from uniquely resolved peaks and/or correlations that could arise from only one pair of atoms within <12 Å (as determined from the initial structures). As required, 3D ¹⁵N–¹³C–¹³C experiments provided additional resolution (24). Overall we assigned 4,002 intraresidue, 1,987 sequential, 425 medium-range, and 711 long-range correlations, representing a total of 888 unique distance restraints. Among the assigned peaks, aromatic residues (especially Tyr CZ, Phe CG, and several Trp resonances resolved in the 1D ¹³C spectrum) proved especially valuable for defining the hydrophobic core, and methyl signals provided a significant number of long-range correlations. In cases where unique assignments could not be made, restraints were explicitly modeled as ambiguous; such sites included the aromatic rings (Phe CD, CE and CZ, and Tyr CD and CE) and the prochiral methyls (Val CG and Leu CD).

Maximum allowed distances in the simulated annealing protocol were assigned to each restraint based both on the mixing time and the intensity of the resonance (Table 2). In analogy with NOE analysis (27), peak intensities in each spectrum were sorted into strong, medium, and weak categories by comparison with resolved cross-peaks with known (≈100%) labeling patterns and distances. The distance ranges were determined by a simple calibration procedure by using the short-mixing-time datasets. For example, in sample D the C′-CB distance in Ala residues is ≈2.48 Å and both sites are ≈100% labeled, as are the CA and CG nuclei of aromatic residues in sample E. Similarly, for ¹⁵N–¹⁵N distance restraints (SI Fig. 10), the interresidue correlations from helical residues in the PDSD spectra were used. The average intensity of each cross-peak type (with a 20% uncertainty) was used to establish the threshold intensity for the strong peaks. Medium and weak peaks were assigned to distance restraints, assuming polarization transfer occurred in the initial rate regime (i.e., linear with respect to time) with 1/r⁶ dependence. This assumption proved valid in classifying the fully labeled CA[i]–CA[i ± 1] pairs, which have a distance (3.8 Å), independent of secondary structure, into the expected distance range. Correlations involving nuclei with fractional labeling were weaker, and therefore were typically classified into larger maximum distance ranges, a safe assumption because no minimum distance range (other than the van der Waals limit) was specified.

Table 2.

Maximum distances^* used in the calculation of GB1 structures

tmix,† ms	Strong,‡ Å	Medium,§ Å	Weak,¶ Å
50	3.3	4.5	5.6
100	4.5	5.1	6.3
200	4.8	5.7	7.0
300	5.3	6.1	7.5
400	5.5	6.4	7.9
500	5.8	6.7	8.2

*A harmonic square well potential with boundaries defined from a minimum of 1 Å to the maximum distance listed here. The energy is defined to be zero within the boundaries, and increases as a harmonic potential outside the specified range by using the scaling factor of 25 kcal within XPLOR-NIH.

^†DARR mixing with a proton irradiation (B₁) field equivalent to the spin rate was utilized.

^‡Peaks with an integrated intensity ≥80% of the calibrated peak intensity, determined as the average of several peaks corresponding to 2.48-Å distances in the spectrum with 50 ms mixing.

^§Peaks with an integrated intensity >20% of the calibrated peak intensity used to define strong peaks.

^¶All other peaks above the noise threshold, not previously classified as strong or medium.

The refined structures based on these distance estimations alone rapidly reached a plateau of ≈1.0 Å bbRMSD (Fig. 2). Further attempts to improve the structure based on the available distance restraint data were unsuccessful; significantly increasing the distance ranges resulted in poorly defined structures, whereas decreasing the ranges resulted in an unacceptably large number of violations, physically unreasonable folds and very high computed structural energies. Overall, this ensemble of structures, as determined with distance restraints alone, had a reasonably accurate fold [based on comparison with previous crystal (15, 28) and NMR structures of GB1 (29); a complete analysis is included in SI Text] but poor definition of backbone dihedral angles.

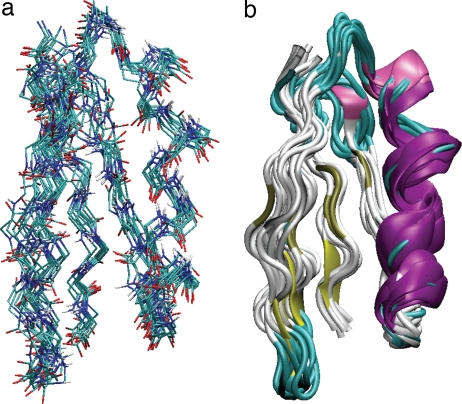
Fig. 2.

Ensemble of the 10 lowest energy structures of GB1, calculated from a total of 7,826 ¹³C–¹³C, ¹⁵N–¹⁵N, and ¹H–¹H distance restraints. The bbRMSD for all residues is 1.01 ± 0.13 Å, and the heavy atom RMSD is 1.52 ± 0.12 Å. (a) Line representation including all backbone carbon (cyan), amide nitrogen (blue), amide proton (white) and carbonyl oxygen (red) atoms. (b) Diagram representation indicating ordered secondary structure elements (helix in purple, strands in yellow, turns in cyan, coil in white).

Refinement with Angular Restraints.

We next investigated the extent to which the structure could be improved by using two types of angular restraints. As investigated (4, 24, 30), empirical chemical shift databases such as TALOS, which were originally developed for solution NMR, generally produce reliable results for solid proteins also; this is a consequence of the good agreement between solution and solid-state isotropic chemical shifts. For GB1, the C′, CA, and CB chemical shifts that are most essential for TALOS show the best agreement (23). TALOS solutions for amino acid residues in regular secondary structures agreed consistently well with the ensembles of structures, although glycine residues and less common conformations (such as the positive φ value for K50) were poorly defined, as reflected in the number of inconsistent solutions found in the TALOS database and the frequency of violations in the computed structures (SI Table 5). With TALOS refinement, the bbRMSD improved to 0.49 ± 0.05 Å.

We next incorporated data from experiments to define the relative orientation of ¹H–¹⁵N and ¹H–¹³C dipolar vectors. Two sets of data were acquired and used. In the first set (15), ¹H–¹⁵N dipolar vectors of neighboring residues were correlated by using a synchronously evolved heteronuclear recoupling sequence [T-MREV (31)], with ¹⁵N–¹⁵N correlations established with PDSD mixing (32). In the second experiment, ¹H–¹⁵N and ¹H–¹³C dipolar vector orientations were determined by a 3D dipolar-shift experiment (33). The site-resolved dipolar-shift spectra were acquired and interpreted as previously described (Fig. 3, SI Fig. 11, SI Text) (15, 33, 34). The line-shape features depend on relative orientation of the dipolar tensors, which can be modeled to better than a few degrees precision in many cases; however, interpretation of these angles in terms of molecular structure requires explicit consideration of several sources of geometrical degeneracy. First, the mirror plane symmetry (a fundamental property of the dipolar coupling) prevents the values θ and 180 − θ from being uniquely distinguished. Second, the functional form for θ depends on multiple backbone dihedral angles; for example, the VEAN relating ¹H–¹⁵N[i] to ¹H–¹⁵N[i + 1] angle is a function of φ[i], ψ[i], and ω [i], which has multiple solutions (15, 34). Finally, the relationship of the dipole vector angle to molecular structure depends on all intervening bond angles and bond lengths, peptide planarity, and amide proton deviation from the peptide plane (35). Therefore, rather than assuming fixed values for all of these parameters, the VEAN was incorporated directly into the simulated annealing algorithm by using the VEAN force field (36). Convergence of calculations including all three types of structural restraints (with simulated annealing for >20 ps) resulted in very good agreement with all restraints (SI Table 7). The final refinement yielded a family of 10 structures with a bbRMSD 0.31 ± 0.06 Å (1.06 ± 0.07 Å heavy atom RMSD) (Fig. 4 and SI Fig. 12) and high structure quality as judged by standard metrics (see SI Text).

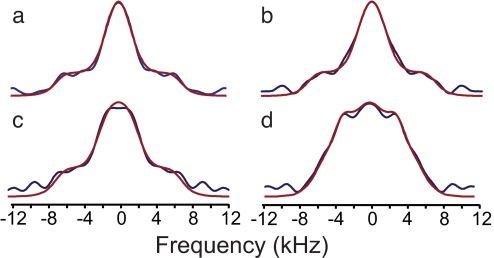
Fig. 3.

Dipolar line shapes from 3D dipolar-shift correlation spectra of GB1, used to derive vector angle (VEAN) restraints. Experimental HN-HACA line shapes (blue) were fit to simulations of the spin dynamics (red), as a function of the relative orientation of the two ¹H-X dipole vectors. The best-fit values for the VEANs are θ = 14.0° ± 2.0° for T51 (a); θ = 21.2° ± 3.1° for V39 (b); θ = 19.5° ± 2.1° for T49 (c); and θ = 42.0° ± 6.3° for V29 (d). Standard errors are determined by Monte Carlo analysis.

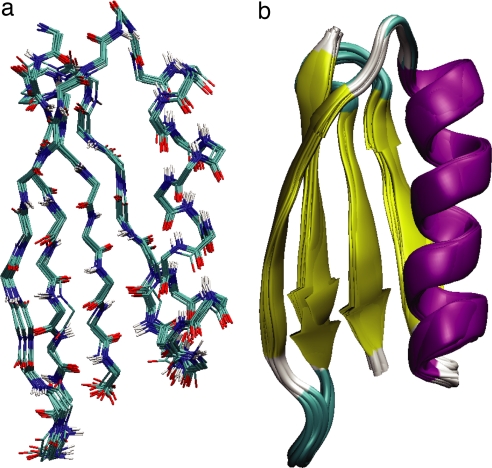
Fig. 4.

Ensemble of 10 GB1 structures determined from distance, TALOS (chemical shift), and VEAN restraints (bbRMSD 0.31 ± 0.06 Å, heavy atom RMSD 1.06 ± 0.07 Å). (a) Line representation; (b) diagram representation. Color coding is identical to Fig. 2.

Structure Analysis and Validation.

The structure quality was evaluated in three ways. First, comparison to the closest related crystal structure (37) (PDB entry 2QMT) yields a bbRMSD of 1.43 ± 0.05 Å (Fig. 5, Table 3, and SI Fig. 13). In all cases, the agreement improves on addition of TALOS or VEAN restraints relative to the structure with distances alone. Second, we compared VEAN distributions in the final structures to the input restraints (SI Figs. 14 and 15). With only distance data, 46 of 108 restraints were satisfied, with a large mean difference of 13.1° and scatter (±13.5°). The addition of TALOS restraints improves agreement (76 of 108, with a mean±standard deviation difference 4.2 ± 6.8°), indicating that TALOS assists in convergence to the correct VEAN results. With the VEAN potential included, 103 of the 108 restraints agree with the average structure, with an average difference of 0.7 ± 1.2° (SI Text). Third, validation of standard peptide geometry was performed with the PROCHECK-COMP (38) suite (SI Text, SI Figs. 16 and 17, and SI Table 4). The addition of either TALOS or VEAN restraints ensured that ≈100% of residues were in most favored or allowed regions of Ramachandran space, in contrast to 76% when only distance restraints were used.

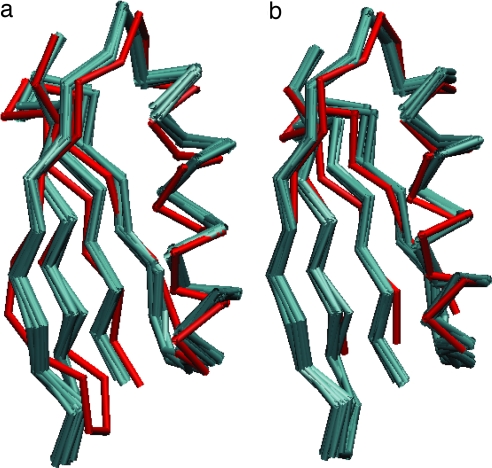
Fig. 5.

Structural alignment of high-resolution SSNMR ensemble (cyan) and the trigonal form crystal structure (2QMT; red). (a) With all residues aligned, the bbRMSD is 1.4 Å. (b) Alignment excluding residues 1, 9–14, and 39–41 (1.1 Å bbRMSD), demonstrating that residues in the β1-β2 turn and helix-β3 loop disrupt the relative positioning of helix and four-stranded β-sheet.

Table 3.

Summary of structure quality

DGSA*		Refinement*		RMSD†
DIHE‡	VEAN§	DIHE	VEAN	Backbone, Å	Heavy atom, Å	Backbone vs. 2QMT, Å	Backbone vs. 2GI9, Å
				1.01 ± 0.13	1.52 ± 0.12	2.20 ± 0.17	2.36 ± 0.16
X		X		0.49 ± 0.05	1.19 ± 0.07	1.32 ± 0.06	1.42 ± 0.08
X			X	0.61 ± 0.09	1.26 ± 0.12	1.57 ± 0.14	1.73 ± 0.14
	X		X	N/A	N/A	N/A	N/A
X	X			1.15 ± 0.09	1.71 ± 0.13	2.14 ± 0.27	2.32 ± 0.31
X	X		X	0.64 ± 0.09	1.29 ± 0.07	1.65 ± 0.19	1.85 ± 0.21
X	X	X	X	0.31 ± 0.06	1.06 ± 0.07	1.43 ± 0.05	1.59 ± 0.06
X	X	X		0.52 ± 0.06	1.18 ± 0.05	1.36 ± 0.08	1.46 ± 0.11

*Distance restraints were included in all calculations. Additional details are available in the SI Text.

^†RMSD is calculated for residues 1–55.

^‡X indicates the inclusion of TALOS dihedral restraints during the indicated period.

^§X indicates the inclusion of vector angle restraints during the indicated period. The calculations including only distance and VEAN restraints failed to converge.

Discussion

Three complete protein structures have previously been solved by multidimensional MAS SSNMR methods. The first study of an SH3 domain (2) reported a precision of 1.6 Å (bbRMSD) and accuracy of 2.6 Å (compared with the most closely related crystal structure); both the precision (0.7 Å) and accuracy (1.2 Å) improved on addition of distance restraints from 3D experiments and TALOS restraints (24). Similar quality structures were obtained for ubiquitin (4) and kaliotoxin (3), in both cases by using distance and TALOS restraints. In our calculations for GB1 with only distance restraints, we obtained a similar result (1.0 Å precision, 2.2 Å accuracy) (SI Figs. 12 and 13 and Table 3) despite substantially larger amounts of data. We attribute this to the fact that NMR structure quality typically is reported for regular secondary structure elements only; the proteins studied previously by SSNMR had significant numbers of residues that were missing in the spectra and therefore not uniquely constrained in the reported structures. For GB1, all backbone and side-chain resonances are observed, and our reported statistics include all residues, including termini, loops, and turns. The values may also differ among studies because of details such as the numbers of structures reported, the type of algorithms and potential functions used, and the duration of the simulated annealing calculations. Unfortunately, no protocols yet exist for evaluation of structure quality among different protein structures solved specifically by SSNMR.

Therefore, we focused subsequent effort on comparisons among GB1 structures calculated with different input data but otherwise identical computational methods (SI Figs. 12 and 13, SI Tables 7 and 8). This process clarified that the precision of ¹³C–¹³C distance estimation methods limited the overall structure quality; although the inherent uncertainty of ± 1 Å for ¹³C–¹³C distances quite reliably reports on long-range interactions (3, 20), this is not sufficient to distinguish among side-chain rotameric states or subtle differences in backbone conformation. Thus, structures calculated with only distance data did not improve beyond ≈1 Å precision, and increasing the number of restraints by an order of magnitude (from ≈500 to ≈7,000 restraints) only incrementally improved the result.

In contrast, ≈100 VEAN restraints greatly improved the structure quality, as realized by using the modified VEAN potential in X-PLOR (36). We found that it was essential to introduce this potential slowly during the high-temperature simulated-annealing, using annealing times of 20 to 90 ps (even so, ensembles of ≈250 structures could be readily calculated in a few hours). The calculations satisfied nearly all VEAN restraints within ±5°. The primary exceptions were mutually exclusive solutions, which may indicate significant variations from canonical bond angle geometry. Although we did not assume bond angles in the interpretation of the dipolar line shapes, X-PLOR assumes bond angles into its standard potential energy functions.

The VEAN restraints could be used to refine the GB1 structure even when TALOS dihedral restraints were removed in the final refinement. Although calculations with VEAN but no TALOS restraints failed to converge, even very conservative TALOS restraints (e.g., doubling all error estimations and removing any restraints with less than perfect agreement with the TALOS database) resulted in very good convergence in the initial phase of high-temperature annealing. Once the structure was properly folded and the backbone dihedrals were within the proper local minimum, the TALOS restraints could be removed and the structure retained high-precision throughout refinement by using only distance and VEAN data (SI Figs. 12c and 15; Table 3). Notably, if at this same stage the VEANs were removed, the structure quality reverted in the refinement stage to that observed with distance restraints alone (SI Fig. 14 and Table 3).

The accuracy of the refined structures also improved significantly, compared with the trigonal form crystal structure (2QMT). With distances alone, the SSNMR structure differed from the crystal structure by 2.2 Å, but the agreement improved to 1.4–1.7 Å with either TALOS restraints, VEAN restraints, or both (Fig. 5a). For the fully refined structure (including NOE, TALOS, and VEAN restraints), fragments of the protein showed even better agreement, with accuracy ranging from 0.4 to 0.6 Å when evaluating the helix alone or individual β-strands β1, β3, and β4. Excluding only the β1-β2 and β3-β4 turns resulted in a 1.0-Å alignment (Fig. 5b). Among the various GB1 crystal structures, the backbone variation is ≈0.5 Å, and our recent study of GB1 microcrystal polymorphs showed that the kinetically favored product in the batch scale preparation is trigonal, yet differs slightly from the single-crystal condition (37). Thus, for most of the protein, the agreement is within error identical to the crystal structure. The remaining discrepancies arise primarily from residues for which TALOS restraints are unavailable (such as glycines) and/or the VEAN restraints were unavailable or in insensitive regimes of the VEAN space (angles of >30°). Additional types of VEAN data such as NCCN (39, 40) and HCCN (41) experiments, as well as higher-precision distance measurements by TEDOR (42) and/or ¹H–¹H restraints (43) would likely address these remaining imperfections in the structure.

Conclusions

Here, we have taken a distinct approach to the problem of high-resolution protein structure determination by SSNMR by using relative dipole tensor orientation information systematically throughout a protein. The ensemble of structures determined with distance restraints alone had a good 1.01 ± 0.13 Å bbRMSD; however, the secondary structure elements were poorly defined, and the loops and turns were badly disordered. Inclusion of empirical chemical shift database restraints (23) improved the structure in the regular secondary structure elements, resulting in an overall 0.49 ± 0.05 Å RMSD, although the turn and glycine residues remained poorly defined. On refinement with VEAN restraints, the bbRMSD improved further to 0.31 ± 0.06 Å. Validation of geometrical parameters in the PRO-CHECK suite (38) also indicated a substantial improvement, a large fraction of which was retained even when the TALOS restraints were removed.

The application of this protocol to noncrystalline solid proteins such as fibrils and membrane proteins opens up new possibilities for atomic-resolution structure determination in context that are often inaccessible to crystallography and solution NMR.

Materials and Methods

Sample Preparation.

Samples of GB1 were prepared as hydrated, nanocrystalline precipitates for SSNMR analysis as described in ref. 18. Several different isotopic labeling schemes were used. Sample A was uniformly ¹³C,¹⁵N-labeled. Sample B was uniformly ¹⁵N-labeled. Sample C was prepared by diluting sample A in natural-abundance protein at a ratio of 1:4 before precipitation. Samples D and E were prepared with uniform ¹⁵N-labeling and fractional ¹³C by using 1,3-¹³C (sample D) or 2-¹³C-glycerol (sample E) as the primary ¹³C source in the respective media (2). Samples A–C were packed in standard 3.2-mm rotors with a 22-μl volume (Varian); samples D and E were packed in limited-speed 3.2-mm rotors with a 36-μl volume.

Solid-State NMR Spectroscopy.

MAS SSNMR experiments were performed at 500, 600, and 750 MHz ¹H frequencies on Varian InfinityPlus (500 and 600 MHz) and Unity Inova (750 MHz) spectrometers, using 3.2-mm Balun (500 MHz), T3 (600 MHz), and BioMAS (44) (750 MHz) probes. Chemical shift assignments were confirmed on all samples by comparison of NC, CC, and NN 2D spectra with those published (18). ¹³C- and ¹⁵N-resolved ¹H–¹H spin diffusion experiments (3) were performed by using sample C at 600 MHz. Two-dimensional CC and 3D NCC correlation spectra with DARR mixing times of 50 to 500 ms were performed with samples D and E at 750 MHz. NN proton-driven spin diffusion (32) and ¹H–¹⁵N dipolar-shift experiments to determine relative amide ¹H–¹⁵N orientations (34) were performed with sample B at 600 MHz. Additional dipolar-shift experiments relating the ¹H–¹⁵N to ¹H–¹³CA (33) were performed on sample A at 500 MHz. The temperature-control point was in all cases set to 0°C, yielding an actual experimental temperature of ≈8 ± 4°C for all experiments. Typical radiofrequency field strengths on ¹H were ≈100 kHz during ¹⁵N–¹³C recoupling periods, ≈70 kHz two-pulse phase modulation (TPPM) (45) during chemical shift evolution periods, and 75 kHz during cross-polarization (CP). As previously shown, tensor values for most backbone resonances are consistent within a few percent of the coupling expected in the rigid lattice limit (18), indicative of rigid protein backbone. High-power decoupling was facilitated by use of the BioMAS probe at high ¹H frequency, which minimized radiation damage to the samples while enabling long evolution and acquisition times (details provided in SI Figs. 7–9).

Structure Calculations.

X-PLOR-NIH version 2.16.0 was used for distance geometry and simulated annealing calculations (21, 22). For each set of experimental restraints, 250 structures were produced with distance geometry subembedding and annealed for 15 ps at 2,500 K, followed by cooling >25 ps to 1,000 K, and refinement with slow (70 ps) cooling from 1,000 to 300 K. The relative pseudoenergy scaling factors for distance (25 kcal) and dihedral angle (100 kcal) restraints were held constant, whereas the vector angle scaling (when used) was gradually increased from 30 to 60 kcal during the high-temperature annealing and from 60 to 90 kcal during refinement.