Population genomics of the wild yeast Saccharomyces paradoxus: Quantifying the life cycle

Abstract

Most microbes have complex life cycles with multiple modes of reproduction that differ in their effects on DNA sequence variation. Population genomic analyses can therefore be used to estimate the relative frequencies of these different modes in nature. The life cycle of the wild yeast Saccharomyces paradoxus is complex, including clonal reproduction, outcrossing, and two different modes of inbreeding. To quantify these different aspects we analyzed DNA sequence variation in the third chromosome among 20 isolates from two populations. Measures of mutational and recombinational diversity were used to make two independent estimates of the population size. In an obligately sexual population these values should be approximately equal. Instead there is a discrepancy of about three orders of magnitude between our two estimates of population size, indicating that S. paradoxus goes through a sexual cycle approximately once in every 1,000 asexual generations. Chromosome III also contains the mating type locus (MAT), which is the most outbred part in the entire genome, and by comparing recombinational diversity as a function of distance from MAT we estimate the frequency of matings to be ≈94% from within the same tetrad, 5% with a clonemate after switching the mating type, and 1% outcrossed. Our study illustrates the utility of population genomic data in quantifying life cycles.

Microbial life cycles are often difficult to study because the organisms involved are so small. Laboratory studies can reveal what a species is capable of doing, but give little information on the frequencies of different modes of reproduction in nature. Instead, we must look at patterns of DNA sequence variation to infer the reproductive system. Pioneered by studies in bacteria, genealogical analyses have been very fruitful in uncovering sex where sexual stages had not been seen, and cryptic species where only one taxon had been recorded (1–4). Quantifying the different aspects of the life cycle, however, has been difficult. Population genomic data now allow accurate measures of mutational and recombinational diversity, and theory predicts that these parameters can be used to estimate the frequencies of different modes of reproduction in the life cycle, including frequencies of sex, outcrossing, and various forms of inbreeding.

The bakers' yeast Saccharomyces cerevisiae has long been a model system in genetics and cell biology; more recently, together with its undomesticated relatives Saccharomyces paradoxus and Saccharomyces cariocanus, it is also becoming a focus of studies in ecology and evolution (5–7). Laboratory studies indicate that when conditions are good the primary mode of reproduction is vegetative budding of diploid cells. Starvation induces meiosis, each diploid cell producing a tetrad of haploid spores of two different mating types (a and α), enclosed within an ascus (8). When conditions improve, the spores germinate and are constitutively ready to mate and return to the diploid state. They can mate with another spore from the same tetrad, or they can be released from the ascus and mate with a spore from another tetrad, which may or may not be from the same diploid clone. It has recently been shown that release of spores from the ascus is facilitated by passage through the gut of an insect (9). If the haploid spores do not mate immediately, they are able to undergo mitoses, during which they repeatedly switch mating types, thus enabling matings between haploid clonemates (haplo-selfing or autodiploidization). This switch is possible because mating type is determined by a system of two cassettes, a and α, both present in the same individual, which alternately insert into the mating type locus (MAT) of chromosome III after being copied from their master loci, HML and HMR, near the two ends of the chromosome (8).

To determine the frequencies of these alternative modes of reproduction in nature, we studied the patterns of DNA sequence variation in two populations of S. paradoxus, from Europe and Far East Asia. Previous work has shown that these two populations are genealogically distinct and ≈1.4% divergent at the nucleotide level (10–12). Isolates from the same population, on the other hand, have well mixed genomes. Strains are readily isolated from the bark of oak trees (13), where both identical and different genotypes coexist as close as 5 cm on a tree (10). Heterozygosity is low, suggesting the species is highly inbred, but it is not known whether matings are predominantly within tetrads or by haplo-selfing (14). In this study, we analyzed sequence variation among 20 isolates for almost the entire third chromosome (≈280 kb; excluding telomeres and subtelomeres). The levels of mutational and recombinational diversity along the chromosome were then used to make two independent inferences of the (effective) population size. If the species was obligately sexual, and under certain assumptions (see Theory), these estimates should be approximately equal. Instead, we find a discrepancy of roughly three orders of magnitude between our two estimates of population size, in both populations, indicating that S. paradoxus goes through a sexual cycle approximately once in every 1,000 asexual generations. In addition, chromosome III contains the MAT locus, and by studying recombinational diversity as a function of distance from MAT we are able to estimate the ratio of intratetrad mating to haplo-selfing to be ≈19:1. To our knowledge, our data provide the most complete quantification of the life cycle yet achieved for any microbe to our knowledge.

Theory

We begin with a review of the relevant theory, which, although not new, will nevertheless aid the understanding of our estimation procedure. Sequence variability in populations is typically described by two parameters, one measuring the variation of nucleotides at the same site (θ) and the other the covariation of nucleotides at different sites (ρ). θ is typically estimated as the average pairwise divergence of sequences in a population (θ_π) or from the proportion of polymorphic or segregating sites (θ_S), whereas there are several different methods of estimating ρ (15, 16). In the standard neutral model (i.e., for sequences sampled randomly from a panmictic population of constant size and no selection), θ_π = θ_S = 4Nu and ρ = 4Nr, where N is the effective population size (of diploid individuals) and u and r are the rates of mutation and recombination per base pair per generation, respectively. That is, θ is twice the number of new mutations occurring at a nucleotide site in the whole population every generation, and ρ is twice the number of new recombination events. Thus the two parameters attempt to quantify the two principal sources of genetic diversity: mutation and recombination. Estimates of u and r can be obtained independently from laboratory observations, and therefore estimates of θ and ρ from population genomic survey data give two (mostly) independent measures of effective population size, N_θ and N_ρ (17, 18).

In populations that deviate from the standard neutral model, the above theoretical expectations may not hold, and some types of deviation will affect estimates of θ and ρ differentially. Three such deviations are important in this article. First, inbreeding has a much larger effect on ρ than on θ, because recombination has a detectable effect only when heterozygous sites are involved. Under inbreeding, the expected parameter values are θ = 4Nu/(1 + F) and ρ = 4Nr(1 − F), where F is Wright's inbreeding coefficient, a measure of deviation from Hardy–Weinberg proportions [F = 1 − H_obs/H_HW, where H_obs is the observed heterozygosity and H_HW is the Hardy–Weinberg expected heterozygosity; F = 0 for random mating and F = 1 for completely inbred populations (19, 20)]. Thus, for S. paradoxus, with F ≈0.98, (recalculated from ref. 14 after excluding identical genotypes; the two-unit support limits are 0.86 and 0.998), ρ is expected to be a 50th of what it would be in an outcrossed population, whereas θ is only reduced by a factor of ≈2. By using these latter equations to estimate N_θ and N_ρ, we take the differential effects of inbreeding into account. Second, selection should have a larger effect on θ than on ρ, because it has a direct effect on reducing nucleotide variation, whereas it is not expected to have such a direct effect on the covariation of nucleotides at different sites (at least in the absence of epistatic interactions). For this reason it is best to estimate N_θ from sequences that are likely to be nearly neutral, whereas all sites can be included in estimates of N_ρ. Finally, and this is the basis of our method for inferring the frequency of sexual reproduction, whether reproduction is sexual or asexual should have little influence on θ (assuming equal mutation rates for mitosis and meiosis), whereas it will have a direct effect on ρ (because recombination does not occur in asexual generations). Thus N_ρ is the effective number of cells in the population derived from mating (i.e., the number of zygotes), whereas N_θ refers to the effective total number of cells, and N_ρ/N_θ estimates the frequency of sexual reproduction.

Further information on the yeast life cycle can be obtained by comparing ρ for regions near and far from MAT (situated ≈85 kb from the centromere, on the right arm of chromosome III). Because of the self-incompatibility of MAT, matings only occur between individuals of different mating types, even when otherwise highly inbred, thus making the MAT locus the most outbred region of the genome. With haplo-selfing, the rest of the genome is made completely homozygous, whereas with other forms of inbreeding the increase in homozygosity is partial and depends on distance from MAT (21–23). That is, different regions of the genome will have different levels of heterozygosity, which in turn should produce different estimates of ρ. If a fraction s_h of zygotes is formed by haplo-selfing, s_i by intratetrad mating, and t = 1 − s_h − s_i by random mating, then the equilibrium heterozygosity at a locus (relative to Hardy–Weinberg proportions) will be 1 − F = 3t/(3 − (2 + e^−3x)s_i), where x is the map distance (in Morgans) between the locus and MAT (21, 23). Because ρ is a linear function of 1 − F, we can therefore estimate the frequency of intratetrad mating by comparing ρ near the MAT to ρ for the whole chromosome [supporting information (SI) Appendix].

Results

Mutational Diversity, Population Structure, and Demographic Equilibrium.

For the European lineage we sequenced chromosomes from 11 isolates from the United Kingdom (U.K.) collected within 10 km² of each other and added one previously published sequence (24). The previously published sequence does not have more unique mutations than the others, so we have included it in our analyses. For the Far East lineage we sequenced eight chromosomes, one of which has already been published (12). The total length of each alignment including all sites (after trimming ends and removing sites at which more than half the strains in the population had an alignment gap) is ≈280 kb. There are 994 polymorphic sites in the European sequences and 640 in the Far East (of which 405 and 312 are singleton sites, i.e., with one strain having a unique mutation, respectively; Table 1). Here, and throughout the article, we consider only nucleotide differences and ignore indels. Both θ_π and θ_S are ≈0.001 in both populations, indicating an average of one difference per 1,000 bp between two random chromosomes in each population. No site has more than two different nucleotides in a population. Four sites are polymorphic in both populations (three of which have the same two nucleotides), all separated by >50 kb from each other on the chromosome. The expected number of polymorphisms coinciding on the same site, assuming independence, is approximately (994/278,654) × 640 = 2.3. Divergence between Europe and the Far East is 1.4% (12).

Table 1.

Polymorphism in the European and Far East populations

Population	Sites*	Segregating sites (S)	Singleton sites†	θπ (×1,000)‡	θS(×1,000)‡	Tajima's D
Whole chromosome
European	278,654	994	405	1.2	1.2	0.02, P = 0.9§
Far East	278,264	640	312	0.9	0.9	−0.06, P = 0.7§
4-fold degenerate (n = 140 protein-coding genes)
European	25,738	158	61	2.1	2.1 (1.6, 2.7)	0.07 (−0.2, 0.3)
Far East	25,649	103	46	1.6	1.6 (1.2, 2.0)	0.07 (−0.2, 0.3)
LTRs (n = 11 intergenic regions)
European	5,802	69	27	3.8	3.8 (2.1, 5.7)	−0.1 (−0.8, 0.6)
Far East	5,474	45	21	3.3	3.2 (1.9, 4.5)	0.04 (−0.5, 0.5)

θ_π, θ_S, and D were calculated by using Variscan [version 2.0.1; option numnuc = 4 (48)], with gaps treated as missing data; numbers in parentheses are 95% C.I. from bootstrapping values from the 140 coding regions or 11 LTR regions.

*Number of sites analyzed, after excluding sites with alignment gaps and sites at which fewer than four strains had data (A, C, G, T); the total length of the alignments is 281,584 and 282,026 bp for Europe and Far East, respectively, and the average number of strains per site analyzed is 11.7 and 7.6 (whole chromosome and 4-fold degenerate) and 10.6 and 7.1 (LTRs).

^†Sites with unique alleles.

^‡θ_π estimated from average pairwise DNA sequence divergence, per bp; θ_S estimated from S, per bp.

^§P values obtained by comparing the observed D with those from 10,000 datasets generated under the neutral coalescent model (49) using the observed parameters: n = 12/8 (Europe/FarEast), r = 865/243 (from the rholike model), S = 755/437, length = 281,584/282,026.

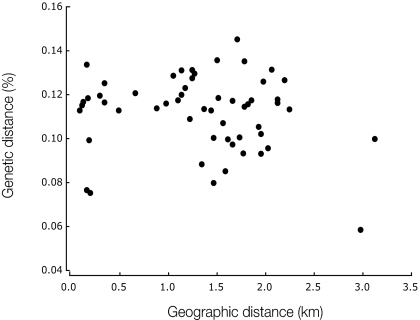
To test how well the data fit the neutral coalescent model we calculated Tajima's D for the entire chromosome in each of the two populations (25) and compared the observed values with the distribution of D values obtained from simulated datasets generated under the neutral coalescent model and using the observed parameters (Table 1). For example, population expansion after a bottleneck would produce an excess of rare variants, and hence a negative D, whereas population subdivision would have the opposite effect (26). The observed D values for both populations are close to 0 and fall well within the distribution of values from the neutrally evolved datasets, revealing no gross deviation from the assumptions of the neutral model. We also tested for isolation by distance among our U.K. isolates and found no correlation between geographic distance and genetic differentiation (Fig. 1).

Fig. 1.

Lack of correlation between genetic differentiation θ_π and geographic distance in the U.K. population. Each point represents a different pair of strains.

Estimating Effective Population Size from the Mutation Parameter θ_S.

For the purposes of estimating population size from θ, it is best to measure variation at neutrally evolving regions of the genome. Remnants of LTR retrotransposable elements are promising candidates, as there is no obvious source of selection acting on them once inserted in the genome (27). We have shown previously that LTRs diverge faster between species than coding regions or other noncoding regions, and at about the same rate as silent sites once codon usage biases are taken into account (12). We thus estimated θ_S from LTR regions in chromosome III, including only those that are fixed within populations. Fixed LTRs are at least as old as the common ancestor of the strains, and therefore contain the full amount of mutational variation since that time.

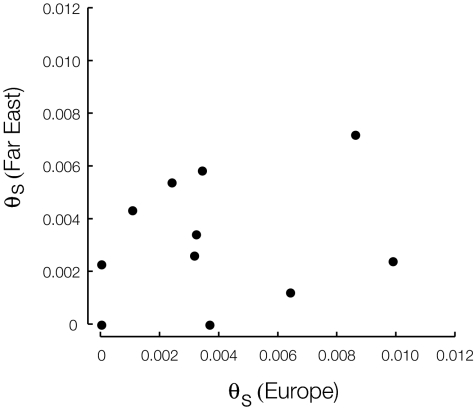
The European and Far East populations have fixed LTRs in the same 11 intergenic regions, 7 of which are separated by at least 15,000 bp. Most are derived from Ty1 and Ty4 elements. These regions can be relatively complex, most having more than one fragment of an LTR, sometimes overlapping or nested. LTRs in the same intergenic region were analyzed together as one observation; these ranged from 93 to 1,076 bp (SI Appendix). The average θ_S is 0.0038 and 0.0032 for the European and Far East populations, respectively, with no significant difference between them (Table 1). These values are about twice those for 4-fold degenerate sites in coding regions and more than three times those for the entire chromosome. Tajima's D is not significant for any of the LTR regions individually nor for all LTRs combined (P > 0.8). We also tested whether there is any correlation between θ_S for Europe and Far East, across the different LTR regions (Fig. 2). A significant correlation would imply violation of some assumption, for example, differential selection among LTR regions, but we found no correlation.

Fig. 2.

Lack of correlation of θ_S from LTR fragments in the European and Far East populations, for regions that were present in both populations. Each point represents fixed LTRs from a different intergenic region (Pearson r = 0.24, P = 0.48).

The mutation rate has been estimated for S. cerevisiae as u = 0.22 × 10⁻⁹ mutations per site per cell division (28), and Wright's F has been estimated for the U.K. population of S. paradoxus as F = 0.98 (above). Assuming S. paradoxus has the same mutation rate as S. cerevisiae, we estimate the effective population size as N_θ = θ(1 + F)/(4u) = 8,600,000 and 7,200,000 individuals for Europe and the Far East, respectively.

Linkage Disequilibrium.

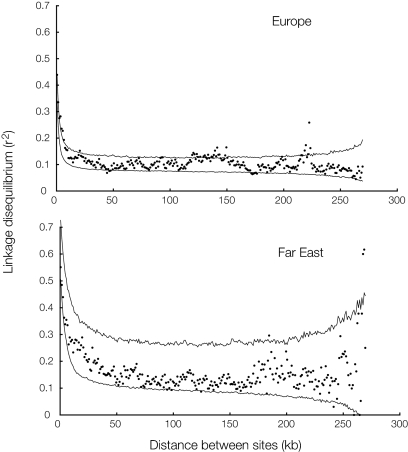
New mutations occur on single chromosomes and therefore, when they first arise, they are statistically associated with particular alleles at any site that is polymorphic in the population at the time. These associations are then broken down by recombination. All else being equal, the further apart two sites are on a chromosome, the higher the rate of recombination between them. We therefore expect linkage disequilibrium to be higher for sites that are near each other than for sites that are further away. We calculated r², a measure of association or linkage disequilibrium (26), for all pairs of polymorphic sites on chromosome III. These values are plotted as a function of physical distance between sites in Fig. 3. The association becomes approximately random for sites that are ≈25 kb (Europe) or ≈50 kb (Far East) apart.

Fig. 3.

Linkage disequilibrium (i.e., correlation of alleles) between pairs of polymorphic sites as a function of physical distance between the two sites. Points are average r² for all pairs within a particular distance, with 1-kb increments. The lines show the two 97.5% upper and 2.5% lower bounds calculated from 1,000 datasets generated under a neutral coalescent model, given the length of sequences, number of polymorphic sites, and the rholike estimate of ρ (from Table 2; using the ms program in ref. 49). The asymptote (i.e., the expected r² when there is no association between alleles) is 1/n, where n is the number of sequences (1/12 = 0.083 for Europe and 1/8 = 0.125 for the Far East).

Comparison to simulated datasets, created by re-evolving chromosome IIIs with the same length, levels of polymorphism, and recombination parameter ρ, reveals an outlier in Europe, between sites that are ≈220,000 bp apart (Fig. 3; for estimation of ρ, see next section). Further analysis shows this is caused by high linkage disequilibrium between sites in the VBA3-YCL068C intergene (which contains the ARS301 silencer of HMLALPHA1) at the 5′ end of the chromosome and sites in the SED4-ATG15 intergene at the 3′ end. The reason for this high linkage disequilibrium is not clear, and it is not apparent in the Far East population.

Estimating Effective Population Size from the Recombination Parameter ρ.

We used three different methods to calculate ρ (Table 2); confidence limits are smallest for the rholike method, and we focus on these estimates. Note that with this method, ρ is more than three times higher in Europe than in the Far East (3.1 vs. 0.9 Morgans/kb, P < 0.05). This result reflects the more rapid decay of linkage disequilibrium in Europe. The recombination rate r has previously been estimated for S. cerevisiae chromosome III as 0.0048 Morgans/kb (http://db.yeastgenome.org/cgi-bin/PGMAP/pgMap). Assuming this also applies for S. paradoxus, and F = 0.98, we estimate the effective population size as N_ρ = ρ/(4r(1 − F)) = 8,100 and 2,300 individuals for Europe and the Far East, respectively.

Table 2.

Estimates of the population recombination parameter ρ (Morgans/kb) for chromosome III

Method	Europe	Far East
Wakeley (50)	1.1 (0.6–4.5)	1.1 (0.4–11.4)
Pairwise (51)*	2.0 (1.1–4.9)	1.0 (0.3–4.4)
rholike (52)†	3.1 (2.2–4.6)	0.9 (0.4–1.9)

Based on analysis of sites with no missing data (229,734 and 211,807 aligned sites in Europe and Far East, respectively, of which 755 and 437 are polymorphic, and 464 and 231 are non-singletons). Singleton sites are uninformative for r² and ρ and were excluded from the analyses, as were sites at which any strain has an alignment gap, except insofar as they contributed to the coordinate system (i.e. the site was considered as missing data). Numbers in parentheses are 95% confidence limits, estimated by using these same methods on simulated datasets with known ρ (see SI Appendix for an example).

*www.stats.ox.ac.uk/∼mcvean/LDhat.

^†www.biostat.umn.edu/∼nali/SoftwareListing.html.

These estimates are more than three orders of magnitude lower than the estimates derived from θ. As discussed above, all cell divisions contribute to mutational diversity, whereas recombinational diversity is generated only by meiotic divisions. This discrepancy therefore implies that the frequency of sex is N_ρ/N_θ = 0.0009 in Europe and 0.0003 in the Far East, or a frequency of sex of approximately once every 1,000 or 3,000 generations, respectively.

Estimating the Frequency of Haplo-Selfing vs. Intratetrad Mating.

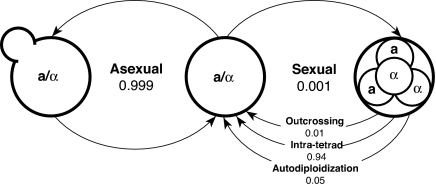
We measured ρ in the 20-kb regions to the left and right of the MAT and there was no significant difference between the two sides in either population (Table 3). In both populations ρ near the MAT was about twice that for the whole chromosome; combining the data from both populations, the ratio of ρ near MAT vs. whole chromosome is 2.1. From this ratio we estimate the frequency of intratetrad mating to be ≈94% (50% C.I.: 88–97%; 95% CI: 41–99.9%; see SI Appendix for calculations). Previously, we estimated the frequency of outcrossing in the U.K. population to be ≈1% (14), leaving 5% for the frequency of haplo-selfing. A summary of all of our estimates is given in Fig. 4.

Table 3.

Estimates of the population recombination parameter ρ (Morgans/kb) in the regions 0–20 kb left and right of the MAT locus (rholike method)

Region	Europe	Far East
Left of MAT	4.7 (1.8–12.8)	1.2 (0.4–6.9)
Right of MAT	7.0 (3.0–14.8)	3.5 (0.8–14.2)
Average	5.9 (2.4–12.8)	2.4 (0.6–8.7)

The MAT locus is defined here as the region with significant homology to HML and includes 800 bp to the left of YCR039C and 190 bp to the right of YCR040W.

Fig. 4.

A quantitative life cycle for the European population of S. paradoxus is shown.

Discussion

This study provides a large-scale survey of sequence polymorphism in a wild yeast. Across the whole chromosome we found θ ≈0.1%, rising to ≈0.35% in the LTRs. Our finding that chromosome III as a whole is about three times less polymorphic than the LTRs [and also diverges three times more slowly (12)] implies that at least two-thirds of sites on the chromosome are under purifying selection. In Drosophila, ≈60% of sites were found to be under purifying selection and in rodents, ≈10% (29, 30). Interestingly, this purifying selection is not apparent from calculating Tajima's D for the whole chromosome.

To estimate the effective population size from mutational diversity (N_θ) we used the value of θ for LTRs and laboratory measurements of mutation rate in S. cerevisiae. Our analysis assumes that the LTRs are neutral, and, consistent with this assumption, we found no significant correlation in θ across LTRs from the two populations and also no significant Tajima's D. Except for the centromere, they are also the most rapidly diverging region of the chromosome (12). In principle, polymorphism of LTRs could be inflated by ectopic recombination between dispersed repeats (31), but synonymous sites diverge at about the same rate after controlling for codon usage bias (12). In this study we found that synonymous sites are about half as polymorphic as LTRs, presumably the result of purifying selection (32). Our analysis also assumes no population structure. We found no correlation between genetic and geographic distance over the 10 km² in which they were collected, although members of the same clone can show spatial aggregation (10). This pattern of aggregated clonemates but dispersed genotypes is expected if sexuals disperse more than asexuals [note that sexual spores survive better than vegetative cells in the gut of Drosophila (9)], although it may also arise from localized expansion of clones, even if there is no difference in dispersal between sexuals and asexuals.

The effective population sizes we estimate (≈10⁷) is broadly comparable with similarly calculated values in other small eukaryotes (33). Given that this many cells can be found in a single colony in the laboratory, it must be much less than the census population size (i.e., the actual number of yeast cells alive at any one time). One possible contributor to this discrepancy is the nonindependence of cells in a colony: perhaps they all live or die together, in which case we are actually estimating the number of colonies, not the number of cells. The effective population size is important in such parameters as the time taken for isolated populations to become genealogically independent and the minimum selection differential needed to overpower random drift (2, 26).

We have analyzed two genealogically independent populations, allowing us to assess the evolutionary stability and repeatability of parameter estimates. The European and Far East populations do not differ significantly in θ, but they do differ in ρ, with the European estimate some three times larger than that for the Far East. This difference could be caused by a higher frequency of sex in Europe or to a higher inbreeding coefficient (F) in the Far East (as discussed above, inbreeding has a greater effect on ρ than on θ). It is less likely that the difference in ρ is caused by a reduced effective population size in the Far East, because then a similar reduction would have been seen in θ. Because ρ is more sensitive to changes in the reproductive system than θ, it is more likely to differ between populations and species.

In both populations, N_ρ is substantially lower than N_θ, from which we estimate the frequency of sex to be about once every 1,000 (Europe) or 3,000 (Far East) generations. This finding of infrequent sex is consistent with the high frequency of identical, spatially aggregated genotypes sampled from several locations (10). It is difficult to put formal confidence limits on these estimates. The mutation and recombination rates (u and r) are from laboratory estimates on another species (S. cerevisiae). In addition, uncertainties in the inbreeding coefficient (F) introduce considerable uncertainty in our calculation of N_ρ (less so in our calculation of N_θ), and our analysis also assumes that the F estimated by Johnson et al. (14), which reflects the mating system over the last few generations, applies to the entire coalescent. Estimates of F from larger samples and multiple populations would be useful in assessing its evolutionary stability. Fortunately, errors in estimating F have opposing effects on estimates of the frequencies of sex and outcrossing, so that the overall probability that a cell is derived from an outcrossed mating (i.e., the frequency of sex multiplied by the outcrossing rate) is largely independent of errors in F. In our study we estimate the absolute outcrossing rate to be ≈10⁻⁵ (Europe) and 3 × 10⁻⁶ (Far East). By comparison, previous work on S. cerevisiae has estimated this frequency to be ≈9 × 10⁻⁵ [from an analysis of a single locus (34)] or 2 × 10⁻⁵ [from a genomewide comparison of three strains (35)].

Estimates of N_θ and N_ρ have previously been compared in a few obligately sexual organisms, where both diversities result from the same (sexual) generations. In these cases the estimates differ by <10-fold, and discrepancies have been attributed to possible effects of selection, nonrandom mating, and population fluctuations (Table 4). The ratio r/u is three or four orders of magnitude higher in yeast than in Caenorhabditis, Drosophila, or humans, reflecting both a high rate of recombination and a low rate of mutation. This high ratio, however, does not result in excessive recombinational diversity, the ratio ρ/θ in S. paradoxus being comparable to or less than that in the other species, because of the high frequencies of asexual reproduction and inbreeding.

Table 4.

Population genomic parameter estimates in different species

Species	u, ×10−9 bp−1	r, ×10−9 Morgans/bp	r/u	LD → 0, kb	θS, kb−1	ρ, Morgans/kb	ρ/θ	Nρ/Nθ
S. paradoxus*
European	0.22	4,800	22,000	25	3.8	3.1	0.81	0.0009
Far East				50	3.2	0.9	0.31	0.0003
Caenorhabditis remanii†	9	23	2.6	1–2	57	35	0.6	0.23
Drosophila melanogaster‡	1.5	23	15	1	9.8–12	47–89	4.6–7.6	0.31–0.51
Humans§	24	13	0.54	30	0.7–1.1	0.6–4.5	0.6–4.1	1.1–7.6

*This study: chromosome III; θ for LTRs only; n = 12 (Europe) and 8 (Far East) strains; u and r from S. cerevisiae.

^†One population, 34 strains, six nuclear loci; u and r from C. elegans (17).

^‡Three African populations, average of 21 alleles per population, 10 X-linked, noncoding loci (53); u and r for loci in the relevant region of the X chromosome from (54).

^§Three populations, 15 individuals in each, 10 noncoding regions, total length ≈25 kb; u calculated as substitution rate from chimpanzees (18); LD → 0 value from ref. 55.

We have also estimated the frequency of the two predominant forms of inbreeding, haplo-selfing and intratetrad mating, by comparing ρ in regions near and far from MAT. Our analysis assumes a constant rate of crossing-over along the chromosome, yet some heterogeneity is known in S. cerevisiae (36). We estimate a high frequency of intratetrad mating (≈94%), which could be caused by such adaptations as the persistent ascus and interspore bridges that keep the four spores together as potential mates (22, 37). The 2-fold higher heterozygosity near MAT, as inferred from a 2-fold higher ρ, is not as extreme a difference as is apparently found in some other species with near-obligate intratetrad mating [e.g., Microbotryum (38)]. The significant frequency of haplo-selfing (≈5%) is consistent with previous findings that all of the isolates are homothallic (ref. 14 and unpublished observations). By contrast, S. cerevisiae strains are often heterothallic [i.e., unable to undergo mating type switching (39)]. Haplo-selfing presumably results from a failure to mate during spore germination, for example if one or more of the meiotic products are inviable, resulting in a “lonely spore”, or if the spores are separated before germination. Ascus dissolution and spore separation are also required for outcrossed matings.

To conclude, our study illustrates how population genomic data can reveal the imprints of different aspects of microbial life cycles, and thus allow insight into their cryptic lives. The quantification of the life cycle presented here should be taken as indicative rather than definitive, as our calculations are based on a number of assumptions. Improvements will come especially from better estimates of the mutation rate, the recombination rate and its heterogeneity along the chromosome, and the inbreeding coefficient. Modern genomic technologies make such improvements increasingly possible (40–42), potentially allowing us to learn almost as much about the reproductive habits of microbes like yeast as can be learned from direct observation of large organisms such as plants and animals.

Methods

Strains.

We studied the same strains as Bensasson et al. (12): the strain sequenced by Kellis et al. (24), 11 other strains of the European lineage, all from Berkshire, United Kingdom (T18.2, T26.3, T32.1, T62.1, T68.2, T76.6, Q4.1, Q6.1, Q14.4, Q15.1, and Q43.5), and 8 strains from the Far East lineage (CBS 8436, 8437, 8438, 8439, 8440, 8441, 8442, 8444). None of these are members of the same clone (10). Strains were made fully homozygous before sequencing by isolating a single spore from a tetrad and allowing it to haplo-self.

DNA Sequencing, Assembly, and Alignment.

The published S. paradoxus chromosome III sequence was used to design primers for PCR amplification and sequencing of the nontelomeric fraction of the chromosome (12). Base-calling was conducted with Phred (43), and sequences were assembled using the Gap4 component of Staden (http://staden.sourceforge.net). Only bases with a consensus Phred quality score ≥ q40 were accepted (probability of miscall <1/10,000), the rest being treated as missing data. DNA sequences have been deposited in GenBank. Sequences were aligned using mlagan, and the alignment was further improved manually using SeaView and BioEdit (44–46). Some analyses rely on the position of the variable nucleotides (e.g., linkage disequilibrium, ρ). So as not to include insertions that are present in a minority of strains, which would disproportionately inflate the distances between some sites, we excluded from the alignment all sites at which more than half the strains had an alignment gap (i.e., >6 strains in Europe and >4 strains in Far East).

LTRs.

LTRs were identified using RepeatMasker [version 3.1.5 (47)] and include all regions in the alignment where at least one strain was identified as having a Ty element. LTRs that were not separated by a gene were analyzed together as one observation (although intervening sequences not related to Ty elements were excluded). Sites with an alignment gap were excluded from the calculation of θ.