Abstract
Estimating the relaxation constant of an exponentially decaying signal from experimental MR data is fundamental in diffusion tensor imaging, fractional anisotropy mapping, measurements of transverse relaxation rates and contrast agent uptake. The precision of such measurements depends on the choice of acquisition parameters made at the design stage of the experiments. In this report, χ2 fitting of multi-point data is used to demonstrate that the most efficient acquisition strategy is a two-point scheme. We also conjecture that the smallest cofficient of variation of the decay constant achievable in any N-point experiment is 3.6 times larger than that in the image intensity obtained by averaging N acquisitions with minimal exponential weighting.
Keywords: exponential decay, T2, diffusion, contrast agent, ptimization methods
Introduction
A wide range of microscopic processes in physiological tissues that can be accessed using MR techniques are characterized by an exponential decay. Determining their relaxation constants from experimental data collected with spin-echo sequences is common in diffusion tensor imaging (DTI) and spectroscopy (DTS) [1–3], measurements of fractional anisotropy (FA) [4], transverse relaxation rates (R2) [5–7], etc. An exponentially decaying signal can be described by two parameters: its amplitude ρ and decay rate λ,
| (1) |
where t is the user-controlled encoding parameter (diffusion weighting or echo time). Therefore, at least two measurements with different encodings t1 and t2 > t1 are needed to estimate λ. It has been shown that within all such “two-point” schemes, the imaging time is used most efficiently when (t2− t1) is chosen to be about 1.29/λ [8]. The method also requires that the number of averages of the acquisition with encoding parameter t2 to be about 18/5 the number of averages with t1.
In this report we examine whether multi-point acquisitions with several (more than two) encodings may be more efficient than two-point schemes in the same total measurement duration. To this end, we use corresponding diagonal element of the covariance matrix of the χ2 fitting procedure as a measure of the precision of the decay rate estimation and demonstrate numerically that the most efficient multi-point scheme, in fact, approaches that of the two-point.
Theory
In a multi-point acquisition N data points, Si, are collected, each with its own encoding parameter ti. Since interchanging the order of these acquisitions does not affect the precision of the estimation we will assume t1 ≤ t2 ≤ t3 ≤ … tN. (The equal sign reflects the possibility that acquisitions with the same encodings may be repeated.) We also assume that all N acquisitions are subject to Gaussian noise with standard deviation σ0 determined by the receiver hardware, spatial resolution and sample properties. Having such data, χ2 fitting can be executed to yield the maximum likelihood estimate of the decay constant [9]. The variance of the estimation is given by the second diagonal element of the 2 × 2 covariance matrix (A+ A)−1 where rows of the N × 2 matrix A are:
| (2) |
The optimal acquisition strategy is specified by a set of ti’s yielding the highest precision in the decay rate, i.e. the smallest . We perform this optimization in the vicinity of the expected decay value λ = λtune and then evaluate σλ at arbitrary λ’s.
It is clear that optimal value of t1 is zero otherwise the amplitude ρ can be redefined as ρe−λt1 and all ti’s as (ti − t1). After this redefinition, ρ is the signal with minimal exponential weighting (i.e. signal acquired with minimal echo time or diffusion weighting allowed by the sequence/hardware) and t1 is zero. Thus, we are left with the problem of finding (N - 1) values of ti, i = 2, 3, …,N minimizing σλ. This search is performed numerically using a brute-force method in (N - 1) dimensions on a uniform grid of λtuneΔt = 0.05 between 0 and 4. The size of the search grid is dictated by the flattening of the signal dependence at large λt, Eq. (1), while its granularity — by the numerical complexity. The optimal values of ti for N between 2 and 10 are given in table 1. Computation of the last line in table 1 took 8 hours on a Pentium IV, 3.4 GHz PC. Making the search grid twice finer would require 210-1 fold more time or about 170 CPU days. The dependence of σλ on λ using several optimal N-point acquisition strategies is shown in Fig. 1.
Table 1.
Optimal encoding parameters ti for estimating decay constant λ in the vicinity of λtunefor several N-point methods. Note that all protocols (except N = 9) are found to be “two-point” ones. The N = 9 case appears different due to the sampling grid granularity: two points out of the three lie on the neighboring grid points.
| N | λtuneti | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | 1.10 | ||||||||
| 3 | 0 | 1.20 | 1.20 | |||||||
| 4 | 0 | 1.25 | 1.25 | 1.25 | ||||||
| 5 | 0 | 1.30 | 1.30 | 1.30 | 1.30 | |||||
| 6 | 0 | 1.35 | 1.35 | 1.35 | 1.35 | 1.35 | ||||
| 7 | 0 | 0 | 1.20 | 1.20 | 1.20 | 1.20 | 1.20 | |||
| 8 | 0 | 0 | 1.25 | 1.25 | 1.25 | 1.25 | 1.25 | 1.25 | ||
| 9 | 0 | 0 | 1.25 | 1.25 | 1.25 | 1.25 | 1.30 | 1.30 | 1.30 | |
| 10 | 0 | 0 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 |
Fig. 1.
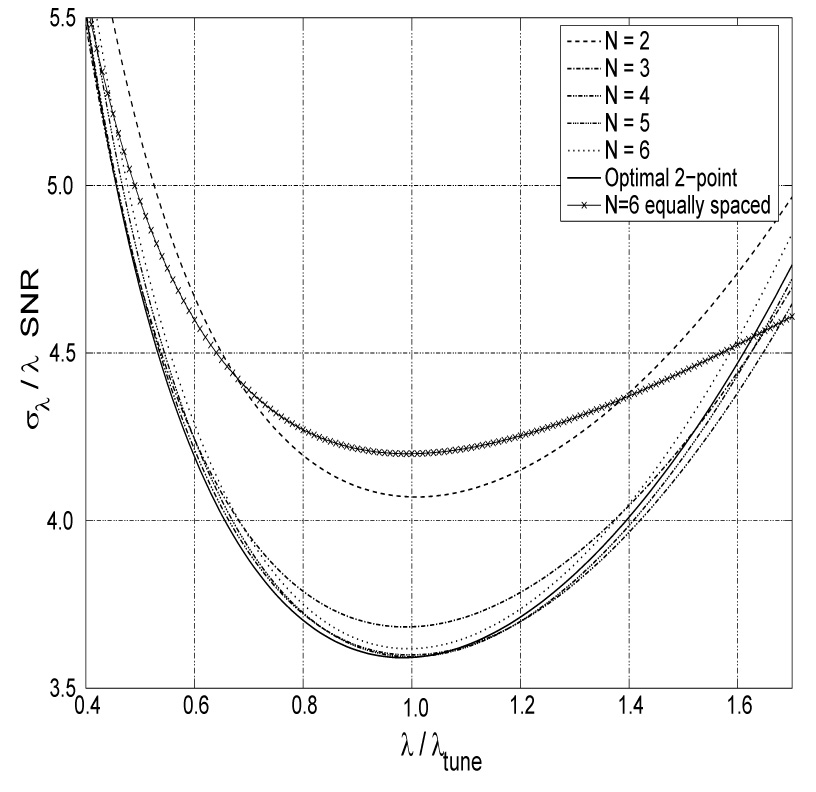
Precision as a function of λ for several N-point protocols tuned for λtune. Here, the SNR is the signal-to-noise ratio of the average of N images with minimal exponential weighting and in general is a function of λ if the minimal weighting is not zero. Note that the precision of protocols with N ≥ 3 is already very close to optimal. Since the convexity of the curves is very small, the precision stays within 15% of the best over a broad interval λ ∈ (0.6, 1.5)λtune. As an example of a commonly used scheme, the precision for optimal 6-equally-spaced-point protocol is superposed.
Results and Discussion
The optimal N-point protocols presented in table 1 reveal that within the search grid all N-point schemes (except N = 9) are, in fact, two-point methods with the appropriate number of averages at each acquisition [1,8]. In the N = 9 case, two out of the three optimal encodings land on the neighboring search grid points 1.25 and 1.30, making this case not too different from a two-point one as well. Performing the search on a finer grid to validate this is computationally intractable as described above. Therefore, we conjecture that the highest precision of exponential relaxation estimation is achieved using the optimal two-point method. The hardware, sample and duration independent measure of this precision can be characterized by the dimensionless normalized coefficient of variation [8] where SNR is the signal to noise ratio obtained by averaging N acquisitions with minimal exponential weighting, S(t1). For example, if averaging N such images delivers signal to noise ratio of 100, then the relative error in the decay constant estimation can not be smaller than . This precision is achieved in the vicinity of the assumed value, λtune, used for tuning the encodings ti as shown in the Fig. 1.
If the actual value of λ deviates from λtune the precision degrades as shown in Fig. 1. Fortunately, the precision loss is only 15% over a wide range λ ∈ (0.6, 1.5)λtune. If the decay constants to be measured are expected to vary by much more than a factor of 1.5/0.6=2.5, the two-point method will be inefficient at the edges of the range of λ’s. Tuning the multi-point method to minimize combined error at the edges of the expected range may yield a flatter ελ and thus more uniform precision across the range. However, for all values of λ in this range the precision will always be worse than the 3.6 achievable with the optimal two-point method. To illustrate this point, superposed in Fig. 1 is the precision for the optimal 6-equally-spaced-point protocol. As expected, the curve is flatter than those achieved by the two-point methods and is above them in the range λ ∈ (0.4, 1.6)λtune. Thus, even if λ lies in this wide range, the two-point method will outperform the equally spaced one. Only outside of this range can the advantage of such protocol be evident. However, the precision is at least 30% worse than could be achieved in the same experimental duration which may render the procedure moot.
The strategy presented assumes a separate spin-echo acquisition for each encoding ti. Although multi-spin-echo experiments are sometimes used to speed up the acquisition, imperfect RF pulses may lead to incomplete refocusing and thus to additional apparent signal decay. Such schemes, therefore, are prone to systematic errors in the relaxation constant estimation.
Measurement of exponential relaxation constants for which the two-point method is found to be the most efficient should not to be confused with the validation of the model of exponential signal decay. The latter is characterized by the goodness of the fit and requires acquisitions at multiple distinct encodings ti.
Being optimal, the two-point scheme lends itself admirably to applications relying on measurement of the change in the relaxation constants such as microvessel density estimation [10]. Indeed, images acquired before and after the relaxation constant is altered, say by administration of a contrast agent, naturally constitute the two points. Image intensity of the first point is given by ρe−λ0t while of the second — by ρe−λ0te−Δλt. Since modification of the encoding parameter t between the points introduces unwanted sensitivity to the unknown “resting” tissue relaxation constant λ0, t has to be common to both acquisitions. The optimal acquisition strategy consists of choosing the value of t to yield the highest precision of Δλ. Interpreting ρe−λ0t as the amplitude of the decay ρ and Δλ as decay constant λ casts the problem in terms of the relaxation constant estimation considered [see Eq. (1)] with one exception: ρ depends on the user selectable parameter t. However, in applications such as microvasculature imaging requiring high doses of contrast agents, λ0 is much smaller than Δλ [10]. Therefore, for optimization purposes in the vicinity of Δλ the t-dependence of ρ can be neglected. Thus, optimal exponential weighting t as well as the number of acquisition averages before and after the relaxation constant alternation are found in table 1 (by replacing λtune with Δλ).
Conclusion
We have considered optimization of N-point data acquisition protocols with N = 2, 3, …, 10 for estimation of exponential relaxation constants. In all but the N = 9 cases two-point scheme was found to be the most efficient. Two encodings out of the three optimal for N = 9 lie on the neighboring search grid points indicating that had a finer grid been used the protocol would perhaps have converged to two points as well. Therefore, we conjecture that the highest precision of exponential relaxation constant estimation is achieved with the optimal two-point acquisition scheme. This yields a coefficient of variation not smaller than 3.6 times the coefficient of variation in image intensity obtained by averaging N acquisitions with minimal exponential weighting (i.e. signal acquired with minimal echo time or diffusion weighting allowed by the sequence/hardware, etc).
Footnotes
This work is supported by NIH grants number EB001015, CA111911 and NS050520.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Xing D, Papadakis N, Huang C, Lee V, Carpenter T, Hall L. Optimized diffusion-weigting for measurement of apparent diffusion coefficient (ADC) in human brain. Magn Reson Imag. 1997;15:771–784. doi: 10.1016/s0730-725x(97)00037-4. [DOI] [PubMed] [Google Scholar]
- 2.Ellegood J, Hastock C, Beaulieu C. Trace apparent diffusion coefficients of metabolites in human brain using diffusion weighted magnetic resonance spectroscopy. Magn Reson Med. 2005;53:1025–1032. doi: 10.1002/mrm.20427. [DOI] [PubMed] [Google Scholar]
- 3.Ellegood J, Hastock C, Beaulieu C. Diffusion tensor spectroscopy (DTS) of human brain. Magn Reson Med. 2006;55:1–8. doi: 10.1002/mrm.20777. [DOI] [PubMed] [Google Scholar]
- 4.Deng X, Farley M, Nieminen M, Gray M, Burstein D. Diffusion tensor imaging of native and degenerated human particular cartilage. Magn Reson Imag. 2007;25:168–171. doi: 10.1016/j.mri.2006.10.015. [DOI] [PubMed] [Google Scholar]
- 5.Mlynarik V, Gruber S, Moser E. Proton T1 and T2 relaxation times of human brain metabolites at 3 Tesla. NMR Biomed. 2001;14:325–331. doi: 10.1002/nbm.713. [DOI] [PubMed] [Google Scholar]
- 6.de Bazelaire C, Duhamel G, Rofsky N, Alsop D. MR Imaging relaxation times of abdominal and pelvic tissues measured in vivo at 3.0 T: Preliminary results. Radiology. 2004;230:652–659. doi: 10.1148/radiol.2303021331. [DOI] [PubMed] [Google Scholar]
- 7.Traber F, Block W, Lamerichs R, Gieseke J, H S. 1H Metabolite relaxation times at 3 Tesla: Measurements of T1 and T2 values in normal brain and determination of regional differences in transverse relaxation. J Magn Reson Imag. 2004;19:537–545. doi: 10.1002/jmri.20053. [DOI] [PubMed] [Google Scholar]
- 8.Fleysher L, Fleysher R, Liu S, Zaaraoui W, Gonen O. Optimizing the precision-per-unit-time of quantitative MR metrics: Examples for T1, T2 and DTI. Magn. Reson. Med. 2007;57:380–387. doi: 10.1002/mrm.21144. [DOI] [PubMed] [Google Scholar]
- 9.Eadie W, Drijard D, James F, Roos M, Sadoulet B. Statistical Methods in Experimental Physics. American Elsevier; 1971. [Google Scholar]
- 10.Jensen J, Chandra R. MR imaging of microvasculature. Magn Reson Med. 2000;44:224–230. doi: 10.1002/1522-2594(200008)44:2<224::aid-mrm9>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]


