Reaction Coordinates for the Flipping of Genetic Switches

Abstract

We present a detailed analysis, based on the forward flux sampling simulation method, of the switching dynamics and stability of two models of genetic toggle switches, consisting of two mutually repressing genes encoding transcription factors (TFs); in one model (the exclusive switch), the two transcription factors mutually exclude each other's binding, while in the other model (general switch), the two TFs can bind simultaneously to the shared operator region. We assess the role of two pairs of reactions that influence the stability of these switches: TF-TF homodimerization and TF-DNA association/dissociation. In both cases, the switch flipping rate increases with the rate of TF dimerization, while it decreases with the rate of TF-operator binding. We factorize the flipping rate k into the product of the probability ρ(q*) of finding the system at the dividing surface (separatrix) between the two stable states, and a kinetic prefactor R. In the case of the exclusive switch, the rate of TF-operator binding affects both ρ(q*) and R, while the rate of TF dimerization affects only R. The general switch displays a higher flipping rate than the exclusive switch, and both TF-operator binding and TF dimerization affect k, R, and ρ(q*). To elucidate this, we analyze the transition state ensemble. For the exclusive switch, the transition state ensemble is strongly affected by the rate of TF-operator binding, but unaffected by varying the rate of TF-TF binding. Thus, varying the rate of TF-operator binding can drastically change the pathway of switching, while changing the rate of dimerization changes the switching rate without altering the mechanism. The switching pathways of the general switch are highly robust to changes in the rate constants of both TF-operator and TF-TF binding, even though these rate constants do affect the flipping rate; this feature is unique for nonequilibrium systems.

INTRODUCTION

Biochemical networks with multiple stable states are omnipresent in living cells. Multistability can provide cellular memory, it can enhance the sharpness of the response to intra- and extracellular signals, it can make the cell robust against biochemical noise, and it allows cells to differentiate into distinct cell types. Although a multistable biochemical network can flip between alternative states due to random fluctuations (i.e., noise), in many cases the states are very stable, and the network typically only switches from one state to the next under the influence of an external signal (1). A key question, therefore, in understanding multistable biochemical networks is what controls the stability of the steady states. To answer this question, we have to elucidate the pathways of switching between steady states. Switching events are, however, intrinsically difficult to study experimentally, because the switching event itself can be much faster than the typical lifetime of the steady state. Computer simulations are a valuable tool for studying biochemical networks, especially for rare processes such as switching. However, precisely because such events are rare, special techniques are required to simulate them. One such technique is forward flux sampling (FFS) (2–4), and in this article, we use FFS in combination with committor distributions to analyze in detail the effect of two important sources of fluctuations—transcription factor dimerization and transcription factor-DNA binding—on the flipping rate and switching pathways of two models of bistable genetic toggle switches. We hope that this analysis may serve as a paradigm for studying multistable biochemical networks as well as other rare events in nonequilibrium systems.

If a biochemical network is bistable, with two stable states A and B, respectively, then it will show a bimodal steady-state probability distribution, ρ(q), of some order parameter q. This order parameter can be the concentration of a species, or a combination of the concentrations of a number of species. It is usually interpreted as a reaction coordinate that measures the progress of the reaction from state A to B. Recently, such bimodal distributions have been measured experimentally for biochemical networks (5–7). These distributions are potentially useful, because they are linked to the rate of switching from one state to the other. In particular, we have recently shown (8) that not only for equilibrium systems, but also for systems that are out of equilibrium such as biochemical networks, the rate of switching from state A to state B, k_AB, can be written as the product of two factors:

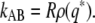(1)

Here, q* denotes the location of the dividing surface, the separatrix (8,9), which separates the two states A and B. The above relation is useful because it shows that the rate of switching from one steady state to the next is given by the probability ρ(q*) of being at the dividing surface, times a kinetic prefactor R that describes the average flux of trajectories crossing the dividing surface. However, while the rate constant k_AB does not depend on the choice of the order parameter q as long as it connects states A and B, both ρ(q*) and R do depend on the choice of q. If q is the true reaction coordinate that accurately describes the switching process, then q* corresponds to the transition state and ρ(q*) and R provide accurate measures for the probability of being at the transition state and the flux of trajectories leaving the transition state for state B (10). A key issue in analyzing rare events in general is therefore identifying the reaction coordinate q that accurately describes the progress of the transition.

FFS can be used to compute k_AB, ρ(q*), R, and to generate members of the transition path ensemble (2–4, 11). To identify the reaction coordinate, the transition paths can be analyzed using committor distributions; this approach is commonly applied in the field of soft-condensed matter physics (10), and we have recently demonstrated how it can be used to analyze the transition pathways of biochemical switches (2). Each configuration x of our system has a commitment probability or committor, P_B(x). This is the probability that a trajectory, fired at random from that configuration, will reach state B before state A. Given P_B(x), we can define the transition state ensemble (TSE) (12), which is the collection of configurations along the reaction pathways which have committor value P_B(x) = 0.5. We can extract TSE configurations from our switching pathways by computing committor values for all the points along the pathways and selecting those points (several per path) with P_B = 0.5. We then try to find an order parameter (or combination of order parameters) that accurately describes these TSE configurations. To test likely order parameters, one can compute the probability distribution for the order parameter for the TSE configurations (2,10). Poorly chosen order parameters will show a broad or even bimodal distribution (13), while good order parameters will show a narrow distribution of values in the TSE.

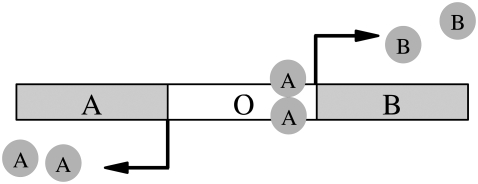
In this article, we apply FFS to study two different models of genetic toggle switches, consisting of two genes A and B that mutually repress each other (2,8,14–20). The genes encode transcription factors (TFs) A and B, respectively. These can form homodimers, in which form they can bind to a regulatory region of the DNA (represented by an operator site O) and regulate transcription. The dimer A₂ represses the transcription of B when bound to O and vice versa (see Fig. 1). In the first model, called the exclusive switch (8,17), the dimers of the two species are not allowed to simultaneously bind to the operator; in the second model, called the general switch, the operator can bind both types of homodimers at the same time (8,17). Both switches have one stable state in which A is abundant, and B scarce, and another stable state in which B is abundant and A scarce. We simulate the switch using the Gillespie algorithm (21), in combination with FFS. The Gillespie algorithm is a widely used and efficient kinetic Monte Carlo scheme (22) for chemical reactions, which generates trajectories in correspondence with the chemical master equation.

FIGURE 1.

Pictorial representation of the model switch, corresponding to the reaction schemes in Eqs. 2a–f. Two divergently-transcribed genes are under the control of a shared regulatory binding site on the DNA (the operator site O). Proteins A and B can bind, in homodimer form, to the operator. Each TF acts to block the production of the other species. In the exclusive switch, only one type of TF can bind at any given time (meaning that the production of both species can never be suppressed), whereas, in the general switch, both types of TF can bind (in which case the production of both species is repressed).

Switching events are driven by random fluctuations. Key fluctuation sources in this network are TF-TF and TF-DNA association and dissociation reactions. By varying the rates of these reactions, while keeping their equilibrium constants fixed, we can vary independently the timescales and hence the correlation times of these fluctuations. The correlation times of fluctuations are important, since they determine the extent to which the fluctuations propagate in the network (23–25).

We therefore begin by calculating how the stability of both switches varies with the rate of TF-TF association and dissociation (dimerization), and with the rate of TF-operator association and dissociation (operator binding). We vary the association and dissociation rates together, keeping their ratio (i.e., the equilibrium constant) unchanged. The switching rate is strongly affected: for both models, k_AB decreases as the rate of operator binding increases, and increases as the rate of dimerization increases. Analyzing the effects on ρ(q*) and R, we find that the two models behave differently: for the exclusive switch, the rate of operator binding changes both ρ(q*) and R, while the rate of dimerization affects only R; for the general switch, the rate of dimerization affects both ρ(q*) and R, while the rate of operator binding predominantly changes ρ(q*).

We then show that the effect of TF-TF and TF-DNA fluctuations on k, R, and ρ(q*) can be understood by elucidating the switching mechanism using committor distributions. We find that for the exclusive switch the difference in total copy number of the two species is not a complete reaction coordinate: the state of the operator is also an important factor in determining the committor value (2). In contrast, we find little evidence that dimerization is an important ingredient of the reaction coordinate. This explains why the rate of operator binding affects both the probability of being at the separatrix and the kinetic prefactor, while dimerization only affects the kinetic prefactor. For the general switch, the situation is markedly different: the switching mechanism is highly robust to changes in both the rate of operator binding and the rate of dimerization. Hence, changing these rate constants does not change the route the switching pathways take in state space, yet does affect the flipping rate. This is a manifestation of the fact that this is a nonequilibrium system—in an equilibrium system the switching rate cannot be changed without changing the switching pathways. The general implication of this observation is that to understand the stability of biochemical switches, we need to understand not only the composition of the transition state ensemble, but also the dynamics of the transition paths.

In the next section, we describe the model genetic switches in more detail. In the subsequent section, we briefly discuss the FFS technique. We then present the results on the switching rate, the kinetic prefactor, and the probability of being at the separatrix for both models, showing how they depend on the rates of operator binding and of dimerization. In the next sections, we discuss switching pathways and reaction coordinates first for the exclusive switch, and then for the general switch. We end with a discussion of the implications of our findings for the modeling of multistable biochemical networks and the study of rare events in other nonequilibrium systems.

MODELS: THE EXCLUSIVE AND THE GENERAL SWITCH

We consider a genetic toggle switch consisting of two genes, each of which represses the other (2,8,14,17,18,26). A switch of this kind has been constructed and shown to be bistable in E. coli (5). We study both the general switch and the exclusive switch, introduced by one of us (8,17). The general switch is represented by the following set of reactions (2,8,17):

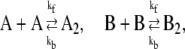(2a)

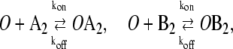(2b)

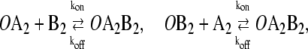(2c)

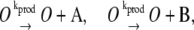(2d)

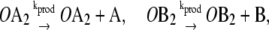(2e)

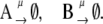(2f)

In this reaction scheme, O represents a DNA regulatory sequence adjacent to two divergently transcribed genes A and B. These code, respectively, for proteins A and B, as shown in Fig. 1. Genes A and B can each randomly produce proteins with the same rate, but whether they do so depends on the state of the operator O. Proteins A and B can each form a homodimer that can bind to the operator. When an A₂ dimer is bound to O, the production of B is blocked, and likewise, when a B₂ dimer is bound to O, the production of A is blocked. When both dimers are bound to the operator, no protein can be produced. Proteins can also vanish (in the monomer form), modeling degradation and dilution in a cell. This model can be modified by removing reactions in Eq. 2c: in this case, transcription factors mutually exclude each other's binding to the operator. We refer to the switch described by the whole set of chemical reactions in Eqs. 2a–f as the general switch; the exclusive switch consists of the same set of reactions, except for reactions in Eq. 2c.

We have assumed in this model that transcription, translation, and protein folding can be modeled as single Poisson processes, neglecting the many substeps that lead to the production of a protein. Warren and ten Wolde (8) discuss the effects of both shot noise and fluctuations in the number of proteins produced per mRNA transcript on the switch stability. We also note here that while mean-field analysis predicts that cooperative binding of the transcription factors to the DNA is essential for bistability (26), it has recently been demonstrated that bistability can be achieved without cooperative binding when the discrete nature of the reactants is taken into account (18).

We choose as the unit of time for our simulations, and we use the volume of the system, V, as the unit of volume. In this article, we will use the following baseline set of parameters: k_f = 5 k_prodV, k_b = 5 k_prod (so that 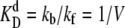), k_on = 5 k_prodV, k_off = k_prod (so that 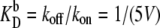), and μ = 0.3 k_prod. These parameters are chosen to be representative of typical cellular values, as discussed in the last section. For simplicity, the model switches are completely symmetrical; rate constants for equivalent reactions involving A and B are the same. The mean field analysis performed in Warren and ten Wolde (8) demonstrates analytically for both systems the existence of three fixed points for the parameter values listed above: two symmetrical stable states, one rich in A and the other rich in B, separated by one unstable state where the total number of A equals the total number of B. This implies that the system can be considered a truly bistable switch. However, while this analysis indicates the regions in parameter space where the system is bistable, it cannot predict the switch stability nor elucidate the switching pathways. For this reason, we carry out stochastic Kinetic Monte Carlo simulations using the Gillespie algorithm (21,22). In previous work, we have shown that the switch stability depends strongly on the mean copy number of species A and B (17), which is given by the ratio of the protein production and decay rates, k_prod/μ. In this article, we investigate its dependence on the other parameters k_f, k_b, k_on, and k_off, which govern key sources of fluctuations in the network—TF-TF and TF-DNA association and dissociation reactions.

METHOD: FORWARD FLUX SAMPLING

Conventional simulation methods are ineffective for studying rare events such as the flipping of biochemical switches, because the vast majority of the computational effort is spent in simulating the uninteresting waiting times in between the events. For this reason, specialized methods are required, and we have recently developed the forward flux sampling (FFS) technique (2–4). FFS is well suited to simulating biochemical networks, since, unlike most other rare event methods (27), it can be used for out-of-equilibrium systems. In this article, we use FFS to calculate rate constants, transition paths, and stationary probability distribution functions for the model genetic switch.

To obtain the rate constant k_AB for a rare transition between two states A and B, FFS exploits the fact that (in steady state) k_AB can be written as the product of two factors:

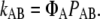(3)

Here, Φ_A is the number of trajectories that leave state A per unit time, while P_AB is the conditional probability that these trajectories subsequently reach state B without returning to A. An order parameter λ must be chosen, which defines states A and B: if λ < λ₀ the system is in state A, while it is in state B if λ > λ_n. The parameter λ is then used to further define a series of nonintersecting interfaces 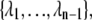with λ_i < λ_i+1, such that any trajectory from A to B has to cross all the interfaces 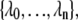without reaching λ_i+1 before it has crossed λ_i. The conditional probability P_AB can be written as

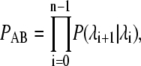(4)

where P(λ_i+1|λ_i) is the conditional probability that a trajectory that comes from A and has crossed λ_i for the first time, will subsequently reach λ_i+1 before returning to A. The factorization of the rate constant k_AB described in Eqs. 3 and 4 was first derived in van Erp et al. (28). Several different algorithms can be used to calculate Φ_A, P(λ_i+1|λ_i) and to obtain transition paths; in this article, we have used the original scheme (2,3). Briefly, one first performs a conventional (i.e., brute-force) simulation to compute Φ_A, which is the number of times that the trajectory crosses λ₀, coming from λ < λ₀, divided by the total simulation time. When one of these crossings occurs, the configuration of the system is stored, so that this simulation run generates not only an estimate for Φ_A, but also a collection of points at interface λ₀. In the next stage, one chooses a point at random from this collection, and fires off a new trajectory from this point, which is continued until the system either reaches the next interface λ₁ or returns to state A. If λ₁ is reached, the system configuration at λ₁ is stored in a new collection. This procedure is repeated a number of times until a sufficiently large number of points at the next interface have been generated. An estimate for P(λ₁|λ₀) is obtained from the number of trials which reached λ₁, divided by the total number of trials fired from λ₀. Starting from the new collection of points at λ₁, one then repeats this whole procedure to drive the system to λ₂, and so on. Eventually, the system reaches state B, upon which the rate constant can be calculated from Eqs. 3 and 4. Furthermore, a (correctly weighted) collection of trajectories corresponding to the transition (i.e., transition paths) can be obtained by tracing back those trial paths that arrive in B to their origin in A.

We have recently shown (11) that this procedure can be used to generate not only the rate constant and transition paths, but also the stationary distribution ρ(q), as a function of a chosen order parameter (or parameters) q. This is achieved by continuously updating a histogram in the parameter q during the trial run procedure, as described in Valeriani et al. (11). To obtain ρ(q), histograms for the forward (A → B) and backward (B → A) transition must be combined. However, since our model switch is symmetric, the two histograms are identical in this case. The parameter q does not have to be the same as λ, although in this article we have chosen q = λ.

In FFS, a series of interfaces are used to drive the system over a barrier, in a ratchetlike manner. The efficiency of the method of course depends on the choice of the order parameter λ, the positioning of the interfaces, number of trials, etc. (4). However, it is important to note that λ does not have to be the true reaction coordinate for the transition. The choice of λ does not impose any bias on the system dynamics: transition paths are free to follow any possible path between states A and B. The choice of λ should not affect the computed rate constant, transition paths or ρ(q). Furthermore, the FFS method does not make a Markovian assumption about the transition paths, or any assumptions about the distribution of state points at the interfaces {λ₀, ···, λ_n}: each point at interface i lies on a true dynamical path which originates in the initial state A. This turns out to be essential for the model genetic switch.

For the FFS calculations presented in this article, we have chosen as λ parameter the difference between the total copy numbers of the two proteins: λ ≡ n_A – n_B, with 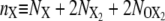the total copy number of species X = A or B in the exclusive switch and 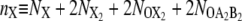the total copy number of species X = A or B in the general switch.

RESULTS

Key sources of fluctuations in this reaction network are TF-TF and TF-DNA association and dissociation reactions. We can vary the influence of these fluctuations on the network dynamics by changing the rate constants for association and dissociation, keeping the equilibrium constant (the ratio of association and dissociation rate constants) fixed, so that the macroscopic dynamics of the system remain unchanged. When these reactions are fast, fluctuations are short-lived on the timescale of the slower protein production and degradation reactions, so that the effect of a fluctuation is lost over just a few production/degradation reactions. However, for slow association-dissociation reactions, fluctuations in, for example, the ratio of monomers to dimers, can persist over the timescale of a series of production/decay reactions, and thus have a strong influence on the dynamics of the whole network. In what follows, we first discuss the effects of varying the rates of operator binding and dimerization on the switching rate for both genetic switch models, and then, to elucidate these effects, we separately discuss the switching pathways for the two cases.

Switching rates

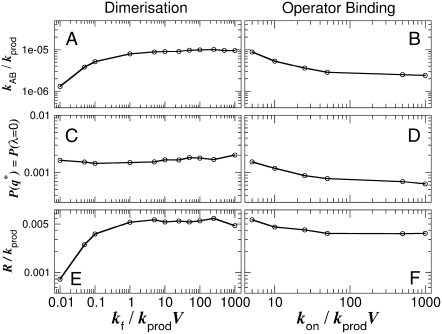
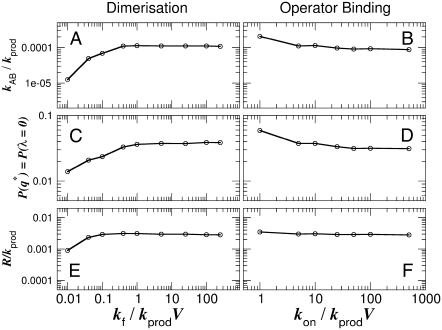
Fig. 2, A and B, shows the flipping rate k_AB for the exclusive switch as a function of the dimerization rate k_f and the operator binding rate k_on, respectively (keeping the dissociation constants constant). The results for the general switch are shown in Fig. 3, A and B. It is clear that for both switches the two sources of fluctuation have very different effects on the stability: while k_AB increases with the rate of dimerization (Fig. 3 A), it decreases with the rate of operator binding (Fig. 2 B). Thus, fluctuations in the TF-DNA association/dissociation reactions tend to destabilize the switch, whereas, counterintuitively, fluctuations in the TF-TF association/dissociation reactions increase the switch stability.

FIGURE 2.

(A and B) Switching rate k_AB for the exclusive switch as a function of the dimerization rate k_f (A) and the rate of operator binding k_on (B). Dissociation rates are scaled such that the equilibrium constants remain constant: 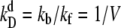and 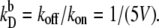Panels C and D show the probability ρ(q*) of being at the dividing surface, as a function of k_f (C) and k_on (D). Panels E and F show the kinetic prefactor, as defined by Eq. 1, as a function of k_f (E) and k_on (F).

FIGURE 3.

(A and B) Switching rate k_AB for the general switch as a function of the dimerization rate k_f (A) and the rate of operator binding k_on (B). Dissociation rates are scaled such that the equilibrium constants remain constant: 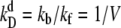and 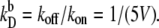Panels C and D show the probability ρ(q*) of being at the dividing surface, as a function of k_f (C) and k_on (D). Panels E and F show the kinetic prefactor, as defined by Eq. 1, as a function of k_f (E) and k_on (F).

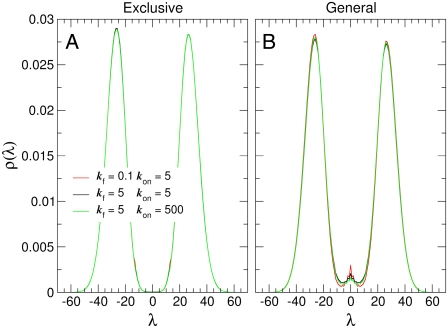
To understand the origin of these effects, we factorize the flipping rate k_AB into the product of the probability of finding the system at the dividing surface ρ(q*) and a kinetic prefactor R, as in Eq. 1. Fig. 4 shows the steady-state probability distribution ρ(λ) of finding the system at a particular value of the order parameter λ, for different values of the dimerization and operator binding rate: Fig. 4 A refers to the exclusive switch and Fig. 4 B to the general switch. These distributions were computed using FFS, as described in Method: Forward Flux Sampling and Valeriani et al. (11).

FIGURE 4.

Probability distribution as a function of the order parameter λ = n_A – n_B, with n_X the total copy number of species X, for the exclusive switch (A) and for the general switch (B). The distributions are obtained with FFS calculations (11), for three different sets of parameters.

We first note that both distributions exhibit peaks at λ ≈ ± 27, corresponding to the two stable states. Secondly, the locations of the two stable states and the shape of the stationary distributions are fairly insensitive to both the rate of dimerization and the rate of operator binding. However, at ∼λ = 0 the distributions, especially that of the general switch, are much more sensitive to changes in the rate constants. Interestingly, the probability of finding the system at the value λ = 0 is markedly differently for the two models: while for the exclusive switch ρ(λ) exhibits a minimum, representing an unstable steady state for the system, in the case of the general switch, the probability distribution has a local maximum, indicating the presence of a metastable steady state (8,18). Finally, we note that for an equilibrium system, fluctuations do not influence the stationary distribution function: the effect of k_f and k_on on ρ(q) is a clear characteristic of the nonequilibrium nature of the dynamics in this system.

From the distribution ρ(q), we compute the probability of being at the minimum of the curve, ρ(q*). For the exclusive switch, this point corresponds to the dividing surface ρ(λ = 0); we show in Fig. 2, C and D, how this quantity varies with k_f and k_on, respectively. In the case of the general switch, the transition happens through the metastable state at λ = 0. However, the rate-limiting step for the flipping is to get to the minimum of ρ(λ), which is now located at λ ≈ ± 5. Therefore, for the general switch, ρ(q*) was computed for q* = λ = 5; it is shown in Fig. 3, C and D. By combining ρ(q*) with Eq. 1, we compute the kinetic prefactor R, shown in Fig. 2, E and F, and Fig. 3, E and F, for the exclusive and general switches, respectively.

We observe that, for the exclusive switch, ρ(q*) depends upon the operator binding rate (Fig. 2 D), but not upon the rate of dimerization (Fig. 2 C), while for the general switch, ρ(q*) depends upon both rate constants (Fig. 3, C and D). In both models, the kinetic prefactor R increases with the rate of dimerization (Figs. 2 E and 3 E), while it decreases with the rate of operator binding (albeit much less so in the general switch; Figs. 2 F and 3 F). One might expect that a change in ρ(q*) reflects a change in the location of the switching pathways in state space. This would suggest that in the general switch, the switching pathways depend upon both the rate of dimerization and the rate of operator binding, while for the exclusive switch the switching mechanism does depend upon the rate of operator binding, but not on the rate of dimerization. While the conclusion for the exclusive switch is correct, that for the general switch is not, as we discuss in the next two sections.

Switching pathways—exclusive switch

To understand the effects of the operator binding and dimerization fluctuations on the switching rate, we would like to determine what the true reaction coordinate is for the switching process and whether it involves these fluctuations. To do this, we need to examine the transition paths for switching, which are also generated by FFS. We will focus on three sets of parameters:

1. The base-line set, with operator binding rate k_on = 5 k_prodV and dimerization rate k_f = 5 k_prodV.

2. A set with slow dimerization, k_f = 0.1 k_prodV and k_on = 5 k_prodV.

3. A set with fast operator binding, k_on = 500 k_prodV and k_f = 5 k_prodV.

As above, in all cases the dissociation rates are scaled such that the equilibrium constants remain constant: 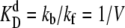and 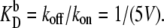In this section, we discuss the exclusive switch, while the next section focuses on the general switch.

To analyze the progress of the system as it flips from one state to the other, we have averaged the switching trajectories in the P_B ensemble. The committor P_B(x) is the probability that a trajectory propagated at random from configuration x reaches state B before state A. The P_B ensemble is formed by those configurations x that have the same value of P_B; 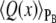thus denotes the average of a quantity Q(x) in the ensemble of configurations x with the same value of P_B. Given an ensemble of switching paths obtained with FFS, we can harvest configurations x with the same value of P_B. Indeed, each transition path has at least one configuration for every value of P_B. The term P_B(x) can be used to characterize the progress of the transition from A to B—in a sense, it is the true reaction coordinate and our task is to identify coordinates that characterize P_B. However, its evaluation is computationally very expensive. We have computed P_B for configurations in the transition paths that were generated using FFS, by firing 100 test trajectories from each configuration. The average paths in the P_B ensemble are rather noisy, precisely because P_B is a stochastic quantity that has to be estimated by a computationally demanding procedure.

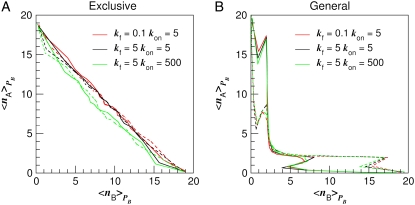
Fig. 5 A shows the average switching pathways for the exclusive switch in the n_A, n_B plane, where n_A and n_B are the total copy numbers of species A and B, respectively (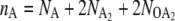 for the exclusive switch and 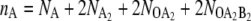for the general switch; similarly for B). Paths are shown for both the A → B (solid lines) and B → A (dashed lines) transitions. Considering the red and black lines in Fig. 5 A, we see that the dimerization rate k_f has little effect on the switching pathways (at least in this representation), whereas, on considering the green and black lines, it is clear that the operator binding rate k_on does strongly influence the switching pathways, especially in the region of the dividing surface, where n_A = n_B: the pathways shift to lower values of n_A and n_B when k_on is increased.

FIGURE 5.

Switching paths projected onto the n_A, n_B surface, for three different sets of parameters. (A) Paths averaged in the P_B ensemble for the exclusive switch, where n_A and n_B are averaged over configurations with the same value of P_B, where n_X is the total copy number of species X. The forward paths, corresponding to transitions from A to B, are shown with solid lines, while the reverse transitions, from B to A, are shown with dashed lines. (B) Switching paths for the general switch. In this projection, the paths are highly insensitive to variations in parameters. The hypersurface λ = 0 is crossed with a lower total number of A- and B-molecules.

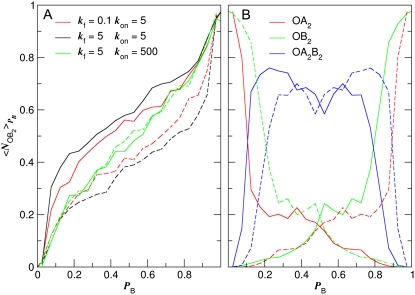
Since it appears from Fig. 5 A that the state of the operator is likely to play an important role in the switching mechanism, we plot in Fig. 6 A the probability that the operator is bound by a B₂ dimer, 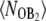as a function of λ. Comparing the solid black and red lines, we see that changing the rate of dimerization has indeed little effect on the transition paths. In contrast, a comparison of the black and green solid lines shows that changing the rate of operator binding has a strong effect on the switching pathways. This indicates that operator state fluctuations play an important role in switch flipping (2,9)—so that the reaction coordinate depends not only on the difference in the number of protein molecules, λ, but also on which protein is bound to the operator.

FIGURE 6.

(A) Exclusive switch: probability that a B₂ dimer is bound to the operator, 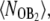as a function of P_B for three different sets of parameters. The solid lines correspond to the transition from A to B, while the dashed lines corresponds to the reverse transition from B to A. (B) General switch: operator occupancies during the transition from A to B and vice versa (the empty state O is not shown since it is always scarcely occupied), for the baseline parameter set; the results for the other parameter sets are indistinguishable.

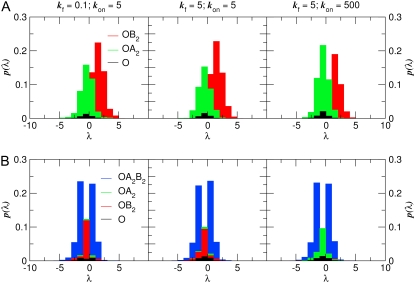
This fact is further illustrated in Fig. 7, which shows histograms for configurations in the TSE of the transition from A to B; members of the TSE are points along the transition paths for which P_B = 0.5. Each panel in Fig. 7 corresponds to a different parameter set—the baseline parameter set in the center, slow dimerization on the left, and fast operator binding on the right. In each case, we divide the collection of TSE configurations according to the state of the operator. For each operator state, we plot histograms for the λ-coordinate, in such a way that the area under a histogram corresponds to the total number of TSE points with that operator state. The histograms are color-coded according to operator state. Considering first the central panel of the upper row (baseline parameter set), we see that the green histogram (OA₂) is shifted toward smaller values of λ than the red histogram (OB₂)— i.e., the state of the operator and λ are correlated in the TSE. This means that if a B-dimer is bound to the operator, then, on average, the number of A-molecules has to exceed the number of B-molecules to have the same value of P_B, and vice versa. We also see that the area under the OB₂ histogram is larger than that under the OA₂ histogram—indicating that the TSE has predominantly B₂ bound to the operator, even though the switch is symmetric. Turning next to the right panel—rapid operator association and dissociation—we see that again the OA₂ histogram is shifted toward smaller values of λ relative to the OB₂. However, in this case, the areas under the two histograms are approximately equal. Thus, increasing the rate of operator binding appears to have caused the transition state for switch flipping to become symmetric in A and B. The left panel shows the results for slow dimerization, k_f = 0.1. This plot is virtually indistinguishable from the baseline parameter results, indicating that changing the dimerization rate has little effect on the transition state ensemble, as suggested by Fig. 6 A. These results unambiguously demonstrate that, for the exclusive switch, fluctuations arising from TF-DNA association-dissociation reactions are central to the flipping mechanism, while those arising from TF-TF association-dissociation reactions have little effect on the flipping mechanism, although they can influence the dynamics of the flipping trajectories and hence the switching rate.

FIGURE 7.

The probability ρ(λ) for the transition state ensemble (P_B = 0.5) for the transition from A to B, where λ = n_A – n_B. (Top row, A) Exclusive switch. (Bottom row, B) General switch. The probability ρ(λ) is split into color-coded contributions from the three operator states; the area under each histogram gives the probability 〈N_OX〉 that the operator is bound to species X (the three areas thus sum to unity). The left panels correspond to the system with slow dimerization k_f = 0.1; the middle panels correspond to the system with the base-line parameters; the panels on the right corresponds to the system with fast operator binding k_on = 500.

Drawing together the observations of Figs. 2, 4 A, 5 A, 6 A, and 7, we can now understand the dependence of the exclusive switch flipping rate on the rate of operator binding (Fig. 2 B). In the limit of slow operator binding and unbinding (2,9), the binding of the minority species to the operator strongly enhances the flipping of the switch: when the minority species happens to bind the operator, it will stay on the DNA for a relatively long time, thus blocking the synthesis of the majority species and allowing the production of the minority species. In this limit, the system can reach the dividing surface with relatively few production/degradation events. As the rate of operator binding and unbinding is increased, each transition involves many operator binding/unbinding events, and consequently proteins of both species are produced and decay during the transition process. Here, the state of the operator is increasingly slaved to the difference in the total number of A- and B-molecules, λ. In the adiabatic limit of fast operator binding, the probability that a molecule of type A or B is bound to the operator is completely determined by λ (9). In this limit, the dividing surface is located at λ ≈ 0 and 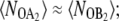to reach the separatrix, the system has to wait for a series of fluctuations in the birth and decay of both species that lead to n_A ≈ n_B. This implies that the total number of copies of A and B at the dividing surface decreases as the rate of operator binding increases (Fig. 5 A). Because a series of production/decay events are required to reach the separatrix, the probability ρ(q*) is decreased as the rate of operator binding increases (Fig. 2 D). In addition, having reached the separatrix, the system requires more production/decay events to take it to the B-state. This increases the probability that it will recross the separatrix and eventually return to A instead of contributing to B—resulting in a decrease in the kinetic prefactor R in Fig. 2 F.

Figs. 5–7 suggest that the rate of dimerization only has a marginal effect on the switching pathways. However, our view of the switching pathways naturally depends on the representation in which we choose to plot them. We have investigated many representations to see whether the rate of dimerization could affect the switching pathways. Perhaps the most important one is the average number of dimers 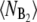as a function of 〈N_B(N_B – 1)〉. However, also in this representation the rate of dimerization only has a very minor effect on the switching pathways; in fact, near the top of the dividing surface, the dimerization reaction is in steady state (data not shown). This supports our conclusion that dimerization affects the rate at which the transition paths traverse state space (and hence R), but not the route they take (and thus not ρ(q*)).

The effect of TF-TF association/dissociation fluctuations on the dynamics of the trajectories can perhaps be understood by considering that to start a switching event from one stable state to the other, two copies of the minority species must be produced. They must then dimerize and bind to the operator, to shut down production of the majority species. If the dimerization rate is comparable to the degradation rate, it becomes increasingly probable that copies of the minority species, once produced, are removed from the system before they can form a dimer. Thus, decreasing the dimerization rate actually reduces the chance that the switch can flip. This effect is truly dynamical in origin. We note that it is also fundamentally different from enhanced switch stability via cooperativity due to nonlinear degradation (29).

Lastly, while operator binding is an equilibrium reaction, it couples to reactions that are out of equilibrium, such as protein production and decay. As a result, the dynamics of operator binding can lead the exclusive switch to behavior that is unique for nonequilibrium systems. This can be seen by comparing the forward paths from A to B with the backward paths from B to A in Fig. 6 A. When the rate of operator binding is fast, the forward and backward paths essentially coincide. This situation differs markedly for the system with the base-line parameter set and for the system with slow dimerization: although the switch is symmetric on interchanging A and B, the transition path ensemble for the transition from A to B does not coincide with that from B to A (2). This is a manifestation of the fact that this switch is a nonequilibrium system: for equilibrium systems that obey detailed balance and microscopic reversibility, the forward and backward paths must necessarily coincide. The fact that the forward and backward paths do not coincide also means that the switching paths do not follow the path of highest steady-state phase space density, which, for equilibrium systems, would correspond to the lowest free-energy path: Since this system is symmetric, this lowest-free energy path is symmetric on interchanging species A and B, while Fig. 6 A shows that the dynamical switching trajectories are not (unless operator binding is fast). This also means that for this system it is essential not to make the Markovian assumption of memory loss, which underlies path sampling schemes such as Milestoning (30) and PPTIS (31).

Switching pathways—general switch

We now turn our attention to the switching pathways for the general switch, again obtained with FFS. Fig. 5 B shows for the three different parameter sets the switching trajectories as averaged in the P_B ensemble and projected onto the n_A, n_B plane. As for the exclusive switch, the forward and backward paths do not coincide, which, as mentioned above, reflects the fact that the genetic switch is a nonequilibrium system. However, in many other respects the pathways of the general switch differ markedly from those of the exclusive switch. Firstly, the switching trajectories of the general switch cross the dividing surface λ = 0 at very low values of n_A and n_B—on average, there is only one dimer of each species at the transition surface. Moreover, the paths display a sharp deviation when they reach the dividing surface. Lastly, paths obtained for different values of the rate constants essentially coincide (the black, red, and green lines overlap). This last observation suggests that the transition paths are rather insensitive to variations in the rate constants of dimerization and operator binding, an observation that should be contrasted with the observation that both ρ(q*) and R do depend upon the magnitude of those rate constants (see Fig. 3).

Fig. 6 B shows the state of the operator for every value of λ during the transition, for the baseline parameter set (the curves for the other parameter sets are virtually indistinguishable). Initially, when the system is still in the basin of attraction of the stable state A, the operator is mostly in state OA₂. However, as the system leaves this basin, the state of the operator rapidly becomes dominated by OA₂B₂. Indeed, this operator state, which is absent in the exclusive switch, plays a pivotal role in flipping the general switch. Its occupancy peaks at λ ≈ −5, corresponding to the top of the barrier that separates the stable state A at λ = −27 from the metastable state at λ = 0. Here, at λ = 0, the occupation statistics of the operator is given by the equilibrium distribution [OA₂]:[OB₂]:[OA₂B₂], with [OA₂] = [OB₂]. As Fig. 7 B shows, the transition state ensemble coincides with the metastable state at ∼λ = 0, and in this ensemble the operator is predominantly in state [OA₂B₂]. As the system leaves the metastable state toward the B-state, the state of the operator progressively moves toward [OB₂].

We are now able to explain the process of flipping the general switch. When a dimer of the minority species is produced, it immediately binds to the operator and drives it in the state OA₂B₂. In this state, the production of both proteins is suppressed, and the system is depleted of almost all its components (17,18). The approach to the transition state is then driven mostly by a decrease of the majority species via protein decay rather than an increase of the minority species via protein production, as in the exclusive switch; this is the reason why the general switch crosses the diving surface at lower values of n_A and n_B than the exclusive switch. Importantly, if one of the two dimers leaves the operator, it can immediately rebind, thereby restoring the previous situation and allowing the transition to continue. By contrast, if the minority species leaves the operator in the exclusive switch, then most likely the majority species will bind the operator, thereby blocking further progress of the transition. This explains why both the pathways and the rate of flipping are much more sensitive to the rate of operator binding in the exclusive switch than in the general switch.

The presence of the state OA₂B₂ also underlies the metastability of the general switch at λ = 0 (Fig. 4 B). As long as both species are present in the system, the state OA₂B₂ is the most stable operator state, and in this state no proteins can be produced. As a consequence, a small fluctuation in λ away from λ = 0 via the unbinding of, say, dimer A leading to the production of protein B, is not sufficient to flip the switch: most likely the dimer will rebind the operator, blocking further production of B; only when the dimer A dissociates and one of its monomers is degraded will the system commit itself to the stable-state B. The probability that the dimer is degraded before it rebinds the operator increases as the rate of dimer dissociation increases; this is the origin of the increase of k_AB, R, and ρ(q*) with increasing dimerization rate k_f for low k_f seen in Fig. 3. Finally, we note that the discrete character of the components in combination with their low copy number is important (32,33): flipping the switch away from the metastable state at λ = 0 requires the unbinding and subsequent degradation of essentially one molecule. The metastability is indeed absent in a mean-field continuum analysis that ignores the discrete nature of the components.

DISCUSSION

In this article, we have analyzed the stability and switch flipping dynamics of two types of bistable genetic toggle switches, as a function of the rates of transcription factor dimerization and operator binding. This allows us to assess the influence of two key sources of fluctuations in the network on the overall system behavior.

We have varied the rate constants of the TF-TF and TF-DNA association/dissociation reactions over greater than three orders of magnitude (see Figs. 2 and 3). This reflects the wide range of observed rate constants for cellular biochemical reactions. For instance, in prokaryotic cells, the inverse rate of protein production, 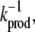is in the range of seconds to minutes (34). Since the size of a typical prokaryote is ∼1 μm³ (based on E. coli), this corresponds to k_prodV = 10⁻² – 10 nM⁻¹/min. The rate of monomer-monomer association, k_f, is ∼10⁻² – 10⁻¹ nM⁻¹/min, while the dimer dissociation rate is ∼k_d = 10⁻² – 10³/min, corresponding to dissociation constants in the range 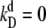– 10² nM (29). This means that k_f = 10⁻² – 10 k_prodV. Figs. 2 A and 3 A show that the switching rate k_AB is fairly insensitive to changes in the dimerization rate when k_f > k_prodV, but is highly sensitive to dimerization rate for k_f < k_prodV. This shows that the rate of dimerization can strongly affect the network stability under biologically relevant conditions. Rate constants for protein-DNA association/dissociation are observed to vary over a similarly broad range (34). Figs. 2 B and 3 B demonstrate that this variation can have a marked effect on flipping rates for multistable networks in living cells.

The steady-state phase space density in the region of the stable states is very robust to every parameter change (Fig. 4). Yet, changing the rate constants does strongly affect the switching between these states. Factorizing the switching rate into the probability ρ(q*) of finding the system at the dividing surface, and a kinetic prefactor R, we find different results for the two versions of the switch: while for the exclusive switch dimerization affects the switching rate predominantly via the kinetic prefactor, for the general switch it affects both the kinetic prefactor and the probability of being at the separatrix; on the other hand, operator binding affects the flipping rate of the exclusive switch both via R and ρ(q*), whereas the effects on the flipping rate of the general switch are exerted predominantly through a modification of its steady-state distribution near the separatrix.

These results can be understood by analyzing the transition paths and the transition state ensemble (TSE). This shows that, in the case of the exclusive switch, changes in the operator binding rate strongly affect the properties of the TSE, while the dimerization rate has little effect on the TSE. We conclude that, for the exclusive switch, operator binding fluctuations play a crucial part in the reaction coordinate, while dimerization fluctuations can affect the dynamics of the transition but have little effect on the route that it takes in phase space. The case of the general switch is rather different: here, the presence of the sterile, doubly-bound state OA₂B₂ makes the flipping pathways rather insensitive to both sources of fluctuations, even though the latter do affect the flipping rate. The resolution of this paradox lies in the fact that the switch is a nonequilibrium system: in contrast to equilibrium systems that obey detailed balance and microscopic reversibility, in nonequilibrium systems the forward and backward transition paths can form a cycle, as observed here; changing microscopic transition rates (i.e., reaction rate constants) can then change the stationary distribution ρ(q) and the flipping rate, even though the location of the transition paths in state space is unaltered. Protein-protein and protein-DNA association and dissociation reactions are a common feature of a wide range of biological control networks. We therefore hope that our results will be useful to understand the factors governing stability in multistable biochemical networks in general.

Genetic switch flipping is an example of a nonequilibrium rare event. Rather few studies have been made of rare events in nonequilibrium systems, but a variety of simulation and analytical approaches have been developed to analyze rare events in equilibrium systems. Here, it is often assumed that one coordinate, the reaction coordinate, is slow, while the other degrees of freedom are fast. In this case, the transition can be modeled by assuming that the reaction coordinate evolves according to a Langevin equation, while the other degrees of freedom play the role of friction. Although the concept of free energy is not applicable to nonequilibrium systems, one can nevertheless define a barrier that corresponds to the maximum of −log ρ(q), as we do in this article. The results presented here show that that barrier crossing in the model toggle switch differs fundamentally from this classical scenario. For the genetic switch, the reaction coordinate consists of at least two parameters, namely the difference in total copy number of species A and B and the state of the operator (2). Moreover, these coordinates evolve on comparable timescales—the operator state fluctuates on timescales similar to those of protein production and decay; in addition, their dynamics mix in a nonequilibrium fashion (9)—the degradation and production of proteins are nonequilibrium processes. This hampers the application of standard theoretical tools to model barrier crossings (9). New theoretical approaches may be required to model such rare events in nonequilibrium systems.