Motions and structural variability within toxins: Implication for their use as scaffolds for protein engineering

Abstract

Animal toxins are small proteins built on the basis of a few disulfide bonded frameworks. Because of their high variability in sequence and biologic function, these proteins are now used as templates for protein engineering. Here we report the extensive characterization of the structure and dynamics of two toxin folds, the “three-finger” fold and the short α/β scorpion fold found in snake and scorpion venoms, respectively. These two folds have a very different architecture; the short α/β scorpion fold is highly compact, whereas the “three-finger” fold is a β structure presenting large flexible loops. First, the crystal structure of the snake toxin α was solved at 1.8-Å resolution. Then, long molecular dynamics simulations (10 ns) in water boxes of the snake toxin α and the scorpion charybdotoxin were performed, starting either from the crystal or the solution structure. For both proteins, the crystal structure is stabilized by more hydrogen bonds than the solution structure, and the trajectory starting from the X-ray structure is more stable than the trajectory started from the NMR structure. The trajectories started from the X-ray structure are in agreement with the experimental NMR and X-ray data about the protein dynamics. Both proteins exhibit fast motions with an amplitude correlated to their secondary structure. In contrast, slower motions are essentially only observed in toxin α. The regions submitted to rare motions during the simulations are those that exhibit millisecond time-scale motions. Lastly, the structural variations within each fold family are described. The localization and the amplitude of these variations suggest that the regions presenting large-scale motions should be those tolerant to large insertions or deletions.

Because of their high affinity and specificity toward their biologic targets, animal toxins have been extensively studied. They exert a wide range of biologic functions from a limited number of frameworks, suggesting that they result from a divergent evolution (Guidebook 1997; Ohno et al. 1998). Most toxins extracted from scorpion venom adopt the same fold, and in snake venom, only six different scaffolds are found (Ménez 1998; Servent and Ménez 2001).

Animal toxins are small-size peptides, generally less than 120 amino acids, have a high content of disulfide bridges, and are stable molecules toward both denaturing conditions and enzymatic attack. Each fold is characterized by a cysteine consensus sequence, which corresponds to a conserved spatial arrangement of the disulfide bridges. Comparison between the known toxin sequences within each structural family shows that in addition to the cysteines, only few residues are conserved. Because they are resistant to degradation and permissive to mutations, they are used as templates for protein engineering (Vita et al. 1995, 1999; Mer et al. 1998; Mourier et al. 2000; Ricciardi et al. 2000).

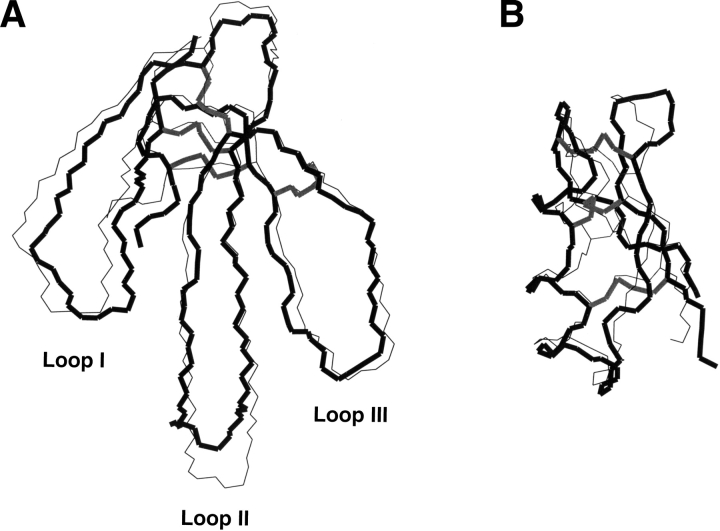
Here we report an extensive study of the structural and dynamic properties of two toxin folds chosen for their different structural properties and different behaviors in protein engineering. The two analyzed folds are the short α/β scorpion fold adopted by scorpion toxins, and the “three-finger” fold from snake venom (Fig. 1 ▶). These two folds differ on several points that make the comparison of their structural and dynamic characteristics particularly attractive. The short α/β scorpion fold is very small (less than 40 amino acids), and presents two types of canonical secondary structure and a very central positioning of the three disulfide bridges that connect the two secondary structure elements. On the opposite, the “three-finger” fold is medium size (around 60 amino acids), contains only β-sheets, and its four disulfide bridges form a knot located at one extremity of the fold. It is characterized by the presence of three large flexible loops. Loops II and III form a three-stranded β-sheet, whereas loop I display few connections to the rest of the structure.

Figure 1.

Structure of (A) toxin α and (B) charybdotoxin adopting the “three-finger” and the α/β scorpion fold, respectively. Backbone superimposition of the X-ray (backbone in black thick line and disulfide bridges in gray) and average NMR structures (thin line and disulfide bridges in dark gray).

As an example of the short α/β scorpion fold and of the snake “three-finger” fold, charybdotoxin from Leiurus quinquestriatus hebraeus and toxin α from Naja nigricollis were respectively chosen (Fig. 1 ▶). The solution structures of charybdotoxin (Bontems et al. 1991) and toxin α (Zinn-Justin et al. 1992) were solved in our laboratory on the basis of NMR data. X-ray studies provide a complementary source of structural information, as the molecule environment and the nature of the experimental data are fundamentally different. The resolution of the crystal structure of toxin α is reported in this article. The crystal structure of charybdotoxin is a personal communication, and will be the subject of a detailed publication by Alda Navaza.

We first describe the X-ray structure of toxin α. Then for toxin α and charybdotoxin, the crystal and solution structure are compared, as the molecular dynamics trajectories started from either the crystal or the solution structures. For both proteins, the crystal structure is better stabilized by hydrogen bonds than the solution structure, and the trajectory starting from X-ray structure is more stable than the trajectory started from the NMR structure. The trajectories started from X-ray structure are in agreement with the experimental NMR and X-ray data available on the toxin dynamics. Analysis of the amplitudes and time scales of the protein internal motions shows that large differences exist between toxin α and charybdotoxin. Such differences seem to be related to the structural variability within each fold family. On the basis of this comparison, the respective structural permissiveness of the two toxin folds is discussed.

Results

Structure and dynamics of toxin α

X-ray structure of toxin α.

The three-dimensional crystal structure of toxin α was solved by X-ray crystallography at 1.8-Å resolution (see Materials and Methods). Toxin α adopts the “three-finger” motif common to other snake toxins. It consists of three loops that protrude from a central core, tightened by four disulfide bridges (Cys3–Cys23, Cys17–Cys40, Cys42–Cys53, Cys54–Cys59). Loops II and III form a three-stranded β-sheet (residues 33–39, 23–30, and 49–54) stabilized by 15 backbone–backbone hydrogen bonds (Table 1). Loop I forms a two-stranded β-sheet (residues 1–5 and 13–17) stabilized by four backbone–backbone hydrogen bonds. Loop I is connected by one backbone–backbone hydrogen bond to loop II and by another one to the C-terminal part.

Table 1.

Main-chain hydrogen bonds in the X-ray, NMR, and simulated structures of toxin α determined using the DSSP program (Kabsch and Sander 1983)

Residue		Hydrogen bond
NH	CO	X-ray	NMR(%)	MD(%)
X1
Q2*		D57.od1	—	D57.od1
C3*	K15	X	X	97
H4*	K58	R60.od1	X	44
N5*	T13	X	X	72
Q6*	T13	Q6.oe1	—	—
Q7
S8	136	X	88	—
S9
Q10*	Q7	X	X	36
P11
P12
T13*	P11	Q6.oe1	—	95
T14
K15*	C3	X	X	X
T16
C17*	X1	X	X	79
P18
G19	C17	—	X	X
Q20	C17	X	X	—
T21
N22*
C23*	C54	X	X	64
Y24*	G39	X	X	X
K25*	N52	X	X	X
K26*	Q37	X	X	X
V27*	K50	X	X	X
W28*	I35	X	X	X
R29*	G48	—	38	—
D30*	G33	X	X	X
H31
R32
G33	D30	X
T34*
I35*	W28	X	X	X
I36*	T34	S8.og	—	41
Q37*	K26	X	X	X
R38*	Q6	—	—	28
G39*	Y24	X	X	95
C40
G41*	N22	X	X	X
C42
P43
T44
V45*
K46*	T44			36
P47
G48	K46		50
I49*	K46	X	X	82
K50*	V27	X	X	95
N52*	K25	X	X	X
C53
C54*	C23	X	X	X
T55
T56*
D57
K58*	Q2	X	50	97
C59	T56	X	75	51
N60*		N60.og		46
N61*		C59.o		C59.o

Residue names with an asterisk are those for which the amide proton is found to be protected from the exchange by NMR. “X” indicates that the hydrogen bond is present in the X-ray structure, or at 100% present in NMR and simulated structures. Percentage of structures presenting the hydrogen bond is indicated for NMR and simulated structures when different from 100%. Identified side-chain acceptors are also indicated.

Comparison of the NMR and X-ray structures.

Figure 1 ▶ shows a superimposition of the three-dimensional solution (Zinn-Justin et al. 1992) and crystal structures of toxin α. The Cα root-mean-square deviation calculated between both structures yields 1.51 Å. This deviation is related to the difference of resolution between the solution and crystal structures (resolution of the X-ray structure: 1.8 Å; equivalent resolution calculated with PROCHECK_NMR (Laskowski et al. 1996) for the NMR structures: 2.5 Å). The most significant differences are found at the tip of loop II: His31 (5.07 Å), Arg32 (5.59 Å); in loop I: Pro11 (2.77 Å), Pro12 (3.30 Å), Thr13 (2.48 Å), and at the C-terminus: Asn61 (3.01 Å). The conformational flexibility of loop II may be partly responsible for these differences. It should also be pointed out that His31 and Thr34 are involved in crystal packing.

The backbone hydrogen bond network is similar for both models (Table 1). The main difference is the presence, in the X-ray structure, of one additional hydrogen bond 33HN–30O in the β-turn of loop II. Furthermore, at residues Cys17 and Lys46, branched hydrogen bonds are observed, for which a carbonyl may have one or two donors depending on the structure. Finally, in the X-ray structure, six amides appear to be hydrogen bonded to a side-chain oxygen atom, while such interactions are not found in solution structure.

It is clear that some hydrogen bonds exist in solution that are not described by the NMR structure of toxin α. Indeed, 35 amide protons exchange sufficiently slowly with the solvent to be observed after 1 h of exchange in D₂O by NMR (Table 1). Most of these protected amide protons are involved in a hydrogen bond in the X-ray structure. For only seven of them no hydrogen bond could be identified. As a comparison, 12 protected amide protons were not involved in a hydrogen bond in the solution structure.

In conclusion, the X-ray structure is more accurate and gives a better description of the hydrogen bond network of the protein compared to the solution structure.

Comparison of the NMR and X-ray trajectories.

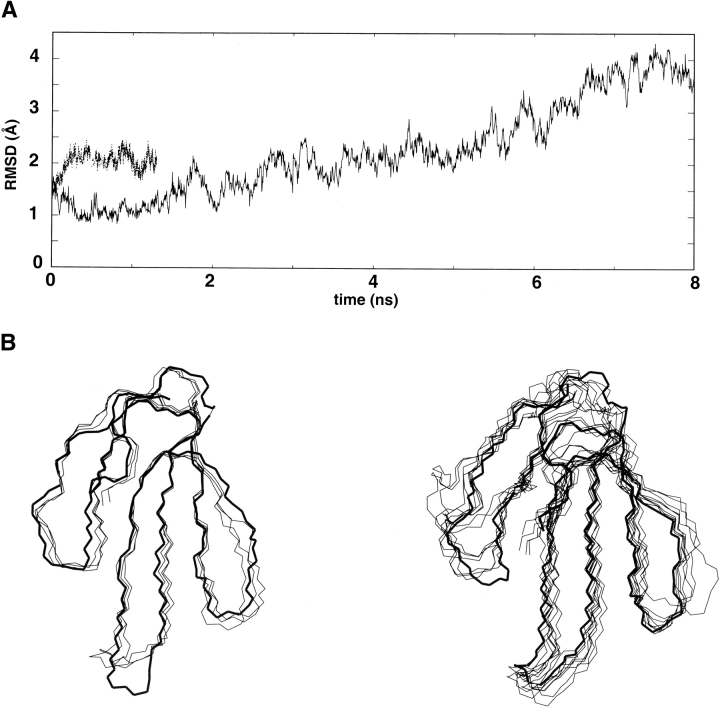
The simulation starting from the crystal structure (named X-ray trajectory) is more stable than the trajectory started from the solution (named NMR trajectory) structure (Fig. 2A ▶). During the NMR trajectory, the root-mean-square deviation increases rapidly to reach 2.3 Å at 1 ns. The superimposition of frames extracted from the NMR trajectory (Fig. 2B ▶) reveals that this deviation is mainly due to structural perturbations in the N- and C-terminal regions and around the β-turn Pro18–Gly19. These perturbations are correlated to the loss of three backbone hydrogen bonds (Cys3.HN–Lys15.O, Cys17.HN–Leu1.O, and Lys58.HN–Glu2.O), leading to a partial unfolding that prevent us from carrying on the trajectory. During the X-ray trajectory, the root-mean-square deviation remains lower than 2.5 Å until 6 ns. In the X-ray structure, the N- and C-terminal regions are stabilized by two backbone–side chain hydrogen bonds (Glu2.HN–Asp57.Od1, His4.HN–Arg60.Od1). The structures extract from the first 6 ns of the X-ray trajectory present their most important deviation in loop I. Analysis of the trajectory shows that: (1) after 2 ns, one backbone–backbone hydrogen bond involving loop I is lost (Ser8.HN–Ile36.O), and (2) between 2 and 6 ns, four backbone–side chain hydrogen bonds observed in the crystal structure of loop I are replaced by backbone–backbone hydrogen bonds (Table 1). The loss of these hydrogen bonds could explain the deviation of the first loop. In conclusion, we propose that the difference of stability observed between the two trajectories is due to the different accuracy of the starting structures, and in particular, to the different quality of definition of the hydrogen bond networks.

Figure 2.

Analysis of the molecular dynamics simulations of toxin α: (A) Variation of the root-mean-square deviation between the backbone atom positions along the trajectories relative to their initial positions (thin and thick lines correspond to trajectories started from NMR and X-ray structures, respectively). (B) Snapshots (one per ns) extracted from the trajectories started from the average NMR structure (left) and X-ray structure (right). The starting structures are represented in thick lines.

Comparison of temperature factors obtained from the X-ray structure and the X-ray trajectory.

B-factor variations along the sequence are similar for crystallographic and simulation data (see Electronic Supplemental Material). Differences are observed only in loop I (residues Asn5 to Lys15) and at the tip of loop II (residues Arg29 to Thr34). Discrepancies in loop II are probably due to intermolecular interactions in the crystal. Such intermolecular interactions are not taken into account in the water box simulation. In loop I, it is clearly due to a deviation from the native structure generated during the simulation.

NH and CαH order parameters obtained from the NMR relaxation data and the X-ray trajectory.

Order parameters reflecting the amplitude of the ps to ns time-scale motions were calculated from the 6-ns trajectory (see Materials and Methods) and are compared in Figure 3 ▶ to experimental values determined from NMR relaxation data (Guenneugues et al. 1999). The agreement between the experimental and simulated values is good. For the NH as for the CαH vectors, the highest values of the order parameters correspond to residues in secondary structure elements, and the lowest ones correspond to residues in loops. Both experimental and simulated order parameter values are lower for the NH than for the CαH vectors. This was already described in other studies, and could be attributed to anticorrelated variations of the phi and psi torsion angles (Fadel et al. 1995; Guenneugues et al. 1999).

Figure 3.

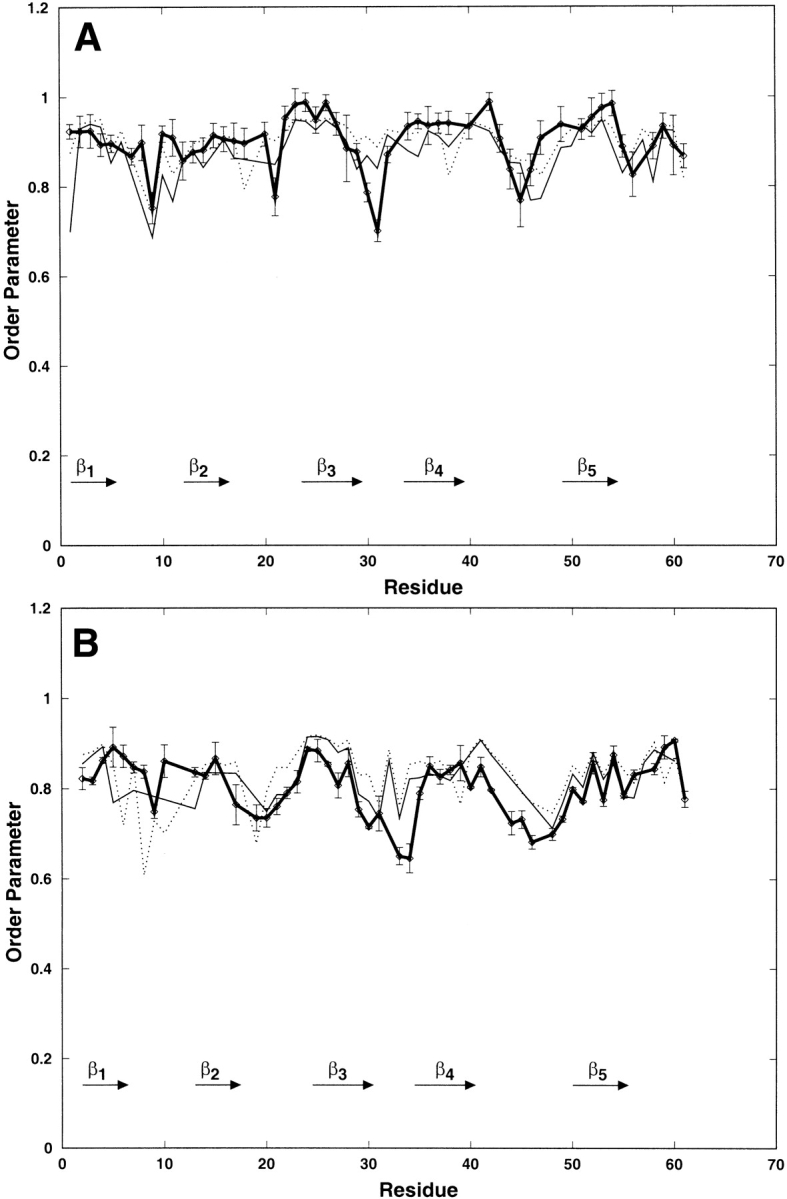
Variation along the sequence of the backbone CαH (A) and NH (B) order parameters of toxin α extracted from the NMR data (thick line) and calculated from the 6 ns trajectory started from the X-ray structure; the order parameters are calculated from correlation functions truncated at 100 ps (thin dotted line) and 600 ps (thin line).

For the CαH vectors, over 52 S² values, several simulated values differ by more than 0.1 from the experimental ones: 8 S²₆₀₀ (residues 1,8,11,15,18, 31, 47, and 61) and 6 S²₁₀₀ (residues 8, 18, 21,30, 31, and 38). These discrepancies essentially concern residues in loop I and at the tip of loop II. In loop I, experimental values are higher than simulated ones, and using a larger part of the correlation functions (600 ps instead of 100 ps) did not improve the agreement. Concerning the tip of loop II, experimental S² values are smaller than the simulated ones, and using a larger part of the correlation function provides a better agreement only for residue 30.

For the NH vectors, over 52 S² values, several simulated ones differ by more than 0.1 from the experimental ones; these correspond to residues 5, 6, 8, 10, 19, 34, and residues 6, 8, 10, 30, 33, 34, and 44 for S²₆₀₀ and S²₁₀₀, respectively. Such discrepancies essentially correspond to residues in loop I and at the tip of loop II. In loop I, S²₁₀₀ is in better agreement with the experimental values than S²₆₀₀. At the tip of loop II, S²₆₀₀ is in better agreement with the experimental values than S²₁₀₀.

Structure and dynamics of charybdotoxin

Comparison of NMR and X-Ray structures.

Superimposition of the three-dimensional structures of charybdotoxin obtained by NMR (Bontems et al. 1991) and X-ray at 2.2 Å (A. Navaza, pers. comm.) is shown in Figure 1B ▶. The Cα root-mean-square distance of the averaged NMR structure superimposed on the X-ray structure is 1.46 Å. This value is related to the difference in resolution of both structures (equivalent resolutions calculated with PROCHECK_NMR (Laskowski et al. 1996) for the NMR structures: 3 Å). The main difference between these structures is located at the β-turn involving residues 30–33 (Asn30 4.5 Å) and concerns the nature of the turn: The NMR structure is characterized by a type I turn, while it has been defined as a type II turn by crystallographic studies.

Analysis of the backbone hydrogen bonds of charybdotoxin in both the NMR and X-ray structures (Table 2) shows that more NMR derived amide protection factors could be explained on the basis of the X-ray structure than on the basis of the solution structure: Seven protected amides are not hydrogen bonded in the NMR structure (residues 5, 6, 25, 26, 28, 31, and 32), while only three of them are not involved in hydrogen bonds in the X-ray structure (residues 6, 28, and 31). In particular, in the NMR structure, only one hydrogen bond has been found in the β-turn between the amide proton of residue Met29 and the oxygen of residue Lys32, while this turn is stabilized by three hydrogen bonds in the crystal structure.

Table 2.

Main-chain hydrogen bonds in the X-Ray, NMR and simulated structures determined using the DSSP program (Kabsch and Sander, 1983)

Residue		Hydrogen bond
NH	CO	X-Ray	NMR	X-MD	NMR-MD
Z1	C35			31	43
F2
T3	C33	X	X	33	X
N4	C33			96
V5*
S6*
C7*	K31	X	—	99	X
T8
T9
S10
K11
E12	T9	—	X	—	—
C13*	T9	X	X	52	—
C13*	S10	—	—	45	—
W14*	S10	X	X	X	37
W14*	K11	X	—	—	31
S15	K11	X	X	89	84
S15	E12	—	—	—	25
V16	E12	X	X	91	88
C17*	C13	X	X	X	X
Q18*	W14	X	X	97	X
R19*	S15	X	X	79	X
R19*	V16	—	—	29	—
L20*	S15	—	—	—	27
L20*	V16	X	X	X	86
H21	C17	X	X	96	—
H21	V16	—	—	—	94
N22	Q18	X	—	—	—
N22	C17	X	—	—	61
T23	C17	X	—	—	X
S24
R25*
G26*	S24	X	—	37	—
K27*	R34	X	X	99	X
C28*
M29*	K27	X	—	95	—
M29*	K32	X	X	X	96
N30	C28	—	—	68	—
K31*
K32*	M29	X	—	84	—
C33*	V5	X	X	X	X
R34*	K27	X	X	99	X
C35*	Z1	X	X	X	88
Y36	R25	X	X	97	59
S37	C35	—	—	49	—

Residue names with an asterisk are those for which the amide proton is found to be protected from the exchange by NMR. “X” indicates that the interaction is present in the X-ray structure, or at 100% present for NMR and simulated structures. Percentage of the structures with the hydrogen bond is indicated for NMR and solution structures when different from 100. Identified side-chain acceptors are also indicated.

In conclusion, as in the case of toxin α, the X-ray structure of charybdotoxin is more accurate and is stabilized by more hydrogen bonds than the solution structure.

Comparison of the NMR and X-ray trajectories.

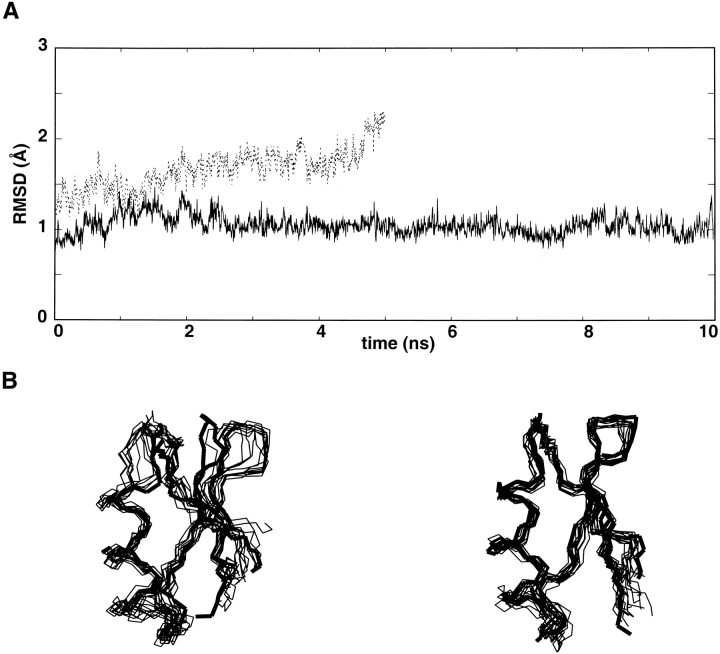
The X-ray trajectory is more stable than the NMR trajectory (Fig. 4A ▶). During the 10-ns X-ray trajectory, the structure remains stable, as indicated by the deviation which fluctuates around 1 Å. Only two hydrogen bonds are lost (Table 2). They correspond to Asn22HN–Gln18O and Thr23HN–Cys17O, and connect the α-helix to the β-sheet. The absence of protection against H–D exchange observed for these amides suggests that these hydrogen bonds are not crucial for structural stability. During the NMR trajectory, the root-mean-square deviation increases rapidly to reach 2 Å before 5 ns. Superimposition of frames extracted from the trajectory (Fig. 4B ▶) reveals that this deviation is mainly caused by structural perturbations around two sites: The β-turn deviates from its initial position, while the first turn of the α-helix exhibits local unfolding. This local unfolding seems to correlate with the rapid loss of the hydrogen bond (i, i + 4) Cys13.HN–Thr9.O. The value of the Cys13 amide exchange rate measured by NMR indicates that this hydrogen bond is stable in solution. Furthermore, this hydrogen bond is observed in 50% of the structures during the X-ray trajectory. Thus, the X-ray trajectory is in better agreement with the experimental H–D exchange rates than the NMR trajectory.

Figure 4.

Analysis of the molecular dynamics simulations of charybdotoxin. (A) Variation of the root-mean-square deviation between the backbone atom positions along the trajectories relative to their initial positions (thick and thin line correspond to trajectories started from X-ray and NMR structures, respectively). (B) Snapshots (one per ns) extracted from the trajectories started from the average NMR structure (left) and X-ray structure (right). The starting structures are represented in thick lines.

Comparison of temperature factors obtained from the X-ray structure and the X-ray trajectory.

A good agreement is found between B-factor variations along the sequence calculated from crystallographic and simulation data (see Electronic Supplemental Material). In particular, in the α-helix, motions are more restricted at the center and increase toward the extremities. Two regions show significant discrepancies between experimental and simulated data: These concern the loop connecting the α-helix and the β-sheet, as well as the β-turn. In these regions, the X-ray B factors are low, probably because of intermolecular interactions in the crystal: The side chains of Arg19 and Asn22 (in the loop connecting the α-helix and the β-sheet) are in contact with the side chains of Lys11 (α-helix), Asn30 (β-turn), and Ser37 (C-terminus) of another molecule.

CαH order parameters obtained from the NMR relaxation data analysis and the X-ray trajectory.

Order parameters reflecting the amplitudes of the ps to ns time-scale motions were calculated from the 10-ns trajectory (see Materials and Methods), and were compared to experimental values determined from NMR relaxation data (Wolff et al. 2000). The experimental and simulated values are in agreement (data not shown). For most residues, both experimental and simulated S² are higher than 0.8 Å. The highest order parameters (∼0.9) are localized in secondary structure elements, and larger motions (∼0.8) are found in loops. Thus, both experimental and simulated data indicate that the amplitude of subnanosecond motions is correlated to the secondary structure.

Discussion

NMR versus X-ray structures

The three-dimensional crystal structure of toxin α was solved by X-ray crystallography at 1.8 Å resolution. X-ray structures of toxin α and charybdotoxin (A. Navaza, pers. comm.) were compared to their corresponding NMR solution structures. In both cases, the X-ray structure is more accurate, as indicated by a better resolution (1.8 versus 2.5 for toxin α; 2.2 versus 3.0 Å for charybdotoxin) and stabilized by more hydrogen bonds compared to the solution structure. It must be stressed that the NMR structures used in these comparisons are from 1991 and 1992, while the crystal structures have been solved recently. The differences in resolution between NMR and X-ray structures, which is a general statement, is emphasized in our study.

Importance of the initial structure accuracy for the stability of a molecular dynamics simulation

Molecular dynamics simulations in water boxes of toxin α and charybdotoxin were performed, starting either from the crystal or from the solution structure. In both cases, the trajectory starting from the crystal structure is more stable than the trajectory derived from the NMR solution structure. This may be related to the accuracy of the structures. The important number of hydrogen bonds present in the X-ray structures appears to be critical for the stability of the trajectories. In addition, the error associated to an X-ray structure is averaged over the entire protein, whereas in NMR, the errors are more local and associated to specific residues. A local error in the NMR structure may induce a local unfolding of the protein during molecular dynamics simulations. To carry the molecular dynamics simulations, the averaged minimized NMR structure was chosen. However, RMSD on the NMR structures of toxin α and charybdotoxin are very low (0.5 and 0.44 Å, respectively) suggesting that similar results would be obtained with any of the individual NMR structures.

Comparison of the experimental and calculated order parameter and B factor

Comparison of experimental and simulated order parameters have been often used to validate molecular dynamics simulations (Philippopoulos et al. 1997). For the two proteins, the X-ray trajectory provides order parameters in very good agreement with the experimental values. The amplitudes of the fast motions (i.e., subnanosecond motions) are well reproduced. These fast motions are present in both toxins with an amplitude correlated to their secondary structures.

B-factors obtained from the X-ray trajectory are also in very good agreement with the experimental values. As expected, for loops which are involved in crystal contacts, simulated B-factors are higher than the corresponding experimental values.

Correlation between experimentally observed microsecond time-scale motions and calculated large structural deviations during the trajectory

After 6 ns of simulation, loop I of toxin α deviates from its initial conformation. The same results were obtained in a recent dynamical study with fasciculin, a toxin also belonging to the “three-finger” fold family: The largest deviations observed during a 2-ns simulation were located at the tip of loop I (Baker et al. 1999). NMR relaxation studies of toxin α show that the three loops of toxin α are submitted to μsec–msec time scale motions, loop I exhibiting mostly μsec time-scale motions and loop III showing particularly large or slow msec time scale motions (Zinn-Justin et al. 1997; Guenneugues et al. 1999). Therefore, rare motions observed in loop I during the simulation could be correlated to the existence of the μsec motions. The behavior of charybdotoxin during its X-ray trajectory is consistent with the suggested correlation: Very few residues are submitted to μsec motions in charybdotoxin and the simulation of charybdotoxin is remarkably stable.

Slow motions and structural variability

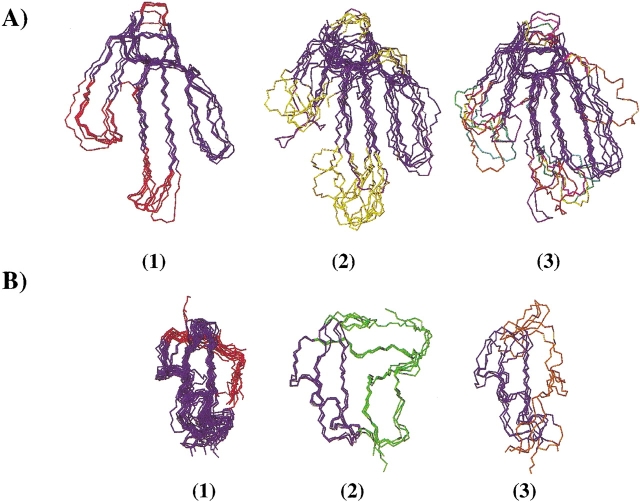
Figure 5 ▶ shows the superimposition of the known three-dimensional structures of the two studied scaffolds.

Figure 5.

(A) Backbone superimposition of proteins adopting the “three-finger” fold. The backbone atoms of the two β-sheets plus the entire loop III and the C-terminus (residues 1–5, 14–18, 21–28, 36–41, 42–60 for toxin α, in blue) were superimposed, (average backbone root-mean-square deviation lower than 2 Å). (1) α-neurotoxins, (2) α/κ-neurotoxins (bucandin in purple), (3) other “three-finger” fold proteins (mambin in orange). (B) Backbone superimposition of proteins adopting the α/β scorpion fold. The backbone atoms from the α-helix to the two stranded β-sheet (residues 5–37 for charybdotoxin in blue) were superimposed, (average backbone root-mean-square deviation lower than 2 Å). (1) short and (2) long scorpion toxins (3) plant, insect, and mollusk defensins.

Figure 5A₍₁₎ ▶ and 5A₍₂₎ ▶ represent snake α-neurotoxins and α/κ-neurotoxins, respectively. These toxins block acetylcholine receptors (Servent and Ménez 2001). For α-neurotoxins, the entire structures superimpose well, while α/κ-neurotoxins structures are strongly different in loop I and at the tip of loop II. The three-finger fold structures of snake toxins blocking acetylcholine receptors is characterized by a conserved structural core and large structural variations in loop I and the tip of loop II (bucandin, a nonconventional neurotoxin, is the only one for which loop III is slightly different). Figure 5A₍₃₎ ▶ shows that proteins belonging to the three-finger fold but having different activities (fasciculins, cardiotoxins, muscarinic toxins, etc.) also present structural variations mainly in loop I and at the tip of loop II. Overall, the “three-finger” fold is characterized by the structural conservation of the β-sheets and the entire loop III (the only exceptions are bucandin and mambin) and by large insertions and variations in loop I and at the tip of loop II. From the NMR data, relaxation experiments indicated that several residues of loop I and of the turn between loops I and II exhibit slow motions that correspond to conformational exchange on a μsec time scale (Zinn-Justin et al. 1997; Guenneugues et al. 1999). We suggest that the slow motions in these loops reflect the permissiveness of the “three-finger” fold. It can be emphasized that the structural variability in loops I and II is the basis of the functional diversity of the “three-finger” fold (Servent and Ménez 2001). For example, the functional determinants of cardiotoxins and fasciculins are located at the tip of loop I, and those of muscarinic and acetylcholine receptor ligands are located at the tip of loops I and II. The exceptional structural variations in loop III of mambin also coincide with the location of the functional residues in this loop.

Figure 5B ▶ displays the superimposition of proteins adopting the α/β scorpion toxin fold. The variations in this α/β fold correspond to large N- and C-terminal extensions and a short insertion in β-turn. Figure 5B₍₁₎ ▶ shows that the entire backbone structure of all short scorpion toxins superimpose well. The long scorpion toxins (Gordon et al. 1998) and plant, insect, and mollusk defensins (Yang et al. 2000) adopt the same fold but with extensions at the N- and C-termini and a slightly longer β-turn (Fig. 5B₍₂₎ ▶ and 5B₍₃₎ ▶). From the NMR data, very few residues exhibit μsec-msec time-scale motions in charybdotoxin: Only three residues—Ser10 (N-terminus of the helix), Cys17, and Gln 18 (C-terminus of the helix)— present fast exchange motions (10–100 μsec), and four residues dispersed in the sequence show slower time scale motions (>250 μsec) (Wolff et al. 2000). The small number of residues exhibiting μsec to msec time-scale motions in charybdotoxin might be correlated with the low structural variability of the short α/β scorpion.

Conclusion

The NMR, X-ray, and molecular dynamics simulation data reported in this article give an image of the structural and dynamical properties of two toxin structural families. The results of the molecular dynamics simulations are convergent with those provided by NMR: (1) simulated rapid motion amplitudes (order parameters) are in good agreement with the experimental NMR values, and are correlated with the secondary structure; (2) charybdotoxin exhibits less rare motions than toxin α during the simulation, and, according to NMR relaxation results, only few residues of charybdotoxin exhibit slow motions while the loop I and of the turn between loops I and II of toxin α present such motions. The presence of rare motions in the simulations and the observation of slow motions in solution by NMR seem to correlate with the structural variability of the scaffold. A large flexibility linked to some structural variability within the fold family is probably a critical property for a structural scaffold in the frame of protein engineering. The possibility of substituting large sequences in the “three-finger” framework is confirmed by several protein engineering results. For example, loops I and II of toxin α were modified to introduce new functional determinants on this structural scaffold. Loop I and part of loop II of fasciculin were transferred at their homologous place in the toxin α sequence, thus contributing to the apparition of an acetylcholine–estherase activity (Le Du et al. 2000; Ricciardi et al. 2000), whereas the grafting of the tip of loop II of a α/κ neurotoxin allowed to transfer part of its neuronal specificity onto the muscular-specific toxin α scaffold (Mourier et al. 2000). The scaffold of short α/β scorpion toxins was not used to insert large sequences, and our study suggests that this would largely destabilize the scorpion framework. By now, engineering of the scorpion toxin scaffold was based on the introduction of ponctual mutations (Vita et al. 1995, 1999; Mer et al. 1998). Suppression of the first six amino acids of charybdotoxin, in conjunction with mutations of 8 residues in the β-sheet, was shown to create important msec time-scale motions on the whole protein, thus deeply modifying the energy landscape of the toxin (Wolff et al. 2000).

Materials and methods

Determination of the X-ray structure of toxin α

Crystallization and data collection

Toxin α was purified from Naja nigricollis venom (Institut Pasteur) as previously described (Fryklund and Eaker 1975). Small crystals of toxin α were grown by the hanging drop vapor diffusion method at 18°C from 4-μL droplets of protein solution (25 mg/mL) containing sodium acetate 100 mM (pH 4.5). The protein solution, diluted with 4 μL of the reservoir solution, was placed on the wall of a siliconized cover slide against a reservoir of the same buffer (sodium acetate 100 mM, pH 4.5) containing ammonium sulfate 2.5 M. These small crystals were used as seeds in 4-μL droplets containing 12.5 mg/mL of toxin in sodium acetate buffer (pH 4.5), 2.4 M ammonium sulfate, and 3% hexane diol. Crystals grew to a size of 0.6 × 0.4 × 0.4 mm within 1 week. The crystals diffract to a 1.65-Å resolution and contain one molecule per asymmetric unit. They belong to the tetragonal space-group P4₃2₁2 with a = b = 40.9 Å, c = 73.5 Å. The value of Vm is 2.19 Å3/Daltons corresponding to a solvent content of 44%. X-ray data were collected at room temperature from a single crystal on a MarResearch imaging plate detector coupled to a Rigaku rotating anode generator. The data processing was carried out with the program HKL (Otwinowski 1993) (Table 3).

Table 3.

Data collection, molecular replacement, and refinement statistics

Data collection
Diffraction limit (last shell)	1.65Å (1.69–1.65)
Number of observed reflections	87663
Number of unique data	7360
Completeness (last shell)	0.920 (0.812)
Rmerge (last shell)	0.090 (0.674)
Molecular Replacement
Rfactor (second solution)	0.436 (0.496)
Correlation coefficient (second solution)	0.462 (0.294)
Refinement
Resolution limit	10–1.8 Å
Rwork	0.19
Rfree	0.24
Total number of atom	780
Number of water molecules	63
Number of sulfate molecule	1
Temperature factor (Å2)
Protein	14.5
Solvent	41.3
Model geometry
rms deviation from ideal geometry of bond length (Å)	0.035
rms deviation from ideal geometry of bond angles (°)	3.081

Structure determination and refinement

The structure of toxin α was solved by molecular replacement with the program AMoRe (Navaza 1994) using the crystal structure of dhydro-trp28–toxin α (M. Gondry, R. Ménez, M.H. Le du, and R. Genet, unpubl.) as a search model. A single, well-contrasted solution was obtained with a correlation coefficient of 0.468, and an R-factor of 0.438 (Table 3).

The model was refined by simulated annealing to 1.8-Å resolution with the program XPLOR (Brünger 1992). Major corrections of the model were performed interactively with the program TURBO-FRODO (Roussel and Cambillau 1989) using 2Fo–Fc and Fo–Fc electron density maps. When the R_work and R_free reached, respectively, 0.25 and 0.30, the water molecules were gradually modeled in peaks of the Fo–Fc electron density map, higher than 3σ. After refinement, the stereochemistry of the model was checked with the program PROCHECK (Laskowski et al. 1993). The statistics of the refinement are summarized in Table 3.

Among the 63 modeled water molecules, 38 are directly bonded to the protein, constituting the first hydration shell of the molecule. Specifically, 27 of the 63 water molecules included in the model are bonded to only one atom, and 11 establish more than one hydrogen bond with atoms of the protein. Of the remaining 25 water molecules, 19 are hydrogen bonded to other water molecules, and two are hydrogen bonded to a sulfate ion. The four oxygen atoms of the sulfate ion are involved in several interactions: O1 with Cys40.N, O2 with His31.NE2 of a symmetry-related molecule and Glu20.OE2 via a water molecule, O3 with Tyr24.OH, and O4 with Lys15.NZ.

Three regions of the protein are implicated in crystal packing: In the first loop, residues 7–10; in loop II, residues 19–26 and 32–38; and the top of loop III, residues 42–44. The five closest contacts (<4 Å) are Thr34.O–Thr44.N, Gln7.Oɛ1–Asn22.Oδ1, Ser8.Oγ–Cys42.O, Glu20.Oɛ2–Arg32.Nη1, Lys26.Nζ–Arg32.O.

The coordinates of X-ray toxin α were deposited at the RCSB Protein Data Bank (entry code 1IQ9).

Molecular dynamics simulations

Calculation of the trajectories

The simulations were carried out using CHARMM software (Brooks et al. 1988) and the all-atom CHARMM22 parameter set (MacKerell et al. 1998). For both toxins, two simulations were carried out, one starting from the NMR solution structure (NMR trajectory) and the other from the X-ray structure (X-ray trajectory). The atomic coordinates were taken from the minimized averaged solution structures determined in our laboratory (Protein Data Bank entry 1NEA and 2CRD for toxin α and charybdotoxin, respectively) and the crystal structures of both proteins (resolutions 2.2 Å and 1.8 Å for charybdotoxin and toxin α, respectively). Hydrogen atoms were added using the IC BUILD routine of CHARMM.

Then, each initial protein structure was placed at the center of an equilibrated box of TIP3 water molecules (Jorgensen 1981). The box size was set to 43 × 43 × 32 Å for charybdotoxin, and 52 × 43 × 33 Å for toxin α, resulting in a system containing 1712 and 2209 water molecules, respectively. Water molecules overlapping the protein, which are those having their oxygen atom within a distance of 2.8Å from any heavy atom of the protein, were removed. The system was minimized in the presence of harmonic restraints on the protein heavy atoms to preserve the global conformation while optimizing water–protein interactions.

The simulation was performed using periodic boundary conditions. The whole system was heated and then equilibrated in the presence of the harmonic restraints. Moreover, for toxin α, to avoid breaking the backbone hydrogen bonds, four distance constraints were added (between Thr13.O–Asn5.HN, Gln7.O–Gln10.HN, Cys3.O–Lys15.HN, and Lys15.O–Thr3.HN). These distances as well as the harmonic constraints were progressively diminished. The heating and the equilibration periods were fixed to 500 and 960 ps for charybdotoxin and toxin α, respectively. A time step of 1 fs was used in conjunction with the SHAKE algorithm. Nonbonded interactions were handled using an 8–12 Å switching function. Coordinates were stored every 0.05 ps, and nonbonded lists, every 0.01 ps.

Autocorrelation functions

Autocorrelation functions were calculated for backbone vectors CαH and NH using the NMR module of CHARMM software. Order parameters and internal correlation times were obtained from our simulations by a nonlinear least-square fitting derived from the model-free approach (Lipari and Szabo 1996). For toxin α, the autocorrelation functions were calculated on the first 6ns of the simulation of the X-ray trajectory and were fitted onto a monoexponential function, using either the first 100 ps (S²₁₀₀) or the first 600 ps (S²₆₀₀) of each function. For charybdotoxin, the autocorrelation functions were calculated on the 10 ns of the simulation of the X-ray trajectory.

Convergence of correlation functions was checked using the method described by Schneider et al. (1999). To estimate the statistical error, two internal correlation functions were obtained for each vector: The first was calculated on the total length of the trajectory, and the second on a 10% smaller trajectory. The error was estimated using the function

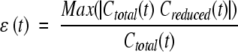The maximum error was empirically set to 2.5%. The internal correlation functions obtained with an error exceeding this value were eliminated because the corresponding motions were considered as insufficiently sampled.

To know if CαH and NH vector positions were influenced by rare motions, the scalar products m(0).m(t) were determined, where m(0) and m(t) are unitary vectors directed along the vector bond at t = 0 and t, respectively. Computation of scalar products shows that nonconvergent correlation functions correspond to rare motions and transitions during the trajectory. In the presence of such movements, simulation shows an artefactual higher mobility than NMR, which describes motions averaged on a large number of molecules.

Temperature factor

The B-factors were calculated from the trajectory according to the formula

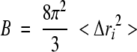where Δr_i represents the average fluctuations of atom i during the trajectory.

Structural comparison of the toxins within each of the two fold families

The “three-finger” fold family

The following proteins adopting the “three-finger” fold were used for our comparison after loading their three-dimensional structures from the RCSB Protein Data Bank: (1) structures of snake toxins blocking acetylcholine receptors: (a) α-neurotoxins: erabutoxin b (1NXB), the two crystal forms of erabutoxin a (1QKE and 1QKD), toxin α (1NEA), cobrotoxin (1COD), Dpp α (1NTX), neurotoxin II (1NOR); (b) α/κ-neurotoxins: NnoI (1NTN), α-cobratoxin (1CTX), α-bungarotoxin (2ABX), LS III (1LSI), toxin b (1TXA); (c) κ-neurotoxins: κ-bungarotoxin (1KBA); (d) nonconventional neurotoxins: bucandin (1F94); (2) structures of three-finger fold proteins: fasciculin 1 (1FSC), cardiotoxin γ (1CXN), muscarinic toxin MTX2, toxin Fs2 (1TFS), mambin (1DRS), cardiotoxin III (2CRT), cardiotoxin V (1CVO).

The short α/β scorpion fold family

Toxins adopting the short α/β scorpion fold and used in our comparison are the following: (1) structures of short scorpion toxins: Hstx1 (1QUZ), maurotoxin (1TXM), pandinustoxin Ka (2PTA), charybdotoxin (2CRD), Bmtx2 (2BMT), Bmtx1 (1BIG), lq2 (1LIR), Ts-κ-toxin (1TSK), noxiustoxin (1SXM), margatoxin (1MTX), agitoxin (1AGT), and kaliotoxin (2KTX), Bmktx toxin (1BKT), P01 (1ACW), P05 (1PNH), scyllatoxin (1SCY); (2) structures of defensins: Rs-Afp1 (1AYJ), Ah-Amp (1BK8), Mgd-1 (1FJN), defensin A (1ICA); (3) structures of long scorpion toxins (1LTB, 1PTX, 1SNB).

Electronic supplemental material

B-factor variations along the sequence are similar for crystallographic and simulation data (Fig. 1 ▶). A good agreement is found between B-factor variations along the sequence calculated from crystallographic and simulation data (Fig. 2 ▶).