Abstract
We investigated the structural determinants of the stability of a designed β-hairpin containing a natural hydrophobic cluster from the protein GB1 and a D-Pro-Gly turn forming sequence. The results of our simulations shed light on the factors leading to an ordered secondary structure in a model peptide: in particular, the importance of the so-called diagonal interactions in forming a stable hydrophobic nucleus in the β-hairpin, together with the more obvious lateral interactions, is examined. With the use of long timescale MD simulations in explicit water, we show the role of diagonal interactions in driving the peptide to the correct folded structure (formation of the hydrophobic core with Trp 2, Tyr 4, and Phe 9 in the first stages of refolding) and in keeping it in the ensemble of folded conformations. The combination of the stabilizing effects of the D-Pro-Gly turn sequence and of the hydrophobic nucleus formation thus favors the attainment of an ordered secondary structure compatible with the one determined experimentally. Moreover, our data underline the importance of the juxtapositions of the side chains of amino acids not directly facing each other in the three-dimensional structure. The combination of these interactions forces the peptide to sample a nonrandom portion of the conformational space, as can be seen in the rapid collapse to an ordered structure in the refolding simulation, and shows that the unfolded state can be closely correlated to the folded ensemble of structures, at least in the case of small model peptides.
Keywords: Protein folding, peptides, protein design, molecular dynamics, hairpin, peptide conformations in water
An essential attribute of biological macromolecules such as proteins is the control that noncovalent forces that govern folding and self-assembly processes have on their structure (Cubberley and Iverson 2001). Understanding not only the reasons for the stabilization of one particular conformation over others, but also the partial destabilization of inappropriate conformations, represents a major effort in modern biophysics and biochemistry. In order to garner deeper insights into the molecular mechanisms governing the stability and dynamics of tertiary structure formation and the relationships between amino acid sequences and three-dimensional conformations, several researchers have focused their attention on short peptide chains showing the ability to fold into well defined structures when studied in isolation in aqueous and alcoholic solutions (Dyson and Wright 1993; Blanco et al. 1998). The fundamental aspects of helix folding have been elucidated in several experimental (Chakrabartty and Baldwin 1995; Parthasarathy et al. 1995) and theoretical (Brooks III and Boczko 1995; Munoz et al. 1996; Zhou and Karplus 1997; Lacroix et al. 1998) studies, and the main thermodynamic and kinetic features of α-helix folding have been clarified (Daura et al. 1998,1999b,Daura et al. c). In contrast, β-sheets are more complex structures than helices (the connections between the β-strands can be well separated along the primary sequence of a protein), and the interactions that stabilize β-sheet formation are less well understood (Smith and Regan 1995). The β-sheet, besides being very diffused as a secondary structure component of proteins (Kabsch and Sander 1983), is involved in the amyloid fibril formation event, a factor in a wide variety of pathological disorders (Booth 1997; Kelly 1997). Therefore the study of a context-free β-hairpin peptide model could be very important in understanding the nature of β-sheet stabilizing interactions. A β-hairpin, that is, two strands linked by a short loop, can be considered a good model of β-sheet secondary structure.
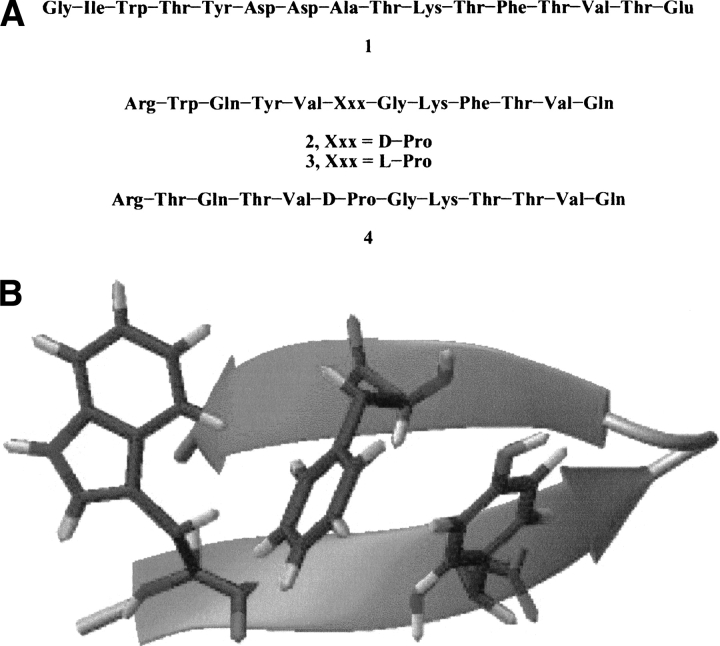
Small designed β-hairpin peptides are proving to be very useful for the analysis of the thermodynamics and kinetics of β-sheet formation (Andersen et al. 1999; Searle et al. 1999). However, natural β-hairpin sequences seldom fold in water when extracted from their native protein context (Gellman 1998). An exception is a 16-residue segment of the protein GB1, 1 (sequence: GIWTYDDATK-TFTVTE; Fig. 1 ▶), which displays a partial population of a β-hairpin conformation (Blanco et al. 1996). Peptide 1 differs from other autonomously folding β-hairpins in the unusually large six-residue loop (Asp-Asp-Ala-Thr-Lys-Thr) that connects the two strand segments; other autonomously folding β-hairpins contain loops of two to four residues (Ramirez-Alvarado et al. 1996; Gellman 1998). Interstrand interactions within the folded conformation of 1 are limited to residues near the termini (Blanco et al. 1996). Clustering among the hydrophobic side chains of Trp 3, Tyr 5, Phe 12, and Val 14 presumably provides a drive for β-hairpin folding, which overcomes the entropic cost of ordering the loop segment. Gellman and coworkers (Espinosa and Gellman 2000) incorporated the residues of the GB1 cluster into a 12-residue sequence, 2 (sequence: RWQYV-DP-G-KFTVQ; Fig. 1 ▶), expected to adopt a more highly defined β-hairpin conformation than 1. The arrangement of the Trp, Tyr, Phe, and Val residues in 2 allows side chain juxtapositions (characterizing the natural peptide 1) if the peptide folds to a β-hairpin conformation with a tight two-residue loop; the D-Pro-Gly segment strongly promotes this type of β-hairpin (Espinosa and Gellman 2000; Das et al. 2001). Espinosa and Gellman (2000) showed by NMR-NOE experiments, chemical shift analysis, and circular dycroism that peptide 2 tends to adopt pairing of antiparallel β-strands similar to that of peptide 1 at two different temperatures of 275K and 315K. The β-hairpin population of 2 was calculated by δHα chemical shift analysis to be 61% at 275K and 45% at 315K. As a negative control, those authors used the diastereoisomer of peptide 2 in which D-Pro was substituted by L-Pro, because L-Pro is expected to disfavor formation of tight β-hairpin conformations.
Figure 1.
(A) Scheme depicting the sequences of the β-hairpin from protein GB1, 1, and the studied peptides 2, 3, and 4. (B) Ribbon representation of the average NMR-determined structure. Aromatic residues are drawn as tubes.
Here we present the results of a study of the stability determinants and folding of the designed peptide 2 using molecular dynamics (MD) simulations in explicit water under periodic boundary conditions at the two different experimental temperatures (280K, 320K). Two 200-nsec simulations were performed at 280K and 320K for the D-Pro-containing peptide, and one control simulation of 100 nsec at 320K was run for the control peptide-containing L-Pro, 3. Moreover, a second control simulation was run on a peptide, labeled 4, in which the residues of the hydrophobic core are substituted by Thr residues, whereas maintaining the D-Pro-Gly sequence in the turn. One refolding simulation of 2 starting from an extended structure was also run to qualitatively investigate the initial stages of folding. MD simulations address the folding problem by only sampling "relevant" (low-energy) regions of conformational space. In cases that are characterized by a limited number of low-energy conformations in rapid equilibrium (on the MD timescale), MD simulations have been demonstrated to provide highly detailed information on the nature of alternative states in solution and the dynamics of spontaneous folding–unfolding (Brooks III and Boczko 1995; Karplus and Sali 1995; Lazaridis and Karplus 1997; Shakhnovich 1997; Zhou and Karplus 1997; Duan and Kollman 1998; Ladurner et al. 1998). In particular, Daura et al. have been able to demonstrate the reversible folding of a helix forming β-heptapeptide in methanol from an arbitrary starting structure under a variety of conditions within 50 nsec (1998, 1999b,c). Computational studies of β-turn-forming sequences (Tobias et al. 1991; Scully and Hermans 1994; Demchuck et al. 1997), as well as β-hairpin-forming sequences (Bursulaya and Brooks III 1999; Dinner et al. 1999; Ibragimova and Wade 1999; Pande and Rokhsar 1999; Roccatano et al. 1999; Sung 1999; Bonvin and van Gunsteren 2000; Ferrara and Caflisch 2000; Ma and Nussinov 2000; Wang and Sung 2000), have addressed different aspects of β-hairpin stability, such as the importance of the turn sequence, hydrogen-bonding patterns, and hydrophobic interactions. In another paper by our group (Colombo et al. 2002), the MD study of the closely related antiparallel three-stranded β-sheet peptide Betanova proved the high flexibility of this kind of peptides in solution and showed that a set of different structures is needed to satisfy nuclear magnetic resonance (NMR)-derived distance restraints. Moreover, MD simulations proved useful in the investigation of the molecular reasons for the stabilization of secondary structure-forming peptides in three fluoro ethanol (TFE)/water mixtures (Roccatano et al. 2002).
Two simulations of 200 nsec for peptide 2 at 280 and 320K (labeled respectively 280D and 320D) and one 100-nsec simulation at 320K for the control peptide 3 [sequence: RWQYV-LP-G-KFTVQ, Fig. 1 ▶; 320L (500 nsec in total plus the refolding simulation)] show extensive sampling of the conformational space around the folded state, and allow us to address issues related to the stability and folding of 2. The second control peptide 4 is used to assess the role of the turn sequence. Based on the analysis of the trajectories, the respective roles of single amino acids, loops, hydrogen bonding, and side chain interactions in determining the stability and the folding mechanism are discussed. In particular, this kind of peptide allows us to probe the effect of side chain–side chain interactions. Prior studies have focused on side chains that are directly across from one another in terms of the β-sheet hydrogen-bonding registry. We refer to such juxtapositions as "lateral" pairings. In this report we consider "diagonal" pairings as well. Diagonal contacts involve side chains which are not directly across from one another in terms of the β-sheet hydrogen-bonding registry. Diagonal interstrand contacts have received relatively little attention in the recent literature (Cootes et al. 1998). Cootes and coworkers found this type of interactions to be present in β-sheets through computational analysis, whereas Gellman and coworkers (Syud et al. 2001) thoroughly investigated their effect on the stabilization of β-hairpins through experimental, synthetic, and spectroscopic approaches. In the case of the peptide under study, the diagonal interactions are the ones between the side chains of Trp 2 and Phe 9 and between the side chains of Tyr 4 and Val 11, and the lateral interactions are the ones between Trp 2 and Val 11 and between Tyr 4 and Phe 9 (Syud et al. 2001). A contact is considered to be present if the minimum distance between the atoms of two side chains is lower than 0.6nm (Bursulaya and Brooks III 1999).
The results of these simulations are first compared with the experimentally derived NMR-NOE data (S. Gellman, pers. comm.), to assess the capability of simulations to sample the conformational space around the experimental conformation. If reasonable agreement is found between simulations and experiment, then simulations can actually be used to reveal factors and phenomena which are difficult to study experimentally, and to derive a model for the description of the factors influencing the folding of β-hairpins. The timerange spanned by these simulations is still short compared to the experimental folding times of β-hairpins (in the order of microseconds, currently out of reach for MD), but the use of long simulations in different conditions, with an explicit representation of all the water molecules in the solvent, should help obtain a clear realistic picture (although partly qualitative) of the role of the different components of the peptide in determining its folding and stability.
Results
Conformational analysis
Table 1 shows the 36 experimental NOE connectivities defining the β-hairpin conformation of peptide 2, together with the respective distance values calculated from simulations 280D and 320D. The interproton distances were calculated for each trajectory separately using ≤r−6>−1/6 averaging. The results of Table 1 clearly show that most NOE constraints are satisfied also at 320K where the amount of ordered β-sheet type of structure is lower than at 280K (Fig. 2 ▶): Three violations are found in simulation 280D (entries 12, 25, and 31), one corresponding to a very weak NOE signal, and the others corresponding to two medium intensities. These latter are however violated by only 0.02 and 0.03 nm, respectively. In 320D, a higher number of violations, five, is found, as expected (entries 1, 17, 26, 31, and 33): one of them corresponds to a strong NOE intensity, the others to weak-medium and medium peaks. The molecule in the 280D and 320D simulations samples a series of conformations basically characterized by a turn and two short strands. Once proved that we could get the experimental NMR structural parameters right, a more thorough investigation of the simulations in terms of the atomistic determinants of folding could be carried out.
Table 1.
NOE connectivities of peptide 2 from NMR experiments in water compared with calculations based on simulations 300A and 300B
| No. | Proton i | Proton j | Exp. intens. | 280D | 320D |
| 1 | CαH W2 | CαH V11 | s | 0.2 | 0.4 |
| 2 | CαH W2 | NH Q12 | w | 0.39 | 0.47 |
| 3 | CβH W2 | CɛH F9 | vw | 0.51 | 0.49 |
| 4 | CβH W2 | CζH F9 | vw | 0.56 | 0.59 |
| 5 | CβH′ W2 | CɛH F9 | vw | 0.51 | 0.49 |
| 6 | Cδ1H W2 | CγH V11 | w | 0.35 | 0.4 |
| 7 | Cδ1H W2 | CγH′ V11 | w | 0.35 | 0.4 |
| 8 | Cδ1H W2 | CαH V11 | vw | 0.32 | 0.47 |
| 9 | Cɛ2H W2 | CγH V11 | vw | 0.42 | 0.39 |
| 10 | Cɛ2H W2 | CαH V11 | vw | 0.34 | 0.47 |
| 11 | Cɛ2H W2 | CαH T10 | w | 0.4 | 0.60 |
| 12 | Cɛ2H W2 | CβH F9 | w | 0.7 | 0.44 |
| 13 | Cɛ2H W2 | Cδ H F9 | w | 0.57 | 0.46 |
| 14 | Cζ2H W2 | CγH V11 | w | 0.36 | 0.44 |
| 15 | Cζ3H W2 | CαH T10 | m | 0.4 | 0.3 |
| 16 | Cη2H W2 | CγH V11 | vw | 0.46 | 0.52 |
| 17 | NH Q3 | NH Q10 | w-m | 0.45 | 0.58 |
| 18 | CαH Y4 | CαH F9 | s | 0.2 | 0.3 |
| 19 | CαH Y4 | CδH F9 | w | 0.31 | 0.42 |
| 20 | CαH Y4 | NH T10 | w | 0.33 | 0.53 |
| 21 | CαH Y4 | CγH T10 | vw | 0.34 | 0.51 |
| 22 | CβH Y4 | CɛH F9 | vw | 0.39 | 0.45 |
| 23 | CδH Y4 | CɛH F9 | w | 0.40 | 0.44 |
| 24 | CδH Y4 | CαH G7 | w | 0.43 | 0.41 |
| 25 | CδH Y4 | CαH K8 | m | 0.43 | 0.4 |
| 26 | CɛH Y4 | CβH F9 | m-s | 0.3 | 0.43 |
| 27 | CɛH Y4 | CβH′ F9 | vw | 0.6 | 0.53 |
| 28 | CɛH Y4 | CɛH F9 | m | 0.36 | 0.37 |
| 29 | CɛH Y4 | CαH G7 | m | 0.30 | 0.33 |
| 30 | CɛH Y4 | CαH K8 | w | 0.40 | 0.54 |
| 31 | NH V5 | NH K8 | m | 0.42 | 0.44 |
| 32 | NH V5 | CγH T10 | vw | 0.7 | 0.53 |
| 33 | CγH V5 | CβH T10 | m | 0.35 | 0.63 |
| 34 | CγH V5 | CγH T10 | w | 0.33 | 0.4 |
| 35 | CβH V5 | CγH T10 | w | 0.41 | 0.62 |
| 36 | NH G7 | NH K8 | m-s | 0.28 | 0.30 |
Experimentally NOE’s are classified according to the following upper distance restraints: strong (s) = 0.25 nm, medium (m) = 0.35 nm, weak-medium (w-m) = 0.5 nm, weak (w) = 0.55 nm, very weak (vw) = 0.6 nm.
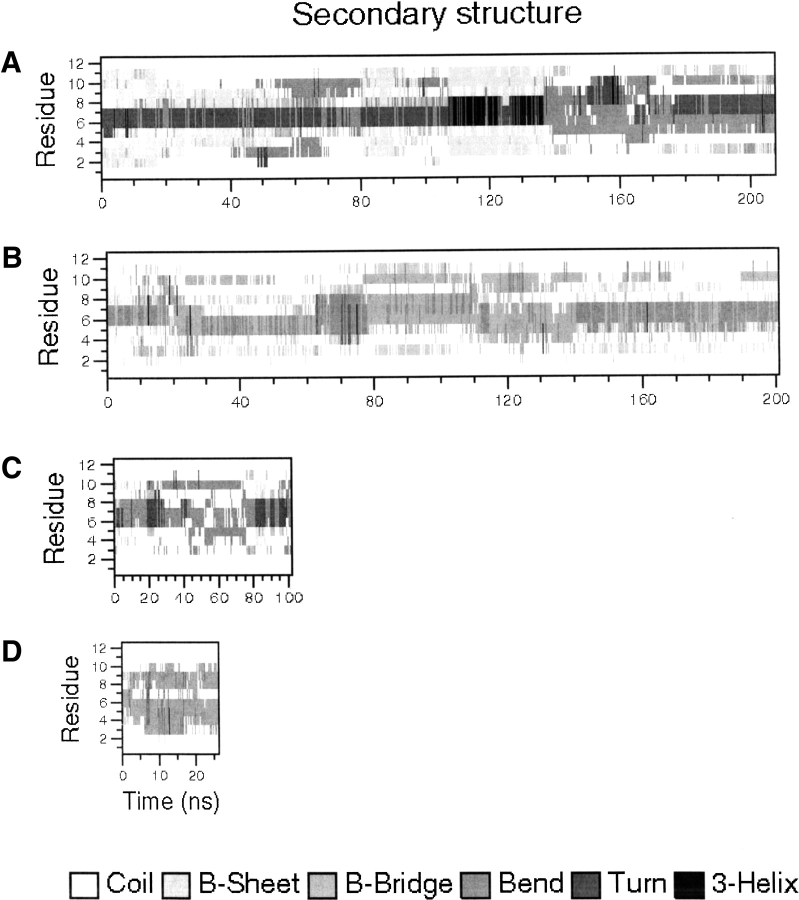
Figure 2.
Secondary structure evolution plots for the simulations 280D (A), 320D (B), 320L (C), and peptide 4.
Table 2 reports the structural properties of the simulated peptides in 280D, 320D, and 320L, and Figure 2A–D ▶ reports the secondary structure evolution as a function of time for 280D, 320D, and 320L and the simulation of peptide 4 based on the DSSP algorithm (Kabsch and Sander 1983). It is evident from these analyses that the particular sequence of peptide 2 favors the formation of an ordered β-sheet structure. In simulation 280D (Fig. 2A ▶), a β-hairpin conformation is recovered at multiple times in the simulation. In addition, simulation 320D displays a similar, although less definite behavior: the β-hairpin structure is present in the first 10 nsec, between 40 and 60 nsec, and in the last 40 nsec of the simulation. In contrast, in both simulation 320L and in the simulation of peptide 4, the absence of either the right turn sequence or the suitable hydrophobic cluster residues determines a fast transition to a disordered structure, even starting from a β-hairpin geometry.
Table 2.
Summary of the structural properties of the simulated peptides
| Radius of gyration (nm) | Accessible surf. area (nm2) | Secondary structure | Hydrogen bonds | ||||
| Sim. | Total | ASA (tot.) | ASA (hydrophob.) | % Beta | % Turn | % Val5-Lys8 | % Gln3-Thr10 |
| 280D | 0.64 ± 0.03 | 8.10 ± 0.52 | 4.9 ± 0.32 | 60 | 55 | 60 | 30 |
| 320D | 0.63 ± 0.03 | 8.12 ± 0.54 | 5.1 ± 0.34 | 25 | 18 | 30 | 10 |
| 320L | 0.65 ± 0.05 | 8.45 ± 0.50 | 5.9 ± 0.32 | 5 | abs | 5 | abs |
The hydrogen bond existence table (Table 2) shows the occurrence of backbone hydrogen bonds between Val 5 and Lys 8 and between Gin 3 and Thr 10 during the simulation time. The ideal structure of this designed hairpin should be formed by a turn (D-Pro and Gly) stabilized by the hydrogen bonds formed by the NH and CO groups of Val 5 with the CO and NH groups of Lys 8, respectively, and by two strands connected by the hydrogen bonds between the NH and CO groups of Gin 3 and the CO and NH groups of Thr 10, respectively. A hydrogen bond is considered present when the angle donor-hydrogen-acceptor is within the cut-off of 60°, and when the distance hydrogen-acceptor is within 0.25 nm. The presence of these hydrogen-bonding interactions is thus a good indication of the tendency of the peptide to populate an ensemble of β-hairpin-type structures. Table 2 shows that the first pair (Val 5 and Lys 8) of hydrogen bonding interactions for peptide 2 is present for about 60% of the simulation time at 280K and for about 30% of the time at 320K, whereas the second pair (Gin 3 and Thr 10) is present for 30% and 10% of the time at 280 and 320K, respectively (Table 2, columns 1 and 2). If the presence of these hydrogen-bonding interactions is considered an index of the presence of a "folded" conformation, these data (besides the direct calculations of the NOE-derived distance constraints) are also consistent with the δHα-based calculations of the folded population based on the variation in the chemical shifts of the α-hydrogens of the "hydrogen-bonded" residues reported by Espinosa and Gellman (2000). As expected, the calculation of the analogous hydrogen bonding existence percentage on peptide 3, which should not have a tendency to form such hydrogen bonds, due to L-Pro, shows that no persistent hydrogen-bond interaction is present during the whole control simulation time, and that the hydrogen-bonding interactions initially present since the structure was built as a β-hairpin are immediately disrupted after a few nsec. In the case of 320D, these interactions are present for the first 10 nsec, and recovered multiple times during the simulation (around 60–80 nsec and 140–200 nsec). The Secondary Structure calculations, based on the DSSP methodology (Kabsch and Sender 1983), also confirm that during simulation 280D the global β-sheet population for the peptide is around 60%, whereas in simulation 320D this population drops to 25%, in good qualitative agreement with the experimental results. The control peptide simulation 320L does not show the peptide significantly populating any β-sheet conformational ensemble, the total percentage of β-sheet structure being only around 5%. The lack of hydrogen-bonding interactions necessary for a β-hairpin motif, combined with the differences in the secondary structure content, clearly shows that the presence of the L-Pro in the control peptide 3 favors an ensemble of conformations lacking the characteristics of the NMR-derived conformation. Peptide 4 completely unfolds because of the absence of the hydrophobic cluster.
In terms of backbone root mean square deviation (RMSD), peptide 2 at 320K shows a backbone RMSD lower than 0.15 nm for the first 26 nsec of the simulation, between 60 and 67 nsec, and several other times for shorter time intervals. Peptide 2 at 280K shows a somewhat lower flexibility due to the lower temperature of the simulation. Nevertheless, it undergoes a transition leading to an RMSD value of 0.2 nm, to come back to around 0.15 nm at around 80 nsec. Another short-term transition to an RMSD value lower than 0.15 nm is observed around 125 nsec. In simulation 280D, the peptide tends to populate an ensemble of structures with an RMSD value centered at 0.10 nm from the NMR structure, representing about 40% of the total population. A second ensemble, centered at 0.20 nm, is also significantly populated, including about 40% of the total population. The RMSD distribution for 320D displays different features: the most populated ensemble of structures is the one centered at 0.18 nm (50% of the total population), but in this case, the ensemble centered at 0.10 nm (thus very close to the NMR structure) is mostly unpopulated, whereas the bins centered at 0.25 nm account for almost all of the remaining 50% of the total population. Peptide 3 shows an average backbone RMSD of 0.3 nm with respect to a hypothetical β-hairpin reference structure, whereas the RMSD value for peptide 4 immediately rises to 0.6 nm, thus showing that the presence of the D-Pro-Gly sequence in the turn is not sufficient to counteract the negative effects of the deletion of the aromatic cluster.
Interestingly, the single comparison of the RMSD would not give a definite distinction between the two ensembles of structures defining peptide 2 at different temperatures, except for the fact that peptide 2 in 280D can come back to RMSD values around 0.1 nm with respect to the NMR structure several times. Hydrogen-bonding interactions are also important in defining the β-hairpin structure of the peptide. The combination of the two properties (the RMSD behavior and the hydrogen-bonding interactions) is actually indicative of the global folding and dynamical characteristics of the system. RMSD, in fact, has been shown to be a good qualitative check of the stability of simulations, yet not a sufficient criterion for the comparison of dynamic molecules such as proteins and peptides (Maiorov and Crippen 1995).
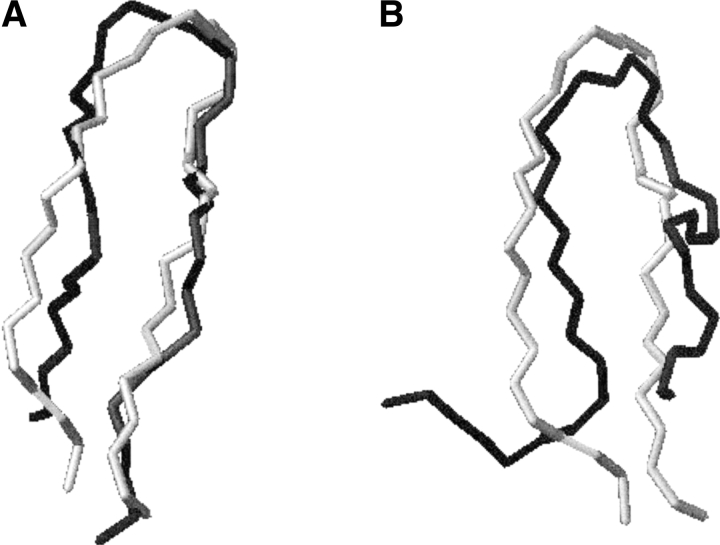
These preliminary calculations should highlight the importance of the turn sequence in keeping the peptide in a close to folded conformation, allowing the formation of favorable hydrogen-bonding interactions between the residues directly bonded to the turn sequence. This interaction, in turn, should drive the formation of other interstrand interactions which could lead to the final folded conformation. Because β-sheets and β-hairpins have folding times in the range of several microseconds (Ramirez-Alvarado et al. 1996; de Alba et al. 1997,1999), our simulations, despite the wide timerange spanned at two different temperatures, are still too short to completely demonstrate reversible folding under realistic conditions. Thus, a conformational clustering algorithm was applied to characterize the conformational space sampled during the simulations. The superposition of the central member structure of the most populated cluster for the two simulations of 2 with the NMR structure shows an RMSD value with respect to the backbone atoms of 0.1 nm in the case of 280K and 0.3 in the case of 320K (Fig. 3A,B ▶). The central member structure of the most populated cluster at 280K is the structure at time 80.9 nsec, whereas for 320K it is the one at 130 nsec. It is worth noting that, despite the structural difference between the central structure of the most populated cluster at 320K and the NMR-derived one, several determinants of the folded state of the peptide are present, such as the hydrogen-bonding interaction between the backbone atoms of residues Val 5 and Lys 8 and "diagonal" hydrophobic-type interactions between the side chains of Trp 2 and Phe 9 and between the side chains of Tyr 4 and Val 11. "Lateral" interactions between Trp 2 and Val 11 and between Tyr 4 and Phe 9 are also present in this particular cluster. The most populated cluster of the simulation at 280K represents an ensemble of low-RMSD structures with respect to the NMR-determined geometry, and can be considered representative of the ensemble of overall folded structures. As expected, the higher conformational mobility of peptide 2 at 320K is reflected in the higher number of conformations (414 clusters) sampled at this temperature than at 280K (214 clusters). The finding that the number of clusters, even at higher temperature, is considerably lower than could be expected from an exhaustive conformational search over all the possible conformers of a peptide of this dimension, and the finding that lateral and diagonal interactions are defined in the most populated conformational family at 320K, suggest that the particular sequence of peptide 2 favors the adoption of a hairpin geometry. This is achieved through the interplay between the propensity of the loop residues to form a well defined turn and the ability to form favorable interactions among hydrophobic residues.
Figure 3.
Backbone superpositions of the central structure of the most populated cluster for the simulations (A) 280D and (B) 320D to the NMR-determined backbone. The structures from the simulations are depicted in black; the NMR structure is in gray.
Lateral versus diagonal interactions
β-hairpin model systems have been used to show that interstrand interactions between side chains of residues facing each other in terms of the β-sheet hydrogen-bonding registry (lateral interactions) confer stability on the antiparallel β-sheet. In the case under examination, the D-Pro-Gly sequence has been shown to be compatible, for stereochemical reasons, with the inset of interactions due to the right-handed strand twist of L-residues. The stereochemical relationship between the turn conformation and the right-handed twist in strands of β-sheets has turned out to be critical in the design of small β-sheet models: the amino acids in the strands of the peptides under study are all Lenantiomers, whereas either D-Pro-Gly or L-Pro-Gly is present in the turn. This diastereoisomeric relation in the turn can cause a change in the "directionality" of the interactions in the strands influencing the folding or the stability of the model peptide. Gellman and coworkers have been able to show that also diagonal side chain–side chain interactions can give significant stabilizing contributions (Syud et al. 2001). Because the structural and dynamical features of the peptides were of primary interest in the present work, the contacts between the side chains are considered in terms of their respective contacts and their timeranges of occurrence. Moreover, Baker (2000) showed that the topology of the folded state is of primary importance in defining the folding-unfolding mechanism of small proteins and peptides. Considering the interactions between hydrophobic side chains only in terms of their force field energies might determine the loss of this kind of topological and dynamical information. Moreover, the approximations introduced in the force field parameterization procedures also lead to approximation errors in defining small energy differences, in particular in the case of hydrophobic side chains, as shown by Mark and coworkers (Villa and Mark 2002).
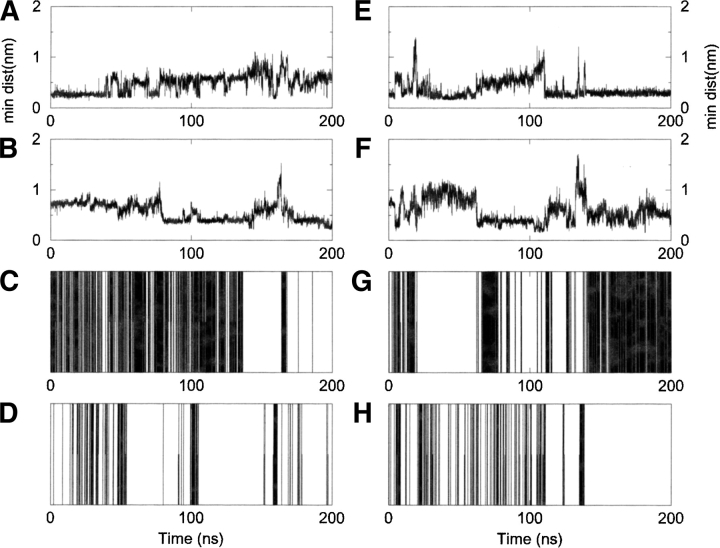
In the peptides under study, the diagonal interactions are between the side chains of Trp 2 and Phe 9 and between the side chains of Tyr 4 and Val 11. In the simulation of 2 at 280K, the contact between the side chains of Trp 2 and Phe 9 is present 47% of the time, whereas the contact between Tyr 4 and Val 11 is present only about 10% of the time in the simulation (Fig. 4A,B ▶). The latter interaction is in fact not present in the list of NMR-NOE-derived contacts recorded at 280K. Interestingly, these values are sensitively higher at 320K; 62% and 23% of the simulation time, respectively, most probably due to a higher mobility of the side chains at higher temperature, which favors the possible encounters between side chains (Fig. 4E,F ▶). The more stable of the two possible diagonal interactions at 280K is between Trp 2 and Phe 9 and involves a partial alignment of the two aromatic planes. Figure 4C,D,G,H ▶, shows the time evolution of the hydrogen-bonding interactions in simulations 280D and 320D, respectively (the same hydrogen bondings as those reported in Table 2). The hydrogen bonds between Val 5 and Lys 8 (Fig. 4C,G ▶) involve the residues directly flanking the D-Pro-Gly motif in the sequence, whereas the ones between Gin 3 and Thr 10 (Fig. 4D,H ▶) are between residues situated in the strands. It is interesting to observe that the presence of the more stable diagonal interaction (between 2 and 9) is paralleled by the presence of a stable hydrogen-bonding interaction between residues 5 and 8. This factor can be considered an index of the formation of the right-turn geometry, favoring the favorable alignment of the hydrogen-bonding donors and acceptors on the 5–8 pair, and of the side chains of Trp 2 and Phe 9. The generation of diagonal interactions is thus correlated with the formation of interstrand hydrogen bonds. The formation of the other interstrand hydrogen-bonding interaction between Gin 3 and Thr 10 participates in stabilizing the correctly folded geometry. The lateral interactions, favored by the proximity in space among the residues involved, are present for a longer time. The contact between Trp 2 and Val 11 is present 75% of the time at both 280K and 320K for peptide 2, whereas the contact between Tyr 4 and Phe 9 is present for 89% and 95% of the time, respectively. The presence of relatively stable diagonal (nonlocal) hydrophobic interactions at 320K can impose conformational restraints on the peptide, together with the particular D-Pro-Gly sequence in the turn, forcing 2 to populate a limited number of possible conformations and driving it to the correct fold. Moreover, the ensemble of these contacts is in good agreement with the experimentally determined contacts reported by Espinosa and Gellman (2000). Nonlocal interactions are also present in the simulation of the control peptide 3. The interactions between Trp 2 and Phe 9 and between Tyr 4 and Val 11 are present for 55% and 32% of the time. However, the lack of a good turn-inducing sequence in the loop makes it impossible for the peptide to form any stable interstrand hydrogen bond, which could lead to the correct folded structure (see Fig. 2C ▶).
Figure 4.
Minimum distance as a function of time between the groups involved in diagonal interactions: (A) Trp 2-Phe 9 at 280K, (B) Tyr 4-Val 11 at 280K, (E) Trp 2-Phe 9 at 320K, and (F) Tyr 4-Val 11 at 320K. The four lower panels represent the hydrogen-bond evolution in time: (C) hydrogen bond Val5-Lys8 at 280K, (D) Gln3-ThrlO at 280K, (G) Val5-Lys8 at 320K, and (H) Gln3-ThrlO at 320K. A black bar is present if an hydrogen bonding interaction is present at that instant.
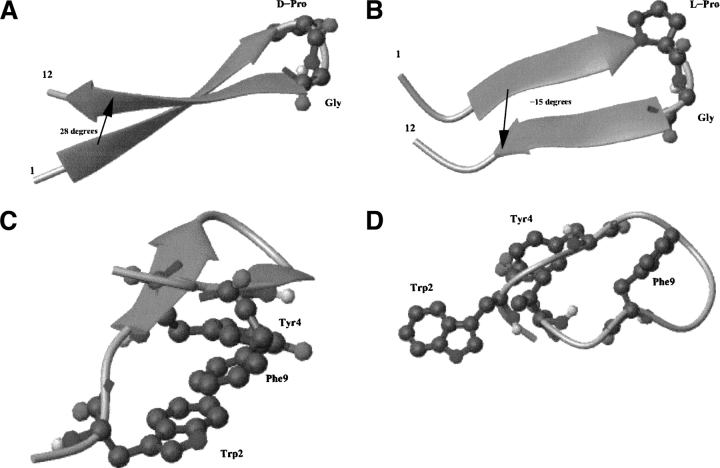
The relationship between the turn sequence and the right-handed β-sheet twist can be important in interpreting these data: the dihedral angle between the two β-strands is on average 28 degrees, as in natural proteins (Chothia 1984) for peptide 2, whereas it assumes an average value of −13 degrees in the case of peptide 3 (Fig. 5A,B ▶, respectively). Moreover, the timeranges in which the angle between the two strands is exactly at 28 degrees coincide with the timeranges in which diagonal contacts are defined in simulations 280D and 320D, a correlation not observed in the case of peptide 3 in simulation 320L. The different orientation of the two strands containing the same sequence of L-residues influences the directionality of the interaction between side chains: whereas in the case of peptide 2, they can interact in a way favorable to and synergistic with the formation of hydrogen bonding interactions, in peptide 3 the same side chains interact simply to remove hydrophobic surface from the contact with water, defining what can be called a misfolded ensemble of conformations. This situation is exemplified in Figure 5C,D ▶, where the representative structures from the simulations are reported for peptides 2 and 3, respectively. From this pictorial representation, the formation of the correct hydrophobic interactions together with the right turn conformation is evident for peptide 2, whereas the absence of these interactions is highlighted for peptide 3. Table 3 summarizes all the observations about the percentage of lateral and diagonal interactions, and should show the importance of the turn sequence in avoiding misfolded conformations such as the case of peptide 3. The complex of these observations highlights that a very delicate balance between the turn propensity of the loop residues and the hydrophobic cluster should exist in order to obtain the correct fold to a β-hairpin structure.
Figure 5.
Schematic representation of the angle between the strands in (A) peptide 2 and (B) 3. The formation of the hydrophobic core is reported in (C) for peptide 2 and (D) for peptide 3.
Table 3.
Summary of percentage of formation of lateral and diagonal interactions in peptides 2 and 3
| Lateral interactions % | Diagonal interactions % | |||
| Sim. | Trp 2-Val 11 | Tyr 4-Phe 9 | Trp 2-Phe 9 | Tyr 4-Val 11 |
| 280D | 75 | 89 | 47 | 10 |
| 320D | 75 | 95 | 62 | 23 |
| 320L | 60 | 20 | 55 | 32 |
Refolding simulation
To investigate the roles of the turn sequence and the nonlocal hydrophobic interactions, a refolding simulation of peptide 2 starting from an extended structure (all backbone angles set to 180 degrees, except naturally for the ones involving D-Pro) (Figs. 6, 7 ▶ ▶) was run at 320K. This kind of simulation can give only qualitative insights into the folding mechanism of the peptide, due to its short time range (50 nsec): It is, in fact, difficult to achieve equilibrium folding/unfolding behavior through all-atom, explicit solvent simulations of systems like the one studied here. Nonetheless, the information obtained from this refolding simulation under realistic conditions (in terms of temperature and of the presence of explicit water molecules) can be useful in gaining mechanistic details regarding the roles of contact formation, turn propensity, and intramolecular interactions.
Figure 6.
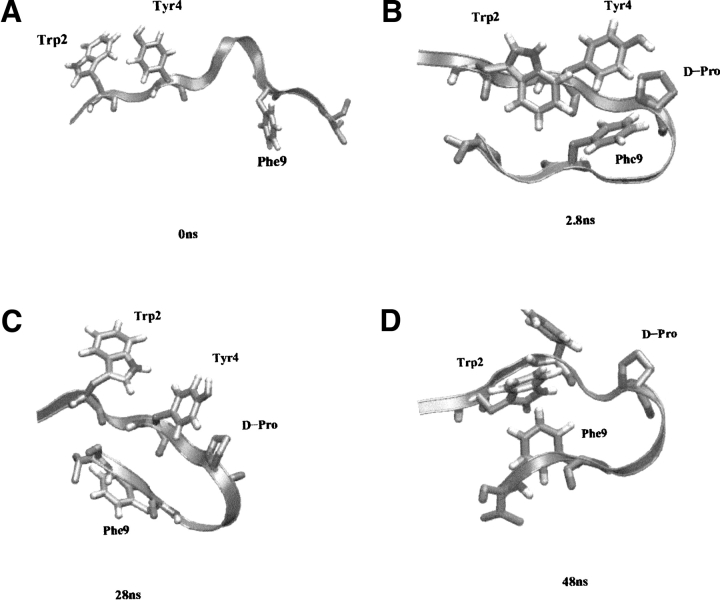
Sample structures from the refolding simulation in a ribbon representation. Trp 2, Tyr 4, and Phe 9, showing the formation of the hydrophobic core, are depicted as tubes. (A) Starting structure, (B) structure at 2.8 nsec, (C) structure at 28 nsec, (D) structure at 48 nsec.
Figure 7.
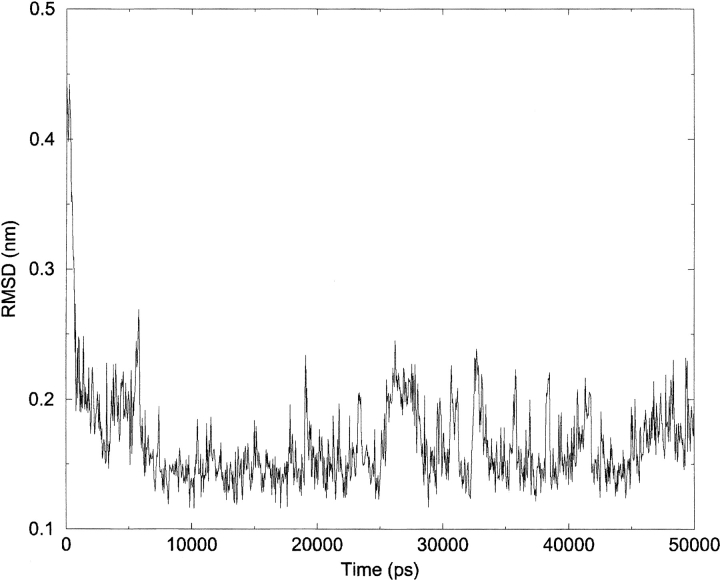
Backbone RMSD of the conformations found in the refolding simulation to the representative structure of the most populated cluster at 280K (folded structure in the force-field).
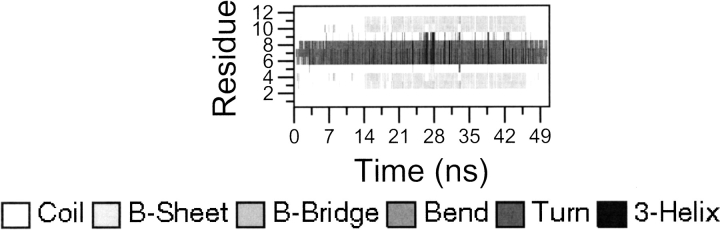
The peptide collapses very rapidly to a compact structure with a backbone RMSD of about 0.2 nm with respect to the central structure of the most populated cluster at 280K (the "folded" ensemble of structures in the force field). At 2.8 nsec, the RMSD value is reduced to 0.l8 nm, and the structure representative of this rapid collapse is displayed in Figure 6 ▶ (structure at 2.8 nsec). This structure shows that the loop sequence is assuming a tight turn conformation and, more importantly, that contacts between the side chains of Trp 2, Phe 9, and Tyr 4 are formed. This type of arrangement contains not only the lateral contact between Tyr 4 and Phe 9, but also the diagonal contact between Trp 2 and Phe 9. Moreover, these three aromatic residues form a "hydrophobic triad" which is representative of the natural hydrophobic cluster found in 41–56 β-hairpin from protein GB1. The average distances between these groups, calculated over the 50 nsec of the simulations, proved that the hydrophobic clustering is quite persistent in the simulation: the distance between Trp 2 and Phe 9 is 0.55 nm, the distance between Tyr 4 and Phe 9 is 0.3 nm, and the distance between Trp 2 and Phe 9 is 0.26 nm. Other authors have also proved the importance of such an arrangement of hydrophobic residues in other proteins via NMR spectroscopy (Ragona et al. 2002). The RMSD evolution with respect to the central structure of the most populated cluster of 280D (representative of the folded ensemble in the force field) is reported in Figure 7 ▶. Figure 8 ▶ reports the secondary structure content (according to the DSSP definition; Kabsch and Sander 1983) as a function of time for the refolding simulation: it is evident that after the collapse and the formation of the hydrophobic interactions, the peptide stabilizes in a β-hairpin type of structure very rapidly. The stable hydrophobic interactions formed at this stage of the refolding simulation involve two residues, Tyr 4 and Val 9, close in the sequence to the loop residues. The particular propensity of the sequence D-Pro-Gly to adopt a tight turn conformation forces the side chains of the proximal residues to come into contact and establish a favorable interstrand folding interaction. This interaction is strengthened by the juxtaposition of the Trp 2 side chain on this preformed hydrophobic complex. The main result of this simulation is the identification of this hydrophobic cluster (present in the NMR-derived conformation) from a starting structure which is completely uncorrelated with the experimental one. This type of nascent structure in water, which can be considered a real folding nucleus, has been observed by other researchers on an independent system using NMR techniques in water and TFE (Ragona et al. 2002). The formation of the hydrophobic core and the parallel formation of a β-hairpin type of backbone is depicted in Figure 6 ▶.
Figure 8.
Secondary structure plot for the refolding simulation.
Discussion
The results of our simulations once again underline the importance of the delicate balance between hydrogen-bonding and hydrophobic interactions in the formation of complex structures such as β-hairpins.
The use of the self-guided molecular dynamics (SGMD; Wu and Wang 1998) simulation method allowed Wu and coworkers (Wu et al. 2002) to simulate and directly observe the folding and unfolding behavior of a related β-hairpin peptide in explicit water, their simulations showing a strong cooperativity in β-hairpin folding. The application of the additional forces used in the SGMD method favors the crossing of energy barriers, reducing the time needed to observe folding events. Previously, β-hairpin folding was studied at high temperature or using implicit solvation models (Sung 1999; Bonvin and van Gunsteren 2000). In our simulations, no additional forces are applied and the system is simulated under realistic conditions with the use of explicit water solvent. Although still short compared to the experimental folding times for related systems, the use of all-atom realistic simulations of the peptide and the water solvent molecules, combined with the use of different temperatures, starting conformations, and long timeranges on the MD timescale (450 nsec in total for peptide 2), shows a good correlation with the experimentally derived NMR parameters (vide infra). These findings, together with the use of control peptides with either a different turn sequence or a deleted hydrophobic core, can yield clear insights into the major factors determining peptide folding and stability.
It is evident from our results that the presence of a tight turn-forming sequence (D-Pro-Gly) is fundamental in driving the formation of the correct set of interstrand hydrogen bonds (simulations 280D and 320D). Substituting D-Pro-Gly with a sequence disfavoring the formation of a tight turn, such as L-Pro-Gly (peptide 3), completely suppresses the formation of the necessary interstrand hydrogen bonds for a correct secondary structure, as reported in the case of the simulation of the L-Pro-Gly-containing diastereoisomer (see Fig. 2 ▶). Our model indicates that the presence of the correct tight turn favors the correlated formation of the right hydrogen-bonding pattern and of the hydrophobic interactions characterizing the NMR-determined structure: lateral interactions involving residues facing each other are found to be stable throughout the dynamics, even in the absence of the correct interstrand hydrogen-bonding pattern. Diagonal interactions, on the other hand, are found to be present for a shorter timerange, but the fact that they can form and be quite stable for large intervals of time, after being broken and reformed in multiple instances, is an indication of their importance as a factor in stabilizing the correct folded conformation.
Diagonal interactions were found to be present also in the simulation of peptide 3. This raises the question of the importance of this kind of interactions in β-hairpin formation and structuring. From our simulations we can infer that diagonal interactions are not sufficient per se to drive the peptide into the β-hairpin conformation. These interactions are present in peptide 3 but not with the right directionality, due to the wrong stereochemistry in the turn sequence. In contrast, the presence of the D-Pro-Gly sequence in peptide 2 results in a different orientation of the planes defined by the two strands, favoring the simultaneous presence of interstrand hydrogen-bonding interactions and the hydrophobic interactions defining the core. Moreover, in peptide 3, lateral interactions are much less stable than in 2 (see Table 3). Hydrophobic interactions are necessary to determine a compact state, but not sufficient to define an ordered structure. The role of diagonal interactions is fundamental in imparting a further stabilization to the structure of the peptide in which the necessary spatial orientation (their relative twist) of the strands, and of the side chains of enantiomerically pure L-residues can be achieved thanks to the presence of the D-Pro-Gly sequence in the turn. It is not by chance that one of the most prevalent turn sequences in natural proteins is Asn-Gly, which determines the formation of the same turn type as D-Pro-Gly (Hutchinson and Thornton 1994). Gellman and coworkers (Syud et al. 2001) examined a very closely correlated system and found for the first time that diagonal side chain–side chain juxtapositions are energetically significant. They estimated that this interaction contributes on the order of 2.0 kJ/mole to the stability of a 12-residue model β-hairpin. Our refolding simulations show that, immediately after the achievement of a correct conformation in the turn, hydrophobic side chain–side chain interactions form between Tyr 4 and Phe 9. Moreover, the juxtaposition of the aromatic side chain of Trp 2 on top of this hydrophobic nucleus (diagonal interaction between Trp 2 and Val 11) stabilizes the partially ordered structure which is formed en route to the folded conformation. The importance of the hydrophobic contacts in preserving the ordered structure of the 41–46 β-hairpin from the domain of protein G had already been observed by Roccatano et al. (1999), who simulated the peptide for shorter times at a range of different temperatures. The juxtaposition of three aromatic (hydrophobic) side chains has been observed on β-hairpin peptides, used by Ragona et al. (2002) to study the folding initiation sites of bovine β-lactoglobulin through NMR spectroscopy in water and TFE. The importance of conserving the hydrophobic packing in determining the secondary structure of peptides even in organic solvents such as TFE was also demonstrated by us via MD simulations of peptides in explicit TFE/water mixtures (Roccatano et al. 2002). The first hydrophobic cluster to be formed, and the more stable in the 200-nsec-long simulations, is the one closest to turn sequence. The stabilization due to the formation of the hydrophobic core provides a major driving force for β-hairpin formation. The hydrophobic cluster is formed almost parallel to the attainment of a good turn conformation, as we already observed in the study of a different system (Colombo et al. 2002). The effect of the hydrophobic stabilization can actually be dependent on the distance in the sequence between the cluster and the turn (Espinosa et al. 2001): this can be a consequence of the compensation between the cost in conformational entropy of forming the β-hairpin and the stabilization produced by interstrand interactions. Bringing together, for instance, Trp 2 and Val 11 would be much more entropically expensive without the constraints imposed on the structure by the partially formed ordered secondary structure. Interstrand clustering reinforced by the diagonal interactions partially compensates for the entropic cost of forming an ordered structure. In peptide 3, the constraints on the structure and the juxtaposition of side chains with the right directionality is absent due to the different diastereoisomeric relationship in that peptide: hydrophobic side chains cluster only to minimize their contact with water, leading to a misfolded structure. The fundamental role of the combination of the turn sequence and the hydrophobic packing is clear from this point of view; in the L-Pro-containing diastereoisomer, as well as in peptide 4, this favorable combination of factors is not present.
Conclusions
We investigated the structural determinants of the stability of a designed β-hairpin containing a natural hydrophobic cluster from the protein GB1. The results of our simulations shed light on the factors leading to an ordered secondary structure in a model peptide, and can give us an atomic resolution picture of the factors determining the folding of such a peptide. We have shown the importance of the so-called diagonal interactions in forming a stable hydrophobic nucleus in the β-hairpin, together with the more obvious lateral interactions. The importance of the diagonal interactions has been underlined a only few times in the previous literature regarding the folding of β-sheet peptides (Cootes et al. 1998; Syud et al. 2001). In particular, Gellman and coworkers (Syud et al. 2001) showed a stabilization due to this factor of about 2.0 kJ/mole. With the use of long timerange MD simulations in explicit water, we have shown the role of diagonal interactions in driving the peptide to the correct folded structure (formation of the hydrophobic core with Trp 2, Tyr 4, and Phe 9 in the first stages of refolding) and in keeping it in the ensemble of folded conformations (Figs. 3, 5 ▶ ▶). The combination of the stabilizing effects of the D-Pro-Gly turn sequence and of the hydrophobic nucleus formation thus favor the attainment of an ordered secondary structure compatible with the one determined experimentally. Moreover, our data underline the importance of the juxtapositions of the side chains of amino acids not directly facing each other in the three-dimensional structure. The combination of these interactions forces the peptide to sample a nonrandom portion of the conformational space, as can be seen in the rapid collapse to an ordered structure in the refolding simulation, and shows that the unfolded state can be closely correlated to the folded ensemble of structures, at least in the case of small model peptides.
Materials and methods
Molecular dynamics simulations and analysis
The starting structure for the simulations (Fig. 1B ▶) was the averaged NMR structure described by Espinosa and Gellman (2000). The peptide was protonated to give a zwitterionic form (with N-terminal NH3+ and C-terminal COO− groups). The peptide was solvated with water in a periodic truncated octahedron large enough to contain the peptide and 0.9 nm of solvent on all sides. All solvent molecules within 0.15 nm of any peptide atom were removed. The total charge on the peptide was +2. No counter-ions were added, as water is a high dielectric and the inclusion of no counter-ions was considered a better approximation to the low-salt experimental conditions. The resulting system was composed of 150 peptide atoms and 3097 water molecules. The control peptide 3 was obtained from peptide 2 by substituting the D-Pro residue in the turn with L-Pro. The system was subsequently energy-minimized with a steepest descent method for 1000 steps. To compare the dynamical behavior of the peptide at different temperatures, simulations at 280K and 320K for 2 (labeled 280D and 320D), and a control simulation at 320K (320L) for 3 were performed. In all simulations, the temperature was maintained close to the intended values by weak coupling to an external temperature bath (Berendsen et al. 1984) with a coupling constant of 0.1 psec. The peptide and the rest of the system were coupled separately to the temperature bath. The GROMOS96 force field (van Gunsteren et al. 1996,1998) was used. The simple point charge (SPC; Berendsen et al. 1987) water model was used. The LINGS algorithm (Hess et al. 1997) was used to constrain all bond lengths. For the water molecules, the SETTLE algorithm (Miyamoto and Kollman 1992) was used. A dielectric permittivity, ɛ = 1, and a timestep of 2 fsec were used. A twin range cut-off was used for the calculation of the nonbonded interactions. The short-range cut-off radius was set to 0.8 nm and the long-range cutoff radius to 1.4 nm for both Coulombic and Lennard-Jones interactions. The cut-off values are the same as those used for the GROMOS96 force field parameterization (van Gunsteren et al. 1998). Interactions within the short-range cut-off were updated every timestep, whereas interactions within the long-range cut-off were updated every five timesteps together with the pairlist. All atoms were given an initial velocity obtained from a Maxwellian distribution at the desired initial temperature. The density of the system was adjusted performing the first equilibration runs at NPT condition (constant number of particles, pressure and temperature) by weak coupling to a bath of constant pressure (P0 = 1 bar, coupling time τP = 0.5 psec; Berendsen et al. 1984). All of the simulations, starting from the average NMR structure, were equilibrated by 50 psec of MD runs, with position restraints on the peptide to allow relaxation of the solvent molecules. These first equilibration runs were followed by other 50-psec runs without position restraints on the peptide. The production runs using NVT conditions, after equilibration, were 200-nsec long for the D-Pro-containing peptide 2 and 100-nsec long for the control peptide 3. The refolding simulation of 2 was started from an extended structure and was run at 320K for 50 nsec.
All of the MD runs and the analysis of the trajectories were performed using the GROMACS software package (van der Spoel et al. 1994). Cluster analysis was performed according to Daura et al. (1999a). The graphical representations of the peptide were realized with the program MOLSCRIPT (Kraulis 1991) and MOLMOL (Koradi et al. 1996).
Acknowledgments
We thank Prof. Sam H. Gellman and Dr. Juan F. Espinosa for providing the experimental data and for helpful discussion, and Prof. Dr. Alan E. Mark for kindly providing computer time.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.0227203/.
References
- Andersen, N.H., Dyer, R.B., Fesinmeyer, R.M., Gau, F., Liu, Z., Neidigh, J.W., and Tong, H. 1999. Effects of hexafluoroisopropanol on the thermodynamics of peptide secondary structure formation. J. Am. Chem. Soc. 121 9879–9880. [Google Scholar]
- Baker, D. 2000. A surprising simplicity to protein folding. Nature 405 39–42. [DOI] [PubMed] [Google Scholar]
- Berendsen, H.J.C., Postma, J.P.M., van Gunsteren, W.F., Di Nola, A., and Haak, J.R. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81 3684–3690. [Google Scholar]
- Berendsen, H.J.C., Grigera, J.R., and Straatsma, T.P. 1987. The missing term in effective pair potentials. J. Phys. Chem. 91 6269–6271. [Google Scholar]
- Blanco, F., Rivas, G., and Serrano, L. 1996. A short linear peptide that folds into a native stable β-hairpin in acqueous solution. Nat. Struct. Biol. 1 584–590. [DOI] [PubMed] [Google Scholar]
- Blanco, F., Ramirez-Alvarado, M., and Serrano, L. 1998. Formation and stability of β-hairpin structures in polypeptides. Curr. Opin. Struct. Biol. 8 107–111. [DOI] [PubMed] [Google Scholar]
- Bonvin, A.M.J.J. and van Gunsteren, W.F. 2000. β-hairpin stability and folding: Molecular dynamics simulations of the first β-hairpin of tendamistat. J. Mol. Biol. 296 255–268. [DOI] [PubMed] [Google Scholar]
- Booth, D. 1997. Instability, unfolding and aggregation of human lysozyme variants underlying amyloid fibrillogenesis. Nature 385 787–793. [DOI] [PubMed] [Google Scholar]
- Brooks III, C.L. and Boczko, E.M. 1995. First-principles calculation of the folding free energy of a three helix bundle protein. Science 269 393–396. [DOI] [PubMed] [Google Scholar]
- Bursulaya, B. and Brooks III, C.L. 1999. Folding free energy surface of a three-stranded β-sheet protein. J. Am. Chem. Soc. 121 9947–9951. [Google Scholar]
- Chakrabartty, A. and Baldwin, R.L. 1995. Stability of α-helices. Adv. Protein Chem. 46 141–176. [PubMed] [Google Scholar]
- Chothia, C. 1984. Principles that determine the structure of proteins. Annu. Rev. Biochem. 53 537–572. [DOI] [PubMed] [Google Scholar]
- Colombo, G., Roccatano, D., and Mark, A.E. 2002. Folding and stability of the three-stranded β-sheet peptide Betanova: Insights from molecular dynamics simulations. Proteins 46 380–392. [DOI] [PubMed] [Google Scholar]
- Cootes, A.P., Curmi, P.M.G., Cunningham, R., Donnelly, C., and Torda, A.E. 1998. The dependence of amino acid pair correlations on structural environment. Proteins 32 175–189. [PubMed] [Google Scholar]
- Cubberley, M.S. and Iverson, B.L. 2001. Models of higher-order structure: Foldamers and beyond. Curr. Opin. Chem. Biol 5 650–653. [DOI] [PubMed] [Google Scholar]
- Das, C., Naganagowda, G.A., Karle, I.L., and Balaram, P. 2001. Designed β hairpin peptides with defined tight turn stereochemistry. Biopolymers 58 335–346. [DOI] [PubMed] [Google Scholar]
- Daura, X., Jaun, B., Seebach, D., van Gunsteren, W.F., and Mark, A.E. 1998. Reversible peptide folding in solution by molecular dynamics simulation. J. Mol. Biol. 280 925–932. [DOI] [PubMed] [Google Scholar]
- Daura, X., Antes, L., van Gunsteren, W.F., Thiel, W., and Mark, A.E. 1999a. The effect of motional averaging on the calculation of nmr-derived structural properties. Proteins 36 542–555. [PubMed] [Google Scholar]
- Daura, X., Gademann, K., Jaun, B., Seebach, D., van Gunsteren, W.F., and Mark, A.E. 1999b. Peptide folding: When simulation meets experiment. Angew. Chem. Int. Ed. 38 236–240. [Google Scholar]
- Daura, X., van Gunsteren, W.F., and Mark, A.E. 1999c. Folding-unfolding thermodynamics of a β-heptapeptide from equilibrium simulations. Proteins 34 269–280. [DOI] [PubMed] [Google Scholar]
- de Alba, E., Jimenez, M.A., and Rico, M. 1997. Turn residue sequence determines β-hairpin conformation in designed peptides. J. Am. Chem. Soc. 119 175–183. [Google Scholar]
- de Alba, E., Santoro, J., Rico, M., and Jimenez, A.A. 1999. De novo design of a monomeric three-stranded antiparallel β-sheet. Protein Sci. 8 854–865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demchuck, E., Bashford, D., and Case, D. 1997. Dynamics of a type VI turn in a linear peptide in acqueous solution. Fold. Design 2 35–46. [DOI] [PubMed] [Google Scholar]
- Dinner, A., Lazaridis, T., and Karplus, M. 1999. Understanding β-hairpin formation. Proc. Natl. Acad. Sci. 96 9068–9073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan, Y. and Kollman, P.A. 1998. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science 282 740–749. [DOI] [PubMed] [Google Scholar]
- Dyson, H.J. and Wright, P.E. 1993. Peptide conformation and protein folding. Curr. Opin. Struct. Biol. 3 60–65. [Google Scholar]
- Espinosa, J.F. and Gellman, S.H. 2000. A designed β-hairpin containing a natural hydrophobic cluster. Angew. Chem. Int. Ed. 39 2330–2333. [DOI] [PubMed] [Google Scholar]
- Espinosa, J.F., Munoz, V., and Gellman, S.H. 2001. Interplay between hydrophobic cluster and loop propensity in β-hairpin formation. J. Mol. Biol. 306 397–402. [DOI] [PubMed] [Google Scholar]
- Ferrara, P. and Caflisch, A. 2000. Folding simulations of a three-stranded antiparallel β-sheet peptide. Proc. Natl. Acad. Sci. 97 10780–10785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gellman, S.H. 1998. Minimal model systems for β-sheet secondary structure in proteins. Curr. Opin. Chem. Biol 7 717. [DOI] [PubMed] [Google Scholar]
- Hess, B., Bekker, H., Fraaije, J., and Berendsen, H. 1997. A linear constraint solver for molecular simulations. J. Comp. Chem. 18 1463–1472. [Google Scholar]
- Hutchinson, E.G. and Thornton, J.M. 1994. A revised set of potentials for β-turn formation in proteins. Protein Sci. 3 2207–2216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibragimova, G.T. and Wade, X.R.C. 1999. Stability of the β-sheet of the ww domain: A molecular dynamics simulation study. Biophys. J. 77 2191–2198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabsch, W. and Sander, C. 1983. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22 2576–2637. [DOI] [PubMed] [Google Scholar]
- Karplus, M. and Sali, A. 1995. Theoretical studies of the protein folding and unfolding. Curr. Opin. Struct. Biol 5 58–73. [DOI] [PubMed] [Google Scholar]
- Kelly, J. 1997. Amyloid fibril formation and protein miniassembly: A structural quest for insight into amyloid and prion diseases. Structure 5 595–600. [DOI] [PubMed] [Google Scholar]
- Koradi, R., Billeter, M., and Wuthrich, K. 1996. MOLMOL: A program for display and analysis of macromolecular structures. J. Mol. Graphics 14 51–55. [DOI] [PubMed] [Google Scholar]
- Kraulis, P.J. 1991. MOLSCRIPT: A program to produce both detailed and schematic plots of protein structures. J. Appl. Cryst. 24 946–950. [Google Scholar]
- Lacroix, E., Viguera, A., and Serrano, L. 1998. Elucidating the folding problem of α-helices: Local motifs, long-range electrostatics, ionic strength dependence and prediction of nmr parameters. J. Mol. Biol. 284 173–191. [DOI] [PubMed] [Google Scholar]
- Ladurner, A.G., Itzhaki, L.S., Daggett, V., and Fersht, A.R. 1998. Synergy between simulations and experiment in describing the energy landscape of protein folding. Proc. Natl. Acad. Sci. 95 8473–8478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazaridis, T. and Karplus, M. 1997. New view of protein folding reconciled with the old through multiple unfolding trajectories. Science 278 1928–1931. [DOI] [PubMed] [Google Scholar]
- Ma, B. and Nussinov, R. 2000. Molecular dynamics simulations of a β-hairpin fragment of protein G: Balance between side-chain and backbone forces. J. Mol. Biol. 296 1091–1104. [DOI] [PubMed] [Google Scholar]
- Maiorov, V.N. and Crippen, G.M. 1995. Size independent comparison of protein 3-dimensional structures. Proteins 22 273–283. [DOI] [PubMed] [Google Scholar]
- Miyamoto, S. and Kollman, P.A. 1992. Settle: An analytical version of the shake and rattle algorithms for rigid water models. J. Comp. Chem. 13 952–962. [Google Scholar]
- Munoz, V., Cronet, P., Lopez-Hernandez, E., and Serrano, L. 1996. Analysis of the effect of local interactions in protein stability. Fold. Design 1 167–178. [DOI] [PubMed] [Google Scholar]
- Pande, V.S. and Rokhsar, D.S. 1999. Molecular dynamics simulations of unfolding and refolding of a β-hairpin fragment from protein g. Proc. Natl. Acad. Sci. 96 9062–9067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parthasarathy, R., Chaturvedi, S., and Go, K. 1995. Design of α-helical peptides: Their role in protein folding and molecular biology. Prog. Biophys. Mol. Biol. 64 1–54. [DOI] [PubMed] [Google Scholar]
- Ragona, L., Catalano, M., Zetta, L., Longhi, R., Fogolari, F., and Molinari, H. 2002. Peptide models of folding initiation sites of bovine β-lactoglobulin: Identification of native-like hydrophobic interactions involving g and h strands. Biochemistry 41 2786–2796. [DOI] [PubMed] [Google Scholar]
- Ramirez-Alvarado, M., Blanco, F.J., and Serrano, L. 1996. De novo design and structural analysis of a model β-hairpin peptide system. Nature Struct. Biol. 3 604–612. [DOI] [PubMed] [Google Scholar]
- Roccatano, D., Amadei, A., Di Nola, A., and Berendsen, H.J.C. 1999. A molecular dynamics study of the 41–56 β-hairpin from bl domain of protein g. Protein Sci. 8 2130–2143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roccatano, D., Fioroni, M., Colombo, G., and Mark, A.E. 2002. The mechanism by which 2,2,2-trifluoroethanol/water mixtures stabilize secondary structure formation in peptides: A molecular dynamics study. Proc. Natl. Acad. Sci. 99 12179–12184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scully, J. and Hermans, J. 1994. Backbone flexibility and stability of reverse turn conformation in a model system. J. Mol. Biol. 235 682–694. [DOI] [PubMed] [Google Scholar]
- Searle, M.S., Griffiths-Jones, S.R., and Skinner-Smith, H. 1999. Energetics of weak interactions in a β-hairpin peptide: Electrostatic and hydrophobic contributions to stability from lysine salt bridges. J. Am. Chem. Soc. 121 11615–11620. [Google Scholar]
- Shakhnovich, E.I. 1997. Theoretical studies of protein-folding thermodynamics and kinetics. Curr. Opin. Struct. Biol. 7 29–40. [DOI] [PubMed] [Google Scholar]
- Smith, C. and Regan, L. 1995. Guidelines for protein design: The energetics of β-sheet side-chain interaction. Science 270 980–982. [DOI] [PubMed] [Google Scholar]
- Sung, S.S. 1999. Monte Carlo simulations of β-hairpin folding at constant temperature. Biophys. J 76 164–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Syud, F.A., Stanger, H.E., and Gellman, S.H. 2001. Interstrand side chain-side chain interactions in a designed β-hairpin: Significance of both lateral and diagonal pairings. J. Am. Chem. Soc. 123 8667–8677. [DOI] [PubMed] [Google Scholar]
- Tobias, D.J., Mertz, J.E., and Brooks III, C.L. 1991. Nanosecond time scale folding dynamics of a pentapeptide in water. Biochemistry 30 6054–6058. [DOI] [PubMed] [Google Scholar]
- van der Spoel, D., van Drunen, R., and Berendsen, H.J.C. 1994. Groningen Machine for Chemical Simulations (GROMACS). Department of Biophysical Chemistry, BIOSON Research Institute, Nijenborgh 4 NL-9717 AG Groningen. e-mail to gromacs@chem.rug.nl.
- van Gunsteren, W.F., Billeter, S.R., Eising, A.A., Hiinenberger, P.H., Kriiger, P., Mark, A.E., Scott, W.R.P., and Tironi, I.G. 1996. Biomolecular Simulation: The GROMOS96 Manual and User Guide. vdf Hochschulverlag, ETH Zurich, Switzerland.
- van Gunsteren, W.F., Daura, X., and Mark, A.E. 1998. GROMOS force field. Encyclopedia of Computational Chemistry 2 1211–1216. [Google Scholar]
- Villa, A. and Mark, A.E. 2002. Calculation of the free energy of solvation for neutral analogues of amino acid side chains. J. Comp. Chem. 23 548–553. [DOI] [PubMed] [Google Scholar]
- Wang, H. and Sung, S. 2000. Molecular dynamics simulations of three-strand-β-sheet folding. J. Am. Chem. Soc. 122 1999–2009. [Google Scholar]
- Wu, X. and Wang, S. 1998. Self-guided molecular dynamics simulation for efficient conformational search. J. Phys. Chem. B 102 7238–7250. [Google Scholar]
- Wu, X., Wang, S., and Brooks, B.R. 2002. Direct observation of the folding and unfolding of a β-hairpin in explicit water through computer simulation. J. Am. Chem. Soc. 124 5282–5283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, Y. and Karplus, M. 1997. Protein folding thermodynamics of a model three-helix-bundle protein. Proc. Natl. Acad. Sci. 94 14429–14432. [DOI] [PMC free article] [PubMed] [Google Scholar]