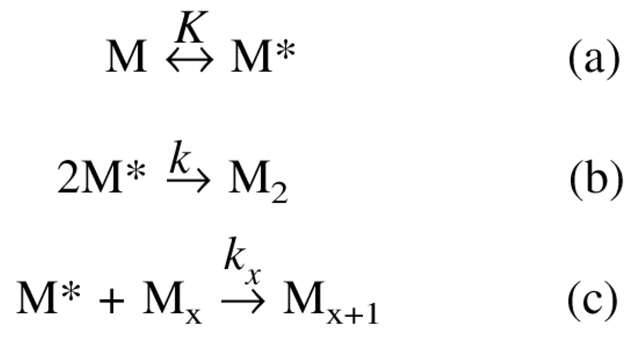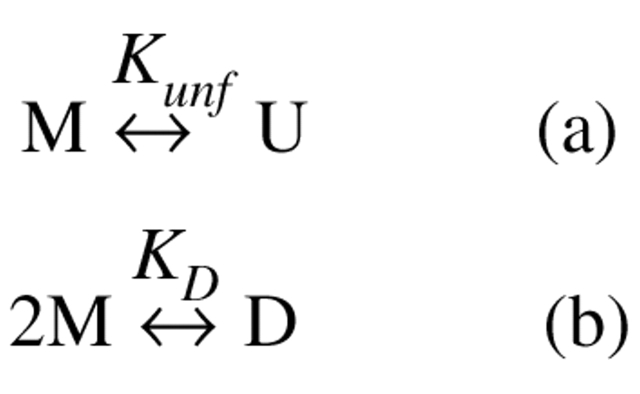Roles of conformational stability and colloidal stability in the aggregation of recombinant human granulocyte colony-stimulating factor

Abstract

We studied the non-native aggregation of recombinant human granulocyte stimulating factor (rhGCSF) in solution conditions where native rhGCSF is both conformationally stable compared to its unfolded state and at concentrations well below its solubility limit. Aggregation of rhGCSF first involves the perturbation of its native structure to form a structurally expanded transition state, followed by assembly process to form an irreversible aggregate. The energy barriers of the two steps are reflected in the experimentally measured values of free energy of unfolding (ΔG_unf) and osmotic second virial coefficient (B₂₂), respectively. Under solution conditions where rhGCSF conformational stability dominates (i.e., large ΔG_unf and negative B₂₂), the first step is rate-limiting, and increasing ΔG_unf (e.g., by the addition of sucrose) decreases aggregation. In solutions where colloidal stability is high (i.e., large and positive B₂₂ values) the second step is rate-limiting, and solution conditions (e.g., low pH and low ionic strength) that increase repulsive interactions between protein molecules are effective at reducing aggregation. rhGCSF aggregation is thus controlled by both conformational stability and colloidal stability, and depending on the solution conditions, either could be rate-limiting.

The aggregation of protein molecules into non-native assemblies in vivo can have profound pathological implications, as in the aggregation of β-amyloid proteins in Alzheimer’s disease and the aggregation of prion protein in numerous neurodegenerative diseases (Smith and Hall 2001). In the biotechnology industry, protein aggregation is encountered routinely during refolding, purification, sterilization, shipping, and storage processes (Manning et al. 1989). Aggregation can occur even under conditions where the protein’s native conformation is favored thermodynamically compared to the unfolded state, and at concentrations well below the protein’s solubility limit (Kendrick et al. 1998; Krishnan et al. 2002). To effectively inhibit aggregation, both in vivo and in vitro, a more complete understanding of the mechanisms by which proteins aggregate and by which varying solution conditions affect this process is needed.

Molecular assembly processes occur as a result of intermolecular forces. Thus, detailed understanding of protein aggregation requires information about the nature and magnitude of these forces. The osmotic second virial coefficient is a measure of nonideal solution behaviors that arise from two-body interactions, and can be derived from statistical mechanics for spherically symmetric forces (McQuarrie 1976):

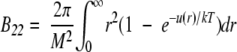(1)

where B₂₂ is the second osmotic virial coefficient with subscripts denoting protein–protein interactions, M is the protein molecular weight, r is the intermolecular separation distance, u(r) is the interaction potential, k is the Boltzmann constant, and T is the absolute temperature. The interaction potential, u(r), describes all of the interaction forces between two protein molecules, which include hard-sphere, electrostatic, van der Waals, and all other short-range interactions. Positive B₂₂ values indicate overall dominance of repulsive forces between proteins, where protein–solvent interactions are favored over protein–protein interactions (George et al. 1997). Negative B₂₂ values reflect attractive forces between proteins, with protein–protein interactions being favored over protein–solvent interactions.

The pioneering work of George and Wilson (1994^; George et al. 1997) showed that solution conditions promoting protein crystallization are characterized by a fairly narrow range of moderately negative B₂₂ values. Proteins are soluble in solutions wherein B₂₂ values are greater than this range, whereas in solutions with B₂₂ values below the range proteins tend to form amorphous precipitates with native protein structures (i.e., “salting out”). B₂₂ is fundamentally linked to protein phase behavior (Rosenbaum et al. 1996; Haas and Drenth 1999) and solubility (Farnum and Zukoski 1999; Guo et al. 1999; Haas et al. 1999; Rosenbaum et al. 1999). B₂₂ values have been used to predict solvent conditions under which chymotrypsinogen will crystallize (Pjura et al. 2000).

The onset of native protein precipitation or crystallization and the morphology of the solid phases are predominantly determined by the mechanisms of molecular approach, reorientation, and incorporation of native proteins, which are governed by the strength and range of protein colloidal interactions (Velev et al. 1998). Assembly of protein molecules into non-native aggregates, resulting in either ordered aggregates (e.g., amyloid fibrils of certain human diseases) or disordered aggregates (e.g., inclusion bodies and amorphous precipitates), by definition involves the formation of higher molecular weight assemblies from initial lower molecular weight species. Thus, the same intermolecular interactions that govern protein crystallization and salting out are also expected to be important in the formation of non-native protein aggregates. For the purpose of this article, these assemblies will be referred to simply as aggregates.

In contrast to crystallization and salting out, aggregation is a more complicated phenomenon. The intrinsic conformational stability of the protein native state plays an important role in its propensity to aggregate. Protein aggregation typically is accompanied by large changes in the secondary and tertiary structures of the protein, with increased non-native intermolecular β-sheet content compared to that for protein in the native state (Fink 1998; Krishnan et al. 2002). Intermediates that are structurally expanded compared to the native state have been found to precede aggregation (Kendrick et al. 1998; Kim et al. 2001; Webb et al. 2001; Krishnan et al. 2002). Sucrose and a number of other solvent additives have been observed to increase protein conformational stability by favoring the more compact native conformation via the preferential exclusion mechanism (Timasheff 1992; Sousa 1995). Preferential exclusion of sucrose has been shown to inhibit aggregation of interferon-γ by disfavoring thermodynamically the expansion of the native state (Kendrick et al. 1997, 1998). Formation of immunoglobulin light chain amyloid fibrils was inhibited by additives (sucrose and betaine) that increased the free energy of protein unfolding (ΔG_unf), and accelerated by additives (urea) that decreased ΔG_unf (Kim et al. 2001). In the presence of sucrose, ΔG_unf for recombinant human granulocyte colony stimulating factor (rhGCSF) was increased and aggregation was slowed (Krishnan et al. 2002).

Protein aggregation is thus the collective effect of at least two processes—an assembly process dominated by intermolecular forces, reflected in the values of B₂₂, and protein structural changes, whose thermodynamics are described by ΔG_unf. In principle, either of these two processes could be rate limiting. In this study, we examined the roles of colloidal stability (reflected by B₂₂) and conformational stability (characterized by ΔG_unf) in the aggregation of rhGCSF. rhGCSF is a pharmaceutically relevant globular protein belonging to a group of growth factors that share the common 4-helix bundle architecture (Hill et al. 1993). It has been found to aggregate rapidly under physiological solution conditions (e.g., pH 7 phosphate-buffered saline and 37°C) where native rhGCSF is both conformationally stable compared to its unfolded state and at concentrations well below its solubility limit (Krishnan et al. 2002). We varied both ΔG_unf and B₂₂ for rhGCSF by systematically varying solution parameters such as pH, salt concentration, salt type, and sucrose concentration, and monitored the protein’s propensity to aggregate.

Results

Aggregation behavior of rhGCSF

Table 1 shows solution conditions under which rhGCSF aggregated during 5 days of incubation at 37°C. In pH 6.9 phosphate-buffered saline (PBS, 10 mM sodium phosphate, and 150 mM sodium chloride [NaCl]), rhGCSF aggregated readily (96% loss of monomer) during 5 days of incubation (Krishnan et al. 2002). In pH 6.1 PBS (protein’s isoelectric point), rhGCSF aggregated as well (30% loss of monomer) during 5 days of incubation. In contrast, in pH 3.5 and low ionic strength solutions (0.32 mM hydrochloric acid [HCl] and 50 to 200 mM sodium acetate), no aggregation was observed during incubation (Table 1). However, at pH 3.5, increasing the ionic strength by the addition of 150 mM NaCl induced aggregation (5% loss of monomers after 5 days of incubation, Table 1). Finally, we have shown previously that in pH 6.9 PBS, sucrose partially inhibited aggregation in a concentration-dependent manner (Krishnan et al. 2002). As expected, aggregation was not observed in pH 3.5 and low ionic strength solutions containing sucrose (0.26 or 0.5 M, Table 1).

Table 1.

Summary of experimental results

						Thermally induced unfolding	Urea-induced unfolding
Solution conditions	Aggregation observed	Refractive index increment dn/dc (mL/g)	Mass averaged molecular weight (kD)	B22 × 103 (cm3mole/g2)	B22/B22HSb	Apparent Tm (M)	Cm (M)	m (kcal/mole/M)	ΔGunf (25°C) (kcal/mole)
pH 3.5 HCl	No	0.187	18.5 ± 3.1	13.5 ± 3.3	85.5 ± 21	74.3 ± 1.7	5.15 ± 0.11	2.19 ± 0.14	11.3 ± 0.71
pH 3.5 HCl 150 mM NaCl	Yes	0.186	N.D.d	N.D.d	N.D.d	64.3 ± 0.19	5.59 ± 0.26	1.77 ± 0.16	9.33 ± 0.63
pH 3.5 HCl 0.26 M Sucrose	No	0.173	30.4 ± 3.0	19.8 ± 1.0	125 ± 6.5	75.4 ± 0.35
pH 3.5 HCl 0.50 M Sucrose	No	0.160	56.5 ± 23	20.9 ± 3.5	264 ± 44c	77.1 ± 0.43
pH 3.5 50 mM NaAc	No	0.186	15.6 ± 1.4	8.98 ± 1.8	56.9 ± 11	75.1 ± 0.49
pH 3.5 100 mM NaAc	No	0.186	16.4 ± 0.70	6.88 ± 0.75	43.6 ± 4.8	74.2 ± 0.92
pH 3.5 150 mM NaAc	No	0.186	17.8 ± 1.6	4.25 ± 1.1	26.9 ± 6.9	72.5 ± 0.41	5.37 ± 0.15	1.96 ± 0.12	10.52 ± 0.40
pH 3.5 200 mM NaAc	No	0.186	19.0 ± 0.56	2.51 ± 0.32	15.9 ± 2.0	73.6 ± 0.96
pH 3.5 200 mM NaAc 0.50 M Sucrose	No	0.163	22.5 ± 1.7	3.39 ± 0.67	21.5 ± 4.2	73.9 ± 0.51
pH 6.1 PBS	Yes	0.190	16.8 ± 0.99	−1.33 ± 0.97	−8.42 ± 6.2	63.4 ± 0.57	5.18 ± 0.13	2.21 ± 0.07	11.4 ± 0.61
pH 6 10 mM Sodium Citrate	Yes	0.196	20.0 ± 0.74	−1.86 ± 0.68	−11.8 ± 4.3
pH 7 PBS	Yes (7.3 ± 0.6)a	0.189	19.7 ± 0.57	−2.34 ± 1.9	−14.8 ± 12	61.1 ± 2.0a	5.88 ± 0.22	1.61 ± 0.05	9.48 ± 0.49
pH 7 10 mM Sodium Phosphate	Yes	0.190	23.9 ± 0.92	−0.72 ± 0.45	−4.57 ± 2.8
pH 7 PBS 0.050 M Sucrose	Yes	0.176	17.9 ± 0.35	−1.52 ± 0.45	−9.63 ± 2.9	60.8 ± 0.49
pH 7 PBS 0.15 M Sucrose	Yes	0.174	18.1 ± 0.45	−1.20 ± 0.33	−7.60 ± 2.1	60.6 ± 1.4
pH 7 PBS 0.25 M Sucrose	Yes (4.8 ± 1.7)a	0.176	33.0 ± 6.7	16.3 ± 3.9	206 ± 49c	63.0 ± 1.3a
pH 7 PBS 0.50 M Sucrose	Yes (2.8 ± 1.5)a	0.179	30.1 ± 14	16.9 ± 1.8	214 ± 24c	63.7 ± 2.0a
pH 7 PBS 0.75 M Sucrose	Yes (1.4 ± 1.3)a	0.163	33.2 ± 11	9.30 ± 7.4	118 ± 94c	65.5 ± 2.1a
pH 7 PBS 1.0 M Sucrose	Yes (0.7 ± 0.2)a	0.155	33.4 ± 11	17.4 ± 4.3	220 ± 55c	68.2 ± 1.8a

^a Results from Krishnan et al. (2002). Numbers in parenthesis of aggregation observed in pH 7 PBS are initial aggregation rates with units μmole/L/day.

^bB₂₂^HS was calculated as four times the molecular volume (V) of rhGCSF using a molecular weight (M) of 19.6 kD for monomers and 39.2 kD for dimers and a protein specific volume (ν) of 0.75 cm³/g (B₂₂^HS = 4V/M² = 4 ν/M).

^cB₂₂ normalized using dimer B₂₂^HS; other calculations were carried out using monomer B₂₂^HS. In pH 7 PBS solutions with 0.25 M and higher sucrose concentrations, extrapolated molecular weights correspond to 40–60 mole % dimer.

^d Could not be reliably determined due to precipitation during sample preparation (dialysis at 4°C) for light scattering experiment.

Errors associated with extrapolated molecular weights and B₂₂ values are standard errors from the linear regression of light scattering data using equation (2). Errors associated with unfolding experiments results are standarddeviations from triplicate samples.

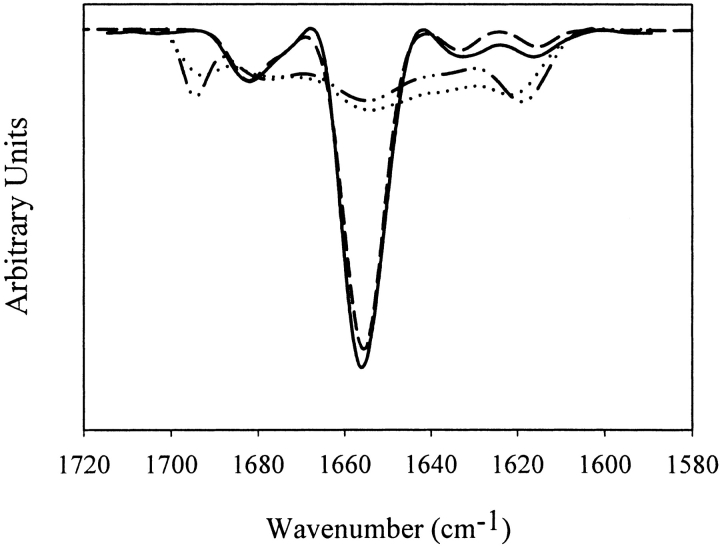
Second derivative Fourier transform infrared (FTIR) spectroscopy was used to examine the secondary structures of soluble rhGCSF in pH 7 PBS and in pH 3.5 HCl with 150 mM NaCl, and aggregates formed during incubation at 37°C in the same solutions (Fig. 1 ▶). Native rhGCSF at both pH 3.5 and pH 7 were predominantly α-helical, as shown by the dominant band at 1656 cm⁻¹ (Dong et al. 2000). Aggregates from both solutions had grossly perturbed secondary structure and dominant levels of non-native intermolecular β-sheet, as evidenced by the strong bands at 1620 and 1695 cm⁻¹ (Dong et al. 2000).

Figure 1.

Structural changes of rhGCSF accompanying aggregation during incubation at 37°C. Area normalized second derivative FTIR spectra of native rhGCSF (solid line, pH 3.5 HCl with 150 mM NaCl; dashed line, pH 7 PBS) show predominantly α-helical structures and aggregated rhGCSF (dotted line, pH 3.5 HCl with 150 mM NaCl; dashed and dotted line, pH 7 PBS) exhibit high levels of intermolecular β-sheet structures. Spectra of soluble and aggregated rhGCSF in pH 7 PBS were taken from Krishnan et al. 2002.

Conformational stability of rhGCSF

Thermally induced unfolding experiments were carried out to assess the conformational stability of rhGCSF in various solution conditions (Table 1). Apparent T_m values (temperature at which 50% of the native rhGCSF was unfolded) of rhGCSF at pH 7, pH 6.1, and pH 3.5 HCl with 150 mM NaCl were approximately 10°C lower than those obtained at pH 3.5 and low ionic strength. These lower T_m values were coincident with irreversible protein aggregation during thermal scans. Solutions with high apparent T_m values showed no aggregation during thermal scans and were 80%–100% reversible. Addition of 0.25 M or higher concentrations of sucrose at pH 7 increased the apparent T_m.

Linear extrapolation of urea-induced unfolding data yielded denaturant m and ΔG_unf values at 25°C in the absence of denaturant (Table 1). Urea concentration at which half of the protein was unfolded, C_m, is also included. rhGCSF unfolding in urea was reversible and essentially complete (circular dichroism [CD] signal at 222 nm was ca. 0) in all solution conditions tested. ΔG_unf values ranged between 9.5 and 11.4 kcal/mole for all conditions. ΔG_unf value of rhGCSF in pH 7 PBS was moderately less—1–2 kcal/mole—than ΔG_unf in pH 3.5 and low salt solutions. ΔG_unf value of rhGCSF in pH 6.1 PBS buffer was the same as in pH 3.5 HCl solution. ΔG_unf values of rhGCSF in pH 3.5 HCl and pH 3.5 HCl with 150 mM NaCl were not significantly different at 95% confidence level from Student’s t-test.

Osmotic second virial coefficients for rhGCSF

B₂₂ values for rhGCSF determined under various solution conditions are summarized in Table 1. Experimental B₂₂ values, as well as values normalized to the hard-sphere contribution, B₂₂/B₂₂^HS, are reported. As shown in Table 1, B₂₂ measured in pH 3.5 solutions were large and positive, indicating strongly repulsive protein–protein interactions. We were not able to reliably determine B₂₂ value for rhGCSF in pH 3.5 HCl with 150 mM NaCl due to intermittent precipitation during sample preparation (dialysis at 4°C). As the pH was increased from 3.5 to pH 6.1 or pH 7, B₂₂ values became negative, indicating that the overall interactions between protein molecules changed from repulsive to attractive. Decreasing total salt concentration, from 160 to 10 mM, in pH 7 and 6.1 PBS did not significantly affect B₂₂ values. With the addition of sucrose above 0.25 M at pH 7, B₂₂ values became positive and very large in magnitude. Increased B₂₂ values were also observed in solutions containing sucrose at pH 3.5.

Refractive index increments (dn/dc) of rhGCSF are also included in Table 1. dn/dc was found to decrease significantly with increasing sucrose concentration while remaining relatively constant with changing salt concentration and pH.

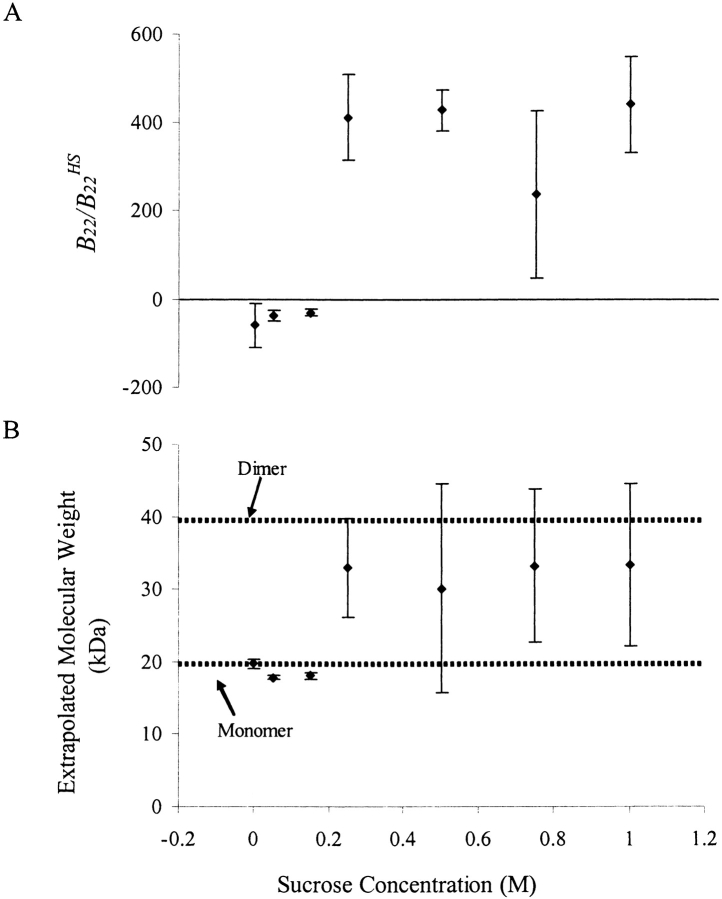
Because all parameters in the Rayleigh equation that was used to analyze static light scattering (SLS) data (equation 2 in Materials and Methods) were determined explicitly, mass averaged molecular weights were also obtained from static light scattering experiments (Table 1). Extrapolated molecular weights in solution conditions without sucrose agreed well with the molecular weight of monomeric rhGCSF (19.6 kD). In the presence of 0.25 M or greater concentrations of sucrose, concomitant with the large changes in B₂₂ value, apparent molecular weights of rhGCSF were greater than 19.6 kD, indicating the presence of higher molecular weight species (Fig. 2 ▶). Assuming that the higher molecular weight species were dimers, the mole % of dimers in equilibrium with monomers ranged from 40 to 60%.

Figure 2.

B₂₂/B₂₂^HS values (A) and extrapolated mass averaged molecular weights (B) of rhGCSF from static light scattering experiments in pH 7 PBS at various sucrose concentrations. Concomitant with the large increase in B₂₂/B₂₂^HS when 0.25 M or more sucrose was added, the apparent rhGCSF molecular weight was higher, indicating the presence of multimeric species. Extrapolated molecular weights for these samples correspond to 40–60 mole % dimers. Thus, B₂₂/B₂₂^HS values measured in these solutions reflect overall two-body interactions, not just from aggregating monomeric species.

Discussion

Mechanism and energetics of rhGCSF aggregation

Native rhGCSF is predominantly α-helical, with 104 of its 174 residues forming a four-helix bundle, and has little or no β-structure (Hill et al. 1993; Fig. 1 ▶). Some of the remaining residues undergo induction to form additional α-helix structures as the pH is lowered from 7.5 to 2.5 (Table 2), while little difference in the four-helix bundle tertiary structure is detected in the pH range of 2 to 7 (Kolvenbach et al. 1997).

Table 2.

Charge and α-helix content of rhGCSF under different pH conditions

	Chargea
pH	+	−	Net	% α-Helix contentb
3.5	14	0	14	84% at pH 2.5
6.1	13	13	0	75% at pH 4.5
7.0	9	13	−4	66% at pH 7.5

^a Charges were calculated based on rhGCSF amino acid composition found in Protein Data Bank. pKa values of charged residues (Asp, Glu, Lys, Arg, and His) were obtained from Lehninger, (Lehninger et al. 1993).

^b % α-Helix contents were taken from Narhi (Narhi et al. 1991).

Although rhGCSF remains conformationally native and compact from pH 2 to 7, its aggregation behavior varies drastically across this pH range. In pH 7 PBS, as depicted in Scheme 1 ▶, native and monomeric rhGCSF (M), first undergoes structural perturbation to form a structurally expanded transition state, M* (Krishnan et al. 2002). M* then dimerizes irreversibly to form an aggregation competent intermediate, M₂. M* also reacts with existing aggregates (M_x) to form larger aggregates (M_x+1), as evidenced by the acceleration in the aggregation rate observed at higher conversions (Krishnan et al. 2002).

Scheme 1:

Aggregation pathway

In addition to aggregation, rhGCSF also participates in two equilibrium reactions (Scheme 2 ▶). It can form a dimer (D) that is favored by the addition of sucrose. rhGCSF can also reversibly unfold to form U in the presence of urea.

Scheme 2:

Equilibrium reactions

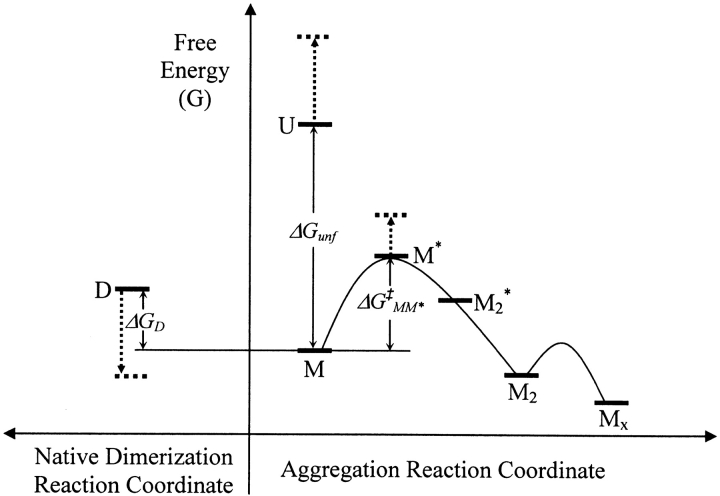
Figure 3 ▶ is a proposed reaction energy profile for Scheme 2 ▶. Because rhGCSF aggregation in pH 7 PBS is spontaneous and rapid, the aggregated state M_x is expected to have the lowest free energy. M is thermodynamically stable compared to U, and their difference in free energy is ΔG_unf. M* is structurally expanded (i.e., it has a higher surface area) relative to M, and as a transition state, must have a higher free energy than either M or M₂. By transition state theory (Atkins 1994), the formation of M₂ is second order in the concentration of M.

Figure 3.

Schematic reaction profile for the aggregation of rhGCSF in pH 7 PBS on an arbitrary free energy y-axis. Curved lines illustrate kinetic energy barriers. M* is a structurally expanded transition state species and ΔG^‡_MM* is the activation free energy of aggregation. The initial rate of irreversible dimer (M₂) formation is second order in native state monomer (M) concentration. Dotted arrows illustrate, relative to M, shifts in the free energies of native dimers (D), unfolded monomer (U), and M* when sucrose is added. The off-path reaction that generates D is depicted to the left of the aggregation reaction coordinate.

Although the mechanism depicted in Scheme 2 ▶ describes the aggregation of rhGCSF, several of its features are expected to be common for the non-native aggregation of other proteins. First, the transformation of a protein that is both soluble and native into non-native aggregates requires conformational changes to the native state. Perturbation to a protein’s native structure to form an aggregation competent species is likely the first conformational change that occurs along the aggregation pathway (Fink 1998; Kendrick et al. 1998). Hence, aggregation is governed by the thermodynamic stability of the native state relative to that of the aggregation competent species. Second, the formation of higher molecular weight aggregates from monomers must involve assembly processes, which are mediated by molecular interactions, and hence, governed by colloidal stability. Aggregation can thus be linked to conformational stability, expressed as ΔG_unf, and colloidal stability, reflected in values of B₂₂. Below, we examine the relative contributions of conformational and colloidal stability in rhGCSF aggregation.

Role of conformational stability in the aggregation of rhGCSF

The addition of sucrose, a preferentially excluded cosolute, shifts the rhGCSF native state ensemble in pH 7 PBS towards more compact, less solvent exposed, structures (Krishnan et al. 2002). As illustrated in Figure 3 ▶, relative to M, sucrose raises the free energies of U and M*. Sucrose thus effectively increases the activation energy barrier, ΔG^‡_MM*, of the aggregation reaction. In addition, sucrose favors the native dimer, D, by about 6.2 kcal/mole relative to M, based on the observation that addition of sucrose increased the mole % dimer to 40%–60% at 25°C. These free energy effects are manifested in the progressively slower rhGCSF aggregation rates in pH 6.9 PBS with increasing sucrose concentration (Table 1; Krishnan et al. 2002). Sucrose also protects rhGCSF from unfolding and aggregating during thermally induced unfolding scans where T_m value increases with the addition of sucrose (Table 1).

Interestingly, ΔG_unf values are not completely predictive of rhGCSF aggregation behavior. ΔG_unf values for rhGCSF in several different solutions (pH 3.5 HCl, pH 6.1 PBS, pH 7 PBS) are comparable. However, aggregation occurs in the pH 6.1 and 7.0 solutions, but not in the pH 3.5 solution (Table 1). In addition, aggregation is observed in solution at pH 3.5 in the presence of 150 mM NaCl, although the change in ΔG_unf caused by addition of salt is statistically insignificant. Thus, rhGCSF aggregation behavior in different solutions cannot be explained by its conformational stability alone.

Role of colloidal stability in the aggregation of rhGCSF

Two major contributions to interactions between colloids in aqueous solutions are Coulombic electrostatic interactions and van der Waals interactions (Israelachvili 1992). The sum of these forces describes the net force acting on colloidal particles and forms the basis of the well-known Derjaguin-Landau-Verwey-Overbeek (DLVO) theory of colloidal stability (Israelachvili 1992; Fig. 4A ▶). Due to the structural, functional, and surface anisotropy of protein molecules, their interactions are often dominated by contributions from relatively few, high-energy intermolecular configurations rather than by the overall colloidal interactions described by the DLVO theory (Neal et al. 1998; Chang et al. 2000). DLVO theory also often fails to describe interactions between proteins at small distances due to either the breakdown of the continuum theory or emergence of non-DLVO forces (Israelachvili 1992; Israelachvili and Wennerström 1996).

Figure 4.

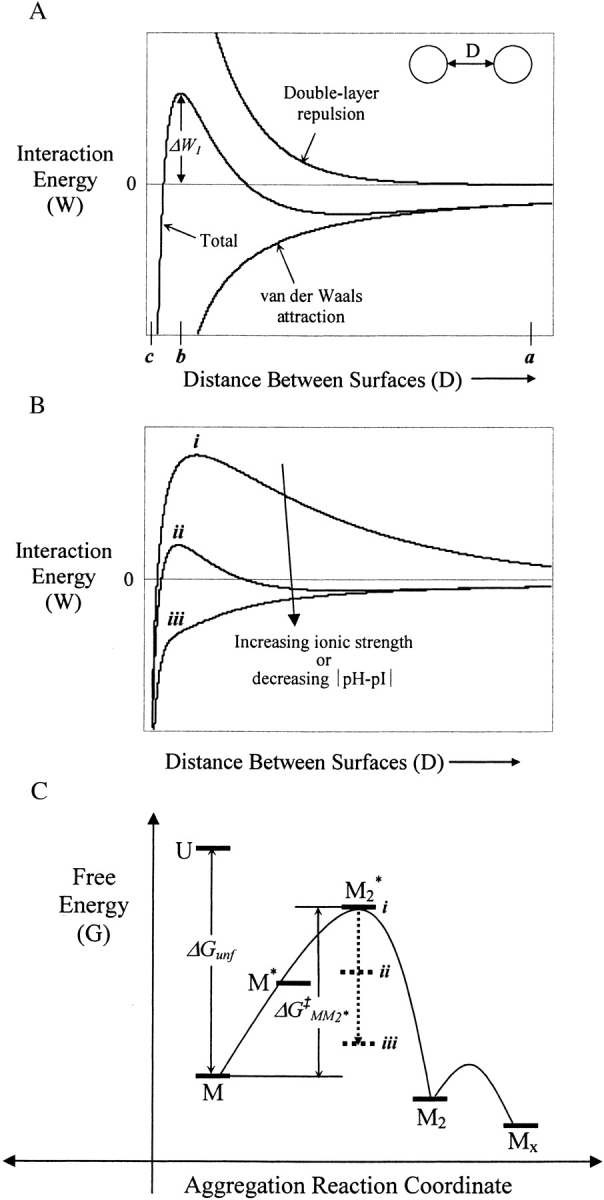
Schematic DLVO interaction energy of two spherical particles interacting at constant and uniform surface potential. (A) Total interaction energy is the sum of electric double-layer repulsion (∝ e^−κD, where κ is the inverse Debye length) and van der Waals attraction (1/6 D; Israelachvili 1992). ΔW₁ represents the maximum interaction energy barrier of the two particles. (B) Increasing salt concentration screens double layer repulsion, resulting in a decrease of ΔW₁. When ΔW₁ < 0 (curve iii), particles become unstable and coagulation occurs. Decreases in ΔW₁ could also be resulted by decreasing the absolute value of the difference between solution pH and the isoelectric point of a protein. (C) Schematic reaction profile for the aggregation of rhGCSF in pH 3.5 HCl on an arbitrary free energy y-axis. Curved lines illustrate kinetic energy barriers. M₂* is the dimeric transition state species and ΔG^‡_MM2* is the activation free energy of aggregation. Dotted arrows illustrate that increases in solution ionic strength (or decreases in |pH-pI|) decrease ΔG^‡_MM2*. At low ionic strength (i), ΔW₁ is large and positive, resulting in a high ΔG^‡_MM2*. Increasing ionic strength sufficiently led to a negative ΔW₁ (iii), lowering ΔG^‡_MM2* enough that M₂* is no longer the transition state of the aggregation reactions. At high ionic strength, M* is expected to be the transition state of aggregation.

As illustrated in Figure 4A ▶, when two isocharged particles such as protein molecules approach each other (e.g., starting from a separation distance marked as point a in Fig. 4A ▶), they need to overcome an energy barrier, ΔW₁ (located at a separation distance marked as position b) to come into physical contact. At distances less than b, molecules experience attractive forces, resulting in coagulation. When ΔW₁ is high, particles remain kinetically stable as dispersed particles (Fig. 4B ▶ i,). Increasing salt concentration decreases electrostatic repulsion and thus lowers ΔW₁ (Fig. 4B ▶) and at high enough concentrations, ΔW₁ becomes negative—particles become unstable and coagulation occurs (Fig. 4B ▶, iii; Israelachvili 1992). Interaction energy between protein molecules thus controls the energetics of their assembly processes. If the energy barrier of collisions between molecules controls protein aggregation (e.g., M₂* has the highest free energy), then ΔW₁ comprises the activation energy of the reaction, ΔG^‡_MM2*, and M₂* is the transition state for the aggregation reaction (Fig. 4C ▶).

At pH 3.5, rhGCSF is highly positively charged (Table 2), resulting in strong protein–protein electrostatic repulsion, as reflected by positive values of B₂₂ (Table 1). Large and repulsive colloidal interactions of rhGCSF in pH 3.5 HCl caused ΔW₁, thus ΔG^‡_MM2*, to be sufficiently high that no aggregation occurred (Fig. 4B,C ▶, case i). This dominant role of colloidal interaction in aggregation is further demonstrated by the observation that even when the native state becomes significantly unfolded during thermal scans, aggregation still does not occur appreciably (data not shown). The addition of 150 mM NaCl (300 mM ion concentration) screens repulsive electrostatic interactions, reducing ΔW₁ (or ΔG^‡_MM2*) sufficiently so that aggregation occurred (Fig. 4B,C ▶, case iii). Under these conditions, transition state is M*, rather than M₂*. Thus, at pH 3.5 and high ionic strength, conformational stability of the native state is the dominant factor governing rhGCSF aggregation (Krishnan et al. 2002).

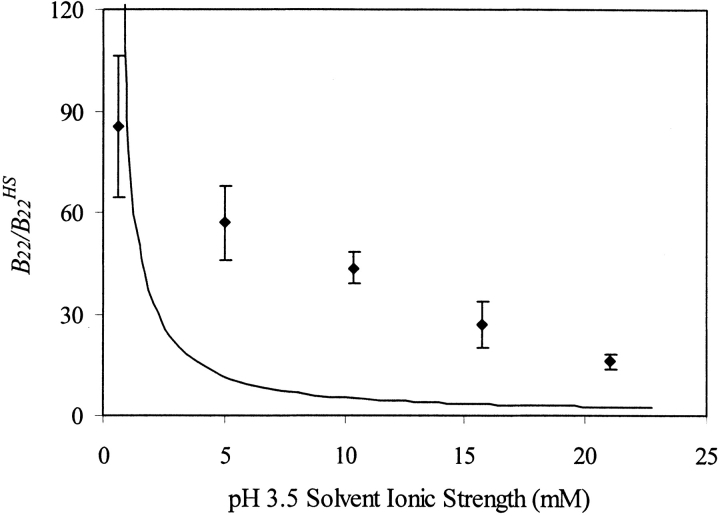
In pH 3.5 solutions at lower ionic strengths (e.g., solutions containing up to 200 mM sodium acetate and pH adjusted to 3.5 with acetic acid at the same molar concentrations), electrostatic repulsion is still sufficiently strong to cause B₂₂ values to be positive (Fig. 5 ▶), which led to large enough ΔG^‡_MM2* that no aggregation occurred on the experimental timescale (Fig. 4B,C ▶, case ii). The strength of this repulsion is reduced in solutions with increased salt concentrations (Fig. 5 ▶). It should be noted that sodium acetate/acetic acid only weakly dissociates. Thus, although concentrations of up to 200 mM sodium acetate at pH 3.5 were used, the ionic strength only reached 24 mM ion concentration. Experimental B₂₂/B₂₂^HS for rhGCSF in solutions containing various concentrations of sodium acetate are larger than those predicted by a simple model that accounts for excluded volume and charge–charge repulsion treating proteins as point charges (Petsev and Denkov 1992; Petsev et al. 2000; Fig. 5 ▶). This could be due to higher order repulsive interaction, such as protein three body interactions, and repulsive two-body interactions with unionized acetic acid that the model did not account for. Additionally, increasing ionic strength may raise the pK_a of ionizable residues (Lee et al. 2002). At pH 3.5, changes in pK_a are expected to have most prominent effects on Asp and Glu residues, where decreases in their side chain acid dissociation are expected. The overall positive charge on rhGCSF thus increases with increasing ionic strength, leading to higher than expected B₂₂ values.

Figure 5.

Comparison between experimental and theoretical B₂₂/B₂₂^HS of rhGCSF at pH 3.5 as a function of ionic strength. Degree of acetic acid ionization was accounted for in calculating the ionic strength of sodium acetate buffers. Error bars on experimental B₂₂/B₂₂^HS (filled diamond) are linear regression standard errors of SLS data using equation 2. Theoretical B₂₂/B₂₂^HS (solid line) was calculated taking into account excluded volume and Coulombic charge–charge repulsion treating proteins as point charges (Petsev et al. 2000).

Although ΔG_unf values for rhGCSF in different pH solutions are comparable, B₂₂ values of rhGCSF change from large and positive in pH 3.5 HCl, where aggregation was not seen, to moderately negative in pH 6.1 PBS and pH 7 PBS, where aggregation occurred. Net charge on rhGCSF changes from +14 to −4 as pH increases from 3.5 to 7 (Table 2). When a protein carries a net charge, electrostatic protein–protein interaction is invariably repulsive, with repulsive force increasing with the square of the net charge. Clearly, electrostatic repulsion cannot be dominant at pH 7, where interactions are overall attractive, as evidenced by the negative B₂₂ value. In addition to electrostatic interactions, anisotropic charge distribution could give rise to highly attractive dipole–dipole interaction configurations (Striolo et al. 2002). This is likely the case with rhGCSF, because the locations of the 9 positive and 13 negative residues in its crystal structure (Protein Data Bank) show highly asymmetric surface distribution at pH 7. Highly attractive dipole–dipole interactions are also likely to be the cause of the negative B₂₂ value measured at pH 6.1, the isoelectric point of rhGCSF. At pH 3.5, all charged residues in the protein are positively charged, thus greatly reducing dipole moments and causing rhGCSF interactions to be repulsive at all separations and orientations.

The effect of pH on protein–protein interaction can also be illustrated by interaction energy curves in Figure 4B ▶. Similar to the effect of increasing ionic strength, decreasing the difference between solution pH and protein pI decreases the energy barrier to protein assembly, or for the case of rhGCSF aggregation, ΔG^‡_MM2* (Fig. 4B,C ▶).

With the addition of 0.05 and 0.15 M sucrose, B₂₂ value of rhGCSF in pH 7 PBS remains negative but increases slightly with increasing sucrose concentration. In solutions with 0.25 M and higher sucrose concentrations, rhGCSF exhibits greatly increased B₂₂ values that are highly positive. Concurrently, 40–60 mole % dimers are detected by SLS (Table 1, Fig. 2 ▶). Dimers are favored at high sucrose concentrations because preferential exclusion of sucrose drives the system to minimize total protein solvent accessible surface area (Timasheff 1992).

rhGCSF in pH 7 PBS incubated at 37°C continues to aggregate when sucrose is added, but at a progressively slower rate with increasing sucrose concentration (Krishnan et al. 2002). The large B₂₂ values obtained in solutions with 0.25 M sucrose or more suggest that the overall colloidal interactions are very repulsive. Why does aggregation still occur when B₂₂ values are large and positive and what accounts for their positive values?

Measured B₂₂ values reflect colloidal interactions between all scattering species, not just from aggregating species. Dimers contribute disproportionally to the apparent B₂₂ and their interactions are likely to be much more repulsive than monomers due to cancellation of attractive dipole interactions that caused B₂₂ to be negative at low concentrations of sucrose. Because it has been shown that these equilibrium dimers do not participate directly in the aggregation pathway (Krishnan et al. 2002), it is not surprising that apparent B₂₂ values measured for solutions that contain primarily dimers do not correlate with monomer aggregation behavior.

Conclusions

Non-native aggregation of a protein involves at least two processes—conformational changes to the protein native state, and assembly of protein molecules into higher order aggregates, and their energetics are controlled by conformational stability and colloidal stability, respectively. The aggregation of rhGCSF in solution conditions where the native state is both conformationally stable compared to its unfolded state and at concentrations well below its solubility first involves the perturbation of its native structure to form a structurally expanded transition state, followed by dimerization to form an irreversible aggregate. The energy barriers of the two steps are reflected in the experimentally measured values of ΔG_unf and B₂₂, respectively. Under solution conditions where conformational stability dominates (i.e., large ΔG_unf and negative B₂₂), the first step is rate-limiting and the activation free energy of aggregation is ΔG^‡_MM*. Increasing ΔG_unf, and thus ΔG^‡_MM*, (e.g., by the addition of sucrose) is effective at decreasing aggregation. In solutions where colloidal stability is high (i.e., large and positive B₂₂ values), the dimerization step is rate-limiting and the activation free energy of aggregation is ΔG^‡_MM2*. Solution conditions (e.g., pH and ionic strength) that increase the colloidal repulsive interactions (and thus B₂₂) between protein molecules are effective at reducing aggregation. rhGCSF aggregation is therefore controlled by both conformational stability and colloidal stability, and depending on the solution conditions, either could be rate-limiting.

Both colloidal and conformational stability are expected to be important in the aggregation of other proteins. To successfully stabilize protein against aggregation, solution conditions need to be chosen to not only stabilize the protein native conformation, but also stabilize protein against attractive intermolecular forces. During development of formulations for therapeutic proteins, the latter goal is often achieved empirically during preformulation studies, where ionic strength, pH, and buffer type are optimized to minimize precipitation and other adverse events (e.g., deamidation). Based on this work, it appears that manipulation of solution conditions during preformulation studies so as to maximize B₂₂ may be useful in development of formulations exhibiting long-term storage stability. We note recently developed techniques for rapid estimation of B₂₂ by Tessier et al. (2002) now permit B₂₂ to be used as a convenient screening tool for preformulation studies.

Materials and methods

Materials

Pharmaceutical grade rhGCSF was produced and purified (>99%) at Amgen, Inc. rhGCSF was obtained as a stock solution at 3 mg/mL in pH 3.25 HCl solution with 5 wt % sorbitol and stored at 4°C. High-purity sucrose was purchased from Pfanstiehl Laboratories, Inc. Other reagents were purchased from Sigma-Aldrich Corporation and Fisher Scientific. All chemicals were of reagent grade.

Solution conditions and aggregation experiments

rhGCSF aggregation was investigated in solution conditions that varied pH, salt type, salt concentration, and sucrose concentration. Solution conditions used were: pH 7 PBS with 0, 0.05, 0.15, 0.25, 0.50, 0.75, and 1.0 M sucrose, pH 6.1 PBS, pH 3.5 HCl with 0, 0.26, and 0.50 M sucrose, pH 3.5 HCl and 150 mM NaCl, pH 3.5 sodium acetate (NaAc) solution at 50, 100, 150, and 200 mM NaAc, and pH 3.5 200 mM NaAc with 0.50 M sucrose. Sodium azide (0.02 wt %) was added to the solutions to prevent microbial growth.

rhGCSF (1.5 mg/mL) was incubated at 37°C in the various solutions described above and the percent monomeric protein remaining as a function of incubation time was determined after centrifugation with size-exclusion high-performance liquid chromatography (SE-HPLC) as described previously (Krishnan et al. 2002).

Second derivative infrared spectroscopy

Secondary structures of rhGCSF in both soluble and aggregated states were assessed with second derivative FTIR. Sample preparation, spectral acquisition, and data analysis were carried out as described by Krishnan et al. (2002).

Osmotic second virial coefficient measurements

B₂₂ values were determined by SLS with a Brookhaven Light Scattering System from Brookhaven Instrument Corporation, equipped with a vertically polarized solid-state laser (wavelength = 523 nm), a BI-200SM goniometer, and a BI9000AT correlator. For dilute solutions consisting of particles that are small compared to the wavelength of incident light (linear dimensions smaller than λ_o/20) such as rhGCSF, scattering is isotropic and the Rayleigh equation is used to interpret SLS data (Hiemenz and Rajagopalan 1997):

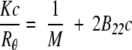(2)

where c is the protein mass concentration, R_θ is the excess Rayleigh ratio, M is the molecular weight of the protein, and K is a constant calculated from optical properties of the system:

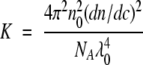(3)

where n_o is the refractive index of the solvent, dn/dc is the protein refractive index increment, N_A is Avagadro’s number, and λ_o is the wavelength of incident laser light. Scattering intensity at 90° was measured to determine B₂₂; scattering at other angles (45, 65, 105, and 135°) was also monitored to verify isotropic scattering from rhGCSF.

Stock solutions of rhGCSF were dialyzed against excess solvent at 4°C for 2 days using 10,000 molecular weight cutoff dialysis cassettes from Pierce. Dialyzed rhGCSF was then diluted to seven different protein concentrations, ranging from 0.5 to 5 mg/mL. The SLS instrument was calibrated with pure toluene before each experiment (B.I. Corporation 1993). R_θ values were determined by subtracting measured scattering intensity of the buffers from those of the respective protein solutions. To minimize scattering from dust, sample vials were washed with 0.02 μm filtered ultrapure water and dried in a dust-free vacuum chamber. Toluene and buffers used during SLS experiments were filtered with 0.02 μm inorganic Anotop 25 syringe filters (Whatman International Ltd.), and all protein solutions were filtered with 0.2μm cellulose acetate syringe filters (Advantec MFS Inc.). Scattering contributions from dust were minimized further by using the built-in statistical criterion of dust-rejection ratio cutoff value of 1.3. Each data point was obtained from the average of no fewer than 30 statistically consistent measurements. Concentrations of protein solutions used during SLS experiments were determined spectrophotometrically (Lambda 35 UV/VIS Spectrophotometer, Perkin Elmer Instrument) using an extinction coefficient of 0.86 at 280 nm and a 1-cm path for a 0.1% solution (Lu et al. 1999). Refractive indices of solvents were determined using a Bausch and Lomb refractometer. dn/dc values for rhGCSF in the different solution conditions were determined independently via the online SE-HPLC light scattering and differential refractometry method described in Kendrick et al. (2001). The DOS version of the BI-ZP Software from B.I. Corporation (1993) was used to collect scattering intensity data. Microsoft Excel was subsequently used to analyze scattering data to extrapolate B₂₂ and mass averaged molecular weight values from least-square linear regression using equation 2.

Free energy of unfolding

The conformational stability of GCSF in various solutions was determined by measuring ΔG_unf by thermally and urea-induced unfolding. Thermally induced unfolding was monitored by far-UV CD (Aviv 62DS) using a 1-mm path-length quartz cuvette at a protein concentration of 0.1 mg/mL. The intensity of CD signal at 222 nm was monitored during unfolding. Temperature was increased at 2°C/min from 25°C to temperatures high enough to obtain adequate post-transition baselines for data analysis; these temperatures ranged from 85 to 95°C depending on solution conditions. CD spectra from 180 to 260 nm were taken for each sample at 25°C before and after heating to determine unfolding reversibility. The percent reversibility was determined from the ratio of intensity at 222 nm for protein before heating and after heating to the maximum temperature and immediate cooling to 25°C. All experiments were carried out in triplicate. For the unfolding of monomeric rhGCSF, unfolding data were analyzed by direct fitting to a modified form of the Gibbs-Helmholtz equation (Pace 1990):

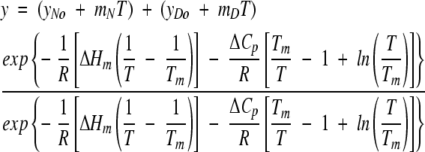(4)

where y is the buffer subtracted CD signal, y_No and y_Do are the pre- and post-transition intercepts, m_N and m_D are pre- and post-transition slopes, T is the absolute temperature, T_m is the temperature at which ΔG_unf is equal to zero, R is the gas constant, ΔH_m is the enthalpy change at T_m, and ΔC_p is the change in heat capacity that accompanies protein unfolding. ΔC_p was estimated to be 2.09 kcal/K/mole, based on the number of amino acid residues in rhGCSF (Krishnan et al. 2002). Direct fitting of unfolding data to equation 4 yielded six parameters: T_m, ΔH_m, and the slopes and intercepts of the pre- and post-transition regions. The free energy of unfolding, ΔG_unf (25°C), was then calculated from the Gibbs-Helmholtz equation (Pace 1990):

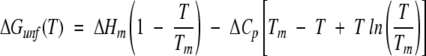(5)

In solution conditions where significant concentrations of dimer (>40%) were determined to be present by SLS (pH 7 PBS with 0.25, 0.50, 0.75 and 1 M sucrose), the transition to the unfolded state (U) was assumed to be coincident with dissociation of the native dimer (D):

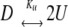(6)

Equilibrium constant for the second order unfolding reaction, K_u, is:

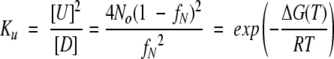(7)

where N_o is the reference state taken as the initial protein concentration of 0.1 mg/mL, and f_N is the fraction of native protein present where f_N = (y_U−y)/(y_U−y_D). Plotting ΔG_unf versus T in the transition region, where f_N is between 0.9 to 0.1, yields a line with y-intercept T_ref (where ΔG_unf is zero) and slope −ΔS_ref. ΔG_unf at 25°C is calculated from equation 5 where ΔH_ref = ΔS_ref/T_ref. Note that T_ref, ΔS_ref, and ΔH_ref obtained from dimer unfolding analysis correspond to 77% unfolded protein. In contrast, T_m, ΔS_m, and ΔH_m obtained from monomer unfolding using equation 4 correspond to 50% unfolded protein.

Urea-induced unfolding experiments were also carried out to determine ΔG_unf, C_m, and m values of rhGCSF. The solubility of urea was observed to decrease with the addition of sucrose (data not shown). Activity of urea is thus increased appreciably by sucrose; we limited the analysis of ΔG_unf by urea-induced unfolding to those solutions that did not contain sucrose (cf. Krishnan et al.). Urea solubility was constant, 9.9 ± 0.1 M, in all other solutions used. Urea unfolding experiments were carried out at a protein concentration of 0.1 mg/mL and urea concentrations ranging from 0 to ca. 9.9 M. Urea concentrations were measured by refractive index (Pace 1986). Protein solutions in urea were equilibrated overnight at room temperature before CD signals at 222 nm and 25°C were collected; all experiments were carried out with triplicate samples. Linear extrapolation was used to analyze rhGCSF unfolding data as a two-state monomer unfolding transition according to Pace and Shaw (2000).

Abbreviations

• rhGCSF, recombinant human granulocyte colony stimulating factor

• SE-HPLC, size-exclusion high-performance liquid chromatography

• FTIR, Fourier transform infrared spectroscopy

• SLS, static light scattering

• CD, circular dichroism

• PBS, phosphate-buffered saline

• DLVO, Derjaguin-Landau-Verwey-Overbeek theory