Abstract
Helices in membrane spanning regions are more tightly packed than the helices in soluble proteins. Thus, we introduce a method that uses a simple scale of burial propensity and a new algorithm to predict transmembrane helical (TMH) segments and a positive-inside rule to predict amino-terminal orientation. The method (the topology predictor of transmembrane helical proteins using mean burial propensity [THUMBUP]) correctly predicted the topology of 55 of 73 proteins (or 75%) with known three-dimensional structures (the 3D helix database). This level of accuracy can be reached by MEMSAT 1.8 (a 200-parameter model-recognition method) and a new HMM-based method (a 111-parameter hidden Markov model, UMDHMMTMHP) if they were retrained with the 73-protein database. Thus, a method based on a physiochemical property can provide topology prediction as accurate as those methods based on more complicated statistical models and learning algorithms for the proteins with accurately known structures. Commonly used HMM-based methods and MEMSAT 1.8 were trained with a combination of the partial 3D helix database and a 1D helix database of TMH proteins in which topology information were obtained by gene fusion and other experimental techniques. These methods provide a significantly poorer prediction for the topology of TMH proteins in the 3D helix database. This suggests that the 1D helix database, because of its inaccuracy, should be avoided as either a training or testing database. A Web server of THUMBUP and UMDHMMTMHP is established for academic users at http://www.smbs.buffalo.edu/phys_bio/service.htm. The 3D helix database is also available from the same Web site.
Keywords: Transmembrane protein topology, burial propensity, topology prediction, hydrophobicity scale
Biological processes are organized through compartmentalization with membranes. Communications and regulation of the communications between inside and outside the membrane are controlled mostly by transmembrane (TM) proteins. Understanding the mechanism of how these proteins function requires the knowledge of their three-dimensional structures. Most TM proteins are helical (TMH) proteins. However, solving their three-dimensional (3D) structures is experimentally challenging because TMH proteins and the membrane are associated by strong hydrophobic interactions. Thus, it is important to develop a reliable theoretical method for predicting the structure of TMH proteins. The importance is highlighted by the finding that 20%–30% of all genes are devoted to encode TMH proteins (Boyd et al. 1998; Wallin and von Heijne 1998; Bairoch and Apweiler 2000; Stevens and Arkin, 2000; Krogh et al. 2001). In this paper, we focus on the determination of the topology of TMH proteins, namely, the membrane spanning regions (MSR) and the amino-terminal orientations. The determination of the topology of a TMH protein is useful for the annotation of its biological function.
Many different methods have been developed to predict the topology of TMH proteins. One widely used method is the analysis based on one or more local properties of amino acids such as hydrophobicity (Argos et al. 1982; Eisenberg et al. 1982; Kyte and Doolittle1982; Nakai and Kanehisa 1992; Cserzo et al. 1997; Jayasinghe et al. 2001b; Juretic et al. 2002), charges (Claros and von Heijne 1994; Hirokawa et al. 1998; Jayasinghe et al., 2001b; Juretic et al., 2002), nonpolar phase helicity (Deber et al. 2001), and multiple sequence alignment (Rost et al. 1995; Persson and Argos 1996). Other investigators use various statistical models [hidden Markov models: TMHMM (Krogh et al. 2001) and HMMTOP (Tusnády and Simon 1998)] and learning algorithms [neural network: PHD (Rost et al. 1996) and model recognition: MEMSAT (Jones et al. 1994)]. These methods were compared in two recent, separate studies by using well-characterized databases (Möller et al. 2001; Ikeda et al. 2002). Both concluded that the most accurate methods are the complex algorithm-based methods such as TMHMM, HMMTOP, and MEMSAT. The result is not surprising because the complex algorithm-based methods use significantly more parameters than local property-based methods. Consensus methods based on multiple prediction algorithms were also developed (Drew et al. 2002; Ikeda et al. 2002; Juretic et al. 2002).
Hydrophobicity is the main local property used to predict TM helices. However, the results largely depend on which hydrophobicity scale is used (Engelman et al. 1986; Degli Esposti et al. 1990; White 1994). This work is spurred by a recent study indicating that helical membrane proteins are packed more tightly than helical soluble proteins (Eilers et al. 2000, 2002). Thus, it may be profitable to use a different scale to predict TM helices, a scale that characterizes the ability of a residue to pack against other residues (packability, H. Zhou and Y. Zhou, in prep.) or, equivalently, the tendency of a residue to be buried by other residues (burial propensity).
Burial propensity is defined here as the average fraction of the buried, solvent-accessible surface area (ASA0–≤ASA>) relative to the total solvent-accessible surface area (ASA0) or 1−≤ASA>/ASA0. Both ASA0–≤ASA> and 1−≤ASA>/ASA0 have been proposed as "hydrophobicity" scales (Chothia 1976; Rose et al. 1985) because of their significant correlations with the oil-to-water transfer free energies. Recent studies (Zhou and Zhou 2002) suggested that ASA0–≤ASA> correlates more strongly with the average contribution of an amino acid residue to the stability of proteins than any hydrophobic scales based on transfer free energies from water to an organic solvent, whereas 1-≤ASA>/ASA0 (burial propensity) correlates strongly with the change in free energy on the change in buried accessible surface area (packability; H. Zhou and Y. Zhou, in prep.). The burial propensity scale (H. Zhou and Y. Zhou, in prep.) was derived from a database of 200 randomly selected proteins from a database of 1011 nonhomologous (<30%) proteins with higher than 2 Å resolution (Hobohm et al. 1992).
In this paper, we develop a topology predictor for TMH proteins using mean burial propensity (THUMBUP). The sliding-window method is used for the profile of burial propensity and a new split-merging-deletion algorithm for identifying TMH segments. A "positive-inside rule" (von Heijne 1986, 1994) is used to determine the orientation of the amino terminus. It was shown that the new scale provides more accurate prediction than other scales commonly used for TMH predictions. More significantly, the accuracy of topology prediction by THUMBUP is essentially the same as the 200-parameter MEMSAT 1.8 and a 111-parameter HMM (UMDHMM) in a database of 73 known 3D crystal and nuclear magnetic resonance (NMR) structures after the parameters of the latter two methods were retrained with the same database. These complex methods, however, if trained with a combination of the partial 3D helix database and a 1D helix database, in which topology information was inferred from gene fusion and other experimental methods, yielded a significantly poorer prediction on the topology of TMH proteins with known structures. Because it is known that the 1D helix database is less accurate than the 3D helix database (Traxler et al. 1993; Jayasinghe et al. 2001b; Chen et al. 2002), our results suggest that the former should be excluded for training and testing of topology prediction algorithms.
Results
Topology prediction
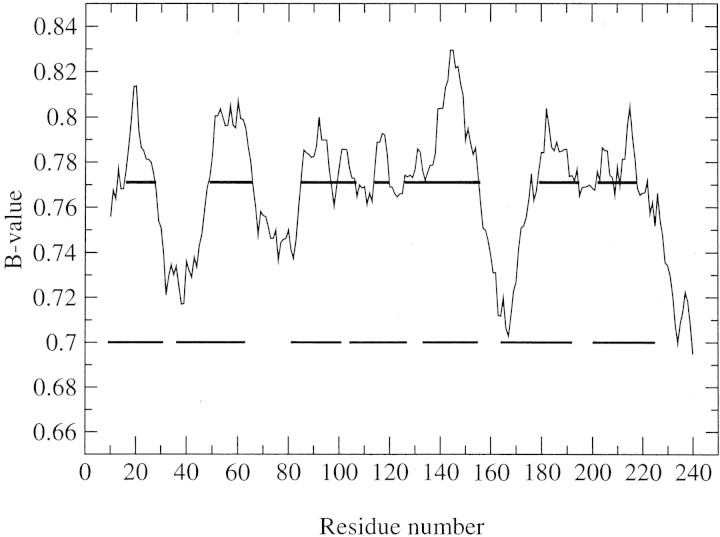
A typical profile of the mean value of burial propensity (shown in Table 1▶) within a 19-residue window (a B-value profile) is shown in Figure 1▶. This plot is very similar to the typical hydropathy plot (e.g., Jayasinghe et al. 2001b). In this example, all seven TMH segments are clearly identified by the peaks of the mean burial propensity.
Table 1.
Amino acid burial propensity (1 − ≤ASA>/ASA0) calculated from 200 randomly selected proteins from a database of 1011 nonhomologous proteins with a higher than 2Å resolution
| Hydrophobic | CYS | MET | PHE | ILE | LEU | VAL | TRP | TYR | ALA | GLY |
| 0.832 | 0.841 | 0.871 | 0.881 | 0.868 | 0.864 | 0.858 | 0.809 | 0.784 | 0.714 | |
| Hydrophilic | THR | SER | GLN | ASN | GLU | ASP | HIS | ARG | LYS | PRO |
| 0.709 | 0.689 | 0.619 | 0.642 | 0.587 | 0.615 | 0.715 | 0.616 | 0.507 | 0.639 |
ASA° is obtained from Shrake and Rupley (1973). Average solvent accessible surface area ≤A> is calculated using Lee-Richards algorithm with 1.4 Å water probe (Lee and Richards 1971).
Figure 1.
The profile of the mean burial propensity and predicted seven TM segments of bacteriorhodopsin. The upper and lower bars indicate the locations of predicted and observed TM segments, respectively. The predicted segments all overlap with the corresponding observed ones for at least five residues long.
Table 2▶ provides a direct comparison between the new method with several well-established methods using the 73-protein 3D helix database. In agreement with two previous assessments (Möller et al. 2001; Ikeda et al. 2002), the method based on hidden Markov model [HMMTOP (Ikeda et al. 2002)] is one of the most accurate methods for topology prediction among the existing methods. We also found that MEMSAT 1.8 is more accurate in predicting the MSR but is less accurate in predicting the amino-terminal orientation than HMMTOP 2.0. Both methods, however, are comparable in predicting the topology of TMH proteins. What is surprising is that THUMBUP is ∼10% more accurate than the complicated HMM methods across all the categories: the amino-terminal orientation, the number of proteins with correct MSR, and the topology. This happens despite the fact that the new method has only 24 parameters, compared to, for example, more than 100 parameters in HMMTOP. Split 4.0, a consensus method based on 15 hydrophobicity scales, is the second most accurate method (behind THUMBUP) for the 3D helix database.
Table 2.
The accuracy of topology prediction in the 3D helix database of 73 proteins by different methods
| Methods | MSRa | Amino-terminal orientationb | Topologyc |
|---|---|---|---|
| TMAPd,e | 49 (67%) | 40 (55%) | 30 (41%) |
| TMprede | 53 (73%) | 40 (55%) | 34 (47%) |
| TopPred IIe | 50 (68%) | 49 (67%) | 39 (53%) |
| SPLIT 4.0e | 62 (85%) | 51 (70%) | 48 (66%) |
| TMHMM 2.0e | 50 (68%) | 49 (67%) | 42 (58%) |
| HMMTOP 2.0d,e | 53 (73%) | 51 (70%) | 44 (60%) |
| MEMSAT 1.8e | 59 (81%) | 48 (66%) | 44 (60%) |
| THUMBUPf | 64 (88%) | 59 (81%) | 55 (75%) |
| THUMBUP (jackknife)f | 63 (86%) | 63 (86%) | 55 (75%) |
| MEMSAT 1.8-3Dg | 62 (85%) | 58 (79%) | 54 (74%) |
a The number (and percentage) of proteins with the correctly predicted membrane spanning region.
b The number (and percentage) of proteins with correctly predicted orientations.
c The number (and percentage) of proteins with correctly predicted topology.
d Only single sequence is used.
e Default settings in respective Web servers were used except that a five-residue overlap is used as a criterion for correct prediction of a TMH segment.
f This work.
g MEMSAT 1.8 using the 73-protein 3D helix database for training and the same database for prediction.
Another way to measure the significance of prediction accuracy is the jackknife cross validation method. A jackknife cross validation is done by using all but one protein for optimization and the two optimized parameters (lcut and B1) are used to predict the topology of the one that was left out. The results are also shown in Table 2▶. The accuracy in prediction from the jackknife test is essentially the same. The 73-protein database was further divided into several different subsets to test whether the performance of THUMBUP depends on the database used. It is found that THUMBUP performs consistently across all different subdivisions of the 73-protein database (see Supplemental Material). Thus, THUMBUP is one of the best algorithms for predicting the topologies of TM proteins with known structures.
The performance of THUMBUP is superior possibly because the parameters in TMHMM, HMMTOP, and MEMSAT were trained from mixed 3D helix and 1D helix databases. Thus, we retrained the 200 parameters of MEMSAT 1.8 with the 73-protein 3D helix database to maximize its performance. The results are shown in Table 2▶. The accuracy of topology prediction by the retrained MEMSAT 1.8 improves significantly over the original MEMSAT 1.8. However, the accuracy is still slightly worse than that of THUMBUP despite the fact that MEMSAT has 200 parameters.
The default hydrophobic scale used in TopPred II is the Goldman-Engelman-Steitz (GES) scale (Engelman et al. 1986). It is possible that the difference of the performance between TopPred II and THUMBUP is not caused by the difference in the scales used but by the difference in the detailed algorithm for splitting, merging, and deleting of candidate TMH segments. Table 3▶ shows the results of four representative scales with the algorithm developed in this study. These four scales [the Eisenberg consensus scale (Eisenberg et al. 1982), the GES scale (Engelman et al. 1986), the augmented WW scale (Jayasinghe et al. 2001b), and the relative frequency JTT2 scale (Jones et al. 1992)] represent the commonly used as well as newly developed scales for predicting TMH segments. The parameters in the algorithm were independently calculated or optimized for each scale using the 40-protein 3D helix database as the parameters in THUMBUP. Table 3▶ indicates that burial propensity is the best in topology prediction among the five scales. The result suggests that burial propensity is likely one of the best scales for predicting the topology of TMH proteins. This is further supported by the fact that burial propensity has a strong correlation (with a correlation coefficient of 0.91) with the knowledge-based scale for amino acid membrane propensity derived from a 3D helix database (Punta and Maritan 2003). The second best scale in Table 3▶ is JTT2, which has the strongest correlation with burial propensity (R = 0.94 ) among the four scales tested. The algorithm used in THUMBUP also appears to be superior to that in TopPred II. With the GES scale, the former correctly predicts 46 of 73 proteins, compared to 39 of 73 proteins in the latter. However, more studies are needed to be certain about the statistical significance of this difference.
Table 3.
The accuracy of topology prediction in the training and test subsets of the 3D helix database of 73 proteins using various physiochemical scales
| Methods |
||||||
|---|---|---|---|---|---|---|
| Database | #a | ECb | GESc | aWWd | JTT2e | Burial propensityf |
| Optimization | 40 | 28 (70%) | 29 (73%) | 25 (63%) | 30 (75%) | 33 (82%) |
| Test | 33 | 16 (48%) | 17 (52%) | 14 (42%) | 21 (64%) | 22 (67%) |
| All | 73 | 44 (60%) | 46 (63%) | 39 (53%) | 51 (70%) | 55 (75%) |
a The number of proteins.
b Eisenberg consensus scale (Eisenberg et al. 1982) with B0 = 0.124 and optimized lcut and B1 (lcut = 6 and B1 = 0.125).
c Goldman-Engelman-Steitz scale (Engelman et al. 1986) with B0 = 0.556 and optimized lcut and B1 (lcut = 6, B1 = 0.556 − 0.584, all yielded same results).
d Augmented WW scale (no salt-bridge included; Jayasinghe et al. 2001b) with lcut = 6, B0 = −0.03, and B1 = −0.03. Note that this is the success rate of topology prediction, rather than prediction of helical segments. The latter often has a success rate of >90%.
e The relative frequency scale (Jones et al. 1992) with lcut = 6, B0 = 1.261, and B1 = 1.283.
f This work.
Although THUMBUP is an exceptionally accurate predictor in the 3D helix database, it performs poorly in a 1D helix database of 261 proteins (Möller et al. 2000) and the 1D helix database of 38 proteins compiled by Jayasinghe et al. (2001a). As shown in Table 4▶, the success rate for its topology prediction in the 261 proteins is only 44%, compared to 55% for MEMSAT 1.8, 70% for TMHMM 2.0, and 66% for HMMTOP 2.0. Similar to THUMBUP, MEMSAT 1.8 retrained with the 73-protein 3D helix database also yielded a poor prediction (43%).
Table 4.
The accuracy of topology prediction in the 1D helix database of 261 proteins that have 1125 assigned TMH segments
| Methods | FPa | FNb | (FP + FN)/# TMHc | MSRd | Amino-terminal orientatione | TM topologyf |
|---|---|---|---|---|---|---|
| TMHMM 2.0 | 42 | 65 | 10% | 201 (77%) | 212 (81%) | 183 (70%) |
| HMMTOP 2.0 | 95 | 24 | 11% | 191 (73%) | 209 (80%) | 172 (66%) |
| MEMSAT 1.8 | 95 | 98 | 17% | 163 (62%) | 198 (76%) | 144 (55%) |
| SPLIT-4.0 | 66 | 65 | 12% | 191 (73%) | 195 (75%) | 162 (62%) |
| THUMBUP | 79 | 150 | 20% | 129 (49%) | 180 (69%) | 114 (44%) |
| MEMSAT-3Dg | 88 | 166 | 23% | 145 (56%) | 175 (67%) | 112 (43%) |
a The number of false-positive TMH segments.
b The number of false-negative TMH segments.
c The fraction of the sum of false positives and negatives in total number of experimentally assigned TMH segments (1125).
d The number (and the percentage) of proteins with correctly predicted TMH segments.
e The number (and the percentage) of proteins with correctly predicted amino-terminal orientations.
f The number (and the percentage) of proteins with correctly predicted topology.
g The parameters are trained from the 73-protein 3D helix database.
To further explore this dramatic change from one database to the other, we study the dependence of the performance of UMDHMMTMHP on its training database (Table 5▶). With a 160-training set used by TMHMM (Krogh et al. 2001; which contains the proteins with and without 3D structures), the accuracy of topology prediction of UMDHMMTMHP is 66% in the 1D helix database of 261 proteins and 63% in the 3D helix database of 73 proteins. The former is lower than that of TMHMM 2.0 (70%), but is the same as that of HMMTOP 2.0, whereas the latter (63% in the 3D helix database) is higher than either that of HMMTOP (60%) or TMHMM (58%). Thus, the accuracy of UMDHMMTMHP is comparable to those of HMMTOP and TMHMM. If UMDHMMTMHP is trained by the 3D helix database, the prediction accuracy is 46% in the 1D helix database of 261 proteins, which is dramatically lower than 78% in the 3D helix database of 73 proteins. Both are only slightly better than the performance of THUMBUP (44% and 75%, respectively). Thus, similar to THUMBUP and the retrained MEMSAT, UMDHMMTMHP trained with the 3D helix database provides a significantly poorer prediction of the topology in the 1D helix database. UMDHMMTMHP trained with the 1D helix database also decreases the accuracy of prediction of the topology in the 3D helix database, although in a less dramatic amount. The accuracy is reduced from 70% in the 1D helix database to 63% in the 3D helix database. Thus, there are intrinsic differences between the proteins in the 1D helix database and those in the 3D helix database.
Table 5.
The accuracy of topology prediction using various HMM methods that are trained by different databases
| Methods training database | HMMTOP default | TMHMM default | UMDHMMTMHP TMHMM default | UMDHMMTMHP 3D helix | UMDHMMTMHP 1D helix |
|---|---|---|---|---|---|
| 1D helix | 66% | 70% | 66% | 46% | 70% |
| 3D helix | 60% | 58% | 63% | 78% | 63% |
One cause for the error in topology prediction is the error in the prediction of the helical segment. The most significant error made by THUMBUP in the 1D helix database is the number of false negatives for helical segments (Table 4▶). It is 150, compared to 98 for MEMSAT 1.8, 24 for HMMTOP 2.0, and 65 for TMHMM 2.0. In other words, THUMBUP failed to identify many TMH segments assigned in the1D helix database. Among the 150 false negatives, 4 were due to misidentified TMH locations, 47 were merged to another TMH segment because the loop is short or hydrophobic, 59 were missed because all residues of the TMH segment have their B-values smaller than B1, and another 40 were missed because the experimentally assigned segment does not contain a segment of a minimum length of six, which satisfies both the lower bound B0 and the upper bound B1 requirements. A dramatic increase from 98 to 166 in false negatives in the same 1D helix database is also observed after the parameters of MEMSAT 1.8 were retrained by the 3D helix database. UMDHMMTMHP, trained with the 3D helix database, on the other hand, yields too many false positives in the 1D helix database (not shown). Thus, it is difficult to pinpoint the exact source that causes the difference between the 1D helix and the 3D helix databases.
Many factors may contribute to the difference between the two databases. For example, the 3D helix database could be biased toward the structures that are potentially easier to solve by X-ray and NMR techniques. More significantly, the topology information in the 1D helix is known to be less reliable than that in the 3D helix database (Traxler et al. 1993). In fact, the average length of TMH segments is 20 in the 1D helix database, compared to 24 in the 3D helix database. This shorter average suggests the influence of hydropathy plots with a sliding window of 19–21 residues (Jayasinghe et al. 2001a). In a 3D helix database, helices often extend beyond the MSR (Jayasinghe et al. 2001b). In a recent paper, Chen et al. (2002) further stated that low-resolution experiments are not much more accurate than prediction methods.
Discrimination
THUMBUP is also tested for its ability to distinguish TMH proteins from other proteins by using a database of 645 soluble and 160 TMH proteins (Krogh et al. 2001). The criterion is the existence of at least one TM segment for a TMH protein. THUMBUP yielded zero false negative but 61 false positives (61/645 = 9.5%). A similar rate of false positives (10.4%) is also observed for a database of 1005 known soluble protein structures. This database is obtained from the database of 1011 nonhomologous (<30%) proteins excluding 6 TMH proteins (Hobohm et al. 1992). This large amount of false positives is not entirely surprising because a TM-like helix can be completely buried inside a soluble protein. Checking the first 23 falsely predicted TMH segments (belonging to 20 soluble proteins), we found that 16 (70%) of them were overlapped with known helices. Nevertheless, a rate of ∼10% false positives is much smaller than the rate of 17%–43% given by several other hydropathy methods (Jayasinghe et al. 2001b).This further supports the use of burial propensity for TMH prediction. Because the length of a TMH segment is usually longer than that of soluble proteins, we can further reduce the number of false positives by introducing a minimum segment length that is required to be a TMH protein. That is, to qualify as a TMH protein, at least one segment should have a length greater than a given value. If this value is set to be 10, the number of false negatives in the 160 TMH proteins becomes one whereas the number of false positives is further reduced to 2.8% (18/645) or 2.9% (29/1005). This result is still not as good as TMHMM. Using the database of 645 soluble and 160 TMH proteins, TMHMM predictions (Krogh et al. 2001) have 5 false positives and 1 false negative, whereas maxH predictions (Boyd et al. 1998; with a maxH cutoff of 1.505) have 3 false positives and 7 false negatives. However, if the cutoff for maxH is chosen so that there is only 1 false negative like TMHMM (the cutoff, then, is 1.410), there are 21 false positives. In this case, the accuracy of maxH will be similar to that of THUMBUP with a constraint of minimum segment length of more than 10.
Discussion
In this paper, we developed a new method (THUMBUP) to predict the topology of TM helical proteins. This is accomplished by using a positive-inside rule for predicting amino-terminal orientations and a simple burial propensity scale for predicting TMH segments. It was shown that the new method yields the most accurate prediction for the proteins with known 3D structures when compared to several commonly used methods with default setting including complex-algorithm-based methods such as hidden Markov models (Tusnády and Simon 1998; Krogh et al. 2001) and model recognition (Jones et al. 1994). The same level of accuracy as THUMBUP is reached by the 200-parameter model recognition method (MEMSAT) and the 111-parameter HMM method only after they were retrained with the 3D helix database. Burial propensity is shown to be one of the best (if not the best) scales for TMH topology prediction. This was concluded based on the results on the 3D helix database using the same algorithm but with four other commonly used scales (Table 3▶). The new split-merging-deletion algorithm also performs better than a slightly different algorithm used in TopPred II. Although the 3D helix database is small, the performance of THUMBUP is robust against various subdivisions of the database. This suggests that the new method is likely (although not for certain) to have a similar performance when a larger database of known structures of TM proteins is available in the future.
The new method, however, produced significantly poorer predictions for the topology of proteins in the 1D helix database. Similar behavior was obtained by Jayasinghe et al. who used an augmented Wimley-White (WW) hydrophobicity scale to predict TM helices of membrane proteins (Jayasinghe et al. 2001b). Significant reduction of prediction accuracy was also observed for MEMSAT and UMDHMMTMHP retrained with the 3D helix database. Thus, an intrinsic difference likely exists between the 3D helix and 1D helix databases. This difference may be contributed to by a possible bias toward experimentally solvable structures in the 3D helix database. However, it is more likely due to the fact that the 1D helix database is not as reliable as the 3D helix database (Traxler et al. 1993; Jayasinghe et al. 2001b; Chen et al. 2002). A significantly higher rate of false negatives of TMH segments for THUMBUP in the 1D helix database than that for TMHMM, HMMTOP, and MEMSAT with default setting suggests that the values of mean burial propensity of some assigned TMH helices in the 1D helix database are close to the values for the helices in soluble proteins. The poor performance of THUMBUP, retrained MEMSAT, and UMDHMMTMHP in the 1D helix database suggests that the 1D helix database should be avoided as either a training or testing database.
If a TMH protein is defined to have a minimum of one TMH segment with a length that is greater than 10, the THUMBUP method has a rate of <1% false negatives and a rate of ∼3% false positives. This rate of false positives is substantially smaller than those given by various hydrophobic scales (17%–43%; Jayasinghe et al. 2001b). The existence of 3% false positives is not surprising because a tightly packed helix may well exist in the hydrophobic core of a soluble protein, similar to the environment of lipid bilayers. The rate of false positives is about three times smaller for TMHMM. This is understandable because TMHMM (Krogh et al. 2001) uses a more sophisticated model to describe TMH.
The positive-inside rule is used here to predict the orientation of the amino terminus. Other variations of the positive-inside rule were also developed. Examples are the charge difference across the first TMH segment (Hartmann et al. 1989), the difference between the amino acid compositions (Nakai and Kanehisa 1992), or the clusters of positive charges (Juretic et al. 2002) between inside and outside loops. Further studies are needed to determine whether these methods could further improve the accuracy of topology prediction.
Materials and methods
Burial propensity of amino acid residues
The burial propensities of amino acid residues (Table 1▶) were derived from a database of 200 randomly selected proteins (H. Zhou and Y. Zhou, in prep.). (A list of 200 proteins can be found in http://www.smbs.buffalo.edu/phys_bio/service.htm.) These values are strongly correlated with the data derived from a database of 23 proteins (Rose et al. 1985; correlation coefficient R = 0.96) and 35 proteins (H. Zhou and Y. Zhou 2002; R = 0.98). All 200 proteins except one (2POR) are soluble proteins. 2POR is a TM β-barrel porin protein.
Database
A 3D helix database refers to a database of proteins with experimentally known 3D structures. A 1D helix database refers to the database of proteins whose topology information was inferred from gene fusion and other methods. We built a 3D helix database of 73 membrane proteins. Among them, 65 proteins are from the TMPDB database (Ikeda et al. 2002; http://bioinfo.si.hirosaki-u.ac.jp/TMPDB/), 2 from MPtopo (http://blanco.biomol.uci.edu/mptopo/; Jayasinghe et al. 2001a), and 6 from the pdb databank (Berman et al. 2000). The amino-terminal locations for the proteins in the mitochondrial inner membrane were assigned incorrectly in TMPDB. (The matrix was assigned as outside and intermembrane as inside.) The errors were corrected. The 73-protein 3D helix database is provided in http://www.smbs.buffalo.edu/phys_bio/service.htm.
We further divide this 73-protein database into a database of 40 proteins for parameter optimization and 33 proteins for independent testing. The 40-protein database is a subset of 43 proteins in the 3D helix database of MPtopo (Jayasinghe et al. 2001a) excluding three proteins (aquaporin, glycerol channel, and KcsA potassium channel) that contain short pore-forming α-helices or loops in the membrane. The 40-protein database was used for the optimization of two parameters in the prediction algorithm. Only two proteins in the 33-protein database have a sequence identity above 30% (33%–38%) with four proteins in the 40-protein database. A high sequence identity does not mean identical topology. In fact, cox1_bovin (in the 33-protein set) has a 38% identity with cyob_ecoli (in the 40-protein dataset), but their topologies are very different from one another. The former has 12 TM helices, whereas the latter has 15 helices. Thus, the 33-protein set can serve as an excellent, independent test database for the algorithm developed in this paper.
As in the MPtopo database, the 73-protein database contains proteins with high sequence identity because subtle differences in sequences can have large effects on hydrophobicity profiles (Edelman and White 1989; Edelman 1993). We also identify a database of 63 proteins that can be considered as nonhomologous proteins [based on clustal w (Thompson et al. 1994)]. This database is used to test the effect of removing homologous proteins in the database. There are 59 proteins whose pairwise sequence identities are <30%. We further include four additional proteins: sensory rhodopsin, psam_synen, cox1_bovin, and cyob_ecoli. These proteins have >30% sequence identities with the 59 proteins. Although, the sequence identity between sensory rhodopsin and psam_synen and between cox1_bovin and cyob_ecoli are 32% and 38%, respectively, the topologies of the proteins are very different. For example, sensory rhodopsin is a seven-helix bundle, whereas psam_synen contains only one TM helix.
A 1D helix database of 261 proteins compiled by Möller et al. (2000; excluding the proteins in level A that belong to the 3D helix database and the proteins without information on the amino-terminal orientation) was used to further test the accuracy of topology prediction.
THUMBUP algorithm
As usual, a sliding window size of 19 amino acids is chosen. This is because a 19-residue segment is close to the thickness of the hydrocarbon core of a lipid bilayer (Jayasinghe et al. 2001b). The mean value of burial propensity within the window is assigned to the central residue of the window (we call it the B-value of the residue). The B-value of the first and last nine residues is not defined. To determine the TM segment and the topology of a protein, we use an algorithm as follows.
Step 1: Determination of candidates
A segment is a candidate TM segment if 1) its sequence length is greater than a cutoff value (lcut), 2) the B-values of the residues in the segment are all greater than B0, and 3) at least one residue in the segment has a B-value greater than B1. We also allow the candidate segment to contain the residues whose B-values are less than B0 if the B-values of the two nearest neighboring residues of the violating residue are greater than B1. The TOPPRED program (von Heijne 1992) also uses two cutoff values but with a different implementation to identify a candidate segment.
Step 2: Merging or deletion
Two candidate segments are merged into one if 1) the two segments are separated by a sequence distance that is less than lcut and 2) the sequence lengths of both segments are ≤19, the window size. On the other hand, the shorter segment of two candidate segments are deleted if 1) the two segments are separated by a sequence distance that is less than lcut and 2) one segment contains more than 19 residues while the other has less than 10.
Step 3: Splitting
A candidate segment will be split into two 19-residue segments (starting from the two ends) if its sequence length is greater than or equal to 2 * 19 + lcut but is less than 3 * 19 + 2 * lcut. It will be split into three 19-residue segments if its sequence length is greater than or equal to 3 * 19 + 2 * lcut. Two of the three 19-residue segments are started from the two ends, whereas the third one is located at the middle of the candidate segment. Steps 2 and 3 are based on the assumption that a TM segment is ∼19 residues long.
Step 4: Screening for possible signal segments
A candidate segment is a signal peptide if it is located within the first ls residue of the protein. This segment is deleted from TM candidate segments. This step takes into account the fact that many signal peptides can be misidentified as a TM segment (Tusnády and Simon 1998).
Step 5. Determination of the orientation of the amino terminus
The orientation of the amino terminus (inside or outside membrane) is determined by the positive-inside rule (von Heijne 1986, 1994). A unit positive charge is first assigned to Arg, Lys, and the first residue of the protein and, then, positive charges are summed over the neighboring loop region of a TMH segment (within 15 amino acid residues; Juretic et al. 2002). If the total positive charge of odd loops is greater than or equal to that of even loops, the amino terminus is inside the membrane enclosed compartment.
The above algorithm contains four parameters in addition to 20 burial propensity parameters for 20 amino acid residues. They are B0, B1, lcut, and ls. B0 is the lower bound of the B-value for a residue in TM helices. We set B0 to 0.771, the average maximal B-value (maxB) of a protein in the database of 1011 proteins (Hobohm et al. 1992), assuming that the B-value for a residue in TM helices should be larger than the average maxB value of soluble proteins. (This database is found to contain six TMH proteins. Without these six proteins, the average value is essentially the same.) A variation of B0 with fixed, optimized B1 and lcut values (given below) indicates that this B0 value provides the best performance. We did not make a systematic search over the space of three parameters (B0, B1, and lcut) to locate globally optimized parameters for a possibly better performance.
To determine the optimal values of lcut and B1, we used a 3D helix database of 40 membrane proteins. During the optimization, we set ls = 0 as we know that there are no signal peptides in the 40-protein database. We use a moderately strict definition for a successful prediction of TM topology. An overlap of at least five residues with the experimentally determined TM segment is required for a correctly predicted TM segment. A range of three to nine overlapping residues has been used in the literature (Tusnády and Simon 1998; Jayasinghe et al. 2001b; Krogh et al. 2001; Möller et al. 2001). The optimized lcut and B1 for the best performance in topology prediction are found to be 6 and 0.781, respectively. We found that the two optimized parameters are insensitive to the database used for optimization. Identical values of lcut and B1 are obtained if the independent 33-protein database (see above) is used for optimization. This suggests that the algorithm developed here is robust.
To obtain the cutoff value for the signal segment ls, we apply the above algorithm to predict the first putative TM segment using the database of eukaryote signal peptides (Nielsen et al. 1997; http://www.cbs.dtu.dk/ftp/signalp). The average residue number of the last residue of the first putative TM segment is found to be 20. Thus, we set ls = 20.
A HMM for topology prediction
To make a more detailed comparison between HMM-based methods with THUMBUP, we developed a HMM that is slightly different from TMHMM and HMMTOP. The main HMM source code is UMDHMM (University of Maryland HMM, version 1.02 obtained from http://www.cfar.umd.edu/kanungo/software/software.html), which was developed to understand the basics of HMMs (Rabiner and Juang 1993). Here, we adapted this program for predicting the topology of TMH proteins. For convenience, we shall label this method UMDHMMTMHP (UMDHMM for topology prediction of TMH proteins).
The implementation is as follows. Each residue can belong to one of the five states: loop inside membrane (in-loop), loop outside membrane (out-loop), tail in-side membrane (in-tail), tail outside membrane (out-tail), and helix. The same five states were used in HMMTOP (Fig. 2; Tusnády and Simon 1998). The probabilities of 20 amino acids in five different states (100 parameters) can be calculated from a training database. The length of the tail is set to six (i.e., a nonhelix residue that is within seven residues away from the TM boundary is counted as a tail residue). A variation around six suggested that the value of six is the best choice.
Each state has substates except in-loop and out-loop. The in-tail and out-tail states have two substates each depending on whether the direction from amino to carboxyl terminus is pointed to inside or outside the membrane. The helix state has 34 substates. The substates ranging from 1 to 17 describe a helix with an amino to a carboxyl direction pointed to outside, whereas the substates ranging from 18 to 34 describe a helix with an amino to a carboxyl direction pointed to inside. This implies that the minimum length of a TMH is 17.
The allowed transitions between substates follow the natural structure of TM proteins (Tusnády and Simon 1998). For example, in-loop is followed by in-tail, helix, out-tail, out-loop, out-tail, helix, and so on. The transitions between two in-tail states and between two out-tail states are also allowed. This requires 10 parameters for transition probability and an additional parameter for the probability of an initial in-loop or out-loop state. The initial values of these 11 parameters were assigned manually so that they yielded a reasonable prediction of TMH topology. These parameters are subsequently optimized with a Monte-Carlo maximization procedure. At each step, all 11 parameters are changed by random numbers (−0.5 to 0.5) multiplied by 0.04. The accuracy of topology prediction for the entire training database is evaluated. The change of the parameters is accepted, if the accuracy increases, and rejected, if otherwise. The procedure is repeated until there is no improvement in accuracy for more than 1000 steps. The above maximization procedure likely leads to a local rather than a global maximum for parameter optimization. This is sufficient here because the goal of this work is not to search for the best HMM-based method but to provide a comparison with THUMBUP. (Several independent runs were unable to improve the accuracy of prediction further.) Here, unlike HMMTOP (Tusnády and Simon 1998) and TMHMM (Krogh et al. 2001), the Baum-Welch (forward-backward) algorithm was not used for parameter optimization and topology prediction. (The Baum-Welch algorithm also leads to local maximum or minimum.) The standard Viterbi algorithm was used for topology prediction (Rabiner and Juang 1993). The Baum-Welch algorithm was not used here because it did not lead to any improvement in accuracy of prediction in the current implementation of HMM. The resulting UMDHMMTMHP method is computationally more efficient than TMHMM and HMMTOP.
Validation, prediction, and comparison
A correct prediction of a TMH segment is defined as an overlap of at least five residues between the predicted TM segment and the experimentally determined one. A correct prediction of the MSR of a protein is defined as one-to-one overlaps between all predicted and experimentally determined TM segments. A correct prediction of TM topology of a protein is defined as the correct prediction of the MSR and the amino-terminal orientation.
We also compare our results with a number of other methods. Results of TMAP (http://bioweb.pasteur.fr/seqanal/interfaces/tmap.html), TMpred (http://www.ch.embnet.org/software/TMPRED_form.html), TopPred II (http://140.129.151.140/pise/emboss/toppred.html), HMMTOP 2.0 (http://www.enzim.hu/hmmtop/), and TMHMM 2.0 (http://www.cbs.dtu.dk/services/TMHMM/) are obtained from their respective Web servers using the default settings. For HMMTOP and TMAP, only a single sequence was used for input. For TopPred II and TMpred, the output of the first topology was selected. MEMSAT 1.8 and SPLIT 4.0 were downloaded from http://www.cs.ucl.ac.uk/staff/d.jones/memsat.html and from http://pref.etfos.hr, respectively.
Acknowledgments
We thank Professor S. H. White for helping us to use his Mpex program, Dr. Tusnády for providing us with his HMMTOP program and helpful discussion, and Dr. Tapas Kanungo and Dr. David Jones for providing their respective software on the Web. This work was supported by a grant from NIH(R01 GM 066049), a grant from Howard Hughes Medical Institute to SUNY Buffalo, by the Center for Computational Research, and the Keck Center for Computational Biology at SUNY Buffalo.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.
Abbreviations
THUMBUP, topology predictor of transmembrane helical proteins using mean burial propensity
UMDHMMTMHP, University of Maryland hidden Markov model for transmembrane helical protein
MSR, membrane spanning regions
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.0305103.
References
- Argos, P., Rao, J.K., and Hargrave, P.A. 1982. Structural prediction of membrane-bound proteins. Eur. J. Biochem. 128 565–575. [DOI] [PubMed] [Google Scholar]
- Bairoch, A. and Apweiler, R. 2000. The SWISS-PROT protein sequence database and its supplement TrEMBL in 2000. Nucleic Acids Res. 28 45–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman, H.M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T.N., Weissig, H., Shindyalov, I.N., and Bourne, P. 2000. The protein data bank. Nucleic Acids Res. 28 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyd, D., Schierle, C., and Beckwith, J. 1998. How many membrane proteins are there? Protein Sci. 7 201–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, C.P., Kernytsky, A., and Rost, B. 2002. Transmembrane helix predictions revisited. Protein Sci. 11 2774–2791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chothia, C. 1976. The nature of the accessible and buried surfaces in proteins. J. Mol. Biol. 105 1–14. [DOI] [PubMed] [Google Scholar]
- Claros, M. and von Heijne, G. 1994. TopPred II: An improved software for membrane protein structure predictions. Comput. Appl. Biosci. 10 685–686. [DOI] [PubMed] [Google Scholar]
- Cserzo, M., Wallin, E., Simon, I., von Heijne, G., and Elofsson, A. 1997. Prediction of transmembrane α-helices in prokaryotic membrane proteins: The dense alignment surface method. Protein Eng. 10 673–676. [DOI] [PubMed] [Google Scholar]
- Deber, C., Wang, C., Liu, L., Prior, A., Agrawal, S., Muskat, B., and Cuticchia, A. 2001. TM finder: A prediction program for transmembrane protein segments using a combination of hydrophobicity and nonpolar phase helicity scales. Protein Sci. 10 212–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degli Esposti, M., Crimi, M., and Venturoli, G. 1990. A critical evaluation of the hydropathy profile of membrane proteins. Eur. J. Biochem. 190 207–219. [DOI] [PubMed] [Google Scholar]
- Drew, D., Sjostrand, D., Nielsen, J., Urbig, T., Chin, C., de Gier, J., and von Heijne, G. 2002. Rapid topology mapping of Escherichia coli inner-membrane proteins by prediction and PhoA/GFP fusion analysis. Proc. Natl. Acad. Sci. 99 2690–2695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelman, J. 1993. Quadratic minimization of predictors for protein secondary structure: Application to transmembrane α helices. J. Mol. Biol. 232 165–191. [DOI] [PubMed] [Google Scholar]
- Edelman, J. and White, S.H. 1989. Linear optimization of predictors for secondary structure. Application to trans-bilayer segments of membrane proteins. J. Mol. Biol. 210 195–209. [DOI] [PubMed] [Google Scholar]
- Eilers, M., Shekar, S.C., Shieh, T., Smith, S.O., and Fleming, P.J. 2000. Internal packing of helical membrane proteins. Proc. Natl. Acad. Sci. 97 5796–5801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eilers, M., Patel, A.B., Liu, W., and Smith, S.O. 2002. Comparison of helix interactions in membrane and soluble α-bundle proteins. Biophys. J. 82 2720–2736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenberg, D., Weiss, R.M., Terwilliger, T.C., and Wilcox, W. 1982. Hydrophobic moments and protein structure. Faraday Symp. Chem. Soc. 17 109–120. [Google Scholar]
- Engelman, D.M., Steitz, T.A., and Goldman, A. 1986. Identifying nonpolar trans-bilayer helices in amino acid sequences of membrane proteins. Annu. Rev. Biophys. Biophys. Chem. 15 321–353. [DOI] [PubMed] [Google Scholar]
- Hartmann, E., Rapaport, T.A., and Lodish, H.F. 1989. Predicting the orientation of eukayotic membrane proteins. Proc. Natl. Acad. Sci. 86 5786–5790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirokawa, T., Boon-Chieng, S., and Mitaku, S. 1998. SOSUI: Classification and secondary structure prediction system for membrane proteins. Bioinformatics 14 378–379. [DOI] [PubMed] [Google Scholar]
- Hobohm, U., Scharf, M., Schneider, R., and Sander, C. 1992. Selection of representative protein data sets. Protein Sci. 1 409–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikeda, M., Arai, M., Lao, D.M., and Shimizu, T. 2002. Transmembrane topology prediction methods: A re-assessment and improvement by a consensus method using a dataset of experimentally-characterized transmembrane topologies. In Silico Biol. 2 19–33. [PubMed] [Google Scholar]
- Jayasinghe, S., Hristova, K., and White, S.H. 2001a. MPtopo: A database of membrane protein topology. Protein Sci. 10 455–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ———. 2001b. Energetics, stability, and prediction of transmembrane helices. J. Mol. Biol. 312 927–934. [DOI] [PubMed] [Google Scholar]
- Jones, D.T., Taylor, W.R., and Thornton, J.M. 1992. A new approach to protein fold recognition. Nature 358 86–89. [DOI] [PubMed] [Google Scholar]
- ———. 1994. A model recognition approach to the prediction of all-helical membrane protein structure and topology. Biochemistry 33 3038–3049. [DOI] [PubMed] [Google Scholar]
- Juretic, D., Zoranić, L., and D.Zucić 2002. Basic charge clusters and predictions of membrane protein topology. J. Chem. Inf. Comput. Sci. 42 620–632. [DOI] [PubMed] [Google Scholar]
- Krogh, A., Larsson, B., von Heijne, G., and Sonnhammer, E.L.L. 2001. Predicting transmembrane protein topology with a hidden Markov model: Application to complete genomes. J. Mol. Biol. 305 567–580. [DOI] [PubMed] [Google Scholar]
- Kyte, J. and Doolittle, R.F. 1982. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 157 105–132. [DOI] [PubMed] [Google Scholar]
- Lee, B. and Richards, F.M. 1971. The interpretation of protein structures: Estimation of static accessibility. J. Mol. Biol. 55 379–400. [DOI] [PubMed] [Google Scholar]
- Möller, S., Kriventseva, E.V., and Apweiler, R. 2000. A collection of well characterized integral membrane proteins. Bioinformatics 16 1159–1160. [DOI] [PubMed] [Google Scholar]
- Möller, S., Croning, M.D.R., and Apweiler, R. 2001. Evaluation of methods for the prediction of membrane spanning regions. Bioinformatics 17 646–653. [DOI] [PubMed] [Google Scholar]
- Nakai, K. and Kanehisa, M. 1992. A knowledge base for predicting protein localization sites in eukaryotic cells. Genomics 14 897–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen, H., Engelbrecht, J., Brunak, S., and von Heijne, G. 1997. Identification of prokaryotic and eukaryotic signal peptides and prediction of their cleavage sites. Protein Eng. 10 1–6. [DOI] [PubMed] [Google Scholar]
- Persson, B. and Argos, P. 1996. Topology prediction of membrane proteins. Protein Sci. 5 363–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Punta, M. and Maritan, A. 2003. A knowledge-based scale for amino acid membrane propensity. Proteins 50 114–121. [DOI] [PubMed] [Google Scholar]
- Rabiner, L.R. and Juang, B.H. 1993. Fundamentals of speech recognition. Prentice-Hall, Englewood Cliffs, NJ.
- Rose, G.D., Geselowitz, A.R., Lesser, G.J., Lee, R.H., and Zehfus, M.H. 1985. Hydrophobicity of amino acid residues in globular protein. Science 229 834–838. [DOI] [PubMed] [Google Scholar]
- Rost, B., Casadio, R., Fariselli, P., and Sander, C. 1995. Transmembrane helices predicted at 95% accuracy. Protein Sci. 4 521–533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rost, B., Casadio, R., and Fariselli, P. 1996. Refining neural network predictions for helical transmembrane proteins by dynamic programming. Proc. Int. Conf. Intell. Syst. Mol. Biol. 4 192–200. [PubMed] [Google Scholar]
- Shrake, A. and Rupley, J.A. 1973. Environment and exposure to solvent of protein atoms. Lysozyme and insulin. J. Mol. Biol. 79 351–371. [DOI] [PubMed] [Google Scholar]
- Stevens, T.J. and Arkin, I.T. 2000. Do more complex organisms have a greater proportion of membrane proteins in their genomes? Proteins 39 417–420. [DOI] [PubMed] [Google Scholar]
- Thompson, J.D., Higgins, D.G., and Gibson, T.J. 1994. CLUSTAL W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, positions-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22 4673–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traxler, B., Boyd, D., and Beckwith, J. 1993. The topological analysis of integral cytoplasmic membrane proteins. J. Membr. Biol. 132 1–11. [DOI] [PubMed] [Google Scholar]
- Tusnády, G. and Simon, I. 1998. Principles governing amino acid composition of integral membrane proteins: Application to topology prediction. J. Mol. Biol. 283 489–506. [DOI] [PubMed] [Google Scholar]
- von Heijne, G. 1986. The distribution of positively charged residues in bacterial inner membrane proteins correlates with the trans-membrane topology. EMBO J. 5 3021–3027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ———. 1992. Membrane protein structure prediction: Hydrophobicity analysis and the positive-inside rule. J. Mol. Biol. 225 487–494. [DOI] [PubMed] [Google Scholar]
- ———. 1994. Membrane proteins: From sequence to structure. Annu. Rev. Biophys. Biomol. Struct. 23 167–192. [DOI] [PubMed] [Google Scholar]
- Wallin, E. and von Heijne, G. 1998. Genome-wide analysis of integral membrane proteins from eubacterial, archaean, and eukaryotic organisms. Protein Sci. 7 1029–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White, S.H. 1994. Hydropathy plots and the prediction of membrane protein topology. In Membrane protein structure: Experimental approaches (ed. S.H. White), pp. 97–124. Oxford University Press, New York, NY.
- Zhou, H. and Zhou, Y. 2002. The stability scale and atomic solvation parameters extracted from 1023 mutation experiments. Proteins 49 483–492. [DOI] [PubMed] [Google Scholar]