Exploring the folding free energy surface of a three-helix bundle protein

Abstract

The multidimensional free energy surface for a small fast folding helical protein is explored based on first-principle calculations. The model represents the 46-residue segment from fragment B of staphylococcal protein A. The relationship between collapse and tertiary structure formation, and the order of collapse and secondary structure formation, are investigated. We find that the initial collapse process gives rise to a transition state with about 30% of the native tertiary structure and 50–70% of the native helix content. We also observe two distinct distributions of native helix in this collapsed state (R_g ≈ 12 Å), one with about 20% of the native helical hydrogen bonds, the other with near 70%. The former corresponds to a local minimum. The barrier from this metastable state to the native state is about 2 k_BT. In the latter case, folding is essentially a downhill process involving topological assembly. In addition, the order of formation of secondary structure among the three helices is examined. We observe cooperative formation of the secondary structure in helix I and helix II. Secondary structure in helix III starts to form following the formation of certain secondary structure in both helix I and helix II. Comparisons of our results with those from theory and experiment are made.

The process of protein organization from the random coil manifold of states to a specific native structure remains an intriguing problem in molecular biology. Because of the vast conformational space available to the protein chain, the time it would require to locate its unique structure by a random search would be astronomical. Different ways of overcoming this search problem have been proposed. Some models such as the framework model (1) and the diffusion-collision model (2) focus on the formation of secondary structural elements followed by their assembly. Others such as the hydrophobic collapse model (3) emphasize the formation of tertiary structure accompanying secondary structure formation. More recently, a theoretical model based on a statistical landscape analysis has been proposed (4). According to this theory, folding can be described by the descent of the folding chain down a folding funnel, with local roughness reflecting the potential for transient trapping in local minima and the overall slope of the funnel representing the thermodynamic drive to the native state. The bottleneck to folding in this funnel picture is the confluence of multiple delocalized “nuclei” at a transition point (the transition state). While the folding funnel model incorporates many aspects of the other folding models, a fully unified view of protein folding has yet to be developed. For example, it is unclear from these models how much secondary structure, resembling that in the native state, is present in the unfolded state. Nor is the degree of similarity between the transition state and the native state well understood. Further, the order of collapse and secondary structure formation is still under debate. Because of the very short time scale for collapse and secondary structure formation, it is difficult to probe these features of folding experimentally (5–7).

Recently, the folding of small helical proteins has been investigated theoretically using a simple statistical mechanical model (4, 8). This work, in conjunction with the development of statistical energy landscape analysis, provides several scenarios for protein folding. Depending upon the ruggedness of the underlying energy landscape, a helical protein can either fold without any significant barrier or can become trapped in local minima in which transitions from these misfolds to the native state become rate-limiting. In addition, these studies indicate that the transition state displays on the order of 90% helicity and roughly 60% of the native contacts (4). The correlation between these theoretical predictions and observations from real proteins has been constructed (9) and can guide experiment and simulation.

Although protein folding simulations have been widely employed, most have focused on simple models that use effective potentials and reduced protein representations (10–17). The analysis of protein unfolding has been carried out using all-atom microscopic models (18–21). However, these studies have not provided detailed thermodynamic properties of protein folding for comparison to experiment or theory. The sole thermodynamic analysis conducted as yet is that of Boczko and Brooks (22) on the three-helix bundle protein that is the focus of this work. In their study, the energetic and entropic contributions for folding from a relatively compact denatured state to the native fold were calculated, and the free energy surface along the radius of gyration (R_g) was explored. However, protein folding is a complex process that requires several coordinates (e.g., degree of compactness, amount of secondary structure, tertiary structure formation, etc.) to describe in detail. Thus, to move beyond the previous study of this model protein, we have performed a more thorough analysis of the free energy landscape along several folding coordinates. The multidimensional free energy surfaces we describe below provide a clear picture of the folding process along several thermodynamic folding coordinates and form the basis for a deeper understanding of folding in small helical proteins.

Model and Methods

We examined the free energy surface of the 46 residue three-helical bundle whose sequence is extracted from fragment B of staphylococcal protein A (23, 24). As illustrated in Fig. 1A, this three-helix bundle protein is simple and small, and therefore is expected to be representative of typical fast folding helical proteins. Thus, it is one of the simplest systems with which to investigate protein folding. We expect that the exploration of the free energy surface and the characterization of the thermodynamic transition state will provide a more complete statistical description of the folding of small helical proteins.

Figure 1.

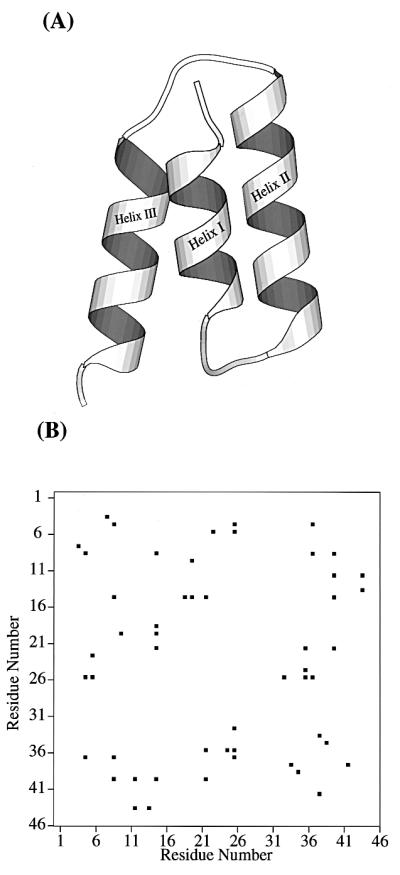
(A) Ribbon model of the native structure of the 46-residue segment of fragment B of staphylococcal protein A. (B) The center of geometry based native contact map from the simulation of two 1.1-ns native trajectories. Only contacts between residues i and j (j ≥ i + 4) are considered.

Our present analysis is based on the earlier simulation studies of Boczko and Brooks (22, 25). We refer the interested reader to these papers for details of their work. However, for completeness, and to illustrate key issues associated with the computational aspects of this study, we provide an overview of the computational protocol used in generating and processing the simulation data.

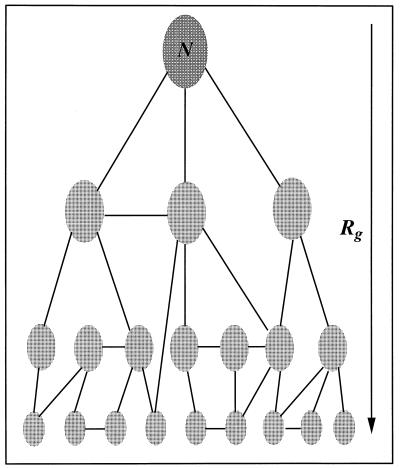
To generate a free energy surface for a process like protein folding one needs to address a number of issues: (i) the definition of a reaction coordinate (or appropriate order parameter) on which to base the progress of folding; (ii) preparation of initial conditions that span this coordinate and provide the starting points for thermodynamic sampling of different regions of the configuration space associated with the reaction coordinate; (iii) generation of sampling within the vicinity of these initial conditions via molecular dynamics; and (iv) a method to combine these data into a meaningful free energy surface and a means to assess the “quality” of this surface. In Fig. 2 we provide a diagrammatic view of the sampling problem for such thermodynamic calculations.

Figure 2.

Diagram illustrating the sampling strategy for free energy calculations of protein folding. The positions of the ellipses represent initial conditions used in generating sampling about conformational basins along the folding reaction coordinate, denoted by R_g and increasing from top to bottom in the figure. The lines illustrate connectivity between sampling of different initial conditions. Both sufficient initial conditions to span the reaction coordinate and a path of connectivity between all sampling basins are requirements for accurate calculation of free energy surfaces for protein folding.

(i) The vertical axis in Fig. 2 is the reaction coordinate, the radius of gyration R_g in the present calculations. This coordinate conveniently divides the conformational space of the protein as it moves between the native basin near R_g = 9.4 Å and the most unfolded states we sampled in these calculations, R_g near 14 Å. While other reaction coordinates such as the number of native contacts (4) could be used, our initial sampling was based upon this reaction coordinate. We will discuss below the free energy surface projected onto other possible reaction coordinates.

(ii) We denote by the ellipses in Fig. 2 representative regions of conformational space to be sampled during the molecular dynamics calculations. These ellipses represent the various initial conditions generated in the first stage of the calculations. Initial conditions were generated by carrying out a series of independent molecular dynamics simulations of the protein and solvent system, the 46 residue protein plus ≈5,600 explicit water molecules in a cubic volume that was periodically replicated. Six such simulations were carried out: two each at 300K, 350K, and 400K for a total simulation time of nearly 7 ns. From the 300K simulations the native basin and corresponding structures of the protein were characterized (see below and Fig. 1B). In addition, we employed a biasing potential that was harmonic in the radius of gyration to generate additional conformational sates that were more expanded (the higher temperature sampling only produced structures with a maximum R_g of about 12 Å). By setting the reference radius of gyration in this potential to a value of 15 Å and evolving the dynamics of seven selected initial structures under the influence of this potential for a period of several hundred picoseconds more expanded conformations were sampled. Initially all of the data, sampled at a frequency of a single structure approximately every 0.04 ps, was binned according to the value of the reaction coordinate into 20 bins. The conformations within each bin were clustered using a hierarchical clustering technique to identify the most representative conformations. These structures defined the initial conditions for subsequent sampling (22, 25). This procedure yielded 79 initial conditions, with between 2 and 7 initial conditions (cluster centers) being present in each bin of the reaction coordinate. While there is no way of assessing the extent of the configuration space covered by this procedure, it is most certainly not complete and becomes less “dense” in the more unfolded regions. Nevertheless, we believe that because we used the natural “denaturant” of temperature to create the ensemble of conformational states for initial conditions they will be representative of those states actually sampled during the folding process. Furthermore, we note that the means by which we combine each thermodynamic sample (i.e., the weighted histogram analysis method) aims at providing the correct statistical weight to each of these samples to give the overall thermodynamic properties. Each initial condition formed the basis for conformational sampling in a specific region of the reaction coordinate and was re-equilibrated at 300K via molecular dynamics over a period of several tens of picoseconds. Thermal equilibration was achieved by reassigning the velocities of the atoms from a Boltzmann distribution characteristic of the target temperature and the extent of equilibration was judged by examining the distribution of energy for each energetic component: protein–protein, protein–solvent, and solvent–solvent. The initial conditions with energy distributions that appeared aberrant—i.e., were significantly different from those characterized from the native state simulations—were further equilibrated.

(iii) Molecular dynamics simulations of duration between 150 and 250 ps were utilized to generate a distribution of configurations in the vicinity of each initial condition. The objective of this sampling procedure was to provide a thermal distribution of conformational states within a specific region of the reaction coordinate and to permit “connections,” denoted by the connecting lines in Fig. 2, to be developed between each initial condition. This condition is necessary for the development of the correct statistical weight of one initial condition relative to others. However, we note that one is not required to sample all regions of configuration space from any given initial condition, only to develop a “connected net” of sampling. To concentrate the sampling in a specific region of configuration space we used umbrella sampling along the radius of gyration coordinate. The biasing potential had the form of a harmonic function centered at a given value of R_g. Twenty such points, evenly distributed between 9.38 and 14.13 Å, were used as the centers of the biasing potential. To assess the “connectivity” of our sampling we examined the distribution of R_g, energy and overall polypeptide conformation. Histograms constructed in R_g, energy and a Mahalonobis distance measure of the pseudo-dihedral angles (unpublished data) composed of four consecutive α carbons were examined for overlap. Where the overlap between neighboring initial conditions for any of these measures was insufficient, more sampling was performed. The total sampling time was in excess of 20 ns for the generation of these distributions. We note that because we are using the statistical mechanical “trick” of biased or umbrella sampling it is not necessary that the sampling time be greater than or equivalent to the anticipated folding time for the protein to provide a good estimate of the thermodynamic aspects of folding. Clearly, to learn about the kinetics of folding, when folding is not under thermodynamic control, it is more essential that the time scales match, or that the specific kinetic bottlenecks be well characterized so that they can be assessed as specific barrier crossing events.

(iv) Combining the data, in the form of histograms of the frequency of occurrence of values of any number of different reaction coordinates (order parameters) describing the folding process, was achieved through the use of the weighted histogram analysis method (WHAM) (27). This method was initially developed by Ferrenberg and Swendsen (28) for problems associated with thermodynamic characterization of phase transitions in two-dimensional Ising spin systems and built upon the work of Bennett (29) from some years earlier. WHAM is a minimum variance estimator of the density of states projected onto specific reaction coordinates. Its usage as a means to compute multidimensional potentials of mean force was first described in earlier work by us (27). The WHAM approach self-consistently optimizes the relative statistical weights of each sample to minimize the variance of the approximate density of states. We have found this method to be a robust means of combining data from numerous simulations to compute thermodynamic properties. Beyond the use of WHAM to combine the data, and the assessment of overlap described above, we examined the convergence of our free energy calculations by randomizing and eliminating portions of the raw data used in the WHAM calculations. We found that nearly 40% of the sampling could be eliminated before dramatic qualitative changes were observed in the potential of mean force projected onto the R_g coordinate. Based on this observation we used sampling from 59 initial conditions for analysis in the present calculations. Throughout our calculations the bin size chosen for the histogram equations was 0.1 Å for the radius of gyration and 1.0 for both the number of native contacts, C_Nat and hydrogen bonds, HB_Nat.

To define the native tertiary structure for the system, we analyzed molecular dynamics simulations of the native state (two independent 1.1-ns trajectories) and from these computed the side chain center-of-geometry-based contact map. The contact map is a simple (binary) representation of the presence/absence of tertiary packing. If two side chain centers-of-mass are separated by less than 6.5 Å, a contact is present. Only long-range contacts—i.e., those between residues i,j (j ≥ i + 4) were considered. In Fig. 1B we display the contact map for protein A, based on these native trajectories. We note the characteristic pattern of short-range i,i + 4 contacts near the diagonal signifying helical structure as well as the regions of contact formation between helices I–II, II–III, and I–III. There are 26 native contacts in protein A.

We have also characterized the formation of native helical hydrogen bonds as folding occurs. In our model, a helical hydrogen bond exists if the atoms comprising the hydrogen bonding pair [(i)C=O· · ·HN(i + 3/4)] are within a distance of 2.5 Å. Analysis of the native dynamics trajectories show that protein A is helical in the region between Gln-9 and His-18 (helix I), Asn-23 and Asp-37 (helix II), and Asn-43 and Asn-52 (helix III). These data on native helix content and contacts form the basis of our subsequent calculations.

The Process of Compaction and Tertiary Structure Formation

Protein folding involves the formation of a well-defined three-dimensional structure from a noncompact unfolded structure. The formation of tertiary structure, that is, the coalescence of residues distant in sequence, dictates the overall folding time. Therefore, it is important to understand the relationship between compaction and tertiary structure formation as folding proceeds. To this end we have calculated the free energy as a function of two reaction coordinates, (i) the radius of gyration (R_g) and (ii) the total number of native contacts (C_Nat). The first coordinate measures compactness of the structure and the second native tertiary structure formation. As evident from Fig. 3A, the folding process is essentially downhill in free energy. There are a few local minima: one located at R_g ≈ 11.8 Å and C_Nat ≈ 2, another at R_g ≈ 12 Å, C_Nat ≈ 5. The barriers to escape these minima are quite small (≈1.0 kcal/mol for the former and ≈0.5 kcal/mol for the latter). Therefore these local minima are not expected to dominate the folding time and the folding process is anticipated to be quite fast.

Figure 3.

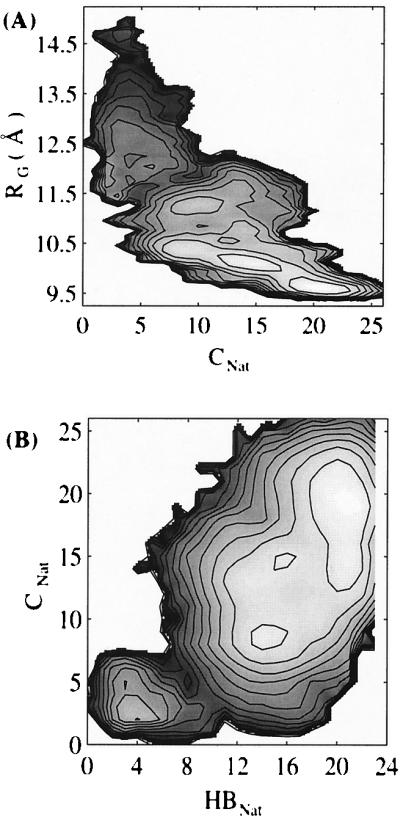
(A) Contour plot of the free energy as a function of total number of native contacts (C_Nat) and radius of gyration (R_g). (B) Contour plot of the free energy as a function of total number of native hydrogen bonds (HB_Nat) and total number of native contacts (C_Nat). Contour levels are drawn at 0.5-kcal/mol intervals.

Experiments suggest that the folding of some proteins may involve an initial fast collapse without formation of any native tertiary structure (30). However the extent to which collapse approaches native compactness is not known in detail. Our result is consistent with this picture of an initially collapsed state with little native tertiary structure. As shown in Fig. 3A, the radius of gyration changes from a large value (R_g ≈ 14 Å) to a smaller one (R_g ≈ 12 Å) and the number of native contacts (C_Nat) does not change significantly. The average number of native contacts in this range of R_g is about four, which should be considered as background because these mostly involve i,i + 4 (or 5) contacts between certain helical residues. As folding progresses toward the transition region (R_g < 12 Å), native contacts begin to form. This will be discussed in the next section.

Characterization of the Transition State

Two broad basins, one corresponding to the denatured state and the other to the native state, appear in the free energy surface shown in Fig. 3A. These basins are connected by a narrow path, which is defined as the transition state in this study. This transition state has about seven native contacts and a radius of gyration equal to 11.7 Å. An analysis of the transition state conformations reveals that 50–70% of the native hydrogen bonds are present in the transition state. Among these hydrogen bonds, those in the center of helix II between residues N28–Q32 and G29–S33 have >90% probability of occurrence. Hydrogen bonds between residues F13–L17, Y14–H18 in helix I and R27–I31, F30–L34, and I31–K35 in helix II have about 80% probability of occurrence. Hydrogen bonds in helix III have a relatively low probability of occurring in the transition state (<50%). We also noticed that a certain amount of nonnative hydrogen bonding is present in the transition state. In particular this involves (i,i + 2), (i,i + 3), (i,i + 4), (i,i + 5) hydrogen bonding. We note that Onuchic and collaborators (4, 8, 9) have pointed out that the compactness and nature (amount of native tertiary structure) of molten globule states, such as the manifold of conformations near the transition state, will provide a bias for the formation of native secondary structure even if the intrinsic tendency for its formation is completely nonspecific.

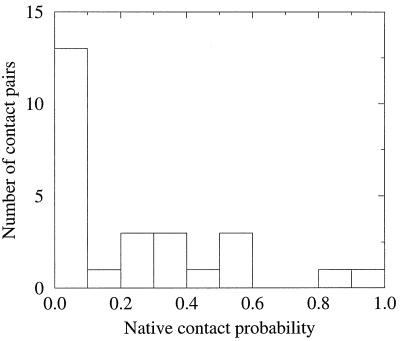
We further analyzed the tertiary contacts that contribute to the transition state. Besides the i,i + 4 (or 5) contacts along helical strands, such as the contact between residue L22 and residue R27 and the contact between residue A12 and residue I16 (which have a high probability to occur in the transition state), several other contacts also occur frequently. These contacts are (i) F13–L34, (ii) L34–L44, and (iii) L34–L45. Fig. 4 displays the distribution of the native contacts in the transition state. This distribution, consistent with the theoretical model for folding of Onuchic et al. (9), is rather delocalized.

Figure 4.

Distribution of native contacts in the transition state.

To select a set of representative conformations for more detailed analysis of the transition state region, we employed a hierarchical clustering technique to naturally group the conformations. The grouping was in terms of (i) the native contacts, (ii) the native hydrogen bonds, and (iii) the solvent accessible surface area. The functional form for the dissimilarity function was the same as that used by Boczko and Brooks (22). Seven clusters were obtained. From each we selected a single conformation as representative of the cluster. This structure had the smallest average distance from other conformations in the same cluster. Thus, the conformations corresponding to each cluster center were considered conformational representatives of the transition state. Graphic display of these transition state structures indicated that they bear native-like global topology, but are more expanded than true native structures. From the values of radius of gyration for native and transition states we find that the transition state volume is about 70% larger than that in the native state, as has been reported in a previous study (22). This too is consistent with experimental observations of the transition state for protein folding (31). It is noteworthy that a less restrictive definition of the transition state, one in which native contacts range from 6 to 8 rather than fixed at 7, was also examined with similar results.

The Cooperative Formation of Secondary and Tertiary Structure

The relationship between the formation of tertiary and secondary structure for this system can be analyzed in terms of the free energy function. The two-dimensional free energy surface along the coordinates, (i) the total number of native contacts (C_Nat) and (ii) the total number of native hydrogen bonds (HB_Nat) is shown in Fig. 3B. This free energy surface is characterized by a small basin in the lower left corner, indicating that there are some hydrogen bonds (approximately three) formed early in the folding process, whereas essentially no native contacts have been formed. The few native contacts that are formed (C_Nat ≈ 3) are those 1–4 (or 5) contacts along helical strands, as has already been discussed. The observation that there is a “channel” along the free energy surface close to the diagonal indicates that, although some native secondary structure is formed early, the predominant development of secondary and tertiary structure does not occur independently. In other words, the formation of secondary and tertiary structure following the initial formation of some secondary structure is cooperative. This is in contrast to the framework model, where secondary structure forms first, followed by tertiary organization. We note that, similar to what is observed in Fig. 3A, there is a broad native basin. We will discuss this further below.

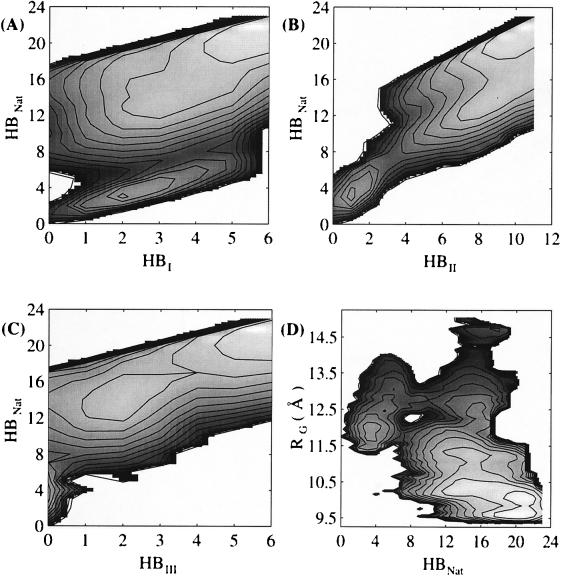
The Formation of Helical Hydrogen Bonds

The total number of hydrogen bonds, such as those shown in Fig. 3B, can be dissected into the number of hydrogen bonds in each constituent helix. To describe the relationship of formation of hydrogen bonds among the three helices, we calculated the free energy surface as a function of (i) the total number of native hydrogen bonds (HB_Nat) and (ii) the number of hydrogen bonds in each helix. Fig. 5 A–C indicates that, statistically, about two native hydrogen bonds in helix I and one hydrogen bond in helix II form first in the early stages of folding. This can be seen from the local minimum near HB_Nat ≈ 3 in these plots. The barrier in going from this minimum to the native state is about 2.0 kcal/mol. This barrier, which is located at HB_Nat ≈ 7, is dominated by the formation of between three and four native hydrogen bonds in both helix I and helix II, while essentially no native hydrogen bonds are present in helix III. This indicates that the early formation of native hydrogen bonds in helix I and helix II is also cooperative. Hydrogen bonds in helix III start to form only after the native helical structure in helices I and II is established (HB_Nat ≈ 13). The stability of helix III in the native state, as show in Fig. 5C, is only about 1.0 kcal/mol, and the free energy barrier for the formation of helix III is also very small (about 0.5 kcal/mol). This feature of the folded protein may have functional significance in relation to Ig recognition and binding (24).

Figure 5.

Contour plot of the free energy as a function of (A) total number of native hydrogen bonds (HB_Nat) and total number of native hydrogen bonds in helix I (HB_I); (B) total number of native hydrogen bonds (HB_Nat) and total number of native hydrogen bonds in helix II (HB_II); (C) total number of native hydrogen bonds (HB_Nat) and total number of native hydrogen bonds in helix III (HB_III); (D) total number of native hydrogen bonds (HB_Nat) and radius of gyration (R_g). Contour levels are drawn at 0.5-kcal/mol intervals.

The Order of Collapse and Secondary Structure Formation

To address the question of the order of collapse and secondary structure formation, we explored the free energy surface along reaction coordinates comprising (i) the radius of gyration and (ii) the total number of native hydrogen bonds. In Fig. 5D two distinct populations of secondary structure appear in nonnative regions. One has about 20% of the native helical content (HB_Nat ≈ 4) and the other about 70% (HB_Nat ≈ 15). Calculation of the probability distribution of the native hydrogen bonds indicates that for the ensemble of molecules with less helical content, the hydrogen bonds predominate near the C-terminal region of helix I and the center of helix II. There is a minimum at R_g ≈ 11.8 Å and HB_Nat ≈ 3. The barrier in going from this minimum to the native state is about 2.0 kcal/mol, or 3 k_BT at room temperature. For the ensemble of molecules with greater helical content, in which almost all hydrogen bonds in helix I and II are present, folding from the compact to the native state is downhill in free energy. This is explained by the extremely low free energy barrier for the formation of helix III following the formation of helices I and II. By simply counting the level sets on the contour surface, we estimate that the population ratio between molecules with lesser and greater helical content is about 3:1. Therefore, we expect that the process with fewer hydrogen bonds will dominate. It appears that in the collapsed state the region with an intermediate amount of secondary structure (6 ≤ HB_Nat ≤ 12) is less likely to be populated, as is evident from the free energy surface peak. This indicates cooperative formation of native secondary structure. It should be pointed out that in addition to the native hydrogen bonds, we also observe a significant amount of nonnative hydrogen bonding present in the unfolded state (both extended and compact states) that involves (i,i + 2), (i,i + 3), (i,i + 4) and (i,i + 5) hydrogen bonding.

The free energy surface of Fig. 5D at large radius of gyration (R_g > 13 Å) should be interpreted cautiously because it is most prone to sampling errors. The broad distribution of the total number of native hydrogen bonds at large R_g indicates the presence of a significant amount of native helix in the rather extended state. However, experiments suggest that helical content in the unfolded state should be low. Our result may arise from insufficient simulation time at the largest values of R_g, or to our use of a simple distance measure to quantitative hydrogen bond content. Clearly, fluctuations about such an average distance can significantly influence experimental measurement of helix as may occur with CD (26).

Discussion

The free energy profiles calculated in this study all suggest that protein A possesses a rather broad native basin. As shown in Fig. 3, native contacts range from 8 to 26 in the native basin and the number of hydrogen bonds varies from 10 to 23. Such a broad native basin indicates that the native state is quite mobile, with a rather fluid architecture in the protein interior. Although interior fluidity has been reported before, the extreme mobility that we have may also arise from the excision of the three-helix fragment from the sequence from segment B of staphylococcal protein A. We believe that the interaction of our model with the rest of the sequence will further stabilize the native structure, an assertion supported by preliminary analysis of on-going simulations of the entire 60-residue polypeptide: the native basin remains very near that observed here, but is clearly more rigid (C.L.B., unpublished work).

The transition state identified here has about 30% of native contacts, which is less than the 60% estimate of Wolynes and coworkers (4, 8). In addition, our calculation of the amount of native secondary structure in the transition state suggests that 50–70% of the helical structure is formed, which is also below the value of near 90% used in the model by Wolynes and coworkers (4, 8). That our detailed findings differ slightly from the theoretical analysis is probably not surprising. The theoretical model represents a rather idealized helical protein and focuses on global determinants of the free energy landscape. Furthermore, this treatment assumes that there is no preference for native helical interactions (compared with nonnative ones). Clearly in real sequences this idealization does not hold, for example there are strong helical tendencies in helix II and strong signals for helical “breaks” due to the presence of proline residues at the junctions between the helices. That many of the ideas regarding compaction and native tertiary/secondary structure formation are quite similar is very encouraging, suggesting that detailed calculations like ours may serve as a bridge between experiment and theory.

Our calculation of the transition state volume is consistent with experimental observation for chymotrypsin inhibitor 2, which indicates a two-third volume expansion of the transition state compared with the native state (31). Our observation that the transition state has a native-like topology is also consistent with the above experiment, which reported that the transition state for folding is a generally expanded form of the folded structure.

Our results for the thermodynamic properties of this helical protein have implications for the kinetics of protein folding in vitro. The findings suggest that kinetic traps are not expected to dominate the folding time for fast-folding helical proteins, and that the folding process involves initial formation of some transient helical structure, segments of which are native-like. The subsequent collapse divides the helical structure into two populations: one bearing less helical content (≈20% in our case), the other possessing greater helical content (≈70% in our case). These two populations of molecules follow slightly differing folding processes. For the population with less native helical content, most of the secondary structure forms only after collapse. The protein encounters a predominantly entropic barrier in progressing from the collapsed to the native state (about 3 k_BT in this study). For the population with greater helical content, folding to the native state is essentially downhill involving barrier-free topological assembly. We should emphasize that we cannot exclude the possibility that the second process mentioned above may be due to the insufficient simulation time or inadequate sampling. Nevertheless, our analysis provides a testable scheme for protein folding that should be useful for fast-folding experiments. It would also be interesting to perform similar analyses on other fast-folding proteins to determine if the features revealed here typify all fast-folders. In addition, our analysis may have important implications for the design of fast-folding proteins.

In concluding, we note that we have focused our attentions in this analysis on the nature of the free energy landscape as it projects onto order parameters (reaction coordinates) such as R_g, C_Nat, and the number of native helical hydrogen bonds. Clearly there are a host of other coordinates that could also be examined, these include quantities specifying the loss of buried surface area and energetic components like the solvent–protein energy or the protein–protein energy. We chose to use the reaction coordinates used throughout this work primarily because they are potentially accessible to experiment and provide the strongest connections to available theoretical models for folding.