Mutational analysis of dendritic Ca²⁺ kinetics in rodent Purkinje cells: role of parvalbumin and calbindin D_28k

Abstract

The mechanisms governing the kinetics of climbing fibre-mediated Ca²⁺ transients in spiny dendrites of cerebellar Purkinje cells (PCs) were quantified with high-resolution confocal Ca²⁺ imaging. Ca²⁺ dynamics in parvalbumin (PV^−/−) and parvalbumin/calbindin D_28k null-mutant (PV/CB^−/−) mice were compared with responses in wild-type (WT) animals. In the WT, Ca²⁺ transients in dendritic shafts were characterised by double exponential decay kinetics that were not due to buffered Ca²⁺ diffusion or saturation of the indicator dye. Ca²⁺ transients in PV^−/− PCs reached the same peak amplitude as in the WT but the biphasic nature of the decay was less pronounced, an effect that could be attributed to PV's slow binding kinetics. In contrast, peak amplitudes in PV/CB^−/− PCs were about two times higher than in the WT and the decay became nearly monophasic. Numerical simulations indicate that the residual deviation from a single exponential decay in PV/CB^−/− is due to saturation of the Ca²⁺ indicator dye. Furthermore, the simulations imply that the effect of uncharacterised endogenous Ca²⁺ binding proteins is negligible, that buffered diffusion and dye saturation significantly affects spineous Ca²⁺ transients but not those in the dendritic shafts, and that neither CB nor PV undergoes saturation in spines or dendrites during climbing fibre-evoked Ca²⁺ transients. Calbindin's medium-affinity binding sites are fast enough to reduce the peak amplitude of the Ca²⁺ signal. However, similar to PV, delayed binding by CB leads to biphasic Ca²⁺ decay kinetics. Our results suggest that the distinct kinetics of PV and CB underlie the biphasic kinetics of synaptically evoked Ca²⁺ transients in dendritic shafts of PCs.

Ca²⁺ transients in dendrites and spines of central neurones represent short-lived and highly compartmentalised signals. They serve a variety of neuronal functions including growth, motility, excitability, synaptic plasticity and gene expression (Berridge, 1998; Wang & Augustine, 1999). In view of this multitude of Ca²⁺-regulated processes, the specific action mediated by a given Ca²⁺ transient is likely to be determined by its amplitude and spatio-temporal pattern. Thus, the kinetics of Ca²⁺ transients will shape their action (Dolmetsch et al. 1997, 1998; Li et al. 1998; Bhalla & Iyengar, 1999). Ca²⁺ kinetics, on the other hand, are shaped by a complex interaction between Ca²⁺ extrusion mechanisms (Fierro et al. 1998), intracellular Ca²⁺ stores (Berridge, 1998), endogenous buffers (Neher & Augustine, 1992; Baimbridge et al. 1992; Markram et al. 1998; Maeda et al. 1999) and diffusion (Maeda et al. 1999; Majewska et al. 2000a,b). A quantitative understanding of the dynamic interplay of these different mechanisms is just beginning to emerge (Zhou & Neher, 1993; Neher, 1995; Markram et al. 1998; Helmchen, 1999).

In many cell types, including hippocampal (Yuste & Denk, 1995; Helmchen et al. 1996; Lee et al. 2000a) and cortical (Markram et al. 1995; Helmchen et al. 1996; Svoboda et al. 1997) pyramidal neurones and the majority of hippocampal interneurones (Lee et al. 2000a), dendritic Ca²⁺ transients return to resting values with a decay that is well described by a monoexponential function. Such monophasic decays were attributed to linear Ca²⁺ extrusion mechanisms and rapid kinetics of Ca²⁺ buffers (Majewska et al. 2000a; Lee et al. 2000b). However, other cell types display more complex Ca²⁺ dynamics that require double exponential fits to faithfully describe their decay. Examples include cerebellar Purkinje cells (Miyakawa et al. 1992; Airaksinen et al. 1997; Maeda et al. 1999) and a subpopulation of hippocampal GABAergic neurones (Lee et al. 2000a). Recent studies have shown that different mechanisms are capable of inducing such biphasic Ca²⁺ kinetics. Depending on the cell type and the cellular compartment studied, diffusion (Majewska et al. 2000a,b), delayed buffering by the slow endogenous Ca²⁺-binding protein (CaBP) parvalbumin (Lee et al. 2000a,b), saturation of high-affinity CaBPs such as calbindin D_28k (Maeda et al. 1999), or non-linear Ca²⁺ extrusion mechanisms (Fierro et al. 1998) were shown to be involved in generating biphasic decay kinetics. However, the exact contribution and dynamic interaction of these mechanisms in shaping physiological Ca²⁺ signals is unclear.

Here we studied cerebellar Purkinje cells (PCs), a cell type well known (i) to have biphasic dendritic Ca²⁺ decay kinetics (Miyakawa et al. 1992; Eilers et al. 1995; Fierro & Llano, 1996; Airaksinen et al. 1997; Fierro et al. 1998; Maeda et al. 1999), (ii) to express high levels of calbindin (CB) as well as parvalbumin (PV; Baimbridge et al. 1992) and (iii) at least in the soma, to possess non-linear Ca²⁺ extrusion mechanisms (Fierro et al. 1998). We used high-resolution confocal imaging of synaptically evoked Ca²⁺ signals in spiny dendrites in combination with numerical simulations to determine the functional role of endogenous Ca²⁺ buffers, diffusion and extrusion mechanisms. Our analysis of wild-type, PV and PV/CB null-mutant mice demonstrates how distinct endogenous CaBPs shape the complex waveform of dendritic Ca²⁺ transients.

METHODS

Animals and slice preparation

Experiments were performed on 18- to 22-day-old parvalbumin-deficient mice (PV^−/−; Schwaller et al. 1999), parvalbumin and calbindin D_28k double-knock-out mice (PV/CB^−/−; Vecellio et al. 2000), and, as control experiments, on Wistar rats, C57BL/6 and PV^+/+ mice (littermates of the PV^−/− animals) of the same age (n = 9, 5 and 4, respectively). Between the control groups, no significant differences in Ca²⁺ dynamics were observed and, consequently, these data were pooled to represent the wild type (WT).

Acute cerebellar brain slices were prepared from animals anaesthetised with Isoflurane. After decapitation the vermis was removed and mounted in a chamber filled with cooled (0-2 °C) artificial cerebrospinal fluid (ACSF; see below). Thick parasagittal slices (200 μm) were cut using a HR2 slicer (Sigmann Elektronik, Germany) and kept in ACSF at 37 °C for 45 min before they were transferred to the recording chamber perfused with ACSF at 19-21 °C. All experimental procedures were carried out according to the animal welfare guidelines of the Max-Planck Society.

Solutions

The ACSF contained (mM): 125 NaCl, 2.5 KCl, 1.25 NaH₂PO₄, 26 NaHCO₃, 1 MgCl₂, 1.8 CaCl₂, 20 glucose, pH 7.3 to 7.4 at 19-21 °C when gassed with 95 % O₂-5 % CO₂. The pipette solution was composed of (mM): 104 potassium gluconate, 8 KCl, 2.5 Mg-ATP, 0.25 GTP, 8 Hepes; 0.2 or 0.05 Oregon Green 488 BAPTA-1 (OGB-1, Molecular Probes, OR, USA) dissolved in purified water (W-3500, Sigma, Munich, Germany). The pH was adjusted to 7.3 (at 19-21 °C) with KOH. The solution was filtered with a syringe filter (Nalge, NY, USA). Using the public domain software WinMaxC 2.1 (http://www.stanford.edu/~cpatton/maxc.html), the free Mg²⁺ concentration in the pipette solution was calculated to be ≈590 μM.

Electrophysiology

Whole-cell patch-clamp recordings were performed in the current-clamp mode with an Axopatch 200A amplifier, a Digidata 1320A AD/DA converter, Clampex 8.0 software (Axon Instruments, CA, USA), and patch pipettes pulled from borosilicate glass (GB150F-8P, Science Products, Germany) on a P-87 puller (Sutter, CA, USA). With our pipette solution the pipette resistances ranged from 4 to 5 MΩ. The amplifier was modified to allow bridge-mode recordings (Axon). Current (up to 300 pA) was injected to hold the cells at membrane potentials of -65 to -70 mV. In order to allow rapid equilibration of the cytosol with the pipette solution, the series resistance was kept below 20 MΩ for at least 15 min after breaking into the cell. A stimulation electrode, filled with 1 M NaCl and connected to a stimulus isolator was used for activation of the afferent climbing fibre (CF). The CF-mediated EPSPs were low-pass filtered at 2-5 kHz and sampled at 10 kHz.

Fluorescence recordings

Fluorescence recordings were performed with a Fluoview-300/ BX-50 confocal laser-scanning microscope (equipped with a × 60, 0.9 NA water immersion objective; Olympus, Tokyo, Japan) between 60 and 120 min after the whole-cell configuration was established. This time window balanced the need for a sufficient but stable dendritic concentration of OGB-1 (70-80 % of the pipette concentration; Rexhausen, 1992), and a minimal washout of PV and CB, which could lead to an underestimation of the functional role of these proteins.

Regions of interest were magnified by a factor of 10 using the zoom function of the Fluoview system. Recordings of 4 s duration were performed either in the line-scan mode with a sampling rate of 500 Hz or in the point-scan mode with a sampling frequency of 500 kHz and subsequent binning to 500 Hz (Schmidt & Eilers, 2002). In order to prevent photodamage, the laser intensity was typically reduced to 0.2 % in line scans and to 0.02-0.06 % in point scans. In recordings that required a direct correlation of the EPSPs and the fluorescence signal (see Fig. 1), the output of the photomultiplier tube of the Fluoview system was filtered at 3 kHz and recorded directly by the electrophysiological system at a sampling frequency of 10 kHz. Further filtering was performed off-line with a digital Gaussian filter set to 500 Hz.

Figure 1. Climbing fibre-mediated Ca²⁺ transients in spines and dendrites of cerebellar Purkinje cells.

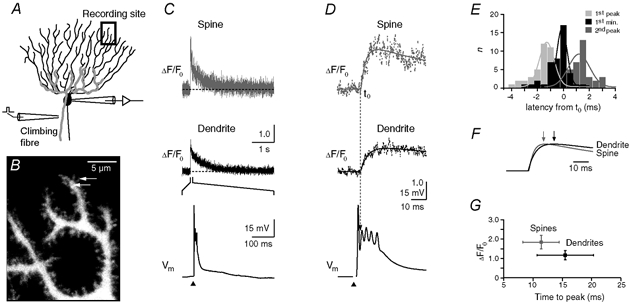
A, schematic drawing of the experimental arrangement. The cells were loaded with the calcium indicator dye Oregon Green BAPTA-1 (OGB-1, 200 μM) via a somatic patch pipette. The climbing fibre (grey), which contacts the Purkinje cell on the proximal dendrites, was stimulated with an extracellular electrode (left) located in the granule cell layer. Ca²⁺ transients were recorded in the distal dendritic branchlets. B, contrast-enhanced confocal image of distal dendrites and adjacent spines. The arrows indicate the spine and the dendritic region from which the Ca²⁺-dependent fluorescence signals were recorded in the point-scan mode (see C and D). C, fluorescence transients (ΔF/F₀) in the spine and the dendrite (upper and middle trace, respectively) evoked by CF activation. The CF-mediated EPSP, with the stimulation artefact blanked, is shown on an expanded time scale in the bottom trace. The arrowhead denotes the time point of synaptic stimulation. D, rising phase of the transients shown in C plotted on the same time scale as the EPSP. The continuous lines represent fits (see eqn (1)) to the transients The dashed line indicates the starting point (t₀) of the dendritic transient estimated by the fit. E, temporal distribution of the peak amplitude of the first and second spike of the CF-EPSP, as well as the start of the second spike (‘1^st min’) relative to t₀ of the fluorescence transients. The continuous lines represent Gaussian fits to the distributions (t₀ = -1.3, -0.1 and 1.2 ms, half-width = 0.8, 0.6 and 1.2 ms for the first peak, the first minimum and the second peak, respectively; n = 43 from five cells from five mice). Note that t₀ correlates best with the start of the second spike. F, comparison of the fitted rising phases of the fluorescence transients shown in D. The responses were normalised to their peak amplitudes. The arrows indicate the time points at which the peak amplitudes were reached. G, peak amplitudes (spine: 1.84, 1.50-2.20; dendrite 1.17, 0.94-1.42; median and IQR) of the fluorescence transients in spines and dendrites (n = 32 and 24, respectively) plotted against the corresponding time-to-peak values (spine: 11.4 ± 3.4 ms; dendrite: 15.5 ± 4.8 ms; mean ± S.D.). Spine transients were significantly larger and reached their maximum earlier than in the dendritic responses (P < 0.001).

Data analysis

The analysis was performed with custom-written routines in Igor Pro 4.0 (Wavemetrics, OR, USA) and SigmaStat 2.0 software (Jandel Scientific, CA, USA). Fluorescence data were expressed as ΔF/F₀, i.e. as background-corrected increases in fluorescence (ΔF) divided by the prestimulus fluorescence (F₀) (Schmidt & Eilers, 2002). The rising phase of the CF-mediated transients (Fig. 1D and Fig. 6E) could be fitted by the product of two exponential terms:

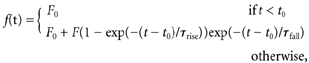(1)

otherwise,where F denotes the peak amplitude of the signal, t₀ the start of the rising phase, and τ_rise and τ_fall the time constants of the rising phase and the first 20 ms of the falling phase of the transient.

Figure 6. Dendritic decay kinetics in parvalbumin/calbindin D_28k null-mutant (PV/CB^−/−) mice.

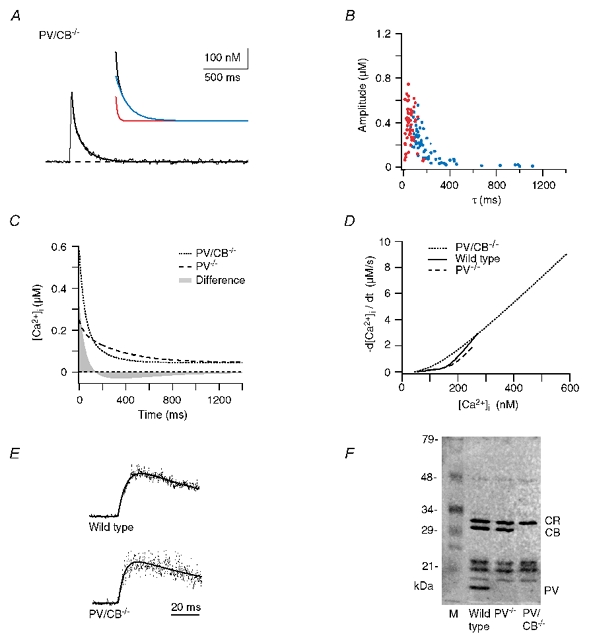
A, example trace. The continuous line represents a double exponential fit to the decay. The inset shows the fast and slow components (red and blue traces, respectively). The fit yielded a fast component of 120 nM with a τ_fast of 19 ms and a slow component of 220 nM with a τ_slow of 135 ms. B, data from double exponential decays from 62 dendrites from six cells from six mice. The fast and slow components are shown in red and blue, respectively. C, calculated median decay in dendrites of PV/CB^−/− mice (dotted trace) compared with the median response in PV mice (dashed trace). The grey area represents the integral of the arithmetic difference between the two decays. D, [Ca²⁺]_i dependence of the [Ca²⁺]_i decay rates in WT (continuous line), PV^−/− (dashed line) and PV/CB^−/− (dotted line) dendrites. The decay rates were calculated from the corresponding median dendritic decays. E, examples of point-scan recordings showing the rising phase of the Ca²⁺ transients in WT and PV/CB^−/− animals. F, ⁴⁵Ca²⁺-overlay assay of cerebella from WT, PV^−/− and PV/CB^−/− mice. ‘CR’ denotes the calretinin bands and ‘M’ the lane containing marker proteins. Note that no PV or PV/CB staining is observed in the mutant mice and that no upregulation of other CaBPs occurred.

ΔF/F₀ values were subsequently filtered using a smoothing kernel of nine points (‘box filter’, Igor Pro) and converted to free intracellular Ca²⁺ concentrations ([Ca²⁺]_i) based on a commercial calibration kit (C-3723, Molecular Probes) and the WinMaxC software. The data from five independent cuvette calibrations performed in our pipette solution were normalised to the peak intensity (F_max) obtained at ≈20 μM [Ca²⁺]_free and fitted to the formula

(2)

where F_min represents the intensity at 0 μM [Ca²⁺]_free. This fit, which yielded a K_D of 325 nM, was used to convert ΔF/F₀ values to [Ca²⁺]_i based on an assumed resting [Ca²⁺]_i of 45 nM (Airaksinen et al. 1997). The dependence of our calibration procedure on a known and stable [Ca²⁺]_rest prevented a pharmacological quantification of dendritic Ca²⁺ extrusion mechanisms. Inhibitors such as cyclopiazonic acid (CPA) and thapsigargin led to variable increases in the resting fluorescence (data not shown; Majewska et al. 2000a) that precluded a quantitative analysis of both ΔF/F₀ as well as the converted [Ca²⁺]_i values. To avoid inaccuracies at higher Ca²⁺ levels, only fluorescence transients that did not exceed a ΔF/F₀ value of 2.5, corresponding to 1.25 μM [Ca²⁺]_i, were included in the analysis. In initial test experiments, performed with an extracellular solution containing 2 mM Ca²⁺, a substantial fraction (about 10 %) of recordings reached this limit. As a consequence, we reduced the extracellular [Ca²⁺] to 1.8 mM. Under this condition, only a few recordings (less than 5 % of spines and no dendritic recordings) had to be discarded. The median amplitude of dendritic transients declined from 285 to 260 nM.

The first 2.5 s of the [Ca²⁺]_i decays were fitted (Levenberg- Marquardt algorithm) with a double and a monoexponential equation. Decays were considered mono- or biphasic depending upon the corresponding χ² values and the additional, more restrictive criterion of an at least three-fold difference between τ_fast and τ_slow for a biphasic decay. All decays and their residuals (data minus fit) were visually inspected to assure that the fits reliably described the data.

At a given recording site, stable and reproducible responses were observed during repeated stimulations. However, different spines and dendritic regions showed considerable variability in their decay kinetics despite stable properties of the complex spike. Therefore, we recorded single responses from many different sites rather than multiple responses from a few sites to strengthen the accuracy of our statistical analysis. Data that showed a standard distribution (Kolmogorov-Smirnov test) were expressed as means ± S.D., otherwise as median and interquartile range (IQR) and tested with Student's t test or the Mann-Whitney U test, respectively.

Single-compartment model

Ca²⁺ dynamics were simulated according to the formalism of Markram et al. (1998) and the parameters given in Table 2. A homogeneous dendritic compartment was approximated by a cylinder with a length of 10 μm and a radius of 1 μm. The Ca²⁺ current (I_Ca) during the CF-mediated complex spike was represented by a Gaussian function adjusted to the time course of the measured complex spike. The increase in the [Ca²⁺]_i caused by the Ca²⁺ influx is given by

(3)

where F is Faraday's constant and V the volume of the cylinder. Ca²⁺ buffering by OGB-1, CB and PV was simulated assuming second-order kinetics for all reactions. The four binding sites of CB and the two binding sites of PV were simulated as individual reaction partners, neglecting possible cooperativity. Under these assumptions, the rate of change in [Ca²⁺]_i due to binding of Ca²⁺ to the jth binding site (BS_j) is given by

(4)

where [BS]_j and [CaBS]_j denote the concentration of the free and Ca²⁺-bound binding sites, and j = 1 for OGB-1, j = 2-5 for CB and j = 6, 7 for PV. For OGB-1 and CB the following relationship between free and Ca²⁺-bound binding sites applies:

(5)

where j = 1-5. For PV the situation is complicated by its medium affinity for Mg²⁺ which significantly affects its Ca²⁺ binding kinetics. The change in the occupancy of PV's binding sites is given by

(6)

where j = 6, 7 and

(7)

Table 2.

Model parameters

Parameter	Value	Notes
[Ca2+]rest	45 nm	Airaksinen et al. (1997)
[Mg2+]i	590 μm	Calculated, held constant
Ca2+ influx
Peak amplitude	36–130 pA
Half-width	4 ms
Extrusion
Michaelis–Menten constant, Km	3 μm
Max. pump velocity dendrite, vmax	30–300 pmol cm−2 s−1
Oregon Green BAPTA-1
Effective concentration	160 μm	80% of pipette conc.
KD	325 nM	This study
Koff	140 s−1	Eberhard & Erne (1991)*
Kon	0.43 × 109 M−1 s−1	Calculated
Calbindin D28k
Effective concentration	40 μm	Maeda et al. (1999)†
Binding sites (non-cooperative)	4	Nägerl et al. (2000)
Ratio of high- and medium-affinity binding sites	2:2	Näet al. (2000)
Koff,medium aff.	35.8 S−1	Näet al. (2000)
Koff, high aff.	2.6 s−1	Nägerl et al. (2000)
Kon, medium aff.	4.35 × 107 M−1 s−1	Nägerl et al. (2000)‡
Kon, high aff.	0.55 × 107m−1 s−1	Nägerl et al. (2000)‡
KD, medium aff.	822nm	Calculated
KD, high aff.	474 nm	Calculated
Parvalbumin
Effective concentration	40 μm	Kosaka et al. (1993)§
Binding sites (non-cooperative)	2
Koff,Ca	0.95 S−1	Lee et al. (200b)
Koff,Mg	25 s−1	Lee et al. (200b)
KD,Ca	9 nm	Lee et al. (2000b)
KD,Mg	31 μm	Eberhard & Erne (1994)
Kon,Ca	10.7 × 107m−1 s−1	Calculated
Kon,Mg	0.8 × 106m−1 s−1	Calculated
Geometry
Volume of spine head	0.1 μm3	Harris & Stevens (1988)
Surface area of spine head	0.9 μm2	Harris & Stevens (1988)
Radius of spine neck	0.1 μm	Harris & Stevens (1988)
Length of spine neck	0.66 μm	Harris & Stevens (1988)
Spine density	3.4 μm−1	Vecellio et al. (200)
Radius of dendritic segment	1 μm
Length of dendritic segment
Single-compartment model	10 μm
Double-compartment model	0.3 μm	Calculated
Diffusional mobility
DCa	223 μm2 s−1	Allbritton et al. (1992)
DOGB	15 μm2 s−1	Holthoff et al. (2002)*
DPV	43 μm2 s−1	Schmidt et al. (2003)
DCB	28 μm2 s−1	Schmidt et al.‖
Fraction of immobile calbindin	0.2	Schmidt et al.‖

^*Data for Calcium Green-1, an indicator dye closely related to OGB-1

^†assuming that their fast buffer is CB, that 33% of CB is occupied by MG²⁺ and that 25% of CB is wahsed out during out wholecell recordings

^‡assuming two-fold slower kinetics in the dendrites compared with the in vitro data (Berggård et al. 2002)

^§assuming 50 % washout of PV during our recordings.

^‖H. Schmidt, B. Schwaller & J. Eilers, unpublished observations.

The intracellular Mg²⁺ concentration was held constant. The starting conditions were calculated from chemical equilibrium at [Ca²⁺]_rest. A single surface-based Ca²⁺ extrusion mechanism was simulated assuming Michaelis-Menten kinetics (Sala & Hernández-Cruz, 1990):

(8)

where K_m is the Michaelis-Menten constant, v_max the maximal pump velocity, and A the surface of the cylinder. In order to maintain a stable [Ca²⁺]_rest, the continuous Ca²⁺ clearance was balanced by a leak current:

(9)

The time course of the total change in [Ca²⁺]_i is given by the sum of eqns (3), (4), (8) and (9). The only free variables in the simulation were the strength of the Ca²⁺ influx (I_Ca) and v_max. These two variables were optimised iteratively until the measured dendritic peak [Ca²⁺]_i amplitudes was reached and the overlap between the measured and the simulated decays was maximal.

Since our fluorometric recordings did not report the ‘real’ [Ca²⁺]_i but the amount of Ca²⁺ bound to OGB-1, we finally converted the simulated changes in the Ca²⁺-OGB-1 complex (i.e. [CaBS₁]) to ‘apparent’ [Ca²⁺]_i values assuming equilibrium conditions (see above; Markram et al. 1998; Yamaguchi & Ichikawa, 1998).

Double-compartment model

The above formalism was extended to a two-compartment model in order to analyse the effects of Ca²⁺ diffusion between the spine and its parent dendrite. The spine and the dendritic shaft were modelled as two homogeneous compartments optionally coupled by diffusion across the spine neck. The length of the dendritic compartment was set to 0.3 μm to correct for the spine density of the terminal dendrites (3.4 μm⁻¹, Vecellio et al. 2000). For a given molecular species X, the diffusional current I_X across the spine neck was modelled as

(10)

where D_X and C_X are the diffusion coefficient and the concentration of the diffusing species, respectively, and r_neck and l_neck are the radius and the length of the spine neck (see Table 2). The rate of change in the concentration of X due to diffusion follows as

(11a)

for the spine and

(11b)

for the dendrite. The simulation included independent diffusion of the free binding sites of OGB-1, CB and PV, of the corresponding Ca²⁺-bound binding sites, of the Mg²⁺-bound binding sites of PV, and of free Ca²⁺. The time course of the total change in [Ca²⁺]_i is given by the sum of eqns (3), (4), (8), (9) and (11a) for the spine and the sum of eqns (3), (4), (8), (9) and (11b) for the dendrite. The strength of the Ca²⁺ influx (I_Ca) was varied independently in both compartments to reach the measured WT peak amplitudes. The dendritic v_max was the same as in the single-compartment model, and the spineous v_max was varied until the overlap between the measured and the simulated spineous decays was maximal. Numerical simulations were performed with Mathematica 4.2 (Wolfram Research, Champaign, IL, USA).

⁴⁵Ca²⁺-overlay assay

Cerebella of adult mice were homogenised in 10 mM Tris-HCl, 1 mM EDTA, pH 7.4 and soluble protein fractions were prepared by centrifugation of homogenates at 30 000 g for 40 min. Soluble proteins (250 μg) were separated by one-dimensional polyacrylamide gel electrophoresis (12.5 % polyacrylamide) on 1.5 mm thick gels, and transferred onto nitrocellulose membrane using a semi-dry transfer system (Hoefer Scientific, CA, USA) according to a transfer protocol described previously (Maruyama et al. 1984). After transfer, membranes were washed (three times, 20 min) in 10 mM imidazole-HCl, 5 mM MgCl₂, 60 mM KCl, pH 6.8 and incubated for 10 min in the same solution containing 40 kBq ml⁻¹⁴⁵CaCl₂ to label high-affinity Ca²⁺-binding proteins as described by Maruyama et al. (1984). Membranes were washed in 50 % ethanol (5 min), dried and analysed by a Molecular Imager system (Bio-Rad, Glattbrugg, Switzerland).

RESULTS

Climbing fibre-mediated Ca²⁺ transients in spines and dendrites of wild-type Purkinje cells

Fluorescence recordings were performed in spiny dendrites (Fig. 1A and B) of wild-type (WT) PCs loaded with the fast and high-affinity Ca²⁺ indicator dye Oregon Green BAPTA-1 (OGB-1, 200 μM). Activation of the afferent climbing fibre (CF) input elicited the characteristic ‘complex spike’, i.e. a large excitatory postsynaptic potential (EPSP) with several spikes, and a concomitant increase in the Ca²⁺-dependent fluorescence of OGB-1 (expressed as ΔF/F₀, see Methods) in dendrites and spines (Fig. 1C and D). As shown previously, the transient in dendritic shafts showed a biphasic (i.e. double exponential) decay (Miyakawa et al. 1992; Eilers et al. 1995; Airaksinen et al. 1997; Maeda et al. 1999). The Ca²⁺ transients in the adjacent spines were also described well by the sum of two exponential functions. In both dendrites and spines the Ca²⁺ signals showed a rapid onset (Miyakawa et al. 1992) that coincided with the onset of the second spike of the EPSP (Fig. 1D and E). This observation is consistent with the notion that the first spike of the CF-EPSP represents a somatic Na⁺ action potential (AP) - which is not associated with dendritic Ca²⁺ signals (Lev-Ram et al. 1992; Eilers et al. 1995) - followed by Ca²⁺ spikes generated in the dendrites of PCs (Llinás & Sugimori, 1980). The peak of the Ca²⁺ transients was reached during the last AP of the complex spike. We never observed a prolonged increase of the Ca²⁺ transients, a signature of Ca²⁺-induced Ca²⁺ release in PCs (Llano et al. 1994). Furthermore, it is unlikely that Ca²⁺ influx through ligand-gated channels contributed to the observed fluorescence signals since the synapses of the CF are only located on the proximal dendrites (Larramendi & Victor, 1967). Thus, the Ca²⁺ transients are probably solely due to Ca²⁺ influx through voltage-operated Ca²⁺ channels (VOCCs). The peaks of the Ca²⁺ transients in spines were significantly larger and occurred earlier than in the corresponding dendrites (Fig. 1F and G). Thus, consistent with immunohistochemical data (Hillman et al. 1991), VOCCs seem to be present in spines.

Conversion of the fluorescence signals to changes in [Ca²⁺]_i

A more quantitative analysis of the fluorescence signals is complicated by the fact that the fluorescence of OGB-1 (like all calcium indicator dyes) exhibits a non-linear dependence on the intracellular Ca²⁺ concentration ([Ca²⁺]_i). Due to this non-linearity, ΔF/F₀ signals do not allow an accurate comparison of kinetic properties of large responses that have different peak amplitudes. To overcome this limitation, we converted the fluorescence signals to changes in [Ca²⁺]_i based on an assumed resting [Ca²⁺]_i ([Ca²⁺]_rest) of 45 nM (Airaksinen et al. 1997) and a cuvette calibration of OGB-1 (Fig. 2; see Methods for details). Besides the possibility that the fluorescent properties of the dye are altered by the cellular environment (see, for example, Maeda et al. 1999), the most critical parameter of our conversion is the assumed [Ca²⁺]_rest. Thus, it is important to note that the presence or absence of buffers does not affect [Ca²⁺]_rest (Chard et al. 1993; Airaksinen et al. 1997) and, therefore, the conversion will also be valid for the recordings we performed in PV and PV/CB null-mutant mice. Furthermore, even a 10 % deviation of [Ca²⁺]_rest from the assumed value will lead only to small errors in the conversion (Fig. 2B, grey lines) as long as the ΔF/F₀ values are smaller than ≈2.5. Therefore, we discarded recordings in which this limit, which corresponds to a [Ca²⁺]_i of 1.25 μM, was exceeded.

Figure 2. Quantification of the fluorescence signals.

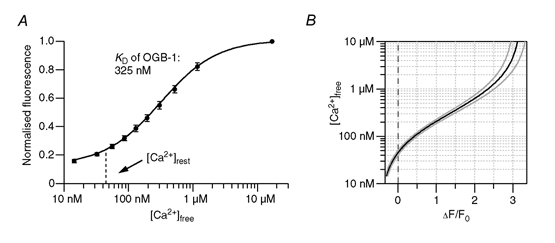
A, fluorescence intensity of OGB-1 in the pipette solution buffered to various free calcium concentrations ([Ca²⁺]_free). Values were normalised to the intensity obtained at ≈20 μM [Ca²⁺]_free. Data points represent means ± S.D. from five independent cuvette calibrations. The continuous line represents a least-squares fit that yielded a K_D of 325 nM (see eqn (2)). The dashed line represents the assumed intracellular resting calcium concentration ([Ca²⁺]_rest) under our experimental conditions. B, conversion (black line) of ΔF/F₀ values to [Ca²⁺]_free for a [Ca²⁺]_rest of 45 nM and the associated F₀. The grey lines represent the error range if the cellular [Ca²⁺]_rest deviates by ± 10 % from 45 nM. Based on the calibration, fluorescence transients that exceeded 2.5 ΔF/F₀ were discarded.

Decay kinetics of the [Ca²⁺]_i signals

The Ca²⁺ dynamics in spines and dendrites may be affected by diffusion between these two compartments (Majewska et al. 2000a). Thus, although the point-scan recordings illustrated in Fig. 1 offer a superior temporal resolution, the following data were obtained in the line-scan mode to allow an exact correlation of spineous and dendritic Ca²⁺ transients. A typical line-scan recording is shown in Fig. 3A-D. The decay of the [Ca²⁺]_i transients in spines and dendrites required a double exponential function for a satisfactory fit (see insets in Fig. 3C and D). In total, the vast majority of the 252 spines and 131 dendrites we analysed in WT PCs (19 cells, 18 animals) showed a biphasic decay (Fig. 3E and F, Table 1). A single exponential function was sufficient to fit the decay in less than 1 % of the spines and 5 % of the dendrites. In these cases the time constants were in the range of the slow components of the double exponential fits and, therefore, were grouped with these data in Fig. 3E-G. On average, the spineous peak amplitudes as well as the amplitudes of the fast and slow components were significantly larger than the corresponding dendritic values (Fig. 3E and F, insets). In addition, the time constants of the fast and slow components were significantly faster in the spines (Fig. 3G).

Figure 3. Double exponential decay kinetics of Ca²⁺ transients in spines and dendrites from wild-type (WT) mice.

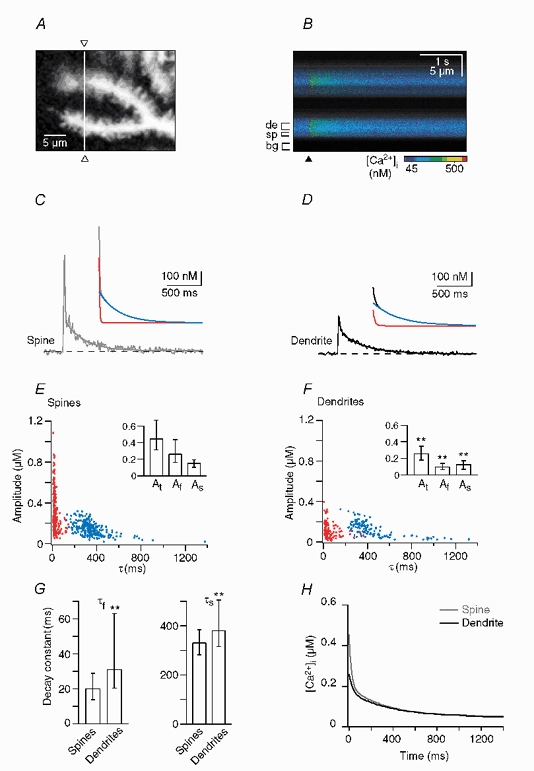
A, confocal image of the dendritic area in which the line-scan recording shown in B-D was performed. The white line and the open triangles indicate the position of the single line that was analysed. B, colour-coded image of the line-scan (i.e. y-t) recording from the region outlined in A. The brackets denote the regions of interest from which the dendritic (‘de’), spine (‘sp’) and background (‘bg’) signals were obtained. The time point of CF stimulation is indicated by the arrowhead. C and D, waveform of the Ca²⁺ transients in the spine (C) and the dendrite (D). The continuous lines represent double exponential fits to the decay; the dashed lines represent the assumed resting [Ca²⁺]_i of 45 nM. The insets show the fits with their corresponding fast and slow components (red and blue traces, respectively) superimposed. In the spine the fit yielded a fast component of 255 nM with a decay time constant (τ_fast) of 17 ms and a slow component of 135 nM with a τ_slow of 330 ms. The corresponding dendritic values were 70 nM and 15 ms (fast component) and 110 nM and 460 ms (slow component). E and F, data for double exponential decays from 252 spines (E) and 131 dendrites (F) from 19 cells from 18 animals. The fast and slow components are plotted in red and blue, respectively. The insets show the median and IQR values of the total amplitude (A_t) as well as the amplitudes of the fast (A_f) and slow (A_s) components. **Statistically different from spines (P < 0.005). G, corresponding values of τ_fast and τ_slow (median and IQR). H, calculated median decay in spines (grey trace) and dendrites (black trace).

Table 1.

Summary of results

Parameter	Wild type		PV−/−	PV/CB−/−
	Dendrite	Spine	Dendrite	Dendrite
Biphasic decays
Fast component
Amplitude (nm)	95(62–135)	258(164–434)	74(61–135)	411(267–490)
Time constant (ms)	31(20–63)	20(13–30)	33(15–60)	43(29–70)
Slow component
Amplitue (nm)	122(64–171)	148(98–190)	149(103–204)	172(56–271)
Time constant (ms)	380(317–508)	330(281–384)	332(301–366)	171(126–328)
Fraction of biphasic decays	0.95(n = 131)	0.99(n = 252)	0.70(n = 48)	0.85(n = 62)
Monophasic decays
Amplitude (nm)	138 (128–197)	135	151 (89–213)	250 (185–315)
Time constant (ms)	379 (281–411)	226	325(265–372)	104 (84–154)

Median values and interquartile ranges.

For the spines and the dendrites we calculated a median decay (Fig. 3H) as a weighted sum of two exponential functions generated from the median values (Table 1) of the double and monoexponential decays, respectively. These median responses emphasise the biphasic nature of the decay in both compartments and provide a simple means for comparing responses between different compartments and animal populations.

In the following we focused on the mechanisms generating the biphasic waveform in dendritic shafts rather than in spines because spineous Ca²⁺ transients are known to be strongly influenced by diffusion of Ca²⁺ between the spine and the parent dendrite (Majewska et al. 2000a,b; Holthoff et al. 2002; Sabatini et al. 2002). The biphasic decay in PC dendrites, however, sharply contrasts with the monophasic time course observed in hippocampal and cortical neurones (see, for example, Helmchen et al. 1996; Lee et al. 2000a; Majewska et al. 2000a,b). Several mechanisms may potentially underlie the biphasic dendritic Ca²⁺ transients in PCs: optical cross-talk from neighbouring spines, diffusion of Ca²⁺, saturation (defined here as higher than half-maximal occupancy of the binding sites) of the Ca²⁺ indicator dye, saturation of and/or delayed Ca²⁺ buffering by endogenous Ca²⁺-binding proteins (CaBPs), or non-linear Ca²⁺ extrusion mechanisms. In the following we addressed each of these possibilities individually.

Optical cross-talk from spines

Individual spines that were oriented horizontally to the optical plane were clearly resolvable (Fig. 1B and Fig. 3A). However, due to the limited axial resolution of our confocal recordings (Rayleigh criterion of 2400 nm, measured with 100 nm fluorescent microspheres, Tetra Speck, Molecular Probes), spines oriented vertically could not be unambiguously distinguished from their parent dendrite. Such ‘hidden’ spines may have contributed to the signals recorded from dendrites and may even have caused the biphasic decay kinetics measured in the dendritic shafts. We estimated the contribution of hidden spines in the different mouse strains based on the spine orientation, the density and geometry of spines (Vecellio et al. 2000), as well as the typical brightness difference between dendrites and spines (>5-fold) in our recordings. On average, ≈5 % of the signal from a single hidden spine contributed to the dendritic signal. Thus, for typical recordings (peak ΔF/F₀ of 1.0 and 2.0 in the dendrite and spine, respectively), the dendritic peak Ca²⁺ increase had been overestimated only by ≈15 nM (compare Fig. 2). In addition, control recordings performed on more proximal dendritic branches (reversed Strahler order 1 to 6), which have a much lower spine density, also revealed biphasic decays (n = 20, five cells, five animals, data not shown, see also Airaksinen et al. 1997). Taken together, the contribution of hidden spines to the dendritic signals was negligible and cannot account for the biphasic decay of the dendritic Ca²⁺ transients.

Diffusion

Similar to the situation in spines (Majewska et al. 2000a,b; Holthoff et al. 2002; Sabatini et al. 2002), the biphasic decay in dendrites could be due to diffusional Ca²⁺ flux from the dendrite to neighbouring compartments that have a lower [Ca²⁺]_i. These compartments could be either adjacent, inactive spines, neighbouring segments of the dendrite under study, or more proximal dendrites, which are known to have lower Ca²⁺ increases during CF stimulation (Miyakawa et al. 1992; Eilers et al. 1995). The first possibility can be excluded because of the amplitudes and kinetics of the spine transients. In almost all cases the CF-mediated Ca²⁺ transients in dendritic shafts were smaller than those in the adjacent spines (Fig. 1G and Fig. 4A). No inactive spines were observed. Moreover, on average the spines showed a higher or equal Ca²⁺ level than the dendrites throughout the CF-mediated transient; no inactive spines were observed (Fig. 3H). Thus, diffusion of Ca²⁺ from dendrites into spines cannot account for the biphasic decay in dendrites.

Figure 4. Influence of Ca²⁺ diffusion and the indicator dye on the decay kinetics.

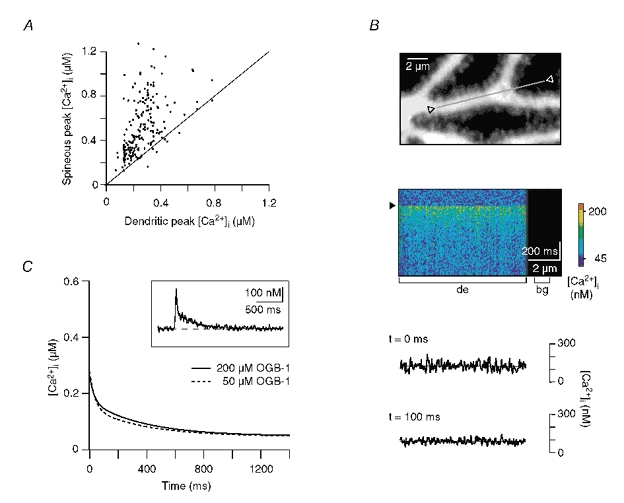
A, plot of the peak amplitude of Ca²⁺ responses in spines versus the peak amplitude in the corresponding dendrites. Note that the dendritic peak amplitude was in almost all cases smaller than in the adjacent spines. B, upper panel: dendritic segment in which the line-scan recording shown below was performed. The grey line and open triangles mark the region from which the fluorescence was sampled. Middle panel: colour-coded image of the line-scan (x-t) recording from the region outlined above. The brackets denote the regions of interest from which the dendritic (‘de’) and background (‘bg’) signals were obtained. The arrowhead indicates the time point of CF stimulation. Lower panel: corresponding Ca²⁺ levels at the peak of the CF response (‘t = 0 ms’) and 100 ms later. The continuous lines represent linear fits to the data. At both time points the slope of the fits was < 1 nM μm⁻¹. C, comparison of the median dendritic decays recorded with a pipette concentration of OGB-1 of 200 μM (same as in Fig. 3H) and 50 μM (n = 69, five cells, three animals, A_f = 131 nM, A_s = 100 nM, τ_fast = 36 ms, τ_slow = 378 ms). The inset shows an example trace recorded with 50 μM OGB-1. A double exponential fit (continuous line) was required to faithfully describe the decay (A_f = 180 nM, A_s = 108 nM, τ_fast = 16 ms, τ_slow = 333 ms).

To test for the possibility that Ca²⁺ diffusion within a given dendritic segment underlies the biphasic dendritic decay, we performed line-scan recordings along longer stretches of distal dendrites (Fig. 4B). These recordings (n = 18, three cells, three animals) revealed homogeneous Ca²⁺ levels within a given segment, with spatial gradients of less than 1 nM μm⁻¹ for at least 10 μm. Thus, on the timescale of CF-mediated Ca²⁺ transients, no significant net diffusion of Ca²⁺ will occur within individual dendritic segments. Finally, diffusional transport of Ca²⁺ towards more proximal dendritic branches, i.e. over distances >10 μm, can be expected to occur on time scales of hundreds of milliseconds (Allbriton et al. 1992; Rexhausen 1992; Berg 1993; Maeda et al. 1999), too slow to account for the fast component of the decay kinetics. Taken together, diffusion of Ca²⁺ towards compartments with lower [Ca²⁺]_i is unlikely to contribute significantly to the biphasic decay kinetics in dendritic shafts.

Effect of the indicator dye

Ca²⁺ indicator dyes act as buffers that compete with endogenous CaBPs and Ca²⁺ extrusion mechanisms for Ca²⁺ binding. Biphasic Ca²⁺ kinetics may result from saturation of the indicator during large Ca²⁺ transients (Neher 1995, 1998; Maeda et al. 1999), an effect that would be augmented by high indicator concentrations. The majority of the Ca²⁺ transients in dendritic shafts, however, had peak amplitudes smaller than the K_D of OGB-1 (Fig. 3F and H), and, thus, did not saturate the indicator dye. Moreover, experiments performed at a four-fold lower dye concentration (35-40 μM in the dendrites) still revealed biphasic dendritic decay kinetics (Fig. 4C; n = 69, five cells from three animals). The median decay kinetics were not significantly different from the decays recorded with the higher dye concentration (Fig. 4C). In conclusion, neither saturation of OGB-1 nor its relatively high concentration appear to make a major contribution to the biphasic character of the decays kinetics in dendritic shafts of WT PCs.

Dendritic decay kinetics in PV null-mutant mice

Neher and co-workers showed that monophasic Ca²⁺ decays in chromaffin cells can be transformed to biphasic ones by perfusing the cells with PV (Lee et al. 2000b). They could attribute this phenomenon to the slow binding kinetics of PV (Eberhard & Erne, 1994) that prevented PV from affecting the peak amplitude of fast Ca²⁺ transients and shifted its action to the decay of the transients. This delayed binding of PV accelerated the early and slowed the later phase of the decay, and, thereby, induced biphasic decay kinetics.

To investigate whether also in PCs, which are well known to express large quantities of PV (Kosaka et al. 1993; de Talamoni et al. 1993), the biphasic decay is attributable to PV, we analysed Ca²⁺ transients in PV null-mutant (PV^−/−) mice. If delayed Ca²⁺ buffering by PV would determine the biphasic character of the decay kinetics (Fig. 1 and Fig. 3), one would expect monophasic decays in PV^−/− mice or at least an assimilation of the time constants.

Figure 5A shows an example of a recording from a dendritic shaft of a PV^−/− PC. Interestingly, the Ca²⁺ decay still required a double exponential function for a satisfactory fit. This was the case for 70 % of the dendritic recordings from PV^−/− mice (n = 48, five cells, five animals, Table 1). The time course of the Ca²⁺ transients in the remaining 30 % of the dendrites, however, could be described by a single exponential equation. As in WT, the fast and the slow components of the fits were clearly separated (Fig. 5B). The calculated median decay (Fig. 5C) had the same amplitude as the WT response and still showed a biphasic time course. However, it significantly deviated from the WT curve during the early decay. This deviation corresponded to a maximal difference of the median responses of 15 nM in the amplitude and 40 ms in the waveform. As a rough approximation (neglecting Ca²⁺-dependent extrusion mechanisms and non-linear interaction of buffers) the integral of this difference (grey shaded area in Fig. 5C) represents the amount of Ca²⁺ that is bound by PV. The observed buffering effect of PV is in good accordance with the model of PV's role in dendritic Ca²⁺ signalling presented by Lee et al. (2000b).

Figure 5. Dendritic decay kinetics in parvalbumin null-mutant (PV^−/−) mice.

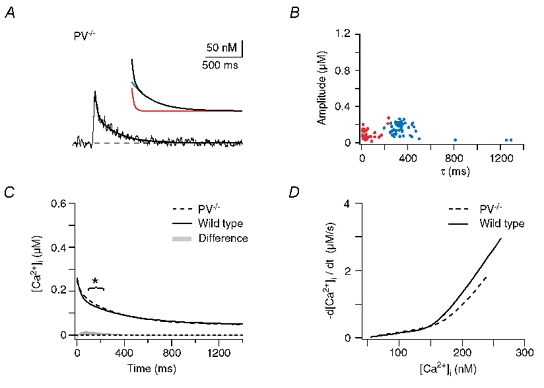
A, example of a dendritic recording. The continuous line represents a double exponential fit to the decay. The inset shows the fit with its corresponding fast (70 nM and 28 ms, red trace) and slow components (90 nM and 280 ms, blue trace) superimposed. B, data of double exponential decays from 48 dendrites from five cells from five mice. The fast and slow components are plotted in red and blue, respectively. C, calculated median decay in dendrites of PV^−/− mice (dashed trace) compared with the median response in WT mice (continuous trace). The grey area represents the integral of the arithmetic difference between the two decays. The bracket denotes the time interval in which a significant difference between the WT and PV^−/− transients occurred (t test, P < 0.025). D, comparison of the [Ca²⁺]_i dependence of the median dendritic decay rates (-d[Ca²⁺]_i / dt; calculated from C) between WT (continuous line) and PV^−/− (dashed line).

Thus, under the assumption that neither Ca²⁺ influx nor Ca²⁺ extrusion were significantly altered in the PV^−/− mice, PV acts as a buffer that is too slow to affect the peak amplitude of the dendritic response but rather accelerates its early decay. While this effect appears to be rather small when inspecting the waveform of the Ca²⁺ transients (Fig. 5C), it becomes evident upon plotting the corresponding Ca²⁺-decay rate (-d[Ca²⁺]_i / dt) versus [Ca²⁺]_i. As illustrated in Fig. 5D, buffering by PV (in the WT) leads to a clear acceleration of the decay at Ca²⁺ levels above 150 nM. However, even in the PV mutants the median decay was clearly biphasic. Thus, delayed buffering by PV is not the only mechanism that induces double exponential decay kinetics in PC dendrites.

Dendritic decay kinetics in PV/CB null-mutant mice

Besides parvalbumin, PCs express high levels of CB (Baimbridge et al. 1992), a buffer with four binding sites (Veenstra et al. 1997) that confer high and medium Ca²⁺ affinity to the protein (K_D values ≈200 and ≈450 nM, respectively; Nägerl et al. 2000, increased by a factor of ≈2 in the presence of physiological concentrations of Mg²⁺; Berggård et al. 2002). The kinetics of the high-affinity binding sites seem to be comparable to those of PV (in the presence of Mg²⁺) while the kinetics of the medium-affinity sites are about an order of magnitude faster (Eberhard & Erne 1994; Nägerl et al. 2000). Maeda et al. (1999) suggested that CB or a Ca²⁺-binding protein with similar properties undergoes saturation during submicromolar and long-lasting Ca²⁺ transients and, thereby, induces biphasic decay kinetics in PCs. However, Airaksinen et al. (1997) showed that in mutant mice lacking CB (CB^−/−) the decay kinetics were still double exponential, an observation that would argue against CB being solely responsible for the biphasic decay. In view of this study, Maeda et al. (1999) suggested that in CB^−/− mice, PV could partially substitute for CB and be responsible for the persistent biphasic decay, an explanation that would be consistent with our results from PV^−/− mice. Thus, both CB and PV would have the potential to induce non-linear decay kinetics.

Therefore, we next analysed mice that lack both buffers, PV as well as CB (PV/CB^−/−, Vecellio et al. 2000). In dendritic shafts of these double-mutant mice the CF-mediated [Ca²⁺]_i transients showed remarkably different kinetics (Fig. 6A and B; n = 62, six cells from six mice, Table 1). A single exponential function was sufficient to fit the time course in 15 % of the responses; the remaining 85 % still required a double exponential function. Whilst in these cases, the fast and slow time constants were significantly different from each other (P < 0.001, Mann-Whitney U test), a clear assimilation of the values was observed (Fig. 6B). The median peak amplitude of the transient was significantly increased (Fig. 6C), but the time-to-peak was not affected (Fig. 6E, mean values of 15.5 ± 4.8 and 15.5 ± 4.1 ms in WT and PV/CB^−/− mice, respectively).

As discussed for the wild-type recordings, optical cross-talk from hidden spines could have contributed to the signals recorded from dendritic shafts. Due to the increased spine size and density in PV/CB^−/− PCs (Vecellio et al. 2000), the average spine signal that contributed to the shaft signal increased (compared with the WT) from ≈5 to ≈7 %. In consequence, for typical PV/CB^−/− recordings (peak ΔF/F₀ of 1.9 and 2.5 in the dendrite and spine, respectively), the dendritic peak Ca²⁺ increase had been overestimated by less than 20 nM. Therefore, also in the PV/CB^−/− recordings, the contribution of hidden spines to the dendritic signals was negligible.

As a rough estimate, the integral of the difference between the median PV/CB^−/− and PV^−/− responses (grey shaded area in Fig. 6C) represents the amount of Ca²⁺ that is bound by and, subsequently, released from CB. Thus, while CB effectively reduces the peak amplitude of the Ca²⁺ transients, it continues to bind Ca²⁺ for ≈150 ms, while later, at lower Ca²⁺ levels, it acts as a Ca²⁺ source. This delayed buffering induces a non-linearity in the dendritic decay that, in the WT, is further amplified by PV (see above). It is important to note that the observed effect of CB represents the net effect of the high- and the medium-affinity binding sites. The high-affinity binding sites alone, for example, which have rather slow binding kinetics, can be expected to exert an effect similar to PV (i.e. delayed binding). Thus, the strong and rapid reduction of the peak amplitude of the Ca²⁺ transients is most likely due to the faster, medium-affinity binding sites of CB. The question whether saturation of CB's binding sites contributed to the non-linear decay kinetics (as during large and long-lasting Ca²⁺ transients; Maeda et al. 1999) could not be answered directly from our recordings. However, our simulations (see below) suggest that neither CB's medium nor its high-affinity sites underwent saturation during the CF-mediated Ca²⁺ transients.

The dendritic Ca²⁺ decay rate in PV/CB^−/− PCs was nearly linearly dependent on [Ca²⁺]_i and the fast and slow time constants of the decay overlapped substantially (Fig. 6D). Thus, the combined effects of PV and CB almost fully accounted for the biphasic decay of the dendritic transients in the WT. However, in the double mutants a slight non-linearity below Ca²⁺ levels of 100 nM remained (Fig. 6D).

Role of unidentified Ca²⁺-binding proteins

Could endogenous buffers other than PV and CB be responsible for the remaining biphasic decay kinetics? Little is known about the expression of additional CaBPs in PCs. Therefore, we performed a Ca²⁺-overlay assay to semi-quantitatively assess the prevalence of CaBPs in the cerebellum of WT as well as PV and PV/CB mutant mice (Fig. 6F). In the samples derived from WT cerebella the three most prominent bands with apparent molecular masses of 30, 28 and 12 kDa correspond to calretinin (CR; 20 % protein concentration, corrected for Ca²⁺ binding sites), CB (20 %), and PV (24 %), respectively. In the mutant animals the deleted CaBPs, i.e. PV and/or CB, are absent, without any significant upregulation of other proteins.

The group of CaBPs ranging from approximately 16 to 24 kDa mainly consists of proteins with four helix-loop-helix Ca²⁺ binding motifs called EF-hand domains. These include calmodulin, calcyphosine and neuronal calcium sensor proteins such as neurocalcin, visinin-like protein 3 or hippocalcin, which were shown to be expressed in PCs (for review see Celio et al. 1996; Burgoyne & Weiss, 2001). Due to the relatively large number of different proteins, all expressed at low levels, this region on the ⁴⁵Ca²⁺ blot appears as a relatively diffuse, almost continuous band. While CB and PV only constitute 44 % of the Ca²⁺-binding proteins in the whole cerebellum of WT mice, their relative concentration in the PC population can be assumed to be considerably higher because in the cerebellar cortex PCs show the strongest expression of PV (Plogmann & Celio, 1993) and are the only cells that express CB (Baimbridge et al. 1992). Furthermore, CR, which is a major constituent of the CaBPs of the whole cerebellum, is not expressed in PCs (Resibois & Rogers, 1992). Taken together, we cannot exclude a role of uncharacterised CaBPs in shaping the dendritic decay kinetics; however, their quantitative contribution is likely to be minor compared with CB and PV.

Ca²⁺ extrusion mechanisms and dye saturation

Assuming that in the PV/CB^−/− mice uncharacterised endogenous CaPBs are not responsible for the residual biphasic decay of dendritic Ca²⁺ transients, two possible mechanism remain: non-linear extrusion mechanisms and saturation of the indicator dye.

Ca²⁺ extrusion mechanisms that generate monophasic decay kinetics are linearly dependent on Ca²⁺, as can be judged by the straight line that is obtained when plotting the Ca²⁺ decay rate (-d[Ca²⁺]_i / dt) against [Ca²⁺]_i. While linear dendritic extrusion mechanisms seem to be operational in most cell types studied so far (see Helmchen, 1999, for review), Llano and co-workers previously analysed Ca²⁺ extrusion mechanisms in somata of PCs and found a significant non-linearity above 200 nM [Ca²⁺]_i (Fierro et al. 1998). Thus, non-linear extrusion mechanisms would be likely candidates to explain the remaining non-linearity in the PV/CB^−/− recordings (Fig. 6D). However, even linear extrusion mechanisms generate biphasic responses if the Ca²⁺ transients saturate the indicator dye (Neher, 1995; Maeda et al. 1999). Unlike the dendritic responses in WT and PV^−/− PCs, the peak amplitudes in PV/CB^−/− recordings were well above the K_D of our indicator dye. Thus, dye saturation may also underlie the remaining non-linearity of the decays in the double mutants.

To judge whether dye saturation in the presence of linear extrusion mechanisms is sufficient to explain the waveform of the decay in the PV/CB^−/− recordings, we performed numerical simulations of Ca²⁺ influx, buffering and extrusion in a dendrite-like structure. Our single-compartment model is largely based on the formalism of Markram et al. (1998). It incorporated a brief Ca²⁺ influx approximated by a Gaussian function, Ca²⁺ buffering by OGB-1 simulated by second-order kinetics, and linear (in the range of CF-evoked Ca²⁺ transients) extrusion mechanisms following Michaelis-Menten kinetics (see Methods and Table 2 for details). As described by Markram et al. (1998), the model allows deduction of how changes in the free [Ca²⁺]_i are reported by the indicator dye (see also Yamaguchi & Ichikawa, 1998). Thus, in the following, the simulated transients represent the Ca²⁺ levels inferred from the calculated dye-Ca²⁺ complex (which corresponds to the fluorescence signals we recorded), not the calculated ‘real’ free [Ca²⁺]_i (see Methods, Markram et al. 1998 and Yamaguchi & Ichikawa, 1998).

We adjusted the Ca²⁺ influx and the extrusion rate so that the peak amplitude of the simulated transient reached the same value as the median response in the PV/CB^−/− recordings and the decay of the measured and the simulated transients overlapped maximally (I_Ca = 78 pA, v_max = 300 pmol cm⁻² s⁻¹). As illustrated in Fig. 7A, the simulated transient well described the waveform of the dendritic PV/CB^−/− response. Importantly, the biphasic nature of the decay was replicated. The inset of Fig. 7A shows that the fractional occupancy of OGB-1 during the transient reached a peak value of 0.65, indicating that saturation of the indicator induced the biphasic decay.

Figure 7. Single-compartment model of Ca²⁺ transients in dendritic shafts.

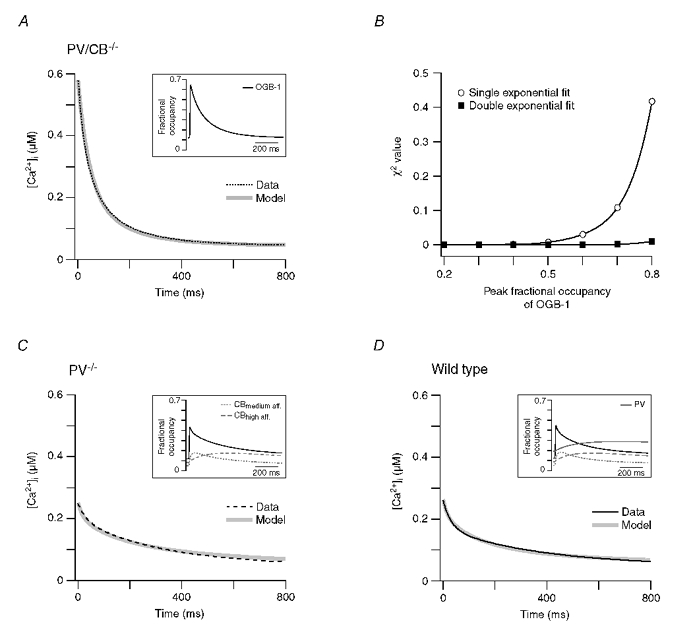
A, median dendritic decay kinetics (dotted black line) and corresponding simulated decay of the [Ca²⁺]_i reported by OGB-1 (grey line) from PV/CB^−/− PCs. The kinetic model incorporated a Gaussian Ca²⁺ influx, OGB-1 and a Ca²⁺ extrusion mechanism that was linear in the range of the Ca²⁺ transient (see Methods and Table 2 for details), reflecting the situation in the double mutant. The inset shows the fractional Ca²⁺ occupancy of OGB-1 during the simulated Ca²⁺ transient. B, χ² values of single and double exponential fits (open and filled symbols, respectively) to increasingly larger Ca²⁺ transients simulated with the model used in A. The lines represent polynomial fits to the χ² values. Note that double exponential fits are required to faithfully describe the decay kinetics once the peak Ca²⁺ concentration reaches the K_D of OGB-1 (>50 % occupancy). C, the median dendritic decay in PV^−/− PCs (black dashed line) was modelled (grey line) by including 40 μM CB with two high- and two medium-affinity binding sites into the simulation described in A. The inset shows the fractional Ca²⁺ occupancy of OGB-1 and CB's high- and medium-affinity binding sites. D, the median dendritic decay in WT PCs (black line) was modelled (grey line) by including 40 μM PV in the simulation described in C. The inset shows the corresponding fractional Ca²⁺ occupancy of OGB-1, of CB's bindings sites and of PV. The simulations of the PV/CB^−/− transients required a two-fold higher extrusion rate than those of the PV^−/− and WT transients (see Results for details).

Using the model, we further quantified up to which peak amplitudes Ca²⁺ transients can be satisfactorily fitted with a single exponential function. As illustrated in Fig. 7B, single exponential fits are sufficient as long as the fractional occupancy of OGB-1 during the peak is smaller than 50 %, corresponding to Ca²⁺ levels of 325 nM, i.e. the K_D of OGB-1 (Fig. 2). At higher Ca²⁺ levels, the decay kinetics require double exponential fits.

Taken together, in the WT and the PV^−/− animals, delayed buffering by PV and/or CB appears to be sufficient to explain the non-linear dendritic Ca²⁺ decay kinetics while saturation of the indicator dye is the most likely mechanism in the double mutant mice. Neither uncharacterised buffers nor non-linear extrusion mechanisms seem to contribute significantly to the waveform of CF-evoked Ca²⁺ transients in dendritic shafts.

Binding kinetics of CB and PV

The integral of the calculated differences in the Ca²⁺ decay kinetics in WT and mutant animals (Fig. 5C and Fig. 6C) already provided a rough estimate of when and to what extend CB and PV bind Ca²⁺ during the Ca²⁺ transients. However, non-linear interactions of the buffers, as described by Markram et al. (1998), complicate a direct comparison of the transients. We, therefore, incorporated CB and subsequently PV into our single-compartment model in order to analyse their buffering kinetics. As for the double mutants, the strength of the Ca²⁺ influx was varied to reach the peak Ca²⁺ amplitudes of the PV^−/− and WT responses. In these simulations the pump velocity had to be reduced (v_max = 150 pmol cm⁻² s⁻¹) in order to obtain satisfactory results, a fact that might indicate compensatory upregulation of extrusion mechanisms in the PV/CB^−/− mice.

We first simulated the situation in the PV^−/− mice by including CB in the single-compartment model. The binding kinetics of CB have been determined by Nägerl et al. (2000) in vitro. We reduced their measured k_on rates by 50 % (which leads to a corresponding increase in the K_D values) to account for the kinetic effects of the Mg²⁺ present in the cytosol (Berggård et al. 2002; see also Lee et al. 2000b). Little is known about the intracellular CB concentration in PCs. Assuming that (i) the fast buffer of PCs identified by Maeda et al. (1999) is indeed CB, (ii) that about one-third of CB complexes Mg²⁺ under physiological conditions (Berggård et al. 2002), and (iii) that about 25 % of CB is washed out during our prolonged whole-cell recordings, we used a CB concentration of 40 μM in our simulations. The exact Mg²⁺ binding kinetics of CB are unknown. Thus we reduced the assumed dendritic CB concentration by 25 % instead of including Mg²⁺ binding in the model. Further uncertainty exists about the ratio of high- and medium-affinity binding sites of CB. Nägerl et al. (2000) proposed a ratio of 2:2 or 3:1. In our simulations a 2:2 ratio invariably gave better results than a 3:1 ratio and, therefore, was used in the simulations. Figure 7B shows the median decay measured in PV^−/− mice and the corresponding result of the simulation. The simulation indicates that in PV^−/− recordings neither OGB-1 nor CB undergoes saturation and that the biphasic Ca²⁺ decay observed in this mutant is due to delayed buffering of CB (inset of Fig. 7C). With the chosen parameters (Table 2), the simulation overlapped satisfactorily with the measured data. It should be noted that double exponential decay kinetics were also obtained by varying the kinetics and/or concentration of CB considerably (data not shown); the simulated decays, however, did not overlap maximally.

We next simulated the WT decay kinetics by including PV in the model. PV's binding kinetics and Mg²⁺ sensitivity are quite well characterised (Eberhard & Erne, 1994; Lee et al. 2002b). Its concentration was set to 40 μM assuming that the native PV concentration is 50-100 μM (Kosaka et al. 1993) and a 50 % washout of the highly mobile PV (Schmidt et al. 2003) occurred. Figure 7D illustrates that the full model, which reflects the interaction of OGB-1, CB, PV and linear extrusion mechanisms, well describes the median decay in the WT animals. The simulation indicates that none of the buffers undergoes saturation and that CB as well as PV induces biphasic decays by delayed buffering (inset of Fig. 7D).

Diffusional coupling of spines and dendrites

Throughout the CF-evoked Ca²⁺ transient, the spineous [Ca²⁺]_i was higher than that in the adjacent dendritic shaft (Fig. 4A). Thus, we finally investigated to what extent diffusional coupling between the spine and the dendritic shaft would attenuate the biphasic waveform of the dendritic Ca²⁺ transients. To address this question we extended our single-compartment model to two compartments - the spine and its adjacent dendrite - optionally coupled by diffusion of Ca²⁺, OGB-1, PV and CB, and their complexes (see Methods and Table 2 for details). In view of the high spine density of terminal dendrites, the length of the dendritic compartment was set to 0.3 μm. We otherwise used the kinetic parameters as in the single-compartment model and again varied only the Ca²⁺ influx and the extrusion rate so that the peak amplitude of the simulated transient reached the same value as the median WT response and that the decay of the measured and the simulated transients overlapped maximally. In the absence of diffusional coupling, the dendritic simulation resembled that of the single-compartment model, i.e. the simulation faithfully reproduced the biphasic Ca²⁺ transient (Fig. 8A). The spineous Ca²⁺ transient, however, could not be satisfactorily simulated. The model invariably failed to reproduce the sharp bend in the early decay of the spine transient (Fig. 8A).

Figure 8. Compartmental model of spino-dendritic Ca²⁺ dynamics.

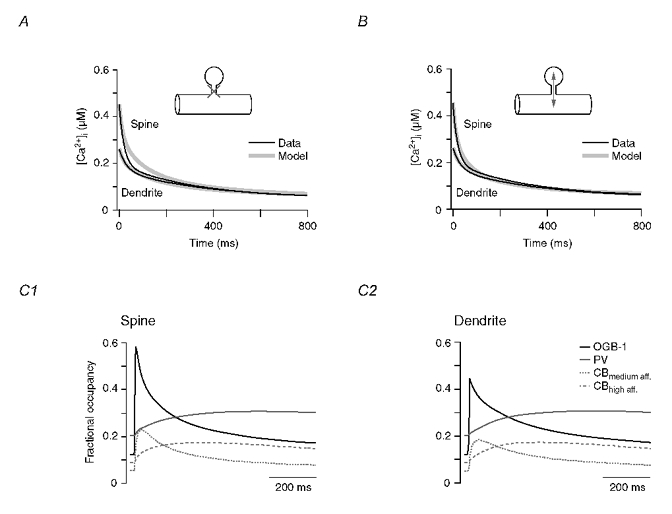
A, measured and simulated Ca²⁺ decay kinetics (black and grey traces, respectively) in spines and dendrites of WT PCs. For the simulation, the diffusional coupling between the spineous and the dendritic compartment was not allowed to occur. Note that the simulation faithfully reproduces the measured dendritic transient (same result as shown in Fig. 7D), but fails to reproduce the spine transient. B, same as A but with diffusional coupling taking place on Ca²⁺ and all buffer species (Ca²⁺- and Mg²⁺-bound as well as free OGB-1, CB and PV) were allowed to diffuse between the spine and the dendrite (see Methods and Table 2 for details). Note that diffusional coupling resulted in a more reliable simulation of the spine transient but did not significantly affect the dendritic decay. C, fractional occupancy of OGB-1, PV and CB's binding sites in the spine (C1) and the dendritic shaft (C2) coupled by diffusion (see B). The only buffer that undergoes saturation (fractional occupancy > 50 %) is the spineous OGB-1.

Once diffusional coupling was included in the simulation, the overlap of the measured and simulated spine transient improved dramatically (Fig. 8B). With all kinetic parameters held constant (only the spineous Ca²⁺ influx was increased slightly), the model could now also reproduce the early phase of the spineous transient. Thus, in agreement with Majewska et al. (2000a), Ca²⁺ diffusion boosts the biphasic nature of spineous Ca²⁺ decays. The Ca²⁺ dynamics in the dendritic shaft were little affected by Ca²⁺ influx from the spine because the volume of the dendritic compartment was ≈10-fold larger than that of the spine. The corresponding changes in the Ca²⁺-buffer complexes (Fig. 8C) indicate that (i) neither of the endogenous buffers PV and CB undergo saturation during CF-evoked Ca²⁺ transients, either in the dendrite or in the spine, (ii) the high-affinity binding sites of CB bind Ca²⁺ with kinetics similar to those of PV, and (iii) the medium-affinity binding sites of CB are capable of reducing the peak amplitude of the Ca²⁺ transients significantly, but they do not fully equilibrate during the rising phase of the transient and continue to complex Ca²⁺ even during the early decay of the transient. Taken together, our results indicate that four mechanisms induce biphasic decay kinetics in spines: saturation of OGB-1 (see Fig. 7B), efflux of Ca²⁺ from the spine (Fig. 8A and B), delayed buffering by CB, and delayed buffering by PV (Fig. 8C1). Biphasic decays in dendritic shafts are induced by two mechanisms: delayed buffering by CB and delayed buffering by PV. Diffusion and/or saturation of buffers appear to make a minor contribution.

DISCUSSION

Biphasic Ca²⁺ decay kinetics

The results presented indicate that a dynamic interaction of PV, CB and linear extrusion mechanisms determines Ca²⁺ kinetics in dendrites of cerebellar PCs. In spines, the biphasic nature of the decay is further amplified by Ca²⁺ diffusion and by saturation of our indicator dye. These findings explain why PCs, but not pyramidal neurones and the majority of interneurones from the hippocampus and cortex, show biphasic dendritic decays. Similar to other neurones, in PC dendrites linear extrusion mechanisms appear to be responsible for Ca²⁺ clearance. In contrast to other neurones, however, Ca²⁺ dynamics in PCs are modulated by high levels of endogenous Ca²⁺-binding proteins (CaBPs), among which CB and PV represent the major fraction (Fig. 6F). The concentration of CaBPs can be quantified in terms of the Ca²⁺-binding ratio (κ_s; Neher, 1992), which ranges from 900 to 2000 in PCs (Fierro & Llano, 1996). Pyramidal cells and interneurones, on the other hand, typically have κ_s values of only 20-60 and 100-300, respectively (Helmchen et al. 1996; Lee et al. 2000a, Kaiser et al. 2001; Sabatini et al. 2002). Thus, in these cells the effect of CaBPs on the decay rate may be negligible and/or obscured by the presence of Ca²⁺ indicator dyes (Neher, 1995; Markram et al. 1998).

Buffering by parvalbumin

We show that in spiny dendrites of PCs, PV acts as a slow buffer that does not affect the peak amplitude of CF-mediated Ca²⁺ transients but accelerates the decay during the first 300 ms (Figs 5C and D, 7D and 8C). This effect is not attributable to saturation of PV but to PV's peculiar Ca²⁺ and Mg²⁺ sensitivity. Parvalbumin binds Ca²⁺ with fast kinetics (Hou et al. 1991) and an extremely high affinity (K_D,Ca ≈9 nM; Lee et al. 2000b). Thus, under resting conditions ([Ca²⁺]_i ≈45 nM) PV would be almost fully saturated with Ca²⁺ (Berrgård et al. 2002). However, PV also has a medium affinity for Mg²⁺ (K_D,Mg ≈30 μM; Eberhard & Erne, 1994) which, under our experimental conditions ([Mg²⁺]_i ≈590 μM), leads to an apparent K_D,Ca for PV of ≈100 nM. Thus, under physiological resting conditions about 76 % of PV is occupied by Mg²⁺, 20 % by Ca²⁺ and only 4 % remains free. As a consequence, buffering of Ca²⁺ transients by PV has to be preceded by Mg²⁺ unbinding, which is an inherently slow process (≈1 s⁻¹; Lee et al. 2000b). This delayed Ca²⁺ buffering explains why, despite the high PV concentration in PCs (50-100 μM; Kosaka et al. 1993), PV only slightly affects the rapid kinetics of synaptically evoked Ca²⁺ transients.

Neher and co-workers described a similar effect of PV in hippocampal interneurones (Lee et al. 2000a). While the majority of interneurones were characterised by monophasic dendritic decay kinetics, a subset showed biphasic waveforms. Probably only these cells expressed PV. In a subsequent study (Lee et al. 2000b) the buffering kinetics of PV were quantified in chromaffin cells and finally incorporated into a numerical simulation of the effect of PV on dendritic decay kinetics. Notably, this model closely predicted our findings.

Buffering by calbindin

Our comparison of PV and PV/CB double-mutant mice revealed that CB affects the peak amplitude as well as the Ca²⁺ decay. We show that CB does not reduce the time-to-peak of CF-mediated Ca²⁺ transients, as had been suggested by Chard et al. (1993). Further, our simulation revealed that under our experimental conditions, the CB-induced non-linearity in the decay kinetics is not attributable to saturation of CB (Fig. 8C) but, similar to PV, to protracted Ca²⁺ binding. At first glance this finding may appear to be in conflict with the results of Maeda et al. (1999), who attributed non-linear Ca²⁺ kinetics in PCs to saturation of an endogenous buffer with similar kinetics as CB. However, compared with the CF-mediated Ca²⁺ signals analysed in our study, Maeda et al. (1999) analysed significantly larger (peak amplitude of 0.5-10 μM) and longer lasting (several seconds) transients. Under these conditions, CB will, like OGB-1 in our PV/CB^−/− recordings (Fig. 7B), induce an additional non-linearity due to saturation. Thus, our results extend, rather than contradict, the conclusions of Maeda et al. (1999). Our simulations predict that the high-affinity binding sites of CB show kinetics similar to those of PV and that even the faster, medium-affinity sites have substantially slower binding kinetics than the indicator dye (Figs 7C and D insets and 8C). Thus, the notion that CB acts as a ‘fast’ buffer in PCs (Airaksinen et al. 1997) holds only in comparison to PV and only for the medium-affinity sites.

Unidentified buffers and Ca²⁺ extrusion

Our results show that biphasic Ca²⁺ decay kinetics in mutant and wild-type PCs can be explained by the interaction of CB, PV and OGB-1 with linear extrusion mechanisms. The model did not require additional buffers or non-linear Ca²⁺ extrusion mechanisms to replicate the measured transients. We cannot rule out, however, that other endogenous proteins (such as calmodulin, for example) influence the dendritic Ca²⁺ kinetics. While our Ca²⁺-overlay assay (Fig. 6F) indicates that in PCs the intracellular concentration of uncharacterised buffers will be low compared with CB and PV, more information about their cellular concentration, localisation and kinetics is required to decisively quantify their role in dendritic Ca²⁺ dynamics. Similarly, exact information about the Ca²⁺ dependence of dendritic extrusion mechanisms will be of critical importance. It is rather surprising that the different neuronal Ca²⁺ extrusion mechanisms (SERCA pumps, plasma membrane Ca²⁺ pumps, Na⁺-Ca²⁺ exchangers and mitochondria), which display distinct, non-linear Ca²⁺ dependencies (Fierro et al. 1998), seem to add up to a linear extrusion (Helmchen, 1999). It is clear, however, that future studies on the contribution of the different extrusion mechanisms should take into account the effects of endogenous and exogenous buffers.

Limitations of our study

Our study is based on quantitative measurements of Ca²⁺ transients in spines and dendrites. Calibrations of non-ratiometric indicator dyes (such as OGB-1) in these compartments rely either on an assumed resting [Ca²⁺]_i (this study) or on measured maximal fluorescence increases (‘F_max‘) during intense stimulation (Maravall et al. 2000). Both methods use cuvette calibrations to determine the K_D value of the indicator under study, and, consequently, are prone to error if the K_D determined in the cuvette differs from that in the cytosol. As pointed out by Neher (1995), in vitro Ca²⁺ calibrations will be wrong by a factor of γ_cuvette/γ_cytosol, where γ denotes the single-ion activity coefficient of Ca²⁺ in the respective media. Unfortunately, little information about γ_cytosol is available. We tried to minimize the influence of the cytosolic environment by performing calibrations in our pipette solutions that will diminish the effects of osmolarity, pH, Mg²⁺ and temperature but not of the protein environment (Thomas et al. 2000). Thus, we may have over- or underestimated the K_D value of OGB-1, which will have resulted in an under- or overestimation of the Ca²⁺ transients. We believe, however, that our conclusions about the effect of the endogenous buffers will nonetheless stand because, firstly, the K_D values of CB's binding sites had been determined in cuvettes and not in the cytosol (Nägerl et al. 2000) and, consequently, were also affected by the cellular protein environment (Neher, 1995). Secondly, our simulations are based on buffer kinetics, not on equilibrium conditions. Thus, even if the absolute Ca²⁺ levels were underestimated, delayed binding by CB and PV will inevitably result in biphasic Ca²⁺ decay kinetics.

A more significant uncertainty concerns the concentration and binding kinetics of PV and CB. The exact dendritic concentrations of these proteins have not been determined so far. For PV we had to rely on data from whole PCs (Kosaka et al. 1993), which will be quite accurate measures of the dendritic PV concentration since PV is freely mobile in PCs (Schmidt et al. 2003). For CB no specific data were available. We used the concentration of the fast buffer estimated in PCs by Maeda et al. (1999), which may be an underestimation since some of CB's binding sites have slow binding kinetics (Table 2). Finally, it is not clear whether CB's binding sites do bind Ca²⁺ in a cooperative manner. The study of Berggård et al. (2002) indicates that cooperativity is weak: from their data a Hill coefficient of < 1.1 can be deduced. We therefore regarded CB's individual binding sites as independent in our simulations.

Functional implications

The impact of endogenous Ca²⁺-binding proteins (CaBPs) and Ca²⁺ extrusion mechanisms on cellular physiology is well established (McBurney & Neering, 1987). For example, altered expression of CaBPs has been shown to result from and/or induce various brain pathologies including dementia, epilepsy and ataxia (for review see Heizmann & Braun, 1992). Yet, the question of how a normal or distorted Ca²⁺ homeostasis mechanistically relates to neuronal function and dysfunction, respectively, could rarely be answered. Generally, CaBPs are thought to exert a neuroprotective function by simply limiting the peak amplitudes of Ca²⁺ responses and, thereby, preventing Ca²⁺-induced cell death (see references in Baimbridge et al. 1992). This view, however, may be an oversimplification as exemplified by the case of homo- and heterozygous CB and PV mutant mice. CB^−/− and CB^+/− mice show a normal gross anatomy and synaptic connectivity with no signs of cell death. However, they develop a graded (CB^+/− < CB^−/−) cerebellar ataxia that is correlated with marked changes in the amplitude and kinetics of synaptically mediated Ca²⁺ transients (Airaksinen et al. 1997). Similarly, muscle cells of PV^−/− and PV^+/− mice (Schwaller et al. 1999) show a normal anatomy with no signs of degeneration. The loss of PV, however, markedly changed Ca²⁺ transients in fast twitching muscles. These altered Ca²⁺ dynamics were associated with a graded (PV^+/− < PV^−/−) increase in twitch tension and prolongation of the relaxation cycle. Additional support for the hypothesis that the waveform of Ca²⁺ critically determines cellular functions is given by recent theoretical and experimental data that show that distinct temporal patterns of Ca²⁺ signals can activate specific second-messenger cascades (Bhalla & Iyengar, 1999) as well as the expression of specific genes (Dolmetsch et al. 1997, 1998; Li et al. 1998).

The waveform of dendritic Ca²⁺ signals also seems to be of critical importance in PCs. We could show that the endogenous Ca²⁺-binding proteins of these cells permit large-amplitude Ca²⁺ signals, but at the same time effectively limit their duration at the cost of a sustained prolongation once Ca²⁺ levels of ≈200 nM have been attained. This ‘distortion’ of dendritic Ca²⁺ transients will directly modulate, for example, distinct types of Ca²⁺-activated K⁺ channels (Vergara et al. 1998) as well as inositol 1,4,5-trisphosphate-mediated Ca²⁺ release, which is known to show a steep dependence on [Ca²⁺]_i (Mak et al. 1998). Thus, the combined action of endogenous Ca²⁺-binding proteins and extrusion mechanisms will significantly influence electrical and biochemical signal integration occurring in the dendrites of PCs (Katz & Clemens, 2001). Once the subcellular distribution and concentration of CaBPs, as well as their mobility (Schmidt et al. 2003) and possible reaction partners are identified, our data will help to establish an exact model of neuronal Ca²⁺ signalling.