A functionally defined model for the M₂ proton channel of influenza A virus suggests a mechanism for its ion selectivity

Abstract

The M₂ protein from influenza A virus forms proton-selective channels that are essential to viral function and are the target of the drug amantadine. Cys scanning was used to generate a series of mutants with successive substitutions in the transmembrane segment of the protein, and the mutants were expressed in Xenopus laevis oocytes. The effect of the mutations on reversal potential, ion currents, and amantadine resistance were measured. Fourier analysis revealed a periodicity consistent with a four-stranded coiled coil or helical bundle. A three-dimensional model of this structure suggests a possible mechanism for the proton selectivity of the M₂ channel of influenza virus.

Ion channels are responsible for the rapid and efficient conduction of ions across phospholipid bilayers. They are generally highly selective for their permeant ions, and are gated by voltage or ligands (1). Although a number of high-resolution structures are available for hemolysins (2) and porins (3)—channel-like proteins that form large, nonselective pores—structural analysis of more selective ion channel proteins is at an early stage. Sequence analysis and low-resolution diffraction data indicate that their conduction pathways often consist of bundles of α-helices (4, 5), but the determination of high-resolution structures of channel proteins has been hampered by their limited availability and large size.

M₂ from influenza virus is an essential component of the viral envelope and forms a highly selective, pH-regulated proton channel that is the target of the anti-influenza drug amantadine (6–9). The influenza virus enters cells through internalization into the endocytic pathway, with virus uncoating taking place in endosomal compartments. The M₂ ion channel activity permits protons to enter the virion interior, and this acidification weakens the interactions of the matrix protein (M₁) with the ribonucleoprotein core (10). By comparison to the channels of excitable tissues, M₂ is quite small (97 residues) and contains but one hydrophobic stretch of 18 residues believed to form a transmembrane (TM) helix (residues 26–43). A wealth of experimental evidence indicates that the M₂ channel

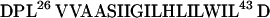consists of a tetrameric array of parallel, TM peptides with their N termini directed toward the outside of the virus (6–9). A synthetic 25-residue peptide spanning the hydrophobic region forms amantadine-sensitive proton channels, indicating that the determinants for assembly of the channel lie within this TM peptide (11). Further, CD spectroscopy indicates that this peptide forms α-helices in membranes (12). Thus, the TM region of the channel appears to consist of a parallel bundle of α-helices.

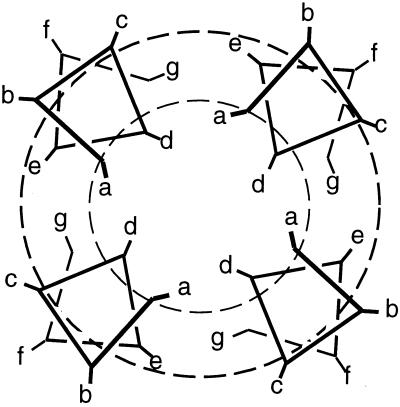
Here we describe the use of Cys-scanning mutagenesis (13, 17, 18) to obtain more detailed information concerning the arrangement of the TM helices within the tetrameric pore. A similar method has been used previously to infer the probable structures of other homo-oligomeric TM proteins, including glycophorin (14) and phospholamban (15). A series of 18 mutants were prepared in which a Cys residue replaced the wild-type residue at successive positions of the TM helix. Cys was used because it does not occur in the TM region of M₂. Further, in subsequent studies, the thiol of Cys could be modified with spectroscopic (16) or chemical (17, 18) probes to obtain structural information. In the present study, we have measured the reversal potential, current amplitude, and amantadine sensitivity of the mutants under conditions where the Cys residues are reduced. Fig. 1 illustrates how mutations might affect the properties of a parallel helical four-stranded ion channel. Alterations to residues lining the lumen of the channel (designated a and d in Fig. 1) are expected to strongly perturb the properties of the channel. Mutation of residues at the helix/helix interfaces (primarily e and g) might have smaller, indirect effects, and the remaining mutations should have little effect. Importantly, the exact mechanism by which a given mutation disrupts the structure is not essential; the effects may range from stabilizing a nonconducting state to disrupting the ability of the helices to oligomerize. The key feature is that the mutations have a perturbing effect on the channel properties, and this effect should be smallest at the lipid-exposed positions.

Figure 1.

Helical wheel diagram showing one heptad of a parallel, four-stranded helical coiled coil (or four-helical bundle assuming a sequence repeat of 7.0 residues) viewed down the bundle axis. The dashed circles demarcate three regions that are predicted to show different perturbational effects (see text).

MATERIALS AND METHODS

Site-Directed Mutagenesis and Protein Expression.

The cDNA encoding the influenza virus A/Udorn/72 M₂ was subjected to site-specific mutagenesis using the Chameleon Double-Stranded, Site Directed Mutagenesis Kit (Stratagene). The nucleotide sequences of the entire coding region of the altered cDNAs were confirmed by nucleotide sequencing. For in vitro transcription, plasmid DNAs were linearized downstream of the T₇ promoter and the M₂ cDNA with XbaI. In vitro synthesis and quantification of ^7mG(5′)ppp(5′)G-capped mRNA was carried out as described (19). Xenopus laevis oocytes were identified individually with an implanted microchip marker (Basic Medic Data Systems, Maywood, NJ). Oocytes were removed from female X. laevis (Nasco, Fort Atkinson, WI), defolliculated by treatment with collagenase B (2 mg/ml; Boehringer Mannheim) and incubated in ND96 (96 mM NaCl/2 mM KCl/3.6 mM CaCl₂/1 mM MgCl₂/2.5 mM pyruvic acid/5 mg/ml gentamycin/5 mM Hepes), pH 7.6, at 19°C. Oocytes at stage V were microinjected with 50 nl of mRNA (1 ng/nl) on the day after defolliculation, incubated for 24 h in ND96 (pH 7.6), and finally incubated for 24 h in ND96 (pH 8.5) at 19°C before use (19). To confirm M₂ expression, oocytes were incubated in ND96 supplemented with [³⁵S]methionine (250 μCi/ml; 1 Ci = 37 GBq) (Amersham) from 24 to 48 h postinjection. Labeled oocytes were homogenized in 75 μl per oocyte of RIPA buffer containing 50 mM iodoacetamide and a mixture of protease inhibitors (phenylmethylsulfonyl fluoride, aprotinin, antipain, pepstatin A, leupeptin, and chymostatin), and extracts were immunoprecipitated using an M₂-specific 14C2 mAb. Samples were analyzed by SDS/PAGE on 17.5% plus 4 M urea polyacrylamide gels (19).

Measurement of Electrical Conductance.

Whole-cell currents were recorded from oocytes 24–48 h after mRNA injection with a two-electrode voltage-clamp apparatus consisting of a differential preamplifier (model MEZ-710I; Nihon Kohden, Tokyo) and voltage-clamp amplifier (model CEZ-1100; Nihon Kohden). Reference and recording electrode were filled with 3 M KCl. Oocytes were bathed in a standard Barth’s solution (1 mM KCl/0.3 mM NaNO₃/0.71 mM CaCl₂/0.82 mM MgSO₄/2.4 mM NaHCO₃/88 mM NaCl/15 mM Hepes, pH 7.5, or 15 mM Mes, pH 6.2). Oocytes were voltage-clamped at −20 mV and whole-cell currents were measured using −120 to −60 mV assay pulses in 10-mV steps. Currents recorded with the −80 mV pulse were used except in the cases of S31C, G34C, H37C and W41C in which case the assay pulse elicited small (<0.5 μA) whole-cell current or complex time and voltage-dependent currents. For these mutants, slowly changing ramps of voltage were applied, and whole cell conductances were determined at V_rev. Amantadine (100 μM; Sigma) treatment was for 2 min prior to recordings.

Periodicity Analysis.

The periodicity of various parameters [e.g., PI(n), see Results] associated with the amino acid side chains vs. their positions in the TM sequence was analyzed by fitting a cosine function (Eq. 1)

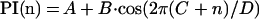1

to the data using kaleidagraph (version 2.0, Synergy Software, Reading, PA) in which A is the midpoint of the curve, B is the amplitude, C is the phase, and D is the period of the cosine wave. Starting parameters were as follows: A = mean of the dependent variable; B = standard deviation of the dependent variable; C = 1.0; D = 3.6. The parameters C and D define the positions in the sequence where PI(n) is maximal (which may be nonintegral in this situation) as defined in Eq. 2, where i is an integer referring to the ith peak in the curve.

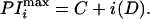2

Generation of M₂ TM Models.

The values of PI_i^max provide constraints for construction of helical bundles when they are mapped onto an α-helix (20–22). Consider a helix with its central axis aligned along the z axis of a Cartesian coordinate system, and the C_β of its first residue lying on the y axis. A smooth curve connecting these points spirals around the helix with a crossing angle or pitch angle (relative to the helical axis) of α as defined in Eq. 3 (22),

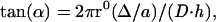3

in which Δ represents the difference between the sequence-defined repeat (D) and the actual repeat of the α-helix (a), r^o is the effective radius of the α-helix, and h is the helical rise per residue.

A number of 4-fold symmetrical helical bundle models were constructed assuming that the positions of maximal perturbility project toward the central axis of the bundle (z_b), and that the stripe defined by PI_i^max is oriented approximately parallel to z_b. Thus, the angle at which the α-helices cross the central axis is −α as defined in Eq. 3. Radially symmetrical helical bundles can adopt shapes resembling either cones or hourglasses, depending on whether the helices approach one another closest near the top or middle of the structure (23). We created a series of helical bundles in which the point of closest approach was coincident with each possible position of PI_i^max as follows: a single TM helix was positioned in a Cartesian coordinate system such that its helical axis was aligned along z, and a vector orthogonal to this axis running through one of the i positions of maximal perturbility was directed along the y axis. The helix was then rotated by α about the y axis and translated by −7, −8, or −9 Å along y, resulting in three model structures for each value of PI_i^max. Application of a symmetry operator completed the construction of the helical bundle. This process was repeated for each possible position of PI_i^max.

We also considered helical bundles in which the helices were straight and arranged with their axes parallel to the central axis, with their most perturbable faces directed toward the central axis (defined using an equation analogous to equation 3 of ref. 20).

We also constructed α-helical coiled coils with a sequence repeat of 7.0 (which is within experimental error of twice the sequence-defined repeat) using methods described previously (24). Three models were generated with a superhelical pitch of 189 Å and a superhelical radius of 7, 8, or 9 Å.

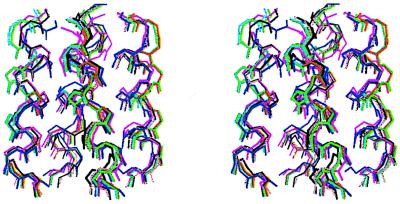
Prior to minimization of the above starting geometries, amino acid side chains were placed in energetically favorable rotamer states (25). Side chains projecting toward the exterior of the bundle were placed in their most probable rotamers, whereas multiple rotamers were examined for the residues projecting toward the interior of the bundle (labeled a and d in Fig. 2). Significantly, three such residues (Val-27, Ala-30, and Gly-34) have no more than one probable rotamer (25). The side chain of His-37 was oriented toward the center of the channel pore with χ₁ = −175° and χ₂ = −90°. Four starting rotamers for Trp-41 (χ₁ = −75°, χ₂ = −90°; χ₁ = −175°, χ₂ = −95°; χ₁ = −180°, χ₂ = 90°; χ₁ = −75°, χ₂ = −100°) were examined, with the resulting structures displaying two major rotamers (χ₁ = −75°, χ₂ = −90°; χ₁ = −170°, χ₂ = 100°). Molecular mechanics were run in vacuo with discover (Biosym Technologies, San Diego) using a combination of steepest descents and conjugate gradient methods. Upon energy minimization, the individual coiled coil and straight helix models converged to a set of structures that differed by 0.1 to 2.2 Å rmsd (backbone atoms) with an average rmsd of 1.1 Å. The seven models closest to the centroid of the cluster are shown in Fig. 3.

Figure 2.

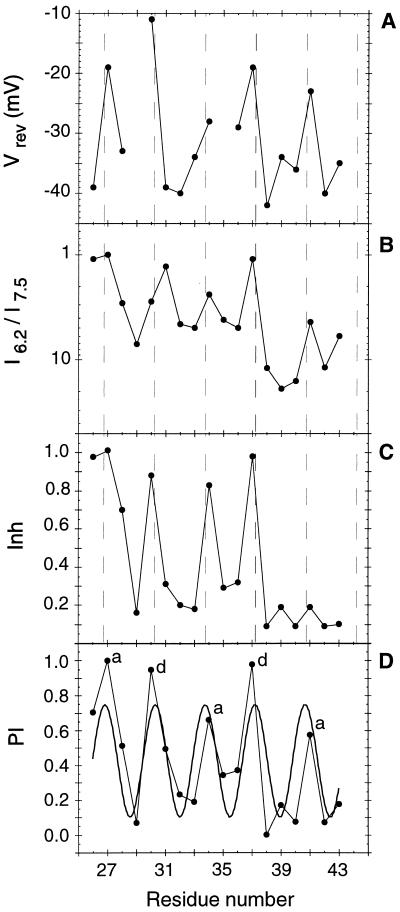
The variation in V_rev (A), I_6.2/I_7.5 (B), Inh (C), and PI(n) (D) as a function of position in the TM helix sequence. The smooth curve through the PI(n) data (D) represents the best fit to a cosine function (Eq. 2) generated using kaleidagraph with initial parameters A = 0.5, B = 1.0, C = 0, and P = 3.6. The dashed lines in A–C show peak positions expected for a 3.5-residue periodicity. Labels a and d in D represent heptad positions in the sequence. The perturbational index [PI(n)] is calculated from the three individual parameters. To combine these three parameters into PI(n), the individual values were normalized so their average values would be zero, then weighted according to their standard deviations. The values of the three parameters for each position were then averaged, and the combined PI(n) scale was normalized to range from 0 to 1. Because the periodic variation of Inh was limited to approximately the N-terminal half of the TM region, only residues 26–38 were included in calculating PI(n).

Figure 3.

Stereoview of the seven representative models of the M₂ proton channel using molscript (26). The backbone atoms of residues 26–41 are shown.

To investigate the effect of protonation of His-37 on the channel structure, molecular minimization was run on a model with one His side chain per four-helix bundle protonated. The pore of the channel was filled with water using the Soak command in insightii. After energy minimization, the resulting structure was virtually superimposable on the unprotonated model.

RESULTS

Cys Scanning Mutagenesis.

The Cys mutations were introduced into DNA encoding the full-length M₂ of influenza virus (19) in which each naturally occurring Cys was already replaced by Ser (27). This mutant behaves identically to wild type after expression in X. laevis oocytes (27) and eliminates the potential complicating issue of forming mixed disulfides with the TM Cys mutations. Electrophoresis of the Cys-containing TM mutants showed that they were predominantly in the monomeric, reduced forms.

The conductance of the mutants was evaluated following expression in X. laevis oocytes. Three distinct and largely independent functional properties of the mutants were measured to determine the degree to which mutations perturbed the structure of the channels. The first involved measuring the ability of the mutants to exclude ions at neutral pH. M₂ is relatively impermeable to ions at neutral pH, but modifications to its structure might lead to an increase in permeability. To test for this possibility, we measured the reversal potential (V_rev) of oocytes expressing the mutants at pH 7.5, and compared the value to that for wild type. If expression of the mutants results in a nonspecific increase in the permeability of the oocyte membrane, the reversal potential at pH 7.5 should decrease in magnitude. We next tested the ability of mutant and wild-type channels to form pH-activated channels by measuring the ratio of the amantadine-sensitive currents measured at pH 6.2 vs. pH 7.5 (I_6.2/I_7.5). Finally, the ability of amantadine to inhibit the channel (Inh) was assessed from the fraction of current observed at pH 6.2, after addition of 100 μM amantadine for 2 min.

Fig. 2 illustrates the variation in V_rev, I_6.2/I_7.5, and Inh with respect to the position of the mutation. The values of these parameters indeed show a periodic variation, and peak at positions a and d as would be expected for an α-helical coiled coil (shown in Fig. 1). The periodic variation of V_rev and I_6.2/I_7.5 extends to near the C terminus of the TM region, indicating that nearly the entire TM region is required for efficient proton transmission. By contrast, the systematic variation of Inh extends only from residues 26 to 38, delimiting the boundaries of the residues involved directly or indirectly in drug binding. All three curves peak at the same positions (±0.2 residues as assessed by fitting the data to a cosine function), indicating that the residues required for binding amantadine are also critical for the transmission of ions.

Periodicity Analysis.

We used periodicity analysis (28) to compare quantitatively the periodic distribution of the electrophysiological parameters with that expected for a coiled coil. The degree of perturbation to a given parameter associated with a mutation at position n is given by the parameters ΔV_rev(n), ΔI_H(n), or ΔInh(n) as defined in Eqs. 4 A–C (in which, for instance, V_rev^cys/V_rev^wt represents the ratio of the reversal potential of cells expressing M₂ mutated at residue n versus wild type). These parameters are zero when the properties of the mutant are identical to wild type and increase as the severity of the perturbation increases.

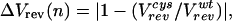4A

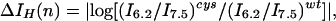4B

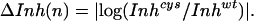4C

The ratio of ionic fluxes is expressed logarithmically in Eqs. 4 B and 4C to allow a better comparison with ΔV_rev(n), which is based on an energetic scale of reversal potentials and thus is also logarithmic. A priori, it is difficult to predict whether a given mutation will increase or decrease a given property of the channel, so ΔV_rev(n), ΔI_H(n), and ΔInh(n) are defined as absolute values. These three parameters were then normalized and combined into an average perturbational index PI(n) (Fig. 2).

Fig. 2D illustrates the variation in PI(n) with respect to sequence position, which is well described by a cosine wave of period 3.46 ± 0.09 residues. Analysis of the individual curves of V_rev, I_6.2/I_7.5, or Inh versus n also gave periods ranging from 3.4 to 3.5 residues. These values are less than the period of an α-helix (3.6 residues). This deviation from α-helical periodicity has been observed previously in the periodicity of coiled coils (24) and is diagnostic of the left-handed interhelical crossing angle in helical bundles and coiled coils (Table 1). The phase of the cosine wave (C) defines the positions of the peaks in the perturbility function. These positions of maximal perturbility are expected to line the lumen of the channel (Fig. 1), providing important experimental constraints to guide the construction of three-dimensional models.

In helical membrane proteins, the faces of TM helices that contact the lipid are generally more hydrophobic than the faces directed toward the protein interior. As a result, the hydrophobicity (Hb) of the side chains shows a periodic distribution, reflecting the structure of the interacting helices (31). Popot and coworkers (21) have also introduced an empirical scale of amino acid side chains (P) describing the preference for a residue to occupy a position facing the membrane lipids versus the interior of the protein. Plots of Hb [using Eisenberg and McLachlan’s hydrophobicity scale (28)] or P versus residue number for seven variants of M₂ also show a sinusoidal distribution, with phases and periods that are remarkably similar to those obtained by mutational analysis (Table 1). Thus, these predictors of structure, which are quite independent of PI, also suggest that the M₂ TM helix forms a left-handed coiled coil or helical bundle and identifies the same set of inward-facing residues.

Modeling the M₂ TM Helical Bundle.

The above analyses suggest that the helices in M₂ adopt a slight left-handed pitch angle, as in coiled coils and four-helix bundles. A total of 27 different models were constructed, each of which was fully consistent with the observed hydrophobic periodicity, while also spanning the geometric variation typically observed in the structures of water-soluble and membrane-spanning helical bundles. Although the geometric differences between coiled coils and helical bundles (in which the helices are tilted relative to the central axis) is not large for 18-residue helices, both were considered. Upon energy minimization, the models converged into a single set of structures with an average rmsd of 1.1 Å. Qualitatively, the initial models with close interhelical distances expanded, whereas those with a larger separation contracted. Similarly, the coiled-coil models straightened somewhat, whereas the models with straight helices curved.

The interhelical crossing angles of the above models (Table 1) were dictated by the periodicity analysis, using well-established procedures of analysis (24, 31). However, to assure that the assumptions implicitly associated with the periodicity analysis did not overly influence the final models, three bundles with straight, strictly parallel helices were also examined. Upon minimization, these models again converged with those obtained using tilted or supercoiled helices as the starting models, showing a pairwise helical crossing angle of 19.5 ± 0.6°, which compares quite favorably with an average of 18.9° calculated from the sequence analysis (Table 1). Thus, the optimization of side chain packing interactions that occurred during energy minimization was alone sufficient to induce a left-handed pitch angle in the bundle. Fig. 3 illustrates seven representative structures generated from straight parallel, straight tilted, or coiled-coil input geometries for energy minimization. They display good pairwise, interhelical packing throughout the length of the structure. The pairwise helical crossing angle between neighboring helices for these structures was 20.8 ± 2.4°, in good agreement with the observed values of 18–24° for interhelical packing in proteins (32, 33). The corresponding mean interhelical distances measured at the point of closest approach in the M₂ model structures and experimentally determined structures were 10.5 ± 0.7 Å and 10.2 Å (33), respectively.

This family of models differs significantly from a previous model of the M₂ TM helical bundle (34), which showed much less extensive helix–helix interactions (interhelical distance of 14 Å vs. 10.5 Å for our model). Also, although His-37 lies within the conduction pathway in our current model, this residue was positioned outside of the central cavity in the earlier model.

Functional Implications of the Model.

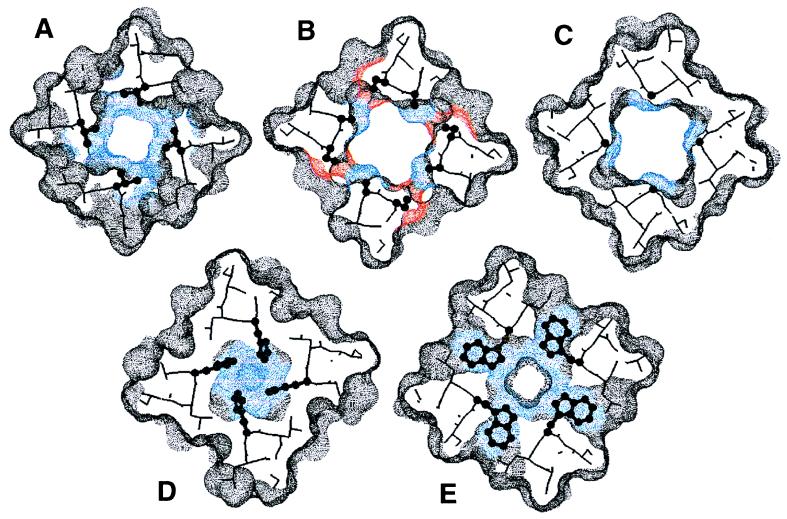
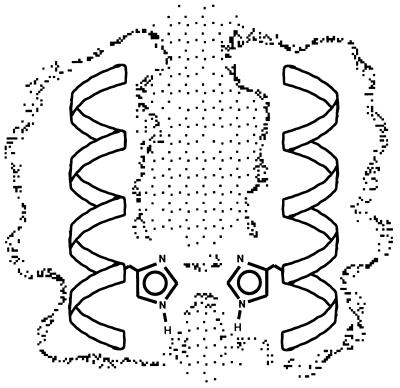
Although there is some variability to the set of models, many features are common to each member. Fig. 4 illustrates 5-Å slices taken through the channel. A continuous channel that is large enough to accommodate a H-bonded chain of water molecules runs down the center of the bundle from the N terminus to His-37. This cavity is largest in the vicinity of Gly-34, where a single amantadine molecule can be accommodated. The only major occlusion of the channel lies at His-37. The planes of the imidazole rings lie roughly parallel to the superhelical axis (Fig. 5), and their orientations within the channel may provide an explanation for the strong proton selectivity of the channel. It would be difficult for alkali metal ions or chloride ions to pass beyond this point, but protons may be transmitted through this site by a proton relay mechanism. A proton entering the channel may protonate a neutral His at the imidazole δ-nitrogen facing the exterior of the virus. Deprotonation of the ɛ-nitrogen would allow translocation of the proton into the viral interior. Finally, tautomerization or a ring flip would complete the cycle, as in the active site of carbonic anhydrase (35, 36). Thus, this model provides an attractive structural hypothesis for the primary, proton-selective conductance of the channel, although other states with larger lumens may be necessary to account for the low-level conductance of other ions by M₂ (9).

Figure 4.

Axial view of the predicted structure of the M₂ proton channel. The individual panels show successive slices (≈5 Å) through the structure. The residues that appear essential from mutagenic analysis—Val-27 (A), Ala-30 and Ser-31 (B), Gly-34 (C), His-37 (D), and Trp-41 (E)—-are shown as ball-and-stick representations. The dotted surface shows the parts of the model accessible to a probe with a 1.4-Å radius. Color designation: blue, Val-27, Ala-30, Gly-34, His-37, and Trp-41; red, Ser-31; gray, all other residues. This figure was generated using insightii.

Figure 5.

Side view of the M₂ proton channel showing a slice through the structure (the other two helices are not shown for clarity).

This model is also consistent with the pH dependence of the M₂ channel conductance. The current passed by M₂ depends sigmoidally on pH with a midpoint near pH 5.8, associated with the pK_a of His-37 (37). The cooperativity of the transition suggests that only one His residue within the tetramer needs to become protonated during the conduction of protons. Also, the saturation of the conductance at low pH might be associated with the limiting rate of tautomerization or torsional rotation of the His side chain.

Further, this model explains the effects of a large number of amantadine-resistant mutations to the TM region. The side chain of each amantadine-resistant mutation identified by Cys scanning projects toward the lumen of the channel. The dimensions of the pore in the vicinity of the amantadine-resistant mutants closely match those of amantadine. These side chains are frequently mutated to larger and more hydrophilic amino acids in amantadine-resistant strains of the virus (6, 7). The increased hydrophilicity and decreased size of the pore is expected to lower the affinity for the drug. In addition, Ser-31, which has been previously identified as a position important for drug binding, is mutated to Asn in amantadine-resistant mutants (7). In this work, we found that the conservative substitution of Ser-31 to Cys did not affect the ability of amantadine to inhibit the channel, although this substitution did decrease proton current at low pH. In the model for the M₂ channel, the hydroxyl oxygen of Ser-31 contributes to the lining of the pore. The hydroxyl proton of Ser-31 forms a hydrogen bond to the backbone carbonyl oxygen of residue 27 in a conformation frequently observed in known protein structures (25). This hydrogen bond orients the lone pair of the Ser hydroxyl oxygen toward the lumen of the channel. A similar hydrogen-bonded geometry has been hypothesized to account for the cation selectivity of a synthetic pore-forming peptide (38).

Conclusion.

The work described herein builds on the previous studies of Lemmon, Brünger, Engelman, and coworkers (14, 15), who used scanning mutagenesis to identify residues important for the association of the TM helix of glycophorin or phospholamban, as assessed by qualitative examination of SDS gels. Molecular dynamics calculations were then used to exhaustively explore conformational space for predicting models of the TM helix. The present work instead focuses on a protein with several well-defined and easily quantified functional properties, which allows a much more quantitative evaluation of the perturbational effects of the mutations. Indeed, these measurements pointed to a parallel four-helix bundle with the helices interacting with a left-handed crossing angle. This conclusion was further confirmed by an analysis of the distribution of Hb and P in the sequence, which are independent predictors of structure. Finally, energy minimization of four-helix bundle models with strictly parallel helices again led to a virtually identical model. The concordance of these independent lines of evidence increase the confidence in the overall features of the model.

Table 1.

M₂ TM bundle parameters obtained from PI(n), hydrophobicity (Hb) (28), and positional propensity (P) (21) analysis

Parameter	C, residues	D, residues	Pitch angle,* α	Pairwise helix crossing angle,† ɛ
PI(n)	2.58  ±  0.91	3.46  ±  0.09	−14.5  ±  9.2	19.4
Hb	2.44  ±  0.82	3.45  ±  0.08	−15.5  ±  8.2	20.5
P	2.65  ±  0.95	3.48  ±  0.10	−12.4  ±  10.3	16.8
Average	2.56  ±  0.51	3.46  ±  0.05	−14.1  ±  5.3	18.9

^*α can be predicted from the sequence-defined period (D), the repeat of the α-helix (a), the effective radius of the α-helix (r⁰), and the helical rise per residue (h) (22, 29) as in Eq. 3 of the text, where r⁰ = 5.5 Å, h = 1.5 Å, and a = 3.60. The errors reflect the uncertainty in α based on the uncertainty in D and a (30).

^†Calculated using equation 11 of ref. 22.

ABBREVIATION

TM

transmembrane

Note Added in Proof

After submission of this paper, a report describing the generation of a similar model of the M₂ TM helical tetramer in the deprotonated and tetra-protonated states (His-37) was published (40).