Evolution of the folding ability of proteins through functional selection

Abstract

An evolutionary process is simulated with a simple spin-glass-like model of proteins to examine the origin of folding ability. At each generation, sequences are randomly mutated and subjected to a simulation of the folding process based on the model. According to the frequency of local configurations at the active sites, sequences are selected and passed to the next generation. After a few hundred generations, a sequence capable of folding globally into a native conformation emerges. Moreover, the selected sequence has a distinct energy minimum and an anisotropic funnel on the energy surface, which are the imperative features for fast folding of proteins. The proposed model reveals that the functional selection on the local configurations leads a sequence to fold globally into a conformation at a faster rate.

Natural proteins are known to fold into unique three-dimensional structures. Though this folding ability must have emerged in the course of evolution, most investigations have focused not so much on the origin as on the mechanism of the folding process.

In dealing with the mechanism of the folding process, recent theoretical work with lattice models (1–4) and with spin-glass ideas (5–8) suggests that completely random heteropolymers do not have the same tendency to fold into a unique conformation as natural proteins do. To attain a single conformation from all the possible ones within a biological time scale, the peptide chain must have an energetically highly distinctive minimum and a so-called folding funnel (2)—i.e., a biased energy surface. This design principle of the energy landscape is called the principle of minimum frustration (5–7). Several hypotheses have been presented of the origin of minimally frustrated peptides (9–11).

Partial successes in obtaining catalytic antibodies (12) and some functional peptides (13, 14) through functional selection imply the possibility that most polypeptides, if not all, have been tuned through positive selections on function during their evolution. Therefore, it is worth asking whether the existence of an accessible unique conformation evolves from random polypeptides when sequences are selected on the basis of their function alone. In fact, one of the authors and his colleagues (15) synthesized random peptides with 140 residues and showed that 10% of those peptides were water soluble. Some of the soluble peptides have weak hydrolyzing activity whose strength depends on the sequence of the random proteins (unpublished results).

The function of a protein is, in general, governed directly by some active site residues. The spatial configuration of each active site is arranged in a certain way to possess a high functional activity. Then, one could ask whether such local configurational adaptation dictates the folding of the whole protein. In other words, does a globally properly folded peptide chain evolve through the restriction on the local configurations? Pande et al. (10) raised a related question whether sequences with a lower total energy of the protein–substrate complex fold more efficiently even without the substrate. In this paper, our simple spin-glass-like model shows that selection based only on the local configurations of active sites is sufficient for the protein to fold without assuming a priori its native conformation to be at the global minimum in the total energy. These results indicate that the Levinthal paradox on the thermodynamics–kinetics controversy (16) can be resolved as a natural consequence of the evolution in protein functions.

MODEL

The model peptide chain consists of N residues. A variable S_i for i = 1 ∼ N represents the spatial configuration of the ith site in a coarse-grained manner. When the ith site is buried inside the globule of the chain, S_i = −1 and when the ith site is exposed outside the globule, S_i = +1. Then, the total energy of the peptide is E = E(S₁, S₂, … , S_N). If E is expanded in terms of {S_i} and is truncated at the 2nd order, we have

1

where the factor 1/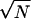 is multiplied to make the last term proportional to the peptide length N. The E_i⁽¹⁾ expresses the change of the energy when the configuration of the ith site is altered and E_ij⁽²⁾ represents the correlation between configurations of the ith and jth sites. Eq. 1 has the form of the Ising spin-glass Hamiltonian, and a similar expression was used in the model of folding of proteins (17). Although Eq. 1 is an extremely simplified expression of the energy of the polymer chain, it has a rugged energy landscape and is able to express the competition between the randomness and coherence.

We adopt the simplest choice for the parameters: E_i⁽¹⁾ = ±1 and E_ij⁽²⁾ = ±1. Because the long-range correlation in sequence plays important roles in determining the global conformation, we assume that S_i and S_j are globally coupled, that is, E_ij⁽²⁾ is nonzero for all i and j. Thus, parameters E_i⁽¹⁾ and E_ij⁽²⁾ carry all the information of the sequences. Mutations in the sequence are equivalent to changes of the signs of E_i⁽¹⁾ and E_ij⁽²⁾. We assume that by a point mutation one of N + N(N − 1)/2 parameters is changed. For computational efficiency, the chain with the short length, N = 15, was used for most of the calculations. Preliminary results with N = 30 suggest that qualitative features do not differ much in the larger system. The model is an extremely simplified one and many points remain to be improved for more precise description: Difference between short- and long-range correlations in sequence should be represented by different values of E_ij⁽²⁾ than ±1. A more general form of spin interaction with different cooperativity from the Ising interaction, such as the Potts spin interaction, should be examined. Effects of the point mutation on E_i⁽¹⁾ and E_ij⁽²⁾ should be statistically inferred from experimental data. The present model, however, is the simplest model and we believe that it captures the essential features to address the problem.

We choose an arbitrary set of three sites, i = a, b, and c, as active sites. The remaining N − 3 sites are assumed to play no direct roles in binding to substrates. When the three active sites take a certain local configuration in their movements, then the peptides bind the substrate, so are functional. We assume for the target configuration, S_a^target = +1, S_b^target = +1, and S_c^target = +1. The arbitrary choices of the active sites and their S_i values do not affect the following conclusion.

Folding is a stochastic process in which each of {S_i} changes its sign in time. {S_i} is randomly assigned to be −1 or +1 as the initial unfolded conformation. The signs of {S_i} are changed by means of the Metropolis Monte Carlo (MC) method at temperature T by using the total energy, E, of Eq. 1. Sequences that more frequently take conformations with the active sites being in the target configuration are searched. To measure the frequency, we observe the configurations at the three active sites from 256 to 512 time steps in the MC simulation and define the following fitness function H,

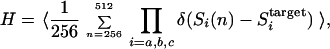2

where δ(S_i(n) − S_i^target) = 0 when S_i ≠ S_i^target and δ(S_i(n) − S_i^target) = 1 when S_i = S_i^target. 〈…〉 is the average over MC trajectories that started from different initial conformations. Thus, H represents the frequency of a certain sequence taking conformations with the correct configurations of the active sites in their motion at temperature T.

Sequences, E_i⁽¹⁾ and E_ij⁽²⁾, are mutated and selected so as to maximize H. For this evolutionary process, a genetic algorithm was employed: (i) For the initial generation, 20 random sequences were prepared by assigning −1 or +1 to E_i⁽¹⁾ and E_ij⁽²⁾ at random. (ii) The “folding” of the sequences was calculated by the MC method. The value of the fitness, H, for each sequence was then measured. (iii) According to the value of H, the sequences were mutated and selected. The sequence with the largest H was passed on to the next generation. The other sequences were mutated by changing the sign of E_i⁽¹⁾ or E_ij⁽²⁾ at random. The value of H is scaled by a parameter T̃, and the mutated sequences were carried over to the next generation with the probability of exp(H/T̃). (iv) All sequences from iii were successively subjected to steps ii and iii for hundreds of generations.

In the following section, we show that the successive selections based only on the local configuration of the active sites lead the peptide chain to be foldable to a single global conformation. That is, a unique conformation represented by a certain {S_i} dominates the thermal motion among 2^N of the possible ones during the evolutionary process. This conclusion was proven not to be affected by the arbitrary choices of the active sites and their S_i values or the time period (from 256 to 512) and the number of folding processes (25).

RESULTS AND DISCUSSION

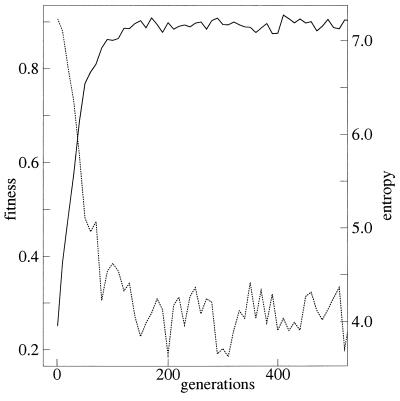
The successive selections create a well-folded conformation. To see the emergence of a single dominant conformation, the conformational entropy, I, for the peptide with the largest H at each generation was calculated by

3

where p_k is the average frequency of the kth conformation from 256 to 512 steps in the 25 MC runs. As shown in Fig. 1, entropy decreases with the increase in fitness. This indicates that the variety of global conformations becomes limited as the local configurations become restricted—hence, the emergence of a single dominant conformation. It goes without saying that the dominant conformation has the target configurations at the active sites. Even after the entropy decreases to a very low level, some minor conformations still exist due to the thermal fluctuation. These minor conformations differ from the dominant one only in a few sites. This result means that through successive selections only on the local configuration at the active sites, the random peptides become foldable globally into a conformation with function.

Figure 1.

The largest value of fitness H of 20 sequences in the pool (solid line), and entropy I (dotted line) are plotted as functions of generation. Data are averaged over 5 selection runs. T = 1.5 and T̃ = 0.1.

As fitness H increases, the conformation with the largest p_k value comes to have the lowest energy. Fig. 2 shows the energy distribution of conformations. At the initial stage of the evolutionary process, the distribution is Gaussian-like, and at the later stage, the low-energy tail of the distribution deviates from it. As the stability gap between the lowest energy state and the center of the distribution grows, the conformation with the lowest energy dominates the thermal motion of the peptide. The minor conformations with nonzero p_k values are situated at a bit higher energy levels than that of the dominant conformation. Hence, the selected sequence has a distinct energy minimum, a thermodynamic requirement for the fast folding process.

Figure 2.

The number of conformations W(E) is shown with the histogram as a function of energy E − E⁽⁰⁾ for an example of selection run, at the 0th generation (a) and at the 600th generation (b). W(E) peaks at E − E⁽⁰⁾ ≈ 0 and only the low-energy tail is shown. T = 1.5 and T̃ = 0.1.

The kinetic characteristics are illustrated by the MC folding trajectory of a selected sequence. The 25 MC trajectories starting from the various random conformations eventually converged around the vicinity of the dominant conformation with lowest energy within 256 MC steps (data not shown). Folding proceeds without significant traps in its course. Thus, the MC trajectories suggest the emergence of what could be called a folding funnel.

The distance between the dominant conformation and the others in the configurations at the active sites is defined as d(active sites) = 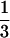∑_{i=a,b, and c} δ(S_i(n) − S_i^dominant), and that at the other sites is d(other sites) = 1/(N − 3) ∑_{i≠a,b, and c} δ(S_i(n) − S_i^dominant). Fig. 3 shows that the active sites attain the configuration of the dominant conformation faster than the other sites, which implies that the emergent funnel is not structureless but has inhomogeneous features. Such a structurally inhomogeneous funnel might be termed an anisotropic funnel.

Figure 3.

An example of the folding trajectory is drawn in the three-dimensional box. The x-, y-, and z-axes represent d(active sites), d(other sites), and energy. The trajectory is drawn with the real line when d(active sites) = 0 and with the broken line when d(active sites) ≠ 0. The arrows indicate the direction of the folding process. The initial structure is represented with ○. The trajectory reaches the lowest energy dominant conformation within 256 MC steps. The sequence used is the same as in Fig. 2b.

The anisotropic funnel should result from the inhomogeneity in the ruggedness of the landscape, hence, from the inhomogeneity in the frustration of interactions among the sites. In our model, two-body interactions are not frustrated when they have the form Ē_ij = − S_i^dominant S_j^dominant. Thus, the degree of frustration F_i at the ith site is estimated by the proportion of the energetically unfavored interactions of the ith site with other sites in the dominant conformation: F_i = 1/2(N − 1)∑_j|E_ij⁽²⁾ − Ē_ij|. 0 ≤ F_i ≤ 1. Values of F_i for the three active sites are 0, 0.133, and 0.133, and for the other 12 sites they are 0.067 ≤ F_i ≤ 0.333. These values indicate that the active sites, in general, are less frustrated than the other sites. The small frustration of the active sites indicates a smooth energy surface in their coordinates, which allows the active sites to attain the target configurations at a faster rate (Fig. 3).

Considering the sites other than the active ones, the shown inhomogeneity in the frustration (0.067 ∼ 0.333) suggests that some of these sites achieved the configuration of the dominant conformation faster than the others. For further investigation, the three sites with the smallest F_i values (0.067, 0.133, 0.133) are named coherent sites and those with the largest (0.333, 0.333, 0.333) are frustrated sites. On the basis of the F_i values, the coherent sites have less rugged surface on the energy landscape in their coordinates than the frustrated ones. The smooth surface of the coherent sites suggests that they can achieve the configurations of the dominant conformations in the folding process faster than the frustrated sites but slower if compared with the active ones. In fact, it is confirmed with the MC folding processes of the selected sequence that the coherent sites attain the configurations of the dominant conformation at a faster rate than the frustrated sites. Therefore, the inhomogeneity in the frustration among the sites clearly shows the existence of an anisotropic funnel on the energy landscape of the selected sequence.

Site dependence of the degree of participation in the ordering at the folding transition state was experimentally measured by the protein engineering technique (18), and it was shown that there are some specific residues that are most ordered in the transition state. These “hot spots” could be called a folding nucleus. It has to be noted, however, that folding nucleation should not be a distinct event from later growth, in contrast to the nucleation in the classical first-order transition of the macroscopic system (19). We here use the term “nucleation” to represent the strong tendency of certain residues to achieve the configuration faster than the other sites. A series of simulations were conducted by fixing any of the sites (active, coherent, or frustrated) in either dominant (correct) or wrong configurations while allowing other unfixed sites to move freely on the energy surface. As shown in Fig. 4a, when the three active sites are fixed at the right configurations, the other N − 3 sites of the selected peptide fold rapidly into the dominant conformation. However, when the active sites are fixed to the wrong configurations, the folding of the other sites does not complete within the observed time scale. The same results hold true for the coherent sites. In contrast, no matter in which configurations the three frustrated sites are fixed, the other N − 3 sites rapidly achieve the dominant configurations (Fig. 4b). These results indicate that the active and coherent sites must be oriented first in the correct configuration to allow the proper folding of other sites. Accordingly, the active and coherent sites are involved in the nucleation during the folding process.

Figure 4.

(a) Distance between the configuration of N − 3 sites other than the active sites and the configuration in the dominant conformation. Two MC trajectories are shown: the trajectory for the case that the active sites are fixed to the target configuration, S_a = S_b = S_c = 1 (dotted line) and the trajectory for the case that the active sites are fixed to the nontarget configuration, S_a = S_b = −1, S_c = 1 (solid line). (b) Distance between the configuration of N − 3 sites other than the frustrated sites and the dominant configuration. The trajectories are for the case that the frustrated sites are fixed to the correct configuration (dotted line) and to the wrong configuration (solid line). The sequence is the same as in Fig. 2b.

To know whether the above results are true with natural proteins, we can examine the configurations at the sites responsible for protein function during nucleation processes. Our results are consistent with Shakhnovich et al. (20), who proposed that the sites involved in the nucleation process were highly conservative because functional sites are usually conserved. In addition, we point out that besides the active sites, some sites, like the coherent sites in our model, may also be involved in the nucleation process. It should be noted that the involvement of the active site and coherent site in the nucleation process does not necessarily imply that the sites should be structurally fitted at the end of the folding process. Because it is the rate of folding that counts, structural fitness of the active and coherent sites may be left open for further adjustment in the course of evolution. Hence, it is important to look further into the relationship among three categories of residues: active sites, nucleation sites, and highly conserved sites in natural proteins.

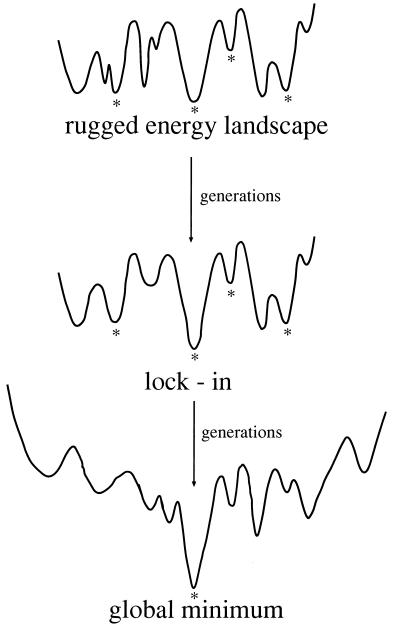
This study shows that the selected sequence has the distinct minimum and the anisotropic funnel on its energy landscape, which are the thermodynamic and kinetic requirements of a fast folder (7). Fig. 5 illustrates the evolutionary history of a random sequence becoming a fast folder. This shows that functional selection alone leads the sequence to have a distinct minimum and an anisotropic funnel on the energy landscape. The initial random sequence possessed a rugged energy landscape such that some functional conformations but also innumerable nonfunctional ones appear randomly in thermal motion. As the frequency of the functional conformations increases during the evolutionary process, there is always one functional global conformation that appears more frequently than the other functional ones. In fact, several series of the successive selections under the same condition result in different conformations with the same native configurations at active sites. In other words, it is the selection on the local configurations that locks in a global functional conformation. Further selections then increase the frequency of the selected conformation, which amounts to lowering of the energy level. Eventually, the selected conformation comes to be a distinct minimum on the energy landscape.

Figure 5.

A scenario of the emergence of the native conformation from a random peptide. A random peptide has some functional conformations designated by ∗ and innumerable nonfunctional ones. The selection on the local configurations at the active sites locks the lowest-energy conformation in one of the functional conformations. With the further selection on the active sites, the conformation grows into the distinctive minimum and the anisotropic funnel develops around it.

As the energy level of the selected conformation decreases, an anisotropic funnel on the energy landscape is created. The decrease in the energy level is mainly due to the stabilization of the configurations at the active sites. Therefore, the energy level of the selected conformation increases with the alteration of the configurations at the active sites more than those at the other sites. This means that the active sites have a smooth surface on the energy landscape. Because some sites, like the coherent sites in the model, contribute to the stability of the configurations at active sites, their energy landscape is also smoothed to some extent. Hence, the energy landscape evolves to have an anisotropic funnel for fast folding.

To distinguish the sequence with a slightly lower energy of the functional conformation in one generation, the thermal fluctuations must be of the same order as the change in the energy level of the functional conformation due to mutations. For too high temperatures, the conformational fluctuations are too large to discriminate any differences in the energy surface of the mutated sequences. With too low temperatures, the conformation tends to be trapped at one of many glassy minima in the folding process. Thus, the temperature T should be above the glass-transition temperature of the initial random sequences to evolve a functional sequence.

The preliminary analysis based on the random energy approximation shows that when T̃ is increased a discontinuous transition from the evolvable phase to the unevolvable phase takes place. Thus, the selection process also depends crucially on the carry-over rate of the mutated sequences.

Natural proteins are thought to have evolved in various ways, such as exon shuffling, gene duplication, selection, and their combination (21). The present study suggests that some proteins could have evolved from random polypeptides as far as Darwinian selection on function proceeded. In addition, our simulations show that a foldable sequence can easily emerge even from a small number of sequences. This indicates that there may be no exhaustive search in the sequence space during the evolution of some natural proteins, but instead, there is a step-by-step increase in the functional ability and so in the folding ability.

It has been shown that the molten globules of some proteins possess functional activities (22, 23). The DNA-binding subunit of a DNA methyltransferase has the characteristics of a molten globule but has the ability to bind DNA in a sequence-specific manner (22). An engineered dihydrofolate reductase possesses all the properties of a molten globule but binds its ligands in a specific way (23). These data indicate that the molten globules retain their active sites at the functional configurations even though most of the other sites take in the fluctuating or misfolded configurations. Therefore, the existence of the functional molten globules supports the evolutionary scenario presented in this paper that shows the strong tendency of the active site to fold into the functional configuration.

The spin-glass-like model presented in this study, therefore, shows that in addition to the uniqueness of the conformation, the distinct energy minimum, and an anisotropic funnel also emerge through the successive selections of sequences based on the local configurations at the active sites. This study brings a new insight into the origins of the thermodynamic and kinetic characteristics of proteins. Evolution of the model polymer chain is now being simulated by using the knowledge-based potential (24) to examine the validity of concepts introduced here. To go into details for the emergence of the shape and density of the globule, secondary structures, and so on, further studies are recommended.