Abstract
The bacterial chaperonin GroEL and the co-chaperonin GroES assist in the folding of a number of structurally unrelated substrate proteins (SPs). In the absence of chaperonins, SP folds by the kinetic partitioning mechanism (KPM) according to which a fraction of unfolded molecules reaches the native state directly while the remaining fraction gets trapped in a potentially aggregation-prone misfolded state. During the catalytic reaction cycle GroEL undergoes a series of allosteric transitions (T ↔ R → R″ → T), triggered by SP capture, ATP binding and hydrolysis, and GroES binding. We develop a general kinetic model that takes into account the coupling between the rates of the allosteric transitions and the folding and aggregation of the SP. Our model, in which the GroEL allosteric rates and SP-dependent folding and aggregation rates are independently varied without prior assumption, quantitatively fits the GroEL concentration-dependent data on the yield of native Rubisco as a function of time. The extracted kinetic parameters for the GroEL reaction cycle are consistent with the available values from independent experiments. In addition, we also obtain physically reasonable parameters for the kinetic steps in the reaction cycle that are difficult to measure. If experimental values for GroEL allosteric rates are used, the time-dependent changes in native state yield at eight different GroEL concentrations can be quantitatively fit using only three SP-dependent parameters. The model predicts that the differences in the efficiencies of GroEL, single ring mutant (SR1), and variants of SR1, in the rescue of mitochondrial malate dehydrogenase, citrate synthase, and Rubisco, are related to the large variations in the allosteric transition rates. We also show that GroE/S mutants that efficiently fold one SP at the expense of all others is due to a decrease in the rate of a key step in the reaction cycle which implies that wild-type GroEL has evolved as a compromise between generality and specificity. We predict that, under maximum loading conditions and saturating ATP-concentration, efficiency of GroEL (using parameters for Rubisco) depends predominantly on the rate of R → R″ transition while the equilibrium constant of the T ↔ R has only a small effect. Both under sub-and super-stoichiometric GroEL concentration enhanced efficiency is achieved by rapid turnover of the reaction cycle which is in accord with the predictions of the Iterative Annealing Mechanism. The effects are most dramatic at sub-stoichiometric conditions (most relevant for in vivo situations) when SP aggregation can out-compete capture of SP by chaperonins.
Introduction
Molecular chaperones are ATP-consuming machines that facilitate the folding of several structurally unrelated substrate proteins (SPs) [1, 2, 3, 4, 5]. The best studied, both structurally [6] and mechanistically, of such machines is the E. coli chaperonin GroEL and the co-chaperonin GroES [7, 8, 9]. GroEL consists of two heptameric rings that are stacked back to back. The coordinated interaction between the two rings in concert with SP and GroES binding and ATP hydrolysis allows for the GroEL machinery to rescue SPs that might otherwise aggregate. Although under maximal loading conditions (presence of SP, ATP and GroES), it is necessary to consider the dual role of both the rings, it is sufficient to use the single ring as the functional unit to describe the conceptual framework underpinning GroEL function [5, 10]. Comparison of the structures [11] in the states GroEL visits during the catalytic cycle of (Fig. 1) shows the spectacular conformational changes that it undergoes in response to the interactions with SP, GroES, and ATP binding and hydrolysis. It follows from Fig. 1 that in order to describe the workings of the GroEL-GroES machine it is important to account for the coupling between the complex allosteric transitions that the GroEL particle undergoes and the fate of the SP during the reaction cycle [4, 12, 13, 14, 15, 16]. Studies that artificially simplify the processes in the GroEL cycle (Fig. 1), such as using SPs that do not require GroES or mutants from which GroES does not dissociate on biologically relevant time scales, while insightful, cannot accurately represent the mechanism of rescue of stringent SPs under non-permissive conditions. Moreover, genetic experiments show that various constituents cannot substitute for GroEL in vivo which further attests to their limitations to serve as surrogate for the wild-type (WT) GroEL [17, 18].
Figure 1.
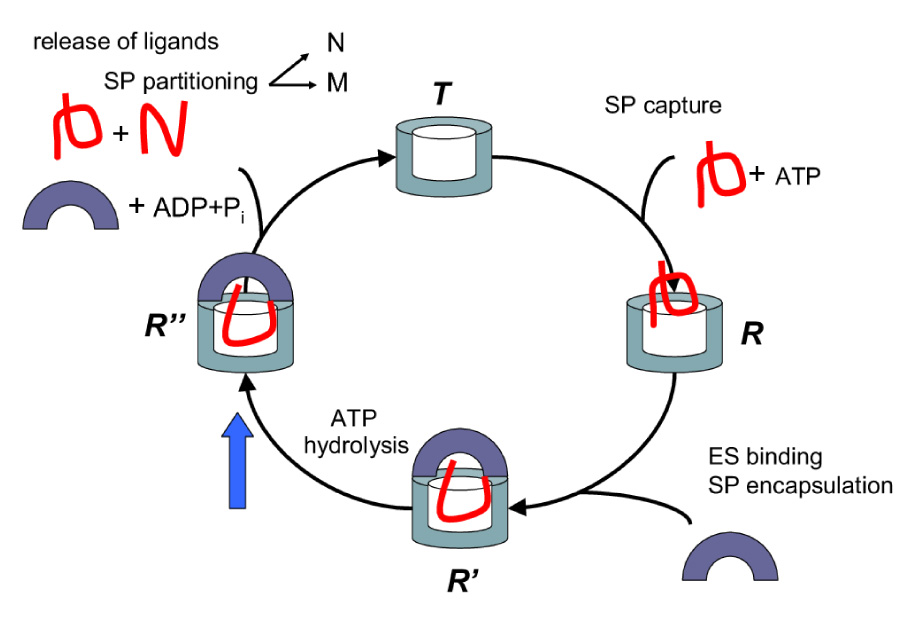
Schematic sketch of the catalytic cycle of GroEL. SP is captured by GroEL in the T state. Binding of ATP triggers the equilibrium T ↔ R transition. Subsequently, GroES binding encapsulates the SP (assuming it can fit into the expanded cavity) leading to the R → R′ transition. Hydrolysis of ATP results in the R′ → R″ transition. The volume of the cavity doubles from 85, 000Å3 in the T state to about 170, 000 Å3 in the R″ (and presumably in R′) state. Folding of SP in the largely hydrophilic cavity in R′ or R″ state can occur with some probability. Interring communication, shown by solid blue arrow, signals release of SP, ADP, and phosphate. Kinetic partitioning of SP, which is shown to occur for clarity in the bulk, could occur in the cell. In other words, folding to the native state or transition to the ensemble of misfolded structures can take place upon SP encapsulation.
Sometime ago, we developed the iterative annealing mechanism (IAM) to provide a quantitative description of the GroEL-assisted folding of SP [19, 5]. The IAM incorporates the consequences of the structural changes in GroEL during the T ↔ R → R″ transitions (Fig. 1), and results from biophysical studies, and theoretical description of monomeric folding. The IAM is based on the premise that GroEL plays an active role in SP folding. The large conformational changes that GroEL undergoes during the catalytic cycle and the experimental observations that, under operating conditions with an imposed load, the SP is ejected from the cavity [20, 21, 22], folded or not, with each round of ATP hydrolysis, attests to the active role of GroEL [21, 23]. It, therefore, follows that these large conformational changes enable the SP to fold under conditions in which spontaneous folding is unlikely. Even in the single ring SR1 mutant, from which GroES dissociates with a lifetime of about 300 min [24], the cavity volume has doubled as a result of GroES binding and ATP hydrolysis. In the process, the microenvironment that the SP feels changes as the GroEL T ↔ R → R″ transition takes place. A consequence of these observations is that, under conditions which place a load on the chaperonin machinery, GroEL is not merely a passive Anfinsen cage but participates actively as a stochastic machine that gives SPs multiple chances to fold by minimizing the possibility of aggregation [19, 20, 25].
The goal of this work is to provide a kinetic framework, that incorporates the coupling between allosteric transitions in GroEL and folding and aggregation of the SPs. Similar kinetic models have been successfully used to analyze experimental data on molecular motors [26, 27] that also undergo complex catalytic cycle in response to ATP binding and force. In order to derive the kinetic model, it is necessary to describe the various time scales whose interplay ultimately determines the efficiency of GroEL function. It is well established, both theoretically [28] and experimentally [29, 30], that in the absence of GroEL the SPs fold by the kinetic partitioning mechanism (KPM) [31]. According to KPM, a fraction of initially unfolded molecules reaches the native state rapidly while the remaining fraction collapses into a manifold of misfolded conformations. The rates of transitions from the kinetically trapped misfolded structures to the native state, that might require partial unfolding of compact structures, are relatively slow. The KPM predicts that the fraction of molecules that do not fold at time t is [28]:
| (1) |
where , kF is the folding rate for the molecules that reach the native basin of attraction (NBA) without being kinetically trapped, ki is the transition time from the ith misfolded conformation to the NBA. Typically, the rate of collapse from the unfolded state to the misfolded ensemble is relatively rapid compared to ki while ki/kF ≪ 1. In general, there may be an ensemble of misfolded structures. However, in practice only a few (one or two) can be experimentally resolved. Here, without loss of generality we will assume that escape from the collection of misfolded structures can be described by a single average rate, kS. Thus, Eq. (1) simplifies to
| (2) |
The KPM, which has also been used to describe RNA folding [31], has been experimentally validated [29, 30].
The first step in the reaction cycle (Fig. 1) is the capture of the misfolded SP by GroEL in the T state. In the second stage, ATP binds to the seven sites in the equatorial domain that triggers movements (localized largely in the apical and the intermediate domains) resulting in the transition to the R state. Recent NMR [32] and theoretical studies [33] show that the SP is disordered and more expanded upon interacting with GroEL than it is in the bulk which further reinforces the active role played by the chaperonins in the rescue of SPs. Two rates, kT−R and kR−T, describe the equilibrium of T → R transition [34, 35, 36]. In the third stage GroES binds. The first of the irreversible steps in the cycle upon GroES binding involves ATP hydrolysis that drives the allosteric transition from R → R″ at a rate kR−R″. Currently, the structure of the R′ (GroEL-(ATP)7-GroES) state is not known although it is suspected that it is similar to the R″ state. In addition, transition rates to or from R′ have not been measured. It is likely that the irreversible steps in the reaction cycle after GroES binds are too rapid to resolve the kR−R′ or kR′−R″ transitions. For these reasons we do not consider the R′ state, the inclusion of which would only increase the number of parameters without providing any increase in the accuracy of the predictions. The release of the SP (folded or not), inorganic phosphate, ADP and GroES requires signal from the lower (trans) ring (indicated by the blue arrow in Fig. 1) [6, 4, 37]. Subsequently, the R″ state relaxes back to the SP acceptor T state on a time scale kR″−T. Thus, events in a single GroEL cycle in concert with changes in SP is minimally described by a number of rates, namely, kF, {ki}, kT−R, kR−T, kR−R″. In the proposed kinetic model communication between rings, which occurs with negative cooperativity, is taken into account using the rate constant kR″−T (see the blue arrow in Fig. 1). Inclusion of SP aggregation and release of SP from GroEL brings additional rate constants into assisted folding (see below).
The reaction cycle in Fig. 1 shows that, even when inter-protein interactions between SPs are neglected, there are a number of distinct time scales that have to be taken into account for a quantitative description of assisted folding. Here, we propose a general kinetic model that accounts for the coupling between SP folding, GroEL allostery and a pathway leading to SP aggregation. The proposed kinetic model is used to analyze experimental data on chaperonin-assisted reconstitution of mitochondrial malate dehydrogenase (mtMDH), Citrate Synthase (CS) and the stringent substrate ribolate biphosphate carboxylase oxygenase (Rubisco). The excellent agreement between the kinetic model and experiments not only validates the kinetic model but also allows us to explore other scenarios for efficient GroEL function. Because of the presence of a large number of time scales that are needed to describe the kinetics of the reaction cycle (Fig. 1) several distinct scenarios for yield enhancement can emerge. We show that changes in the rate constants in the catalytic cycle, which depend on intrinsic folding properties of monomeric proteins, the concentrations of SPs, and the SP and ATP-dependent GroEL allosteric rates, can dramatically change the efficiency of the function of this remarkable machine. Finally, we show that optimization of yield of a particular protein at the expense of decrease in efficiency for other SPs can be achieved by tuning the kR−R″ rate (Fig. 1).
Results
Steady-state solutions of the kinetic equations
In order to reveal the interplay between the allosteric transition rates and SP folding in a transparent manner we first obtain analytical expressions for the concentrations of the folded SPs and aggregated species in the steady-state limit. The applicability of the results obtained in the steady-state limit depends on the actual time scales. The cell doubling time of E. coli, under minimal glucose conditions, is on the order of 30 min which is the most relevant biological timescale. The results obtained in the steady-state limit provide some insights into the more complex kinetic model. If the protein folding and chaperonin reaction rates are significantly faster than 30 min then the relatively simple approach is meaningful. Below we analyze the steady-state results for two specific situations.
Superstoichiometric Chaperonin Concentration
If the chaperonin concentration exceeds that of the SP, we can approximate [ELT] ≈ [EL0], and linearize the protein binding reaction (Eq.(11)) λB[ELT] ≈ λB[EL0] = kB. In this limit, the native states and the aggregates are produced at rates that are independent of the chaperonin allostery related timescales, . The steady-state rates of production of aggregates (υMA) and folded SPs (υN) are:
| (3) |
where we have assumed that nascent proteins are introduced to the cell at the rate υ0, and the parameter w is:
| (4) |
Spontaneous folding without chaperonins corresponds to w = 0.
The solutions have a few of properties that are useful to point out. First, the production rate of the native proteins depends strongly on the effective SP binding rate kB. For large kB (compared to λA), w (Eq. (4)) becomes large and υMA → 0, υN → υ0, according to Eq. (3) i.e. all proteins fold successfully. Thus, any mutation in the SP or GroEL that increases the binding rate would increase the native state yield. Second, mutations that directly affect the protein release rates without affecting the folding rate in the cavity (i.e. that would effect kN and kM by the same factor), would have no effect on the native state yield. In other words, the yield and aggregation depend on the ratio kM/kN, that is the partitioning of the ejected SPs only. Third, chaperonins cannot aid folding in the steady-state limit if folded proteins are not ejected from the cavity (w → 0 as kN → 0). Finally, chaperonin effectiveness can be enhanced by increasing the ratio kN/kM. In the limit, kN ≫ kM, w → kB and the effectiveness is determined solely by the binding rate.
Substoichiometric Chaperonin Concentration
The steady-state solutions for a low chaperonin concentration yield a lengthy expression for the reaction rates. However, if the second order aggregation reaction rate can be replaced with an effective first order rate kA ≈ λA[M], simple expressions for the production of native states and aggregates can be found. In these expressions, the allosteric timescales appear in the form:
| (5) |
One can show that the native state production rate increases as A decreases. It follows from Eq. (5), which is derived in Appendix A, that A can be decreased if the rates kT−R, kR−R″ increase or upon decrease of kR−T. Thus, when the concentration of GroEL is less than SP then faster turnaround of the allosteric cycle leads to a bigger yield as was predicted based on lattice simulations and the IAM. Because of the paucity of the number of GroEL/S particles in E. coli, it is likely that the substoichiometric condition is most appropriate for in vivo situation. In this situation, even the steady-state solutions, clearly show that rapid GroEL turnover leads to yield enhancement of the folded SP. Thus, in general, speeding up of the kT−R and kR−R″ should lead to increased efficiency (measured by the amount of native SP yield in a given time) of chaperonins. These predictions are borne out by solving the time-dependent kinetic equations (see Methods).
The allosteric kinetic model accounts for [EL]-dependent folding kinetics of Rubisco
Although the steady-state solutions give insights into the variables in the reaction cycle that control the native state yield, it is necessary to solve the coupled kinetic equations in order to compare the predictions with experiments. To explore the full effect of GroEL dynamics, from now on, we use the coupled time-dependent equations (Eq. (12)). In vitro experiments can be used to measure the time-dependent yield of the native state of SPs as a function of GroEL, GroES and ATP concentrations. In order to validate the kinetic model, we first analyze the measured yield of Rubisco as a function of time at various GroEL concentrations. In the process, we extract kinetic rates in the reaction cycle that are very difficult to measure.
Since the differential equations (see Methods) cannot be solved analytically, we integrate the kinetic equations (Eq. (12)) numerically. The model is used to extract parameters using experimental data on Rubisco [19], whose folding was probed at various GroEL concentrations under non-permissive conditions. It is, however, important to keep in mind that variations in the experimental conditions such the temperature or the concentrations of cochaperonins, nucleotides, cations could affect the specific rates significantly. Other SPs will have different intrinsic folding timescales and can also affect the GroEL allosteric rates (see below). Nevertheless, many of the qualitative results obtained here also provide predictions or illustrations of trends and dependencies of the GroEL efficiency on allosteric transitions or spontaneous folding rates of SP.
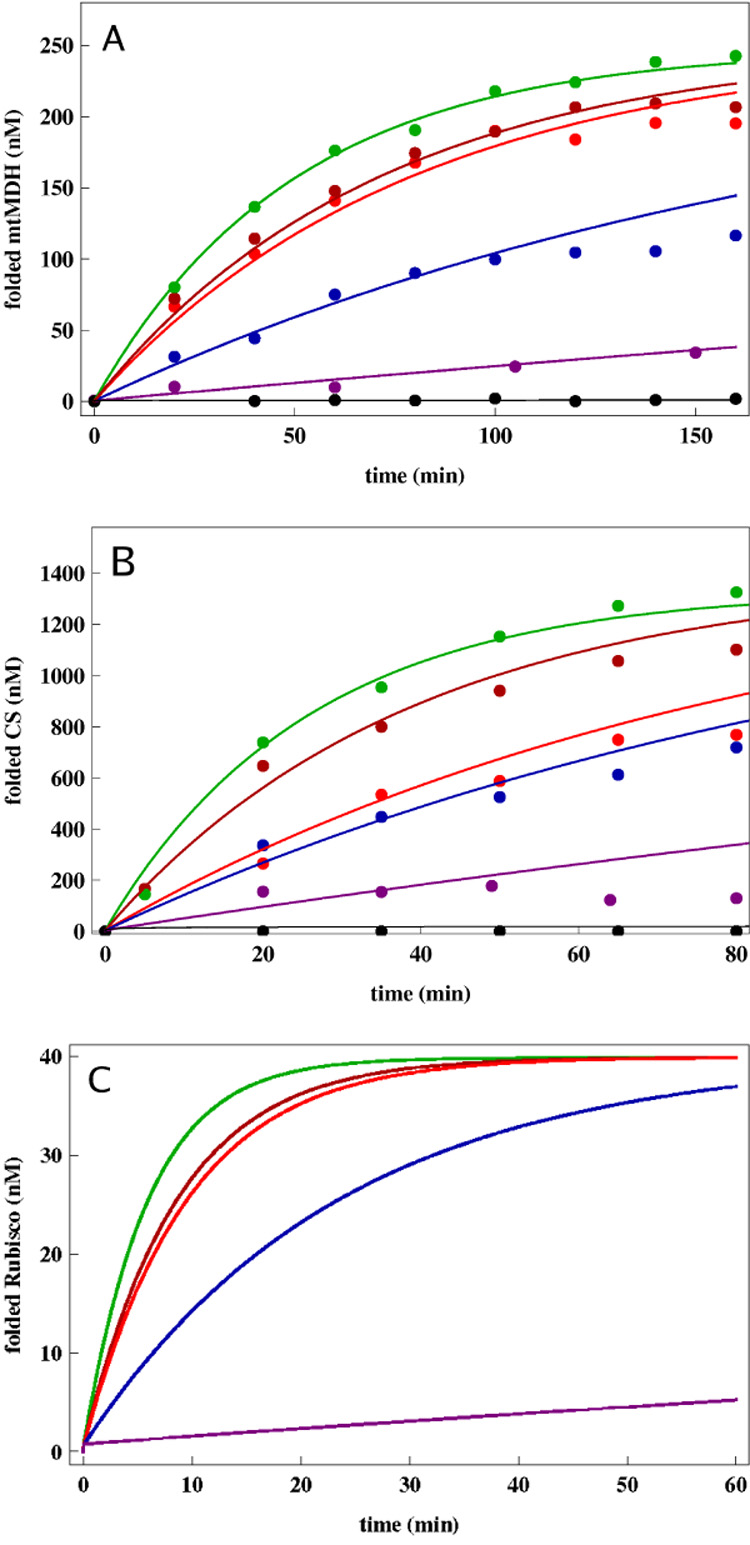
The data at eight values of GroEL concentration in Figure 5 of Ref. [19] allows us to demonstrate that our model can reproduce the observed time-dependent yield of the native state of Rubisco and its dependence on the concentration of GroEL. In the process, we can extract the nine kinetic parameters (Eq. (12). Fortunately, the number of measurements reported in [19] is large enough that an unbiased fit to the equations can be carried out. In the first test of Eq. (12) we varied, without prejudice, the nine parameters to fit all eight curves at different [EL] concentrations. Further tests of the robustness of our model are described below. In assessing the validity of the model, it is not only important to check the quality of the fits but also ensure that the values of the parameters are physically reasonable. Our kinetic model fits the experimental data extremely well (Fig. 2). We should emphasize that all the data points were globally fit using only one set of parameters, describing the kinetic reaction cycle of GroEL and intrinsic Rubisco rates. By fitting the experimental data using our kinetic model we obtain physically reasonable reaction rates for Rubisco (see Table 1). The intrinsic time scales associated with Rubisco are in accord with theoretical expectations. For example, the time scale for the fast process is in the range of time expected for a 491-residue protein [38]. The value kS is consistent with measurements that monitored spontaneous folding of Rubisco in the presence of chloride ion [39]. The ratio, kF/kS ≈ 104 ≫ 1, is in accord with the predictions of KPM. Recall that kS is an average rate for the transition from the ensemble of misfolded structures to the native state. It is likely a small fraction of misfolded states can fold more rapidly i.e., 1 ≪ kF/kS < 10 4. The requirement that, under experimental conditions, Rubisco folding requires the chaperonin machinery implies that the aggregation must compete with transition from misfolded structures especially considering that the partitioning factor Φ = 0.02 is small. Indeed, the pseudo first order process for aggregation kA ≈ λA[SP] > kS when [SP]0 ≈ 40nM as in the experiments [19]. Efficient function of GroEL also requires that the binary rate constant for [ELSP] formation must exceed the low order aggregation rate. Our fits show that λB = 0.6nM−1min−1 ≫ λA, and hence GroEL can effectively rescue stringent substrates.
Figure 5.
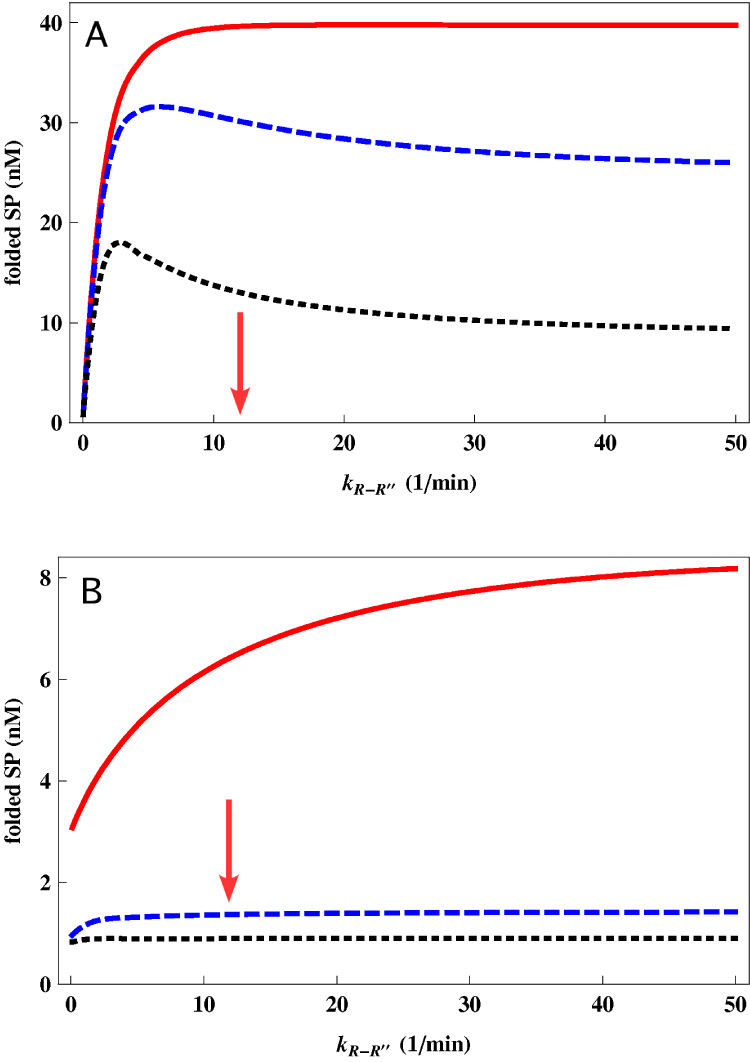
Prediction of the effect of kR−R″ on the yield of folded SPs over cell doubling time (30 min). (A): Red line, obtained using Eq. (12) and Eq. (8) is for the expected yield of Rubisco as kR−R″ is varied. All other parameters are taken from Table 1. Dashed blue curve shows yield for a protein whose aggregation rate λA = 0.1nM−1min−1 which is hundred fold greater than Rubisco. Dotted black curve shows yield for a protein whose aggregation rate λA = 1nM−1min−1 which is a thousand times that of Rubisco. The concentration of chaperonin [EL0] = 100nM which exceeds the initially unfolded concentration of SP (40nM). (B): Same as (A) except [EL0] = 1nM. In this case, even rapid cycling does not significantly yield of a rapidly aggregating protein. Yet, the paucity of chaperonins makes it best to increase the cycling rate. The arrows give the value of kR−R″ for WT GroEL (see Table 1).
Figure 2.
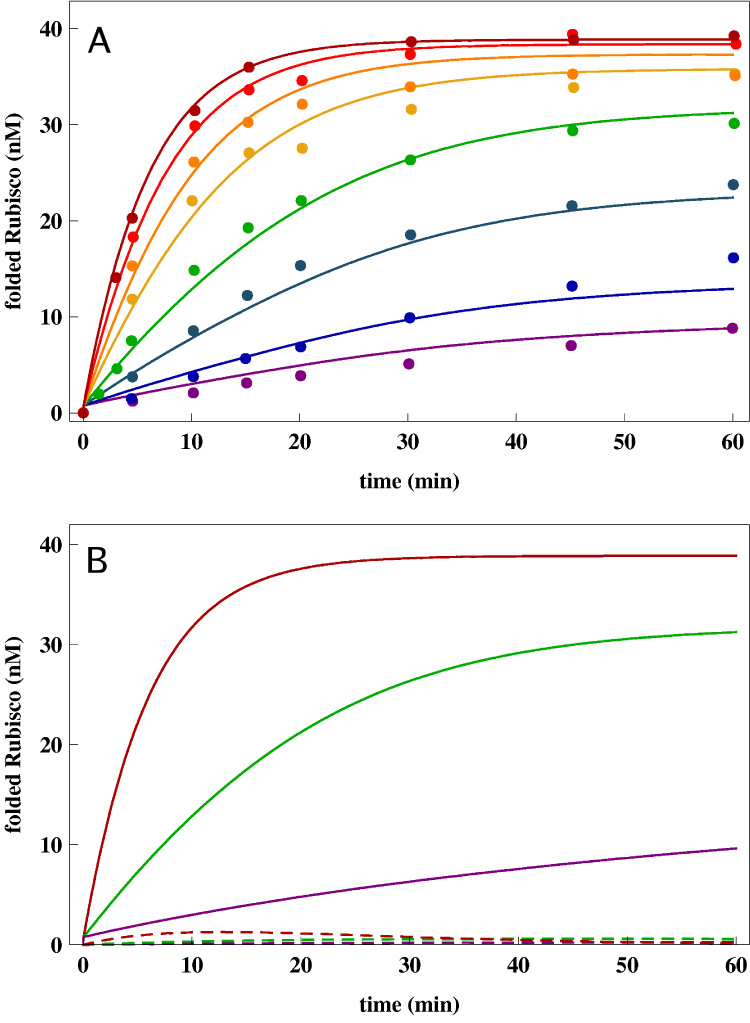
(A) Native state yield of Rubisco as a function of time at different chaperonin concentrations. The points are experimental data from Ref. [19]. The lines are the fits to the data using the kinetic model. The set of parameters that provides a global fit to all eight data set is given in Table 1. The initial concentration of Rubisco is 40nM. The chaperonin concentrations for the curves from bottom to top are: EL0 = 1nM, EL0 = 2nM, EL0 = 5nM, EL0 = 10nM, EL0 = 20nM, EL0 = 30nM, EL0 = 50nM, EL0 = 100nM corresponding exactly to Ref. [19]. (B) Results of sensitivity analysis of the kinetic model (Eq. (12)) using Rubisco parameters (Appendix B). The time-dependent native state yield [N](t), solid curves, for three chaperonin concentrations, EL0 = 1nM, EL0 = 10nM, EL0 = 100nM, is compared to the robustness measure Δ[N](t), dashed curves (Eq. (23)). The small values of δ[N](t)/[N](t) for all t and at various [EL] concentrations suggest that the allosteric model is robust to changes in the kinetic parameters around the values that provide the best fit in (A).
Table 1.
Folding and aggregation rates of Rubisco and allosteric transition rates of GroEL.a
| kF(min−1) b | 100 |
| kS(min−1) | 0.003 |
| Φ | 0.02 |
| λA(nM−1min−1) c | 0.001 |
| λB(nM−1min−1) d | 0.6 |
| kR−R″(min−1) | 12 |
| kT−R(min−1) | 5000 |
| kR−T(min−1) | 1 |
| kR″−T(min−1) | 60 |
| Φ e | 0.02 |
| χ f | 0.37 |
The theoretical fits and experimental data are compared in Fig. 2.
kF, kS are Φ are defined in Eq. (2).
The extracted aggregation rate.
Parameters that characterize the reaction cycle (Fig. 1).
Probability of folding to the native state with .
where M is the number of experimental data points.
Extracted kinetic parameters are in accord with experiments
We further calibrate our model by comparing the extracted parameters for GroEL allostery with rates that have been obtained by independent measurements. In particular, the transition R → R″ is believed to be the rate-limiting step in the GroEL allosteric cycle. Our fits yield kR−R″ = 12min−1 (Table 1) or which is consistent with the GroE hemicycle time. The load-dependent GroEL allosteric cycle time τ1 is usually estimated to be ∼ 10–15s [40]. The value of τ1 can be as small as 6 seconds depending on the nature if ligand that is bound to the trans ring (J. Gresham, J. Grason, and G. H. Lorimer, unpublished data). The chaperonin binding rate has been measured to be in the range λB ≈ 107 – 108 M−1 s−1 [9]. The binding constant λB = 107 s−1 M−1 obtained from our fits (Table 1) falls within this range. The TT ↔ TR transitions have been characterized extensively by Yifrach and Horovitz [41] who found that, for various GroEL mutants, kT−R ∼ 2000 – 9000min−1. The value of kT−R = 5000min−1 (Table 1) is consistent with their measurements. We also find that kR−T ≪ kR−R″ to favor the forward reaction from the R state in the presence of ATP and GroES. Incidentally, our fits are not sensitive to the precise values of kR−T and kT−R as long as they remain non-rate-limiting in the reaction cycle. The final ejection of ligands is associated with the release of SP (folded or not), ADP, inorganic phosphate, and the transition from R″ back to the T state. We found that this transition timescale is on the order of 1s which is in accord with expectations [40].
Independent estimate of Φ agrees with fits to experimental data
According to the IAM, in the limit , the native state yield in the case of super-stoichiometric chaperonin concentration can be approximated as:
| (6) |
where n = t/τ1 is the number of GroEL cycles within the time t. Alternatively, the yield of the GroEL-assisted folding of the native SP can be fit using an exponential function, and thus is characterized by an effective folding timescale τE. Thus, in this limit, the kinetic partitioning Φ can be estimated using:
| (7) |
For the data in Fig. 2 at the highest chaperonin concentration, we found τE = 6.3min. The independent estimate of Φ = 0.02 is consistent with our fitted value. We should stress that the quality of our fits may not change as long as Φ < 0.05 which was the value reported in our earlier study [19].
Coupling to GroEL allostery is required for accurate predictions of Rubisco yield
We should point out that kinetic schemes that completely ignore the GroEL reaction cycle can also be constructed to fit the experimental data on Rubisco (see Methods). The solutions to such a simple kinetic scheme does not provide as good fits to the data as in Fig. 2, and lead to unphysical values of the scales. More importantly, Eq. (14) and even simpler conceivable schemes cannot account for dramatic efficiency using GroEL mutants that clearly affect the allosteric transition rates [41, 17].
Average rate kS describes transitions for the misfolded state ensemble to the native state
The KPM predicts that there ought to be an ensemble of misfolded conformations so that escape from these kinetic traps should be specified by a collection of rates {ki} (Eq. (1)). In deriving the kinetic model, we replaced those by an average rate (Eq. (1) and Eq (2)). Mathematically, including separate misfolded species as in Eq. (1), only complicates the solutions (the summation over discrete misfolded species have to be explicitly taken into account) without adding any new insight. More importantly, bulk experiments cannot resolve these states. Here, we further justify using an average kS for the misfolded ensemble using experimental data on Rubisco [19]. Figure 4 in Ref. [19] shows the time-dependent Rubisco folding yields after the addition of GroEL at t = 0, and after a delay of 15 minutes and 30 minutes. Each data set can be fit using a single exponential, giving an effective folding timescale (data not shown). Since the effective timescale does not vary significantly between the sets, we can conclude that the population of GroEL-binding misfolded species does not change over time and our assumption that we can use an average kS for the misfolded states ensemble, while approximate, is fully justified.
Figure 4.
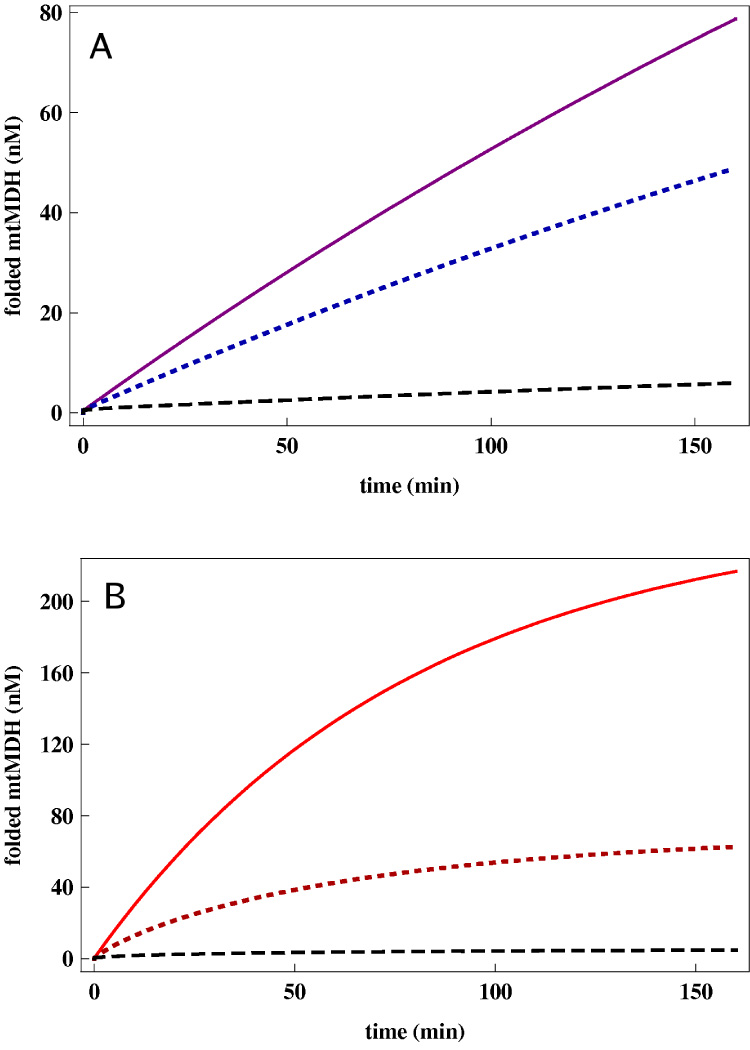
(A):Theoretical predictions for the expected yield of mtMDH at various concentrations of SR1. The concentrations of SR1 are 1500nM (solid purple line), 150nM (dotted blue line), and 15nM (dashed black line) where the initial unfolded mtMDH concentration is 300nM. The allosteric transition rates for SR1 are obtained from the theoretical fits in Fig. 3A. (B): Same as (A) except the expected yield of mtMDH at various concentrations of SR1 mutant SR-A399T, instead of SR1. (The solid red line corresponds to 1500nM SR-A399T, dotted red to 150nM of SR-A399T and dashed back to 15nM of SR-A399T.) The predictions are based on the predicted allosteric transition rate kR″−T = 11min−1, obtained from fits to Fig. 3A.
Assessing the robustness of the kinetic scheme
The complexity of the reaction cycle (Fig. 1) and the intrinsic folding rates of the SP require minimally nine parameters (see Methods). If some of the parameters are constrained to known experimental values then the number of parameters required to analyze the Rubisco data can be reduced. We reanalyzed the experimental data for assisted Rubisco folding by using known values of the allosteric rates (kT−R, kR−T, kR−R″ and kR″−T) in the GroEL reaction cycle. In particular, we fixed the values of the ATP-dependent rates kR−T and kT−R, kR−R″ and kR″−T at values in the middle of the experimental range. The partition factor, Φ, which can be independently determined from experimental data was set to 0.02. With these values fixed, there are only four Rubisco-dependent parameters, namely, kS, kF, λA, and the binding rate, λB. The best fit obtained by varying these parameters is indistinguishable from the results shown in Fig. 2 (data not shown). The consistency between the results obtained using the full kinetic model in which all parameters are varied to obtain the best fit and the ones obtained by constraining the allosteric rates and Φ to experimental values gives additional credence to the proposed kinetic model. It should be emphasized that the proposed kinetic scheme is a general minimal model that can not only be used to analyze available data but also is useful in predicting experimental outcomes especially in situations where GroEL concentration is less than SP (see below).
We also performed sensitivity analysis (see Appendix B for details) to identify the kinetic parameters that most strongly influence the time-dependent changes in the native state yield, and assess their effect on the yield curves in Fig. 2. The changes in the native state yield to variations in the kinetic parameters around the optimum values (those that produce the fits shown in Fig. 2) depend on GroEL concentration. For all values of [EL]0/[SP]0, the values of δ[N]/δkα (α = R − T,T − R,R − R″, or R″−T) are relatively small. The largest value, over the time course (0 < t < 60min) corresponds to δ[N]/δkR−R″ which lies in the range (0 < |δ[N]/δkR−R″| < 0.8) nM min. Thus, the native state yield is nonsensitive to small changes in the allosteric rates. The derivatives, δ[N]/δkα are larger for SP-dependent parameters, especially for the binary aggregation rate λA. However, the cumulative effect on the time-dependent changes in the native state yield is very small (Fig. 2B). We have calculated the time-dependent changes in the native state yield Δ[N](t) (see Eq. (23) in Appendix B) due to variations in the kinetic parameters for three values of [EL]. At all values of [EL], Δ[N](t)/[N](t) ≪ 1 for all t. Both the sensitivity analysis and the ability to reproduce the experimental results with merely four parameters for a large data set by using measured allosteric rates in the reaction cycle attest to the robustness of the kinetic model.
Single ring mutant (SR1) can reconstitute Rubisco with decreased efficiency
The single-ring mutant of GroEL, called SR1, has been used as a surrogate to probe assisted folding [24, 42, 18]. The inability to discharge the ligands implies that in the GroEL allosteric cycle inter-ring negative cooperativity is suppressed. The allosteric cycle of SR1 is similar to that of GroEL. Just like GroEL, SR1 can bind SPs and GroES in the presence of ATP and undergo the structural changes shown in Fig. 1. Yet, without the trans ring, and hence a signal from it, SR1 is missing a ”timer” and cannot readily discharge the ligands. Several studies have shown that when SR1 [24, 42] and SR1 mutants [18] are present in excess of SP they can aid in the folding of stringent substrates. However, the efficiency of SR1 is greatly compromised [18]. Nevertheless, SR1 and other mutants of SR1 have been useful in providing insights into the role confinement effects play in the SP folding as a result of the expanded cavity in the R″ state. Our theoretical model can be used to explore folding in SR1 and assess the extent to which yield enhancement occurs when the SP is sequestered in the central cavity for a long time. It should be borne in mind that even in SR1 the microenvironment of SP is altered from hydrophobic to hydrophilic as a consequence of allosteric transitions from T → R → R″. In terms of IAM cycling in SR1 corresponds to n = 1, and kR″−T ≈ 0 (Fig. 1).
In terms of the kinetic model, the SR1 mutant undergoes the complete allosteric cycle (Eq. (11)) but the R″ → T transition, characterised by kR″−T has been prolonged to approximately 300 min [24]. Thus, during the transitions from R → R″ → T, the SP is encapsulated within GroEL cavity where it can fold in the restricted space [42]. Rates of SP folding in a hydrophilic cavity are typically greater than in the bulk [43, 44, 45] assuming that the interaction between SP and the walls of cavity is repulsive. Even in the most favorable case the confinement-induced folding rate remains within an order of magnitude of the bulk rates. Because these changes are much smaller than the lifetime of the SR1 mutant we assume that folding inside the cavity is not very different from folding in the exterior, except that aggregation is suppressed. The consequence of changes in SP folding in confined space is explored later. With this assumption, after time , we find that the fraction of misfolded and folded concentrations are:
| (8) |
We have used the notation to emphasize that the interior (in the cavity) and bulk rates may differ. We have also assumed that SP folding inside the cavity follows the kinetic partitioning mechanism.
In almost all cases, 300 min is sufficient for SPs to fold inside the cavity and thus mostly folded SPs would be ejected from it. For instance, for Rubisco, even under the assumption that there is no effect of confinement in the hydrophilic cavity (), 300 min is sufficient for 61% of the SPs to fold using the parameters in Table 1. A modest enhancement of the slow folding timescale upon confinement would increase the partitioning to the folded states even more. Thus, our kinetic model predicts that SPs can fold in the central cavity as in the SR1 mutant. However, from Eq. (8) it follows that even in this case the yield of the folded states depends not only on the intrinsic folding characteristics of the SP (kF, kS and Φ and their values upon encapsulation) but also on kR−R″ i.e., SP folding and GroEL allostery are coupled. More importantly, the efficiency of SR1 in producing Rubisco in the native state, even after 300 min ∼ 10 times the cell doubling time, is far less than for the WT GroEL. Efficiency of SR1 mutants is linked to decrease in kR″−T (see below).
Efficiency of SR1 and its variants in folding mtMDH and CS depends on intrinsic GroEL allosteric rates
In the quest to find single ring constructs that can substitute for GroEL in vivo Lund and coworkers used genetic experiments to screen for SR1 mutants from which GroES can disassociate [18]. Two of the three SR1 mutants, namely SR-D115N and SR-A399T, were judged to be nearly as efficient as GroEL [18] in that they facilitated folding of mtMDH and citrate synthase (CS) almost as well as GroEL. They could also function well in vivo at 37°C. The third one, SR-T522I, while considerably more efficient than SR1, was unable to sustain growth of E. coli. The experiments were performed under non-permissive conditions so that spontaneous folding of mtMDH and CS was negligible (see Fig. 5 and Fig. 6 in Ref [18]). The time-dependent changes in the activity of mtMDH, which presumably mirrors the yield of the folded state, in the presence of GroEL, SR1, SR-D115N, SR-A399T and SR-T522I were reported in Fig. 5 of Ref. [18].
Figure 6.
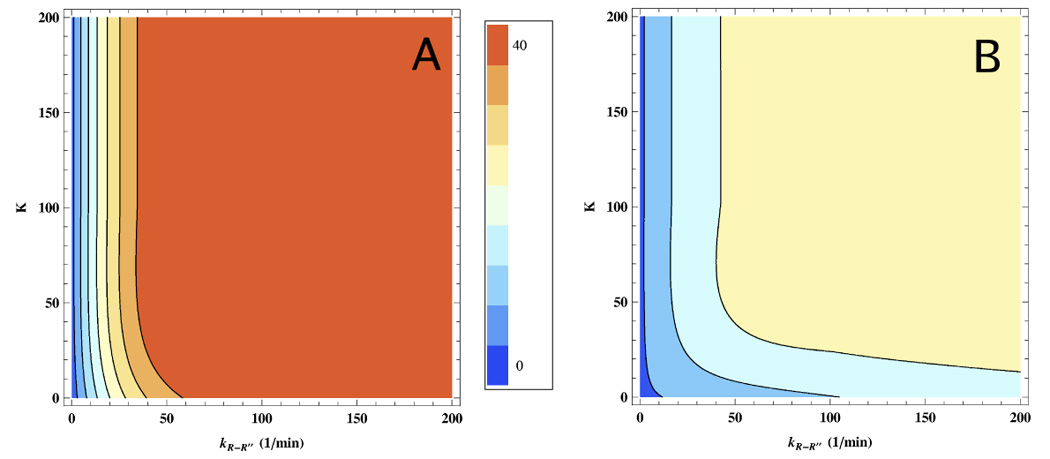
Theoretical predictions on yield of the native SP for Rubisco. (A) The extent of SP folding as a function of the equilibrium constant K in the T ↔ R and kR−R″ are varied. The GroEL concentration is 100nM. (B) Same as (A) except the concentration of GroEL is lowered to 2nM. In both (A) and (B) the GroEL parameters, expect those that are varied, are taken from Table 1. The scale reporting the yield of folded Rubisco, whose initial unfolded concentration is 40nM, is given in the middle.
mtMDH
We fitted the experimental data using our kinetic model, with the same GroEL parameters (varying only kR″−T for different mutants, see below) as we obtained in the analysis of Rubisco (Table 1) and treating mtMDH folding within the single ring cavity using Eq. (8). In particular, we analyzed Fig. 5 of Ref. [18] data in two steps. First, we used the data of spontaneous folding and GroEL assisted folding from the figure to determine the intrinsic rates of mtMDH folding. While GroEL allosteric rates are dependent on the SP and on the specific experimental conditions, we used the rates λB, kR−R″, kT−R, kR−T, kR″−T from Table 1 for the WT GroEL. Thus, for mtMDH the intrinsic folding rates are: kF = 100min−1, kS = 0.0012min−1, Φ = 0.002, λA = 0.021nM−1min−1. Consistent with those rates, the values for kN and and for GroEL are: and kR″−T = 60min−1. For SR1, we used the same λB, kR−R″, kT−R, kR−T, however, . The corresponding data and curves are shown in in Fig. 3.
Figure 3.
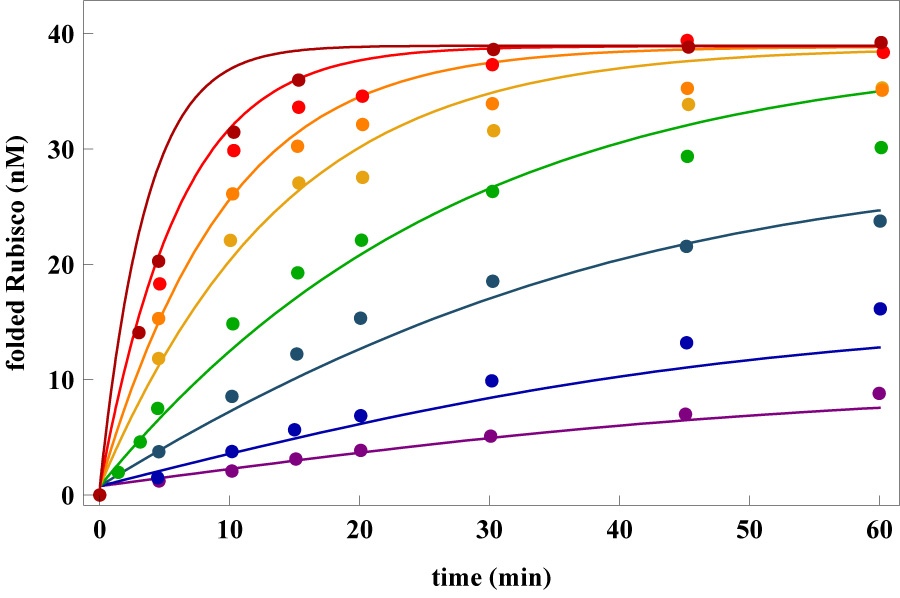
Yield of SPs as a function of time. (A) The points are taken from the experimental measurements [18] for folding mitochondrial malate dehydrogenase (mtMDH). The lines are fits to the data using the kinetic model. Black line is for spontaneous folding. Assisted folding in the presence of GroES and SR1 (purple), SR-T522I (blue) and SR-A399T (red) and SR-D115N (dark red) were used to assess the efficiencies of these three single ring chaperonins relative to GroEL (green). (B) The same as (A) except the folding of CS instead of mtMDH is analyzed. The only GroEL allosteric rate that is varied in obtaining the results in (A) and (B) is kR″−T while all others are taken from Table 1. (C) Predictions for the time-dependent yield of Rubisco for GroEL (green) and the single-ring mutants SR-T522I (blue), SR-A399T (red), SR-D115N (dark red), and SR1 (purple) based on chaperonin allosteric rates. The values of kR″−T were taken by analyzing the mtMDH data in (A). In (A) and (B) superstoichiometric concentrations of chaperonins were used.
Second, we fitted the yield data for mtMDH for the three SR1 mutants (SR-D115N, SR-A399T and SR-T522I), using only one free parameter each, namely, the R″ → T transition rate, kR″−T which reflects the kinetic efficiency of inter-ring communication. For the mutant SR-T522I the fits yielded kR″−T = 2.5min−1, for SR-A399T kR″−T = 11min−1, and for SR-D115N kR″−T = 14min−1. The fits are shown in Fig. 3. While it is likely that other SR1 kinetic rates were also altered as a result of these mutations, we chose the kR″−T transition rate because it is most closely related to the GroES dissociation rate (Ref [18], Table 5). The GroES Kd measurements for these mutants (Table 5 of Ref [18]) indicate an increased dissociation rate for the mutants compared to SR1. Larger GroES dissociation rate would correspond to speeding up of the R″ → T transition rate compared to SR1. Thus, our kinetic model, with physically reasonable parameters, accounts for folding in number of single ring mutants of GroEL. Increased efficiency of GroEL, SR1 mutants and SR1 correlate with decreasing values of kR″−T, i.e. the values of kR″−T can be arranged in the order as GroEL > SR-D115N > SR-A399T > SR-T522I > SR1.
CS
Lund et al also report the efficiency of the same GroEL mutants (SR-D115N, SR-A399T and SR-T522I) in assisted folding of CS (see Figure 6 in Ref. [18]). We analyzed the CS data using exactly the same procedure described for mtMDH. As before, for kR−T, kT−R, kR−R″, kR″−T and the binding rate, λB we use the values from Table 1. We fitted the GroEL-assisted and spontaneous folding data and obtained the CS intrinsic folding rates (kS = 0.01min−1, kF = 100min−1, Φ = 0.003 and λA = 0.01nM−1min−1). We then fitted the dataset for each mutant by varying only one reaction rate, kR″−T. For CS, the effective rates associated with the transition from R″ to the T state were: 10min−1 for SR-D115N, 0.8min−1 for SR-A399T, and 0.1min−1 for SR-T522I. For SR1, we used as before. The fits are shown in Fig. 3B. While the precise values of the allosteric rate constant depend on the SP, the trends in kR″−T using mtMDH and CS, namely GroEL > SR-D115N > SR-A399T > SR-T522I > SR1, are the same.
The experiments with SR1 are generally performed with highly superstoichiometric chaperonin concentrations. Figs. 4 are plots of predicted mtMDH yields with super- and sub-stoichiometric concentrations of SR1 (Fig. 4A) and SR-A399T (Fig. 4B).When present in excess molar concentrations ([EL]0/[SP]0 > 1), SR1 and SR-A399T can prevent aggregation as they isolate misfolded SPs (data not shown). However, experiments [18] and the theoretical analysis here show that fast cycling rates are required for efficient chaperonin-aided SP folding, especially in in vivo situations where typically [EL]0/[SP]0 < 1.
SR1 is least efficient in the folding of Rubisco
Normalized activity of Rubisco in the presence of SR1 has been previously reported [42]. However, to our knowledge, time-dependent increases in the absolute yield (or activity) for SR1-assisted folding of Rubisco does not exist in the literature. Using the allosteric transition rates for SR1, SR1 mutants (SR-D115N, SR-A399T and SR-T522I) we can predict the trend in the yield as a function of time for single-ring assisted folding of Rubisco using the kinetic model. With the initial concentration of 100 nM for the chaperonins and 40 nM for unfolded Rubisco we find that SR1 is the least efficient in folding this stringent SP (Fig. 3C). Numerically, we used the kR″−T rates from mtMDH data its. Just as with refolding mtMDH and CS, the SR-D115N can lead to yields that are similar to that obtained using GroEL. The yield of folded Rubisco at long times, in the presence of SR-A399T is somewhat less than that obtained using GroEL or SR-D115N. These predictions also reinforce that ease and frequent discharge of the SP from the central cavity is the most efficient way of enhancing chaperonin-assisted yield in finite (less than cell doubling) time.
Rate of kR−R″ of substrate-optimized chaperonin is greater than wild-type GroEL
It is well established that the WT GroEL machinery can assist in the folding of a variety of proteins that do not share sequence or structural similarity. The ability of GroEL to function as a general chaperone for a range of substrates might render it inefficient for a given SP. To probe the basis of the conflict between the generality and specificity for selected SPs, Weissman and coworkers [17] performed rounds of in vivo and in vitro directed evolution to identify GroEL/S mutants that can reconstitute a particular SP, namely green fluorescent protein (GFP) more efficiently than WT GroEL (see Fig. 2B of Ref. [17]). However, the enhanced efficiency of GFP comes at the expense of GroE3−1 (the mutant that refolds GFP more efficiently than WT) not being able to fold other natural GroEL SPs as well. It was argued that efficient folding of GFP by GroE3−1 is related to changes in the ATPase activity in GroE3−1 compared to the WT and enhanced hydrophilic character of the GroE3−1 cavity [17]. Thus, mutation-induced alterations in the kinetics of the GroEL reaction cycle can be used to increase the yield for a particular SP at the expense of others. The specific residues that were altered in the directed evolution experiments resulting in GroE3−1 were located in the equatorial (D490G) and intermediate (A163V) domains near a hinge region that is critical to the chaperonin allosteric transitions. The accompanying cochaperonin, GroES-Y71H, had a single mutated residue that putatively changed the polarity of the chaperonin cavity.
While it is difficult to ascertain the specific allosteric kinetic rates in the reaction cycle and the extent to which they were altered in GroE3−1, our model can explain how changes in the rates may affect the folding efficiency of a specific SP in a positive way while hindering the folding of others. For instance, based on the location of the GroEL mutated residues in GroE3−1, we propose that the allosteric transitions determining rates, kR−R″ in particular, is altered. In addition, we can presume that the associated mutation in GroES changed the folding rates and/or the kinetic partitioning of GFP inside the cavity. With the assumption that kR−R″ is altered in the GroE3−1 chaperonin we can explore, using the kinetic model, whether optimal value of the rate for one SP (say GFP) compromises efficiency for others. Thus, a given SP (kF and kS are fixed) chaperonin efficiency is determined by kR−R″ and λA (binary aggregation rate) assuming that all other parameters do not change dramatically with GroE3−1. Optimum value of kR−R″ should arise only if the SP, under the experimental conditions, is aggregation prone (see below).
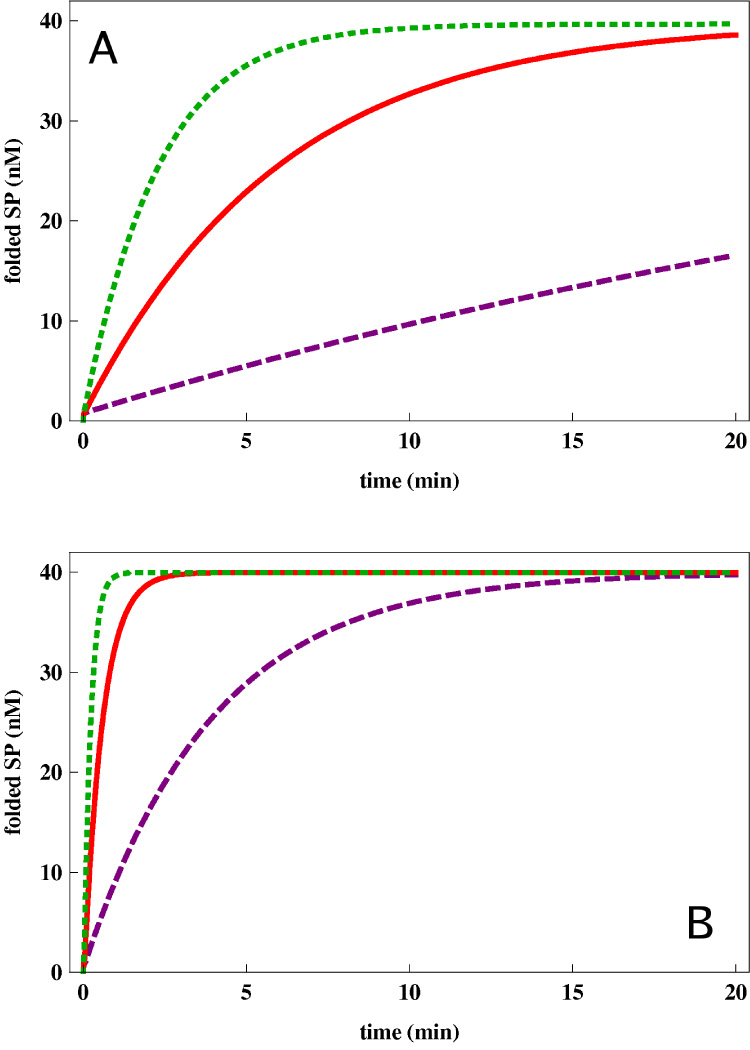
Typically, enhancement in kR−R″ increases the yield of folded SPs. Solid red line in Fig. 5 is an example of the dependence of the native state yield after 30 min for a SP (we used the Rubisco parameters in Table 1) using superstoichiometric chaperonin concentration (100 nM of GroEL and 40 nM of Rubisco). From this result we surmise that optimizing the efficiency of the chaperonin cannot be achieved unless λA (or other rates) are also changed. For instance, the dashed curve in Fig. 5 shows the dependence on the native state yield (also at 30 min) on kR−R″ for a highly aggregation prone protein (we used λA = 0.1nM−1min−1) with superstoichiometric chaperonin concentration. In this case, it is better to prolong the time the protein spends in the cavity in order to reduce the amount of misfolded species in the bulk (Fig. 5B). The presence of a maximum in the yield curve in Fig. 5, indicating an optimum timescale for the chaperonin allosteric transition, can be understood as a competition between two effects. On one hand, a small kR−R″ would result in most SPs remaining captive within GroEL and not being ejected quickly enough for sufficient yield. On the other hand, if kR−R″ is large then most SPs are released in a misfolded state, and hence would aggregate because λA is large. Our calculation (dashed curves in Fig. 5) demonstrates the plausibility of an optimum value of kR−R″ and is consistent the experiments of Weissman and coworkers [17]. These calculations show that optimized chaperonin activity not only depends on the time scales in the reaction cycle of GroEL but also on aggregation and folding characteristics of the SP. It is important to emphasize that for proteins that are only moderately aggregation prone, the yield increases as the cycling rate increases. The experimental observation that the folding of other SPs was not as efficient with GroE3−1 is also consistent with this observation (solid red curve in Fig. 5).
The results in Fig. 5A are obtained using concentration of chaperonins in excess of the SP. We predict in Fig. 5B the yield for the same SPs at the same time in the case of sub-stoichiometric chaperonin concentration (we used 1 nM of chaperonin). The presence of an additional competing factor – the availability of chaperonins – favors faster chaperonin turnover, and hence we see that even in the case of a highly aggregation prone SP, it is better to increase the chaperonin cycling rate. It is expected that in in vivo situations, the amount of chaperonins is rather limited. Therefore, we predict that even for aggregation-prone SPs, the most efficient chaperonin function in vivo requires fast cycling.
Discussion
The interplay between the ligand-dependent (ATP and SP) time scales describing the GroEL allosteric transition rates in the reaction cycle (Fig. 1) and those that determine the fate of SPs determines the efficiency of chaperonins. Our work shows that the kinetics of assisted folding of SPs, under non-permissive conditions, can be used to accurately describe a number of experiments, provided the coupling between allosteric transitions and SP folding and aggregation is taken into account. The dependence of Rubisco folding on the EL concentration can be quantitatively obtained only by including the coupling between the kinetic processes in the reaction cycle. More importantly, using our kinetic model, we can also account for SP folding assisted by SR1 and SR1 mutants and link the efficiency of these chaperonins to the kinetic rates in the reaction cycle. Finally, our model also explains naturally, in terms of the rates of the allosteric transitions that depend on the nature and the concentrations of ligands and the tendency of SPs to aggregate, the observations that enhanced efficiency of GroEL mutants for a particular SP comes at the expense of their inability to rescue other SPs. Although the full kinetic model is complicated (Eq. (12)), the variations in the efficiency of the chaperonins is, to a large extent, determined by the rate limiting step in the reaction cycle (it is typically kR−R″ under maximal loading conditions), the capture rate of the SP, and the concentration-dependent rate of SP aggregation. Most of the readily available yield data can be quantitatively explained primarily by varying these parameters. The availability of the complete theoretical model allows us to explore other possibilities that can be experimentally realized through directed evolution or targeted mutation of GroEL and GroES.
Chaperonin concentration and binding rate of SP determine GroEL efficiency
Misfolded proteins either fold to the native state or aggregate. Chaperonins provide an additional pathway out of the misfolded states. Only if the flux along that path is significant, can chaperonins substantially reduce aggregation. Thus, quantitatively, chaperonins can measurably reduce aggregation only if λBC0 > λA[X0]. In other words, the product of chaperonin concentration and binding rate determines how effectively chaperonins can isolate the misfolded SPs. The criterion λBC0 > λA[X0] is a necessary kinetic criterion for efficient function of chaperonins.
Given a sufficient amount of chaperonins, the binding rate, λB, has a large effect on aggregation prevention illustrated by steady-state solutions to the kinetic equations. We expect that binding to the misfolded proteins, and hence isolating them from the aggregation-prone environment is beneficial. In most cases, increasing λB or the concentration also increases the yield. In Fig. 2 we show the native state yield increase as the chaperonin concentration increases. Theoretically, however, it is also possible to find a regime where increasing the chaperonin concentration or increasing λB may not necessarily increase the native state yield. Such a possibility is realised if the chaperonin allosteric cycle is very slow, slower than the characteristic timescale kS−1 associated with the protein escaping from the misfolded conformations spontaneously. The effect of chaperonin concentration on yield and aggregation is larger in the sub-stoichiometric cases, i.e. if C0 < [X0]. If C0 > [X0] then GroEL-GroES can fold all SPs (Fig. 2).
T ↔ R equilibrium constant has only a moderate effect on SP folding yield in the presence of excess ATP
A consequence of IAM [43] is that it is generally beneficial to speed up the chaperonin allosteric cycle, so that, when needed, chaperonin can perform multiple rounds of binding and release. This can result in a rapid enhancement in yield of native state SP (Eq. (6)). In the context of the T → R transition, this means that, upon SP binding, driving the equilibrium towards the R state should enhance efficiency of SP folding. Yifrach and Horovitz have shown (see Fig. 1 in Ref. [41]) how the rate of refolding of mDHFR increases as the TT → TR conformational transition is sped up. Using our kinetic model, we have analytically shown (Eq. (5)) in the steady-state limit, that the native state yield can be increased (and aggregation reduced) upon increasing kT−R and reducing kR−T. For WT GroEL, under non-permissive conditions in the presence of saturating ATP and GroES, the T → R transition does not appear to be the rate determining step in the catalytic cycle. We have varied both the equilibrium constants K = kT−R/kR−T and kR−R″ to predict the changes in yield of the folded SP (Fig. 6). Under superstoichiometric conditions even large changes in K do not have significant effect on the SP native state yield (Fig. 6A). Even when C0 < [X0], alterations in SP yield are relatively small except perhaps when K and kR−R″ are greatly changed (Fig. 6B). It is unclear if this situation can be easily realized. Thus, we predict that changes in K do not significantly affect GroEL efficiency at least for stringent SPs. Even for non-stringent substrates which do not require GroES, the SP folding rate changes by only a small factor even as K varies greatly. These conclusions are only valid when ATP concentration is large so that the T ↔ R occurs readily. If the ATP concentration is very low or GroEL mutations slow the first steps in the reaction cycle, it is likely that the efficiency of GroEL can also be greatly reduced.
R → R″ transition rates and confinement-induced changes in SP folding dramatically alter native state yield
The efficiency of chaperonin function changes dramatically as kR−R″ , which includes GroES binding, SP encapsulation, and ATP hydrolysis, is varied. During the events that occur on the time scale , the characteristics of SP folding can also be different than in the bulk. In particular, as discussed in the context of SR1, it is possible that kN and kM are functions of kR−R″ . It is of interest to explore the efficiency of assisted folding as SP-dependent rates and kR−R″ are simultaneously altered. It was argued [5], using the IAM, that during the T → R transition, a SP is pulled out of a misfolded state. The stretching occurs because ATP favors the R state while SP, which has high affinity for the T state, resists the T → R transition. During the R → R″ transition SP is encapsulated in the central cavity where it can refold on a time scale ∼ . At the end of the R → R″ transition, the concentrations of SP in various states to be released from the cavity are given by Eq. (8). In general, the folding rates and kinetic partitioning factor inside the cavity can be different from the bulk values. Detailed computations show that rates of folding inside a cavity change at best by a factor of 10 [46, 47]. Using the kinetic model we explore two possibilities (Fig. 7). First, assuming that the folding rates inside the cavity are the same as outside, we plot the native state yield as a function of time for three different kR−R″ in Fig. 7A. The yield increases as kR−R″ increases. Thus, even in this case where the rates are not altered by confinement, it is beneficial to speed up the chaperonin allosteric cycle. For comparison, we also plot, in Fig. 7B, the native state yield in the case where the folding rates inside the cavity are different. It has been shown that confinement and the hydrophobicity of the cavity walls [43] affect folding rates, probably by favoring the native states. We use , so the population of the misfolded states is somewhat suppressed. We can see from Fig. 7B that chaperonins increase the native state yield even more. Benefits of confinement-induced changes in SP and multiple iterations have a cooperative effect on SP folding. However, regardless of the changes in the intrinsic confinement-induced folding characteristic of the SP yield enhancement is only possible if kR−R″ increases. This central result, obtained in experiments (Fig. 2 and Fig. 3A) and in the exploration of the complete kinetic model (Eq. (12)), shows clearly that when presented with SP, ATP, and GroES efficient function of GroEL requires frequent cycling – a prediction that follows from the IAM [5, 19].
Figure 7.
Effect of variations of kR−R″ on native yield of Rubisco. The concentration of unfolded SP is 40nM and that of GroEL is 100nM. (A) The folding characteristics inside the central cavity are the same as in the bulk (for values see Table 1). The values of kR−R″ are 1.2min−1 (dotted green line), 12min−1 (solid red line), and 120min−1 (dashed purple line). (B) Same as in (A) except the enhancement in confinement induced folding of SP is taken into account. Specifically, we used the same value of kF and , and In both cases frequent cycling, as predicted by IAM, greatly enhanced yield of folded Rubisco. The combined effect of multiple iterations and favorable values of folding in a cavity results in more rapid production of the native state.
Methods
Allosteric Kinetic Model
In order to derive the kinetic model we have to translate the steps in the catalytic cycle (Fig. 1) into a set of kinetic equations. In addition to the time scales that characterize the kinetic partitioning mechanism for the SP (kF, {ki}) and the GroEL allostery (kT−R, kR−T and kR−R″) we have to include the rates of binding and release of SP (linked to the R″ → T transition) for a complete description of the kinetic model. It is possible to solve the kinetic equations assuming that there are distinct structures in the misfolded ensemble. In this case the kinetic processes associated with the misfolded ensemble would involve summations over the discrete structures like in Eq. (1). Experimental resolution of the various misfolded ensembles is difficult if not impossible, and treating the discrete misfolded structures explicitly does not provide new insights into the GroEL function. As a result, we assume that the transition to the NBA from the ensemble of misfolded conformations is given by an average rate kS. Because of the commonly made assumption that the R′ state (GroEL-(ATP)7-GroES) and the R″ state (GroEL-(ADP)7-GroES) are not structurally that different, we do not consider the R′ state explicitly. Even with these physically motivated simplifications, there are 10 distinct time scales that can vary depending on the SP and binding conditions (concentrations of SP, ADP, and GroEL). From general considerations, we can anticipate that the dynamic range of possibilities for assisted folding is large. As a consequence, a number of scenarios can emerge depending on the values of the rate constants.
In the absence of GroEL and under non-permissive conditions, a small fraction of unfolded molecules folds directly to the native state and the remaining molecules misfold into long-lived metastable state, i.e., SP folding is described by the KPM [28]. The misfolded molecules can also aggregate. Using X, N, M and Ma to denote unfolded, native, ensemble of misfolded conformations and the aggregates respectively, the relevant reactions are:
| (9) |
We have assumed that along the fast track (X → N) specific collapse and folding occur nearly simultaneously. In addition, the commitment to partitioning which also results in M, occurs on time scale kF, i.e., time scale for non-specific collapse ∼ kF. Explicit simulations using coarse-grained models [48] and theoretical considerations lend support to these assumptions. For simplicity, we have also ignored the higher order aggregation reactions such as M2 + M → M3, etc. For our purposes it suffices to include aggregation process as a pathway that prevents the formation of the native structure. The inclusion of higher order aggregation reactions does not alter the conclusions relating to GroEL. First order rate constants are denoted by kα (α = S, F, …), second order rate constants by λα. The kinetic equations for the reaction scheme in Eq.(9) are:
| (10) |
The case λA = 0, kF ≫ kS describes SP folding by the KPM for which Pu(t) is given by Eq. (2). Throughout the paper we assume that a single rate constant (kS) describes the transition from misfolded state to N.
In the presence of GroEL additional reactions that reflect the coupling between allosteric transitions and the fate of SP, have to be taken into account. The minimal set of GroEL allosteric state-dependent reactions that account for the major steps in the reaction cycle in Fig. 1, is:
| (11) |
where EL stands for GroEL, the subscript on EL indicates its allosteric state, and a substrate protein in an unknown state is denoted by SP. Note: kN, which is the rate for reaching the native state either in the cavity or upon release from the cis cavity is assumed to be different from kF.
In our model, EL can bind misfolded proteins (the first step in Eq. (11)), it then undergoes allosteric transitions T → R → R″ (the next two reactions). The SPs that are ejected from the chaperonin cavity are either misfolded (M) or folded (N). We have assumed that while the chaperonin may unfold the SP during the initial steps of the allosteric cycle, the collapse from the unfolded state X into M or N is fast (commitment to partitioning occurs rapidly) and thus even if there are unfolded proteins ejected from the cavity, they will partition into M and N quickly.
The kinetic equations that describe assisted folding that include SP folding by KPM, GroEL allostery and SP aggregation are:
| (12) |
Using the conservation of the number of EL particles: [EL0] = [ELT] + [ELTX] + [ELRX] + [ELR″ X], where [EL0] is the initial (and total) chaperonin concentration, the coupled nonlinear differential equations Eq. (12) need to be solved consistently to obtain time-dependent concentrations of the different molecular species. There are, in principle, 10 independent reaction rates that are needed to solve the seven coupled differential equations. The interplay between these rates creates a number of possibilities, several of which may not be always experimentally realizable or biologically relevant. Physical arguments show that λB/λA ≫ 1 to prevent aggregation. In other words, the rate of SP recognition must exceed the binary SP aggregation rates. Although chaperones belonging to the other heat shock protein family (HSP70 for example) may break up aggregates, there is no evidence that GroEL can facilitate such process. Even with physically motivated values for the rate constants there are a number of factors that determine GroEL efficiency.
Kinetic Model Without Allostery
Even though the kinetic model that takes into account coupling between the kinetic steps in the well established reaction cycle and SP folding quantitatively fits the experimental data for Rubisco and mtMDH (Fig. 2 and 3) it is legitimate to wonder if a reduced description suffices. Before we consider models that ignore GroEL allostery it is important to state the reasons for deriving a complete kinetic model for GroEL-assisted folding. The multi-timescale model agrees better with experimental data. An example of a model without chaperonin allostery (see below) does not provide as good a fit of Rubisco folding into Ref. [19] data. Moreover, the rates in our kinetic model have a physical meaning. The steps in the GroEL allosteric cycle are distinct, and their rates can be separately measured and/or manipulated by mutations. Our extracted rates for the allosteric transitions agree with independent experiments. In addition to giving less accurate results for chaperonin concentration and time dependent yield profiles, a fit using a reduced model results in reaction rates that cannot be easily interpreted or used to make predictions. It is unclear how to predict the effects of mutations in the GroEL-GroES system using the model that ignores allostery. Experiments on various mutants of GroEL-GroES have linked their efficiencies to alterations in ATPase activity that are intrinsic to GroEL function. Nevertheless, we have considered a simplified reaction scheme to see if the experimental data can be fit without accounting for allosteric transitions.
In the absence of allosteric transitions, the chaperonin-related reactions reduce to:
| (13) |
It is conceivable that kinetic schemes in which EL plays a passive role can be proposed. Because such schemes do not even account for GroEL concentration-dependent yield of SP, they do not warrant further discussion. The kinetic equations that describe assisted folding and include SP folding by KPM, GroEL without allostery, and SP aggregation, corresponding to the reactions Eq. (13) are:
| (14) |
The solutions to Eq. (14) were used to fit the data for Rubisco. Although the quality of fits in Fig. 8 (especially at intermediate concentrations of EL) is not as good as in Fig. 2 it appears that the reduced set of equations can approximately account for experimental observation. The parameters extracted from the fits are: kF = 100min−1, kS = 0.0003min−1, Φ = 0.02, λA = 0.0003nM−1 min−1, λB = 6nM−1min−1, kM = 1400min−1, and kN = 1min−1.
Figure 8.
Rubisco native state yield at different chaperonin concentrations. Data points are from Ref. [19], curves are fits based on a kinetic model without allostery (Eq. (14) in Methods).
There are notable differences between the extracted parameters using Eq. (14) and the one which includes allosteric transitions (Eq. (12). In particular, the value of kS obtained for the reduced kinetic model is a factor smaller than shown in Table 1. The much smaller value of kS would result in the prediction that SR1 would not be able to fold Rubisco to any measurable degree which is in apparent contradiction with reports by Brinker et al [42]. More importantly, the kM value in the reduced model is far greater than all other time scales, and is unphysical. Perhaps the greatest drawback with the kinetic scheme in Eq. (14) is that it cannot be used to predict or understand the effect of GroEL/S mutations that have profound effect on the efficiency of chaperonin function. The mutations alter the rates in the reaction cycle of GroEL. Only by taking those changes into account can the action of WT GroEL and its variants be obtained (Fig. 3–Fig. 7)
Acknowledgements
We have benefitted greatly from discussions with George H. Lorimer. RT is a Ruth A. Kirschstein postdoctoral fellow and her work was supported by the National Institute Of General Medical Sciences (1F32GM082009). DT is grateful to the National Science Foundation (CHE 05-14056), Air Force Office of Scientific Research, and the National Institutes of Health (1R01GM067851-01) for support.
Appendix A
Derivation of Eq. (5) (Steady-state, substoichiometric limit)
If we assume that the second order aggregation reaction rate can be replaced with an effective first order rate kA ≈ λA[M], Eq. (12) in the steady-state limit becomes:
where we have included υ0, υN and υMA as the rates of introduction of nascent, unfolded proteins and the rates of production of native and aggregated proteins respectively. From the above equations we obtain
| (15) |
| (16) |
Using these equations we obtain
| (17) |
By using the conservation of chaperonin concentration, [EL]0 = [ELT] + [ELTSP] + [ELRSP] + [ELR″SP], Eq. (17) can be rewritten as,
| (18) |
By substituting Eq. (15) and Eq. (16), Eq. (18) becomes
| (19) |
or
| (20) |
where (see also Eq. (5))
| (21) |
Combining the first two steady-state equations along with Eq. (17) and Eq. (20), yields the following quadratic equation for the concentration for the misfolded species:
| (22) |
Because Φ and all the rates are positive, the only physical solution for [M] is a monotonically increasing function of A. The native state yield decreases as [M] increases and thus the native state production increases as A decreases.
Appendix B: Sensitivity analysis of the kinetic model (Eq. (12))
We have assessed the effects of the changes in the kinetic parameters around the optimal values, that produce the best fits to the Rubisco data (Fig. 2 and Table 1), by performing a local sensitivity analysis. We computed the time-dependent change in the native state yield, Δ[N](t), in response to variations in the kinetic parameters. The change Δ[N](t) is computed by using
| (23) |
where Δpα is the variation in the kinetic parameter pα (Eq. (12)), and (δ[N]/δpα) is the time-dependent derivative of the native state yield with respect to pα. The magnitude of Δ[N](t) is an estimate of the variation in the native state yield in response to fluctuations Δpα. The magnitude of (δ[N]/δpα) is an indication of the extent to which the parameter pα affects Δ[N](t). We computed Δ[N](t) by varying each rate constant by ±5% around the values given in Table 1. The derivatives, obtained using a simple finite difference scheme, depend on [EL]. Among the allosteric rates in the reaction cycle, the largest value corresponds to |δ[N]/δkR″−T| when [SP]0 < [EL]0. The maximum value (≈0.8) is found at t ≈ 10min. Similarly, the values of |δ[N]/δλA| changes from 40nM2min at early times to 120nM2min for t ≳ 20min. Even these seemingly large values produce negligible changes in Δ[N](t) (Fig. 2B). All other derivatives are much smaller. Using all the values of δN/δpα we have calculated Δ[N](t) (using Eq. (23)). The time dependent changes Δ[N](t), which are residuals in the best fit of the data using Eq. (12), are small. Thus, the kinetic scheme is robust to variations in the kinetic parameters.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Lin Z, Rye HS. GroEL-mediated protein folding: making the impossible, possible. Crit. Rev. Biochem. Mol. Biol. 2006;41:211–239. doi: 10.1080/10409230600760382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Saibil H. Molecular chaperones: containers and surfaces for folding, stabilizing or unfolding proteins. Curr. Opin. Struct. Biol. 2000;10:251–258. doi: 10.1016/s0959-440x(00)00074-9. [DOI] [PubMed] [Google Scholar]
- 3.Horwich AL, Farr GW, Fenton WA. GroEL-GroES-mediated protein folding. Chem. Rev. 2006;106:1917–1930. doi: 10.1021/cr040435v. [DOI] [PubMed] [Google Scholar]
- 4.Horovitz A, Willison KR. Allosteric regulation of chaperonins. Curr. Opin. Struct. Biol. 2005;15:646–651. doi: 10.1016/j.sbi.2005.10.001. [DOI] [PubMed] [Google Scholar]
- 5.Thirumalai D, Lorimer GH. Chaperonin-mediated protein folding. Ann. Rev. Biophys. Biomol. Struct. 2001;30:245–269. doi: 10.1146/annurev.biophys.30.1.245. [DOI] [PubMed] [Google Scholar]
- 6.Xu Z, Sigler PB. GroEL/GroES: structure and function of a two-stroke folding machine. J. Struct. Biol. 1999;124:129–141. doi: 10.1006/jsbi.1998.4060. [DOI] [PubMed] [Google Scholar]
- 7.Viitanen PV, Gatenby AA, Lorimer GH. Purified chaperonin 60 (GroEL) interacts with the nonnative states of a multitude of Escherichia coli proteins. Protein Sci. 1992;1:363–369. doi: 10.1002/pro.5560010308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lorimer GH. A quantitative assessment of the role of the chaperonin proteins in protein folding in vivo. FASEB J. 1996;10:5–9. doi: 10.1096/fasebj.10.1.8566548. [DOI] [PubMed] [Google Scholar]
- 9.Fenton WA, Horwich AL. GroEL-mediated protein folding. Protein Science. 1997;6:743–760. doi: 10.1002/pro.5560060401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lorimer GH. Protein folding with a two-stroke motor. Nature. 1997;388:720–721. doi: 10.1038/41892. [DOI] [PubMed] [Google Scholar]
- 11.Xu Z, Horwich AL, Sigler PB. The crystal structure of the asymmetric GroEL-GroES-(ADP)7 chaperonin complex. Nature. 1997;388:741–750. doi: 10.1038/41944. [DOI] [PubMed] [Google Scholar]
- 12.Kipnis Y, Papo N, Haran G, Horovitz A. Concerted ATP-induced allosteric transitions in groel facilitate release of protein substrate domains in an all-or-none manner. Proc. Nat. Acad. Sci. USA. 2007;104:3119–3124. doi: 10.1073/pnas.0700070104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Amir A, Horovitz A. Kinetic analysis of ATP-dependent inter-ring communication in groel. J. Mol. Biol. 2004;338:979–988. doi: 10.1016/j.jmb.2004.02.076. [DOI] [PubMed] [Google Scholar]
- 14.Chennubhotla C, Bahar I. Markov propagation of allosteric effects in biomolecular systems: application to GroEL-GroES. Mol. Sys. Biol. 2006;2:36. doi: 10.1038/msb4100075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Keskin O, Bahar I, Flatow D, Covell DG, Jernigan RL. Molecular mechanisms of chaperonin GroEL-GroES function. Biochemistry. 2002;41:491–501. doi: 10.1021/bi011393x. [DOI] [PubMed] [Google Scholar]
- 16.Hyeon C, Lorimer GH, Thirumalai D. Dynamics of allosteric transitions in GroEL. Proc. Nat. Acad. Sci. USA. 2006;103:18939–18944. doi: 10.1073/pnas.0608759103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang JD, Herman C, Tipton KA, Gross CA, Weissman JS. Directed evolution of substrate-optimized GroEL/S chaperonins. Cell. 2002;111:1027–1039. doi: 10.1016/s0092-8674(02)01198-4. [DOI] [PubMed] [Google Scholar]
- 18.Sun Z, Scott DJ, Lund PA. Isolation and characterisation of mutants of GroEL that are fully functional as single rings. J. Mol. Biol. 2003;332:715–728. doi: 10.1016/s0022-2836(03)00830-1. [DOI] [PubMed] [Google Scholar]
- 19.Todd MJ, Lorimer GH, Thirumalai D. Chaperonin-facilitated protein folding: Optimization of rate and yield by an iterative annealing mechanism. Proc. Nat. Acad. Sci. USA. 1996;93:4030–4035. doi: 10.1073/pnas.93.9.4030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Todd MJ, Viitanen PV, Lorimer GH. Dynamics of the chaperonin ATPase cycle: implications for facilitated protein folding. Science. 1994;256:659–666. doi: 10.1126/science.7913555. [DOI] [PubMed] [Google Scholar]
- 21.Weissman JS, Kashi Y, Fenton WA, Horwich AL. GroEL-mediated protein folding proceeds by multiple rounds of binding and release of nonnative forms. Cell. 1994;78:693–702. doi: 10.1016/0092-8674(94)90533-9. [DOI] [PubMed] [Google Scholar]
- 22.Bukau B, Weissman JS, Horwich A. Molecular chaperones and protein quality control. Cell. 2006;125:443–451. doi: 10.1016/j.cell.2006.04.014. [DOI] [PubMed] [Google Scholar]
- 23.Burston SG, Weissman JS, Farr GW, Fenton WA, Horwich AL. Release of both native and non-native proteins from a cis-only GroEL ternary complex. Nature. 1996;383:96–99. doi: 10.1038/383096a0. [DOI] [PubMed] [Google Scholar]
- 24.Weissman JS, Hohl CM, Kovalenko O, Kashi Y, Chen S, Braig K, Saibil HR, Fenton WA, Horwich AL. Mechanism of GroEL action: Productive release of polypeptide from a sequestered position under GroES. Cell. 1995;93:577–587. doi: 10.1016/0092-8674(95)90098-5. [DOI] [PubMed] [Google Scholar]
- 25.Fedorov AN, Baldwin TO. GroE modulates kinetic partitioning of folding intermediates between alternative states to maximize the yield of biologically active protein. J. Mol. Biol. 1997;268:712–723. doi: 10.1006/jmbi.1997.1007. [DOI] [PubMed] [Google Scholar]
- 26.Kolomeisky AB, Fisher ME. Molecular motors: A theorist’s perspective. Ann. Rev. Phys. Chem. 2007;58:675–695. doi: 10.1146/annurev.physchem.58.032806.104532. [DOI] [PubMed] [Google Scholar]
- 27.Wu Y, Gao YQ, Karplus M. A kinetic model of coordinated myosin V. Biochemistry. 2007;46:6318–6330. doi: 10.1021/bi700526r. [DOI] [PubMed] [Google Scholar]
- 28.Guo Z, Thirumalai D. Kinetics of protein folding: Nucleation mechanism, time scales, and pathways. Biopolymers. 1995;36:83–102. [Google Scholar]
- 29.Kiefhaber T. Kinetic traps in lysozyme folding. Proc. Nat. Acad. Sci. USA. 1995;92:9029–9033. doi: 10.1073/pnas.92.20.9029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Matagne A, Radford SE, Dobson CM. Fast and slow tracks in lysozyme folding: insight into the role of domains in the folding process. J. Mol. Biol. 1997;267:1068–1074. doi: 10.1006/jmbi.1997.0963. [DOI] [PubMed] [Google Scholar]
- 31.Hyeon C, Thirumalai D. RNA and protein folding: Common themes and variations. Biochemistry. 2005;44:4957–4970. doi: 10.1021/bi047314+. [DOI] [PubMed] [Google Scholar]
- 32.Horst R, Bertelsen EB, Fiaux J, Wider G, Horwich Al, Wüthrich K. Direct NMR observation of a substrate protein bound to the chaperonin GroEL. Proc. Nat. Acad. Sci. USA. 2005;102:12748–12753. doi: 10.1073/pnas.0505642102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Stan G, Lorimer GH, Thirumalai D, Brooks BR. Coupling between allosteric transitions in GroEL and assisted folding of a substrate protein. Proc. Nat. Acad. Sci. USA. 2007;104:8803–8808. doi: 10.1073/pnas.0700607104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yifrach O, Horovitz A. Nested cooperativity in the ATPase activity of the oligomeric chaperonin GroEL. Biochemistry. 1995;34:5303–5308. doi: 10.1021/bi00016a001. [DOI] [PubMed] [Google Scholar]
- 35.Inbar E, Horovitz A. GroES promotes the T to R transition of the GroEL ring distal to GroES in the GroEL-GroES complex. Biochemistry. 1997;36:12276–12281. doi: 10.1021/bi9714870. [DOI] [PubMed] [Google Scholar]
- 36.Yifrach O, Horovitz A. Mapping the transition state of the allosteric pathway of GroEL by protein engineering. J. Amer. Chem. Soc. 1998;120:13262–13263. [Google Scholar]
- 37.Ma J, Sigler PB, Karplus M. A dynamic model for the allosteric mechanism of GroEL. J.Mol. Biol. 2000;302:303–313. doi: 10.1006/jmbi.2000.4014. [DOI] [PubMed] [Google Scholar]
- 38.Li MS, Klimov DK, Thirumalai D. Thermal denaturation and folding rates of single domain proteins: size matters. Polymer. 2004;45:573–579. [Google Scholar]
- 39.Viitanen PV, Lubben TH, Reed J, Goloubinoff P, O’Keefe DP, Lorimer GH. Chaperonin-facilitated refolding of ribulosebisphosphate carboxylase and ATP hydrolysis by chaperonin 60 (groEL) are K+ dependent. Biochemistry. 1990;29:5665–5671. doi: 10.1021/bi00476a003. [DOI] [PubMed] [Google Scholar]
- 40.Rye HS, Roseman AM, Furtak K, Fenton WA, Saibil HR, Horwich AL. GroEL-GroES cycling: ATP and non-native polypeptide direct alternation of folding-active rings. Cell. 1999;97:325–338. doi: 10.1016/s0092-8674(00)80742-4. [DOI] [PubMed] [Google Scholar]
- 41.Yifrach O, Horovitz A. Coupling between protein folding and allostery in the GroE chaperonin system. Proc. Nat. Acad. Sci. USA. 2000;97:1521–1524. doi: 10.1073/pnas.040449997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Brinker A, Pfeifer G, Kerner MJ, Naylor DJ, Hartl FU, Hayer-Hartl M. Dual function of protein confinement in chaperonin-assisted protein folding. Cell. 2001;107:223–233. doi: 10.1016/s0092-8674(01)00517-7. [DOI] [PubMed] [Google Scholar]
- 43.Betancourt MR, Thirumalai D. Exploring the kinetic requirements for enhancement of protein folding rates in the GroEL cavity. J. Mol. Biol. 1999;287:627–644. doi: 10.1006/jmbi.1999.2591. [DOI] [PubMed] [Google Scholar]
- 44.Takagi F, Koga N, Takada S. How protein thermodynamics and folding mechanisms are altered by the chaperonin cage: Molecular simulations. Proc. Nat. Acad. Sci. USA. 2003;100:11367–11372. doi: 10.1073/pnas.1831920100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Jewett AI, Baumketner A, Shea J-E. Accelerated folding in the weak hydrophobic environment of a chaperonin cavity: Creation of an alternate fast folding pathway. Proc. Nat. Acad. Sci. USA. 2004;101:13192–13197. doi: 10.1073/pnas.0400720101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Klimov DK, Newfield D, Thirumalai D. Simulations of beta-hairpin folding confined to spherical pores using distributed computing. Proc. Nat. Acad. Sci. USA. 2002;99:8019–8024. doi: 10.1073/pnas.072220699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cheung MS, Klimov DK, Thirumalai D. Molecular crowding enhances native statetability and refolding rates of globular proteins. Proc. Nat. Acad. Sci. USA. 2005;102:4753–4758. doi: 10.1073/pnas.0409630102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Guo Z, Thirumalai D. Kinetics and thermodynamics of folding of a de novo designed four helix bundle. J. Mol. Biol. 1996;263:323–343. doi: 10.1006/jmbi.1996.0578. [DOI] [PubMed] [Google Scholar]


