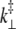Abstract
The elastic properties (stretching and bending moduli) of myosin are expected to play an important role in its function. Of particular interest is the extended α-helical coiled-coil portion of the molecule. Since there is no high resolution structure for the entire coiled-coil, a study is made of the scallop myosin II S2 subdomain for which an x-ray structure is available (Protein Data Bank 1nkn). We estimate the stretching and bending moduli of the S2 subdomain with an atomic level model by use of molecular simulations. Results were obtained from nonequilibrium molecular dynamics simulations in the presence of an external force, from the fluctuations in equilibrium molecular dynamics simulations and from normal modes. In addition, a poly-Ala (78 amino acid residues) α-helix model was examined to test the methodology and because of its interest as part of the lever arm. As expected, both the α-helix and coiled-coil S2 subdomain are very stiff for stretching along the main axis, with the stretching stiffness constant in the range 60–80 pN/nm (scaled to the 60 nm long S2). Both molecules are much more flexible for bending with a lateral stiffness of ∼0.010pN/nm for the S2 and 0.0055pN/nm for the α-helix (scaled to 60 nm). These results are expected to be useful in estimating cross-bridge elasticity, which is required for understanding the strain-dependent transitions in the actomyosin cycle and for the development of three-dimensional models of muscle contraction.
INTRODUCTION
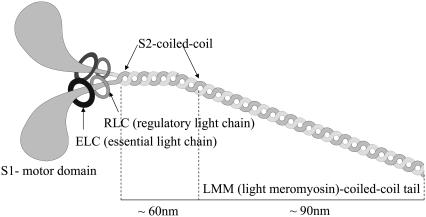
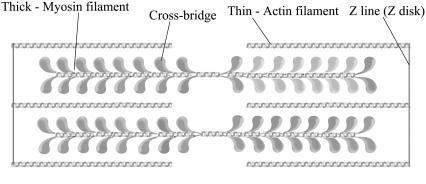
The primary proteins involved in the process of muscle contraction are myosin II (1) and actin, although other proteins, such as tropomyosin and troponin, also play important roles in regulation of muscle contraction. Myosin II consists of two heavy polypeptide chains and two pairs of light chains (two essential (ELC) and two regulatory (RLC) light chains). By proteolytic cleavage (with enzymes such as trypsin or papain), myosin II can be divided into several subfragments; they are the S1 subfragment (the motor domain of myosin II with the ATP and actin binding sites), the S2 subfragment (the N-terminal portion of the myosin tail, which has an α-helical coiled-coil structure), and light meromyosin (LMM) (the myosin tail beyond the S2 subfragment). Heavy meromyosin (HMM) is a common name for two head domains (S1) connected by their subfragment-2 (S2) regions and two pairs of light chains, ELC and RLC. A schematic representation of myosin II and its subfragments is given in Fig. 1. Actin filaments (F-actin) are polymers of monomer units called G-actin. Two parallel strings of actin monomers twist around each other, forming microfilaments, while groups of microfilaments form the so-called thin filament. The sarcomere lattice is an assembly of myosin (thick) filaments and actin (thin) filaments, as shown in Fig. 2. The filaments can slide relative to each other and they are interconnected by cross-bridges (2–6), formed by the S1 and S2 subfragments. The actomyosin cycle, which involves the cyclic binding and unbinding of myosin to actin, provides the driving force for muscle contraction. It is regulated by the binding and hydrolysis of ATP and the resulting conformational changes of myosin, which lead to the force-generating transition or “power stroke”. A crucial aspect of the interaction of myosin with actin concerns the way in which mechanical forces affect its chemistry and vice versa. This part of the cycle is not well understood, in part because x-ray structures are not available. It has been suggested that the rates of some key transitions (myosin binding to actin, power stoke, ADP release, and myosin detachment from actin) depend on the force acting upon a cross-bridge.
FIGURE 1.
Schematic representation of the myosin II protein and its subfragments (adapted from http://www.mrothery.co.uk/images/Imag108.gif).
FIGURE 2.
Schematic representation of the sarcomere lattice (adapted from http://www.cytoskeleton.com/products/actinbind/images/myosindrawing.jpg).
Significant progress has been made in understanding the structural, biochemical, kinetic, and mechanical aspects of muscle contraction. An outline mechanism of the actomyosin cycle was given by Lymn and Taylor (7) before knowledge of any high resolution structures. Since 1993, a number of x-ray and cryoelectron microscopy states have been reported (8–11) and used for making specific models for the elements of the Lymn-Taylor cycle.
These biochemical and structural findings, taken together with the cross-bridge forces, the sliding distance generated in each enzymatic cycle of the actomyosin ATPase, and the duration of cross-bridge attachment measured in motility assays, set the stage for development of sliding-filament models of muscle contraction. The coupling between the biochemical cycle and sarcomere mechanics is complicated by the strain dependence of the actomyosin cycle (12). The cross-bridge stiffness (determined by the stretching stiffness of S2, the lateral stiffness (bending) of the lever arm, and the elasticity of the unstructured segment between lever arm and the S2 subdomain) are the key elements in the strain-dependent transition rates. Estimates of the total cross-bridge stiffness from motility assays and intact fibers span a range from 0.5 to 5 pN/nm (13–17). This has made it difficult to develop a precise model for the behavior of a muscle fiber.
For many years, sliding filament models assumed that actin and myosin filaments were rigid and that cross-bridge compliance resided entirely in the S2 myosin subfragment. Even in this simplified model, mechanical measurements of muscle stiffness were insufficient to precisely separate cross-bridge stiffness from the number of attached cross-bridges. It has been established that both actin and myosin filaments exhibit extensibilities comparable to or larger than the cross-bridge itself (18,19). Goldman and A. F. Huxley (20) have pointed out that this new evidence invites reexamination of the theory of muscle contraction at the most basic level. In a model study, one of the authors (21) has shown, for example, that when filaments are extensible, small rapid length changes of the sarcomere are not experienced simultaneously or to the same extent by all attached bridges. The distortion effect imposed by the extensibility of thin and thick filaments further complicates the comparison between in vitro measurements and measurements in intact fibers. For example, the estimate of cross-bridge stiffness of ∼0.7 pN/nm derived from early tension recovery measurement (22,15–17) may actually be three times greater if filament extensibility is taken into account (21,23). Considering these uncertainties, it is clear that independent estimates of the cross-bridge stiffness from a study of its parts and their complexes are needed to determine the contributions to the overall cross-bridge compliance of S2, the lever arm (24), the unstructured segment between the lever arm and the S2 subdomain (the so called “neck region”), the myosin motor domain, and the actin-myosin connection.
The major focus of this study is on the elastic properties of the S2 subdomain and to a lesser degree on the elasticity of an α-helix, which is an essential part of the lever arm of the S1 subdomain. The elasticity of both S2 and the lever arm contributes to the overall elasticity of a cross-bridge in two ways. It contributes to the compliance of the cross-bridge, and more importantly to lateral flexibility of a cross-bridge necessary for effective binding of myosin heads to actin sites in the three-dimensional sarcomere lattice. The S2 domain has an α-helical coiled-coil structure (25–27). Coiled-coil structural motifs are diverse; most commonly they are composed of two intertwined α-helices. Ideally, each of the α-helices has a heptad repeated sequence (a-b-c-d-e-f-g), where a and d are usually nonpolar amino acids, which stabilize the coiled-coil structure through strong “knob into hole” nonpolar interactions (25–27). The lever arm consists of a single α-helix associated with two regulatory and essential light chains (28). Here we consider the elasticity of an α-helix, composed of 78 Ala residues, as an estimate of the lower bound of the lever arm elasticity.
Another possibility is that the stability of S2 may play a role in the actomyosin cycle. One group of experimental studies (29,30) supports the idea that the unwinding, as well as bending, of the S2 subfragment is needed for the proper mechanical and regulatory function of myosin II. Another group of studies (31,32) concludes that S2 is stable and that, at least beyond the first heptad, uncoiling is not necessary for its proper function. Knowledge of the elastic properties of the S2 subfragment should aid in resolving this conflict.
This article is organized as follows: The following section describes the general methods used for the calculations, the systems studied, and the computational details of the simulations. Then we give the results for the stretching and bending moduli of the S2 subfragment and the α-helix. This is followed by a Concluding Discussion section.
METHODS
Theory
The main goal of this study is to obtain the stretching and bending elastic properties of an α-helix and the myosin II S2 subdomain. For detailed definitions and descriptions of the theory of elasticity of homogeneous material, the reader is referred to classic texts (33,34). Only the key equations of the elasticity theory relevant for our study are presented.
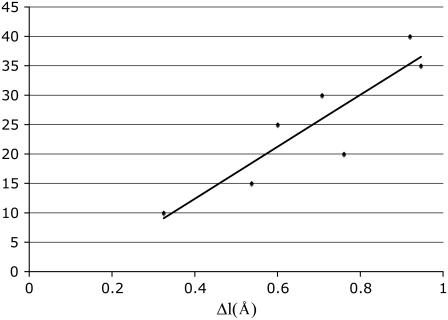
According to Hooke's law, the strain (the change of unit length) is proportional to the stress (force per unit surface area) and the ratio of the two is, therefore, a constant that is commonly called Young's modulus. By definition, Young's (stretching) modulus, EII, relates the tensile stress, the force per unit cross-sectional area of the material, and the strain, the increase in length due to the stretching of a standard rod divided by the rod original length:
 |
(1) |
where FII is force (along the rod axis), A is the cross-section area, L is length, and ΔL is change in the length (i.e., the elongation or displacement of the rod end).
In addition to Young's modulus, the stiffness or spring constant (kII) is commonly used to express the stretching elasticity of the material. The stiffness (kII), is defined as the proportionality constant between the force (F) and displacement (ΔL):
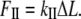 |
(2) |
Combining Eqs. 1 and 2, one gets the relationship between kII and EII:
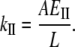 |
(3) |
Analog expressions can be derived for the bending of a cantilevered rod (beam). First, the relation between the bending force and the cantilever deflection is:
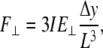 |
(4) |
where 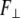 is perpendicular (bending) force,
is perpendicular (bending) force, 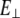 is Young's modulus estimated from bending, I is the cross-sectional moment of inertia estimated from the circular cross-section area of α-helix of 0.95 nm2, or from cross-section area of coiled-coil (35) of 1.9 nm2 and double helix geometry as described in Table 1, and Δy is the displacement (deflection) of the beam free end in the direction perpendicular to the beam axis. Because of possible uncertainties associated with calculation of I, we first determine the flexural rigidity
is Young's modulus estimated from bending, I is the cross-sectional moment of inertia estimated from the circular cross-section area of α-helix of 0.95 nm2, or from cross-section area of coiled-coil (35) of 1.9 nm2 and double helix geometry as described in Table 1, and Δy is the displacement (deflection) of the beam free end in the direction perpendicular to the beam axis. Because of possible uncertainties associated with calculation of I, we first determine the flexural rigidity 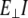 and then estimate
and then estimate 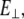 which can be compared to
which can be compared to 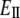 obtained from stretching.
obtained from stretching.
TABLE 1.
Summary of the S2 and α-helix parameters
| A (nm2) | L (nm) | M (10−27 kg) | I (nm4) | |
|---|---|---|---|---|
| S2 subdomain | 1.90 | 9.48 | 29802.87 | 0.32 |
| α-Helix | 0.95 | 10.00 | 9236.23 | 0.07 |
A is cross-section area, L is length, and I is the cross-sectional moment of inertia 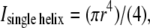 where r is helix radius, whereas
where r is helix radius, whereas 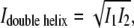 where
where 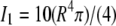 and
and 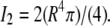 All parameters were obtained from the model used in the simulations.
All parameters were obtained from the model used in the simulations.
Next, in analogy with Eqs. 2 and 3, the lateral stiffness (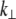 ) is defined as proportionality constant between force,
) is defined as proportionality constant between force, 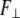 and lateral displacement, Δy, is defined as follows:
and lateral displacement, Δy, is defined as follows:
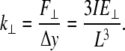 |
(5) |
The above expressions are only valid for small displacements and small deflections. For the bending, it is also assumed that the beam is long in comparison with the cross-section dimension.
There are several methods that can be used to obtain Young's modulus, or equivalently, the stiffness from known atomic structure. It is important to compare different approaches to obtain a measure of sensitivity of the estimated parameters to the approximations inherent in each of the methods.
Normal mode analysis
The first step in a normal mode (NM) analysis is to obtain and classify normal modes according to the type of motion they represent, e.g., stretching, bending, and torsion. Ideally the types are well resolved and there is no mixing between them. Once the normal mode vectors and the corresponding frequencies are obtained, they can be used to calculate the elastic properties, in particular, to assess Young's modulus from stretching (EII) and from bending the flexural rigidity (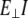 ) and then assess
) and then assess 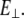 To connect NMs and their frequencies with the mechanical coefficients of an ideal rod, vibrational analysis of an isotropic, homogeneous rod was used. Details of the derivation of the formulas connecting
To connect NMs and their frequencies with the mechanical coefficients of an ideal rod, vibrational analysis of an isotropic, homogeneous rod was used. Details of the derivation of the formulas connecting 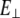 and the bending frequency can be found in various studies of bending (e.g., DNA (36) and β-sheet (37,38, and references therein)). The equation that connects the angular frequency (bending mode) and the flexural rigidity
and the bending frequency can be found in various studies of bending (e.g., DNA (36) and β-sheet (37,38, and references therein)). The equation that connects the angular frequency (bending mode) and the flexural rigidity 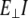 (Nm2) is
(Nm2) is
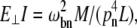 |
(6) |
where ωbn (s−1) is the angular bending frequency of mode n, M is the total mass (kg), L is the length of the rod (m), and pnL = 4.730, 7.853, 10.996, … (for n = 1, 2, 3 …) (35).
The frequencies of accordion-like vibrations can be related to Young's modulus (39–41), EII. The stretching vibrational frequency, 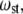 is connected to the EII through the following equation:
is connected to the EII through the following equation:
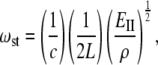 |
(7) |
where ωst (m−1) is the stretching frequency of a given mode, c (m/s) is the speed of light, and r (kg/m3) is the density. Young's modulus and stiffness are converted from the International System of Units (SI) (N/m2 and N/m) into more convenient units of pN/nm2 and pN/nm, respectively.
Forced molecular dynamics simulations
The direct connection between the stiffness constants and the results of applying a force comes from the basic equations of the theory of elasticity for an elastic rod: Eqs. 1 and 2 for stretching, and 5 for bending. For these simple relations to hold, the deformation has to be small, so that linearity is preserved. Stiffness constants are obtained as the slope of the curves representing the external force as a function of change in length (or deflection) with respect to a reference value; the linearity of this curve determines whether this is in the small deformation regime or not.
Equilibrium molecular dynamics
Nonequilibrium dynamic simulations (see above) introduce an unphysical timescale by inducing dynamic changes in the system much faster than they would happen in an experimental setting. It is not clear how much this will affect the elastic properties, but it is important to compare the values obtained from equilibrium molecular dynamics (MD) simulations, in which only “naturally” occurring fluctuations are considered. It is possible to show that Young's modulus can be related to the equilibrium fluctuations. The resulting equations are
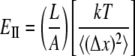 |
(8a) |
 |
(8b) |
where k (J/K) is the Boltzmann constant, T is temperature (K), and 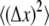 (m2) and
(m2) and 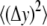 (m2) are the mean-squared axial (stretching) and lateral (bending) equilibrium fluctuations, respectively.
(m2) are the mean-squared axial (stretching) and lateral (bending) equilibrium fluctuations, respectively.
Combining Eqs. 8a and 3, with Δx = ΔL = (Lt − Lave), where Lave is the time average over dynamic trajectory of the defined length and Lt is the instantaneous value over the time, the axial stiffness is given:
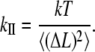 |
(9) |
Computational methods
The S2 coiled-coil subdomain (terminal segment of the scallop myosin II, Protein Data Bank (PDB) code name 1NKN, ∼10 nm long) (42) of myosin II was used for this study. This was the only existing crystal structure for even part of the myosin II S2 domain, which is 60 nm in length, when this article was completed. Since then, a crystal structure for the human β-myosin S2 fragment appeared (PDB code name 2FXM) (43); this structure is not considered here. For the simulation, only two chains (A and B) were extracted from the crystal structure, which consists of a dimer of coiled-coils. The total number of amino acid residues is 150 in the coiled-coil (75 per chain). The sequence of the fragment used in the simulations is given in Appendix A. All calculations presented here were done with the CHARMM program (44). Both vacuum and implicit solvent calculations were used. To treat the effects of solvent, the EEF1 (45) implicit solvent model was used with the CHARMM 19 force field. Nonbonded interaction parameters were set to EEF1 default values. The distance cutoff in generating the pair list is 10 Å, the distance at which the switching function reduces the interactions to zero is 9 Å, and the distance at which the smoothing function begins to reduce a contribution is 7 Å. Besides being very fast, the EEF1 method has analytical second derivatives, which provides an accurate and rapid way of calculating the Hessian matrix required for calculating the normal modes.
S2 subdomain
NM analysis. To obtain the NM of the S2 subdomain, the crystal structure was energy minimized. It is ideal to have true minima (all translational/rotational modes equal to zero), without at the same time deviating too much from the crystal structure. A balance between the two requirements was achieved with an energy gradient of 0.002 kcal/molÅ for the gas phase system, and 0.00003 kcal/molÅ with EEF1; the calculated translational/rotational frequencies were <0.06 cm−1 in both cases. The root mean-square deviations (for the minimized structures) were ∼2.6 Å and ∼1.3 Å for gas phase and EEF1, respectively. After minimization, the mass weighted second derivative of the energy (Hessian) matrix was diagonalized and the lowest frequency modes (1000 out of a total of 4665) were obtained. The lowest frequency modes were inspected and classified according to the types of motion they represent. The frequencies for the first bending and stretching modes were used to calculate bending (according to Eqs. 6 and 5) and stretching elasticity (according to Eqs. 3 and 7).
Equilibrium MD. After a short energy minimization of the crystal structure (1000 Adopted basis Newton-Raphson (ABNR) steps), to eliminate large forces due to possible atomic overlaps, the system was gradually heated from 0 to 300 K in 10 K increments for 200 ps in the presence of harmonic restraints (mass weighted force constant of 5 kcal/molÅ2), which were applied on all heavy atoms (to prevent thermal uncoiling of the system). The time step for the MD simulation was 1 fs and coordinates were saved every 100 steps. An equilibration phase of total length 2 ns was calculated during which the harmonic restraints were gradually reduced to zero. To achieve and test convergence of the equilibrium MD simulation, canonical ensemble (Nose-Hoover thermostat) (46,47) simulations were done for 5 and 10 ns.
Nonequilibrium MD. The same setup was used for the MD simulations with external force. Ten snapshots (at 100 ps intervals) were taken from the equilibrium MD simulations and used as initial conformations for the forced MD simulations. During the nonequilibrium MD, the molecule was oriented along the x axis and the C-terminal end was fixed (as it is in the thick filament of the myosin II tail). Starting from 10 different initial geometries, nonequilibrium MD simulations were run for 2 ns using the atomic force microscopy (48,49) CHARMM constant force module to investigate stretching properties and the PULL command (imposes externally applied (pulling) force in a specified direction) to investigate bending properties (constant force applied in the y direction). The essential element in these methods is an additional energy term of the form 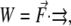 where
where 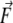 is the external force and
is the external force and 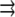 is the pulling direction, added to the molecular mechanics Hamiltonian. Force is applied on two atoms (stretching) and it is equal in magnitude and acts in the opposite direction. For more details on the implementation and theoretical background the reader is referred to Nose (46) and Hoover (47). In the case of bending, forces defined in the PULL command pull selected atoms in the specified direction.
is the pulling direction, added to the molecular mechanics Hamiltonian. Force is applied on two atoms (stretching) and it is equal in magnitude and acts in the opposite direction. For more details on the implementation and theoretical background the reader is referred to Nose (46) and Hoover (47). In the case of bending, forces defined in the PULL command pull selected atoms in the specified direction.
To obtain flexural rigidity, lateral stiffness, and elastic modulus (from bending) of the coiled-coil S2 subdomain, the molecule was oriented along the x axis, and an external force was applied in the y direction; 2 ns forced MD simulations were performed for each value of force (2, 4, 5, and 6 pN) starting from 10 different initial conformations. The C-terminal Cα atoms of A and B chains were fixed to mimic experimental conditions, such as those used by Schwaiger et al. (50). Ten atoms close to the N-terminal end of S2 were chosen for an additional averaging of the y direction displacement. Specifically, the experimental coordinates of Cα and Cβ atoms: 852–856 (residue number) were used for this purpose; the residue numbers of the A chain of the S2 fragment go from 846 to 919 (42). For each of those atoms, fluctuations were averaged over 10 initial geometries. To scale the result from each length of the S2 subdomain (L), which is equal to the distance between the C-terminal (Cα residue 918) and atom (852–856) on the N-terminal), to the so-called long S2 (60 nm long S2 subdomain) (51), the lateral stiffness was multiplied by the conversion factor: (L nm/60 nm)3, assuming that the flexural rigidity ( ) is uniform along the S2 fragment. Since both the distances (L) and the fluctuations are almost independent of the type of atom (Cα versus Cβ), results are presented only for the Cα atoms.
) is uniform along the S2 fragment. Since both the distances (L) and the fluctuations are almost independent of the type of atom (Cα versus Cβ), results are presented only for the Cα atoms.
To obtain the stretching stiffness, a constant force in the range of 10–40 pN (5 pN steps) was applied. These values of the forces were chosen because they are expected to be in the elastic regime. This assumption was tested by graphing the change in length along the main coiled-coil axis as a function of the applied force. The linearity of this graph supports the assumption that for small forces, the coiled-coil (S2 fragment) behaves as an elastic rod. The change in length of the S2 coiled coil for each force is given by
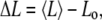 |
(10) |
where Lo (nm) is the initial end-to-end distance (defined as 10 different lengths—the Cα atom of residue 852 (nine amino acids from the N-terminus) and the Cα atom of residue 910 (nine amino acids from the C-terminus): Cα 854–Cα 908, Cα 856–Cα 906, Cα 858–Cα 904, Cα 860–Cα 902, Cα 862–Ca 900, Cα 855–Cα 912, Cα 855–Cα 911, Cα 855–Cα 910, and Cα 855–Cα 909; with residue numbers the same as in the original PDB file. 〈L〉 refers to the corresponding length time averaged over a forced MD simulation.
Choosing 10 different Ls helps to avoid “end effects”, such as uncoiling, and gives better statistics. Axial stiffness was estimated as the slope of the 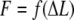 graph. Once the slope is obtained for each value of
graph. Once the slope is obtained for each value of 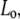 it was multiplied by the corresponding length, to get the “length independent” stiffness (so that different sets of results could be compared directly).
it was multiplied by the corresponding length, to get the “length independent” stiffness (so that different sets of results could be compared directly).
α-Helical test system
We have chosen 78-residue long poly-alanin α-helix as a model system, because α-helices have been studied extensively, both experimentally (39–41) and theoretically (52). Also it is of interest because the lever arm part is a long α-helix (∼88 Å). The choice of this particular α-helix was based on the study of Choe and Sun, who examined its elastic properties (52). The calculated flexural rigidity and lateral stiffness could directly be compared with their results, and served as a test for the S2 stiffness calculations. Only certain methods that were applied on the S2 fragment were tested on this model system (as given below).
The poly-Ala α-helix, consisting of 78 amino acid residues, was constructed by fixing the dihedral angles to typical α-helix values (φ = −57°, ψ = −47°). The EEF1 solvation model was used, as for the S2 subdomain, so that similar assumptions are introduced in the treatment of both systems. Nonbonded interaction cutoffs were set to the default values for the EEF1 model (given above).
NM and quasiharmonic NM analysis. Once a minimized structure for the poly-Ala helix was obtained, all atom diagonalization of the Hessian matrix was performed and NM vectors and frequencies were obtained. Since NM frequencies are approximate, in the sense that anharmonic effects are not taken in account, it was desirable to check their values against some more accurate method. We have chosen to compare the NM analysis (NMA) results with quasiharmonic values (from converged, 30 ns, constant temperature, equilibrium MD simulations described below). Quasiharmonic frequencies of the normal modes were obtained from the equilibrium MD simulation to be compared to NMA, which was performed on the minimized poly-Ala α-helix (generalized root-mean square = 0.0001 kcal/molÅ). The 1000 lowest frequency normal modes were obtained and compared.
Equilibrium MD. The poly-Ala helix was minimized for 1000 steepest descent steps, followed by 1000 ABNR steps. The heating phase was run for 200 ps, using a 1 fs time step with the same harmonic constraint as in the S2 case. During the equilibration phase, the harmonic constraints were gradually reduced to zero, with the exception of terminal Cα atoms. Atoms on the C- and N-termini were restrained by use of geometrical (internal) restraints on the last three O-N pairs, for example: distance O(1)–N(5) (1 and 5 are residue numbers) was kept to ∼3 Å, to keep proper helical geometry and to keep from spontaneous uncoiling during the simulations. Equilibrium MD simulations were performed for 30 ns and 60 ns to check the convergence of the simulations.
RESULTS
The lateral and stretching stiffness for the α-helical model system and the S2 subdomain are reported. Both the bending and stretching values are determined by nonequilibrium, equilibrium, and normal mode analysis. The structural parameters used for the α-helix and S2 coiled coil are given in Table 1.
Model system results
Normal mode analysis and equilibrium MD were used for the α-helix.
NM analysis—lateral stiffness (bending)
The normal modes of poly-Ala α-helix are well resolved, so that certain normal modes (and their frequencies) of the helix could be easily associated with the particular type of motion. The first two NMs with the nonzero frequencies, which correspond to bending in lateral directions, are almost degenerated with a frequency of ∼0.8cm−1 (these modes are shown as a movie file in the Supplementary Material (see Movie S1 and Figs. S2 and S3 in Supplementary Material, Data S1). Using this bending frequency and Eqs. 5 and 6, the lateral stiffness for the 10 nm long the poly-Ala α-helix is ∼1.2 pN/nm. This result is in excellent agreement with the study of Choe and Sun (52); their estimate from the calculated persistence length (∼100 nm) is ∼1.23 pN/nm.
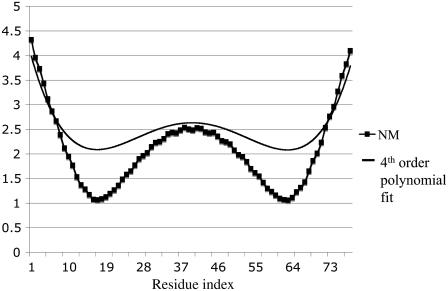
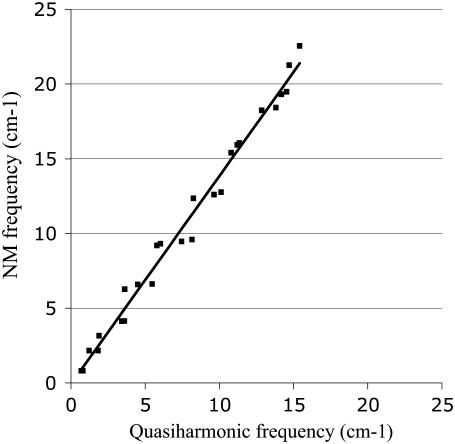
Fig. 3 shows the overall root mean-square fluctuation (RMSF) for the Cα atoms calculated from NM, quasiharmonic, and MD simulations at 300 K; the quasiharmonic modes were obtained from the latter. In Fig. 3, a fourth-order polynomial fit to the MD RMSF is shown. Detailed results are presented in Fig. S1 (Data S1); the values for the individual Cα atoms fluctuate with the helical periodicity. The quasiharmonic approximation results are essentially identical to those of full MD simulations and the NMA follows the general behavior shown in Fig. S1 (Data S1), but with overall larger fluctuations. Since the MD simulation is expected to be the most reliable, the vibrational analysis based on the quasiharmonics approximation should be also. In Table S1 (Data S1), the overlap matrix for the first 25 normal mode vectors from NMA and quasiharmonic analysis is given. Many of the lowest modes are similar (large overlap), or interchanged in frequency, or involve mixing of two modes; the higher modes are more mixed. Fig. 4 compares the vibrational frequencies obtained from two models. The values of the NM are in excellent agreement with the quasiharmonic frequencies for the lowest bending modes (0.70 cm−1 vs. 0.80 cm−1 and 0.81 cm−1 vs. 0.80 cm−1). These results suggest that the frequency-based (frequencies obtained from NMA) calculations of the lateral stiffness should be also reasonably accurate for the S2 construct. However, overall the NM frequencies tend to be higher, as expected, so the slope of the line in Fig. 4 is 1.39.
FIGURE 3.
Magnitude of the RMSF for Cα atoms of the 78-residue poly-Ala α-helix from NM and fourth-order polynomial fit of the RMSF obtained from the MD simulations. Quasiharmonic and MD curves are essentially identical (see also Fig. S1).
FIGURE 4.
Frequencies from NM and quasiharmonic analysis.
Stretching stiffness: NM analysis
Analysis of NM vectors shows that vibrational mode 17 is an accordion mode, describing stretching motion along the helix axis (see Movie S2 in Data S1). An analogous mode was also found in the quasiharmonics analysis (mode 25). The frequencies of the stretching mode are 9.19 cm−1 in NMA and 5.47 cm−1 in the quasiharmonic analysis. These values are much larger than the first bending frequency, as expected. The ratio between the quasiharmonic and NM frequencies is ∼1.7. The calculated stretching stiffness and Young's modulus for a 10 nm long α-helix, obtained from Eq. 7, are 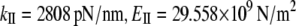 from the NMA and
from the NMA and 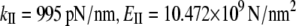 from the quasiharmonic analysis. Scaled to 60 nm long, the α-helix NMA gives
from the quasiharmonic analysis. Scaled to 60 nm long, the α-helix NMA gives 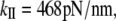 whereas the quasiharmonic analysis gives
whereas the quasiharmonic analysis gives 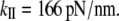 The values for
The values for 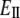 are in good agreement with those obtained in earlier studies ((41) (23.1 × 109 N/m2)). The difference between harmonic and quasiharmonic values suggests that the stretching motion is significantly more anharmonic than the bending motion. The importance of anharmonicity in the fluctuations was observed previously (53) in studies of shorter α-helical systems. However, the fact that even the quasiharmonic approximation gives too high a value for the Young's modulus relative to the full equilibrium dynamics (see below) indicates that the stretching energy surface is quite complex.
are in good agreement with those obtained in earlier studies ((41) (23.1 × 109 N/m2)). The difference between harmonic and quasiharmonic values suggests that the stretching motion is significantly more anharmonic than the bending motion. The importance of anharmonicity in the fluctuations was observed previously (53) in studies of shorter α-helical systems. However, the fact that even the quasiharmonic approximation gives too high a value for the Young's modulus relative to the full equilibrium dynamics (see below) indicates that the stretching energy surface is quite complex.
Stretching stiffness: equilibrium-MD simulation
A 30 ns equilibrium (EQ)-MD simulation with a fixed C-terminus (the first three Cα atoms) was performed and Eq. 9 was used to determine the stretching stiffness. Ten different pairs of atoms were chosen to represent the axial coordinate. These atom pairs are residues 6 and 72 (6 residues from the N-and C-termini), 8 and 70 (8 residues from the N-and C-termini), 10 and 68 (10 residues from the N-and C-termini), 12 and 66 (12 residues from the N-and C-termini), 14 and 64 (14 residues from the N-and C-termini), 16 and 62 (16 residues from the N-and C-termini), and combinations 10 and 72, 10 and 70, 10 and 66, and 10 and 64. Even though these distance fluctuations are not independent because of the correlated motion of the atoms, the averaging provides better statistics. To minimize end effects, all of the chosen pairs were at least 6 residues from the N-and C-termini.
Changes in distance (length) between pair of atoms (L), time average length (〈L〉), and apparent stretching modulus (the stretching constant multiplied by the length, i.e., 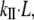 a distance independent variable so that it can be easily compared) are given in Table 2. Once multiplied by corresponding distances, the average apparent stretching modulus is ∼3850 ± 785 pN. For an α-helix that is 60 nm long (in analogy to the S2 length) the corresponding stiffness (spring constant) value is kII ∼ 64 pN/nm. Even for 30 ns, however, there are still convergence issues: apparent stretching modulus (for the first 10 ns) ∼5376 pN, (for the second 10 ns) ∼5010 pN, and (for the third 10ns) ∼3158 pN. To further check convergence, a 60 ns EQ-MD simulation with a fixed end (as above) was performed. The average apparent stretching modulus is ∼4024 ± 837 pN, slightly larger than the 30 ns value. For an α-helix, 60 nm long,
a distance independent variable so that it can be easily compared) are given in Table 2. Once multiplied by corresponding distances, the average apparent stretching modulus is ∼3850 ± 785 pN. For an α-helix that is 60 nm long (in analogy to the S2 length) the corresponding stiffness (spring constant) value is kII ∼ 64 pN/nm. Even for 30 ns, however, there are still convergence issues: apparent stretching modulus (for the first 10 ns) ∼5376 pN, (for the second 10 ns) ∼5010 pN, and (for the third 10ns) ∼3158 pN. To further check convergence, a 60 ns EQ-MD simulation with a fixed end (as above) was performed. The average apparent stretching modulus is ∼4024 ± 837 pN, slightly larger than the 30 ns value. For an α-helix, 60 nm long, 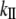 is ∼67 pN/nm. Since the 30 ns and 60 ns simulations give almost the same stretching stiffness, the results appear to be relatively well converged. An analysis that measures fluctuations of the contour length of the α-helix gave a result in reasonable agreement (
is ∼67 pN/nm. Since the 30 ns and 60 ns simulations give almost the same stretching stiffness, the results appear to be relatively well converged. An analysis that measures fluctuations of the contour length of the α-helix gave a result in reasonable agreement (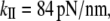 for a 60 nm long α-helix). This additional analysis was done by dividing the α-helix into parts that are ∼10 amino acids long, following the length of these parts during the MD trajectory and adding the lengths together to get the total length of the helix. Its fluctuations are calculated as a standard deviation of the total length.
for a 60 nm long α-helix). This additional analysis was done by dividing the α-helix into parts that are ∼10 amino acids long, following the length of these parts during the MD trajectory and adding the lengths together to get the total length of the helix. Its fluctuations are calculated as a standard deviation of the total length.
TABLE 2.
Stretching stiffness of 78 residue poly-Ala α-helix
| Segment residue numbers | 〈(L–Lo)2〉 (Å2) | Length L (Å) | Apparent modulus (pN) |
|---|---|---|---|
| 6–72 | 1.29 | 96.65 | 3100.3 |
| 8–70 | 1.16 | 90.85 | 3248.9 |
| 10–68 | 1.09 | 85.06 | 3217.2 |
| 12–66 | 0.90 | 79.27 | 3636.9 |
| 14–64 | 0.74 | 73.49 | 4086.0 |
| 16–62 | 0.52 | 67.73 | 5369.5 |
| 10–72 | 1.14 | 90.86 | 3292.2 |
| 10–70 | 0.87 | 88.04 | 4171.5 |
| 10–66 | 0.69 | 82.28 | 4950.9 |
| 10–64 | 0.96 | 79.27 | 3416.6 |
From 30 ns MD simulations; L is the axial length and Lo is the average length; see text for details. Stretching stiffness multiplied by length.
When the above values (60–80 pN/nm) are compared to the stretching stiffness calculated from vibrational analysis (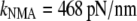 and
and 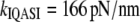 ), it is seen that the vibrational methods overestimate stiffness by ∼6-fold (NMA) or ∼2-fold (quasiharmonic). The change is large (three times) when the anharmonicity is taken into account approximately with the quasiharmonic method, but it still does not reach MD value. In comparison to the bending surface, the energy surface involved in stretching seems to be more complex (53).
), it is seen that the vibrational methods overestimate stiffness by ∼6-fold (NMA) or ∼2-fold (quasiharmonic). The change is large (three times) when the anharmonicity is taken into account approximately with the quasiharmonic method, but it still does not reach MD value. In comparison to the bending surface, the energy surface involved in stretching seems to be more complex (53).
S2 subdomain—lateral stiffness (bending)
NM analysis of S2 subdomain
The lowest frequency normal modes of a given system generally describe the most important conformational fluctuations of a molecule (54). In the case of the S2 subdomain, as for the α-helix, the first normal mode (with frequency different than zero) clearly corresponds to a bending motion and can be used to estimate flexural (bending) rigidity according to Eq. 6. The frequency of this mode is 0.76 cm−1. Taking into account the parameters of the system (see Table 1), the estimated lateral stiffness is 3.1pN/nm for 9.48 nm long construct. This stiffness is of the same order as the lateral stiffness of the α-helix of similar length ∼1.2 pN/nm (L = 10 nm). The S2 subdomain is a coiled-coil structure made of two α-helices, so this system is expected to be stiffer than a single α-helix. To obtain the lateral stiffness of the 60 nm long S2, the calculated value for the 9.48 nm long S2 (3.1 pN/nm) should be scaled by (9.48 nm/60nm)3, according to Eqs. 5 and 6. This yields the lateral stiffness for S2 of 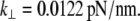
Equilibrium MD
The lateral stiffness can be estimated through the equilibrium fluctuations of a chosen coordinate for a particular set of atoms (close to the N-terminus, with the C-terminus clamped in the equilibrium position; see above). Combining Eqs. 8 b and 5, the lateral stiffness constant is given:
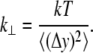 |
(11) |
Atomic fluctuations over set of five atoms, close to the N-terminus (as described in the previous section), were chosen to represent the bending coordinate. Five 10 ns EQ-MD simulations, described above, were used to extract time averages of the y fluctuations in the chosen atomic positions. Table 3 gives the summary (average over five 10 ns EQ-MD simulations) of those fluctuations and corresponding lateral stiffness. For an average S2, L = 9.48 nm, the average lateral stiffness is 2.63 pN/nm, in excellent agreement with a non-EQ-MD value of 2.2 pN/nm. Scaling up to a 60 nm long S2 gives k⊥ (long S2) = 2.63 × (9.48/60)3 = 0.0104 pN/nm.
TABLE 3.
Bending (lateral) stiffness analysis for S2 from EQ-MD
| Atom studied | 〈(Y–Yo)2〉 (Å)2 | Lateral stiffness (k⊥) (pN/mm) |
|---|---|---|
| 852 CA | 181.50 | 2.4 |
| 853 CA | 174.88 | 2.5 |
| 854 CA | 165.13 | 2.7 |
| 855 CA | 160.06 | 2.8 |
| 856 CA | 153.40 | 2.9 |
| 852 CB | 186.82 | 2.4 |
| 853 CB | 179.70 | 2.5 |
| 854 CB | 168.80 | 2.7 |
| 855 CB | 165.45 | 2.7 |
| 856 CB | 157.60 | 2.8 |
Averages over five 10 ns EQ-MD with fixed C-terminus; 〈(Y–Yo)2〉 are squared fluctuations in the y direction. For lateral stiffness calculations, see Eq. 11
Nonequilibrium MD
Since one end has to be fixed to study the effect of applying an external force, fixing different numbers of terminal Cα atoms was studied for 5pN force and the results are summarized in Table 4. As can be seen from the table, fixing 4, 6, 8, or 12 Cα atoms at the C-terminus does not influence the final result for the lateral stiffness to a large extent. The minimal number of Cα atoms that could be fixed without rotation developing on the C-terminal was four, and all the following calculations were done with four C-terminal Cα atoms fixed.
TABLE 4.
Influence of fixing different numbers of Cα-terminal atoms on the bending characteristics of the S2 subdomain
Five data sets for the  values as a function of the force were generated and slopes of those graphs were obtained (see Fig. 5). The quantity
values as a function of the force were generated and slopes of those graphs were obtained (see Fig. 5). The quantity 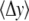 is a geometrical parameter determining the flexural rigidity and lateral stiffness,
is a geometrical parameter determining the flexural rigidity and lateral stiffness, 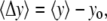 where
where 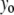 is the value of the y coordinate in equilibrium (starting geometry from corresponding EQ-MD) and
is the value of the y coordinate in equilibrium (starting geometry from corresponding EQ-MD) and 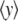 is the time average over a 2 ns MD simulation. The linearity of the plot is in accord with the S2 coiled-coil behavior as an elastic rod in this force regime. Each of these slopes is then multiplied with the corresponding average length of S2 (60 nm), and a “distance independent” (
is the time average over a 2 ns MD simulation. The linearity of the plot is in accord with the S2 coiled-coil behavior as an elastic rod in this force regime. Each of these slopes is then multiplied with the corresponding average length of S2 (60 nm), and a “distance independent” (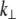 ) lateral stiffness was obtained; one example is given in Fig. 5 (for point: Cα residue No. 152, B chain).
) lateral stiffness was obtained; one example is given in Fig. 5 (for point: Cα residue No. 152, B chain).
FIGURE 5.
Bending stiffness of an S2 from the non-EQ-MD simulations. The force was applied to the N-terminus perpendicular to the coiled-coil axes and 〈ΔY〉 is the average lateral displacement obtained in the simulations (for details see text).
Slopes from five graphs described above for different lengths, lateral stiffness (slope of the graphs), apparent modulus (slope times length L), and Young's modulus (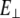 ) estimated from the flexural rigidity (
) estimated from the flexural rigidity (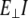 ) are given in Table 5. The length-independent apparent bending modulus is introduced so that results obtained for different values of L can be compared directly. As can be seen from the table, these apparent moduli are very similar and all fluctuate around an average value of 21.2 pN. For an S2 fragment studied here, which is 9.48 nm long, the average lateral stiffness is 2.2 pN/nm. To interpolate to long S2, assumptions are that all variables from Eq. 5 are the same in the short and long fragment, except length. The lateral stiffness for long S2 (60 nm) is ∼2.2 × (9.48 nm/60nm)3 ∼ 0.00866 pN/nm. The lateral stiffness is much smaller (∼104 times) than stretching stiffness (see below) of the S2 subdomain. Young's modulus,
) are given in Table 5. The length-independent apparent bending modulus is introduced so that results obtained for different values of L can be compared directly. As can be seen from the table, these apparent moduli are very similar and all fluctuate around an average value of 21.2 pN. For an S2 fragment studied here, which is 9.48 nm long, the average lateral stiffness is 2.2 pN/nm. To interpolate to long S2, assumptions are that all variables from Eq. 5 are the same in the short and long fragment, except length. The lateral stiffness for long S2 (60 nm) is ∼2.2 × (9.48 nm/60nm)3 ∼ 0.00866 pN/nm. The lateral stiffness is much smaller (∼104 times) than stretching stiffness (see below) of the S2 subdomain. Young's modulus, 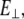 is estimated using Eq. 5 (taking I = 0.317 nm4) to be ∼1967 pN/nm2.
is estimated using Eq. 5 (taking I = 0.317 nm4) to be ∼1967 pN/nm2.
TABLE 5.
Apparent bending modulus from non equilibrium MD simulations (see text)
| Point* | Slope* (pN/Å) | L* (Å) | Apparent modulus† (pN) |
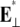 (pN/nm2) (pN/nm2) |
|---|---|---|---|---|
| CA 152 | 0.217 | 96.9 | 21.1 | 2057 |
| CA 153 | 0.216 | 96.1 | 20.8 | 1997 |
| CA 154 | 0.222 | 95.1 | 21.1 | 1989 |
| CA 155 | 0.230 | 92.6 | 21.3 | 1902 |
| CA 156 | 0.237 | 91.3 | 21.7 | 1879 |
Point is defined as Cα residue number 152 (153, 154, …, 156) on the B chain used to measure 〈Δy〉; the slope of the graph of 〈Δy〉 (lateral displacement) as a function of the applied force; L is the length, and E⊥ is Youngs bending modulus (see text).
Value of the apparent module is obtained as product of slope and L (length) values; it represents length independent of stiffness (see text).
The results from three applied techniques, described above, are in very good agreement: the calculated lateral stiffness k⊥ (nonequilibrium) = 0.0086 pN/nm, k⊥ (EQ-MD) = 0.0104 pN/nm, and k⊥ (NM) = 0.0122 pN/nm.
S2 subdomain—stretching stiffness
NM analysis
The vibrational analysis shows that mode 24 is an accordion mode, describing the stretching motion along the coiled-coil axis. The frequency of this mode is 6.92 cm−1. The calculated stretching stiffness obtained from Eq. 7 is 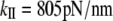 (for a 60 nm long S2 subdomain). Taking the ratio between the quasiharmonic and NM analysis, obtained in the α-helix calculations (1.7), one can estimate that the quasiharmonic frequency for the S2 would be 4.07cm−1 and the corresponding stiffness constant would be
(for a 60 nm long S2 subdomain). Taking the ratio between the quasiharmonic and NM analysis, obtained in the α-helix calculations (1.7), one can estimate that the quasiharmonic frequency for the S2 would be 4.07cm−1 and the corresponding stiffness constant would be 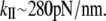 As for the α-helix, the stiffness calculated from NM (or estimated from the quasiharmonic modes) analysis is >3 times larger than from the other methods, indicating that anharmonic contributions are significant (53).
As for the α-helix, the stiffness calculated from NM (or estimated from the quasiharmonic modes) analysis is >3 times larger than from the other methods, indicating that anharmonic contributions are significant (53).
Equilibrium MD
To obtain the axial stiffness from the equilibrium simulations, fluctuations of the distance between two end points (length) were extracted from 10 ns MD, and using Eq. 9, the stretching stiffness is calculated.
Table 6 gives a summary of squared, averaged fluctuations of the length (averaged over five different “end to end” distances) and apparent stretching modulus. The average value of the apparent stretching modulus is ∼3448 pN (average of the last column from Table 5). This value is averaged over five, 10 ns EQ-MD simulations, with the C-terminal fixed (Cα atoms on the C-terminal of both the A and B chain), starting with four different initial geometries. For 10 ns MD simulations, the averaged value of the axial stiffness for long S2 fragment is ∼58 pN/nm. This is also in good agreement with both the experimental estimate (lower bound) ∼60 pN/nm and the non-EQ-MD calculation of ∼80 pN/nm.
TABLE 6.
Axial stiffness analysis for S2 from EQ-MD
| Residue numbers* | 〈(L–Lo)2〉 (Å2) | Length Lo (Å) | Apparent stretching modulus (pN) |
|---|---|---|---|
| 854–908 | 1.26 | 79.61 | 2789.7 |
| 856–904 | 1.00 | 68.04 | 3142.6 |
| 960–902 | 0.59 | 62.03 | 4759.6 |
| 862–900 | 0.56 | 56.75 | 4307.9 |
Averages over four 10 ns EQ-MD with Cα atoms on the C-terminus of both the A and B chain fixed; Lo is the equilibrium axial length, 〈(L–Lo)2〉 are squared length fluctuations.
Residue numbers refer to the number of the residues that were followed in the simulations to obtain the length fluctuations (see text).
Nonequilibrium MD
Details of the simulations and the methodology used to obtain stretching stiffness are described in the Computational Methods (Nonequilibrium MD) section. The average value (over 10 distances) for the apparent stretching modulus is ∼4800 pN. The fluctuation in the axial distance between end points as a function of the force is given in Fig. 6. Again, linearity of the graph confirms the assumption that the S2 fragment acts as an elastic rod in this force regime (10–40 pN). For an S2 fragment (L ∼ 9.48 nm), 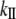 is ∼506.3 pN/nm. The stretching stiffness of long S2 (∼60 nm) is ∼80 pN/nm. This value is used to estimate
is ∼506.3 pN/nm. The stretching stiffness of long S2 (∼60 nm) is ∼80 pN/nm. This value is used to estimate 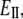 from Eq. 3, and for long S2, taking that A = 1.9 nm2,
from Eq. 3, and for long S2, taking that A = 1.9 nm2, 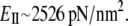
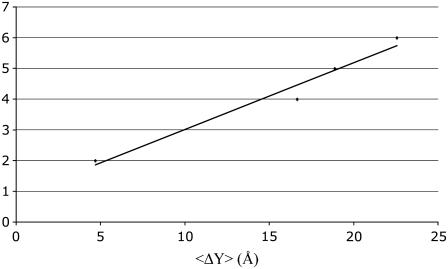
FIGURE 6.
Stretching stiffness of S2 from the non-EQ-MD simulations. The force was applied to the N-terminus along the coiled-coil axes and 〈Δl〉 is the average axial displacement obtained in the simulations (for details see text).
The experimentally estimated stretching stiffness from coiled-coil persistence length (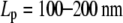 ) (35) and also from overall stiffness of the myosin filament is in the range between 60 and 80 pN/nm for 60 nm long S2.
) (35) and also from overall stiffness of the myosin filament is in the range between 60 and 80 pN/nm for 60 nm long S2.
CONCLUSIONS
Several different methods (i.e., NM analysis, equilibrium, and nonequilibrium MD) were used to study the stretching and bending elasticity of an α-helix and the structurally characterized S2 subfragment of myosin II. Test calculations using the same methodology for a 78-residue poly-Ala α-helix model showed that results of satisfactory accuracy could be obtained. This conclusion is based on a comparison of the results presented here with estimates from experimental studies and other published simulations. Interestingly, the bending motion appeared to be better described using the harmonic approximation than the stretching motion. The energy surface that describes stretching was found to be significantly anharmonic in a previous study (53).
For the S2 subdomain, which is of primary interest, the flexural rigidity and lateral stiffness results calculated with the three methods (non-EQ-MD, EQ-MD, and NM) are in very good agreement. This finding is particularly important because for systems like the whole S2 subdomain (60 nm), the required MD simulations would be very time consuming. The results indicate that an NM analysis, which provides an affordable alternative, can be used to estimate the flexural rigidity and lateral stiffness (I. Adamovic, unpublished). Very high flexibility (small lateral stiffness ∼0.01 pN/nm for L = 60 nm) shows the importance of incorporating bending motion in a model of actomyosin in a three-dimensional sarcomere lattice.
Our results are in very good agreement with previous experimental studies (55–57) of the elastic properties of different coiled-coil structures. These studies estimated persistence length of various coiled-coil (tropomyosin, myosin tick filament, S2 subdomain) to be in the range from 130 to 170 nm, which translates into a lateral stiffness of ∼0.008–0.01 pN/nm, in very good agreement with the calculated lateral stiffness k⊥ (nonequilibrium) = 0.0086 pN/nm, k⊥ (equilibrium MD) = 0.0104 pN/nm, and k⊥ (NM) = 0.0122 pN/nm. Based on our study and the comparison with the experimental studies just cited, it appears that there is a “generic” value of the coiled-coil bending stiffness in the range from 0.008 to 0.01 pN/nm. Specific value may depend on the particular amino acid sequence, but this was not investigated in this report.
When stretching stiffness is determined and the results are compared with literature values, the main conclusion is that both the α-helix and S2 coiled-coil are much stiffer in the axial direction than in the lateral direction. An experimental study by Hvidt et al. (55) found that the stretching Young's modulus is 1.3 109 N/m2, which translates into a stretching stiffness of kII of 32 pN/nm (for 65nm long S2). This result, when scaled by (65/60)3 to obtain a value for 60 nm long S2, is ∼41 pN/nm. When compared with other experimental estimates of 60–80 pN/nm (35), their value appears somewhat too low.
Young's moduli for stretching (EII ∼ 2.526 109 N/m2) and for bending (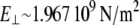 ) have similar values. The difference between
) have similar values. The difference between 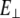 and EII reflects the specific geometry of the cross section of S2 at the molecular level.
and EII reflects the specific geometry of the cross section of S2 at the molecular level.
A comparison of the bending modulus of the coiled-coil and α-helix was made in the study by Wolgemuth and Sun (58). They found that the coiled-coil bending modulus is lower than twice that of the α-helix. Lateral stiffness constants from our study are k⊥ (nonequilibrium) = 0.0086 pN/nm, k⊥ (equilibrium MD) = 0.0104 pN/nm, and k⊥ (NM) = 0.0122 pN/nm, whereas the α-helix estimate is 0.0056 pN/nm (NM). Thus, our results also indicate that the stiffness of S2 is less than or equal to (depending on the method) twice that of the α-helix.
The cross-bridge stiffness includes the stretching stiffness of S2, the lateral stiffness of the lever arm, and the elasticity of the neck region (the unstructured part between the lever arm and the S2 subdomain). The stretching stiffness of S2 is much larger than the lateral stiffness of the lever arm and probably the stiffness of the neck of the myosin head. Thus, the stretching elasticity of S2 is expected to play a minor role in cross-bridge stretching. This is fortunate because the stretching stiffness is more difficult to calculate since the simple vibrational approximation has been shown not to be very accurate, e.g., the NM method tends to overestimate stretching stiffness. By contrast, the lateral stiffness of S2 could be of crucial importance in the binding of myosin to actin in three-dimensional sarcomere lattice.
An important finding is that S2 and α-helix (model for the lever arm) have similar elastic properties. Both the stretching and lateral stiffness of these two elements are the same orders of magnitude. This indicates that in correct contractile models, the elasticity both of these elements needs to be taken in account.
It is expected that the results obtained here will aid in developing improved models of muscle function.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Dr. W. Hwang for helpful comments based on a careful reading of the manuscript. Also, we thank Dr. J. J. Fredberg for a critical reading of the manuscript.
This study is supported in part by the National Institutes of Health (NIH) Training grant 5 T32 HL007118-30. (I.A.), NIH grant AR048776 (S.M.M.) and National Institutes of Health and Human Frontiers Science Program grants to Harvard University and the Universite Louis Pasteur, respectively (M.K.).
APPENDIX A
Sequence of the scallop myosin II S2 subdomain in three-letter code:
MET LYS GLU GLN LEU LYS GLN MET ASP LYS MET LYS GLU ASP LEU ALA LYS THR GLU ARG ILE LYS LYS GLU LEU GLU GLU GLN ASN VAL THR LEU LEU GLU GLN LYS ASN ASP LEU PHE GLY SER MET LYS GLN LEU GLU ASP LYS VAL GLU GLU LEU LEU SER LYS ASN TYR HIS LEU GLU ASN GLU VAL ALA ARG LEU LYS LYS LEU VAL GLY GLU ARG GLU GLU GLU MET LYS GLU GLN LEU LYS GLN MET ASP LYS MET LYS GLU ASP LEU ALA LYS THR GLU ARG ILE LYS LYS GLU LEU GLU GLU GLN ASN VAL THR LEU LEU GLU GLN LYS ASN ASP LEU PHE GLY SER MET LYS GLN LEU GLU ASP LYS VAL GLU GLU LEU LEU SER LYS ASN TYR HIS LEU GLU ASN GLU VAL ALA ARG LEU LYS LYS LEU VAL GLY GLU
Editor: Gregory A. Voth.
References
- 1.Craig, R., and R. Padron. 2004. The structure of contractile filaments. In Myology, A. G. Engel and C. Franzini-Armstrong, editors. McGraw-Hill, New York. 129–166.
- 2.Huxley, H. E., and J. Hanson. 1954. Changes in the cross-striations of muscle during contraction and stretch and their structural interpretation. Nature. 173:973–976. [DOI] [PubMed] [Google Scholar]
- 3.Huxley, A. F., and R. Niedergerke. 1954. Structural changes in muscle during contraction: interference microscopy of living muscle fibers. Nature. 173:971–973. [DOI] [PubMed] [Google Scholar]
- 4.Huxley, A. F. 1957. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 7:255–318. [PubMed] [Google Scholar]
- 5.Huxley, A. F., and R. M. Simmons. 1971. Proposed mechanism of force generation in striated muscle. Nature. 233:533–538. [DOI] [PubMed] [Google Scholar]
- 6.Holmes, K. C., and M. A. Geeves. 2000. The structural basis of muscle contraction. Philos. Trans. R. Soc. Lond. B Biol. Sci. 355:419–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lymn, R. W., and E. W. Taylor. 1971. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry. 10:4617–4624. [DOI] [PubMed] [Google Scholar]
- 8.Rayment, I., H. M. Holden, M. Whittaker, C. B. Yohn, M. Lorenz, K. C. Holmes, and R. A. Milligan. 1993. Structure of the actin-myosin complex and its implications for muscle contraction. Science. 261:58–65. [DOI] [PubMed] [Google Scholar]
- 9.Rayment, I., W. R. Rypniewski, K. Schmidt-Base, R. Smith, D. R. Tomchick, M. M. Benning, D. A. Winkelmann, G. Wesenberg, and H. M. Holden. 1993. Three-dimensional structure of myosin subfragment-1: a molecular motor. Science. 261:50–58. [DOI] [PubMed] [Google Scholar]
- 10.Spudich, J. A. 1994. How molecular motors work. Nature. 372:515–518. [DOI] [PubMed] [Google Scholar]
- 11.Geeves, M. A. 1991. The dynamics of actin and myosin association and the cross-bridge model of muscle contraction. Biochem. J. 274:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Geeves, M. A., and K. C. Holmes. 1999. Structural mechanism of muscle contraction. Annu. Rev. Biochem. 68:687–728. [DOI] [PubMed] [Google Scholar]
- 13.Molloy, J. E., J. E. Burns, J. C. Sparrow, J. Kendrick-Jones, R. T. Treager, and D. C. White. 1995. Movement and force produced by the single myosin head. Nature. 378:209–212. [DOI] [PubMed] [Google Scholar]
- 14.Veigel, C., M. L. Bartoo, D. C. White, J. C. Sparrow, and J. E. Moloy. 1998. The stiffness of rabbit skeletal actomyosin cross-bridges determined with an optical tweezers transductor. Biophys. J. 75:1424–1438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lombardi, V., G. Piazzesi, M. A. Ferenczi, H. Thirlwell, I. Dobbie, and M. Irving. 1995. Elastic distortion of myosin heads and repriming of the working stroke in muscle. Nature. 374:553–555. [DOI] [PubMed] [Google Scholar]
- 16.Steffen, W., A. Lewalle, and J. Sleep. 2008. Single-molecule measurement of the stiffness of the rigor myosin head. Biophys. J. 94:2160–2169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Piazzesi, G., M. Reconditi, M. Linari, L. Lucii, P. Bianco, E. Brunello, V. Decostre, A. Stewart, D. B. Gore, T. C. Irving, M. Irving, and V. Lombardi. 2007. Skeletal muscle performance determined by modulation of number of myosin motors. Cell. 131:784–795. [DOI] [PubMed] [Google Scholar]
- 18.Huxley, H. E., A. Stewart, H. Sosa, and T. Irving. 1994. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys. J. 67:2411–2421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wakabayashi, K., Y. Sugimoto, H. Tanaka, Y. Ueno, Y. Takezawa, and Y. Amemiya. 1994. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys. J. 67:2422–2435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Goldman, Y. E., and A. F. Huxley. 1994. Actin compliance: are you pulling my chain? Biophys. J. 67:2131–2133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mijailovich, S. M., J. J. Fredberg, and J. P. Butler. 1996. On the theory of muscle contraction: filament extensibility and the development of isometric force and stiffness. Biophys. J. 71:1475–1484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lombardi, V., and G. Piazzesi. 1990. The contractile response during steady lengthening of stimulated frog muscle fibres. J. Physiol. 431:141–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huxley, A. F., and S. Tideswell. 1996. Filament compliance and tension transients in muscle. J. Muscle Res. Cell Motil. 17:507–511. [DOI] [PubMed] [Google Scholar]
- 24.Uyeda, T. Q., P. D. Abramson, and J. A. Spudich. 1996. The neck region of the myosin motor domain acts as a lever arm to generate movement. Proc. Natl. Acad. Sci. USA. 93:4459–4464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Crick, F. H. C. 1953. The Fourier transform of a coiled coil. Acta Crystallogr. 6:685–689. [Google Scholar]
- 26.Crick, F. H. C. 1953. The packing of α-helices: simple coiled coils. Acta Crystallogr. 6:689–697. [Google Scholar]
- 27.Lupas, A. 1996. Coiled coils: new structures and new functions. Trends Biochem. Sci. 21:375–382. [PubMed] [Google Scholar]
- 28.Reference deleted in proof.
- 29.Lauzon, A. M., P. M. Fagnant, D. M. Warshaw, and K. M. Trybus. 2001. Coiled-coil unwinding at the smooth muscle myosin head-rod junction is required for optimal mechanical performance. Biophys. J. 80:1900–1904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Liu, J., T. Wendt, D. Taylor, and K. Taylor. 2003. Refined model of the 10S conformation of smooth muscle myosin by cryo-electron microscopy 3D image reconstruction. J. Mol. Biol. 329:963–972. [DOI] [PubMed] [Google Scholar]
- 31.Chakrabarty, T., M. Xiao, R. Cooke, and P. R. Selvin. 2002. Holding two heads together: stability of the myosin II rod measured by resonance energy transfer. Proc. Natl. Acad. Sci. USA. 999:6011–6016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chakrabarty, T., C. Yengo, C. Baldacchino, L. Q. Chen, H. L. Sweeney, and P. R. Selvin. 2003. Does the S2 rod of myosin II uncoil upon two-headed binding to actin? A leucine-zippered HMM study. Biochemistry. 42:12886–12892. [DOI] [PubMed] [Google Scholar]
- 33.Feynman, R. P. The Feynman Lectures on Physics. Addison-Wesley, Reading, MA.
- 34.Landau, L. D., and E. M. Lifshitz. 1986. Theory of Elasticity. Pergamon Press, Oxford, New York.
- 35.Howard, J. 2001. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates, Sunderland, MA.
- 36.Matsumoto, A., and N. Go. 1999. Dynamic properties of double-stranded DNA by normal mode analysis. J. Chem. Phys. 110:11070–11075. [Google Scholar]
- 37.Park, J., B. Kahng, R. D. Kamm, and W. Hwang. 2006. Atomistic simulation approach to a continuum description of self-assembled β-sheet filaments. Biophys. J. 90:2525–2533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Choe S., and S. X. Sun, 2007. Bending elasticity of anti-parallel β-sheets. Biophys. J. 92:1204–1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Itoh, K., and T. Shimanouchi. 1970. Vibrational frequencies and modes of α-helix. Biopolymers. 9:383–399. [DOI] [PubMed] [Google Scholar]
- 40.Suezaki, Y., and N. Go. 1976. Fluctuations and mechanical strength of α-helices of polyglycine and poly(L-alanine). Biopolymers. 15:2137–2153. [DOI] [PubMed] [Google Scholar]
- 41.Schaufele, R. F., and T. Shimanouchi. 1967. Longitudinal acoustical vibrations of finite polymethylene chains. J. Chem. Phys. 47:3605–3610. [Google Scholar]
- 42.Li, Y., J. H. Brown, L. Reshetnikova, A. Blazsek, L. Farkas, L. Nyitray, and C. Cohen. 2003. Visualization of an unstable coiled coil from the scallop myosin rod. Nature. 424:341–345. [DOI] [PubMed] [Google Scholar]
- 43.Blankenfeldt, W., N. H. Thoma, J. S. Wray, M. Gautel, and I. Schlichting. 2006. Crystal structures of human cardiac β-myosin II S2-{Delta} provide insight into the functional role of the S2 subfragment. Proc. Natl. Acad. Sci. USA. 103:17713–17717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 45.Lazaridis, T., and M. Karplus. 1999. Effective energy function for proteins in solution. Proteins. 35:133–152. [DOI] [PubMed] [Google Scholar]
- 46.Nose, S. 1984. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 52:255–268. [Google Scholar]
- 47.Hoover, W. G. 1985. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A. 31:1695–1697. [DOI] [PubMed] [Google Scholar]
- 48.Paci, E., and M. Karplus. 1999. Forced unfolding of fibronectin type 3 modules: an analysis by biased molecular dynamics simulations. J. Mol. Biol. 288:441–459. [DOI] [PubMed] [Google Scholar]
- 49.Paci, E., and M. Karplus. 2000. Unfolding proteins by external forces and temperature: the importance of topology and energetics. Proc. Natl. Acad. Sci. USA. 97:6521–6526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Schwaiger, I., C. Sattler, D. R. Hostetter, and M. Rief. 2002. The myosin coiled-coil is a truly elastic protein structure. Nat. Mater. 1:232–235. [DOI] [PubMed] [Google Scholar]
- 51.Bagshaw, C. R. 1993. Muscle Contraction, 2nd ed. Chapman & Hall, New York, NY.
- 52.Choe, S., and S. X. Sun. 2005. The elasticity of α-helices. J. Chem. Phys. 122:244912–244919. [DOI] [PubMed] [Google Scholar]
- 53.Levy, R. M., D. Perahia, and M. Karplus. 1982. Molecular dynamics of an α-helical polypeptide: temperature dependence and deviation from harmonic behavior. Proc. Natl. Acad. Sci. USA. 79:1346–1350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Brooks, B. R., and M. Karplus. 1983. Harmonic dynamics of proteins: normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc. Natl. Acad. Sci. USA. 80:6571–6575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hvidt, S., F. H. Nestler, M. L. Greaser, and J. D. Ferry. 1982. Flexibility of myosin rod determined for dilute solution viscoelastic measurements. Biochemistry. 21:4064–4073. [DOI] [PubMed] [Google Scholar]
- 56.Swenson, C. A., and N. C. Stellwagen. 1989. Flexibility of smooth and skeletal tropomyosins. Biopolymers. 28:955–963. [DOI] [PubMed] [Google Scholar]
- 57.Philips, G. N., Jr., and S. Chacko. 1996. Mechanical properties of tropomyosin and implication for muscle regulation. Biopolymers. 38:89–95. [DOI] [PubMed] [Google Scholar]
- 58.Wolgemuth, C. H., and S. X. Sun. 2006. Elasticity of α-helical coiled-coils. Phys. Rev. Lett. 97:248101. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.