Single-molecule nonequilibrium periodic Mg²⁺-concentration jump experiments reveal details of the early folding pathways of a large RNA

Abstract

The evolution of RNA conformation with Mg²⁺ concentration ([Mg²⁺]) is typically determined from equilibrium titration measurements or nonequilibrium single [Mg²⁺]-jump measurements. We study the folding of single RNA molecules in response to a series of periodic [Mg²⁺] jumps. The 260-residue catalytic domain of RNase P RNA from Bacillus stearothermophilus is immobilized in a microfluidic flow chamber, and the RNA conformational changes are probed by fluorescence resonance energy transfer (FRET). The kinetics of population redistribution after a [Mg²⁺] jump and the observed connectivity of FRET states reveal details of the folding pathway that complement and transcend information from equilibrium or single-jump measurements. FRET trajectories for jumps from [Mg²⁺] = 0.01 to 0.1 mM exhibit two-state behavior whereas jumps from 0.01 mM to 0.4 mM exhibit two-state unfolding but multistate folding behavior. RNA molecules in the low and high FRET states before the [Mg²⁺] increase are observed to undergo dynamics in two distinct regions of the free energy landscape separated by a high barrier. We describe the RNA structural changes involved in crossing this barrier as a “hidden” degree of freedom because the changes do not alter the detected FRET value but do alter the observed dynamics. The associated memory prevents the populations from achieving their equilibrium values at the end of the 5- to 10-sec [Mg²⁺] interval, thereby creating a nonequilibrium steady-state condition. The capability of interrogating nonequilibrium steady-state RNA conformations and the adjustable period of [Mg²⁺]-jump cycles makes it possible to probe regions of the free energy landscape that are infrequently sampled in equilibrium or single-jump measurements.

RNA molecules perform both regulatory and catalytic functions (1). Adopting the proper conformation(s) is crucial for their function. Determining the mechanisms by which RNA searches for and finds the proper tertiary structure (i.e., native state) remains a challenging problem (2). Cations, such as Mg²⁺, are essential to the RNA folding process; nonspecifically bound cations neutralize the highly charged RNA phosphate backbone while specifically bound cations help form and stabilize tertiary interactions and structures (3, 4). The electrostatic and hydrogen-bond (base pairing) interactions create a free energy landscape that determines both the conformational search process and the dynamics related to function.

Like proteins, the free energy landscape of RNA is believed to be rugged. It has been shown that protein dynamics/kinetics can be power law distributed (5, 6) whereas RNA conformational changes tend to exhibit discrete behavior (7, 8). Spontaneous conformational fluctuations associated with thermal motion are observed in equilibrium measurements. Whereas the region near the minimum of the free energy landscape is primarily sampled in equilibrium measurements, nonequilibrium perturbation or (buffer) concentration-jump experiments might probe a larger region as the molecules move farther from their initial equilibrium conformation(s). The nonequilibrium relaxation to new conformations more directly reveal the pathway(s) that RNA molecules take to the new minimum free energy state.

Ensemble concentration-jump measurements using rapid mixing techniques have been widely applied to study RNA and protein folding (9–14). The population relaxation process is assumed to be well described by the fluctuation-dissipation theorem, which, together with detailed balance, allows determination of the equilibrium rate constants (15). The measured ensemble-averaged kinetics allow constructing (minimal) kinetic schemes to describe folding or unfolding.

Single-molecule fluorescence resonance energy transfer (FRET) measurements of surface immobilized RNA have been a powerful approach for studying equilibrium conformational dynamics of DNA and RNA (7, 14, 16–18). By contrast, only a few single-molecule concentration-jump experiments have been reported for RNA (19–21). In these, a single concentration-jump perturbation was applied to the RNA molecules and the subsequent relaxation behavior was observed. These experiments allowed direct observation of an RNA folding pathway.

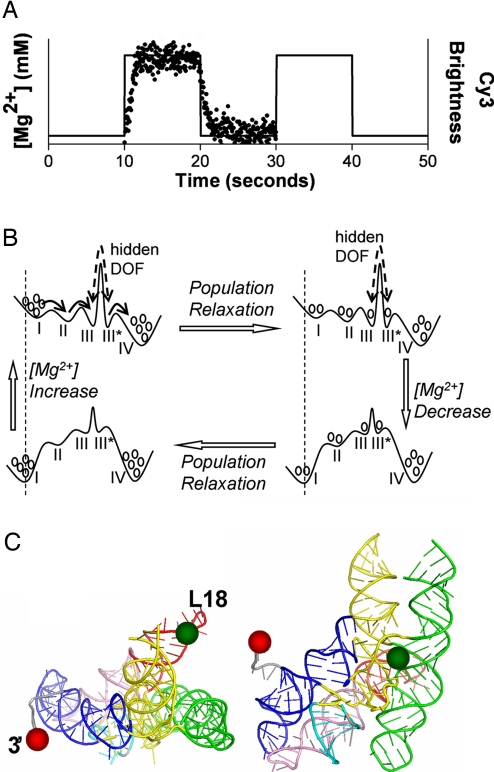
Here, we use FRET to observe the structural response of single RNA molecules to periodic Mg²⁺ concentration ([Mg²⁺]) jumps (Fig. 1A) to study the folding of the 260-residue catalytic domain of the thermophilic RNase P RNA [termed CthermoL18; for details, see refs. 22 and 23, and supporting information (SI) Materials and Methods and Fig. S1]. The kinetic scheme shown in Fig. 1B illustrates the experiment: each [Mg²⁺] jump induces a change of the free energy landscape on which the RNA population subsequently redistributes. Alternating forward and reverse jumps create a cycle (24). When the period of the [Mg²⁺] jumps is longer than the slowest relaxation process, the periodic [Mg²⁺]-jump measurement gives information equivalent to the single-jump experiment. However, when the [Mg²⁺]-jump period is shorter, the distribution of configurations of the RNA molecules before each [Mg²⁺] jump will be different compared with the single-jump experiment. Therefore, such nonequilibrium steady-state measurements allow probing regions of the free energy landscape that may otherwise escape detection via poor sampling.

Fig. 1.

Schematic of the periodic [Mg²⁺]-jump experiment and cycling of the energy landscape. (A) [Mg²⁺] profile applied in the experiments. The lengths of the high and low [Mg²⁺] intervals are both 10 sec with a 50 μl/min flow rate for all of the experiments reported here. The solid line shows the idealized [Mg²⁺] change over time. The overlaid dotted data show the averaged brightness of isolated Cy3 molecules in one field of view. (B) Schematic free energy landscape for the periodic [Mg²⁺]-jump experiment. Circles represent the population in each E_FRET level. The vertical dashed lines show that the E_FRET value of each E_FRET state shifts to a higher value at higher [Mg²⁺] due to electrostatic relaxation. The solid arrows (upper left) represent the folding pathways observed for molecules starting from the low or high E_FRET state. These two cases are separated by a high barrier associated with the hidden DOF. The dashed double arrows are meant to indicate that transitions over the high barrier of the hidden DOF are seldom observed within the 10-sec [Mg²⁺] step. The number of basins, exact barrier heights or well depths, E_FRET values, and population at each E_FRET state are different for the three [Mg²⁺]-jump conditions. (Note: the coordinates to the left and right of the large barrier are different due to the presence of the state of the hidden DOF. The figure is a 1D representation of a 2D energy landscape.) (C) Locations of the L18 loop (Cy3, green spheres) and 3′ end (Cy5, red spheres) on the tertiary structure model of Cthermo from ref. 25.

For the experiments reported here, the full [Mg²⁺]-jump period is 20 sec; 10 sec each for the low and high [Mg²⁺] intervals. For CthermoL18, this period is too short for the system to achieve equilibrium before the next jump. This is observed with striking clarity in the kinetics of relaxation associated with each [Mg²⁺] interval. The range of [Mg²⁺] jumps used, from 0.01 mM (i.e., low [Mg²⁺]) to 0.1, 0.4, or 1.0 mM (i.e., high [Mg²⁺]), allows probing relatively simple conformational changes (i.e., two-state behavior at 0.1 mM) and complex multistate behavior (at ≥0.4 mM). A general electrostatic response of the RNA structure is immediately observed upon the change in ionic condition. We observe subsequent exponential kinetics in each [Mg²⁺] interval, but the relaxation at high [Mg²⁺] is incomplete. Furthermore, by considering the FRET value just before the jump, we identify conformations that are slowly interconverting and therefore separated by a high free energy barrier. The species on either side of this barrier have indistinguishable FRET efficiency (E_FRET) values but very different dynamics. Therefore, for single-molecule FRET measurements, the barrier functions as a “hidden” degree of freedom (DOF) that exhibits long memory of the RNA structure and hence influences the individual molecule's dynamics and the kinetics of population relaxation.

Results

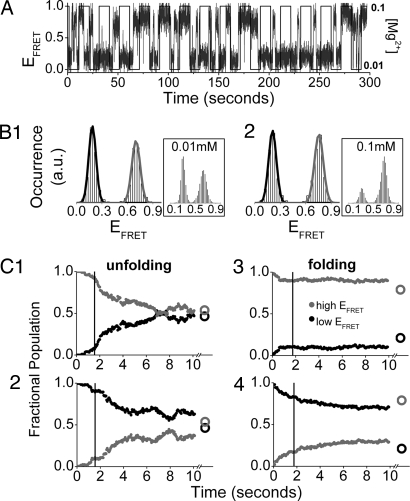
Measurements were conducted at three [Mg²⁺]-jump conditions: 0.01 ↔ 0.1, 0.01 ↔ 0.4, and 0.01 ↔ 1.0 mM (see Fig. 1 and SI Materials and Methods for details). We refer to the conformational changes of RNA molecules after a [Mg²⁺] decrease as unfolding, and to those after a [Mg²⁺] increase as folding. For analysis, trajectories are segmented into unfolding and folding intervals, and these intervals further separated into two cases according to whether the molecule occupied the low or high E_FRET state immediately before the [Mg²⁺] jump (see Fig. 2C). The averaged relaxation properties of the resulting four sorted sets (unfolding starting low E_FRET, unfolding starting high E_FRET, folding starting low E_FRET, and folding starting high E_FRET) are calculated separately and yield key insights into the alternate folding pathways.

Fig. 2.

The 0.01 ↔ 0.1 mM [Mg²⁺]-jump experiment. (A) Typical single-molecule trajectory. The [Mg²⁺] profile (solid square wave) superimposed on the FRET trajectory for a single RNA molecule. (B) Cumulative E_FRET histograms for folding and unfolding. The histograms are constructed from all of the single-molecule E_FRET trajectories in one field of view (≈100 RNA molecules are observed simultaneously). (Insets) Equilibrium E_FRET histograms. (C) Population relaxation kinetics of the low (black) and high (gray) E_FRET states. These curves are constructed by sorting all folding and unfolding trajectory segments according to E_FRET state before the [Mg²⁺] jump, and calculating the fraction of molecules that occupy this state at each later time point. The decays are well approximated by exponential fits after the 1- to 2-sec [Mg²⁺]-transition time. (C1 and C2) Unfolding from the high (C1) or low (C2) E_FRET states. (C3 and C4) Folding from the high (C3) or low (C4) E_FRET state. Circles after the split of the time axis show the equilibrium population distributions. Vertical lines at ≈2 sec show when the [Mg²⁺]-transition period ends.

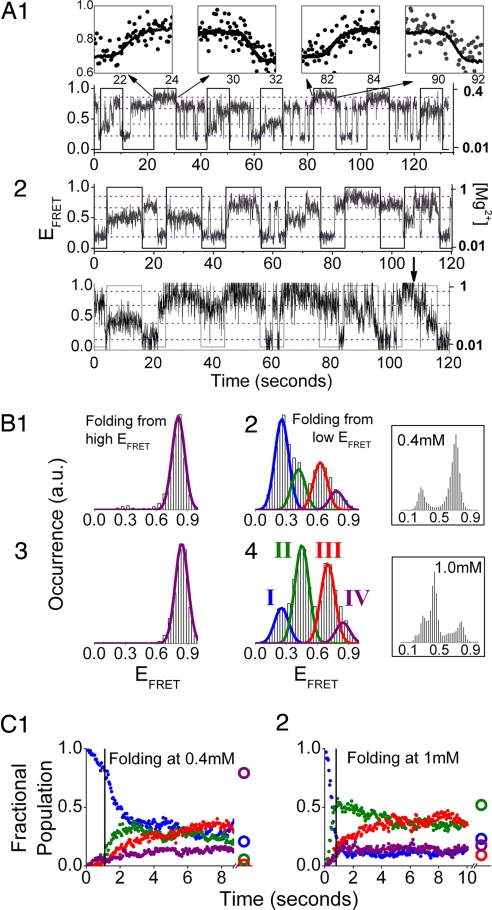
We observed two classes of RNA conformational change: (i) discrete transitions characteristic of barrier-crossing events that are observed during each constant [Mg²⁺] interval and (ii) smooth transitions only observed during the 1-sec [Mg²⁺]-transition time (see Fig. S2). The smooth transitions track the [Mg²⁺] change (Fig. 3A1 Inset) in a manner consistent with electrostatic relaxation (i.e., collapse or expansion) of RNA structure due to a change in the ionic condition.

Fig. 3.

[Mg²⁺]-jump experiments for 0.01 ↔ 0.4 mM (A1, B1, B2, and C1) and 0.01 ↔ 1.0 mM (A2, B3, B4, and C2). (A) Representative single-molecule trajectories. (A1 Insets) Smooth E_FRET change (dots) due to electrostatic relaxation overlap with the measured [Mg²⁺] profiles (solid lines). The last high [Mg²⁺] step of the lower trajectory in A2 shows a rarely observed transition (arrow) over the high barrier associated with the hidden DOF (Fig. 1B) whose signature is a transition from the state IV to state III. (B) Cumulative E_FRET histograms for molecules folding from the high (B1 and B3) and low (B2 and B4) E_FRET states. (Insets) Equilibrium E_FRET histograms. Blue, state I; green, state II; red, state III; purple, state IV (state definition: ref. Table 1). (C) Population relaxation kinetics for molecules folding from the low E_FRET state. Molecules starting from the high E_FRET state only show occasional transitions to state III* and negligible transitions to other E_FRET states (data not shown). Two-state behavior similar to that observed in the 0.01 ↔ 0.1 mM experiment (Figs. 2 B1, C1, and C2) is observed at the low [Mg²⁺] interval for these two jump conditions (data not shown).

Two-State Unfolding and Folding for [Mg²⁺] = 0.01 ↔ 0.1 mM.

E_FRET trajectories (Fig. 2A; also see Fig. S3) and cumulative E_FRET histograms (Fig. 2B) show that the RNA exhibits single-transition, two-state behavior for both unfolding and folding in the 0.01 ↔ 0.1 mM experiment. Two-state behavior is consistent with the expectation from our equilibrium study (Fig. 2 Insets) (22). The high E_FRET peak is more dominant in the folding interval (Fig. 2B2) than in the unfolding interval (Fig. 2B1), although it is apparent from the peak amplitudes that the population has not yet achieved equilibrium (Fig. 2B2 Inset).

The kinetics of population relaxation are clearly different depending on the initial E_FRET state immediately before the [Mg²⁺] jumps, and this difference is especially apparent in the folding interval. If an RNA begins its folding interval from a high E_FRET state (Fig. 2C3), it tends to stay in the high E_FRET state with a population relaxation time constant much longer than the 10-sec jump interval. RNA folding from the low E_FRET state (Fig. 2C4), in contrast, exhibits relatively fast relaxation. The long-lived high E_FRET state observed in the first case is obviously a different conformation than the actively fluctuating high E_FRET state visited in the second case. These two high E_FRET conformations, distinguished only by their kinetics, reveal a property that we call the “hidden” DOF in CthermoL18. Sensitivity of the relaxation rate and pathways on initial state was observed in previous single-jump studies (19–21).

RNA Conformational Change: Electrostatic Relaxation vs. Barrier-Crossing Process.

Electrostatic compaction into a nonspecifically collapsed structure has been shown by time-resolved SAXS to occur in <100 msec (13). When E_FRET states at low and high [Mg²⁺] are grouped together according to their electrostatic relaxation connectivity (Table 1), the E_FRET values in each group show a monotonic increase with [Mg²⁺]. This is consistent with a progressively more collapsed RNA structure at higher [Mg²⁺] due to better electrostatic screening of the RNA phosphate backbone. This E_FRET shift with [Mg²⁺] is also observed in the E_FRET histograms of the equilibrium FRET measurements of the same RNA (22), although in that case the relationship between E_FRET states cannot be directly observed.

Table 1.

E_FRET values at the peak positions of the E_FRET histograms in Figs. 2B and 3B

[Mg2+], mM	EFRET value
0.01	0.19			0.7
0.1	0.21			0.76
0.4	0.25	0.41	0.62	0.8
1	0.25	0.45	0.7	0.85
(State)	(I)	(II)	(III)	(IV)

Error: ± 0.02 (upper bound). The E_FRET states are separated into four groups (I–IV) according to their structural relation by electrostatic relaxation.

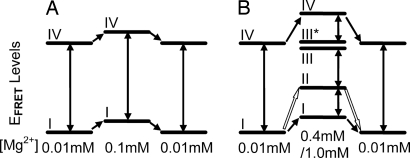
For the [Mg²⁺] intervals with only two E_FRET states populated, the E_FRET states are referred to as low and high. For simplicity, in the case of [Mg²⁺] intervals with multiple E_FRET states, we use group numbers (I–IV) instead of the specific E_FRET values (see Table 1 and Fig. 4). The transitions between E_FRET states from different groups (see Table 1 and Fig. 4) are barrier-crossing processes that occur during the constant [Mg²⁺] intervals whereas the transitions between E_FRET states within the same group are electrostatic relaxation processes observed only during the ≈1-sec [Mg²⁺]-transition time. An exception is the conformational change between states I and II for the [Mg²⁺] = 0.01 ↔ 1.0 mM jump condition, which happens both during the constant [Mg²⁺] interval (i.e., barrier crossing) and during the [Mg²⁺]-transition time (i.e., barrier crossing happening concurrently with the electrostatic relaxation).

Fig. 4.

Connectivity between E_FRET states for the three [Mg²⁺]-jump conditions. (A) [Mg²⁺] = 0.01 ↔ 0.1 mM. (B) [Mg²⁺] = 0.01 ↔ 0.4 mM/1.0 mM. The solid double-headed arrows represent RNA conformational fluctuations that happen during the constant [Mg²⁺] interval and involve barrier crossing with time constants on the order of seconds. The solid single-headed arrows represent electrostatic relaxation of the RNA structure, which follows the [Mg²⁺]-transition curve. In B, for the [Mg²⁺] = 0.01 ↔ 1.0 mM condition, the barrier crossing between state I and state II also happens during the [Mg²⁺]-transition time, simultaneously with the electrostatic relaxation. This is different from other barrier crossing processes (shown as solid double-headed arrows) and thus is represented by open single-headed arrows. States III and III* in B have indistinguishable E_FRET values within experimental error but differ in dynamic behavior because of difference in hidden DOF. The transitions between III and III* are very rarely observed and thus not represented by arrows. For E_FRET states that are not connected by single-headed arrows at [Mg²⁺] jump, direct transitions between them during [Mg²⁺]-transition time are rarely observed in experiments.

Two-State Unfolding and Multistate Folding for [Mg²⁺] = 0.01 ↔ 0.4 and 0.01 ↔ 1.0 mM.

The single-molecule trajectories of Fig. 3A show that the 0.01 ↔ 0.4 and 0.01 ↔ 1.0 mM jump experiments exhibit two-state unfolding. E_FRET histograms and population relaxation kinetics are very similar to those of the unfolding interval for 0.01 ↔ 0.1 mM just described and thus are not shown, for brevity. In contrast, both jump conditions exhibit complicated multistate folding (Fig. 3). Multistate folding is unexpected for the 0.01 ↔ 0.4 mM jump experiment because equilibrium measurements for [Mg²⁺] ≤ 0.4 mM (22) show only two-state trajectories for the majority of single molecules. This dramatic deviation from equilibrium behavior is a first indication that the periodic-jump technique is able to probe regions of the free energy surface that are virtually unsampled at equilibrium.

E_FRET histograms (Fig. 3 B1 and B3) and trajectories show that RNA molecules folding from the high E_FRET state (IV) always go to the highest E_FRET state (state IV) with only very infrequent transitions to state III* (Fig. 4). In contrast, molecules folding from the low E_FRET state (I) evolve to populate four E_FRET states (Fig. 3 B2 and B4), some of which are “intermediate states” not observed in equilibrium measurements (Fig. 3B Insets). The folding kinetics for the two-jump conditions will be discussed separately below.

During the [Mg²⁺] = 0.4 mM folding interval (Fig. 3C1), RNA molecules that fold from state I primarily go to state II within 3 sec, and the subsequent population relaxation is predominantly to state III. There is also a slow but steady increase in the population of state IV within the 10-sec interval consistent with the expectation from our equilibrium measurements (Fig. 3B2 Inset). States II and III are thus intermediates along the folding pathway with state II preceding state III. Because the populations of E_FRET states II and III decrease with increasing period of the perturbation (data not shown), one should also consider that these intermediates are sampling conformations in what would be the transition state region at equilibrium.

Folding under the 0.01 ↔ 1.0 mM jump condition (Fig. 3C2) is similar, and molecules initially in state I again strongly favor going to state II. The transition is fast, complete within the ≈1-sec [Mg²⁺]-transition time. The RNA molecules in state II fold to state III, which continues to accumulate within the 10-sec interval. The difference between folding at 0.4 mM and folding at 1 mM is that the native state is thermodynamically stable and populated at equilibrium at 1 mM. The native state is characterized by an E_FRET value of 0.45 (22), indistinguishable from the E_FRET value of state II (Fig. 3B4 Inset), suggesting similarity in conformation (or distance between dye molecules) for these two states as probed by FRET. However, the population of state II does not increase monotonically in the folding interval, as would be expected for the native state (see ref. 22). This contradiction is strong evidence that state II is not identical to the native state, and that these two states differ in some hidden DOF. We conclude that the observed axis responds rapidly to the [Mg²⁺] change while equilibration of the hidden DOF is slower. A much longer time (≫10 sec) is required for both the observed axis and the hidden DOF to relax to the native state.

Variation of [Mg²⁺] Period.

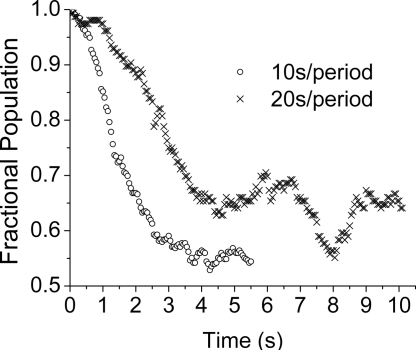
To further establish the sensitivity to hidden DOFs and non-Markovian dynamics, we varied the period of the perturbation. Fig. 5 shows a comparison of the low E_FRET, low [Mg²⁺] subensemble results for 20- and 10-sec periods (i.e., 10- and 5-sec intervals at the high and low [Mg²⁺] condition). If the dynamics were a two-state (Markovian) process, one would expect the relaxation rates to be the same. However, the shorter-period data relax much faster. In comparison to the shorter high [Mg²⁺] interval, the RNA molecules are driven further from the low [Mg²⁺] steady-state (almost equilibrium) position in the longer high [Mg²⁺] interval. Because the observed DOF then has more time to “couple” with the hidden DOF, the dynamics of the observed DOF become slower (or more non-Markovian). In the language of this article, the more time the molecules are allowed to fold during the high [Mg²⁺] interval, the more the single molecules change their conformations along the hidden DOF(s), and hence the slower the unfolding during the low [Mg²⁺] interval.

Fig. 5.

Relaxation kinetics depend on period length. Shown are the fractional population of the low E_FRET state for molecules that are unfolding from the low E_FRET state in a 0.01 ↔ 0.1 mM jump experiment with either 10-sec (○) or 20-sec () periods.

Discussion

Folding at High [Mg²⁺] Is Slow and Multistate Whereas Unfolding at Low [Mg²⁺] Is Fast and Two-State.

For the unfolding interval, all three jump experiments exhibit two-state kinetics, and the population distributions at the end of the 10-sec interval are close to the equilibrium result (Fig. 2 C1 and C2; unfolding intervals for the 0.01 ↔ 0.4 and 0.01 ↔ 1 mM [Mg²⁺] are not shown for brevity). This population shift indicates that at low [Mg²⁺], relaxation appears to be nearly complete within the 10-sec interval regardless of the initial E_FRET state or original high [Mg²⁺]. Folding, however, is more complicated; multiple intermediate states are involved and events originating from the low or high E_FRET states behave very differently. Unfolding involves spontaneous opening of the RNA structure, while folding is entropically unfavorable, requiring structural elements to assemble in the correct order. The E_FRET population distributions at the end of the high [Mg²⁺] interval for all three jump conditions (Figs. 2 C3 and C4 and 3C) are far from their equilibrium distributions. Thus, the RNA population does not achieve equilibrium in the 10-sec high [Mg²⁺] interval. This is consistent with previous observations that folding is slower and more complex than unfolding (21).

Hidden Degrees of Freedom and Long Memory Effect.

The crystal structure of RNase P RNA (25) suggests that the positions labeled with the FRET dyes (3′ end and L18 loop) are not directly involved in the formation of the core structure. However, it is reasonable to expect that the observed (i.e., labeled) DOF can report on the structure and dynamics of the unlabeled parts of the RNA due to structural connectivity (22). All three jump experiments reported here indicate that the structural changes of the unlabeled parts of the RNA molecule affect the observed dynamics of the labeled axis but not the E_FRET values. Folding at [Mg²⁺] = 0.1 mM is characterized by two kinetically distinct high E_FRET states: molecules that fold from an initial high E_FRET state end up in a stable long-lived high E_FRET state whereas molecules that fold from the low E_FRET state fluctuate quite actively between low and high E_FRET states. These two behaviors result from conformational differences in the hidden DOFs. Folding at [Mg²⁺] = 1 mM includes transient population of a E_FRET state (state II) with the same E_FRET value as the native state, although it behaves as a kinetic intermediate. Further structural changes in a hidden DOF require much longer than 10 sec to attain the native state.

Slow dynamics in the hidden DOFs give rise to long memory effects in the single-molecule E_FRET trajectories. Fig. S4 shows RNA molecules that retain dramatically different dynamics in the observed FRET DOF for several minutes; some molecules remain in the low or high E_FRET states (Figs. S4 a and b) whereas other molecules synchronize with the periodic [Mg²⁺] jumps and switch between low and high E_FRET states (Fig. S4c). Persistent behavior is likely to result from structural/conformational differences in some hidden DOF.

Stabilizing Effects of Mg²⁺ on RNA Structure and Cooperative RNA Folding.

Mg²⁺ ions stabilize RNA structure by allowing tertiary contacts to form through specific ion binding, and by electrostatically screening the phosphate backbone (3). For all three jump conditions, the RNA molecules were observed to become compact upon an increase in [Mg²⁺] (Fig. 4). This compaction is likely due to the nonspecific electrostatic relaxation of the RNA structure, but it has been shown for other RNA molecules that some tertiary interactions might also be formed during the electrostatic relaxation process (4, 26). Achieving high cooperativity in folding (27, 28) requires some preorganization of the structure. We believe that topological constraints of the native state require formation of the following helices: P4 first, then P2, then finally P5, with a number of noncanonical stabilizing interactions (22). Formation of these helices in different order or combinations may result in intermediate states that are kinetically stable.

No ensemble kinetic experiments have been reported for the Cthermo thermophilic ribozyme. However, a rate-limiting step along the folding pathway of a mesophilic homologue has been characterized in ensemble measurements. A folding (29) and unfolding (30) intermediate was directly observed and deduced from a [Mg²⁺]-chevron analysis (12). The rate-limiting step to the native state was described as a small-amplitude conformational change (i.e., no change in radius of gyration or burial of surface area) between these two intermediate states (29). No additional Mg²⁺ ions are bound in this step, which argues for a local consolidation of RNA structure around a prebound Mg²⁺ ion. This lack of change in global structural dimensions is consistent with the indistinguishable E_FRET values of states III and III* and would suggest that these states lie on either side of the major barrier (Fig. 1B).

In the mesophilic homologue, the folding rate at high [Mg²⁺] is more than one order of magnitude slower than the unfolding rate at very low cation concentration (29). This difference is qualitatively consistent with our observation that for all three jump conditions, unfolding is largely complete within the 10-sec low [Mg²⁺] interval whereas folding is far from equilibrium within the 10-sec high [Mg²⁺] interval (Figs. 2C and 3C). Thus, our observation that the folding barrier is higher under folding conditions compared with the unfolding barrier under unfolding conditions in the [Mg²⁺] jump experiments of CthermoL18 RNA agrees with the ensemble kinetic measurements of the mesophilic homologue.

Free Energy Landscape.

The connectivity of the E_FRET states along the folding pathway (Figs. 2C, 3C, and 4) and the rate constants for interconversion between two connected E_FRET states (Table S1) are readily obtained from the single-molecule RNA response to [Mg²⁺] jumps monitored over time. Although each jump experiment differs in detail (e.g., the barrier heights and number of free energy basins), a qualitative free energy landscape with the major features of all three jump experiments can be illustrated as in Fig. 1B. A [Mg²⁺] change causes the free energy landscape to shift with subsequent RNA population redistribution toward equilibrium on the new free energy landscape. Molecules traverse different regions of the landscape depending on which E_FRET state [low (I) or high (IV)] a molecule occupies before the [Mg²⁺] jump. The two regions are separated by a high barrier that corresponds to a structural change in some hidden DOF. During folding, this barrier is so high that transitions over it are only rarely observed. For the 0.01 ↔ 0.4 mM and 0.01 ↔ 1.0 mM jump conditions, the E_FRET histograms (Fig. 3B), connectivity of the E_FRET states (Fig. 4), and (rare) observation of transitions over the barrier (Fig. 3A2, lower trajectory, arrow) allow assignment of the barrier between states III and III*—they possess the same observed E_FRET value but are kinetically distinct and therefore on opposite sides of the barrier.

Probing Regions of the Free Energy Landscape That Are Inaccessible to Equilibrium Results.

In contrast to perturbation experiments with only a single jump, the period of the periodic-jump experiment can be used to probe macromolecular free energy landscapes. When the period of [Mg²⁺] jumps is shorter than the time scale for relaxation, the distribution of RNA conformations at the end of an interval will not have reached equilibrium. The response of this nonequilibrium distribution of starting conformations to the next [Mg²⁺] jump will depend on how far the system is from each of the two asymptotic equilibrium distributions. The system's “distance” from equilibrium is controlled by the length of the periodic [Mg²⁺] jumps. Fig. 5 shows that the ribozyme is perturbed less during the 5-sec interval (vs. 10-sec interval), and so it relaxes more quickly. If one assumes linear response (but near equilibrium), then the relaxation rate should be independent of perturbation. The observed dependence of relaxation kinetics on the length of the [Mg²⁺]-jump period is evidence that a nonlinear (or non-Markovian) response describes the RNA dynamics in this experiment. Additionally, the RNA populations driven for different periods cannot be equilibrating to the same distributions of states. Therefore, different regions of the free energy surface are probed with different period lengths. The result of the period dependence is a direct manifestation of memory in the dynamics. With a long enough sequence of periodic-jump cycles, the molecules are best described by a nonequilibrium steady-state distribution of conformations (31). Because the effective steady-state landscape is different from either equilibrium limit, one can picture that the set of conformations sampled may be those close to the transition state separating the basins (note state II in Fig. 3C1).

Conclusions

We developed and applied a single-molecule periodic [Mg²⁺]-jump method to study the Mg²⁺-induced folding of CthermoL18 RNA. The observed connectivity of E_FRET states and the associated rate constants allow construction of new details of the free energy landscape. We find that molecules starting from the two different interconverting conformations (i.e., the low and high E_FRET states) before a [Mg²⁺] increase traverse two distinct regions of the landscape, which are separated by a very high free energy barrier. This rate-limiting step involves only changes in the hidden DOF and does not induce detectable change in the E_FRET value. The slow dynamics, apparent in the hidden DOF, give rise to more details of the free energy landscape and clearly reveal long memory effects in the single-molecule E_FRET trajectories. The fact that the relaxation dynamics depend on the magnitude (duration) of the perturbation for a fixed [Mg²⁺] clearly indicates that the response is non-Markovian as is expected for a nonequilibrium steady-state system with long memory.

Many important RNA folding questions can be studied with this approach, such as the origin and properties of long memory effects, and cooperative folding of large RNAs at high [Mg²⁺]. Quantitative modeling of the observed dynamics, such as a generalized Langevin equation simulation with a memory kernel (32), will provide more insights into RNA folding mechanisms. Finally, measurements with a set of different [Mg²⁺]-jump periods will allow construction of a more comprehensive free energy landscape that is inaccessible from equilibrium measurements and traditional single-jump techniques.

Materials and Methods

The experimental methods are briefly described here and in detail in SI Materials and Methods. A microfluidic channel ≈800-μm-wide with two short input branches in a “Y”-shape was cut into an adhesive spacer (Grace Biolabs). The flow chamber was completed by coupling the spacer to a polyethylene glycol (PEG)-coated coverslip and to a glass slide. Holes were drilled through the glass slide to allow connection of the two input channels of the flow chamber via polyethylene tubing to individual syringes filled with buffers of the desired [Mg²⁺]. Two computer-controlled PHD2000 syringe pumps (Harvard Apparatus) were used to achieve the desired flow profile (see Fig. 1A).

RNA molecules labeled with the FRET dye pair and biotin were attached to Streptavidin molecules that have been immobilized to the coverslip. The FRET measurement was conducted on a home-built objective-type total internal reflection fluorescence (TIRF) microscope, using an EM-CCD detector (Andor Technology). Time trajectories of donor and acceptor molecules were extracted from the images for each RNA molecule by using a routine written in MATLAB (MathWorks).