Evolution of graded refractive index in squid lenses

Abstract

A lens with a graded refractive index is required for vision in aquatic animals with camera-type eyes. This optical design entails a radial gradient of protein density, with low density in external layers and high density in internal layers. To maintain the optical stability of the eye, different material properties are required for proteins in different regions of the lens. In low-density regions of the lens where slight protein aggregation causes significant light scattering, aggregation must be minimized. Squid lens S-crystallin proteins are evolutionarily derived from the glutathione S-transferase protein family. We used biochemistry, optical modelling and phylogenetics to study the evolution and material properties of S-crystallins. S-crystallins are differentially expressed in a radial gradient, suggesting a role in refractive index. This gradient in S-crystallin expression is correlated with their evolutionary history and biochemistry. S-crystallins have been under positive selection. This selection appears to have resulted in stabilization of derived S-crystallins via mutations in the dimer interface and extended electrostatic fields. These derived S-crystallins probably cause the glassy organization and stability of low refractive index lens layers. Our work elucidates the molecular and evolutionary mechanisms underlying the production and maintenance of camera-like optics in squid lenses.

1. Introduction

Aquatic animals with camera-type eyes require high-powered lenses to decrease the size and increase the sensitivity of these eyes (Land & Nilsson 2002). However, the greater the optical power of a homogeneous refractive index lens, the more spherical aberration it produces, resulting in blurred images (Hecht 1989). Aquatic animals have resolved this issue with a spherical, graded refractive index lens that simultaneously achieves small eye size, high sensitivity and excellent imaging (figure 1; Gordon 2000). These ‘Matthiesen's ratio’ lenses have a radial gradient of lens crystallin protein concentration which results in a low refractive index at their periphery and a high refractive index at their centre (Matthiesen 1886).

Figure 1.

Image quality of single versus graded refractive index spherical lenses. (a) An image formed by a spherical glass bead with a single refractive index. (b) The same image at the same magnification, through the lens of a fish, a spherical lens with a graded refractive index. The fish lens has much less spherical aberration than the single refractive index lens.

Transparency is structurally correlated with high refractive index. Biological lenses achieve transparency with a liquid-like ordering of lens crystallins, producing a proteinaceous glass (Delaye & Tardieu 1983). This glassy order is required to maintain transparency, because fluctuations in density on spatial scales longer than approximately half the wavelength of incident light cause observable light scattering, making the material cloudy or opaque (Benedek 1971). Since organelles and protein aggregates also scatter light, biological lenses contain few of the former and go to great lengths to avoid the latter. Thus, lens proteins cannot turn over, denature or aggregate for the lifetime of the animal (Bettelheim & Siew 1983). In the exterior of a lens, where protein concentration is low, a small amount of protein aggregation produces significant opacity, because the refractive index mismatch between the protein aggregate and the cytoplasm is high. In the interior of the lens, soluble proteins are densely packed, hence aggregated proteins cause little scattering since the refractive index mismatch between the aggregates and the cytoplasm (saturated with soluble protein) is low. A paradox of lens biology, therefore, is how do lenses maintain a glassy structuring of their proteins across a large concentration gradient without replacing them?

We addressed this by investigating the biochemical and resulting material properties of the major protein constituents of squid lenses (dubbed crystallins). The crystallin protein components for many animal lenses have been identified and are primarily structural proteins that raise the protein concentration and therefore the refractive index of the lens (Tomarev & Piatigorsky 1996; Graw 1997). In many cases, these lens crystallins have been evolutionarily co-opted from housekeeping enzymes with other metabolic, rather than structural functions (Tomarev & Piatigorsky 1996). A central, unanswered question is why some proteins were co-opted for lens expression and not others. A consensus has emerged that proteins suited for lens expression are small, globular housekeeping enzymes that are often upregulated during stress responses and relatively resistant to denaturation (Wistow 1995). However, this explanation does not fit all cases of lens crystallins, for instance J-crystallins in cubozoan jellyfish and ι-crystallin in geckos (Piatigorsky et al. 1993; Werten et al. 2000). J-crystallins are related to saposins, which are small, membrane-bound glycoproteins. In addition, it does not explain why protein sequences usually change once they are expressed in the lens.

The questions of how, why and in what manner have lens crystallins evolved from housekeeping enzymes point to essential questions in our understanding of protein folding and stability. When a protein serves as a refractive function in the lens, it is freed from the constraints of its original enzymatic function, but is under new pressure to fold efficiently and stably to avoid denaturation and aggregation. Therefore, the evolutionary study of lens crystallins is an excellent way to study trade-offs between the protein function and the thermodynamics of its folding.

An understanding of the evolution of the material and optical properties of lens crystallins has been complicated by the fact that vertebrate lenses are a mixture of three different families of proteins, the α-, β- and γ-crystallins. In addition, each major group of vertebrates has multiple, varying copies of each of these three types of crystallin. Squid, however, have one major type of lens crystallin, S-crystallin. Therefore, we chose Loligo opalescens, the market squid, as a model for investigating the contributions of protein evolution to lens evolution.

S-crystallins in L. opalescens are an evolutionary radiation of approximately 25 lens-specific proteins that are descended from a single-copy glutathione S-transferase (GST) liver enzyme (Tomarev et al. 1995). In L. opalescens, these S-crystallins have an average of approximately 81% amino acid identity to each other and 40% amino acid identity to a liver-expressed GST enzyme. The overall tertiary and quaternary structures of the GST enzyme appear to be conserved in S-crystallins, but S-crystallins have an evolutionarily novel exon inserted between the N-terminal and the C-terminal folding domains of GST (figure 2). This exon appears to code for an unstructured cytoplasmic loop bridging these two conserved folding domains and varies from 10 to 20 amino acids in length (Ji et al. 1995).

Figure 2.

Alignment and structure of the S-crystallin radiation. 1GSQ is the sequence used in the crystal structure of the O. pacificus GST (Ji et al. 1995). The remaining sequences are S-crystallins from L. opalescens lenses. Negatively charged residues are coloured red and positively charged residues are coloured blue in both the alignment and the ribbon diagrams. Shaded residues in the alignment indicate the novel third exon and were excluded from all phylogenetic analyses. The novel third exon of the S-crystallins is marked with asterisks in the alignment and ribbon diagrams. Black vertical lines indicate residues that are involved in the dimer interface in O. pacificus GST and are functionally conserved in L. opalescens S-crystallin. (a) Monomeric crystal structure of 1GSQ. (b) Monomeric homology model of the Lops6 S-crystallin. (c) Monomeric and dimeric homology models of the Lops8 S-crystallin sequence.

We sought to understand how this evolutionary radiation and resulting variation of S-crystallins in squid might have contributed to its graded refractive index optics. Since the transition from an enzyme to a structural lens protein involved many structural mutations, there is no straightforward biochemical assay of lens crystallin function. Therefore, S-crystallins do not lend themselves to ancestral reconstruction and bacterial expression, as has been done for opsins, fluorescent proteins and other protein families (Chang et al. 2002; Ugalde et al. 2004). Instead, we used a diverse array of techniques from molecular evolution, protein biochemistry, optical modelling, electrodynamics and light scattering theory to understand the function of mutations leading from an enzymatic liver-expressed protein to a structural lens-expressed protein. This approach allowed us to examine patterns of selection on S-crystallins and their electrostatic properties and to model their behaviour in situ and the optical properties of their ensembles. We show that positive selection on S-crystallins has resulted in proteins with variable electrostatic properties that affect the transparency and refractive index of different regions in the squid lens. These properties may have been the object of selection that produced graded refractive index optics and contributed to acute vision in squid.

2. Material and methods

2.1 Animal sampling and eye dissection

Fresh specimens of the myopsid squid L. opalescens were obtained from commercial catches via the Coastal Pelagic Species Division of the California Department of Fish and Game or Phil's Fish Market, Moss Landing, CA. L. opalescens is the major fishery squid in North America, where they are abundant off of the coast of California. Lenses were excised from the suspending muscle and bisected along the membrane that separates the anterior and the posterior halves. The posterior half of the lens was dissected on ice into four concentric hemispherical layers that were digitally photographed alongside a millimetre rule. The lens layers were then placed in an appropriate buffer for the experiment being conducted, as follows.

2.2 Lens protein concentration gradient determination

Dissected lens layers were placed in a known volume 0.2 M NaOH/2.5% SDS solution sufficient to entirely dissolve the lens, and then diluted 1 : 500 in sucrose buffer. The absorbance of this dilution at 280 nm was measured. The average extinction coefficients of long- and short-loop S-crystallins were determined empirically using the measured extinction coefficients of tryptophan and tyrosine in the experimental buffer. Average extinction coefficients for long- and short-loop S-crystallins were then calculated. An appropriate extinction coefficient for each layer of the lens was estimated by taking a weighted average of the long- and short-loop S-crystallin extinction coefficients from the relative quantities of long- and short-loop S-crystallins present in each layer in SDS-PAGE (see §2.4). This method resulted in extinction coefficients of 51 350 cm⁻¹ M⁻¹, 49 880 cm⁻¹ M⁻¹, 49 150 cm⁻¹ M⁻¹ and 48 420 cm⁻¹ M⁻¹ for the four layers of the lens, moving from the outside to the inside of the lens. The volume and average radius of each hemispherical lens layer were determined from digital photographs using the following procedure. First, two-dimensional coordinates of the perimeter of each lens layer were obtained from the digital images using Geometer's Sketchpad (KCP Technologies, Inc., Emeryville, CA) and then fitted to a polynomial curve. The volume of the lens layer, V, was then determined using a volume of revolution,

$$V=\pi \int c_{\text{outer}}{(x)}^2-c_{\text{inner}}{(x)}^2\text{d}x,$$ (2.1)

where c_outer and c_inner are points on the outer and inner surface of the layer, respectively, and x is lens radius. The average radius of each hemispherical layer was also determined from these coordinates by taking the average distance between c_outer and c_inner. The numerical density of S-crystallins in each lens layer was then calculated from the total protein concentration of each layer and the volume of each layer.

2.3 Gel chromatography

Loligo opalescens lens layers were placed into several volumes of potassium phosphate buffer (10 mM K₂PO₄, 100 mM KCl, 0.05% NaN₃) and shaken overnight at 8°C. Samples were centrifuged at 12 600 g for 25 min. Supernatant (750 μl) from a single dissolved lens layer was loaded onto an 18 mm×180 mm column of Sephadex 200 calibrated with Gel Filtration Standard (Bio-Rad) according to the manufacturer's instructions. The column was run with potassium phosphate buffer at a rate of approximately 60 ml h⁻¹, with 1 ml fractions collected. Absorbance at 280 nm was measured and the extinction coefficients as determined above were used to determine protein concentration of these fractions.

2.4 SDS-PAGE

Lens layers were placed in 1 ml of sucrose buffer (0.32 M sucrose, 10 mM HEPES, 2 mM EDTA, 40 μg ml⁻¹ AEBSF, 20 μg ml⁻¹ leupeptin, 20 μg ml⁻¹ pepstatin), incubated overnight at 4°C then diluted 1 : 2 in Laemmli buffer (Bio-Rad Laboratories, Hercules, CA). Dithiothreitol was added to a concentration of 400 mM and samples were heated to 95°C for 5 min. Samples were then loaded on a Bio-Rad Criterion 10.5–14% gradient Tris–HCl 12+2-well gel (Bio-Rad Laboratories). Samples were loaded in a series of five twofold dilutions for each of the four lens fractions. Gels were electrophoresed for 105 min at 180 V and stained with Bio-Safe Coomassie (Bio-Rad Laboratories). Digital scans of the gels were analysed with the TotalLab 1-D gel software package (Nonlinear USA, Inc., Durham, NC) to determine the percentage of total protein content contained in each band of S-crystallin. The mass ratios of S-crystallin bands for each lens fraction were determined by averaging the ratios in all five lanes run for each fraction.

2.5 MALDI–TOF mass spectrometry

Our SDS-PAGE gels of L. opalescens lens layers were submitted to the University of North Carolina at Chapel Hill Proteomics Core Facility for MALDI–TOF mass spectroscopy analysis. At this facility, the 27 and 25 kD bands from each of the four dissected lens layers were submitted to tryptic digest and MALDI–TOF mass spectroscopy. To determine which S-crystallin sequences were present in which of the eight bands resulting from the four concentric lens layers, each of the eight resulting peak lists were searched against the theoretical tryptic peptides of the 20 S-crystallin and GST sequences in our gene tree using the MS-Fit function of the Protein Prospector proteomics data mining server (Clauser et al. 1999). All mass peaks within a sample that matched more than one tryptic peptide in the gene tree were excluded from the dataset. In matching experimental mass peaks to theoretical tryptic digests of proteins from our alignment, we used broad search criteria: a mass tolerance of +/−130 p.p.m., two possible missed cleavages, and considered only oxidized methionine as a possible side chain modification. These broad criteria make this analysis conservative because only mass peaks that were very likely to be unique to a single peptide were included.

2.6 Molecular evolution

We used a Bayesian MCMCMC approach to build a gene tree of L. opalescens S-crystallin genes, using the liver-expressed GST enzyme sequence from the oegopsid squid Ommastrephes pacificus as the outgroup (Larget & Simon 1999; Huelsenbeck & Ronquist 2001). All known sequences of S-crystallin and GST from L. opalescens from GenBank were aligned by eye. Prior work on L. opalescens S-crystallins used the naming convention of ‘Lops’ followed by an isoform number to refer to individual S-crystallin gene copies, and we retain their S-crystallin labels in this work (Tomarev et al. 1995). To make an alignment for our gene tree, we had to consider the novel, rapidly evolving third exon in lens-expressed S-crystallins. All L. opalescens S-crystallin genes, with the exception of Lops4, have what appears to be an evolutionarily novel third exon inserted between the first two exons encoding the N-terminal domain and the last two exons encoding the C-terminal domain of the protein. In addition, these novel exons do not align well with one another, although they appear to comprise two major groups whose members are more similar to one another than to those of the other group (figure 2). Since the exon appears to encode a cytoplasmic loop bridging the two folding domains of GST, we refer to these two groups of genes as ‘long-loop’ and ‘short-loop’ S-crystallins. To prevent the topology of our gene tree from being inappropriately influenced by the unalignable novel S-crystallin exon, we excluded this exon from all alignments and phylogenetic analyses, making our results a very conservative estimate of their evolution. The resulting alignment comprises 612 nucleotides encoding 204 amino acids in 20 proteins. Gaps were treated as missing data in both our phylogeny estimation and selection analyses. Based on the nucleotide sequences, we used an MCMCMC approach to estimate historical relationships between S-crystallin and GST copies within a Bayesian framework (Huelsenbeck & Ronquist 2001). A hierarchical likelihood ratio test comparing 56 models of nucleotide substitution inferred that the best-fit model was general time reversible (GTR) with a discrete gamma distribution to model rate heterogeneity. Two sets of four MCMCMC chains (three ‘heated’) were run in MrBayes v. 3.1 for 2 000 000 generations (Larget & Simon 1999; Huelsenbeck & Ronquist 2001). At the conclusion of these 2 000 000 generations, we estimated that the Markov chains had converged upon a stable set of parameters by calculating the potential scale reduction factor using MrBayes. Trees were sampled every 200 generations along the Markov chains. From these 10 000 trees, we identified the most frequently sampled topology and used this topology in all subsequent analyses. The tree generated by an F81 nucleotide substitution model was also within the most likely set of trees generated by MrBayes. At all highly supported nodes discussed in this paper, it was identical to the tree that resulted from the GTR model with the exception that some short-loop S-crystallins in the F81-based tree group cluster as a clade instead of a grade as in the GTR model. Our data do not provide resolution of relationships among short-loop S-crystallins. We used this F81-based tree in our figures for a more concise graphical presentation of the data, but either tree produces identical results in our subsequent analyses.

We used lineage and lineage-site based analyses of codon evolution in phylogenetic analysis by maximum likelihood (PAML) to test the hypothesis that selection acted differently on the branch leading to the L. opalescens S-crystallin radiation containing extra exons and, separately, the branch leading to one subclade within the radiation (Yang & Nielsen 2002). This model assumes that all codons in all lineages belong to one of four evolutionary rate classes: class 0 for codons with a dN/dS ratio less than one, or purifying selection; class 1 for codons with a dN/dS ratio of approximately one, for sites that are drifting; and classes 2a and 2b, for codons with a dN/dS ratio of significantly greater than one, to identify sites that are under positive selection.

2.7 Protein homology and electrostatics modelling

S-crystallin sequences were aligned as dimers to the sequence of the dimeric crystal structure of the Ommastrephes sloani enzymatic GST (Protein Data Bank accession number 1GSQ). The sequence of the target dimer was threaded onto the structure of the GST dimer found in the PDB file 1GSQ using Swiss PDB-Viewer v. 3.7 (Schwede et al. 2003). The alignments used for homology modelling are shown in figure 2. The initial model obtained for the target dimer was further refined using SWISS-MODEL (Schwede et al. 2003). Hydrogen atoms were added and optimized using the Monte Carlo routines implemented in the PDB2PQR (Dolinsky et al. 2004) script included with APBS (Baker et al. 2001). Electrostatic potential surfaces of these models were computed using a finite difference Poisson–Boltzmann calculation with the software APBS. Atomic radii and charges were taken from PARSE (Sitkoff et al. 1994). Protein and water dielectric constants were set to 2 and 78.54, respectively. The mobile ion species concentration was set to 0.01 M with an exclusion radius of 2.0 Å. Images of isoelectric surfaces of these electrostatic models at ±0.5 kT/e were constructed with visual molecular dynamics (Humphrey et al. 1996). For simplicity and clarity in illustrating the electrostatic differences between S-crystallin sequences, we modelled S-crystallin homodimers.

2.8 Electrodynamics modelling

After modelling the electrostatic properties of individual S-crystallin proteins, we considered their likely behaviour in vivo by calculating a radial distribution function for a modelled lens cell. The amino acids that are thought to directly govern dimerization are quite conserved in all the S-crystallin sequences, making dimers between any two S-crystallin sequences plausible. Therefore, we consider it likely that in vivo, S-crystallins form indiscriminate heterodimers of all S-crystallins present in a given lens fibre. Thus, in this simulation of S-crystallin packing behaviour in the lens, we modelled the most probable S-crystallin heterodimers for a lens with S-crystallins similar to enzyme GST proteins and extant, derived S-crstayllins. We treated S-crystallin dimers as spheres with radii of 25 Å. This radius was measured directly from the crystal structure 1GSQ and from our homology models. For a model of the peripheral layers of the lens, 1000 spheres were placed in a 1100×1100×1100 Å box on a simple cubic lattice where the distance between lattice points is 110 Å, which corresponds to a density of 7.44×10⁵ proteins μm⁻³, according to experimental concentration data. For a model of the central layers of the lens, we used the same 1100 Å per side box and 25 Å spheres, but increased the density of the lattice, placing 14 000 spheres on a simple cubic lattice where the distance between lattice points is 45 Å, which corresponds to a density 1.10×10⁷ proteins μm⁻³, also according to experimental concentration data. Owing to the difficulties inherent in measuring small volumes and the necessity of estimating an extinction coefficient for a complex protein mixture, we plotted our experimental concentration data as a histogram using arbitrary units in figure 3; however, for these electrodynamics models, we used the highest and the lowest values obtained from our experiments measuring the lens' concentration gradient described above. These concentrations are consistent with the ability of the squid lens to form a sharp image in water as well as with our experimental results, making them reasonable. We chose the size of the box according to the cross-sectional dimension of squid lens cell fibres in transmission electron microscopy (Willekens et al. 1984). For both protein densities, we modelled a scenario with spheres of charge +4 and a scenario with spheres of +8. The +4 models are a hypothetical case of a squid lens with no derived, highly charged S-crystallin dimers. The +8 models are an estimate of L. opalescens lens with a one-to-one ratio of high-charge/long loop to low-charge/short loop S-crystallins with dimers combining high- and low-charge S-crystallins. Of the four models, the +8 low-density model and the +4 high-density model are our best estimates of the periphery and the centre, respectively, of extant squid lens. Impenetrability of spheres was enforced via an R⁻¹² repulsive function between sphere centres with a cut-off of 90 Å. Molecular dynamics simulations were run under periodic box conditions for 1000 picoseconds at a temperature of 298K and a dielectric of 78.5 to account for the screening effect of water. A radial distribution function for the last 500 picoseconds of a simulation was calculated using the Radial program in Tinker to probe the average density of spheres at distances relative to any given sphere in the simulation (Ponder & Richards 1987).

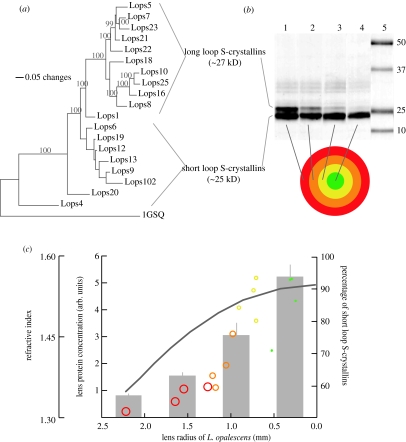
Figure 3.

S-crystallin gene tree, expression and density in squid lens. (a) Consensus Bayesian gene tree of S-crystallins from L. opalescens. There are two main groups of S-crystallin, corresponding to sequences with long cytoplasmic loops (27 kD) and those with short cytoplasmic loops (25 kD). Numbers above branches indicate Bayesian support values. Although a GTR model of nucleotide substitution best fit the data in our tree, here we show a tree based on an F81 model. The F81 model produces all the same basal nodes but shows some resolution in short-loop S-crystallins, resulting in a more concise graphical presentation of the data. (b) Representative gel with lanes 1–4 loaded with protein samples from four concentric lens layers, colour coded with red, orange, yellow and green for the outermost to the innermost region. Lane 5 contains molecular weight standard. There is a decrease in the relative expression of 27 kD S-crystallin from the outside to the inside of the lens. (c) Relationships between lens protein concentration, refractive index and relative S-crystallin expression. The circular symbols show the percentage of short novel exon S-crystallin in total S-crystallin expression in L. opalescens according to the layers in which they were found. The solid grey line shows the relationship between lens radius and refractive index for a Matthiesen's ratio lens. The grey bars show relative amino acid concentrations of L. opalescens lens layers in arbitrary units, with standard error indicated by the fine line.

2.9 Rayleigh scattering

In order to quantify the effects that protein aggregation has on lens clarity as a function of lens concentration, we used a Rayleigh scattering approach, following Bettelheim & Siew 1983. This work calculated the Rayleigh ratio, R(θ), the proportion of light scattered at an angle θ relative to total incident light, generated by protein aggregates as a function of their volume fraction in solution. We modified this approach to estimate the scattering of these same aggregates as a function of total protein concentration and radius of the squid lens. Following the original work, we used 600 nm for the wavelength of incident light, calculated R(θ) at a scattering angle of 10° and assumed a value for protein aggregate diameter of 1000 Å. We estimated the radius of S-crystallin to be 25 Å; the refractive increment of protein to be 0.2; the refractive index of cytoplasm to be 1.34; and the refractive index of protein to be 1.55. We calculated the Rayleigh ratio along the radius of the squid lens considering an arbitrary 0.000003% of the total mass of protein at each position along the radius to be aggregated into 1000 Å spheres of high refractive index. We then converted this Rayleigh ratio to total scattering through a 1 mm section of lens made out of a given lens layer by calculating the Mie scattering cross-section of the 1000 Å spheres, calculating scattering in a and accounting for the shadowing effects of overlapping large scatterers.

3. Results/discussion

3.1 Evolution of L. opalescens S-crystallins

Our gene tree shows that S-crystallins in L. opalescens fall into two major groups. These groups correspond to S-crystallin genes with short and long novel exons, suggesting that the folding domains and the novel cytoplasmic loops are evolving in concert (figure 3). This third exon does not bear any sequence similarity to previously described protein domains, but its polar and charged residue content is consistent with its encoding a loop in tertiary structure (Branden & Tooze 1999). The two groups also differ in net charge: the short-loop S-crystallins have an average net charge of +2.8, while the long-loop S-crystallins have an average net charge of +4.8. The branching order of the gene tree shows that there was an initial introduction of an extra exon into a GST-like protein. This exon then lengthened and the S-crystallins radiated into a clade of long loop and high charge. Since the low-charge short-loop S-crystallins are basal to the high-charge long-loop S-crystallins, and the enzymatic ancestor has no loop and low charge, it appears that S-crystallins have been gaining loop length and charge over their evolutionary history. There appear to have been two coordinated important jumps in loop length, net S-crystallin charge and S-crystallin diversity: the first occurred with the introduction of the novel exon to the gene and the second occurred with the lengthening of this exon and a marked increase in positive surface charge on the protein. A detailed estimation of the net charge and loop length of the ancestral S-crystallin was not possible, however, because the net charge of the derived proteins is determined in part by the content of the unalignable extra exon.

3.2 Spatial expression of S-crystallins

Since the refractive index of squid lenses varies regularly with their radius, it was possible to dissect squid lenses into four concentric layers of differing refractive index and study the proteins in each layer. Owing to their bipartite development and the resulting adult anatomy, squid lenses are particularly well-suited to correlating geometry, optics and biochemical properties. Since the squid lens develops from two separate populations of cells (West et al. 1995), there is a transparent membrane separating its anterior and posterior halves, making it possible to easily and reliably split spherical lenses into two clean hemispheres. After a near-perfect posterior lens hemisphere is obtained in this manner, onion-like layers of lens fibre cells can be neatly removed from the lens with forceps, leaving behind a smaller, denser hemisphere of lens tissue. A size-calibrated photograph of the hemisphere before each removal of a sample of fibre cells can then be used to determine the position and refractive index of each fibre cell sample.

There is a spatial correlation among refractive index, the topology of the S-crystallin gene tree and the expression of S-crystallin isoforms in the lens. SDS-PAGE gels from all the four lens layers showed two major bands, one at 25 kD and a second at 27 kD, corresponding closely in size to the short- and long-loop S-crystallin groups. Short- and long-loop S-crystallins are equally expressed at the periphery of the lens, but long-loop S-crystallin expression diminishes along the radial aspect of the lens until it is nearly absent in the centre (figure 3b). We confirmed that the two major bands of S-crystallin seen in SDS-PAGE resulted from the sequences of the two groups of S-crystallins using MALDI–TOF mass spectroscopy (electronic supplementary material). Most of the mass fragments from the 27 kD bands in each layer of the lens were matches to tryptic peptides from the long-loop S-crystallins, and mass fragments from the 25 kD band in each region of the lens were matches to tryptic peptides from the short-loop S-crystallins.

3.3 Positive selection on S-crystallins

S-crystallins in L. opalescens have been evolving under the influence of positive selection (table 1). First, the lineage leading from a liver-expressed GST to lens-expressed S-crystallins experienced positive selection. Subsequent to that, the lineage leading to S-crystallins with high charge and long loops also experienced positive selection. In the evolutionary model with the greatest likelihood, 30% of all codons in the ancestral S-crystallin lineage appear to have experienced positive selection. The rate of evolution for these codons was estimated to be 4.4 non-synonymous nucleotide substitutions for every synonymous substitution (dN/dS). In the lineage leading to the long-loop S-crystallin clade, 7% of the codons experienced very strong positive selection, with an estimated dN/dS of 17.6. In contrast, the background rate of substitution was consistent with purifying selection, with an estimated dN/dS of 0.08. The net positive charge in the S-crystallins is not correlated with the topology of the branching of the long-loop high-charge clade of the gene tree, suggesting that after a certain set of mutations under positive selection occurred, positive charge accumulated randomly on the surface of the protein (results not shown).

Table 1.

Parameter estimates for likelihood models.

model	degrees of freedom	−ln L	parameter estimates	sites under positive selection
M0-one ratio	1	5405.615867	dN/dS=0.1042	n.a.
lineage models
S-crystallin radiation	2	5404.427823 (n.s. at p>0.95)	dN/dS0=0.1007	n.a.
			dN/dSLops=0.2226
S-crystallin radiation with large novel exons	3	5402.761598 (n.s.)	dN/dS0=0.0969	n.a.
			dN/dSLops=0.2337
			dN/dSbig=0.1939
lineage-site models
null (nearly neutral)	1	5346.035715	p0=0.93115	n.a.
			pdN/dS=1=0.06885
basal S-crystallin radiation	3	5337.710662	p0=0.3551	21, 22, 40, 44, 45, 49, 64, 65, 100, 106, 112, 116, 160, 170, 172, 180, 193, 203, 204 (at p>0.9)
			p1=0.004824
			p2+3=0.2966
			dN/dSLops=4.3962
S-crystallins with large novel exons	3	5330.530338	p0=0.86896	87, 89, 93, 126, 153, 166, 198 (at p>0.9)
			p1=0.06071
			p2+3=0.07033
			dN/dSbig=17.52815

The analysis of our gene tree using computational methods to detect positive selection (PAML) allowed us to identify amino acid residues that were critical for the transition from enzyme GSTs to stable refractive S-crystallins. It appears that positive selection has been acting on mutations that contribute to the overall stability of S-crystallin tertiary and quaternary structure in order to accommodate high positive charge on a small dimerizing protein. None of the set of changes that were under positive selection during the transition from short-loop S-crystallins to long-loop S-crystallins are mutations from neutral or negative amino acids to positively charged amino acids. However, after this set of mutations occurred, positive charge accumulated on the surface of the long-loop proteins without respect to the topology of the gene tree in a new radiation of the long-loop S-crystallins. In keeping with this mechanism, most of the residues under positive selection (residue numbers 87, 89, 93 and 126) on the lineage leading to the derived long-loop high-charge clade of S-crystallins lie in the region of the protein responsible for the dimer interface (figure 4; table 1). The other residues under positive selection (residue numbers 153, 166 and 198) are located in turns stabilizing the end of helices in the C-terminal domain of the protein. Interestingly, four of six residues responsible for stabilizing the dimer (residue numbers 70, 91, 94 and 131; Ji et al. 1995) are conserved. The other two residues (132 and 135) vary between the GST sequence and S-crystallins.

Figure 4.

Locations of residues under positive selection in the tertiary and quaternary structures of S-crystallin. The molecule in this figure is Lops8 S-crystallin, one of the derived, high-charge S-crystallins. Orange residues are those homologous to residues in the crystal structure of GST, directly responsible for dimmer–dimer interactions. Green residues are those under positive selection in high-charge S-crystallins. One monomer of the dimer is shown desaturated to indicate where the dimer interface lies. Four of six residues under positive selection lie directly in the dimer interface. The other two residues under positive selection lie at the ends of an external helix probably prone to unfolding.

The liver-expressed squid sigma-class GST is not an obvious evolutionary candidate for a lens crystallin protein. Unlike other enzymes that have been co-opted for refractive function in the lens, it is unstable and relatively susceptible to thermal and solvent-induced denaturation (Stevens et al. 1998; Mei et al. 2004). Interestingly, increasing the stability of the dimer interface is probably the best way to generate increased stability of the entire protein complex. In all studied classes of GST, including squid GSTs, the dimer interface is an integral contributor to the stability of the enzyme (Kaplan et al. 1997; Luo et al. 2002; Mei et al. 2004). The irreversible denaturation of these proteins first requires the concentration-dependent dissociation of the component monomers, and conversely, the interactions at the protein interface determine the overall stability of the dimer. Therefore, the interactions leading to stability of the dimer interface are an integral part of the stability of the protein complex (Kaplan et al. 1997; Stevens et al. 2000). Accordingly, in the transition from an enzymatic GST to a highly stable lens crystallin, we should expect to see the observed changes in the dimer interface that probably stabilize the tertiary structure interactions of the component monomers and prevent disassembly of the quaternary complex. It appears that the ancestral interactions mediating the dimerization of two S-crystallin monomers are under strong purifying selection, and other changes at the dimer interface subsequently further stabilized this interaction. These secondary, stabilizing mutations maintained by positive selection may have been a precondition for the accumulation of positive charge on the surface of the protein.

3.4 In situ concentration and dimerization of S-crystallins

Our measurements of protein density as a function of lens radius showed that squid lenses have a density distribution consistent with a Matthiesen lens. Although a graded refractive index has been measured in Octopus lenses, this is the first time that it has been demonstrated in a squid (Jagger & Sands 1999). S-crystallins exist in situ as dimers in all layers of the lens, as demonstrated by a single peak at 54 kD (2×27 kD) in all the four samples of our gel chromatography experiment.

3.5 Novel cytoplasmic loop of S-crystallins

The cytoplasmic loop encoded in a novel third exon in S-crystallin genes plays a critical role in our analysis as a marker for the spatial distribution of the two groups of S-crystallins. However, much is not known about possible functions of this loop. Cytoplasmic loops are an efficient, effective way to alter the properties of a protein without changing its stable folding topology (Branden & Tooze 1999). Although we can only speculate on the possible functions of this loop, it seems useful to do so. We hypothesize that by a combination of three mechanisms, this cytoplasmic loop contributes to the overall stability of the S-crystallin dimeric complex. One possibility is that this loop folds down to occupy the enzyme's substrate-binding pocket and stabilize it. Consistent with this hypothesis is the fact that inserting a cytoplasmic loop into a functional GST enzyme removes enzyme activity. In studies of squid GST unfolding, a flexible, poorly formed alpha-helix bordering the active site of the enzyme undergoes some unfolding before the dimer dissociation occurs. The flexibility of this helix may be necessary for enzyme function, and binding of a substrate analogue greatly reduced this flexibility and stabilized the enzyme (Stevens et al. 1998). Therefore, the occupation of the substrate-binding pocket and stabilization of this flexible helix by the novel cytoplasmic loop could prevent denaturation of the S-crystallin dimeric complex.

Another possibility is that the novel cytoplasmic loop functions in the S-crystallin folding landscape. S-crystallin must fold by the N-terminal and C-terminal domains folding independently, and then the two of these domains subsequently folding down on one another, with the linkage between the two domains acting as a fulcrum (Baker 2000). In a derived S-crystallin expressed in the exterior of the lens, an N-terminal domain with charge of +3 must interact with a C-terminal domain of +5. In the enzyme GST, an N-terminal domain with charge of −3 must interact with a C-terminal domain of +6. It is possible that the extra cytoplasmic loop in the derived S-crystallins is required to provide enough kinetic energy for two highly charged domains to interact with one another. We have also considered the possibility that these cytoplasmic loops may interact across the dimer interface, further stabilizing it.

3.6 Electrostatic properties of S-crystallins

As might be predicted from the differences in net charge, there are striking differences between the electrostatic potentials of the long- and the short-loop S-crystallins (figure 5). The long-loop S-crystallins have highly extended positive electrostatic fields compared with the short-loop S-crystallins, which look similar to the enzymatic GST ancestor. Moreover, the electrostatic fields of the proteins change markedly at nodes in the tree adjacent to lineages where positive selection occurred. Calculations of protein electrostatic fields consider both the distribution of the protein's atoms and the medium's dielectric constant. Therefore, these differences are not only due to the differences in net charge among the S-crystallins but also due to the evolving position and number of charged residues within the tertiary structure of the protein.

Figure 5.

Electrostatic evolution of S-crystallins. (a) Dimeric homology model of Lops8. All molecular models in this figure are in this same relative orientation. (b) Models of the electrostatic potentials of L. opalescens S-crystallins in relation to the S-crystallin gene tree and isoelectric potential, net charge and the length of the novel third exon in number of amino acids. Positive isopotential surfaces are shown in blue and negative isopotential surfaces in red. The magnitudes of the positive and negative isopotential surfaces are the same for each homology model and are an equal arbitrary value (+/−0.5 kT/e). S-crystallin sequences with short novel exons have relatively small electrostatic fields and resemble the ancestral liver enzyme sequence 1GSQ. Arrows indicate lineages where positive selection occurred; branches with black lines indicate strong evidence of directional selection.

3.7 Ordering of S-crystallins in situ

The radial distribution function is a measure of the order in a material. It measures the average density of a material as a function of radius from any given molecule. The radial distribution function is directly correlated to the optical properties of the lens, since it quantifies density discontinuities relevant to the scattering of transmitted light (Bettelheim & Siew 1983). Therefore, our models of the radial distribution functions of an extant and ancestral lens periphery are also estimates of the abilities of these lens regions to avoid aggregation and light scattering and of their optical properties. Our modelling of the periphery of an extant squid lens (with +8 charge) shows a more periodic ordering of S-crystallins than does our modelling of the periphery of a squid lens containing enzymatic GSTs (with +4 charge). We expect that models of ordering in intermediate radial layers of the lens will exhibit intermediate packing characteristics between the +8 external lens model and the +4 internal lens model. The peripheral +8 simulation is more characteristic than the peripheral +4 simulation of the distributions of molecules seen in liquids and glasses. This +8 simulation would also result in a more transparent material because there are fewer random thermal fluctuations in the material's density (figure 6; Delaye & Tardieu 1983). Charge–charge repulsion between highly charged molecules in the periphery also presumably reduces the total number of intermolecular collisions that occur here over the lifetime of the animal. This reduction in the number of intermolecular collisions combined with a glassy structuring should prevent the tiny amounts of aggregation (e.g. just 0.000003% of total protein) that cause lens opacification. Our model demonstrates that even in the low density and low refractive index periphery, there is a glassy structuring of S-crystallin molecules. Our modelling of the central region of the lens shows that since proteins here are so densely packed, their charge does not matter, because their distribution is governed by the rules of near closest-spherical packing. In fact, the high density of packing in the centre of the lens may require proteins with a lower charge to reduce the forces resulting from charge–charge repulsion. It is interesting to note that in the central region of the lens, there is also a glassy ordering and a reduction of density fluctuation due to random thermal movement. This is not surprising, given that at these concentrations, proteins are approaching closest-spherical packing, and a glassy ordering is required.

Figure 6.

Light scattering caused by protein aggregation as a function of lens radius. This model of Mie scattering through a squid lens assumes that a constant proportion of lens protein occupies 1000 Å, light-scattering protein aggregates. The black line shows the per cent scatter of a 1 mm layer of lens for a given position and correlated refractive index and protein concentration. Since a cornea provides most of the optical power of a human eye, a human lens has a much shallower gradient of refractive index than a squid lens. In this model of lens cataract, cataract is always most severe at a refractive index of 1.41 or protein concentration of 35% regardless of the exact crystallin composition or index gradient of the lens. This refractive index occurs at the centre of human lenses, but near the periphery of squid lenses. Accordingly, humans are very prone to nuclear cataracts, whereas squid are resistant to cataracts in general, but when cataracts do occur, they occur in the periphery of the lens.

3.8 Protein aggregation and transparency in aquatic lenses

In order to generate the refractive index gradient necessary for sharp aquatic vision, protein concentration in squid lenses must vary from nearly 0% to close to 100%, compared with approximately 40% in human lenses. As described above, the physical requirements of proteins for transparency vary significantly over this range. Therefore, the evolution of lens clarity and the evolution of the protein density gradient required for sharp vision are closely related.

Figure 7 shows light scattered by protein aggregates as a function of squid lens protein concentration and refractive index. Since S-crystallins are dimers that are small relative to the wavelengths of visible light and have primarily repulsive interactions, in the absence of aggregation, light scattering in the lens is negligible. However, when even a tiny amount of aggregation occurs in some lens regions, it results in lens opacity. At the low and intermediate refractive indices found in the periphery of the squid lens, the mismatch between the high index of protein aggregates (approx. 1.5) and the low index of the cytoplasmic medium (1.34) causes significant light scattering. Maximum scattering occurs at the critical refractive index of 1.40, which is found in the centre of the human lens, but near the outside edge of squid lenses (Smith 2003). At this refractive index, there is enough protein to cause significant aggregation, but the refractive index mismatch between protein aggregates and the cytoplasmic background is still quite high. As our calculations show, as little as 0.00003% of the total protein in aggregated plaques in these lens regions will cause a nearly opaque lens. In contrast, in the squid lens centre, owing to its extremely high background refractive index not found in human lenses (approx. 1.55), high refractive index protein aggregations scatter 2–7% much light compared with aggregations in the exterior and centre of the lens (figure 7). At the periphery of the squid lens, selection for properties that prevent aggregation and light scattering resulted in thermodynamically stable proteins with high net charge. It is possible that in the centre of the lens, proteins are so tightly packed that charge–charge repulsion requires proteins expressed here to have low total charge in order to prevent intracellular pressure from becoming untenably high. These findings reinforce the idea that in the squid, the protein content in central, very high refractive index layers may matter little, because protein aggregates cause little scattering, and that a single high refractive index lens may be ancestral because it is less sensitive to the effects of random protein aggregation. In the exterior of the lens, however, where there is evidence for positive selection on its derived constituent proteins, protein content matters a great deal, because it is only here where cataracts can form.

Figure 7.

Radial distribution functions modelling S-crystallin distribution in L. opalescens lens. (a) An estimate of the radial distribution function (RDF) of lens proteins at a numerical density found in the exterior of the squid lens. (b) The same estimate for the numerical density found in the centre of the squid lens. The dashed lines show the RDF calculated for proteins with a charge of +4, and the solid lines show the RDF for proteins with a charge of +8. The +8 simulation is our best estimate of the periphery of an extant squid lens. (a) shows that in the exterior of the lens, proteins with a charge of +4 result in a completely diffuse and random distribution of proteins, while proteins with a charge of +8 exhibit glass-like interactions. Here, the +4 simulation is our best estimate of the centre of an extant squid lens. In the centre of the lens, proteins are so dense that they are nearly closest-spherically packed and have glass-like interactions independent of protein charge.

4. Conclusion

We believe that our data describe a comprehensive mechanism for the evolution of graded refractive index and camera optics in squid eyes. We assume that the ancestor to coleoid cephalopods had a pinhole-camera design, like their extant sister group, the nautiloids. Our data support a scenario of the evolution of spherically corrected camera optics in the following sequence. First, GST or a closely related paralogue was expressed in the pinhole aperture in front of the retina at high concentrations, forming a high refractive index, transparent, structure. This development would increase the aperture and thus sensitivity of squid eyes, and possibly introduce some imaging ability. Subsequent to expression of GST or a close paralogue in the lens, the novel third exon of uncertain function was introduced into the gene, which marked the evolution of S-crystallins. Then, there were several maintained duplications of this gene. These initial gene duplications may have been maintained due to selective pressure for the extremely high expression required for high refractive index, rather than for any novel biophysical properties. These duplications may have occurred in concert with an enlargement of this refractive region in the aperture of the pinhole eye, since selective pressure for the pinhole aperture to be small would be released with the insertion of a refractive sphere (Nilsson & Pelger 1994). This first group of S-crystallins may have resembled the extant low-charge, short-loop, centrally expressed S-crystallins. Lower concentrations of these proteins in the exterior of the lens could have produced the graded refractive index seen in extant lenses. However, it seems probable that lower concentrations of these proteins would result in aggregation and opacity within the lifetime of the animal, given their lack of charge–charge repulsion and the effects of aggregation on light scattering in low-index regions of the lens. Subsequently, one member of this group of ancestral S-crystallins acquired ‘stability mutations’ at the dimer interface and at the ends of external helices. These mutations were maintained by positive selection as shown by our analysis using PAML. Once these mutations were present, positive charge accumulated over the surface of the protein and these genes were duplicated, resulting in the second radiation of high-charge, long-loop, peripherally expressed S-crystallins. The scenario we present here is consistent with a detailed stepwise physical mechanism of camera-like eye evolution. This problem has stymied biologists since Darwin identified it as one of the problems with his theory of evolution (Darwin 1859). As copies with increased positive charge appeared in the genome, they were expressed in the periphery of the growing lens, resulting in layers with low refractive index that were nevertheless optically stable over the lifetime of the animal. In this iterative manner, each introduction of a new, lower refractive index layer of the lens due to the introduction of new, more highly charged and highly stable S-crystallins would increase the imaging capability in the eye. While an incremental gradualist mechanism as modelled by Nilsson & Pelger is possible given our data, they could also be consistent with a more rapid, punctuated story of camera-like eye evolution (Nilsson & Pelger 1994). Instead of a gradual accumulation of thin layers of steadily lower refractive index, a relatively thick layer of low refractive index could have appeared rather suddenly on the surface of an existing low index lens. This more punctuated interpretation of our data is supported by the sudden burst of derived, high-charge S-crystallin diversity seen in our gene tree and by the imperfectly graded series of protein expression from the interior to the exterior of the lens (figure 3).

We suspect that this mechanism of evolution of graded refractive index involving gene duplications followed by electrostatic evolution may have occurred in other invertebrate phyla. Each of the four sense organs of box jellyfish has several eyes. Two of these eyes have lenses, one larger than the other. The large lens has been shown to have a well-developed refractive index gradient, while the gradient in the small lens is poorly developed (Nilsson et al. 2005). Just as in squid lenses, there is a gradient of positive charge in the jellyfish crystallins composing these lenses: jellyfish J-crystallins range in charge from +4 to +19 (Piatigorsky et al. 1993; Piatigorsky et al. 2001), although the J-crystallin with +19 charge is seemingly evolutionarily unrelated to the others. Interestingly, the J-crystallin with +19 charge is only expressed in the large lens with a highly developed refractive index gradient (Piatigorksy et al. 1989).

This is one of the first studies to investigate links between the physical properties of lens crystallins and the optical properties of the lens. The data describe how the duplication and electrostatic evolution of squid S-crystallins may have led to the graded refractive index lens required for high resolution, high sensitivity vision in aquatic animals. Over the history of the L. opalescens S-crystallin family, there has been an increase in the number of positively charged residues on the surface of the proteins and positive selection on residues that probably support stable folding with this high net protein charge. The strong electrostatic fields of these proteins impart a glass-like stability to the peripheral lens tissues where they are highly expressed. In addition to increasing the glassy order of the lens tissue, these proteins, possibly because they collide less often with other proteins, may be less likely to denature and aggregate, causing cataract. Accordingly, we found that squid lenses form cataracts much less readily when damaged than fish lenses do.

Supplementary Material

Isoform distribution of S-crystallin in L. opalescens lens

Peptides identified from MALDI-TOF mass spectroscopy are shown across the top of the grid, with their starting position in the amino acid alignment shown in parentheses. The bold vertical line divides peptides identified in the 26 kD SDS-PAGE band from those identified in the 27 kD band. The left side of the grid shows the S-crystallin gene tree with theoretical molecular weights shown in parentheses. The bold horizontal line divides long loop/high charge S-crystallin sequences from short loop S-crystallins. Circles in the grid represent the same lens layers used in figure 2, and indicate the layer of the lens in which a particular peptide was found. Overall, the 27 kD band seen with SDS-PAGE contains S-crystallins from the clade with long loops, and the 26 kD band contains S-crystallins from the clade with short loops