Computational stabilization of human growth hormone

Abstract

Recombinant human growth hormone (hGH) is used worldwide for the treatment of pediatric hypopituitary dwarfism and in children suffering from low levels of hGH. It has limited stability in solution, and because of poor oral absorption, is administered by injection, typically several times a week. Development has therefore focused on more stable or sustained-release formulations and alternatives to injectable delivery that would increase bioavailability and make it easier for patients to use. We redesigned hGH computationally to improve its thermostability. A more stable variant of hGH could have improved pharmacokinetics or enhanced shelf-life, or be more amenable to use in alternate delivery systems and formulations. The computational design was performed using a previously developed combinatorial optimization algorithm based on the dead-end elimination theorem. The algorithm uses an empirical free energy function for scoring designed sequences. This function was augmented with a term that accounts for the loss of backbone and side-chain conformational entropy. The weighting factors for this term, the electrostatic interaction term, and the polar hydrogen burial term were optimized by minimizing the number of mutations designed by the algorithm relative to wild-type. Forty-five residues in the core of the protein were selected for optimization with the modified potential function. The proteins designed using the developed scoring function contained six to 10 mutations, showed enhancement in the melting temperature of up to 16°C, and were biologically active in cell proliferation studies. These results show the utility of our free energy function in automated protein design.

Human growth hormone (hGH) is a polypeptide hormone that is synthesized by the somatotropic cells of the anterior pituitary. It plays an important role in somatic growth through its effects on the metabolism of proteins, carbohydrates, and lipids. hGH is currently used for the treatment of pediatric hypopituitary dwarfism and in children suffering from low levels of hGH (Hindmarsh and Brook 1987). It is believed that hGH functions by direct action on bone and soft tissue to cause uniform growth and by indirect stimulation of insulin-like growth factor-1 (Pearlman and Bewley 1993).

The most prevalent form of pituitary hGH is a single-chain polypeptide containing 191 amino acids, internally cross-linked by two disulfide bonds. The molecular mass is ∼22 kD, with pI near 5.3. Approximately 55% of the polypeptide backbone exists in a right-handed α-helical conformation. The hormone is a four-helix bundle showing an up-up-down-down topology. Activation of transmembrane receptors for hGH (hGHbp) occurs when dimerization of receptor chains is triggered by binding of hGH to a ligand-binding domain on the receptor. The crystal structure of the wild-type hGH in 1:2 complex with its receptor was determined to 2.8-Å resolution (de Vos et al. 1992). There are other crystal structures of the protein, its mutants, and complexes available in the literature and the Protein Data Bank (PDB; Sundstrom et al. 1996^; Atwell et al. 1997^; Clackson et al. 1998).

Met-hGH and hGH are produced recombinantly and are available worldwide for clinical use. Both forms have therapeutic activity that is equivalent to the pituitary-derived material (Jorgensen 1987). Because hGH is a protein, it is not absorbed orally to any significant extent (Moore et al. 1986) and must be administered by injection. It is typically given subcutaneously or intramuscularly several times a week over an extensive period. It has limited stability in solution (for ∼2 weeks at 2°C to 8°C) and is commonly stored in freeze-dried form. Development has therefore focused on more stable or sustained-release formulations and alternatives to injectable delivery that would increase bioavailability and make it easier for patients to use. In this study, we have redesigned hGH computationally to improve its thermostability. A more thermostable variant of hGH could have improved utilization time or a longer shelf-life, which would translate into decreased costs for the manufacturer and added convenience and compliance for patients. Thermostability, described in terms of T_m, or the denaturation temperature of unfolding, has been used to predict the best long-term storage conditions for protein pharmaceuticals (Schrier et al. 1993; Remmele et al. 1998). A more stable variant of hGH could also have improved pharmacokinetics or be more amenable to use in alternative delivery systems and formulations.

There are two components required for computational design: (1) accurate scoring functions to rank sequences and (2) high-speed optimization methods to rapidly find the best sequences from the enormous combinatorial search space (Dahiyat 1999). We use our Protein Design Automation (PDA) method (Dahiyat and Mayo 1996, 1997a; Dahiyat et al. 1997), which incorporates the dead-end elimination (DEE) algorithm (Desmet et. al 1992; Goldstein 1994). Using a rotamer description of the side-chains, an optimal sequence for a backbone can be found by screening all possible sequences of rotamers, in which each backbone position can be occupied by each amino acid in all possible rotameric states.

The scoring functions used for protein design were recently reviewed by Gordon et al. (1999). Although nonenergy terms such as secondary structure propensities can be used, the most successful designs use energy functions based on molecular mechanics force field terms (van der Waals, hydrogen bonding, electrostatics, bond and angle energy), that is, potential energy terms, or their combinations with free energy terms such as solvation (Dahiyat and Mayo 1996) or entropy (Hellinga and Richards 1994; Dahiyat and Mayo 1996; Kono et al. 1998). Here we use a previously developed scoring function that includes potential energy terms (van der Waals, hydrogen bonding, electrostatics) and solvation terms (polar hydrogen burial and nonpolar exposure penalties, nonpolar burial energy) augmented with a term that accounts for the loss of backbone and side-chain conformational entropy. Before side-chain selection, residues are identified as core, surface, or boundary using the RESCLASS residue classification program (Dahiyat and Mayo 1997a).

Combining potential energy and free energy terms to estimate the free energy of folding or binding assumes both additivity and proportionality of potential energy and free energy terms. This necessarily raises the question of proper weighting factors for the terms. In the simplest treatment, the weighting factors are assumed to be equal to one (Kono et al. 1998). Alternatively, the factors can be derived by regression to experimental free energy data (Dahiyat and Mayo 1996; Filikov and James 1998; Filikov et al. 2000). Here we use a different approach: The weighting factors are optimized by minimizing the number of mutations designed by the algorithm.

The loss of entropy on formation of the folded protein is believed to be the principal force opposing folding (Stites and Pranata 1995). Therefore, inclusion of side-chain and main-chain entropy terms into the scoring function with proper weighting factors could improve scoring of designed sequences. A side-chain entropy term has been incorporated into protein design energy functions previously (Hellinga and Richards 1994; Kono et al. 1998). The change in side-chain entropy on folding can be modeled as the change in the number of rotatable bonds, assuming that conformational freedom is completely restricted in the folded state (Hellinga and Richards 1994). An empirical approach is based on the entropy of fusion of small organic compounds (Sternberg and Chickos 1994). Alternatively, the change in entropy can be derived from the distribution of side-chain rotamers in crystal structures (Pickett and Sternberg 1993) or in Monte Carlo simulations (Creamer and Rose 1992; Creamer 2000). These and other methods of estimating conformational entropy have been described recently (Creamer 2001) and were shown to correlate extremely well, despite different methods of derivation. In this study, we use both side-chain and backbone entropy terms based on scales introduced by Pickett and Sternberg (1993) and by Stites and Pranata (1995), respectively (Table 1).

Table 1.

Values of TΔS (kcal/mol) for the amino acids at 20°C

Amino acid	Side-chain TΔSa	Backbone TΔSb	Total TΔSc
Ala	0.0	−0.71	−1.21
Arg	−2.03	−0.51	−3.44
Asn	−1.57	−0.18	−3.31
Asp	−1.25	−0.29	−2.88
Cys	−0.55	−0.29	−2.18
Gln	−2.11	−0.48	−3.55
Glu	−1.81	−0.64	−3.09
Gly	0.0	0.0	−1.92
His	−0.96	−0.21	−2.67
Ile	−0.89	−0.59	−2.22
Leu	−0.78	−0.55	−2.15
Lys	−1.94	−0.42	−3.44
Met	−1.61	−0.51	−3.02
Phe	−0.58	−0.31	−2.19
Pro	0.0	−0.82	−1.10
Ser	−1.71	−0.28	−3.35
Thr	−1.63	−0.29	−3.26
Trp	−0.97	−0.44	−2.45
Tyr	−0.98	−0.32	−2.58
Val	−0.51	−0.57	−1.86

^a Taken from Pickett and Sternberg (1993).

^b Taken from Sites and Pranata (1995).

^c Obtained by summing up the side-chain scale and the backbone scale, corrected for the glycine backbone entropy loss (−1.92 kcal/mole) taken from D'Aquino et al. (1996); TΔS = TΔS_side-chain + (−1.92 − TΔS_backbone).

Results

The scoring function used in this work is a sum of the following terms: van der Waals interaction, hydrogen bond potential, distance-dependent Coulombic electrostatics, polar hydrogen burial penalty, nonpolar burial energy, nonpolar exposure penalty, and entropy. A detailed description of all the terms, except the entropy term, is given elsewhere (Dahiyat and Mayo 1997a,b). Here we optimize the weighting factors for the entropy (λ_S) and polar hydrogen burial penalty (ΔG_H) terms, and the dielectric constant (ɛ) for the electrostatic term. In the following sections, we describe independent optimization of each parameter, beginning with the entropy term. Although simultaneous optimization of the three weighting factors is a possibility, such an approach is often problematic because of correlations between parameters. Here, by focusing on different sets of residue classes that are predominantly dependent on one of the parameters, we are able to optimize each parameter independently, thus minimizing the possibility of spurious results. Furthermore, simultaneous optimization is significantly more computationally intensive because it requires that a much more extensive set of calculations be performed and analyzed.

Weighting factor for the entropy term

We optimized the weighting factor for the entropy term by minimizing the number of mutations designed by the algorithm. This approach is based on the assumption that the wild-type sequence is reasonably close to the global energy minimum (GEM) in the sequence space of a particular fold (Kuhlman and Baker 2000), and by minimizing the distance from the wild-type sequence, we minimize the distance from the GEM sequence. The wild-type sequence often is not the GEM sequence, because stabilizing mutations for numerous proteins are known. For example, in this work we find two sequences that are considerably more thermostable than the wild type. Without knowing the GEM sequence, however, a reasonable option is to use the wild-type sequence as a target for optimization of the algorithm parameters. To derive and validate a broadly applicable parameter set, a number of different proteins should be used to optimize parameter values. Here we derive a parameter set based only on hGH, which will be tested more extensively in future work.

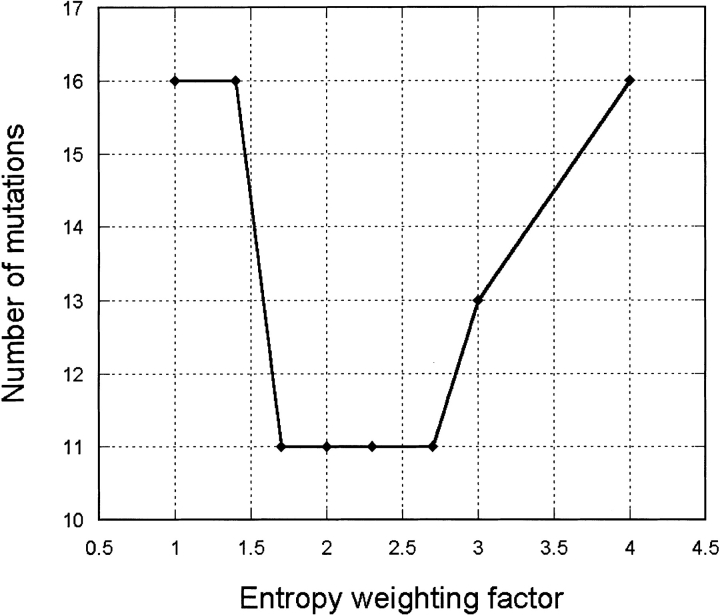
We selected 45 residues buried in the core of hGH for entropy calculations. Residue classification with RESCLASS gives 71 core residues for hGH (PDB structure 3HHR). To make the calculations faster and to focus the optimization on residues for which the entropy term is isolated from the electrostatic and polar hydrogen energies, we reduced this list to 45 positions by eliminating residues involved in hydrogen bonds and residues with significant exposure to the solvent. Several rounds of design were performed with PDA using different weighting factors for the entropy term in the range of one to four. For each round of design, the DEE algorithm was run to completion; that is, the global energy minimum sequence (GEMS) was identified. The number of mutations contained in the GEMS strongly depends on the entropy term weighting factor and has a clear minimum centered at 2.2 (Table 2; Fig. 1 ▶). At smaller entropy weighting factors (<1.7), the GEMS tends to contain a lot of methionine residues (methionine is very flexible and can fill cavities of a wide variety of shapes). Simultaneously, the loss of total entropy on folding (TΔS) for methionine is very high (−3.02 kcal/mole). Frequent appearance of methionines in the GEMS is the most obvious consequence of neglecting the entropy term in the scoring function. At higher entropy weighting factors (>3), the GEMS tends to have larger residues mutated to smaller ones, that is, to less entropically rich residues: Ile→Val, Leu→Ala, and Met→Ala (see Table 2). The optimal value for the entropy weighting factor is in the range of 1.7 to 2.7, as can be seen from Figure 1 ▶.

Table 2.

Global energy minimum sequences found by PDA for different entropy weighting factors (λs)

		λs
Positiona	Wild type	1	1.4	1.7	2	2.3	2.7	3	4
6	Leu	—b	—	—	—	—	—	—	—
10	Phe	—	—	—	—	—	—	—	—
13	Ala	Val	Val	Val	Val	Val	Val	Val	Val
17	Ala	—	—	—	—	—	—	—	—
20	Leu	Met	Met	—	—	—	—	—	Ile
24	Ala	—	—	—	—	—	—	—	—
27	Thr	Val	Val	Val	Val	Val	Val	Val	Val
28	Tyr	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe
31	Phe	—	—	—	—	—	—	—	—
36	Ile	—	—	—	—	—	—	—	—
44	Phe	—	—	—	—	—	—	—	—
54	Phe	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr
55	Ser	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala
58	Ile	—	—	—	—	—	—	Val	Val
73	Leu	—	—	—	—	—	—	Ala	Ala
75	Leu	—	—	—	—	—	—	—	—
76	Leu	—	—	—	—	—	—	—	—
78	Ile	—	—	—	—	—	—	—	—
79	Ser	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala
80	Leu	—	—	—	—	—	—	—	—
81	Leu	—	—	—	—	—	—	—	—
82	Leu	—	—	—	—	—	—	—	—
83	Ile	—	—	—	—	—	—	—	Val
85	Ser	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala
90	Val	Ile	Ile	—	—	—	—	—	—
93	Leu	—	—	—	—	—	—	—	—
96	Val	—	—	—	—	—	—	—	—
97	Phe	—	—	—	—	—	—	—	—
105	Ala	—	—	—	—	—	—	—	—
110	Val	Met	Met	—	—	—	—	—	—
114	Leu	Met	Met	Met	Met	Met	Met	—	Phe
117	leu	Met	Met	—	—	—	—	—	—
11	Ile	Val	Val	—	—	—	—	—	—
124	Leu	—	—	—	—	—	—	—	—
157	Leu	—	—	—	—	—	—	—	—
161	Gly	Met	Met	Met	Met	Met	Met	Met	Met
162	Leu	—	—	—	—	—	—	—	—
163	Leu	—	—	—	—	—	—	—	—
166	Phe	Leu	Leu	Leu	Leu	Leu	Leu	Met	Leu
170	Met	—	—	—	—	—	—	Leu	Ala
173	Val	—	—	—	—	—	—	—	—
176	Phe	—	—	—	—	—	—	—	—
177	Leu	—	—	—	—	—	—	—	—
180	Val	—	—	—	—	—	—	—	—
184	Ser	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala

^a The residues are numbered as in 3HHR file from Brookhaven Protein Databank.

^b "—" indicates the wild-type residue.

Fig. 1.

Number of mutations versus weighting factor for the entropy term.

Weighting factor for the electrostatic term

The same approach was used for optimization of the weighting factor for the electrostatic term. However, the set of core residues used for the entropy calculations cannot be used to optimize the electrostatics term, because there are few polar residues in the core. For these calculations, we selected a set of 28 boundary residues. These were obtained by running the RESCLASS algorithm, which gives 41 boundary residues for hGH, and eliminating the residues within 5 Å of the receptor and Gly104, because it has unusual φ and ξ angles. The result is a set of 28 residues that are predominantly buried: The solvent accessible fraction of the residue surface is 32.7% on average. Therefore, we assume that for these residues all the entropy of the unfolded state is lost on folding and treat them no differently from core residues in this respect.

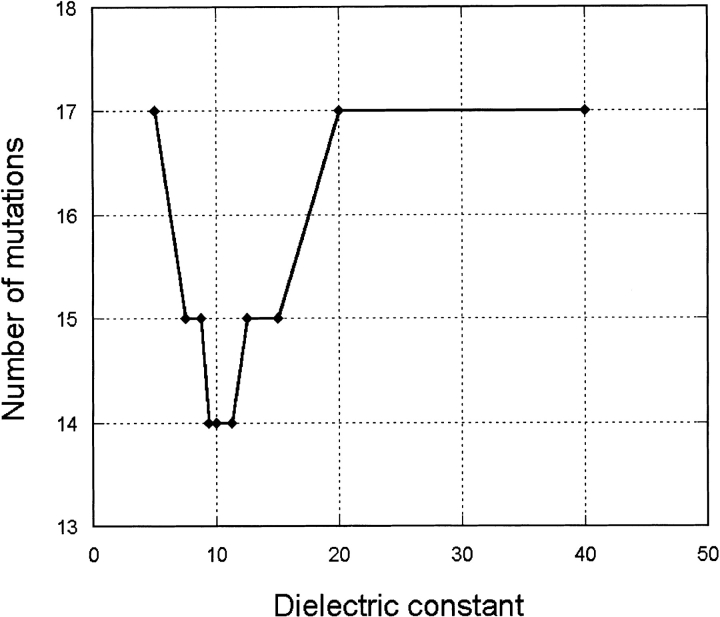
Ten rounds of design were performed using different values of the dielectric constant for the electrostatic term in the range of 5R to 40R, where R is the interatomic distance (varying ɛ is equivalent to varying the weighting factor). The weighting factor for the entropy term was set to 2.3, the midpoint of the optimal values found previously (Fig. 1 ▶). For each round of design, the DEE algorithm was run to completion. The number of mutations contained in the GEMS is plotted versus the dielectric constant in Figure 2 ▶. As can be seen, the curve has a distinct minimum at ɛ/R = 10.3 ± 0.9.

Fig. 2.

Number of mutations versus dielectric constant.

At low dielectric constants, PDA tends to place charged or polar residues; at higher constants, these mutate to wild-type or non–wild-type uncharged or apolar residues (see Table 3). Examples of this trend include positions 34, 35, 71, 84, and 157. On the other hand, at high constants, some charged positions, including the wild-type ones, mutate to apolar amino acids. Examples of this trend include positions 74 and 118. Superposition of these two trends results in a curve with a minimum at ɛ/R = 10.3 ± 0.9.

Table 3.

Global energy minimum sequences found by PDA for different dielectric constants (ɛ)

		ɛ/R, R = interatomic distance
Positiona	Wild type	40	20	15	12.5	11.25	10	9.37	8.75	7.5	5
6	Leu	—b	—	—	—	—	—	—	—	—	—
14	Met	Phe	Phe	Leu	Leu	Leu	Leu	Leu	Leu	Leu	Leu
26	Asp	—	—	—	—	—	—	—	—	—	—
30	Glu	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp
32	Glu	—	—	—	—	—	—	—	—	—	—
34	Ala	—	—	—	—	—	—	—	Ser	Ser	Hsp
35	Tyr	—	—	—	—	—	—	—	—	—	Asp
40	Gln	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp
50	Thr	Met	Met	Met	Met	Met	Met	Met	Met	Met	Met
56	Glu	—	—	—	—	—	—	—	—	—	—
57	Ser	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr
59	Pro	Val	Val	Val	Val	Val	Val	Val	Val	Val	Val
66	Glu	—	—	—	—	—	—	—	—	—	—
71	Ser	Thr	Thr	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp
74	Glu	Phe	Phe	—	—	—	—	—	—	—	—
84	Gln	Ile	Ile	Ile	Ile	Ile	Ile	Ile	Ile	Lys	Lys
92	Phe	—	—	—	—	—	—	—	—	—	—
107	Asp	Ala	Ala	Ala	Ala	—	—	—	—	—	—
109	Asn	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe
113	Leu	—	—	—	—	—	—	—	—	—	—
118	Glu	Phe	Phe	—	—	—	—	—	—	—	—
125	Met	—	—	—	—	—	—	—	—	—	—
130	Asp	His	His	His	His	His	His	His	His	His	His
139	Phe	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala
143	Tyr	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala
157	Leu	—	—	—	—	—	—	—	—	—	Hsp
158	Lys	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe
183	Arg	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp

^a The residues are numbered as in 3HHR file from Brookhaven Protein Databank.

^b "—" indicates the wild-type residue.

Polar hydrogen burial penalty term

To optimize the polar hydrogen burial penalty term, we ran 11 rounds of design with values of the penalty from 0 to 3 kcal/mole. The dielectric constant was set to 10.3R, the optimal value obtained previously (Fig. 2 ▶). The entropy term weighting factor and other parameters were the same as in the optimization of the dielectric constant, as were the residues selected for design (28 boundary residues). The number of mutations contained in the GEMS is plotted versus the polar hydrogen burial penalty in Figure 3 ▶. The optimal value for the penalty is 1.6 ± 0.6 kcal/mole.

Fig. 3.

Number of mutations versus polar hydrogen burial penalty.

At low values of the penalty, charged or polar residues appear at some positions and become apolar or less polar as the penalty increases (see Table 4). This is the case for positions 40, 57, 71, 84, 139, 143, and 157. At high values of the penalty (ΔG_H ≥ 2.5), wild-type Glu at position 74 mutates to Phe; that is, a charged residue mutates to an apolar one. Superposition of these two trends results in a curve with a minimum at 1.6 ± 0.6 kcal/mole.

Table 4.

Global energy minimum sequences found by PDA for different polar hydrogen burial penalties (ΔGH)

		ΔGH (kcal/mole)
Positiona	Wild type	0	0.5	0.75	1	1.25	1.5	1.75	2	2.25	2.5	3
6	Leu	—b	—	—	—	—	—	—	—	—	—	—
14	Met	Leu	Leu	Leu	Leu	Leu	Leu	Leu	Leu	Leu	Leu	Leu
26	Asp	—	—	—	—	—	—	—	—	—	—	—
30	Glu	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp	Trp
32	Glu	—	—	—	—	—	—	—	—	—	—	—
34	Ala	—	—	—	—	—	—	—	—	—	—	—
35	Tyr	—	—	—	—	—	—	—	—	—	—	—
40	Gln	Arg	Arg	Arg	Arg	Arg	Arg	Arg	Arg	Arg	Arg	Arg
50	Thr	Phe	Phe	Phe	Met	Met	Met	Met	Met	Met	Met	Met
56	Glu	—	—	—	—	—	—	—	—	—	—	—
57	Ser	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr	Tyr	Ala	Ala	Ala
59	Pro	Val	Val	Val	Val	Val	Val	Val	Val	Val	Val	Val
66	Glu	—	—	—	—	—	—	—	—	—	—	—
71	Ser	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Thr	Thr
74	Glu	—	—	—	—	—	—	—	—	—	Phe	Phe
84	Gln	Arg	Lys	Lys	Lys	Lys	Lys	Ile	Ile	Ile	Ile	Ile
92	Phe	—	—	—	—	—	—	—	—	—	—	—
107	Asp	—	—	—	—	—	—	—	—	—	—	—
109	Asn	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Tyr	Tyr
113	Leu	—	—	—	—	—	—	—	—	—	—	—
118	Glu	Leu	—	—	—	—	—	—	—	—	—	—
125	Met	—	—	—	—	—	—	—	—	—	—	Val
130	Asp	His	His	His	His	His	His	His	His	His	His	His
139	Phe	His	His	His	His	His	His	His	Ala	Ala	Ala	Ala
143	Tyr	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala	Ala
157	Leu	Arg	Arg	Arg	—	—	—	—	—	—	—	—
158	Lys	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe	Phe
183	Arg	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp	Hsp

^a The residues are numbered as in 3HHR file from Brookhaven Protein Databank.

^b "—" indicates the wild-type residue.

Redesign of the core of hGH

To enhance the thermostability of hGH, we used PDA to computationally redesign 45 residues in the core of the protein (the same set that was used in the entropy weighting factor optimization). We used the parameters optimized as described above: entropy term with weighting factor of 2.3, penalty for polar hydrogen burial of 1.6 kcal/mole, and dielectric constant of 10.3R. The surface-based nonpolar exposure penalty and nonpolar burial benefit were set to 0.048 kcal/mole/Ų. The calculation resulted in 11 mutations (Table 5). We selected sequences for experimental testing by ranking the mutations according to their contribution to lowering the energy of the wild-type sequence. The six highest-ranking mutations were selected for the CORE1 sequence; two others were added to obtain CORE2; and another two were added to obtain CORE3 (Table 5). The model structure and 10 mutations of the CORE3 protein are shown in Figure 4 ▶.

Table 5.

Global energy minimum sequence found by PDA using optimized parameters for a core design of hGHa (Design) and experimentally tested sequences (CORE1, CORE2, CORE3)

Positionb	Wild type	Design	CORE1	CORE2	CORE3
6	Leu	—c	—	—	—
10	Phe	—	—	—	—
13	Ala	Val	Val	Val	Val
17	Ala	—	—	—	—
20	Leu	—	—	—	—
24	Ala	—	—	—	—
27	Thr	Val	Val	Val	Val
28	Tyr	Phe	—	—	Phe
31	Phe	—	—	—	—
36	Ile	—	—	—	—
44	Phe	—	—	—	—
54	Phe	Tyr	—	—	Tyr
55	Ser	Ala	—	Ala	Ala
58	Ile	—	—	—	—
73	Leu	—	—	—	—
75	Leu	—	—	—	—
76	Leu	—	—	—	—
78	Ile	—	—	—	—
79	Ser	Ala	Ala	Ala	Ala
80	Leu	—	—	—	—
81	Leu	—	—	—	—
82	Leu	—	—	—	—
83	Ile	—	—	—	—
85	Ser	Ala	—	Ala	Ala
90	Val	Ile	Ile	Ile	Ile
93	Leu	—	—	—	—
96	Val	—	—	—	—
97	Phe	—	—	—	—
105	Ala	—	—	—	—
110	Val	—	—	—	—
114	Leu	Met	—	—	—
117	Leu	—	—	—	—
121	Ile	—	—	—	—
124	Leu	—	—	—	—
157	Leu	—	—	—	—
161	Gly	Met	Met	Met	Met
162	Leu	—	—	—	—
163	Leu	—	—	—	—
166	Phe	—	—	—	—
170	Met	—	—	—	—
173	Val	—	—	—	—
176	Phe	—	—	—	—
177	Leu	—	—	—	—
180	Val	—	—	—	—
184	Ser	Ala	Ala	Ala	Ala

^a Protein Data Bank structure 3HHR.

^b The residues are numbered as in 3HHR file from Brookhaven Protein Databank.

^c "—" indicates the wild-type residue.

Fig. 4.

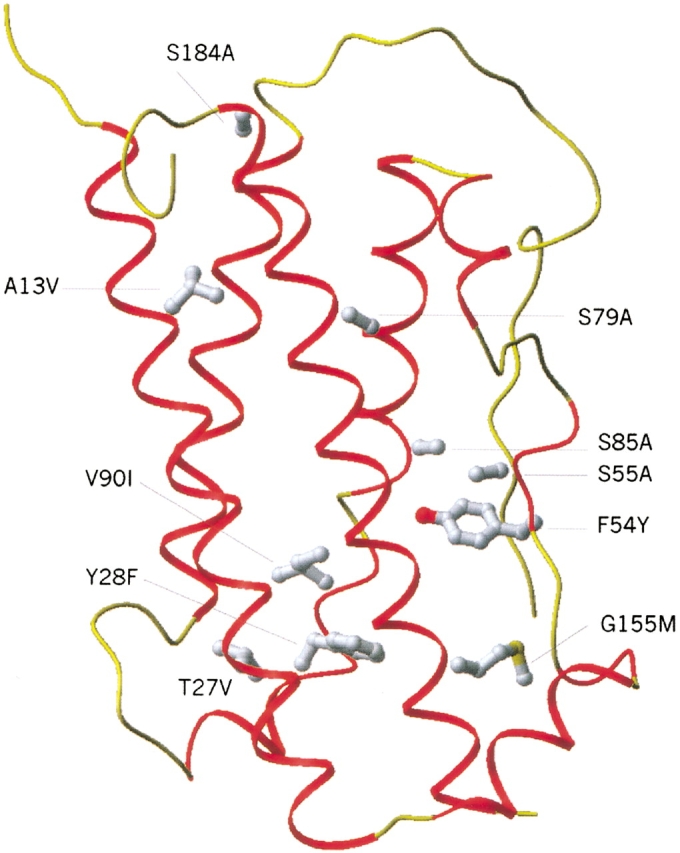
Structure of CORE3 protein (a model generated by PDA, our computational design method). The 10 mutations are shown in ball-and-stick representation (hydrogen atoms are not shown).

Thermal stability

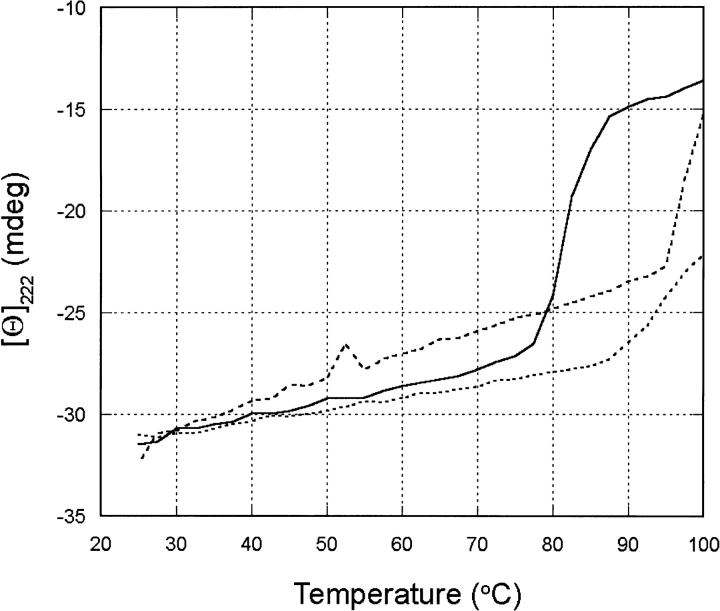
CORE1, CORE2, and CORE3 proteins and wild-type hGH were expressed and isolated as described in Materials and Methods. The far-ultraviolet circular dichroism spectra for the proteins were nearly identical to each other and to the wild-type protein, indicating highly similar secondary structure and tertiary folds (data not shown). Thermal denaturation was monitored at 222 nm for wild-type hGH, CORE1, and CORE2 (Fig. 5 ▶; data was not obtained for CORE3).

Fig. 5.

Thermal denaturation monitored by circular dichroism at 222 nm for wild-type hGH (solid line), CORE1 (dashed line), and CORE2 (dotted line).

The melting temperatures (T_ms) were estimated graphically by finding the midpoints on the transition region of the melting curve. Because the T_ms for the mutants are close to 100°C and the ends of the transition regions of the curves are beyond the experimental range, only the lower bounds of the T_ms can be estimated. This gives the following values: wild-type T_m = 82°C, CORE1 T_m ≥ 98°C, and CORE2 T_m ≥ 95°C. The designed proteins thus showed enhancements of 13°C to 16°C. It should be noted that thermal melting was not reversible as measured; therefore, the T_m values given here are not rigorous thermodynamic parameters. However, these values are indicative of the improved thermostability of the designed proteins.

Biological activity

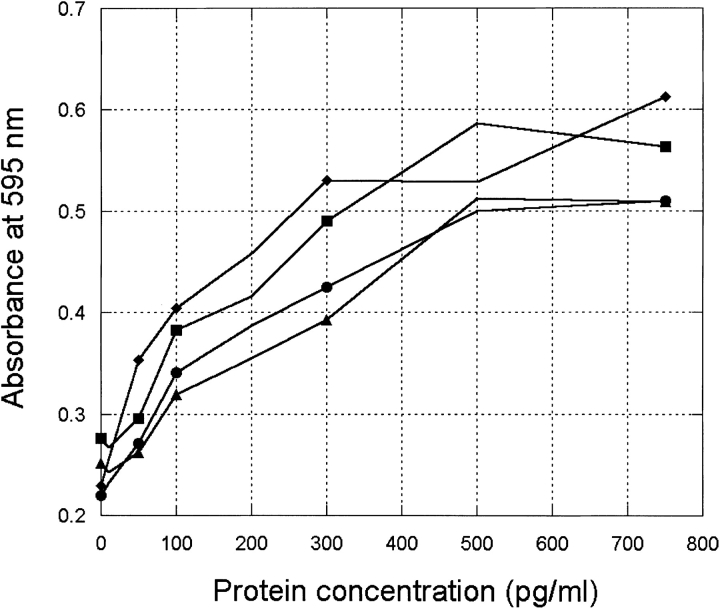
The biological activity of CORE1, CORE2, and CORE3 proteins was determined in vitro by quantitating cell proliferation as a function of protein concentration. Figure 6 ▶ shows the dose-response curves of CORE1, CORE2, CORE3, and wild-type hGH in a representative assay. EC₅₀ values were determined by nonlinear least-squares fit of sigmoidal parts of the averaged curves to a four-parameter sigmoidal equation as described in Materials and Methods. The designed proteins showed comparable activity to wild-type hGH (Table 6).

Fig. 6.

Proliferation of BAF/B03 cells expressing the hGH receptor in response to wild-type hGH (diamonds), CORE1 (squares), CORE2 (triangles), and CORE3 (circles). Each point represents the average of three replicates.

Table 6.

Biological activity of the designed proteins

Protein	EC50 (pg/mL)
Wildtype hGH	220 ± 20
CORE1	320 ± 30
CORE2	260 ± 50
CORE3	230 ± 50

Discussion

This study has two purposes: (1) improving our sequence energy scoring function by both adding an entropy term and optimizing the relative weights of the energy terms, and (2) improving the thermostability of hGH. We designed only the core residues of the protein, rather than the surface-exposed residues, to reduce the probability of an immunogenic response to the mutated protein. Designing only core residues simplified implementation of the entropy penalty. Core residues can be modeled simply as losing all entropy relative to the free side-chain, whereas boundary and surface residues require correction factors, such as scaling based on accessible surface area (Abagyan and Totrov 1994), to account for remaining conformational flexibility in the folded state. Designing only core residues also simplified electrostatic modeling. Optimization of the weighting factor for electrostatic energy showed that a large distance-dependent dielectric (ɛ/R ∼10) was necessary to reduce the magnitude of the electrostatic energy and mitigate inaccuracies in the charge model, a weakness of all force fields. Because no charged residues were in the core design, the inaccuracies of force field approaches for charge-charge interactions were eliminated from our hGH variants.

In this work, we optimize the weighting factors by minimizing the number of mutations designed by the algorithm. That is, we assume that the wild-type sequence approximately corresponds to the global energy minimum in the sequence space. This is more correct for highly stable proteins, which were optimized for stability by nature. Therefore, further development of this idea should include calculations on a test set of several highly stable proteins with known high-resolution X-ray structures. An alternative approach to optimize the weighting factors is the use of mutagenesis data to correlate mutant stability with the energy function predictions. Of particular interest, of course, is testing the stability of the sequences designed by the algorithm. Unfortunately, this is a very time-consuming approach.

The increased stability seen with CORE1 and CORE2 results from improved van der Waals packing interactions and increased burial of hydrophobic groups (A13V, T27V, V90I, G161M) and from replacement of unsatisfied hydrogen bond donors or acceptors with hydrophobic residues (T27V, S55A, S79A, S85A, S184A). It should be noted that our design resulted in the replacement of one threonine and four serines, residues that do not seem to form hydrogen bonds in the native protein. Although the role of these T→A and S→A mutations has not been determined individually, the considerable improvements in the T_ms obtained indicate that these mutations are beneficial for stability.

We obtained highly stabilized variants of hGH, a result of considerable practical interest and potential clinical significance. An equipotent, but more robust, hGH molecule could have improved pharmacokinetics or better storage properties or be more amenable to use in alternative delivery systems and formulations, thus providing added convenience and improved patient compliance. Also, the large increase in T_m (≥16°C) shows the utility of our optimized energy function in automated protein design.

Materials and methods

Entropy term

We used the side-chain entropy scale taken from Pickett and Sternberg (1993) and the backbone entropy scale from Stites and Pranata (1995). Both scales were derived by analyzing the distribution of side-chain rotamers and backbone angles in crystal structures. We assume that all the entropy is lost on folding, because all the designed residues in the current work are mostly buried in the core of the protein. Therefore, our entropy scale is obtained by summing up the side-chain entropy scale and the backbone entropy scale, corrected for the glycine backbone entropy loss taken from D'Aquino et al. (1996; Table 1). The correction does not influence the ranking of the designed sequences, because it only results in a constant offset. The following parameters were used in the calculations for optimization of the entropy weighting factor: distance-dependent electrostatic term with ɛ = 40R (R is the interatomic distance), penalty for polar hydrogen burial of 2 kcal/mole, and surface-based nonpolar exposure penalty and nonpolar burial benefit of 0.0232 kcal/mole/Ų. The following amino acids were allowed at the designed positions: Ala, Val, Phe, Ile, Leu, Tyr, Trp, Met, and Ser.

Weighting factor for the electrostatic term

The following parameters were used: entropy term with weighting factor of 2.3, penalty for polar hydrogen burial of 2 kcal/mole, and surface-based nonpolar exposure penalty and nonpolar burial benefit of 0.048 kcal/mole/Ų. The following amino acids were allowed at the designed positions: Ala, Val, Leu, Ile, Phe, Tyr, Trp, Asp, Asn, Glu, Gln, Lys, Ser, Thr, His, Hsp, Arg, and Met.

Weighting factor for the polar hydrogen burial penalty

The following parameters were used: entropy term with weighting factor of 2.3, dielectric constant of 10.3 R, and surface-based nonpolar exposure penalty and nonpolar burial benefit of 0.048 kcal/mole/Ų. The amino acids allowed at the designed positions were the same as for the optimization of the electrostatics term.

Computational design

The crystal structure of hGH (Brookhaven Protein Data Bank code 3HHR) was used as the starting point. The program BIOGRAF (Molecular Simulations Inc.) was used to generate hydrogens on the structure and to minimize it (50 steps of conjugate gradient minimization with the Dreiding II force field; Mayo et al. 1990). Residues were classified as core, surface, or boundary using the RESCLASS program (Dahiyat and Mayo 1997a). The parameters not specified in the Results section are described in other work (Dahiyat and Mayo 1996, 1997a). An expanded version (Dahiyat and Mayo 1996) of the backbone-dependent rotamer library of Dunbrack and Karplus (1993) was used in all the calculations.

Cloning and expression

A gene for hGH was synthesized from partially overlapping oligonucleotides (∼100 bases) that were extended and PCR amplified. Codon usage was optimized for Escherichia coli, and several restriction sites were incorporated to ease future cloning. These partial genes were cloned into a vector and transformed into E. coli for sequencing. Several of these gene fragments were then cloned into adjacent positions in an expression vector (pET17 or pET21) to form the full-length gene for hGH and transformed into E. coli for expression. Protein was expressed in E. coli in insoluble inclusion bodies, and its identity was confirmed by immunoblot of SDS-PAGE using a commercial mAb against hGH (Santa Cruz Biotechnology).

Refolding

The protein inclusion bodies were dissolved and washed consecutively using wash buffer A (100 mM Tris at pH 8, 2% Triton, 4 M urea, 5 mM EDTA, 0.5 mM DTT) and wash buffer B (100 mM Tris at pH 8, 0.5 mM DTT), and the solvents were removed by centrifuging at 20,000g for 30 min. The pellet was resuspended with extraction buffer (50 mM glycine, 0.0156 M NaOH, 5 mM glutathione reduced, 8 M GdnHCl at pH 9.6). The supernatant was dialyzed for 12 to 16 h against folding buffer A (50 mM glycine, 0.0156 M NaOH, 10% sucrose, 1 mM EDTA, 1 mM glutathione reduced, 0.1 mM oxidized glutathione, 4 M urea at pH 9.6). The supernant was dialyzed for 6 to 8 h in buffer B (60 mM Tris, 10% sucrose, 1 mM EDTA, 0.1 mM reduced glutathione, 0.01 mM oxidized glutathione at pH 9.6).

Purification

A size exclusion column (10 mm × 300 mm loaded with Superdex prep 75 resin purchased from Pharmacia) was loaded with protein and eluted at a flow rate of 0.8 mL/min using the column buffer (100 mM Na₂SO₄, 50 mM Tris at pH 7.5). The peaks were monitored at dual wavelengths of 214 and 280 nm. Albumin, carbonic anhydrate, cytochrome C, and aprotinin were used to calibrate the molecular size of proteins versus elution time. The monomeric peak that elutes around the expected elution time for each protein was collected for biophysical characterization. The proteins were >98% pure as judged by reversed-phase high performance liquid chromatography on a C₄ column (3.9 mm × 150 mm), with a linear acetonitrile-water gradient containing 0.1% TFE. The identities of all proteins were confirmed by comparing the molecular mass measured by mass spectrometry with the corresponding molecular mass calculated using the protein sequences.

Spectroscopic characterization

Protein samples were 50 μM in 50 mM sodium phosphate (pH 5.5). Concentrations were determined using ultraviolet spectrophotometry. Protein structure was assessed by circular dichroism. Circular dichroism spectra were measured on an Aviv 202DS spectrometer equipped with a Peltier temperature control unit using a 1-mm path length cell. Thermal stability was assessed by monitoring the temperature dependence of the circular dichroism signal at 222 nm. The data were collected every 2.5°C, with an averaging time of 5 sec and an equilibration time of 3 min. The T_m of each protein was derived from the derivative curve of the ellipticity at 222 nm versus temperature. T_m values were reproducible to within 2°C for the same protein at the concentrations used.

Cell proliferation assay

Cell proliferation assays were performed using an interleukin 3–dependent murine proB cell line, BAF/B03, stably transfected with the full-length human growth hormone receptor (Behncken et al. 1997) according to the method of Rowlinson et al. (1995, 1996). Cells were maintained in RPMI-1640 medium with 5% fetal calf serum (FCS), 1 μg/mL gentamicin, and 50 units/mL interleukin 3. In preparation for the assay, exponentially growing cells were washed twice in PBS and resuspended in hGH-free and phenol red–free RPMI-1640 media with 5% FCS and 1 μg/mL gentamicin. Serial diluted hGH was then added to 96-well microtiter plates containing 2.5 × 10⁴ cells/well. After 24 h of incubation at 37°C in 5% CO₂, cell proliferation was quantified using the MTT assay. In each assay, the wild type and all three of the designed variants of hGH were tested in triplicate on the same plate. The entire assay was repeated three times. EC₅₀ values were determined using KaleidaGraph (Synergy Software) by nonlinear least-squares fit of sigmoidal parts of the averaged curves to a four parameter equation:

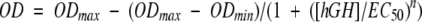as performed by Young et al. (1997).