Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction

Abstract

The distance-dependent structure-derived potentials developed so far all employed a reference state that can be characterized as a residue (atom)-averaged state. Here, we establish a new reference state called the distance-scaled, finite ideal-gas reference (DFIRE) state. The reference state is used to construct a residue-specific all-atom potential of mean force from a database of 1011 nonhomologous (less than 30% homology) protein structures with resolution less than 2 Å. The new all-atom potential recognizes more native proteins from 32 multiple decoy sets, and raises an average Z-score by 1.4 units more than two previously developed, residue-specific, all-atom knowledge-based potentials. When only backbone and C_β atoms are used in scoring, the performance of the DFIRE-based potential, although is worse than that of the all-atom version, is comparable to those of the previously developed potentials on the all-atom level. In addition, the DFIRE-based all-atom potential provides the most accurate prediction of the stabilities of 895 mutants among three knowledge-based all-atom potentials. Comparison with several physical-based potentials is made.

The solution of the protein folding problem requires an accurate potential that describes the interactions among different amino acid residues. The potential that would yield a complete understanding of the folding phenomena should be derived from the laws of physics. However, the use of such physical-based potentials (Brooks et al. 1983; Weiner et al. 1986; Jorgensen et al. 1996; Scott et al.1999) for ab initio folding studies is limited by available computing power (Duan and Kollman 1998). Their applications to the recognition of native structures from nonnative conformations (Moult 1997; Hao and Scheraga 1998; Lazaridis and Karplus 2000; Petrey and Honig 2000; Wallqvist et al. 2002), however, yielded results comparable to knowledge-based statistical potentials that extract interactions directly from known protein structures (Tanaka and Scheraga 1976). Knowledge-based statistical potentials are attractive because they are simple and easy to use. Knowledge-based potentials can be categorized into distance-independent contact energies (Miyazawa and Jernigan 1985; DeBolt and Skolnick 1996; Zhang et al. 1997; Skolnick et al. 2000) and distance-dependent potentials (Hendlich et al. 1990; Sippl 1990; Jones et al. 1992; Samudrala and Moult 1998; Lu and Skolnick 2001). Both residue level (Miyazawa and Jernigan 1985; Hendlich et al. 1990; Sippl 1990; Jones et al. 1992) and atomic level (DeBolt and Skolnick 1996; Zhang et al. 1997; Samudrala and Moult 1998; Lu and Skolnick 2001) potentials were developed and applied to fold recognition and assessment (Hendlich et al. 1990; Sippl 1990; Casari and Sippl 1992; Jones et al. 1992; Bryant and Lawrence 1993; Samudrala and Moult 1998; Miyazawa and Jernigan 1999; Lu and Skolnick 2001; Melo et al. 2002), structure predictions (Sun 1993; Simons et al. 1997; Skolnick et al. 1997; Lee et al. 1999; Tobi and Elber 2000; Vendruscolo et al. 2000; Pillardy et al. 2001), and validations (Luthy et al. 1992; Sippl 1993; MacArthur et al. 1994; Rojnuckarin and Subramaniam 1999), docking and binding (Pellegrini et al. 1995; Wallqvist et al. 1995^; Zhang et al. 1997), and mutation-induced changes in stability (Gilis and Rooman 1996,Gilis and Rooman 1997; Zhang et al. 1997).

This work focuses on distance-dependent, residue-specific, all-atom, knowledge-based potentials. This is because in protein–structure selections, all-atom–based potentials perform better than residue-based potentials (Samudrala and Moult 1998; Lu and Skolnick 2001), and distance-dependent potentials better than distance-independent ones (Melo et al. 2002). The derivation of a distance-dependent, pairwise, statistical potential 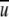(i,j,r) starts from a common equation given by

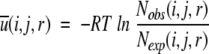(1)

where R is the gas constant, T is the temperature, N_obs(i,j,r) is the observed number of atomic pairs (i,j) within a distance shell r − Δr/2 to r + Δr/2 in a database of folded structures, and N_exp(i,j,r) is the expected number of atomic pairs (i,j) in the same distance shell if there were no interactions between atoms (the reference state). Clearly, the method used to calculate N_exp(i,j,r) is what makes one potential differ from another because the method to calculate N_obs(i,j,r) is the same (except minor differences in database and bin procedures). Samudrala and Moult (1998) used a conditional probability function

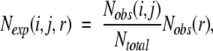(2)

where N_obs(r) ≡ ∑_i,j N_obs(i,j,r), N_obs(i,j) ≡ ∑_r N_obs(i,j,r) and N_total ≡ ∑_i,j,r N_obs(i,j,r). Lu and Skolnick (2001) employed a quasi-chemical approximation:

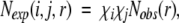(3)

where χ_k is the mole fraction of atom type k. The common approximation made by the above two potentials is that ∑_i,j N_exp(i,j,r) ≡ N_obs(r). This approximation has its origin in the "uniform density" reference state used by Sippl (1990) to derive the residue-based, distance-dependent potential. In this approximation, the total number of pairs in any given distance shell for a reference state is the same as that for folded proteins. In other words, the distance dependence of the pair probability distribution of the reference state is an averaged distribution over all residue or atomic pairs. This reference state is a noninteracting ideal-gas reference state only if the average interaction of all residue or atomic pairs is zero (i.e., attractive and repulsive interactions cancel each other). However, it is highly unlikely that attractive and repulsive interactions could cancel each other exactly. These missing residual interactions may well be important for an accurate potential.

To explore the missing residual interactions, we establish a noninteracting reference state without using the above-mentioned assumption. This is done by using uniformly distributed noninteracting points in finite spheres. The reference state coupled with a simple distance scaling method is employed to derive an all-atom potential of mean force from 1011 known protein structures (Hobohm et al. 1992). It is shown that the new atomic potential is slightly more attractive than other knowledge-based all-atom potentials (Samudrala and Moult 1998; Lu and Skolnick 2001). This small residual interaction leads to an improved potential of mean force for structure selections from single and multiple decoy sets and for the prediction of the changes in the stabilities of 895 mutants.

Methods

Fundamental equations of statistical mechanics

The observed number of pairs of atoms i and j, N_obs(i,j,r), between spatial distances r − Δr/2 and r + Δr/2 is related to the pair distribution function g_ij(r) as follows (Friedman 1985).

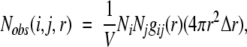(4)

where V is the volume of the system and N_i and N_j are the number of atoms i and j, respectively. Because the atom–atom potential of mean force, 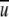(i,j,r), is equal to −RTln g_ij(r) (Friedman 1985), we have

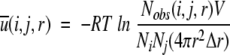(5)

When the interaction is turned off (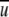(i,j,r) = 0), we have

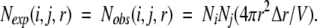(6)

This is a simple expression for an ideal mixture of atoms i and j that have a uniform number of densities of N_i/V and N_j/V, respectively.

Finite ideal-gas reference state

The above equations from liquid-state statistical mechanics cannot be directly applied to proteins. Proteins are finite systems, and as a result, N_exp(i,j,r) will not increase in r² as in an infinite system (Equation 6). We remedy this problem by assuming that N_exp(i,j,r) increases in r^α with a to-be-determined constant α. Thus, Equation 6 becomes

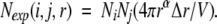(7)

This leads to (cf. Equation 5)

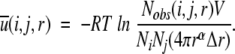(8)

Equation 8 can be further simplified by assuming that 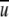(i,j,r) is a short-range interaction with a cutoff distance of r_cut. That is, 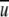(i,j,r ) = 0 for r ≥ r_cut. In this case, Equation 8 can be rewritten in terms of variables at r = r_cut as below:

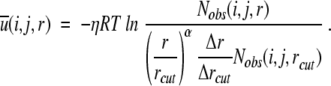(9)

Here, a constant factor η is placed in front of RT to facilitate a quantitative comparison with mutation-induced changes in stability. This factor is needed because temperature is a free parameter in potentials derived from static structures. Equation 9 implies a new equation for N_exp(i,j,r):

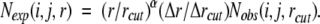(10)

Unlike early expressions for N_exp(i,j,r) (Equations 2 and 3), this equation does not contain any distance-dependent information from protein structures but is a natural extension of the ideal-gas reference state (Equation 6) to a finite system. We shall call this reference state the Distance-scaled, Finite Ideal-gas REference (DFIRE) state. A potential generated from Equation 9 is called the DFIRE-based potential. DFIRE-A and DFIRE-B denote the residue-specific all-atom–based and backbone + C_β atom-based potentials, respectively.

Structural database

The common approximation used in all structure-derived potentials is that the structures of different proteins are belong to an ensemble of the thermodynamically equilibrated structures of one system. We employ a structural database of 1011 nonhomologous (less than 30% homology) proteins with resolution <2 Å that was collected by Hobohm et al. (1992) (http://chaos.fccc.edu/research/labs/dunbrack/culledpdb.html). The DFIRE-based potentials are generated by calculating the total number of observed i,j pairs N_obs(i,j,r) from all 1011 proteins. Contacting pairs between the atoms within the same residue are excluded from the statistics. If N_obs(i,j,r) is found to be zero, the potential of mean force is set to 10η kcal/mole.

One can also calculate N_obs(i,j,r) and 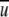(i,j,r) for each protein and then obtain an ensemble-averaged potential afterward. We do not use this approach because the number of pairs in a single protein is too small to yield accurate statistical results for individual (Lu and Skolnick 2001).

Atom types, r_cut and bin procedure

As in Samudrala and Moult (1998) and Lu and Skolnick (2001), residue-specific heavy atom types were used. This results in 167 atom types in DFIRE-A. In DFIRE-B, only backbone and C_β atom types are employed. In this paper, the cutoff distance r_cut is set to 14.5 Å. The bin width Δ r is 2 Å for r < 2 Å, 0.5 Å for 2 Å < r < 8 Å, and 1 Å for 8 Å < r < 15 Å. The total number of bins is 20. In this work, no attempt is made to optimize bin width and r_cut for better performance (also see discussion below).

The value of α

The value of α is estimated from uniformly distributed points in 1011 spheres; each corresponds to a protein. The radius of each sphere is cR_g, and the sphere contains an evenly distributed n_hv points. Here, c is a to-be-determined constant, R_g and n_hv are the radius of gyration and the number of heavy atoms of the corresponding protein, respectively. Constant c is determined by the number of atomic pairs in a noninteracting uniform system. The latter can be calculated from the number of atomic pairs in 1011 protein structures in the cutoff distance shell of 14–15 Å because at that distance, we assumed zero interactions between atoms. There are about 61 million atomic pairs for 1011 proteins. c is found to be 1.17 by setting the number of atomic pairs in 1011 spheres in the 14–15 Å distance shell to 61 million.

The number of pairs as a function of spatial separation, N(r), can be obtained from the evenly distributed points in the 1011 spheres. We further define the reduced distance-dependent function f(r) (=N(r)/r^α) and the relative fluctuation, δ of f(r).

where 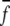= ∑_r f(r)/n, and n is the total number of distance shells. The relative fluctuation δ as a function of α and f(r) as function of r are shown in Figures 1A and 1B ▶, respectively. The minimum of δ corresponds to α = 1.57 (1.57 ≈ π/2 by coincidence). Because there is no distinction between different atoms in the ideal-gas limit, the value of 1.57 is applied to any atomic pair. We also assess the new potential at α = 1.45 and 1.70 to ensure that α = 1.57 gives the best performance. The positive outcome (see below) validates the overall approach used to obtain α.

Fig. 1.

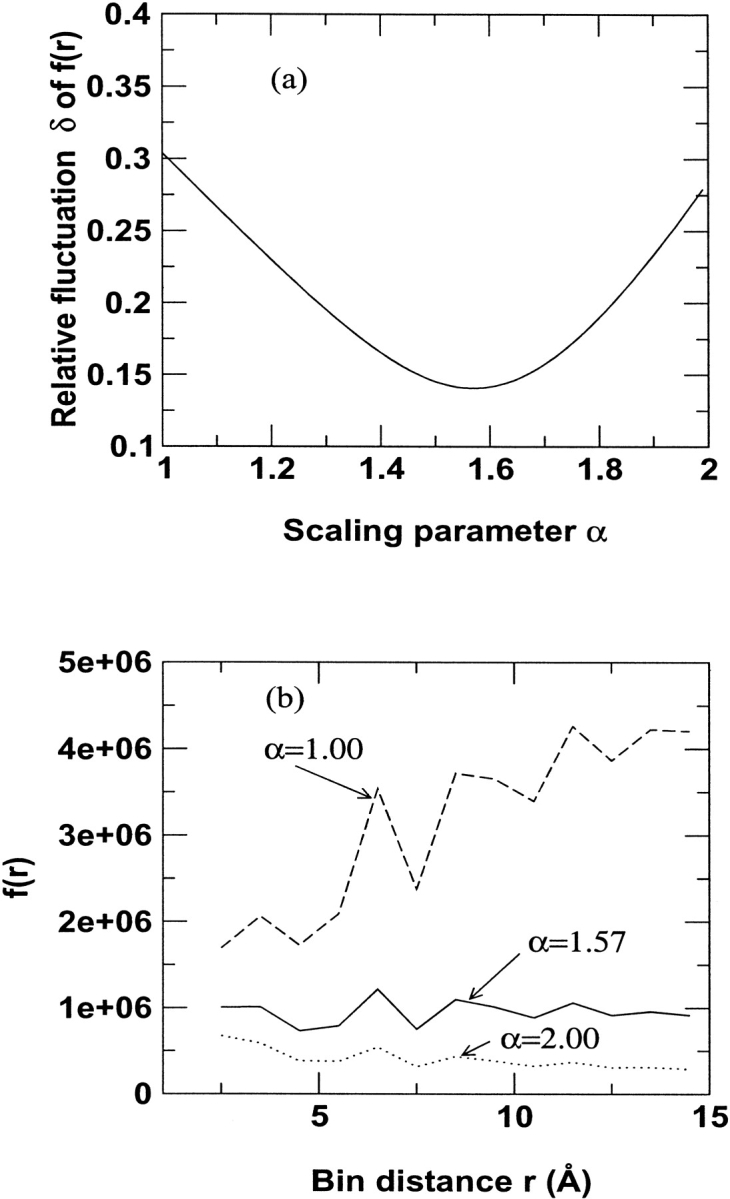
Scaling behavior of uniformly distributed heavy atoms in 1011 spheres. Number of pairs was counted in every 1 Å shell, and r is the middle point of the shell. (a) Relative fluctuation δ, and (b) reduced distance-dependent function f(r) = N(r)/r^α.

One approximation made in this derivation is that the contributions of backbone entropy and the structure of denatured state to stability are not included. These terms are difficult to evaluate, and are not included in other distance-dependent knowledge-based potentials as well.

Structure selections from decoys and stability prediction

In structure selections from decoy sets, the total atom–atom potential of mean force, G, is calculated for each decoy

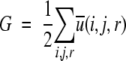(11)

where the summation is over atomic pairs that are not in the same residue. The native state is correctly identified if its structure has the lowest value of G. Z-score is defined as 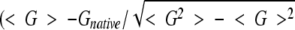, where ≬ denotes the average over all decoy structures of a given native protein, and G_native is the total atom–atom potential of mean force of the native structure. Z-score is a quantitative measure of the free-energy bias against nonnative conformations.

The predicted free energy change due to mutation is calculated by G_mutant − G_native assuming no structural relaxation after mutations. Only those mutations that have a decreased number of atoms are used in prediction. This is to avoid the possible strains associated with small-to-large mutations (Liu et al. 2000) and the uncertainty about the placement of extra atoms.

The RAPDF and atomic KBP potentials

To compare the DFIRE-based potentials with the RAPDF (Samudrala and Moult 1998) and atomic KBP (Lu and Skolnick 2001) potentials, we regenerate the two potentials using the procedures described below. For RAPDF (Samudrala and Moult 1998), the first bin covers 0–3.0 Å, the distance between 3.0–20 Å is binned every 1 Å. The total number of bins is 18. All 18 bins with a cutoff distance of 20 Å are used for scoring. For atomic KBP (Lu and Skolnick 2001), the distance between 1.5 to 14.5 Å, is binned every 1 Å and the last bin is from 14.5 Å to infinite. The total number of bins is 14. The first and second sequence neighbors are excluded while backbone atoms are included in counting contacts. When used in scoring, only the bins covering 3.5–6.5 Å are used. In all cases, contacts between atoms within a single residue are excluded from the counts and scoring. In case of zero pairs, both potentials are set to be 2η kcal/mole. The structural database is the 1011 structures described above for the DFIRE-based potentials rather than 265 proteins used in RAPDF and 1291 proteins used in atomic KBP in respective original publications. As we discussed below, the change of the database has little effect on the overall accuracy of the RAPDF and atomic KBP potentials.

Results

Single decoy sets

In this paper, both single and multiple decoy sets are used to assess DFIRE-based potentials. We did not exclude the homologous proteins to the test decoy sets from the 1011 training database because the exclusion has very little effect on the results. For example, 1ctf is in the training database and also in many of the decoy sets to test the potential; the results for 1ctf with a database that includes or excludes 1ctf are essentially the same. The large database of 1011 proteins makes the contribution of a single protein to the number of pairs observed too small to have any bias toward the protein.

The single decoy sets are obtained from the PROSTAR website, http://prostar.carb.nist.gov/. Results are compiled in Table 1. For decoy sets misfold (Holm and Sander 1992), asilomar (Mosimann et al. 1995), pdberr & sgpa (Avbelj et al. 1990), all three potentials (RAPDF, Atomic KBP, and DFIRE-A) achieved 100% correct identifications.

Table 1.

Number of correctly identified decoys from single decoy sets by different potentials

	RAPDFa	Atomic KBPb	DFIRE-Ac	DFIRE-A1.45d	DFIRE-A1.70e	DFIRE-Bf
Misfold	25/25g	25/25	25/25	25/25	25/25	23/25
Asilomarh	33/33	33/33	33/33	33/33	33/33	32/33
Pdberr & sgpa	5/5	5/5	5/5	5/5	5/5	5/5
Ifu	31/44	33/44	34/44	32/44	34/44	18/44

^a All atom potential from Samudrala and Moult (1998)).

^b All atom potential from Lu and Skolnick (2001).

^c All-atom DFIRE-based potential (α = 1.57).

^d DFIRE-based potential (α = 1.45)

^e DFIRE-based potential (α = 1.70)

^f DFIRE-based potential (α = 1.57) for backbone and C_β atoms.

^g The first number and the second number in each cell are the number of correctly identified decoys and the total number of decoys, respectively.

^h As in (Petrey and Honig, 2000), the native structure of protein NDK is replaced by the structure of PDB code 1nue; the following eight decoys were excluded from the original set because of mismatched sequences: crabpi_vriend, edn_biosym, edn_weber, mchpr_vihinen, ndk_abagyan, ndk_vihenen, p450_abagyan, p450_weber.

The worst performance for all three potentials is in the ifu decoy set (Pedersen and Moult 1997). DFIRE-A is slightly better than RAPDF and KBP. It identified 34 out of 44, compared to 31 for RAPDF and 33 for atomic KBP. The results of RAPDF and atomic KBP shown here are identical to the performance of the original RAPDF and atomic KBP potentials derived from different structural databases (Lu and Skolnick 2001). The relatively poor performance made by the knowledge-based potentials in the ifu decoy set is perhaps because the "independent folding units" are peptide fragments (between 10–20 residues) that may not be foldable when isolated (Samudrala and Moult 1998).

Multiple decoy sets

The Park and Levitt 4state_reduced decoy set contains seven proteins and each has 600 to 700 decoys. The set was built using a 4-state off-lattice model (Park and Levitt 1996). RAPDF and atomic KBP correctly identified all seven proteins (Table 2, A). DFIRE-A identified six out seven proteins. Although the native state of 3icb was ranked as the fourth lowest energy by DFIRE-A, three lower energy decoys all have rmsd within 1.7 Å from the 3icb native structure that has a 2.3 Å resolution. Moreover, the native structure 4icb, a higher resolution version (1.6 Å) of the same protein (Svensson et al. 1992), is correctly identified as the lowest energy by DFIRE-A. In term of the bias against nonnative structures, DFIRE-A has the highest Z-score (3.49), followed by atomic KBP (3.24), and RAPDF (3.01).

Table 2.

Native rank and Z-score of different potentials using multiple decoy sets

	RAPDF	Atomic KBP	DFIRE-A	DFIRE-A1.45	DFIRE-A1.70	DFIRE-B
(A) 4state-reduceda
1ctf	1/3.26b	1/3.53	1/3.86	1/3.33	1/4.01	1/3.03
1r69	1/3.49	1/3.76	1/4.23	1/3.76	1/4.10	1/2.95
1sn3	1/3.26	1/3.50	1/3.79	1/3.83	1/3.13	1/3.40
2cro	1/2.93	1/2.91	1/3.29	1/2.97	1/3.24	2/2.74
3icb	1/2.22	1/2.41	4/2.28c	1/2.15	4/2.29	24/1.68
4pti	1/3.12	1/3.47	1/3.62	1/3.54	1/3.16	1/3.15
4rxn	1/2.79	1/3.12	1/3.33	1/2.78	1/3.42	19/1.88
d	3.01	3.24	3.49	3.19	3.34	2.69
(B) fisae
1fc2	497/−2.74	413/−1.05	254/0.23	406/−0.91	60/1.05	1/2.76
1hdd-C	17/2.00	25/1.78	1/4.50	1/3.77	1/4.45	1/6.76
2cro	14/1.93	24/1.64	1/6.33	1/5.47	1/6.08	1/7.84
4icb	1/3.89	6/2.46	1/6.91	1/6.34	1/6.96	1/8.47
d	1.27	1.21	4.49	3.67	4.64	6.46
(C) fisa_caspf
1bg8-A	1/4.39	2/2.84	1/5.35	1/5.13	1/4.92	1/3.82
1bl0	1/3.19	215/0.76	1/4.50	1/4.01	1/4.32	3/2.27
1jwe	1/4.69	4/2.64	1/6.26	1/5.96	1/5.94	1/4.81
d	4.09	2.08	5.37	5.03	5.06	3.63
(D) lmds
1b0n-B	359/−0.45	74/1.03	430/−1.17	398/−0.82	438/−1.33	261/0.03
1bba	501/−11.11	500/−3.51	501/−16.28	501/−18.34	501/−11.78	501/−21.38
1fc2	501/−7.75	501/−8.86	501/−5.72	501/−6.32	501/−4.19	441/−1.22
1ctf	1/2.84	1/3.45	1/3.54	1/3.56	1/3.42	1/2.77
1dtk	116/−0.08	31/1.16	1/2.62	62/0.56	1/3.69	5/2.46
1igd	1/4.21	1/4.16	1/5.16	1/5.54	1/4.26	1/4.69
1shf-A	1/5.15	2/2.83	1/6.68	1/6.01	1/6.29	1/5.44
2cro	416/−0.96	175/0.40	1/4.70	109/0.85	1/6.51	1/4.50
2ovo	4/2.76	1/2.86	1/3.21	1/3.27	1/2.92	27/1.48
4pti	157/0.20	13/1.75	1/3.96	5/2.18	1/4.72	1/3.47
d	−0.52	0.53	0.67	−0.35	1.45	0.22
(E) lattice_ssfitg
lbco	1/9.79	1/9.47	1/12.09	1/10.80	1/7.36	1/7.95
1ctf	1/6.99	1/7.20	1/10.05	1/7.26	1/8.13	1/6.89
1dkt-A	1/6.78	1/6.78	1/6.87	1/6.38	1/4.50	1/4.92
lfca	1/5.57	1/3.36	1/7.18	1/6.13	1/5.26	1/5.30
1nkl	1/8.33	1/8.16	1/9.29	1/7.15	1/7.15	1/5.83
1pgb	1/8.42	1/6.86	1/11.87	1/8.60	1/9.18	1/9.64
1trl-A	1/4.84	1/5.58	1/6.32	1/4.81	1/5.00	1/3.73
4icb	1/6.68	1/5.65	1/7.81	1/6.12	1/7.06	1/4.25
d	7.18	6.61	8.94	7.16	6.70	6.06
Summary
# Correct/Total	22/32	18/32	27/32	25/32	27/32	23/32
h	2.83	2.87	4.27	3.31	3.91	3.32

^aPark and Levitt, 1996.

^b The first number in each cell is rank and the second number is the Z-score.

^c See text for discussion.

^d The average Z-score for the decoy set.

^eSimons et al., 1997.

^fSimons et al., 1997.

^gXia et al., 2000.

^h The average Z-score for all 32 decoy sets.

DFIRE-A, atomic KBP, and RAPDF are tested using 25 additional multiple decoy sets listed on the website http://dd.stanford.edu/. It includes fisa (Simons et al. 1997), fisa_casp3 (Simons et al. 1997), lmds, and lattice_ssfit (Xia et al. 2000). The fisa (Simons et al. 1997), fisa_casp3 (Simons et al. 1997), and lmds decoy sets are more challenging than the 4state_reduced and lattice_ssfit decoy sets (Table 2, B–E). The relative performance of RAPDF to that of atomic KBP is different for different decoy sets. Atomic KBP performs better in the 4state_reduced and lmds decoy sets, while RAPDF is better in the fisa, fisa_casp3, and lattice_ssfit sets. Thus, many decoy sets are needed to be certain about the overall quality of a potential. DFIRE-A is consistently the best based on the average Z-core and the number of correctly identified native structures. In summary, DFIRE-A significantly improves over the previous potentials in the multiple decoy sets (Table 2). The most significant improvement is in the average Z-score. The average Z-score is 4.27 for DFIRE-A, compared to 2.83 for RAPDF and 2.87 for atomic KBP. Further, it correctly identified 27 native conformations out of 32 decoy sets. The corresponding number is 22 for RAPDF and 18 for atomic KBP, respectively. Only five proteins were missed by DFIRE-A. They are 3icb in 4state_reduced, 1fc2 in fisa, 1b0n-B, 1bba, and 1fc2 in lmds. The failure to identify 3icb is not really a failure, as discussed above. The other four proteins were missed by all three potentials. For example, 1bba and 1fc2 were all ranked as either the 500th or the 501st lowest energy. All residue-based statistical potentials also failed to recognize these four proteins (Tobi and Elber 2000). The reason for this massive failure is not entirely clear. Perhaps, this is because 1bba is an atypical small protein without a significant hydrophobic core while the other three proteins have many missing coordinates (≥15 residues) in their native structures, and the number of residues with coordinates is less than 45.

Another multiple decoy set is loops (Moult and James 1986; Fidelis et al. 1994) from http://prostar.carb.nist.gov/. They consist of conformations of short (four or five residues) loops in protein structures. The challenge is to locate the low rmsd structure from a large database of a few hundred to 70 thousand possible conformations. Results are compiled in Table 3. For DFIRE-A, the rmsds of the lowest energy structure are all within 1Å from the lowest rmsd of the decoy. This is better than either RAPDF or atomic KBP. For example, the rmsd of the lowest energy structure of 3dfr for the residue range from 64 to 67 is 2.32 Å (2.61 Å) for RAPDF (atomic KBP), compared to 1.24 Å for DFIRE-A. Significant improvement of DFIRE-A over RAPDF and atomic KBP is also observed for selecting the loop structure in protein 2fbj.

Table 3.

The rmsd (Å) of the lowest energy conformation from the loops decoy set (Moult and James 1986; Fidelis et al. 1994)

PDB ID	Residue range	rmsd range	RAPDF	Atomic KBP	DFIRE-A	DFIRE-A1.45	DFIRE-A1.70	DFIRE-B
3dfr	20–23	0.75–4.58	0.88	0.88	0.75	1.63	0.75	4.17
3dfr	27–30	0.81–3.47	0.87	1.69	1.69	1.69	1.10	1.27
3dfr	64–67	0.89–4.19	2.32	2.61	1.24	2.41	1.14	1.82
3dfr	120–124	0.57–2.91	0.75	1.28	1.18	0.62	1.18	1.25
3dfr	136–139	1.39–2.15	1.57	1.71	1.54	1.54	1.67	1.66
2sga	35–39	1.20–3.17	1.32	1.22	1.28	1.28	1.28	1.23
2sga	97–101	0.60–3.34	0.79	3.34	0.63	0.63	0.61	1.08
2sga	116–119	0.47–4.91	0.99	1.09	0.99	0.99	1.05	4.28
2sga	132–136	0.97–2.58	1.29	1.56	1.62	1.62	1.42	1.53
2fbj	265–269	0.96–3.90	3.90	3.67	1.03	2.15	1.03	2.15
2hfl	264–268	1.11–2.81	1.46	1.50	1.50	1.50	1.50	1.58

The correlation between the scores and rmsd values of the decoys is another way to assess knowledge-based potentials. Of all the multiple decoy sets tested here, we found that only the 4state_reduced and loops sets have significant correlations between scores and rmsd values. This is because the secondary structures in these two decoy sets are mostly unchanged and rmsd values are small while most decoys in the other sets have large rmsd values. The correlation coefficients between the scores and rmsd values obtained from the RAPDF, atomic KBP, and DFIRE-A potentials are given in Tables 4 and 5 for the 4state_reduced and loops sets, respectively. The three potentials yield comparable correlations for the 4state_reduced set. The average correlation coefficients are 0.67, 0.65, and 0.63 for the RAPDF, atomic KBP, and DFIRE-A potentials, respectively. For the loops decoy set, the DFIRE-A potential yields the most significant correlation among the three potentials. The average correlation coefficients are 0.51, 0.41, and 0.74 for the RAPDF, atomic KBP, DFIRE-A potentials, respectively. Thus, DFIRE-A is potentially useful for loop modeling and structural refinement.

Table 4.

The correlation coefficients between the scores and the rmsd values for the 4state_reduced set

PDB ID	RAPDF	Atomic KBP	DFIRE-A
1ctf	0.73	0.67	0.70
1r69	0.72	0.70	0.68
1sn3	0.47	0.49	0.32
2cro	0.76	0.73	0.75
3icb	0.86	0.83	0.83
4pti	0.52	0.53	0.45
4rxn	0.61	0.59	0.66
Ave.	0.67	0.65	0.63

Table 5.

The correlation coefficients between scores and rmsd values for the loops decoy set

PDB ID	Residue range	rmsd range	RAPDF	Atomic KBP	DFIRE-A
3dfr	20–23	0.75–4.58	0.83	0.60	0.91
3dfr	27–30	0.81–3.47	0.60	0.56	0.71
3dfr	64–67	0.89–4.19	0.48	0.20	0.76
3dfr	120–124	0.57–2.91	0.93	0.84	0.93
3dfr	136–139	1.39–2.15	0.61	0.14	0.66
2sga	35–39	1.20–3.17	0.61	0.72	0.79
2sga	97–101	0.60–3.34	0.83	0.44	0.93
2sga	116–119	0.47–4.91	0.82	0.82	0.75
2sga	132–136	0.97–2.58	0.30	0.08	0.26
2fbj	265–269	0.96–3.90	−0.84	−0.10	0.82
2hfl	264–268	1.11–2.81	0.45	0.23	0.61
Ave.			0.51	0.41	0.74

Dependence on α

For single decoy sets, the performance of DFIRE-A at α = 1.70 is the same as that of DFIRE-A (at α = 1.57), while DFIRE-A at α = 1.45 identified 32 out of 44 in the ifu decoy set (Table 1). For multiple decoy sets, other choices of α will lead to a reduction of the average Z-score at both α = 1.45 and α = 1.70 (Table 2). Thus, indeed, α = 1.57 produces the most accurate potential.

Dependence on atomic detail

For single decoy sets, the performance of the DFIRE-B potential based on backbone and C_β atoms is significantly worse than that of the RAPDF and atomic KBP potentials. The former did not achieve 100% correct in structure selections in misfold and asilomar decoy sets, similar to other residue-based potentials (Samudrala and Moult 1998; Lu and Skolnick 2001). However, the DFIRE-B potential, performs slightly better for 32 more-challenging multiple decoys sets. The average Z-score of the 32 decoy sets is 3.32 for DFIRE-B, compared to 2.83 for RAPDF and 2.87 for atomic KBP. Thus, the accuracy of the DFIRE-B potential (with a reduced representation) is comparable to the RAPDF and atomic KBP potentials with full atomic detail.

Mutation-induced change in stability

Mutation-induced change in stability can be predicted as described in the Methods section assuming that there is no structural relaxation after mutation. We use a database of 895 large-to-small mutations defined by a decreased number of heavy atoms upon mutation (a list is provided in http://www.smbs.buffalo.edu/phys_bio/paper.html). The measured changes in stability are compared with predicted ones in Figure 2 ▶. In generating Figures 2a, 2b, and 2c ▶, different scaling factors are used so that the regression slope is equal to 1. At T = 300 K, η = 0.025 for RAPDF, 0.026 for atomic KBP, and 0.017 for DFIRE-A. The scaling factor for DFIRE-A is close to 0.015, the inverse of the coordination number at r = r_cut (the number of pairs per atom), which was the physical quantity used to scale the structure-derived atomic contact energy (Zhang et al. 1997). The correlation coefficient between experimental measured and theoretical predicted changes in stability is 0.67 for DFIRE-A (Fig. 2c ▶). The corresponding coefficients are 0.52 for RAPDF (Fig. 2a ▶) and 0.55 for atomic KBP (Fig. 2b ▶), respectively. The root-mean-squared deviation between the experimental data and theoretical predictions is 1.52 kcal/mole for DFIRE-A, compared to 1.89 kcal/mole for RAPDF, and 2.11 kcal/mole for atomic KBP. Thus, DFIRE-A provides the most accurate prediction. One obvious improvement of the DFIRE-A potential over the other two potentials is in predicting the strongly stabilizing mutations (ΔG << 0). RAPDF predicts that no mutation can produce more than 2 kcal/mole improvement in stability. Atomic KBP and DFIRE-A raised this limit to 5 and 6 kcal/mole, respectively. Experimentally, the largest increase in stability is about 8 kcal/mole.

Fig. 2.

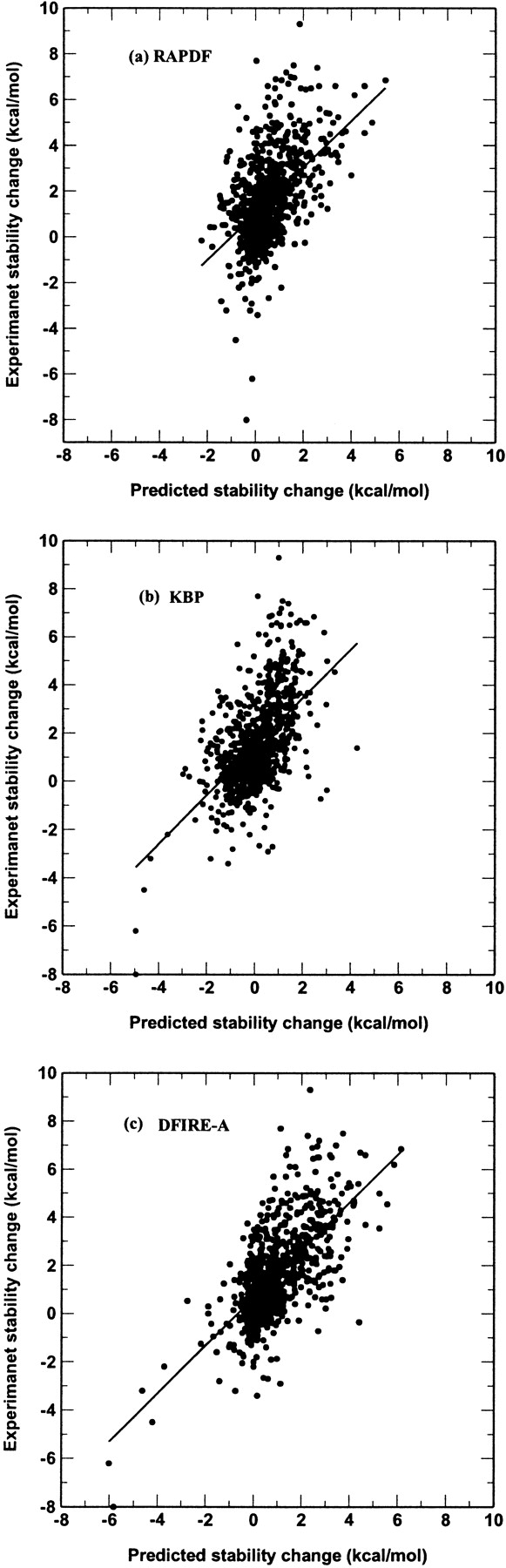
The experimentally measured changes in stability versus theoretically predicted ones in a database of 895 large-to-small mutations. (a) RAPDF, (b) atomic KBP, (c) DFIRE-A. Lines represent the results from linear regression fit. The correlation coefficients are 0.52, 0.55, and 0.67 for RAPDF, atomic KBP and DFIRE-A, respectively.

Distance dependence of potentials

To reveal the difference among three knowledge-based all-atom potentials, we plot the potentials as a function of distance for several atomic pairs. In Figure 3 ▶, all three potentials between the polar backbone atoms of N in Cys and O in Trp show very rich distance dependence. They all have a stable minimum around 3 Å and another weaker minimum around 7 Å. The potentials between atom C_α in Ile and atom C_δ2 in Leu are simpler with one minimum near 6 Å. The results of RAPDF in this figure are essentially the same as those given in Figure 8 of Samudrala and Moult (1998). Samudrala and Moult used a structural database of 265 proteins, and we regenerated their potential using 1011 protein structures. This suggests that increasing the size of the structural database has little effect on the distance dependence. In Figures 3a and 3b ▶, the value of the DFIRE-A potential is somewhat in between the values of the RAPDF and atomic KBP potentials.

Fig. 3.

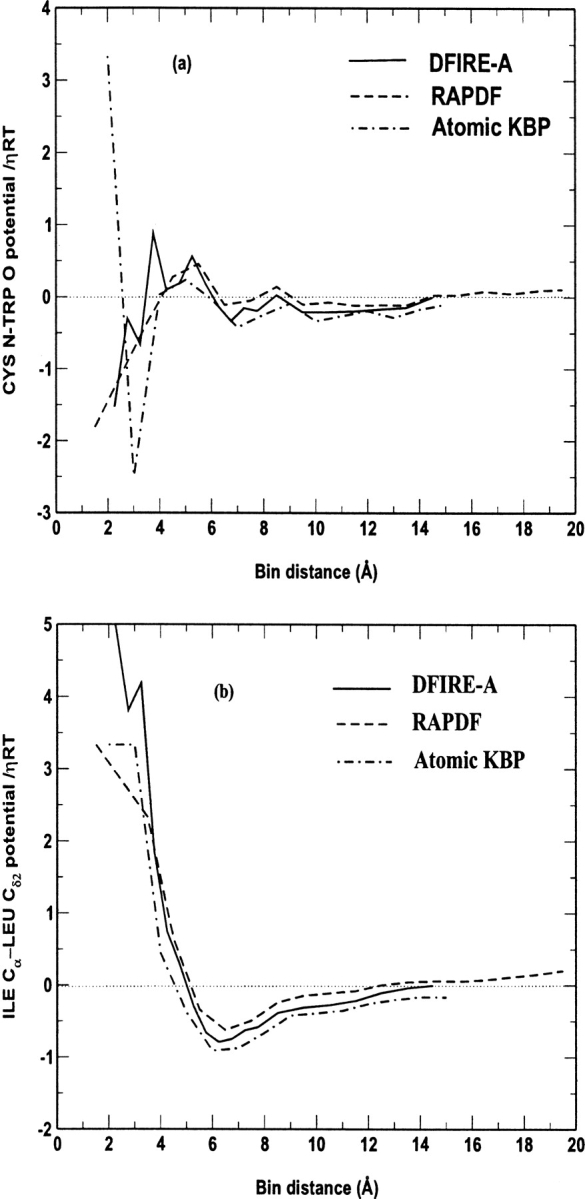
The distance dependence of three knowledge-based potentials (a) between atom N of residue Cys and atom O of residue Trp, and (b) between atom C_α of residue Ile and atom C_δ2 of residue Leu.

The potentials between nonpolar atom C_β in Leu and atom C_β in Ile show two stable minima at about 6 and 10 Å, respectively (Fig. 4A ▶). Similar results are found for the potentials between atom C_β in Leu and atom C_β in Asp. However, because Asp is a hydrophilic residue and Leu is a hydrophobic residue, the interaction between Leu-C_β and Asp-C_β is weaker and significantly shorter ranged than that between Leu-C_β and Ile-C_β. The results of atomic KBP in Figures 4A and 4B ▶ are essentially the same as those given in Figure 2 ▶ of Lu and Skolnick (2001) except near the core and the tail portions. The value of the DFIRE-A potential is no longer between those of the atomic KBP and the RAPDF potentials, but can be either closer to that of the atomic KBP potential (Fig. 4A ▶) or closer to that of the RAPDF potential (Fig. 4B ▶). Thus, the effect of different reference states on the distance dependence is different for different atomic pairs. However, in general, the distance dependences of the three potentials are qualitatively similar. Thus, the approximation that the average interaction is zero is a reasonable approximation. This explains in part the success of atomic KBP and RAPDF potentials.

Fig. 4.

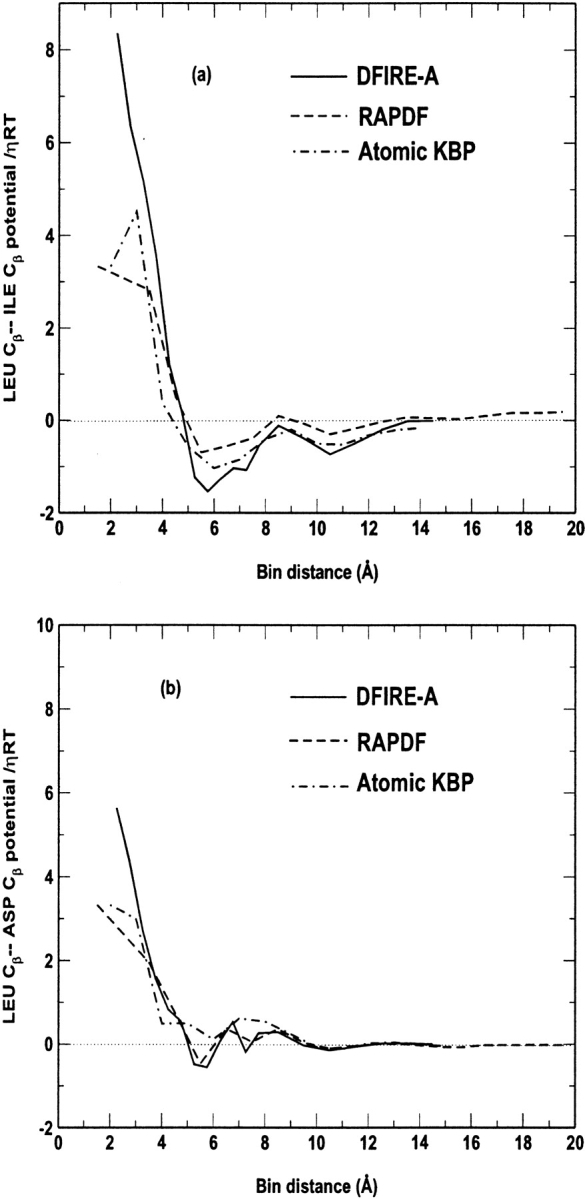
The distance dependence of three knowledge-based potentials (a) between C_β atoms of Leu and Ile residues, and (b) between C_β atoms of Leu and Asp residues.

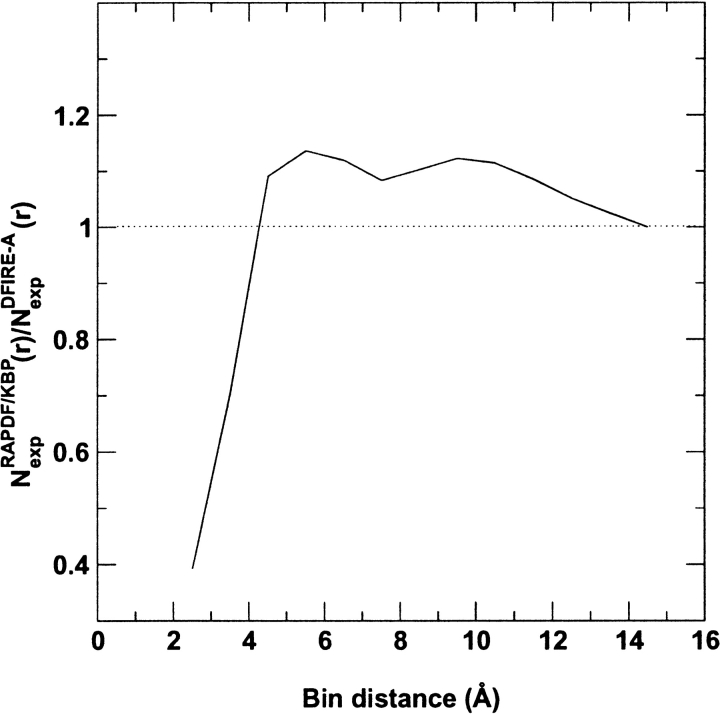
To further understand what makes the DFIRE-A potential quantitatively different from the atomic KBP and the RAPDF potentials, we calculate the ratio of the number of expected pairs at a given distance, N_exp(r) (=∑_i,j N _exp(i,j,r)) of the RAPDF and atomic KBP to that of the DFIRE-A potential. For the RAPDF and atomic KBP, N_exp^RAPDF/KBP(r) = N_obs(r). For the DFIRE-A potential, N_exp^DFIRE-A(r) = (r/r_cut)^α(Δr/Δr_cut)N_obs(r_cut). Figure 5 ▶ shows that in the distance range of 4–12 Å, both RAPDF and atomic KBP overestimate the expected number of pairs by about a constant value of 10% more than the DFIRE-A potential. This means that RAPDF and atomic KBP underestimate attractive interactions among atoms. This constant value explains the qualitatively similar distance dependence observed in Figures 3 and 4 ▶ ▶. It is noted that the ratio significantly differs from 1 in the range of 0–4 Å as well. This difference, however, is not as important as the difference in the distance range of 4–12 Å because the number of pairs in the former is negligibly smaller than that in the latter.

Fig. 5.

The distance dependence of N_exp^RAPDF/KBP(r)/N_exp^DFIRE-A(r).

To verify whether the 10% difference in the range of 4–12 Å is the source for the different performance between the RAPDF/KBP and DFIRE-A, we assume that the number of expected pairs of atomic types i and j, N_exp(i,j,r), is uniformly overcounted by 10% for RAPDF or KBP in the distance range of 4–12 Å. In other words, the RAPDF or KBP potential can be improved by subtracting −η RTln(1/1.1) ≈ 0.1η RT in this range. Indeed, such a modified RAPDF increases the average Z-score from 2.83 to 4.11 and the number of correctly identified proteins from 22 to 27. Both results are close to or the same as those from the DFIRE-A potential (4.27 and 27, respectively). The improvement of the atomic KBP is also visible, although it is not as significant. The average Z-score increases from 2.87 to 3.14 and the number of correctly identified proteins from 18 to 20. Because the atomic KBP only uses the 3.5–6.5 Å window to calculate scores, we also make a double shift of 0.2η RT to account for the 6.5–12Å window. The atomic KBP is further improved with an average Z-score of 3.32 and 24 identified proteins. Thus, a slightly more attractive potential in the region of 4–12 Å leads to the superior performance of the DFIRE-A potential.

Discussion

Comparison with other knowledge-based potentials

In this paper, we used a finite ideal-gas reference state to derive knowledge-based potentials. Early methods due to Sippl (1990)), Samudrala and Moult (1998), and Lu and Skolnick (2001) are all based on a reference state that can be better characterized as a residue (atom)-averaged state. A residue (atom)-averaged state can be approximated as a noninteracting ideal-gas state, assuming that all interactions cancel each other during average. Here we employed an ideal-gas state directly. The new potentials are tested by using decoys and mutation database. The results show that the DFIRE-based all-atom potential consistently performs better than previous all-atom knowledge-based potentials. The latter’s performance is comparable to that of the DFIRE-B potential based on backbone and C_β atoms only. The most significant improvement is in the average Z-score of 32 multiple decoy sets. A larger Z-score indicates a stronger bias against decoys. A large Z-score is a necessary condition for a potential to be useful in structure prediction (Lu and Skolnick 2001).

Perhaps, more significantly, the DFIRE-A potential can provide a reasonably accurate prediction of mutation-induced change in folding stability. Both stabilizing and destabilizing mutations are predicted reasonably well (Fig. 2 ▶). This indicates that it is possible to use knowledge-based potentials to interpret and predict mutation-induced change in stability as has been demonstrated previously (Gilis and Rooman 1996, Gilis and Rooman 1997; Zhang et al. 1997). In particular, Gilis and Rooman (1996^{, 1997}) found that a distance-dependent potential is less accurate in predicting the change in stability due to the mutation of solvent exposed residues. Similar results are found for RAPDF, KBP, and DFIRE-A potentials. The correlation coefficients between experimentally measured and theoretical predicted changes in stability upon the mutations of solvent exposed residues are 0.14, 0.22, and 0.44 for RAPDF, KBP, and DFIRE-A, respectively. These values are significantly smaller than the corresponding values of 0.53, 0.56, and 0.68 for the mutations of buried residues. Here, a solvent-exposed residue is defined as a residue that has more than 40% of its accessible surface area exposed. There are 293 mutants used in calculations. Recently, Guerois et al. (2002) used a training database of 339 mutants to optimize the parameters and weighting factors for a given functional form of interaction potentials. The correlation coefficient between predicted and experimental measured changes in stability is 0.73.

Comparison with physical based potentials

The single and multiple decoy sets have also been used to assess several physical-based potentials. In the misfold decoy set, the success rates for the CHARMM 19 vacuum parameter set (Neria et al. 1996), CHARMM 19 with the effective energy function (CHARMM 19-EEF1) (Lazaridis and Karplus 1999), vacuum OPLS all-atom force field (OPLS-AA) (Jorgensen et al. 1996), and OPLS-AA surface generalized Born solvation model (OPLS-AA/SGB) (Ghosh et al. 1998; Zhang et al. 2001) are 19/22 (Lazaridis and Karplus 1998), 21/22 (Lazaridis and Karplus 1998), 24/25 (Wallqvist et al. 2002), and 25/25 (Wallqvist et al. 2002), respectively. These success rates are comparable to the success rate of 25/25 for the DFIRE-A potential. In the 4state_reduced multiple decoy set, the success rates are 6/6 for CHARMM 19-EEF1, 4/7 for a simplified PEEF (Petrey and Honig 2000), 4/7 for vacuum OPLS-AA, 7/7 for OPLS-AA/SGB (Wallqvist et al. 2002), and 7/7 for CHARMM-GB (Dominy and Brooks 2002), respectively. OPLS-AA/SGB, CHARMM-GB, and CHARMM19-EEF1 have an average Z-score of 3.66 for 7 proteins (Wallqvist et al. 2002), 3.38 for 7 proteins (Dominy and Brooks 2002), and 3.27 for 6 proteins (Lazaridis and Karplus 1998), respectively. RAPDF, atomic KBP, and DFIRE-A have comparable average Z-scores ranging from 3.01 to 3.49. For the lmds decoy set, the Z-scores for 1bba, 1fc2, 1ctf, 1igd, 1shf-A, 2cro, 2ovo, and 4pti from OPLS-AA/SGB are −3.29, −0.68, 2.63, 4.06, 3.32, 2.85, and 14.42, respectively (Felts et al. 2002). The corresponding values from DFIRE-A are −16.28, −5.72, 3.54, 5.16, 4.70, 3.21, and 3.96, respectively. These two sets of results are comparable. It should be noted that in physical-based potentials, Z-scores were calculated from minimized structures. On the other hand, no minimizations were performed for knowledge-based potentials because of their discretization.

Cutoff and long-range interactions

One approximation used in DFIRE-based potentials is one cutoff distance for all atomic pair potentials of mean force. Potential of mean force, unlike pair interaction potential, is long-ranged potential due to presence of solvent (Friedman 1985). Here, we choose r_cut = 14.5 Å because f(r) starts to systematically deviate from a constant for r > 15 Å. The occurrence of the deviation is perhaps because the average radius of gyration of 1011 proteins is about 20 Å. (That is, the final finite-size effect occurs before the edge of a protein is reached). It is not clear if a database of large proteins would allow us to use a longer cutoff distance and whether or not a longer cutoff would improve the performance of the DFIRE-based potential, a subject that requires further studies.

The cutoff problem in potential of mean force has been investigated by a number of other researchers. Samudrala and Moult (1998) found that a long cutoff of 20 Å improves the performance of their potential. A 30-Å cutoff is proposed by Melo et al. (2002) for residue-based potentials. In contrast, Lu and Skolnick (2001) showed that a short cutoff (6.5 Å) yields the best performance of their potential. Thomas and Dill (1996) pointed out that a potential derived from the Sippl approximation would produce an anomalous behavior of long-range repulsion between hydrophobic residues as a result of hydrophobic/polar partitioning. Simons et al. (1997) corrected this effect by incorporating the environmental effect of residue pairs. The RAPDF potential seems to have the problem of a long-range repulsive tail between hydrophobic residues (Figs. 3 and 4 ▶ ▶). On the other hand, the atomic KBP appears to have a long-range attractive tail. The extent of the problem in our potential is not clear as a result of cutoff. Incorporating the environmental effect (Simons et al. 1997) into DFIRE-based potentials did not yield any improvement in the performance of the DFIRE-based potential. This is done by further dividing residues into surface and core residues (40 residue types). The result suggests that hydrophobic/polar partitioning does not produce any major error in the DFIRE-based potential.