Scaling of tree vascular transport systems along gradients of nutrient supply and altitude

Abstract

A recent metabolic scaling theory predicts that plants minimize resistance to hydraulic conduction in the bulk transport network by narrowing the diameter of xylem conduits distally. We hypothesized that trees growing at high altitude or on nutrient-depleted soils would prioritize survival over minimizing hydraulic resistance, and that their vascular systems would be structured differently from those of trees growing under more benign conditions. In fact, conduits were observed to narrow towards the periphery of vascular system within all 45 trees of three species we investigated, and scaling relationships were indistinguishable across a range of environments. Thus, conduit tapering relationships appear to be invariant with respect to environmental conditions.

1. Introduction

The West–Brown–Enquist theory (henceforth WBE theory) endeavours to use the basic principles of physics and biology to provide a mechanistic explanation for the scaling relationships found in many organic structures and metabolic processes (West et al. 1999). This hotly debated theory assumes that natural selection has acted to minimize resistance to hydraulic flow, and that the optimal strategy adopted by all plants is to taper conduit diameters towards the periphery of the vascular transport system (Enquist 2002; McCulloh & Sperry 2005). The principle behind this concept is that resistance to laminar flow scales as the fourth power of conduit diameter (the Hagen–Poiseuille law), so extra lengths of pipe can be added to a network (starting from the base of the leaves) without creating much additional resistance, provided that these pipes are wider than the ones to which they are joined.

WBE theory is calculated from the first principles so that if C is the mean diameter of conduits within a stem and D is the diameter of that stem, then the scaling relationship C∝D^α must have an exponent of at least 1/6 (i.e. 0.17) to minimize hydraulic resistance, and it should be as close as possible to 0.17 (Enquist 2002). They reached this conclusion by making the simplifying assumption that a plant branches in a similar way to volume-filling fractals, and conduit diameters within petioles are similar in all plant species. Alternatively, Anfodillo et al. (2006) derived a formula based on the distance from the top of a tree, H: the scaling relationship C∝H^β must have an exponent of at least 0.20. The few papers that have tested these scaling relationships in trees have strongly endorsed their invariant predictions (Anfodillo et al. 2006). However, we suggest several reasons why the same conduit-scaling relationships may not be found in plants growing in extreme environments. First, xylem exposed to winter freezing is vulnerable to cavitation unless conduits are narrow (Pittermann & Sperry 2003), and this may place an upper limit on C in cold (e.g. high altitude) environments if cavitated conduits impact fitness. Second, slow-growing trees associated with nutrient-poor soils require low rates of mortality to survive to reproductive maturity. In windy, low-nutrient environments trees may reduce the risk of wind-throw by having narrow conduits in their xylem that increase mechanical strength; this may also place an upper limit on C in nutrient-poor soils. The aims of this paper are to test whether (i) conduits narrow distally within tree vascular systems according to the scaling relationship predicted by WBE theory and (ii) tapering patterns are invariant along environmental gradients, by examining the xylem anatomy of the two tree species that occur naturally along a soil fertility gradient and another species of tree that grows along an altitudinal gradient.

2. Material and methods

The samples were collected from 10 Picea abies and 10 Pinus sylvestris trees growing on islands in northern Swedish lakes. Previous work has shown that smaller islands are depleted in plant-available nutrients; the explanation being that they burn infrequently because lightning is unlikely to hit them, and that recalcitrant humus accumulates as a result, sequestering nutrients in plant-unavailable forms (Wardle et al. 1997, 2003). Small islands (less than 0.1 ha) have four times more nitrogen sequestered in humus than large islands (more than 1.0 ha), and have half the tree productivity of large islands. Five small and five large islands were chosen from the lake system, and on each island wood samples from one randomly selected mature tree of P. abies and one P. sylvestris were collected. The height of each tree was measured, and samples were taken at specific distances from the tip of the terminal branch to fit a logarithmic scale: 2; 8; 32; 128; 256; 512 and 1024 cm. At each sampling point, diameter was recorded and wood samples were collected (short cores if the diameter was larger than roughly 10 cm or otherwise a sawed disc).

Nothofagus solandri var. cliffortioides samples were collected from forests in the Southern Alps, New Zealand. In these relatively dry eastern ranges where peaks reach heights above 2000 m, N. solandri occurs in naturally monospecific stands from around 650 m in altitude to treeline at roughly 1400 m (Wardle 1984). Mean temperature drops by approximately 0.6°C for every 100 m rise in altitude (Wardle 1984). Five mature trees were selected from low- (approx. 700 m), mid- (approx. 1000 m) and high-altitude bands (approx. 1400 m). Wood samples and diameter measurements were taken using the methods described previously, with the exception that wood cores were removed at equal distances along the length of each tree, rather than being logarithmically spaced. Confocal microscopy was used to determine the tangential diameters of early- and latewood vessels of N. solandri and of earlywood tracheids of P. abies and P. sylvestris. Thin transverse sections of the outer rings of each wood core were cut with a razor blade, selecting rings of approximately the same age for measurements, stained with Safranin O (0.01% in water) and then wet-mounted onto a microscope slide. Digital images of the wood were obtained using a Leica confocal microscope, the diameters of approximately 20 conduits were measured and hydraulic weighted means were calculated (Anfodillo et al. 2006).

Data were log transformed before analysis, and allometric relationships were estimated by standard major axis (SMA; type II) regression in the Smatr package (R foundation; see http://www.r-project.com). Smatr includes functions for testing whether SMA regression lines differ from one another, and it gives an estimate of the common intercept and slope of a group of lines (Warton et al. 2006). This allowed us to estimate a single scaling relationship using data from all 15 Nothofagus trees we sampled, thereby reducing the confidence intervals and increasing our ability to reject null hypotheses (i.e. reducing type II errors; Niklas 2004). Some of the relationships appeared curvilinear on log–log axes, so we tested for nonlinearity by fitting a least-squares regression model containing log(D), log(D)² and log(D)³ terms and testing for significance of the cubic term using ANOVA.

3. Results

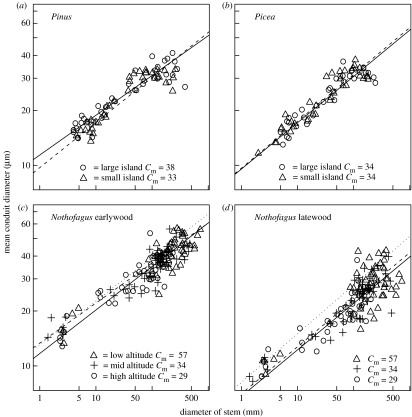
Conduits were narrower towards the periphery of the transport system of all three species (figures 1 and 2). In the case of the relationships between conduit and tree diameters, we were unable to reject the null hypotheses that trees within an environmental category had a common scaling exponent (see electronic supplementary material), or that scaling exponents were invariant along our environmental gradients (N. solandri earlywood p=0.52, N. solandri latewood p=0.91, P. sylvestris p=0.19, P. abies p=0.86). In contrast, intercept values differed significantly among trees (see electronic supplementary material). When lines were fitted for the individual trees, the 95% confidence intervals of the estimated scaling exponents were wide, and many overlapped with 1/6 (7 out of 10 Picea trees, 4 out of 10 Pinus trees and 9 out of 30 Nothofagus trees). Estimates of common slopes for groups of trees had much narrower confidence intervals, and these were systematically and significantly greater than 1/6 (see electronic supplementary material). The relationships for the conifers were not accurately described by allometric functions; the data were strongly curvilinear on log–log axes, and a cubic function of log H was significantly better than a straight-line relationship (table 1).

Figure 1.

The relationship between tree stem diameter (D, mm) and mean hydraulically weighted conduit diameter (C, μm) for three species: (a) Pinus sylvestris, (b) Picea abies, (c) and (d) Nothofagus solandri. The lines are the SMA regression lines for the trees on large (open circles) and small (open up triangles) islands in (a) and (b) and low- (open up triangles), mid- (plus) and high-altitude trees (open circles) in (c) and (d). C_m is the 95th quantile of the range of C values shown, calculated for each environmental category.

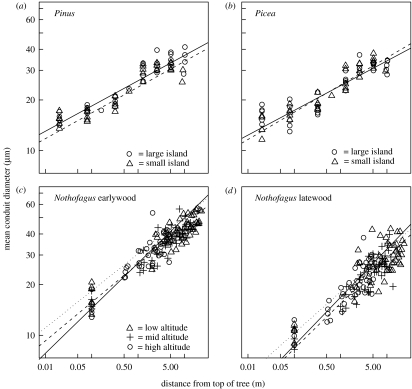
Figure 2.

The relationship between the distance from the treetop (H, m) and the mean hydraulically weighted conduit diameter (C, μm) for three species: (a) Pinus sylvestris, (b) Picea abies, (c) and (d) Nothofagus solandri. The lines are the SMA regression lines for the trees on large (open circles) and small (open up triangles) islands in (a) and (b) and low- (open up triangles), mid- (plus) and high-altitude trees (open circles) in (c) and (d).

Table 1.

Estimates of the scaling exponents α and β in C∝D^α and C∝H^β, where C is the hydraulically weighted conduit diameter; D is stem diameter; and H is the distance from the treetop. (The estimates are the averages (with 95% confidence intervals) obtained from 15 trees of Nothofagus solandri and 10 trees of Pinus sylvestris and Picea abies, and these were obtained by type II regression of log–log transformed data. The column labelled p indicates whether a cubic function gave a better fit to the transformed data than a linear function (^*p=0.01, ^**p=0.001).)

species	α (95% CI)	p	β (95% CI)	p
Nothofagus (earlywood)	0.23 (0.22–0.25)	n.s.	0.24 (0.22–0.25)	n.s.
Nothofagus (latewood)	0.26 (0.24–0.28)	*	0.27 (0.25–0.29)	*
Pinus	0.23 (0.21–0.25)	**	0.15 (0.14–0.17)	**
Picea	0.26 (0.23–0.28)	**	0.16 (0.14–0.18)	**
WBE theory	>0.166	>0.20

A similar picture emerged from the analyses of C in relation to distance from the treetops. We were unable to reject the null hypothesis that allometric slopes were invariant, either within environmental categories (with the exception of Nothofagus earlywood at low altitude; see electronic supplementary material) or between different altitudes and island sizes (N. solandri earlywood p=0.06, N. solandri latewood p=0.34, P. sylvestris p=0.78, P. abies p=0.32). Slopes were indistinguishable from 0.20 in the case of 8 out of 10 Pinus trees, 9 out of 10 Picea trees and 22 out of 30 Nothofagus trees (at p>0.05). When greater precision was obtained by pooling replicates within the different environment categories, or by pooling all data for a given species, we found the slope estimates greater than 0.20 for Nothofagus trees, but less than 0.20 for the conifers (table 1; see electronic supplementary material). Again, the relationships for the conifers were not accurately described by allometric functions; a cubic function of log H was significantly better than a linear function (table 1).

Nothofagus tree height declined with altitude (23, 12.5 and 5.5 m at low, medium and high altitudes, respectively) and the largest conduits in the stem also declined along this gradient (figure 1). Similarly, the conifers were shorter on the small islands, where plant-available nutrients were scarce, compared with the large islands (Picea 7.6 versus 10.5 m, Pinus 8.2 versus 11.4 m), and this was associated with a decrease in diameter of the largest conduits in the case of Pinus, but not Picea (figure 1).

4. Discussion

Conduits narrowed towards the periphery of the branching systems of the three species examined, consistent with previous studies (see Zimmermann 1978; Weitz et al. 2006). These data support the general thrust of WBE theory, namely that vascular systems have evolved to minimize hydraulic resistance (Tyree & Ewers 1991; West et al. 1999; Anfodillo et al. 2006). However, our results contain an apparent contradiction: while the values of α were greater than 1/6, suggesting optimal tapering, the β-values for the two conifers were less than 0.20, indicating ‘sub-optimal’ tapering. This discrepancy might have arisen owing to the difficulties associated with applying any abstract theory to real plants. In particular, the WBE theory assumes that trees branch to fill volume in a fractal-like manner, whereas real trees have more complex branching architectures. Recently, Weitz et al. (2006) predicted that optimal scaling exponents vary with branching design, so it is quite possible that a more realistic model for the conifer species, taking account of their strong apical dominance, would have an optimal β-value less than 0.2, in which case no apparent contradiction would arise. Therefore, while WBE theory is gaining considerable support in a general sense, ‘testing’ it on real trees presents a challenge (Niklas 2006).

Our results depart from WBE theory, in that conifers had narrower conduits at their bases than further up the trunk resulting in curvilinear relationships of log–log axes (figures 1 and 2). Other studies have reported that conduits are narrower near the base of mature trees, as a result of secondary thickening of cells to increase structural support (Spicer & Gartner 2001), but the implications for hydraulic flow are unclear. It may be that tapering conduits allow hydraulic resistance to be minimized when trees are small, but that hydraulic resistance increases once trees reach maturity, and this increase has a negative impact on height growth (Anfodillo et al. 2006).

Our most novel finding was that conduit tapering relationships were indistinguishable among the sites. Invariance cannot be attributed to us selecting too narrow a range of environmental conditions to have any tangible effect on plant physiology, because some plant properties, such as tree height, varied substantially along these two gradients. Our hypothesis was that freezing and nutrient deprivation would place an upper constraint on conduit diameters, and thereby alter the scaling relationship (e.g. Pittermann & Sperry 2003). We found that maximum conduit diameters did indeed decline with high altitude, but that this was associated with a reduction in tree height rather than a change in scaling function. It appears that trees reduce the cavitation risk at high altitude by having reduced stature and minimize hydraulic resistance within these shortened vascular systems by having tapering conduits within the xylem.

Supplementary Material

Detailed analyses of regression relationships

SMA regression relationships for Nothofagus trees at three altitudes, and Picea and Pinus trees on small and large islands