A MATHEMATICAL ANALYSIS OF SELEX

Abstract

SELEX (Systematic Evolution of Ligands by Exponential Enrichment) is a procedure by which a mixture of nucleic acids can be separated into pure components with the goal of isolating those with specific biochemical activities.

The basic idea is to combine the mixture with a specific target molecule and then separate the target-NA complex from the resulting reaction. The target-NA complex is then separated by mechanical means (for example by nitrocellulose filtration), the NA is then eluted from the complex, amplified by PCR (polymerase chain reaction) and the process repeated. After several rounds, one should be left with a pool of [NA]that consists mostly of the species in the original pool that best binds to the target. In Irvine et al. (1991) a mathematical analysis of this process was given.

In this paper we revisit Irvine et al. (1991). By rewriting the equations for the SELEX process, we considerably reduce the labor of computing the round to round distribution of nucleic acid fractions. We also establish necessary and sufficient conditions for the SELEX process to converge to a pool consisting solely of the best binding nucleic acid to a fixed target in a manner that maximizes the percentage of bound target. The assumption is that there is a single nucleic acid binding site on the target that permits occupation by no more than one nucleic acid. We analyze the case for which there is no background loss, (no support losses and no free [NA] left on the support.) We then examine the case in which such there are such losses. The significance of the analysis is that it suggests an experimental approach for the SELEX process as defined in Irvine et al. (1991) to converge to a pool consisting of a single best binding nucleic acid without recourse to any a-priori information about the nature of the binding constants or the distribution of the individual nucleic acid fragments.

1. Introduction

In this paper we present an alternative approach to that used in Irvine et al. (1991) to analyze mathematically the process of SELEX. Our goal is to simplify the mathematical analysis and to thereby provide the experimentalist a means of improving upon the success of this process.

First we provide a detailed description of the SELEX process as it is performed in the laboratory. Then we develop a mathematical framework to describe and analyze this process by which nucleic acids with new functions can be selected from a large random pool of nucleic acid sequences.¹ The plan of the paper is as follows:

• Section 2: The SELEX process is introduced and a mathematical overview of the paper is given.

• Section 3: Here the notation and the equilibrium equations are given. The notion of the efficiency of the selection process is defined.

• Section 4: The SELEX process is defined mathematically as an iteration scheme.

• Section 5: A necessary and sufficient condition for the convergence of this iteration scheme is given in the case that there are no losses of products through the support or binding of free nucleic acid to the support (partitioning). This case is the mathematical ideal.

• Section 6: Here partitioning is precisely defined as in Irvine et al. (1991).

• Section 7: The two major theorems on the convergence of the SELEX process are given when there are losses through the support or free nucleic acid binding to the support are stated. These theorems give necessary and sufficient conditions for the convergence of the SELEX process. Although they are asymptotic results, in concrete cases they give practical information as is shown in the simulations.

• Section 8: We give upper and lower bounds on the number of rounds needed to raise the concentration fraction of the best binding nucleic acid from a very small fraction of the total pool (as little as one molecule in 10¹² for example) to a very large fraction of the total pool.

• Section 9: In this section, a number of simulations are given based on a very simple Matlab program that illustrate the theorems and approximations discussed in the preceding sections.

• Section 10: A discussion of SELEX from a geometric point of view is given.

• Section 11: The proofs of Theorems 1, 2, and 3 are given.

• Section 12: The simple Matlab programs are given. There is one main program and three small function subprograms.

• Section ??: In this section, mostly out of curiosity, we replace the discrete iteration scheme by an analogous system of ordinary differential equations. The results analogous to Theorems 1, 2, and 3 are deduced from the solution of the system of ordinary differential equations.

2. The SELEX process and mathematical overview

2.1. The SELEX Process

Antibodies have served medical science extremely well for diagnostics and, in some special cases, as medications. More recently it has been discovered that certain single-stranded nucleic acids can adopt similar properties to antibodies in having high affinity and high specificity for their target molecule. Although they were only discovered in 1990, aptamers are already being developed as analytical agents (Tombelli et al,, (2005)) and for clinical treatments (Cerchia et al. (2002)). One aptamer, that recognizes vascular endothelial growth factor, is now in clinical use to treat macular degeneration (Zhou et al.(2006)). Among the many advantages of aptamers over antibodies are the stability of aptamers for diagnostics and their lack of immunogenicity for clinical treatments. Another important characteristic of aptamers is that they can be selected in vitro by a process called SELEX. Although most frequently depicted in the double helical structure of chromosomal DNA, nucleic acids (NA) are capable of forming many alternate structures; to whit the ribosome, transfer RNAs, ribosomes and aptamers. Aptamers are short single-stranded nucleic acids that behave like antibodies, binding their target molecules with high affinity and high specificity. However, antibodies and aptamers differ substantially in their stability and in the means by which they are obtained. Aptamers are prepared synthetically whereas antibodies still require an animal for their production.

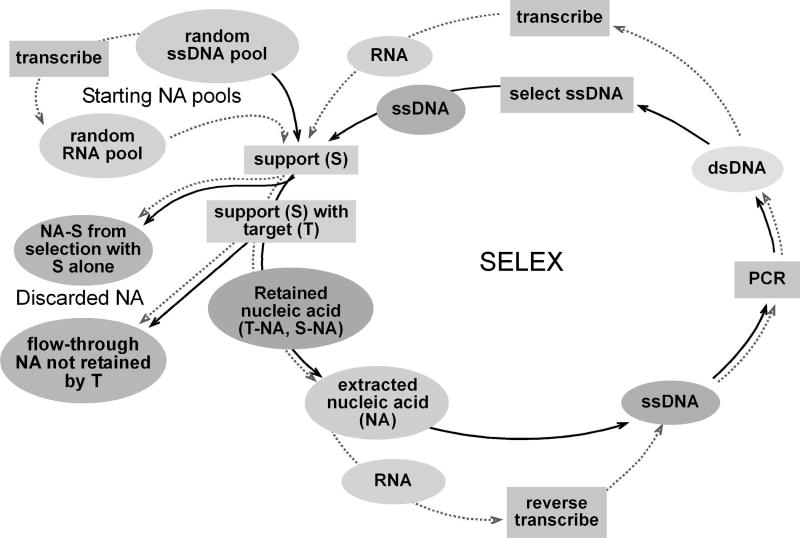
Aptamers are selected by a selection process called SELEX (systematic evolution of ligands by exponential enrichment) an (Ellington et al. (1990) and Teurk et al. (1990)). This is a reiterative process of selection and amplification that can be combined with mutagenesis to expand the pool of possible NA for selection. Here we will deal only with the selection aspects of this process, which starts with a randomized pool of nucleic acids that has been prepared synthetically. Each molecule in the pool is of the same length, but varies in an internal sequence (generally 40–80 bases long) in which positions along the polymer are randomly assigned to one of the four bases (A, G, C, T/U )². Although the technology for producing and amplifying the pool differs depending on whether the molecules in the pool are RNA or DNA, the same basic steps are performed to isolate aptamers that bind a target (T) with high affinity and specificity (Figure 1).

Figure 1.

The steps of SELEX are demonstrated in this figure. Starting in the top left corner of the figure, the blue and pink ovals represent the initial NA pools. SELEX can be done for RNA or single stranded DNA (ssDNA) molecules. Both protocols are represented here. The RNA selection protocols can be followed by the red dashed arrows and the ssDNA protocols by the black arrows. The square yellow selection step [support (S) with or without target (T)] is used to select the S-NA complex in combination with or without the T-NA complex. The S-NA complex, selected in the absence of T is discarded as is the NA that flows through the support-target combination. Retained extracted NA is taken through a SELEX round that includes the PCR amplification step and that generates the next NA pool, which is again selected against the support and or support plus target. SELEX protocols can vary greatly, depending on the desired characteristics of the selected aptamer. Not all rounds of SELEX include an initial selection against support, although this is a recommended practice (Pollard et al. (2000)).

The first step in SELEX is to use T attached to a solid support (S) such as a filter or a column to select molecules with sequences that promote their folding into structures that bind T. The interaction between T and NA is assumed to be at equilibrium and thus can be represented as T + NA_i ⇆ T:NA_i in which NAi is the ith NA in the pool. The equilibrium constant (Kd) for each NAi is different and characteristic of the NAi sequence. Because the use of S is often technically necessary to achieve the separation, there is also the possibility that certain NA sequences will fold to structures that bind S. Thus, another set of equilibria that occurs in every incubation of T and S with NA is S + NAi ⇆ S:NA_i with a variety of Kd’s that are characteristic of the individual NAi.

In each round of SELEX, the goal is to select for the NAi with the highest affinity (lowest Kd) for T. Therefore, after incubating T and NA the T:NA complexes are separated from T and NA, generally with the aid of S. The S:NAi is retained and captured together with the T:NAi. In some selection protocols, T:NA is then separated from S and S:NA. The bound NA is then extracted from T and S. When T:NA cannot be first separated from S and S:NA, the extracted pool contains NA that was bound to T (the desired aptamers) and NA that was bound to S (undesired background). Thus, part of the SELEX process is to minimize the number of background molecules and maximize the number of desired aptamer molecules.

Three general approaches are used to eliminate background in SELEX. The most common approach is to remove the background NA by incubating with S alone then discarding NA:S (Conrad, (1994)). Another approach is to associate T to S through a reversible linkage that can be broken prior to extracting NA from T:NA (Bock et al. (1992)). A third approach, that has more recently been developed, is to dispense with S by using capillary electrophoresis to separate T from T:NA (German et al. (1998)). Thus in some cases, one can dispense with S and, hence, as in Irvine et al. (1991), we will not include equilibrium S+NA_i ⇆ S:NA_i in our analysis.

After NA has been extracted from T (and S) this new NA population is amplified by polymerase chain reaction (PCR) to make more NA of the same sequences. PCR utilizes a heat stable DNA polymerase and the predefined sequences that are present at the termini of each NA molecule in the pool. With primers that are complementary to the predefined sequences, and by going through multiple cycles of annealing, polymerization and melting, the PCR protocol grows the population to a size that is equal to or larger than the original SELEX population. This amplified population is then used for a new round of SELEX in which the binding species are again selected from the population as just described.

Once it is determined that a binding population has evolved (by measuring K_D and the bound fraction [T:NA]/[ NA]) the population is cloned, which produces a sample set of NA from the population. Each molecule in the sample set is sequenced and all the sequences are aligned in a search for identities. The presence of identical sequences amongst the sample set of groups identifies members of the population that have likely been selected through the process. If the population contained two or more molecules with similar $K_d^{\prime }\text{s}$ then two or more sub populations will be found in the sample set. Putative aptamer sequences identified in this way are chemically synthesized and tested for their ability to bind the target.

Although it is a matter of luck that the original NA population contains one or more NA sequences that have a high affinity for T, some aspects of SELEX protocols can be optimized for successful selection of an aptamer from the pool. Examples of these factors are the concentrations of T and NA and their ratios. Success in SELEX is also influenced by background binding NA:S, which should be as low as possible. This paper presents a mathematical analysis of SELEX with the intent of providing practical guidance for SELEX experiments in the laboratory.

2.2. Mathematical overview

We show that, under ideal conditions, selection will occur in all cases. The target concentration also tends to zero with increasing round number in an ideal selection. However, if the selection conditions are not ideal and some bound target passes through the support, or some unbound nucleic acid binds to the support (nonspecific binding), the selection will fail if the decrease in target from round to round is not done within a range of increments that can be defined mathematically.

The underlying goal of the mathematical analysis is to give a formula for the number of rounds needed to raise the concentration of a pool of nucleic acids that consists of at least one molecule per unit volume of the best binding NA to a pool that consists of some specified percentage of the best binding NA. Such an ideal formula would depend on (1), the desired percentage; (2), the ratio of target concentration to total pool concentration, and (3), the errors or losses in passing from round to round, i.e. the fraction of NA molecules that bind to the support and on the capture fraction by the support of the bound target-nucleic acid complex; (4), the initial distribution of nucleic acids in the pool and finally (5); the dissociation constants themselves, which, like the distribution of nucleic acids in the original pool, may not be known, or known only approximately. (In the latter situation, one may have some idea of the ratio of the largest to the smallest dissociation constant in the pool.)

Precise conditions for a successful non-ideal SELEX experiment are given in this paper. Theorems 2 and 3 provide the basis for an experimental SELEX protocol that requires little prior knowledge of the nature of the binding constants or the numerical distribution of the concentrations of each nucleic acid component in the pool.

In Irvine et al. (1991), the authors resort to solving a large nonlinear system of equations numerically to illustrate the mathematical underpinnings of the SELEX method. We show that one needs only to solve a single nonlinear equation in the free target for its sole positive root. Once this is known, it is a simple matter to calculate the bound target from the total target and to then to track how the concentration ratios [NA_i]/[NA₁] vary from round to round where [NA_i] denotes the concentration of the i^th nucleic acid species. The assumption here is that the first species binds better to the target than all the other species in the pool. We also give some upper and lower bounds for the round number needed to reach a specified pool fraction of the best binding nucleic acid.

Other modeling approaches have been made to the SELEX problem, (Djordjevic et al. (2006), Levitan (1997) and Sun et al.(1994)), but we believe our theoretical and computational approaches offer the advantages of simplicity and ease of applicability for the practitioner as it rests on mass action considerations (i.e. the law of large numbers) rather than individual probabilistic considerations. One approach, based on probability arguments is given in (Sun et al. (1994)) in the case in which there is no loss through the support of captured target and no nonselective retention of nucleic acids. If the optimal nucleic acid is very rare in the first round of SELEX, one may miss it entirely. Thus there is a very real need for a probabilistic model that goes beyond that of Sun et al. (1994)). In this paper, the assumption is that we are operating in the range of the law of large numbers so that we may use the Law of Mass Action with impunity.

We believe however, that our results provide a practical algorithm for carrying out the SELEX process in the laboratory. This is especially important because the individual binding constants are generally not known, although free energy considerations were used to estimate them in some special cases in (Sun et al. (1994)) for example.

Finally we remark that the SELEX process is, in some ways, mathematically analogous to to multicomponent distillation processes. See McCAbe et al. (2001).

3. Chemistry

Here we establish the following equivalence: Selection will be approached at maximum target efficiency if and only if the overall dissociation constant converges to the smallest dissociation constant and the concentration of the total target converges to zero. This equivalence is established near the end of this section in subsection 3.2. In order to do this, we need to define our terms and our problem carefully. (For example, allowing the total target to approach zero in the continuum sense is not a physical notion any more than the terminology ”infinite dilution” is.)

3.1. Notation and Mathematical overview

The notation is given in Table 1.

Table 1. Notation and problem formulation for a single SELEX round.

We extend the notation of Irvine et al. (1991) to permit a more general discussion. Thus the protein (P) is replaced by a target (T) and RNA by NA (nucleic acid).

species	quantity (See (Irvine et al. 1991).)
starting target	[T]
starting NAi	[NAi]
starting NA	[NA]
free NAi	[NAfi]
free NA	[NAf]
bound NAi	[{T:NAi}]
free target	[Tf]
bound NA (max.avail for PCR)	[T:NA]

Here we frame the underlying chemistry of a single SELEX round in terms of chemical equilibria. Following Irvine et al. (1991), we exclude the possibility of nucleic acid binding to the support S. We envisage an initial pool of N nucleic acids, NA_i, for i = 1, 2, … N. Here NA stands for nucleic acid which could be DNA or RNA. These are called nucleic acid ligands. They bind to a target molecule T via the dissociation-association:

$$\{T:N{A}_i\}\underset{k_i}{\overset{k_{-i}}{\rightleftharpoons }}Tf+NA{f}_i,$$ (3.1)

assumed to be in equilibrium. The dissociation constant for each of the N nucleic acids is given by:

$$K_{di}=\frac{k_{-i}}{k_i}=\frac{[NA{f}_i][Tf]}{[\{T:N{A}_i\}]}$$ (3.2)

where

$$[N{A}_i]=[NA{f}_i]+[\{T:N{A}_i\}].$$ (3.3)

Thus, solving for the bound target:

$$[\{T:N{A}_i\}]=\frac{[N{A}_i][Tf]}{K_{di}+[Tf]}=[NA]\frac{[F_i][Tf]}{K_{di}+[Tf]}.$$ (3.4)

where we have set

$$F_i=\frac{[N{A}_i]}{[NA]},$$

the fraction of the i^th nucleic acid. It is assumed that the dissociation constants are ordered: 0 < K_d1 < K_d2 ··· < K_dN. Otherwise, they are to be regarded as unknown. Ordering them is done simply for mathematical convenience. Any set of N distinct numbers can be ordered.

In addition there is the overall dissociation constant given by

$$K_d=\frac{[\mathit{NAf}][Tf]}{[\{T:NA\}]}$$ (3.5)

where

$$\begin{array}{l}[NA]=\sum _{i=1}^N[N{A}_i],\\ [\mathit{NAf}]=\sum _{i=1}^N[NA{f}_i],\\ [\{T:NA\}]=\sum _{i=1}^N[\{T:N{A}_i\}]\end{array}$$ (3.6)

denote the total NA, the total free NA and the total bound target respectively. The total bound target can be determined under the stoichiometric assumption that there is only one NA bound to a target molecule, an assumption made here and in Irvine et al. (1991). In a given round of the SELEX process, one begins with a pool of nucleic acids for which one knows the initial total concentration of nucleic acids, the initial concentration of binding target, and the overall dissociation constant. Thus

$$\begin{array}{l}[NA]=[\{T:NA\}]+[\mathit{NAf}],\\ [T]=[\{T:NA\}]+[Tf].\end{array}$$ (3.7)

Thus, using (3.5), (3.6) and (3.7)

$$\frac{[NA][Tf]}{K_d+[Tf]}=[\{T:NA\}]=\sum _{i=1}^N[\{T:N{A}_i\}]=[Tf][NA]\sum _{i=1}^N\frac{F_i}{K_{di}+[Tf]}.$$ (3.8)

Thus

$$\frac{1}{K_d+[Tf]}=\sum _{i=1}^N\frac{F_i}{K_{di}+[Tf]}=\mathscr{H}(\overrightarrow{F},[Tf])$$ (3.9)

where $\mathscr{H}$ is defined by the left hand side and where F⃗ = (F₁, F₂,…, F_N ). Thus the overall constant K_d depends only on the free target, the individual dissociation constants, and the fractions of each nucleic acid in the pool. Note also that ${\sum }_{i=1}^N{F}_i=1$. Because ${\sum }_i{F}_i=1,\hspace{0.17em}1/(K_{d1}+[Tf])>\mathscr{H}(\overrightarrow{F},[Tf])=1/([Tf]+K_d)>1/(K_{dN}+[Tf])$ it follows that

$$K_{d1}<K_d(\overrightarrow{F},[Tf])<K_{dN},$$ (3.10)

i. e., the overall dissociation constant must lie between the largest and smallest such constants.

The overall constant K_d is also a function of the total target, the total nucleic acid and the free target in the given pool:

$$K_d=\frac{([NA]+[Tf]-[T])[Tf]}{[T]-[Tf]}.$$ (3.11)

Thus, one can eliminate K_d between (3.9), (3.11) to obtain a single nonlinear equation for the free target. This is easily found as follows: From the second equation in (3.7) and the far right hand expression for the bound target as a sum in equation (3.8) one finds

$$[T]=[Tf]+[Tf]\sum _{i=1}^N\frac{[N{A}_i]}{K_{di}+[Tf]}=[Tf]+[Tf][NA]\sum _{i=1}^N\frac{F_i}{K_{di}+[Tf]}.$$ (3.12)

The extreme ends of this equation give a single nonlinear equation for the free target. The bound target concentration is then

$$[T]-[Tf]=[\{T:NA\}]=[Tf][NA]\sum _{i=1}^N\frac{F_i}{K_{di}+[Tf]},$$

the maximum concentration of nucleic acid available for amplification by PCR.

Turning to the individual fractions, new concentration fractions of nucleic acids are related to the old via

$$F_i^{\prime }=\frac{[\{T:N{A}_i\}]}{[\{T:NA\}]}=\frac{[NA]}{[\{T:NA\}]}=\frac{[Tf]}{K_{di}+[Tf]}\frac{[N{A}_i]}{[NA]}=\frac{K_d([Tf])+[Tf]}{K_{di}+[Tf]}{F}_i.$$ (3.13)

From a mathematical point of view, one only has to follow the ratios F_i/F₁, i.e.

$$\frac{F_i^{\prime }}{F_1^{\prime }}=\frac{[\{T:N{A}_i\}]}{[\{T:N{A}_1\}]}=\frac{K_{d1}+[Tf]}{K_{di}+[Tf]}\frac{F_i}{F_1}.$$

The beauty of PCR from the chemist’s point of view is that the ratios [{T:N A_i}]/[{T:NA}] do not change under PCR. Therefore we can adjust (at least in principle) the concentration of the new pool to be the same as the concentration of the original pool without changing the ratio $F_i^{\prime }/F_1^{\prime }$. Thus the concentration of [NA] can be regarded as constant from round to round.

Because the dissociation constants increase in i the ratio in [Tf] is smaller than unity and is a minimum at [Tf] = 0. This formula needs to be modified when there is nonselective binding of nucleic acids by the support, or losses of bound target (Irvine et. al., 1991). We revisit it in Section 6.

Unlike the procedure followed in Irvine et al. (1991), we adopt a different approach. Equation (3.12) is a single nonlinear equation of the form F([Tf], [NA]) = [T]. If the pool concentration [NA] is given, the fractional distributions of the nucleic acids and the values of the dissociation constants are known (or at least estimable) then, given the target concentration [T], it is a simple matter to use Newton’s method (for example) to calculate [Tf]. Once this is found, all the new ratios are easily computed. (Notice that

$$F_1^{\prime }\left(1+\sum _{i=2}^N\frac{F_i^{\prime }}{F_1^{\prime }}\right)=1$$

so that if one knows F₁, …, F_N and $F_2^{\prime }/F_1^{\prime },\dots ,F_N^{\prime }/F_1^{\prime }$, then one knows all the fractions at the next round.)

In the laboratory, one usually fixes [NA] and takes [T] → 0 as the round number increases. What justifies such a protocol? The ratios

$$R_j=\frac{[T:N{A}_j]}{[T:NA]}=\frac{[Tf][NA]\frac{F_j}{K_{dj}+[Tf]}}{[Tf][NA]{\sum }_{i=1}^N\frac{F_i}{K_{di}+[Tf]}}=\frac{1}{1+{\sum }_{i\ne j}^N\frac{(F_i/F_j)(K_{dj}+[Tf])}{K_{di}+[Tf]}}$$

represent the fraction of bound NA_j to total bound NA. (These can also be viewed as the relative likelihood of binding one NA type to the binding of any type.) One sees that when j = 1, this ratio will be a maximum at [Tf] = 0 because

$$\frac{d}{d[Tf]}\sum _{i=2}^N\frac{(F_i/F_j)(K_{d1}+[Tf])}{K_{di}+[Tf]}=\sum _{i=2}^N\frac{(F_i/F_j)(K_{di}-K_{d1})}{{(K_{di}+[Tf])}^2}$$

is strictly positive unless we are at selection. Hence R₁ is decreasing in [Tf] and has its maximum at [Tf] = 0. Likewise, if we compute d[R_N]/d[Tf] we see that this ratio is strictly increasing in [Tf] and hence has its maximum when Tf] = [T] = + ∞.³ This justifies the protocol. It also says that maximum probability for binding the best binder occurs when the free target is small while the probability of binding the poorest binder will be at a minimum when the free target is small. (The concept is closely related to the concept of maximum bound target efficiency as defined below.)

The argument above does NOT say that R₁ > R_N. To take an extreme example, if we have only one target molecule, a pool consisting of two species of nucleic acids, one that bind with an affinity of only 1/100 that of the the other but the concentration of the poorer binder is 10⁶ times that of the better binder, the interaction of the pool with the target is going to lead to the target bound to the poorer binder far more often than to the to the target bound to the better binder. (For the example, R₁ = 10⁻⁴ and R₂ ≈ 0.999998 when Tf ≈ 0. The reader should keep in mind that we are talking about equilibrium thermodynamics here and not kinetics.)

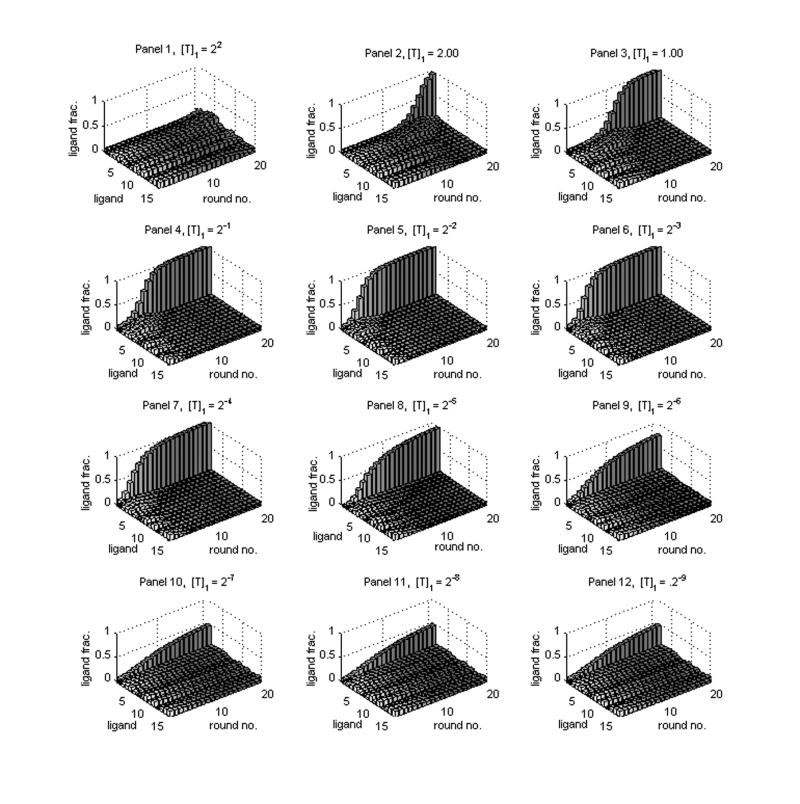
In theory as one decreases the target from round to round, the fraction of best binding molecules in the pool should increase relative to the others because of the greater likelihood that they will be bound to the target than those of lower affinity. But, as the above example shows, one might miss the the best binder altogether as one lowers the target. Another manifestation of this can be seen in Figure 8. We see that as the initial target is decreased, the round number to achieve a fixed level of selection first decreases and then increases. The decreasing of the round number reflects the the improved opportunity given to the best binder while the increasing of the round number as the initial target level continues to fall reflects the fact that R₁ is much smaller than R_N (at zero free target) and more rounds are needed to change this inequality.

Figure 8.

As the initial target is decreased progressively from panel 1 through panel 6, selection takes fewer rounds to achieve. Further increases in the initial target result in increases in the round number (the number of rounds required to reach a fixed percentage of ligand 1), begins to increase. This illustrates the point that simply increasing target over the concentration of the initial pool or else reducing it considerably will not necessarily decrease round number.

The fundamental issue remains. How do we choose the target from round to round? The theorems we develop here tell us that in the absence of information about the dissociation constants, there is, at least in principle, a way to reduce the target concentration from round to round, fixing the total pool size, in such a way as to insure that selection occurs. This is the subject of Section 5 and Section 7.

We sometimes suppress the argument F⃗ in K_d(F⃗, [Tf]) and in [Tf](F⃗, [T]) in the interest of readability.

3.2. Efficiency and selection

Operating under the assumption that at most one nucleic acid binds to a single target, the SELEX process can be monitored by following either the relative concentration of bound NA or the overall dissociation constant and the free NA. To see this define the fraction of bound target as [{T:NA}]/[T] = ([T] − [Tf])/[T]. Then

$${[T]}_b\equiv \frac{[T]-[Tf]}{[T]}=\frac{[NA]\mathscr{H}(\overrightarrow{F},[Tf])}{1+[NA]\mathscr{H}(\overrightarrow{F},[Tf])}=\frac{[NA]}{K_d(\overrightarrow{F},[Tf])+[Tf]+[NA]}.$$ (3.14)

We can write:

$$K_d([T],{[T]}_b)=(1-{[T]}_b)([NA]-[T]{[T]}_b)/{[T]}_b.$$ (3.15)

Equation (3.15) tells us that if we monitor [T], [T]_b, we can monitor the overall dissociation constant. From (3.14) we see that ${lim}_{[Tf]\to 0}[Tf]/[T]=1/(1+[NA]\mathscr{H}(\overrightarrow{F},0))$ and thus [Tf] → 0 if and only if [T] → 0 when [NA] is fixed.

Consequently

$$\frac{K_{d1}}{K_{d1}+[NA]}<\underset{[Tf]\to 0}{lim}\frac{[Tf]}{[T]}<\frac{K_{dN}}{K_{dN}+[NA]}$$

equality holding at one side or the other according as F⃗ = (1, 0, …, 0, 0) or F⃗ = (0, 0, …, 0, 1).

From (3.14), because the ratio on the right is increasing in $\mathscr{H}$ and $\mathscr{H}$ is decreasing in [Tf], the ratio is a maximum when [Tf] = 0. Whatever the value of [Tf], the maximum value of the relative concentration must occur at F⃗ = (1, 0, …, 0). Thus

$$\begin{array}{l}max\{{[T]}_b\mid 0\le [Tf]\le [T]<\infty \}=\frac{[NA]}{K_d(0)+[NA]}\hspace{0.17em}\text{and}\\ \text{max}\left\{{[T]}_b\mid \sum _{i=1}^N{F}_i=1,F_i\ge 0\right\}=\frac{[NA]}{K_{d1}+[Tf]+[NA]}\end{array}$$ (3.16)

while

$$max\{{[T]}_b\mid 0\le [Tf]\le [T]<\infty ,\sum _{i=1}^N{F}_i=1,F_i\ge 0\}=\frac{[NA]}{K_{d1}+[NA]}.$$ (3.17)

We call $\frac{[NA]}{K_{d1}+[NA]}$ the maximum bound target efficiency.

Thus, we approach selection at maximum bound target efficiency (i. e. at the maximum value of the bound fraction) if and only if K_d → K_d1 and [Tf] → 0 (or [T] → 0).

4. The selection process as an iterative scheme

The sequential process, selection, PCR, selection …, can be written an iterative scheme. To do this, we introduce notation that suitably represents this process. For the initial step, we have NA fractions, $\overrightarrow{F^{(1)}}=\{F_1^{(1)},\dots ,F_N^{(1)}\}$, with ${\sum }_i{F}_i^{(1)}=1$ and a starting concentration of target [T]₁. After the initial pool is exposed to the target (in the presence or absence of a support), we obtain as output, new NA fractions, $\overrightarrow{F^2}=\{F_1^{(2)},\dots ,F_N^{(2)}\}$ and some free target that is then discarded. (The free target can be viewed as output from the first round. However, it is notationally simpler to call it [Tf]₁.) We then select a new target [T]₂. More generally, we are given a fixed sequence of target fractions ${\left\{{[T]}_r\right\}}_{r=1}^{\infty }$ with [T]₁ ≤ [NA]. We make any assumptions on this sequence that can be realized in the laboratory. At the r^th step we have NA fractions, $\overrightarrow{F^{(r)}}=\{F_1^{(r)},\dots ,F_N^{(r)}\}$, with ${\sum }_i{F}_i^{(r)}=1$. We obtain a new pool, $\overrightarrow{F^{(r+1)}}=\{F_1^{(r+1)},\dots ,F_N^{(r+1)}\}$ defined as follows: First we compute the free target left over from the reaction at the r^th step by solving

$${[T]}_r={[Tf]}_r(1+[NA]\mathscr{H}(\overrightarrow{F^{(r)}},{[Tf]}_r))$$ (4.1)

for [Tf]_r in terms of [T]_r. This value is then used to compute the fractions in the new pool from those in the old pool by evaluating the right hand sides of

$$F_i^{(r+1)}=\frac{K_d(\overrightarrow{F^{(r)}},{[Tf]}_r)+{[Tf]}_r}{K_{di}+{[Tf]}_r}{F}_i^{(r)}$$ (4.2)

for i = 1, …, N. This is much simpler than the procedure described in (Irvine et al. 1991).

5. Convergence of the selection process in the case of no background interference

The proof of Theorem 1 is given in Appendix B (Section 11).

Theorem 1

Assume that there is no loss through the support, that $F_1^{(1)}>0$ and [T]₁ ≥ [T]_r for r ≥ 2. Then the iterative scheme will converge to a pool consisting only of the best binding nucleic acid and

$$\underset{r\to +\infty }{lim}{K}_d(\overrightarrow{F^{(r)}},{[Tf]}_r)=K_{d1}.$$ (5.1)

The two conclusions above are equivalent. The convergence to selection, when it occurs, will be at maximum target efficiency if and only if [Tf]_r → 0. (See subsection 3.2).

Remark 1

From the proof of Theorem 1 one sees that the convergence to selection is very rapid. Indeed, from equation (11.7) in Appendix 11 one has for N ≥ i ≥ 2

$$\frac{F_i^{(r+1)}}{F_1^{(r+1)}}÷\frac{F_i^{(1)}}{F_1^{(1)}}=\frac{{\prod }_{k=1}^r(K_{d1}+{[Tf]}_k)}{{\prod }_{k=1}^r(K_{di}+{[Tf]}_k)}<{\left(\frac{K_{d1}+{[Tf]}_1}{K_{d2}+{[Tf]}_1}\right)}^r=e^{-rQ}<1$$

where Q = ln(K_d2 + [Tf]₁)/(K_d1 + [Tf]₁). Thus the decay to zero of the mole fractions of all except the best binding aptamer is at least exponentially fast. This will be the case if $K_d^{(r)}$ is close to K_d1 and [Tf]_r is small. Thus it is important to monitor K_d approach selection at maximum bound target efficiency.

Remark 2

Given a sequence of input targets, {[T]_r} with [T]_r < [T]₁ for r ≥ 2, the corresponding sequence of overall dissociation rate constants will converge to the dissociation constant of the best binding nucleic acid and the concentrations of the nucleic acid pool will approach that of a pool consisting solely of the best binding nucleic acid. However, the approach will be optimal (at maximum target efficiency) if and only if [T]_r → 0.

6. Partitioning

In practice, there are experimental losses. When the sample is passed through a support, some free NA will be bound to the support. Also, some of the product will be lost through the support. Following (Irvine et al. 1991), we say that the NA pool has been partitioned. Again following (Irvine et al. 1991), we express the individual NA relative concentrations in the form:

$${[\{T:N{A}_i\}]}^{\mathit{part}}=b_g[NA{f}_i]+c_p[\{T:N{A}_i\}]=b_g{F}_i[NA]+(c_p-b_g)[\{T:N{A}_i\}].$$ (6.1)

where, in the author’s notation, c_p is the percent of captured target caught by the i^th NA species that is eluted from the support and b_g is the percent of background free NA_i that is used for PCR by being nonselectively trapped by the support. In principle c_p and b_g should be species dependent. However, at the outset, following (Irvine et al. 1991), we assume they are not because it is difficult to measure them individually. Then summing (6.1) over all species, we have

$${[\{T:NA\}]}^{\mathit{part}}=b_g[NA]+(c_p-b_g)[\{T:NA\}].$$ (6.2)

In order to compute the percent of NA_i available for PCR we now define δ = b_g/(c_p − b_g) and ε = δ/(1+δ) = b_g/c_p:

$$F_i^{\prime }=\frac{{[\{T:N{A}_i\}]}^{\mathit{part}}}{{[\{T:NA\}]}^{\mathit{part}}}=\frac{\delta F_i[NA]+[\{T:N{A}_i\}]}{\delta [NA]+[\{T:NA\}]}=F_i\frac{\delta +[Tf]/(K_{di}+[Tf])}{\delta +[Tf]\mathscr{H}(\overrightarrow{F},[Tf])}$$ (6.3)

where again $[\{T:NA\}]=[T]-[Tf]=[Tf]\mathscr{H}(\overrightarrow{F},[Tf])$ and set (suppressing the arguments in [T f](F⃗, [T]) and in K_d(F⃗, [T f]) on the right hand side)

$$E_i([Tf],\delta )=\frac{F_i^{\prime }}{F_i}=\frac{\delta +[Tf]/(K_{di}+[Tf])}{\delta +[Tf]/(K_d+[Tf])}=\left(\frac{\epsilon K_{di}+[Tf]}{K_{di}+[Tf]}\right)\left(\frac{K_d+[Tf]}{\epsilon K_d+[Tf]}\right).$$ (6.4)

Notice that the last term consists of the product of two factors, the first is always less than unity (when 0< ε < 1 and [T f] > 0) while the second is always larger than unity for this range of ε. Notice that 1 < E_i([T f], δ) < E_i([T f], 0) if and only if K_di < K_d. Thus, it is better to use

$$\frac{F_i^{\prime }}{F_1^{\prime }}=\frac{[\{T:N{A}_i\}]}{[\{T:NA\}]}=\left(\frac{K_{d1}+[Tf]}{K_{di}+[Tf]}\right)\left(\frac{\epsilon K_{di}+[Tf]}{\epsilon K_{d1}+[Tf]}\right)\frac{F_i}{F_1}$$ (6.5)

When δ > 0 we see that as [T f] → 0 or as [T f] → +∞, the ratio E_i/E₁ →1. Thus the extreme values of E_i/E₁ must occur for nonzero values of the free target. It is an easy exercise in calculus to show that each ratio has unique minimum value of

$${\left(\frac{\sqrt{\epsilon }+\sqrt{K_{d1}/K_{di}}}{1+\sqrt{\epsilon K_{d1}/K_{di}}}\right)}^2$$

which occurs at $[Tf]=\sqrt{\epsilon K_{d1}{K}_{di}}$.

7. Convergence of the selection process in the case of NA partitioning

There are, as when ε= 0, zero, a number of fixed points for the scheme, each having the form $F_i^j={\delta }_{ij}$ with K_d = K_dj for j = 1, 2, … N. (Here δ_ij = 1 or δ_ij = 0 according as i = j or i ≠ j.) The goal is to determine necessary and sufficient conditions for the convergence of the iterative sequence to converge to the fixed point corresponding to the case j = 1.

We establish two theorems. In the first theorem, we assume that [T]₁ ≥ [T]_r ≥ [T]₀ > 0 with round number. In the second, it is assumed that [T]_r → 0 with round number.

Theorem 2

Suppose, in the selection process we define input target concentrations [T]_r recursively by the rule ${[T]}_{r+1}=(1-s_r){[T]}_r={{\prod }_1^r(1-s_k)[T]}_1$. Suppose also that [T]_r → [T]₀ > 0. That is, the series Σ_r s_r is convergent. Suppose also that $F_1^{(1)}>0$. Then the iterative scheme will converge to a pool consisting only of the best binding nucleic acid and

$$\underset{r\to +\infty }{lim}{K}_d(\overrightarrow{F^{(r)}},{[Tf]}_r)=K_{d1}.$$ (7.1)

The two conclusions are equivalent. The convergence to selection, when it occurs, will fail to be at maximum bound target efficiency because {[T f]_r} is bounded below by a positive constant.

Theorem 3

Suppose, in the selection process we define input target concentrations [T]_r recursively by the rule ${[T]}_{r+1}=(1-s_r){[T]}_r={\prod }_1^r(1-s_k){[T]}_1$. Suppose also that [T]_r → 0 with round number. (Equivalently, Σ_r s_r is a divergent series.) Then a necessary and sufficient condition for the SELEX method to converge to the best binding nucleic acid is that the series

$$\sum _{r=1}^{\infty }\left[\prod _{k=1}^r(1-s_k)\right]$$ (7.2)

is divergent. Moreover, if the series is divergent: The convergence of the iterative scheme to a pool consisting only of the best binding nucleic acid and

$$\underset{r\to +\infty }{lim}{K}_d(\overrightarrow{F^{(r)}},{[Tf]}_r)=K_{d1}$$ (7.3)

are equivalent statements. The convergence to selection, when it occurs, will be approach maximum bound target efficiency because [T f]_r → 0. (See subsection 3.2.)

A useful corollary is the following:

Corollary 1

If ${\left\{z_r\right\}}_{r=0}^{\infty }$ satisfies

$$z_r\ge z_{r+1}>0\hspace{0.17em}\mathit{and}\hspace{0.17em}\underset{r\to \infty }{lim}{z}_r=0,$$

with

$$\sum _{r=1}^{\infty }{z}_r=+\infty ,$$

then

$${\left\{s_r\right\}}_{r=1}^{\infty }={\left\{1-\frac{z_r}{z_{r-1}}\right\}}_{r=1}^{\infty }$$

satisfies the conditions of Theorem 3. Conversely, if ${\left\{s_r\right\}}_{r=1}^{\infty }$ is a sequence such that this theorem holds, then the sequence given by recursively by z₀ = 1, z_r+1 = s_r+1z_r satisfies the above conditions.

Thus it is relatively easy to generate sequences for which one can satisfy the conditions of the theorem.

For example, if z_r = 1/(r + 1), then s_r = 1/(r + 1), (the harmonic sequence) then Σ_r s_r = Σ_r 1/(r + 1) is a divergent series. Furthermore, the series in (11.11) reduces to this same series and hence selection will take place. The harmonic sequence {1/(r + 1)} is not the only one with this property. For example, z_r = 1/(r+1) ln(r+2)) will give a sequence with s_r = 1 − r ln r/(r+1) ln(r+1)) ≈ 1/r for large r also satisfies the conditions of the theorem. Thus, in the absence of any information about the dissociation constants, the harmonic sequence is a good choice for target reduction in each round in SELEX.

However, if the input target is reduced by a fixed fraction 1 − c at each step, then the series in (11.11) is a convergent geometric series and selection is not possible. (That is, it is not possible in the mathematical sense although clearly, the more slowly the (11.11) converges, i.e., the closer c is to unity, the more likely we are to get something approaching perfect selection.

In Section 9 we illustrate these results with numerical simulations.

8. Partial selection - Likelihood of success

Here we want to consider how many rounds will be needed to achieve a concentration of the best binding NA that is a large multiple σ of the other nucleic acid concentrations in pool. Our approach to this problem is somewhat different than that of (Irvine et al. 1991). We can write

$$\frac{F_i^{(r)}}{F_1^{(r)}}=\frac{F_i^{(1)}}{F_1^{(1)}}\prod _{k=1}^r\frac{(K_{d1}+{[Tf]}_k)(\epsilon K_{di}+{[Tf]}_k)}{(K_{di}+{[Tf]}_k)(\epsilon K_{d1}+{[Tf]}_k)}=\frac{F_i^{(1)}}{F_1^{(1)}}\prod _{k=1}^r\left(1-\frac{(K_{di}-K_{d1})(1-\epsilon ){[Tf]}_k}{(K_{di}+{[Tf]}_k)(\epsilon K_{d1}+{[Tf]}_k)}\right)=P_{i,r}\frac{F_i^{(1)}}{F_1^{(1)}}$$ (8.1)

where P_i,r denotes the indicated product.

Notice that the products P_i,r satisfy

$$P_{2,r}>P_{3,r}>\cdots >P_{N,r}.$$

Because ${\sum }_1^N{F}_1^i=1$ it follows that

$$\begin{array}{l}{F}_1^{(r)}(1+\mathrm{\Theta }{P}_{N,r})\le \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1,\\ F_1^{(r)}(1+\mathrm{\Theta }{P}_{2,r})\ge \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1\end{array}$$ (8.2)

where we have set

$$\mathrm{\Theta }=\frac{{\sum }_{i=2}^N{F}_i^{(1)}}{F_1^{(1)}}=\frac{1-F_1^{(1)}}{F_1^{(1)}}.$$ (8.3)

Thus

$$\frac{1}{1+\mathrm{\Theta }{P}_{2,r}}\le F_1^{(r)}\le \frac{1}{1+\mathrm{\Theta }{P}_{N,r}}$$ (8.4)

We want good upper bounds for P_2,r (in order to get good lower bounds for $F_1^{(r)}$) and good lower bounds for P_N,r.

To get a good upper bound on P_2,r note that

$$\begin{array}{l}\frac{(K_{d1}+{[Tf]}_k)(\epsilon K_{d2}+{[Tf]}_k)}{(K_{d2}+{[Tf]}_k)(\epsilon K_{d1}+{[Tf]}_k)}=1-\frac{(K_{d2}-K_{d1})(1-\epsilon ){[Tf]}_k}{(K_{d2}+{[Tf]}_k)(\epsilon K_{d1}+{[Tf]}_k)}\\ \approx 1-\frac{(K_{d2}-K_{d1})(1-\epsilon )}{({[Tf]}_k+K_{d2})}\\ \le 1-(1-K_{d1}/k_{d2})(1-\epsilon )\equiv (1-{\mathrm{\Lambda }}_2).\end{array}$$

when we assume that K_d2 ≫ [T f]_k ≫ εK_d1. If ${[Tf]}_k\approx \sqrt{K_{d1}{K}_d}$, this inequality will hold if $K_{d2}^2/(\epsilon K_{d1}>K_d)$ and K_d > εK_d1. The latter inequality is always true since K_d > K_d1. The former will be true if $K_{d2}>\sqrt{\epsilon K_{d1}{K}_{dN}}$, a claim that will always hold if the background is small enough. On the other hand, it may take a number of preliminary rounds in order to get to the level for which K_d2 ≫ [T f]_k ≫ εK_d1.

In this case, P_2,r ≤ (1 − ⋀₂)^(r).

To get a good lower bound on P_N,r we note that for any value of [T f]_r

$$\frac{(K_{d1}+{[Tf]}_k)(\epsilon K_{dN}+{[Tf]}_k)}{(K_{dN}+{[Tf]}_k)(\epsilon K_{d1}+{[Tf]}_k)}\ge {\left(\frac{\sqrt{\epsilon }+\sqrt{K_{d1}/K_{dN}}}{1+\sqrt{\epsilon K_{d1}/K_{dN}}}\right)}^2\equiv {(1-{\lambda }_N)}^2$$

where

$${\lambda }_N=\frac{(1-\sqrt{\epsilon })(1-\sqrt{K_{d1}/K_{dN}})}{1+\sqrt{\epsilon K_{d1}/K_{dN}}}.$$ (8.5)

Therefore

$$\frac{1}{1+\mathrm{\Theta }{(1-{\mathrm{\Lambda }}_2)}^{(r)}}\le F_1^{(r)}\le \frac{1}{1+\mathrm{\Theta }{(1-{\lambda }_N)}^{2r}}$$ (8.6)

or

$$\mathrm{\Theta }{(1-{\mathrm{\Lambda }}_2)}^{(r)}\le \frac{1-F_1^{(r)}}{F_1^{(r)}}\le \mathrm{\Theta }{(1-{\lambda }_N)}^{2r}.$$ (8.7)

Suppose that 0 < σ < 1. Then we can be sure that $F_1^{(r)}\ge \sigma$ if

$$r\ge r_U=\frac{ln[\sigma \mathrm{\Theta }/(1-\sigma )]}{ln[1/(1-{\mathrm{\Lambda }}_2)]}=\frac{ln\{(\sigma /F_1^{(1)})[(1-F_1^{(1)})/(1-\sigma )]\}}{ln[1/(1-{\mathrm{\Lambda }}_2)]}$$ (8.8)

Whereas $F_1^{(r)}\le \sigma$ provided

$$r\le r_L=\frac{1}{2}\frac{ln[\sigma \mathrm{\Theta }/(1-\sigma )]}{ln[1/(1-{\lambda }_N)]}.$$ (8.9)

Thus we define the interval of uncertainty as the interval (of integers) (r_L, r_U) where the value of the round number must belong in order for $F_1^{(r)}$ to achieve the value σ. It is important to keep in mind that (8.8) holds only under the hypothesis that K_d2 ≫ [T f]_k ≫ εK_d1. Consequently, the number r_U may understate the number of rounds needed for $F_1^{(r)}\ge \sigma$. That is, we must allow for a certain number K of rounds say to take place before we can assert that K_d2 ≫ [T f]_k ≫ εK_d1. Thus, the interval of uncertainty is (r_L, r_U + K).

Notice that as ε → 0⁺,

$$\frac{r_U}{r_L}\to \frac{ln(K_{dN}/K_{d1})}{ln(K_{d2}/K_{d1})}$$

which ratio is unity when N = 2. Thus at least one of the two numbers r_U, r_L cannot give the required minimum number of rounds needed for $F_1^{(r)}$ to achieve the value σ unless there are only two nucleic acids present in the initial pool and ε = 0.

Now suppose in our initial pool we have M molecules per unit volume of [NA]. We are going to look at some distribution scenarios. We compute the interval of uncertainty with data from (Irvine et al. 1991).⁴ First, suppose also that all but 1 of them are of the poorest binding type while the sole exception is of the best binding type. That is $F_1^{(1)}=1/M$ and $F_N^{(1)}=(M-1)/M$ while none of the intermediate binders are present. Then Θ = M − 1.

The number nucleotides, with distinct binding constants is taken as N = 5. The pool size is [NA] = 3(10⁻⁵)M. In order to take [NA] = 1, the dissociation constants have to be rescaled to this concentration. K_d1 = 4.8(10⁻⁹)M/[NA] = 1.6(10⁻⁴), K_d2 = 12.0(10⁻⁹)M/[NA] = 3(10⁻⁴), K_d3 = 17.0(10⁻⁹)M/[NA] = 5.7(10⁻⁴), K_d4 = 27.0(10⁻⁹)M/[NA] = 9(10⁻⁴), K_d5 = 3.2(10⁻⁷)/[NA] = 1.6(10⁻²) where ε ≈ 0.1/80 = 1.25(10⁻³). The input or target concentration, [T] = [NA]10⁻³ = 3(10⁻⁸)M = [T]₁[NA]. Hence [T]₁ = 1.0(10⁻³). If the initial distribution is such that $F_1^{(1)}=1/65536$ with $F_2^{(1)}=F_3^{(1)}=F_4^{(1)}=0,\hspace{0.17em}{F}_5^{(1)}=65535/65536$, then $(1-F_1^{(1)})/F_1^{(1)}\approx 65535$. In order to find [T f] we need to solve the equation arising from (3.9)

$${[T]}_1=[Tf]\left(1+\frac{F_1^{(1)}}{K_{d1}+[Tf]}+\frac{1-F_1^{(1)}}{K_{dN}+[Tf]}\right)$$

which, in this case leads to a cubic in [T f]. However, using the values for [T]₁, K_d1, K_dN, $F_1^{(1)}$ we can easily estimate the value of [T f] as [T f] ≈ 1.6(10⁻⁵). Thus K_dN ≫ K_d1 > [T f] ≫ εK_d1 ≈ 2.0(10⁻⁷). If one seeks a pool consisting of 84% of the best binding nucleic acid, then σ = 0.84 Then σ/(1 − σ) = 5.25. With M = 65536, ln(Θ σ/(1 − σ)) = 12.7485. We find that ln[1/(1 − ⋀₂)] ≈ ln[K_d2/K_d1] = ln[1.875] = 0.628 and this gives r_U ≈ 12.7485/0.628 ≈ 21.0. On the other hand $\sqrt{K_{d1}/K_{dN}}=0.1$ while ε = 1.25(10⁻³) so that1 − λ₅ = 0.135/(1 + 0.00354) ≈ 0.135. Thus 2 ln(1/(1 − λ₅)) = 4.04 and hence r_L ≈ 3.18. Thus we obtain 84% selectivity in not less than three nor more than 20 rounds.

Notice that if we only demand a 50% pool of the best binding aptamer, then σ = 0.5 and ln(Θσ/(1 − σ)) = ln(65535) so that r_U ≈ 18 while r_L = 2.7.

Using pubmed (http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?db=PubMed) as the search engine, a review of the recent literature (2003 through mid-2006) revealed 26 publications describing successful SELEX experiments (Boyce et al.(2006), Chen et al.(2003), Cerchia et al. (2005), Cui et al. (2004), DeStefano et al. (2004), Eulberg et al. (2005), Fan et al. (2004), Gening et al. (2006), Gopinath et al. (2006), Jarosch et al. (2006), Kim et al. (2003), Kulbachinskiy et al. (2004), Lee et al. (2004), Lee et al. (2005), Mi et al. (2005), Mochizuki et al. (2005), Moreno et al. (2003), Mori et al. (2003), Ogawa et al. (2004), Pileur et al. (2003), Rhie et al. (2003), Skrypina et al. (2004), Surugiu-Warnmark et al. (2005), Vo et al. (2003), Yang et al. (2006) and White et al. (2001)). In all instances the targets were proteins. The number of rounds prior to cloning varied from 7 to 22 with a mean of 12 ± 4 and a median of 12. These results identify the round at which each group of investigators identified binding activity of the aptamer(s) in the oligonucleotide pool and decided to clone the sequences. The decision to clone can vary depending on the results obtained from previous rounds of the SELEX experiment and does not indicate that a certain percentage of the oligonucleotides in the pool are aptamers of the highest a, nity form. Because it is prohibitively time consuming to test every oligonucleotide sequence in the cloned pool, the information regarding percent best binding aptamer sequences in the pool is usually sketchy at best. However, the collective results from a number of SELEX experiments should provide a view of the number of rounds it generally takes to obtain a population with measurable (greater than about 10%) binding activity. With the understanding that the experimental data is not uniform, the results from the mathematical model are consistent with the experimental data. The concordance of experimental results with mathematical predictions that are based only on chemical equilibria suggest that, in most SELEX experiments, the binding equilibrium is the major factor determining selection, whereas the evolution enabled by in vitro mutagenesis might not have a major impact on the rate of aptamer selection.

As a second example, suppose that we compare the best binding nucleic acid with the worst binding nucleic acid. Then ⋀₂ = ⋀_N = (1 − ε) K_d1/K_dN and λ_N is given in (8.5). Suppose we have a pool consisting of 10⁽¹⁾2 nucleic acids, 10^k of which are the best binder and the rest are of the worst binding type. Then $F_1^{(1)}={10}^{k-12}$ and Θ = 10^{12 − k} − 1. If we seek a pool of 50% of the best binding aptamer, we have K_d1/K_dN = 10⁻². Then ln(σ Θ/(1 − σ)) ≈ (12 − k) ln 10 = 2.303(12 − k) while − ln(1 − ⋀_N) = − ln(1 − 0.95(.99)) = − ln(0.0595) = 2.821 and ${\lambda }_N=(1-\sqrt{(}0.05))(1-0.1)/(1+\sqrt{(}0.05(.01))=0.69875/1.02236=0.682468$ and − ln(1 − ⋀_N) = 1.14766. Thus 0.5(1.14766)2.303(12 − k) ≥ r ≥ 2.303(12 − k)/2.821 or

$$1.32(12-k)\ge r\ge 0.816(12-k).$$ (8.10)

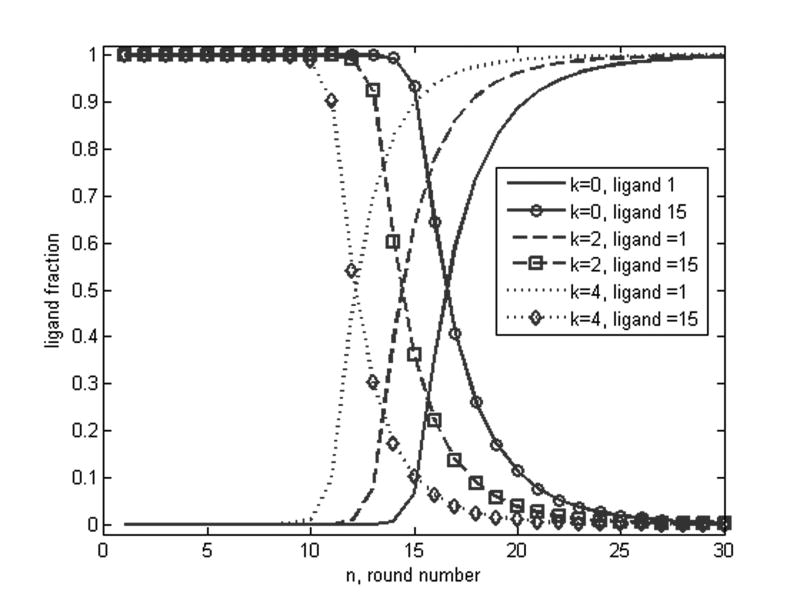
Thus when k = 0 we should need not fewer than 10 rounds nor no more than 16 rounds to get a pool consisting of 50%. of the best binding aptamer. If we have 10 molecules of the best binder so that k = 1, then 9 ≤ r ≤ 15. See Figures 11, 12.

Figure 11.

A plot of the overall dissociation constant as a function of round number for six different initial fractions of best binding nucleic acid. 10^k=number of best binding [NA] molecules in a pool of = 10¹² molecules. There are fifteen nucleic acid types.

Figure 12.

A plot of the best and poorest binding fractions as a function of round number for three different initial fractions of best binding nucleic acid. Here 10^k=number of best binding [NA] molecules in a pool of = 10¹² molecules. There are fifteen nucleic acid types. Clearly the round number at which the nucleic acid fractions of the best and worst binders are each 1/2 of the pool falls with in the range predicted by the inequalities in (8.10)

9. Simulations

In this section, we present some simulations. We take a fixed number N = 15 of nucleic acids and a fixed linear ordering of the dissociation constants. In Figures 2–8 we use K_di = (1.6+2.2(i − 1))10⁻⁴, i = 1,…, N (rescaled to a fixed pool size of [NA] = 3(10⁻⁵M). We started with a nucleic acid pool generated by using a random number generator. Once the pool is selected, it is fixed for the Figures 3–9.

Figure 2.

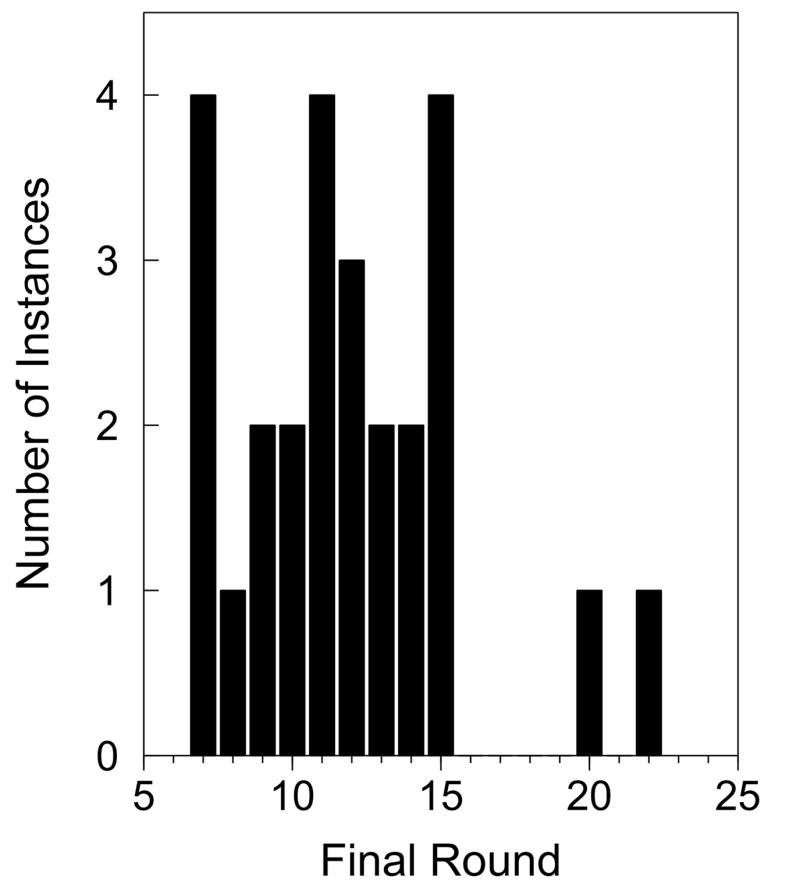
Survey of Rounds to Completion in SELEX Experiments. Plotted is a summary of 26 publications from 2003 to mid-2006 in which SELEX experiments were reported that resulted in the cloning of one of more aptamers. The number of rounds performed before the aptamers were cloned was determined for each instance and the number of instances is plotted against the number of rounds prior to cloning. The number of rounds prior to cloning varied from 7 to 22 with a mean of 12 ± 4 and a median of 12.

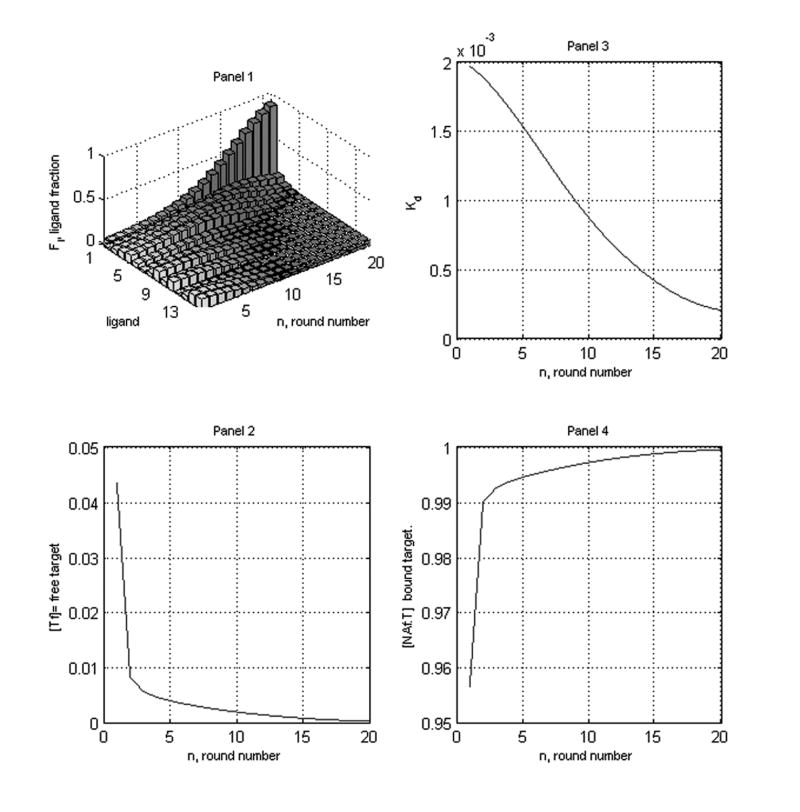
Figure 3.

The decrease in target concentration from round to round is very slow but nevertheless, selection is occurring, nearly all but the first and second nucleic acids being essentially gone after 10 rounds. In panels 2, 4 the plots begin at round numbers 2 and 3. This was done for convenience of scale. In particular, in Panel 4, we see that the maximum target efficiency is 1/(1 + K_d1 + [Tf](20)) < 1/(1 + K_d1) at twenty rounds.

Figure 9.

We use formula $[Tf]=\sqrt{\delta K_{d1}{K}_d(0)}$ for the initial target in every round. That is, s_r = 0. The initial pool is again random and ε = 0.05. The first panel demonstrates improved selection over all the panels in Figure 7.

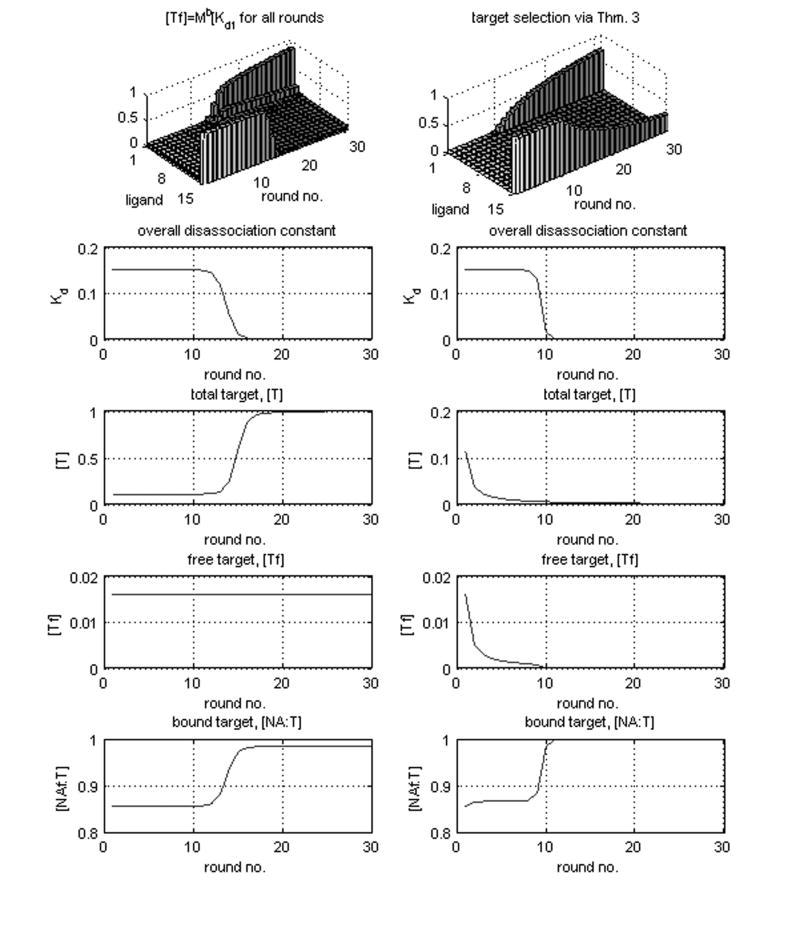
In Figures 11–16 we increased the spread of the dissociation constants by a factor of 10, i. e. we used This range is consistent with the data used in (Irvine et al. 1991), figure 4. We also looked at the worst case pool distribution, i. e. $F_1^{(1)}=\dots F_N^{(1)}={10}^{-12}$ and $F_N^{(1)}=1$.

Figure 16.

The top row of figures illustrates the effect of increasing the ratio K_dN / K_d1 on the round number at which selection becomes significant. The the round number for which 50% selection is achieved decreases from 14 to around 8 over six orders of magnitude. The input target at subsequent rounds was dictated by Theorem 3. The bottom row of figures was generated by using the solution $[Tf]=\sqrt{\epsilon K_{d1}{K}_d([Tf])}$ of to generate the free target at each round.

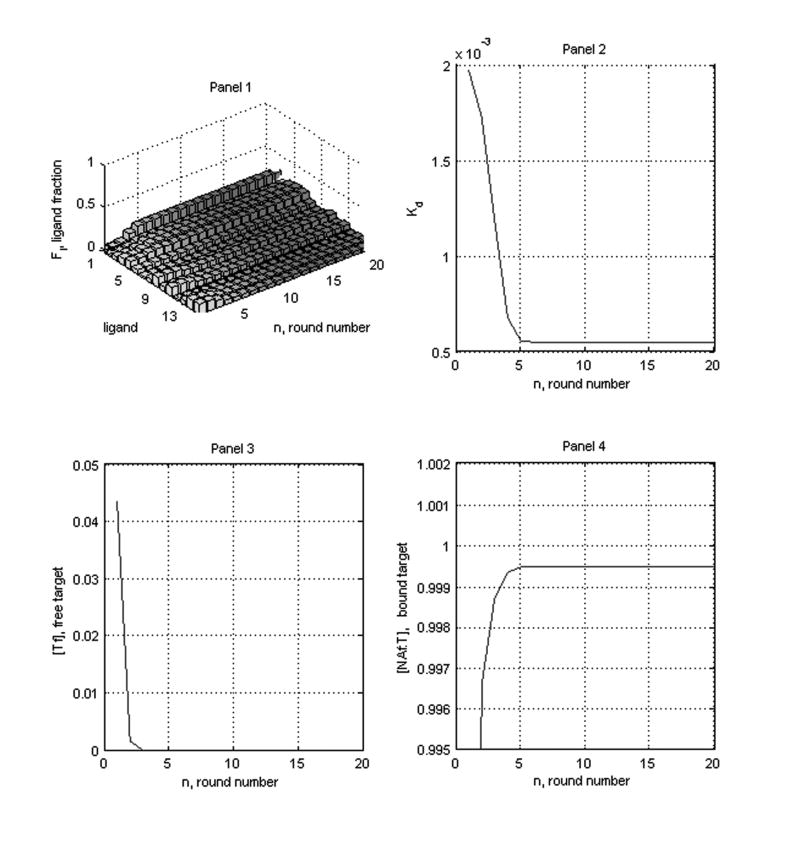
Figure 4.

The decrease in target concentration from round to round is such that the series in (7.2) is convergent. Clearly selection is not taking place. Notice the scale on the vertical axis in Panel 1. Notice also that almost all of the free target is used up after four rounds. Panel 2 (incorrectly) suggests that we have achieved selection as the overall (rescaled) dissociation constant has fallen to 0.6(10⁻³). If we didn’t have other information we might be inclined to conclude that this value is K_d1. In fact, for this experiment, K_d1 = 1.6(10⁻⁴). Although all of the free target is exhausted, the maximum bound target fraction is not unity, but rather 0.9995 ≈ 1/(1.00006), a number smaller than the maximum target efficiency, 1/(1 + K_d1).

Because we do not need to solve a large system of equations, the Matlab program we use runs very rapidly. Figures 3–11 are organized as follows:

1. In the first set of experiments, we take ε = 0.05, [T]₁ = 1.0 and vary the reduction sequence. The choices for ${\left\{s_r\right\}}_{r=1}^{\infty }$ are ${\{1/{(r+1)}^{5/2}\}}_{r=1}^{\infty }$ (to illustrate Theorem 2), ${\{r^2/(r^2+1)\}}_{r=1}^{\infty }$ (Theorem 3, series in (7.2) is convergent, no selection) and ${\{1/(2r+1)\}}_{r=1}^{\infty }$ (Theorem 3, series in (7.2) is divergent, selection). We give the graphs of K_d, [T f], [T]_b, as functions of round number.

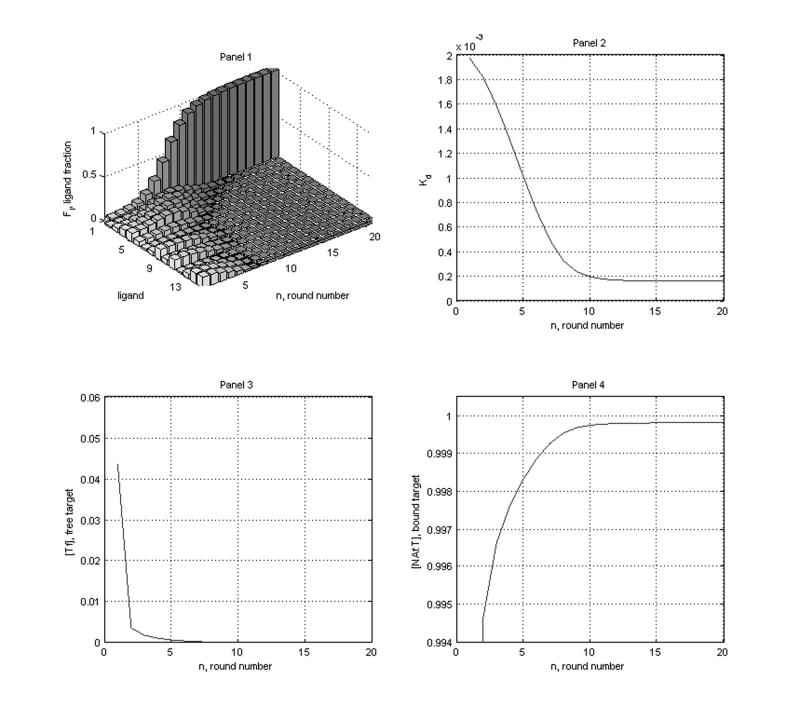
   In Figures 3 and 5 we have selection. However, while the panels 2 in both figures indicate that the overall dissociation constant, K_d, is converging to the smallest such constant, K_d1 with round number, the convergence is faster in the case of Figure 4. Also, there is much less free target left and more efficient binding in the case of Figure 5 as compared to Figure 3 (compare panels 3, 4 in both figures).

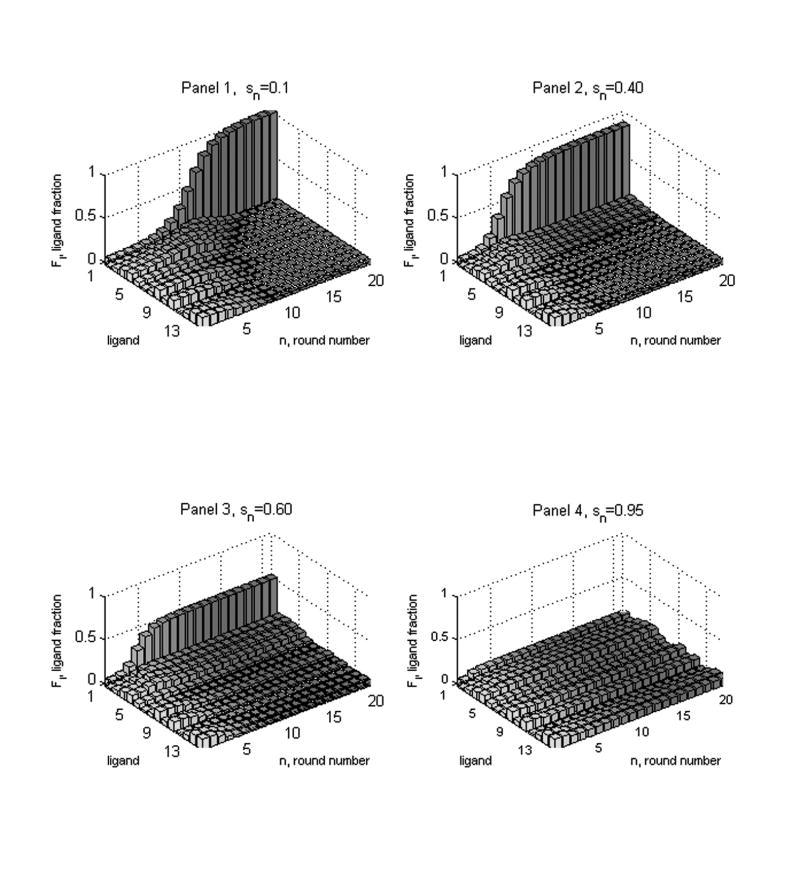
2. For the second set of experiments, Figure 6, with [T]₁ = 1.0, we examine the case that ${\{s_r=s\}}_{r=1}^{\infty }$, a series of constants. We compare slow reduction s = 0.1, 0.4, 0.6 and s = 0.95. While we are led to geometric series in (7.2) in all four cases, the rate of convergence of the series accelerates as s increases toward unity.

   Notice how, as we move from panel to panel in Figure 6, the number of rounds for which the poorer binders survive increases. Notice also that nearly perfect selection of the first nucleic acid becomes impossible to achieve in less than twenty rounds when s > 0.5.

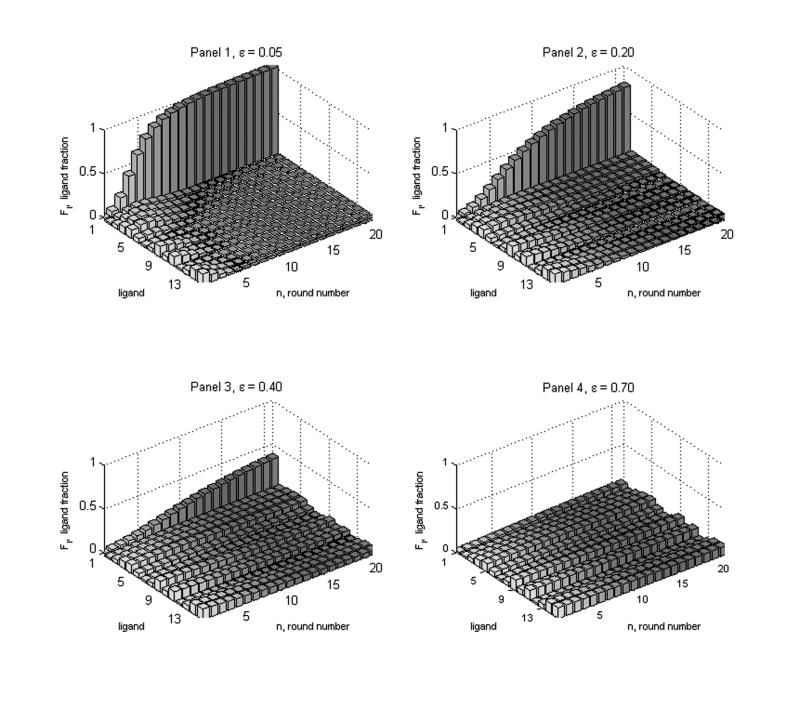
3. In the third set of experiments, we start simulations with [T]₁ = 0.1 and with ε variable over the four values 0.05, 0.20, 0.40, 0.70 s_r = 0.1 for all round numbers r. In the panels in Figure 7, we see the effect of increasing ε ≈ b_b/c_p on selection.

4. In the fourth set of experiments, we start simulations with ε = .05 and with [T]₁ = 4^−k for k = −2, −1, 0, 1, 2,…2, 9. We reduced the target by 10%(s_r = 0.1) in every case. See Figure 8.

   We see from Figures 8 that there is an optimal starting value for [T]₁ lying in the interval (1/16, 1/4) for which the round number leading to selection will be minimal. Much of the discussion in (Irvine et al. 1991), pages 749–753, is concerned with estimating this optimal starting value.

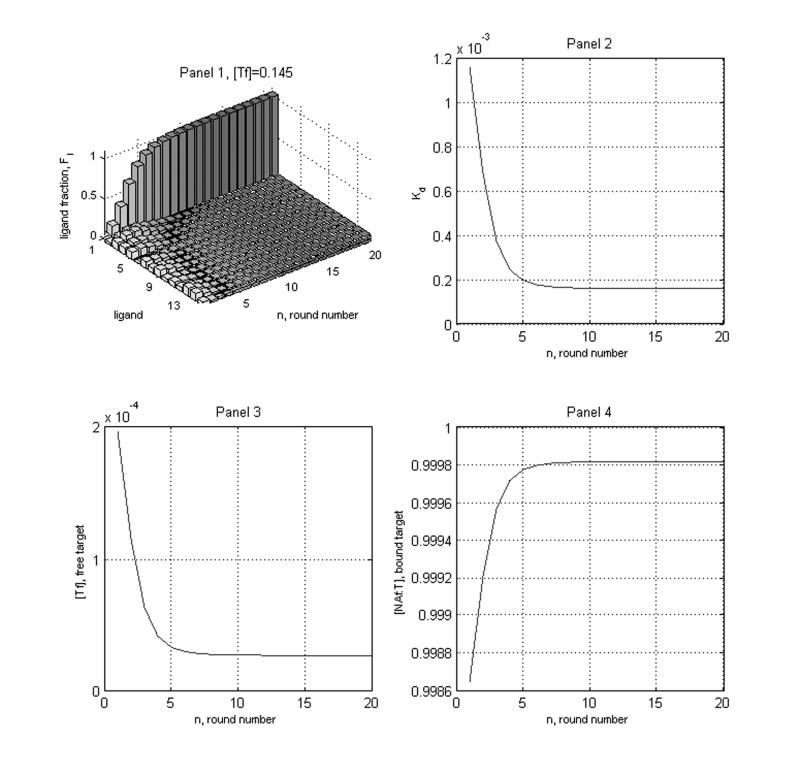
5. If we use the formula $[Tf]=\sqrt{\delta K_{d1}{K}_d(0)}$ in every round, we are led to fixing [T](r) ≈ 0.1451 for every round. That is, we are setting s_r = 0. In Figure 9 we have given the nucleic acid fractions for a random pool with this fixed value for the input target with ε = 0.05.

   Although in this case there is no reduction in initial target from round to round, one needs to have a reasonable idea of the background and capture fractions as well as the geometric mean, $\sqrt{K_{d1}{K}_{dN}}$, of the smallest and largest dissociation constants in order to implement this in the laboratory. Notice also that in this case all the free target is not consumed nor is the binding fraction as close to unity as they are in Figure 5. (Compare panels 3 in Figures 5, 9 and panels 4 in Figures 5, 9.) Because we do not have convergence of the free target to zero (Figure 9, panel 3) we do not obtain convergence of the overall dissociation constant to K_d1. (Compare Figure 5, panel 2 with Figure 6, panel 2.)

6. In Figures 11 and 12 we use the values K_di = (1.6 + 22 (i − 1))10⁻⁴, i = 1,…, N and the starting value [T]₁ = 1. We chose s_r = 2/(2r + 1) so that selection is assured. Here the pool is chosen in such a way that, $F_1^{(1)}={10}^{k-12}$ for k = 1, 2,… 5 and $F_N^{(1)}=1$ while $F_j^{(1)}={10}^{-12}$ for 2 ≤ j ≤N −1. Figure 9 illustrates how the increase in the number of best binding molecules in the initial pool affects the overall dissociation constant as a function of round number. Figure 11 illustrates how the increase in the number of best binding nucleic acid in the initial pool affects the number of rounds need to bring the pool to a size consisting of 50% or more of best binding nucleic acid.

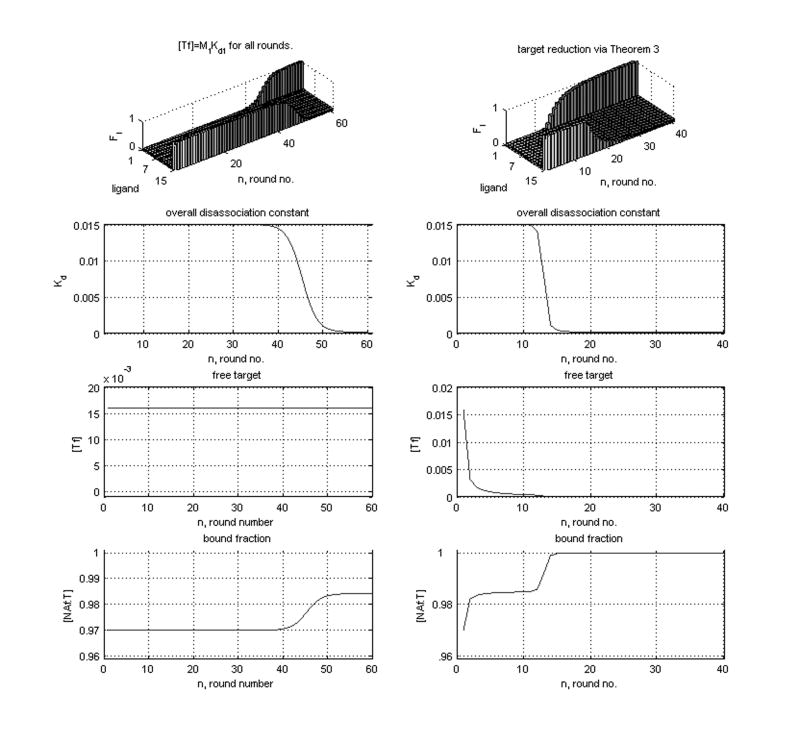
7. In Figure 13, we have taken K_dN/K_d1 = 93 and M^b = 99 in the first column of figures. We took $F_r^{(1)}={10}^{-12}$ if n < 15 and $F_N^{(1)}=1$ if N = 15 as the initial pool distribution in all cases. M_b/(1 + M_b) is the probability of binding one molecule of [NA₁]. (See (Irvine et. al., 1991) for details.)

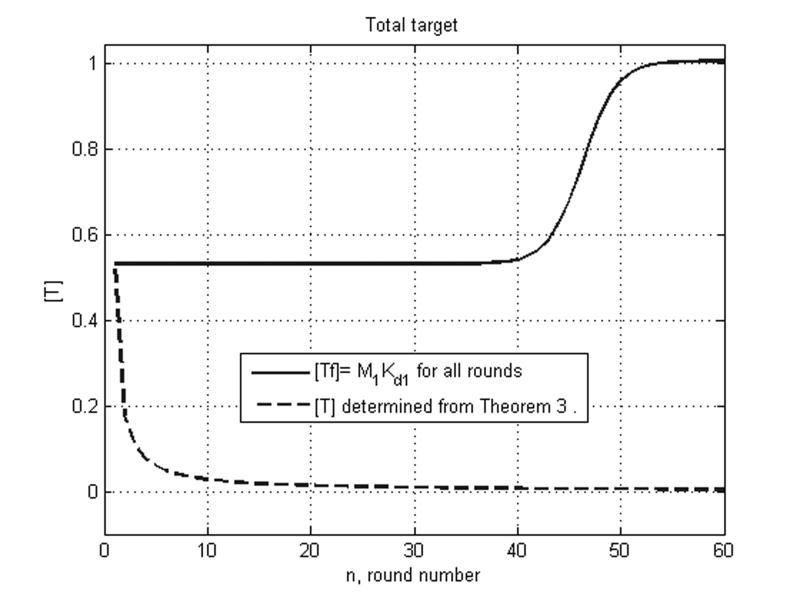
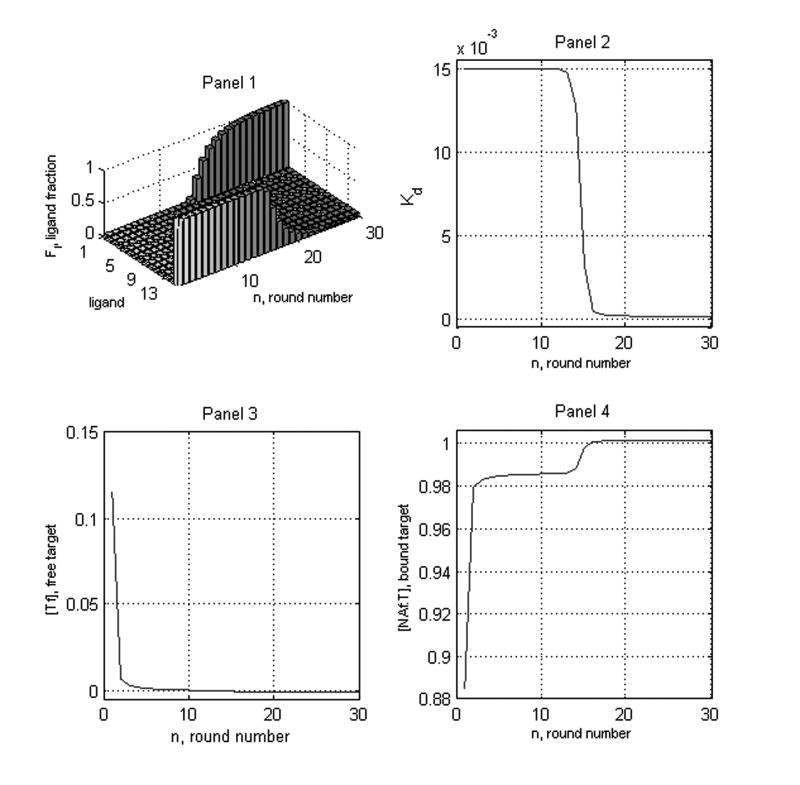
   We follow the strategy of (Irvine et al. 1991) in that K_d is updated from round to round while [T]₁ = M_bK_d1 + M_bK_d1[NA]/(M_bK_d1 + K_d([T f])) is fixed in every round. This choice gives [T]₁ = 0.5304 as the initial target value. In the second column, we used this as a starting ratio along with s_r = 2r/(2r + 1). In the first case we do not achieve even a 50-50 pool until after around 45 rounds while in the second case, we achieve this pool in less than 20 rounds. On the other hand, in Figure 14, we took K_dN/K_d1 = 9300 and M_b = 99. Here [T](1) = 0.1117. We see that this time it is better to follow the strategy of (Irvine et al. 1991). Notice the shapes of the curves for K_d, [T]_b are very similar. It appears from the second panel in the first row as though Theorem 3 is violated. In fact, selection does occur here also but it takes many more than 30 rounds to achieve it because the initial target value [T](1) is so small. See Figure 8.

8. Figures 16 and 17 indicate that either the use of Theorem 3 (with s_r = 2/(2r + 1) here) or use of equation $[Tf]=\sqrt{\epsilon K_{d1}{K}_d([Tf])}$ of (Irvine et al. 1991) to select the free target from round to round, leads to very nearly the same round number for the nucleic acid pool to consist of 50% of the best binding molecule when there is only one initially present. The agreement is better, the larger the ratio K_dN/K_d1 is. When this ratio is relatively small, of order 10 or less, it is probably better to resort to some other method for discriminating between aptamers such as cloning unless one has sufficient information about K_d1 and K_d in order to be able to invoke $[Tf]=\sqrt{\epsilon K_{d1}{K}_d([Tf])}$. Both methods for computing the round number at 50% lead to larger and larger values for the round number but once at least one of the methods gives an estimate 20 or more rounds, one should perhaps consider whether the time and expense of using the SELEX method is worth the expected outcome.

Figure 5.

The decrease in target concentration from round to round is such that the series in (7.2) is divergent. Almost all of the target is gone after seven rounds and that only the best binding nucleic acid remains in the pool after eight or nine rounds. Now we see from Panel 4, that the maximum target efficiency (≈ 0.9998) has been attained.

Figure 6.

The results of uniform reduction from round to round. Selection becomes harder to achieve if we reduce the starting target from round to round too quickly.

Figure 7.

The effects of partitioning (losses). As the loss fraction (ε), increases from 0 to 1, it becomes harder to achieve selection.

Figure 13.

In this set of figures the starting value for the target is taken as the starting value of the target dictated by demanding a probability of 0.99 for one molecule of the best binding nucleic acid to bind in order to generate the starting target value as dictated by (Irvine et al. 1991). The ratio K_dN/K_d1 ≈ 100 was used for these figures. Again, we need to interpret the bound target graphs carefully. The maximum value in the bottom panel in the first column here is clearly smaller than unity, as it should be. In the bottom panel in the second column, it appears to reach unity, but is in fact, smaller than unity, being approximately 1/(1 + K_d1) as the free target is nearly zero near the last few rounds.

Figure 14.

In this figure we plot the total target as a function of round number for the two cases illustrated in Figure 13.

Figure 17.

Here all the relevant plots are given for the case K_dN /K_d1 = 10³, a case not included in Figure 16. The same comments concerning the graphs of [T]_b in the figure caption for Figure 13 apply here also.

Figure 10.

A plot of the best and poorest binding fractions as a function of round number with only one molecule of each nucleic acid present except the poorest binder and there = 10⁻² molecules of it. There are fifteen nucleic acid types. Notice the unusual kink in the graph in Panel 2. It occurs at about the value of the round number for which the pool size is roughly evenly divided.

Figure 15.

The effect of using the small starting value of the target dictated by demanding a probability of 0.99 for one molecule of the best binding nucleic acid to bind in order to generate the starting target using Theorem 3. To generate this figure the ratio K_dN /K_d1 ≈ 10⁴ was used. The same comments concerning the graphs of [T]_b in the figure caption for Figure 13 apply here also.

10. Appendix A. Geometric observations

The entire SELEX iteration scheme can be viewed to take place in the Cartesian product of two sets $\mathcal{T}\times \mathcal{S}$. The set $\mathcal{T}$ is given by

$$\mathcal{T}=\left\{\overrightarrow{F}\in R^N\mid F_i\ge 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}\sum _{i=1}^N{F}_i=1\right\},$$ (10.1)

the simplectic triangle in Euclidian N space.

The set $\mathcal{S}$ can be described as follows: In the three dimensional orthant determined by the inequalities [Tf] ≥ 0, [NA] ≥ 0, [T] ≥ 0, there are two surfaces S₁, S_N say, defined by the equations

$$[T]=[Tf]+\frac{[NA][Tf]}{K_{d1}+[Tf]}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}[T]=[Tf]+\frac{[NA][Tf]}{K_{dN}+[Tf]}$$

respectively. Then

$$\mathcal{S}=\left\{([Tf],[T],[NA])\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\parallel \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}[Tf]\ge 0,\hspace{0.17em}[NA]\ge 0,\hspace{0.17em}[T]\ge 0,\hspace{0.17em}\frac{[NA][Tf]}{K_{dN}+[Tf]}\le [T]-[Tf]\le \frac{[NA][Tf]}{K_{d1}+[Tf]}\right\}$$ (10.2)

is the region between and including the two surfaces S₁, S_N.

The surface S defined by

$$[T]=[Tf]+\frac{[NA][Tf]}{K_d(\overrightarrow{F},[Tf])+[Tf]}$$

must be between these two surfaces because K_d1 < K_d < K_dN. Likewise the remaining N-2 surfaces S_i defined by [T] = [Tf]+([NA][Tf])/(K_di +[Tf]) for i = 2, …, N-1 sit between these two surfaces. All N +1 surfaces intersect along the straight line ([Tf], [NA], [T]) = (0, [NA], [0]). When one fixes [NA] = [NA]₀ > say, the surfaces S_i intersect this plane in curves C_i, which are branches of hyperbolae. These curves are asymptotic to lines parallel to [T] = [Tf] as [Tf] becomes large. They have different limiting slopes [T]′(0) = 1 + [NA]/K_di at [Tf] = 0, . The surface S has limiting slope 1 + [NA]/K_d(F⃗, 0).

Depending on how one chooses [T]_r → 0 and determines [Tf]_r (from 3.12) and $\overrightarrow{F^{(r)}}$ (from (6.5)), one can obtain a limiting ratio [T]_r/[Tf]_r that is different from 1 + [NA]/K_d1, the desired limiting ratio for selection. (This cannot happen when s = 0.) The theorems give necessary and sufficient conditions on the sequence {[T]_r} in order to obtain the correct limit. Equation (3.12) defines a functional dependence of [Tf] on [NA], [T] as independent variables because the left hand side is a strictly increasing function of [Tf]. By means of implicit differentiation:

$$\begin{array}{l}\frac{\partial [Tf]}{\partial [NA]}=-\frac{[\{T:NA\}]}{[NA]}{\left(1+[NA]\sum _{i=1}^N\frac{F_i{K}_{di}}{{(K_{di}+[Tf])}^2}\right)}^{-1}<0,\\ \frac{\partial [Tf]}{\partial [T]}={\left(1+[NA]\sum _{i=1}^N\frac{F_i{K}_{di}}{{(K_{di}+[Tf])}^2}\right)}^{-1}>0.\end{array}$$ (10.3)

Therefore there is no extreme value for the free target in the region determined by [NA] > 0 and [T] > 0.

Likewise, using (3.9)

$$\frac{\partial K_d}{\partial [Tf]}=\left[\sum _{i=1}^N\frac{F_i}{{(K_{di}+[Tf])}^2}-{\left(\sum _{i=1}^N\frac{F_i}{K_{di}+[Tf]}\right)}^2\right]{(K_d+[Tf])}^2=S^2{(K_d+[Tf])}^2.$$ (10.4)

Viewing K_d = K_d([NA], [T]) after elimination of [Tf] from (3.9) and implicit differentiation again, we find

$$\frac{\partial K_d}{\partial [NA]}=S^2{(K_d+[Tf])}^2\frac{\partial [Tf]}{\partial [NA]},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial K_d}{\partial [T]}=S^2{(K_d+[Tf])}^2\frac{\partial [Tf]}{\partial [T]}.$$ (10.5)

It follows from (10.4), (10.5) and Schwarz’s inequality⁵ that the extreme value for K_d in $\mathcal{S}$ occur if and only if one of the fractions F_i vanish and the exception is unity, i.e. when F⃗ is a vertex of $\mathcal{T}$. When this happens, K_d([NA], [T]) = K_di for some i. The smallest value of K_d([NA], [T]) occurs when i = 1. In this case ([Tf], [T], [NA]) must be a point on S₁, one of the boundary surfaces, i. e. ([T] − [T f ])/[T] = [NA]/(K_d1 + [T f ] + [NA]). The maximum value of this expression, the maximum target efficiency, occurs at ([Tf], [T], [NA]) = (0, 0, [NA]) for fixed [NA] and increases to unity as [NA] → ∞.

11. Appendix B.Proofs of Theorems

Because the value of [NA] plays no role in the proofs of the theorems, we take [NA] = 1 in this section.

11.1. Proof of Theorem 1

If we strike the ratio $F_i^{(r+1)}/F_1^{(r+1)}$ we see that

$$\frac{F_i^{(r+1)}}{F_1^{(r+1)}}=\frac{K_{d1}+{[Tf]}_r{F}_i^{(r)}}{K_{di}+{[Tf]}_r{F}_1^{(r)}}.$$ (11.6)

We see that for i ≥ 2,

$$\frac{F_i^{(r+1)}}{F_1^{(r+1)}}÷\frac{F_i^{(1)}}{F_1^{(1)}}=\frac{{\prod }_{k=1}^r(K_{d1}+{[Tf]}_k)}{{\prod }_{k=1}^r(K_{di}+{[Tf]}_k)}<\frac{{\prod }_{k=1}^r(K_{d1}+{[Tf]}_k)}{{\prod }_{k=1}^r(K_{d2}+{[Tf]}_k)}<{\left(\frac{K_{d1}+{[T]}_1}{K_{d2}+{[T]}_1}\right)}^r<1$$ (11.7)

Because K_d2 ≤ K_di and the ratio (a + x) / (b + x) is increasing in x when a, b, x are all positive and a < b, except when i = 1, the coefficient of $F_i^{(r)}/F_1^{(r)}$ is bounded above by (K_d1 + [T]₁) / (K_di + [T]₁) < 1. Hence, i ≠ 1, lim_r→+∞ ${lim}_{r\to +\infty }{F}_i^{(r)}=0$. since the sums ${\sum }_i{F}_i^{(r)}=1$, this implies that ${lim}_{r\to +\infty }{F}_1^{(r)}=1$.

The convergence of the overall dissociation constants then follows from:

$$K_d(\overrightarrow{F^{(r)}},{[Tf]}_r)-K_{d1}=\frac{{\sum }_{i=2}^N(K_{di}-K_{d1})F_i^{(r)}/(K_{di}+{[Tf]}_r)}{{\sum }_{i=1}^N{F}_i^{(r)}/(K_{di}+{[Tf]}_r)}$$ (11.8)

since the denominators on the right hand side are all bounded away from zero by K_d1 and above by K_dN +[T]₁.

Conversely, if ${lim}_{r\to +\infty }{K}_d(\overrightarrow{F^{(r)}},{[Tf]}_r)-K_{d1}=0$, we must have $li{m}_{r\to \infty }{F}_i^{(r)}=0$ for i ≥ 2. This establishes the equivalence.

11.2. Proof of Theorem 2

Again we strike the ratio $F_i^{(r+1)}/F_1^{(r+1)}$ to find

$$\frac{F_i^{(r+1)}}{F_1^{(r+1)}}÷\frac{F_i^{(1)}}{F_1^{(1)}}=\prod _{k=1}^r\frac{(K_{d1}+{[Tf]}_k)(\epsilon K_{di}+{[Tf]}_k)}{(K_{di}+{[Tf]}_k)(\epsilon K_{d1}+{[Tf]}_k)}$$ (11.9)

If {[T]_r} is a convergent sequence with a nonzero limit, then the same is true of the sequence {[Tf]_r}. Thus we can assume that 0 ≤ [T]₀ ≤ [Tf]_r ≤ [T]₁. Because the function

$$f_i(x)=\frac{(K_{d1}+x)(\epsilon K_{di}+x)}{(K_{di}+x)(\epsilon K_{d1}+x)}$$

satisfies f_i(x) < 1 for 0 < x < ∞ if 0 < ε < 1, we know that on [[T]₀, [T]₁] there is a constant ℓ_i such that f_i(x) ≤ ℓ_i < 1. Consequently, we have ${lim}_{r\to \infty }{F}_i^{(r)}=0$ if i > 1. This implies that lim_{r → ∞} K_d(F⃗, [T f]_r) = K_d1 as before. Likewise, if this limit holds, then from (11.8) it follows that ${lim}_{r\to \infty }{F}_i^{(r)}=0$ for i ≥ 2.

11.3. Proof of Theorem 3

If [T]_r → 0, then [T f]_r → 0 and the functions f_i([T f]_r) converge to unity. Hence we cannot assume that we have selection in this case. Thus the selection of the sequence {[T]_r} is more delicate. We write [T]_r+1 = [T]_r(1 − s_r).

First we show that the sequence of vectors $\left\{\overrightarrow{F^{(r)}}\right\}$ converges to some vector and that the sequence $\{K_d(\overrightarrow{F^{(r)}},{[Tf]}_r)\equiv K^{(r)}\}$ converges to some limit, L.

We have again

$$\frac{F_i^{(r+1)}}{F_1^{(r+1)}}÷\frac{F_i^{(1)}}{F_i^{(1)}}=\prod _{k=1}^r\frac{(K_{d1}+{[Tf]}_k)(\epsilon K_{di}+{[Tf]}_k)}{(\epsilon K_{d1}+{[Tf]}_k)(K_{di}+{[Tf]}_k)}=G_{i,r}.$$

The k^thfactor in G_i,r can be written in the form

$$\frac{(K_{d1}+{[Tf]}_k)(\epsilon K_{di}+{[Tf]}_k)}{(\epsilon K_{d1}+{[Tf]}_k)(K_{di}+{[Tf]}_k)}=1+\frac{(1-\epsilon )(K_{d1}-K_{di}){[Tf]}_k}{(\epsilon K_{d1}+{[Tf]}_k)(K_{di}+{[Tf]}_k)}.$$ (11.10)

A theorem of analysis says that if |b_r| < 1, then the infinite product ${\prod }_{r=1}^{\infty }(1+b_r)$ converges to a non zero constant if and only if the series ${\sum }_{r=1}^{\infty }\mid b_r\mid$ is convergent. (This follows from the inequality ln(1 + |b_r|) ≤ |b_r| ≤ ln(1 + 2|b_r|) valid for 0 ≤ |b_(r)| ≤ 1.)

Recall that lim_{r → ∞}[T f]_r/[T]_r is positive and finite and suppose first that ${\sum }_{r=1}^{\infty }{\prod }_{k=1}^r(1-s_k)<\infty$, i.e. the numbers [T f]_r form the terms of a convergent series or equivalently,

$$\sum _{r=1}^{\infty }\frac{(1-\epsilon )(K_{di}-K_{d1}){[Tf]}_r}{(K_{di}+{[Tf]}_r)(\epsilon K_{d1}+{[Tf]}_r)}<\infty .$$ (11.11)

Then for each i, ${lim}_{r\to +\infty }{F}_i^{(r)}$ exists and is not zero.(The series in (11.11) will not converge if ε = 0.) Setting ${lim}_{r\to +\infty }{F}_i^{(r)}=B_i(\epsilon )>0$, it follows that

$$\underset{r\to +\infty }{lim}{K}_d(\overrightarrow{F^{(r)}},{[Tf]}_r)={\left\{\sum _{i=1}^N\frac{B_i(\epsilon )}{K_{di}}\right\}}^{-1}>K_{d1}.$$ (11.12)

Hence selection does not occur in this case.

Suppose next that ${\sum }_{r=1}^{\infty }{\prod }_{k=1}^r(1-s_k)$ diverges. Because the coefficients of $F_i^{(1)}/F_1^{(1)}$ are G_i,r and the series (11.11) is now divergent, we conclude that the infinite products G_i,r diverge to zero. Hence $F_i^{(r)}\to 0$ if i ≥ 2 and consequently $K_d(\overrightarrow{F^{(r)}},{[Tf]}_r)\to K_{d1}$. Thus selection occurs in this case.

Remark 3

It is of some mathematical interest to examine the total derivative of K_d as a function of F⃗, [T f] along the iteration trajectory in $\mathcal{T}\times \mathcal{S}$. We show that:

$$\frac{\partial K_d(\overrightarrow{F},[Tf])}{\partial [Tf]}\mathrm{\Delta }[Tf]+\sum _{i=1}^N\frac{\partial K_d(\overrightarrow{F},[Tf])}{\partial F_i}\mathrm{\Delta }{F}_i=-s[Tf]{\left(\frac{S}{\mathscr{H}}\right)}^2-[Tf]{\left(\frac{S}{\mathscr{H}}\right)}^2\left(\frac{(1-\epsilon )(K_d+[Tf])}{\epsilon K_d+[Tf]}\right).$$ (11.13)

where

$$S^2=\left(\sum _{i=1}^N\frac{F_i}{{(K_{di}+[Tf])}^2}\right)-{\left(\sum _{i=1}^N\frac{F_i}{K_{di}+[Tf]}\right)}^2,$$

and use this to establish a relationship between the terms of the series ${\sum }_{r=1}^{\infty }{\prod }_{k=1}^r(1-s_k)$ and the rate of convergence of the sequence $\{K_d((\overrightarrow{F^{(r)}},{[Tf]}_r))\}$ to its limit.

We see from (11.13) that the first term describes how the differential changes in $\mathcal{S}$. The second term describes how this differential changes in $\mathcal{T}$. However, the change is being driven by how [T f] → 0 at a rate that clearly depends on the background parameter ε. The closer ε is to unity, the less influential changes in of the F_i in $\mathcal{T}$ are on K_d.

In our iteration scheme, a sequence $\left\{\overrightarrow{F^{(r)}}\right\}$ is generated using the formulas involving the products G_i,r which tells us how to calculate the vector c→ and gives us specific information on the rule for determining $\mathrm{\Delta }\overrightarrow{F^{(r)}}=\overrightarrow{F^{(r+1)}}-\overrightarrow{F^{(r)}}$. Suppose therefore that $\overrightarrow{F^{(r)}}\to \overrightarrow{C}\in \mathcal{T}$ and [T]_r → 0. Then

$$\frac{1}{K^{(r+1)}+{[Tf]}_{r+1}}\to \sum _{i=1}^N\frac{c_i}{K_{di}}\equiv \mathscr{H}(\overrightarrow{c},0)$$ (11.14)

as r → +∞. Likewise, $\{K_d(\overrightarrow{F^{(r)}}),{[Tf]}_r\}\equiv K^{(r)}\to 1/\mathscr{H}(\overrightarrow{c},0)\equiv L$.

Using the shorthand ${\mathscr{H}}^{(r)}=\mathscr{H}(\overrightarrow{F^{(r)}}),{[Tf]}_r)$, we have

$${[Tf]}_r(1+{\mathscr{H}}^{(r)})={[T]}_r={[T]}_{r+1}+s_r{[T]}_r={[Tf]}_{r+1}(1+{\mathscr{H}}^{(r+1)})+s_r{[tf]}_r(1+{\mathscr{H}}^{(r)}).$$

Thus

$$\frac{{[Tf]}_{r+1}}{{[Tf]}_r}=(1-s_r)\frac{1+{\mathscr{H}}^{(r)}}{1+{\mathscr{H}}^{(r+1)}}=(1-s_r)\frac{({[Tf]}_{r+1}+K^{(r+1)})({[Tf]}_r+K^{(r)}+1)}{({[Tf]}_r+K^{(r)})({[Tf]}_{r+1}+K^{(r+1)}+1)}$$

and hence, for any index m

$$\frac{{[Tf]}_{r+m}}{{[Tf]}_r}=\prod _{l=1}^m\frac{{[Tf]}_{r+l}}{{[Tf]}_{r+l-1}}=\frac{({[Tf]}_{r+m}+K^{(r+m)})({[Tf]}_r+K^{(r)}+1)}{({[Tf]}_r+K^{(r)})({[Tf]}_{r+1}+K^{(r+m)}+1)}\prod _{l=1}^m(1-s_{l+r-1}).$$

The overall dissociation constants satisfy $K_d(\overrightarrow{F^{(r)}},{[Tf]}_r)\equiv K^{(r)}\to L\ge K_{d1}$ as [T f]_r → 0. Hence for all m and all sufficiently large r,

$$\frac{{[Tf]}_{r+m}}{{[Tf]}_r}\approx \prod _{l=1}^m(1-s_{l+r-1})$$ (11.15)

We abandon the round number index r temporarily for readability. We approximate ΔK_d to first order in ΔF_i, Δ[T f] directly from the equation $K_d=-[Tf]+1/(\mathscr{H}(\overrightarrow{F},[Tf]))$. The components of the gradient of K_d in these variables are:

$$\frac{\partial K_d}{\partial [Tf]}=\frac{{\mathscr{H}}^2+{\mathscr{H}}_{[Tf]}}{{\mathscr{H}}^2}=\frac{S^2}{{\mathscr{H}}^2}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial K_d}{\partial F_i}=\frac{-1}{(K_{di}+[Tf]){\mathscr{H}}^2}$$

where S² is defined in (10.3) and is positive unless one of the F_i = 1 and all the others vanish.

We write s = s_r, [T f] = [T f]_r, [T f]_r+1 = [T f]+ Δ[T f], $\overrightarrow{F^{(r)}}=\overrightarrow{F},\hspace{0.17em}\overrightarrow{F^{(r+1)}}=\overrightarrow{F}+\mathrm{\Delta }\overrightarrow{F}$ in order to calculate the total differential of K_d. We need formulas for ΔF_i and Δ[T f]. Recalling from (6.4) the definition of E_i there results:

$$\mathrm{\Delta }{F}_i=(E_i-1)F_i=\frac{[Tf](1-\epsilon )}{(\epsilon K_d+[Tf])}\frac{(K_d-K_{di})}{(K_{di}+[Tf])}{F}_i.$$

We have

$$K_d(\overrightarrow{F}+\mathrm{\Delta }\overrightarrow{F},[Tf]+\mathrm{\Delta }[Tf])-K_d(\overrightarrow{F},[Tf])\approx \frac{\partial K_d(\overrightarrow{F},[Tf])}{\partial [Tf]}\mathrm{\Delta }[Tf]+\sum _{i=1}^N\frac{\partial K_d(\overrightarrow{F},[Tf])}{\partial F_i}\mathrm{\Delta }{F}_i$$

Hence from equation (11.15) with m = 1,

$$\begin{array}{l}{\mathscr{H}}^2(\overrightarrow{F},[Tf])\mathrm{\Delta }{K}_d=S^2\mathrm{\Delta }[Tf]-\frac{[Tf](1-\epsilon )}{\epsilon K_d+[Tf]}\sum _{i=1}^N\frac{K_d-K_{di}}{{(K_{di}+[Tf])}^2}{F}_i,\\ =-s{S}^2[Tf]-\frac{[Tf](1-\epsilon )}{\epsilon K_d+[Tf]}\sum _{i=1}^N\frac{(-[Tf]+1/\mathscr{H})-K_{di}}{{(K_{di}+[Tf])}^2}{F}_i,\\ =-s{S}^2[Tf]-\frac{[Tf](1-\epsilon )}{\epsilon K_d+[Tf]}\left\{\frac{1}{H(\overrightarrow{F},[Tf])}\sum _{i=1}^N\frac{F_i}{{(K_{di}+[Tf])}^2}-\sum _{i=1}^N\frac{F_i}{(K_{di}+[Tf])}\right\},\end{array}$$

Finally, returning to the index notation:

$$K^{(r+1)}-K^{(r)}=-{[Tf]}_r{\left(\frac{S^{(r)}}{{\mathscr{H}}^{(r)}}\right)}^2\left(\frac{(1-\epsilon )(K^{(r)}+{[Tf]}_r)}{\epsilon K^{(r)}+{[Tf]}_r}+s_r\right).$$ (11.16)

Thus the terms of the sequence {K^(r)} decreases to L. Therefore for sufficiently large r

$$K^{(r)}-K^{(r+m)}=L^2{[Tf]}_r\sum _{l=1}^m\left(\frac{1}{\epsilon }-(1-s_{l+r})\right){\left(\frac{S^{(r+l)}}{{\mathscr{H}}^{(r+l)}}\right)}^2\left[\prod _{j=1}^l(1-s_{j+r-1})\right]$$

Letting m + ∞

$$\frac{K^{(r)}-L}{{[Tf]}_r}=L^2\sum _{l=1}^{\infty }\left(\frac{1}{\epsilon }-(1-s_{l+r})\right){\left(\frac{S^{(r+l)}}{{\mathscr{H}}^{(r+l)}}\right)}^2\left[\prod _{j=1}^l(1-s_{j+r-1})\right].$$ (11.17)

Thus we have an expression for $K_d(\overrightarrow{F^{(r)}},{[Tf]}_r)-L$ in terms of [T f]_r. The first coefficient on the right in (11.17) is bounded above by 1/ε and below by (1 − ε)/ε. Thus

$$\sum _{l=r+1}^{\infty }{\left(\frac{S^{(l)}}{{\mathscr{H}}^{(l)}}\right)}^2\prod _{j=r}^{l-1}(1-s_j)=\sum _{l=r+1}^{\infty }\frac{\partial K^{(l)}}{\partial [Tf]}\prod _{j=r}^{l-1}(1-s_j)$$

must be convergent for all large indices r and hence (since 1 − s_k ≤ 1) for every index r.

The sequence of coefficients $\{S^{(l)}/{\mathscr{H}}^{(l)}\}$ is convergent since F⃗^(r) → c→. Thus, if the series ${\sum }_{r=1}^{\infty }{\prod }_{k=1}^r(1-s_k)$ is divergent, $S^{(l)}L\approx S^{(l)}/{\mathscr{H}}^{(l)}\to 0$. That is, the divergence of the series forces the convergence of the iteration scheme to one of the vertices of $\mathcal{T}$ along one of the hyperbolic curves C_i defined in Section 10, Appendix A.

The role of ε on the absolute convergence of (11.17) is easily seen. When s_r = 1/(r + 1) and ε = 1, the series on the right in (11.17) will converge whether or not $S^{(l)}/{\mathscr{H}}^{(l)}\to 0$. (The reason is that the coefficients $S^{(l)}/{\mathscr{H}}^{(l)}$ are bounded above and the series $\sum l=r^{\infty }\frac{1}{l(l+r)l}$ is convergent.) As ε decreases from unity, the partial sums ${\sum }_{l=r}^m[1/\epsilon -(l+r-1)/(l+r)]1/l$ increase. Thus the coefficients $S^{(l)}/{\mathscr{H}}^{(l)}$ in the partial sums of (11.17) decrease more rapidly and hence, for the entire series, decrease more rapidly to zero as ε decreases. From Theorem 3 c₁ = 1 and L = K_d1.

If the series ${\sum }_{r=1}^{\infty }{\prod }_{k=1}^r(1-s_k)$ is convergent, nothing can be said about L or S² from (11.17). This is to be expected since from Theorem 3, selection cannot occur.

12. Appendix C. Matlab code

We include the programs we used here. Notice that only a single nonlinear equation is to be solved by Newton’s method.

13. Appendix D. A continuous analog of the SELEX iteration scheme

The mathematical and scientific literature abounds with examples of continuous time processes being modeled as the limit of discrete time processes as a time step is allowed to go to zero. Conversely, continuous processes are frequently approximated as discrete time processes.

In that spirit, we can think of the round number as a continuous parameter (time). Our goal is to determine the dynamical system of ordinary differential equations that corresponds to the selection process. We replace the discrete time notation $F_i^{(r)}$, s_r, [T]_r, [Tf]_r, $K_d^{(r)}$ by the continuous time notation F_i(r), s(r), [T](r), [Tf](r), K_d(r) and convert differences to time derivatives by replacing” difference quotients” of the form $(F_i^{(r+1)}-F_i^{(r)})/1$ by $(F_i^{(r+\mathrm{\Delta }r)}-F_i^{(r)})/\mathrm{\Delta }r$ and let Δr → 0. Thus, we should expect to have, for the continuous dynamics, the following:

$$\begin{array}{l}\frac{d{F}_i}{dr}=(E_i(r)-1)F_i(r)\\ \frac{dT}{dr}=-s(r)[T](r)\end{array}$$ (13.18)

where

$$E_i(r)=\frac{\epsilon K_{di}+[Tf](r)}{K_{di}+[Tf](r)}\frac{K_d(r)+[Tf](r)}{\epsilon K_d(r)+[Tf](r)},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{K}_d(r)=\frac{([T](r)-[Tf](r)+1)[Tf](r)}{[T](r)-[Tf](r)},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1=\sum _{i=1}^N{F}_i(r)$$

and where

$$\frac{1}{K_d(r)+[Tf](r)}=\sum _{i=1}^N\frac{F_i(r)}{K_{di}+[Tf](r)}=\frac{[T](r)-[Tf](r)}{[Tf](r)[NA]}=\mathscr{H}(r).$$

Then

$$\frac{F_i(r)}{F_1(r)}=\frac{F_i(1)}{F_1(1)}exp\left(-{\int }_1^r[E_1(s)-E_i(s)]ds\right).$$ (13.19)

Because the disassociation constants are ordered, [Tf](r) ≤ [T](r) ≤ [Tf](r)(1 + [NA]/K_d1) and [T](r) ≤ [T](1) and one can show that L[Tf](r) ≤ E₁(r) − E_i(r) ≤ U[Tf](r) where L, U are constants given by

$$L=\frac{(K_{d2}-K_{d1})(1-\epsilon )}{(K_{d2}+[T](1))(K_{d1}+[T](1))}\hspace{0.17em}\text{and\hspace{0.17em}}U=\frac{1-\epsilon }{\epsilon }\frac{K_{dN}-K_{d1}}{K_{dN}{K}_{d1}}$$

From these simple inequalities and the fact that $[T](r)=[T](1)exp\left(-{\int }_1^{r}s(\rho )d\rho \right)$ it follows immediately that F_i(r) → 0 for i ≥ 2 as r → +∞ if and only if

$${\int }_1^{\infty }exp\left(-{\int }_1^{r}s(\rho )d\rho \right)dr=+\infty .$$ (13.20)

Two cases obtain:

1. ${\int }_1^{\infty }s(\rho )d\rho <\infty$ and (13.20) holds. Then K_d(r) + [Tf](r) → K_1d + [Tf](r) so K_d(r) → K_d1. Consequently, [T](r) → T_∞ > 0 and [Tf](r) → [Tf]_∞ where K_d1(T_∞ − [Tf]_∞) = [Tf]_∞ (1 + T_∞ − [Tf]_∞), a quadratic easily solved for T_∞ > 0. In this case

   $$\underset{r\to +\infty }{lim}\frac{[T](r)-[Tf](r)}{[T](r)}=\frac{[NA]}{{[Tf]}_{\infty }+K_{d1}+[NA]}<\frac{[NA]}{K_{d1}+[NA]},$$

   i.e. maximum bound target efficiency is not obtained.

2. ${\int }_1^{\infty }s(\rho )d\rho =+\infty$. In this case we still must require that (13.20) holds. Then T_∞ = 0 = [Tf]_∞ and

   $$\underset{r\to +\infty }{lim}\frac{[T](r)-[Tf](r)}{[T](r)}=\frac{[NA]}{K_{d1}+[NA]},$$

   i.e. maximum bound target efficiency is obtained.

If we take s(r) = s₀/r² where s₀ ∈ (0, 1) then ${\int }_1^{\infty }s(r)dr=s_0<1$ and we have the first case. If we take s(r) = 1/r we are in the second case. In both cases, (13.20) holds. Notice that when s(r) = s₀ where s₀ ∈ (0, 1) the result says that selection cannot occur.

Finally, a calculation shows that

$$\frac{d{K}_d(r)}{dr}=-[Tf](r){[K_d(r)+[Tf](r)]}^2{(S(r))}^2\left(\frac{(1-\epsilon )(K_d(r)+[Tf](r))}{\epsilon K_d(r)+[Tf](r)}+s(r)\right)$$

where

$$S^2(r)=\left[\sum _{i=1}^N\frac{F_i(r)}{{(K_{di}+[Tf](r))}^2}-{\left(\sum _{i=1}^N\frac{F_i(r)}{K_{di}+[Tf](r)}\right)}^2\right].$$

This tells us that $K_d^{\prime }(r)/[Tf](r)\to 0$ if and only if selection occurs.

Finally, after a little algebra we find

$$\frac{F_1(1)}{[1-F_1(1)]exp\left(-L{\int }_1^r[Tf](s)ds\right)+F_1(1)}\le F_1(r)\le \frac{F_1(1)}{[1-F_1(1)]exp\left(-U{\int }_1^r[Tf](s)ds\right)+F_1(1)}.$$

From these inequalities it is possible to get upper and lower bounds on how large r must be in order that F₁(r) reach a fixed fraction. Notice that as ε increases to unity, these upper and lower bounds on r must recede to infinity as L, U → 0 with ε ↑ 1.