Nucleation-dependent Tau Filament Formation

Abstract

Filamentous inclusions composed of the microtubule-associated protein tau are found in Alzheimer disease and other tauopathic neurodegenerative diseases, but the mechanisms underlying their formation from full-length protein monomer under physiological conditions are unclear. To address this issue, the fibrillization of recombinant full-length four-repeat human tau was examined in vitro as a function of time and submicromolar tau concentrations using electron microscopy assay methods and a small-molecule inducer of aggregation, thiazine red. Data were then fit to a simple homogeneous nucleation model with rate constant constraints established from filament dissociation rate, critical concentration, and mass-per-unit length measurements. The model was then tested by comparing the predicted time-dependent evolution of length distributions to experimental data. Results indicated that once assembly-competent conformations were attained, the rate-limiting step in the fibrillization pathway was tau dimer formation. Filament elongation then proceeded by addition of tau monomers to nascent filament ends. Filaments isolated at reaction plateau contained ∼2 tau protomers/β-strand spacing on the basis of mass-per-unit length measurements. The model suggests four key steps in the aggregation pathway that must be surmounted for tau filaments to form in disease.

Tau is a microtubule-associated protein that normally functions as a monomer in conjunction with the microtubule cytoskeleton (1). In Alzheimer disease (AD),4 however, tau dissociates from its binding partner tubulin and aggregates to form filamentous inclusions within neuronal cell bodies and processes (2). Tau molecules that become subunits of filaments, termed protomers, adopt the parallel, in register cross-β-sheet structure typical of amyloid aggregates (3–5). On the basis of morphology and mass-per-unit length measurements, mature tau filaments, termed PHFs, consist of two protofilaments wound around each other (6, 7). Because PHF formation correlates with both neurodegeneration and cognitive decline (8, 9), tau is a useful marker for AD-associated events at the molecular and cellular levels.

AD is primarily a sporadic disease with a significant environmental contribution to relative risk. Therefore, the mechanisms through which tau fibrillizes may provide clues to the initiating stresses that precede neurodegeneration. Detailed characterization of the tau fibrillization reaction has been hampered, however, by the failure of full-length tau proteins to spontaneously aggregate over experimentally tractable time periods at physiological concentrations (10). This limitation has been overcome by the addition of anionic polymers such as heparin (11, 12) and micelle-forming anionic surfactants (13) that appear to support heterogeneous nucleation (i.e. the foreign anionic substance facilitates filament nucleation on its surface). Anionic inducers also facilitate seeding reactions (6, 14), suggesting they promote conformational changes in full-length tau protein separate from direct effects on putative nucleation events. Intramolecular conformational change has been found to be the rate-limiting step for spontaneous aggregation of poly-Gln peptides (15) and for cellular retinoic acid-binding protein 1 (16) as well, but in neither case have the subsequent steps in the aggregation pathway been elucidated. In fact, protein aggregation can be mediated by distinct pathways once assembly competent conformations form, reflecting either kinetic or thermodynamic barriers. In the classic equilibrium nucleation-elongation model elaborated for linear polymer formation, assembly-competent monomer is in rapid equilibrium with a thermodynamically unstable species termed the nucleus (17). Once the critical nucleus cluster size is reached, subsequent additions to the nascent filament ends are energetically favorable, and elongation proceeds efficiently. This pathway leads to peaked distributions of filament lengths early in the reaction time series followed by slow relaxation toward exponential distributions at equilibrium (18). Protein aggregation also can be mediated by energetically favorable steps in a “downhill” reaction. Both tubulin polymerization and transthyretin monomer aggregation are mediated by this pathway, which supports stable formation of small soluble aggregates (19, 20). This pathway also yields peaked filament length distributions (21). Finally, aggregation rates can be limited by secondary nucleation events, which occur on existing aggregates. The rate of sickle cell hemoglobin aggregation, for example, is limited by secondary nucleation along the length of nascent fibrils, resulting in time-dependent increases in filament mass but not length (22).

It is not clear which of these mechanisms mediate tau aggregation once assembly-competent conformations are populated in part because of its dependence on exogenous anionic inducers (10). For example, heparin strongly binds tau monomer at typical assay ionic strength (24), and so the extent of aggregation depends in part on the heparin/tau ratio (25, 26). Recently, we showed that the barrier to spontaneous aggregation of full-length tau proteins can be overcome by the addition of small-molecule fibrillization agonists such as thiazine red (27). These agents, which can stabilize aggregation-prone protein conformations (28), drive full-length tau aggregation at submicromolar concentrations in the absence of tau point mutations, truncations, or macromolecular inducers such as heparin. These data suggest that adoption of assembly competent conformations, perhaps associated with enriched β-sheet content, can be driven by small diffusible ligands in a process that approximates homogeneous nucleation (i.e. that the presence of inducer can be neglected). Consistent with this hypothesis, the extent of tau aggregation in the presence of thiazine red does not depend on tau/thiazine red ratios (27). Furthermore, the resultant tau filaments are relatively well separated and amenable to assay by electron microscopy methods (27). These assays are time-consuming (29), but the resultant length distribution data can be used to assess the contribution of secondary pathways and also to provide an independent check on rate constants deduced from time-dependent evolution of filament mass (21, 30).

Here we characterize the fibrillization pathway for full-length htau40 in the presence of thiazine red under near physiological buffer conditions and reducing environment using electron microscopy methods. Results indicate that under these conditions the assembly reaction can be approximated by a simple nucleation-dependent mechanism.

EXPERIMENTAL PROCEDURES

Materials—Recombinant polyhistidine-tagged human htau40 (31) was prepared as described previously (32). Aggregation inducer thiazine red (Chemical Abstract Service registry number 2150-33-6) was obtained from TCI America (Portland, OR).

Tau Fibrillization Assays— htau40 (0.4, 0.5, 0.6, 0.8, and 1 μm) was incubated at 37 °C without agitation in assembly buffer (10 mm HEPES, pH 7.4, 100 mm NaCl, and 5 mm dithiothreitol) with aggregation induced by the addition of thiazine red (100 μm final concentration). Aliquots were removed at the indicated time points, fixed with glutaraldehyde, adsorbed onto Formvar/carbon-coated grids, stained with 2% uranyl acetate, and examined by transmission electron microscopy as described previously (29). Adsorbed filaments >10 nm in length were quantified from at least 3 fields captured for each tau concentration and time point using Optimas 6.5 imaging software (Media Cybernetics, Silver Spring, MD). Interfacial filament concentration (Γ_f) is defined as the summed lengths of all completely resolved filaments per field and is reported ±S.D. Filament length distributions were calculated using 10-nm wide bins. Data points above the distribution mode were fit to the negative exponential function (22),

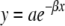(Eq. 1)

where y is the percentage of all filaments in a bin of length interval x, and β is a semi-logarithmic constant reported in units of length^-1 ± S.E.

Dissociation Rates—Tau filaments prepared as described above (1.6 μm tau, 24-h aggregation) were diluted 10-fold into assembly buffer and incubated at 37 °C. Aliquots were withdrawn as a function of time up to 5 h post-dilution and subjected to electron microscopy assay for filament length. After the disaggregation time series was fit to an exponential decay function to obtain k_app, the pseudo-first order rate constant describing the time-dependent decrease in filament length, the dissociation rate constant k_e- was estimated as described previously (33, 34).

STEM Analysis—Tau filaments prepared as described above (8 μm tau; 24-h aggregation) were gel-filtered through Sephacryl S500 beads (pre-equilibrated in 10 mm HEPES, pH 7.4, 100 mm NaCl) to remove unincorporated protein monomers. Filtered samples were then flash-frozen in an ethanol/dry ice bath and sent to Brookhaven National Laboratory (Upton, NY) for imaging. Mass per unit length was measured for filaments relative to a TMV standard using the program PC Mass 29 as described previously (7).

Kinetic Analysis—Aggregation time series were fit to a scheme that included equilibrium nucleation (Scheme 1) and monomer addition (elongation, Scheme 2) steps,

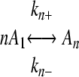SCHEME 1

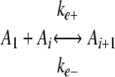SCHEME 2

where A₁ represents assembly competent tau monomer, where A_n represents the thermodynamic nucleus of cluster size n (17), defined as the least stable species reversibly interconverted with assembly competent monomer by forward and reverse rate constants k_n+ and k_n-, and where A_i represents aggregates >n in size that extend through the addition of activated monomers with forward and reverse rate constants k_e+ and k_e-. The rate constants do not distinguish between filament ends and, therefore, correspond to the overall rate constants for both ends. The term seed refers to the aggregate species n + 1, where the rate constants describing monomer association/dissociation change from k_n+/k_n- to k_e+/k_e- (35).

Nucleus cluster size was estimated from initial aggregation rate (i.e. the first third of the progress curve) by plotting total filament length as a function of t² as described by Ferrone (17),

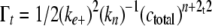(Eq. 2)

where Γ_t is total filament length adsorbed on assay grids at time t, K_n is a dissociation equilibrium constant describing the monomer-nucleus equilibrium, c_total is the bulk tau concentration, and n is the nucleus cluster size. Plots of Γ_t as a function of t² yield curves with slope m,

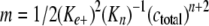(Eq. 3)

Nucleus cluster size was estimated from double-log replots of m versus c_total according to the function

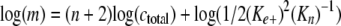(Eq. 4)

where the replot slope and y intercept provided estimates of n + 2 and log(½(k_e+)²(K_n)^-1), respectively.

To model the tau fibrillization time series, data were first converted from total filament length to molar concentration using the estimated critical concentration, K_crit. Because K_crit represents the concentration of monomer (c₁) remaining unincorporated into filaments at reaction plateau (36), it was used to estimate protomer concentration, c_p^*, by assuming that all protein above the critical concentration formed aggregates,

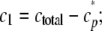(Eq. 5)

The relationship between Γ_f and c_p^* was then used to calibrate c_p^* for each individual time point. Data were then fitted to the simplified homogeneous nucleation scheme of Wegner and Engel (37),

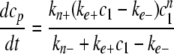(Eq. 6)

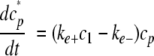(Eq. 7)

where c_p represent tau filament concentration (37). Parameter estimates were obtained by fitting experimentally determined values of c_total, c_p^*, and k_e- to Equations 5, 6, 7 in JACOBIAN™ modeling software (Numerica Technology, LLC, Cambridge, MA). The simulation yielded estimates of k_n- and k_n+, with the ratio k_n-/k_n+ recorded as K_n.

Simulation of Tau Fibrillization Dynamics—To simulate the time-dependent evolution of length distribution, a system of ordinary differential equations was derived assuming reversible association of monomers (30, 35),

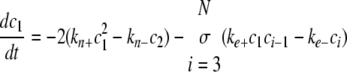(Eq. 8)

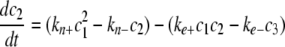(Eq. 9)

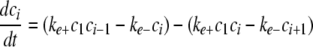(Eq. 10)

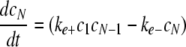(Eq. 11)

where c_i is the concentration of filaments of length i protomers. The number of equations was limited to N = 500, whereas tau concentrations were fixed by c_total and the conservation condition

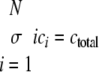(Eq. 12)

The relative concentration of each species from c₁ to c_N as a function of time was calculated in XPP (University of Pittsburgh, Pittsburgh, PA) using Equations 8, 9, 10, 11, 12 and experimentally estimated values for parameters k_e+, k_e-, k_n+, and k_n-, and c_total. Data from the XPP output matrix were visualized in MATLAB (The Mathworks, Natick, MA).

RESULTS

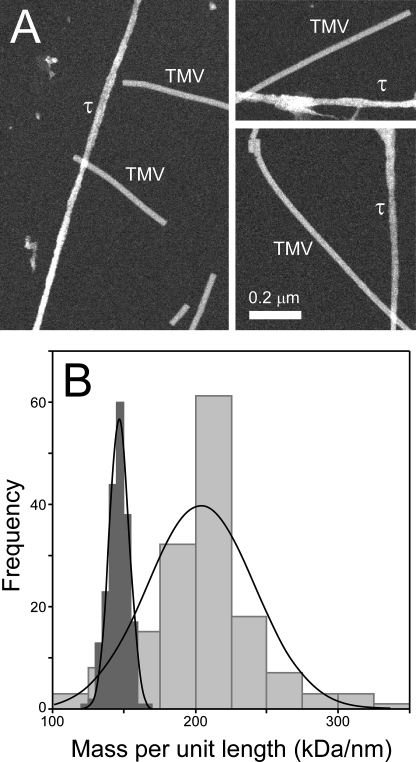
Initial Characterization—Thiazine red and other small-molecule tau aggregation agonists induce the formation of tau filaments with twisted ribbon morphology (27). To characterize this filamentous morphology, the mass-per-unit-length of filaments formed from htau40 in the presence of thiazine red was estimated by STEM using TMV as calibrant. Mean mass per unit length of TMV was measured as 145 ± 7 kDa/nm (200 observations) with a value of 205 ± 38 (151 observations) for tau filaments (Fig. 1). The established value of 131 kDa/nm for TMV was used to calibrate these values (7), resulting in an estimated mass-per-unit length for thiazine red-induced tau filaments of 185 ± 34 kDa/nm. On the basis of monomer molecular mass (48,013 Da (38)), this value corresponds to 3.85 ± 0.71 molecules per nm or 1.81 ± 0.33 molecules per β strand of a cross-β-sheet polymer and is in general agreement with recent estimates for authentic brain-derived PHFs (39) and synthetic Aβ_1–40 filaments (40). Thus, thiazine red-induced filaments resembled mature filaments composed of two protofilaments with respect to mass-per-unit length.

FIGURE 1.

STEM analysis. htau40 (8 μm) was incubated in assembly buffer without agitation in the presence of 100 μm thiazine red for 24 h at 37 °C. Samples were then gel-filtered, flash-frozen, and subjected to STEM analysis along with TMV standard as described under “Experimental Procedures.” A, STEM images from which mass-per-unit length measurements were made. B, histograms relating frequency to mass-per-unit length for tau filaments (151 observations; light graybars) and TMV (200 observations; dark gray bars). Raw average mass-per-unit length values for tau filaments (205 ± 38 kDa/nm) and TMV (145 ± 7 kDa/nm) were estimated assuming Gaussian distributions (solid lines).

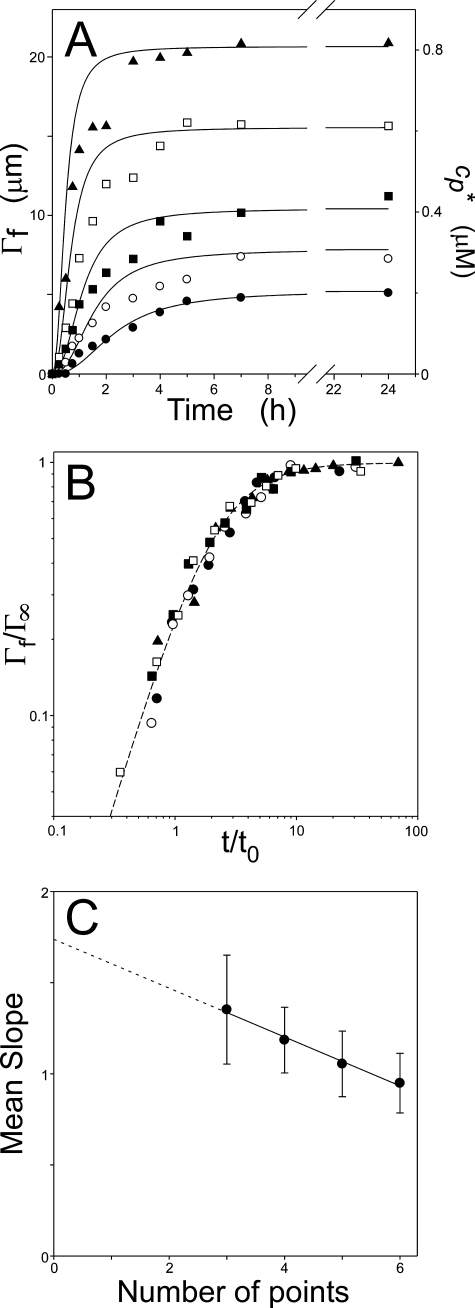
To characterize the tau aggregation reaction, 0.4–1.0 μm bulk tau concentrations were incubated in the presence of thiazine red inducer for 24 h under near physiological conditions of pH, ionic strength, and reducing environment. These concentrations were chosen because they were above the minimal tau concentration necessary to support the reaction (27) but within normal physiological bulk tau concentrations (41, 42). Samples were not agitated in an effort to minimize shear forces that can foster filament breakage. Time-dependent fibrillization of tau was then quantified in units of filament number and length using transmission electron microscopy methods (29). At each tested concentration, the total length of all filaments increased to a plateau within ∼4 h (Fig. 2A), with the rate of formation and plateau both dependent on tau concentration. To gain preliminary information on mechanism, each time series was normalized on the basis of plateau length (Γ_∞) and a characteristic time (t₀) as described by Flyvbjerg and Jobs (21) and plotted on double-log axes. The resultant normalized curves collapsed on one another (Fig. 2B), indicating that each time series could be related to another by simply scaling the data. These results indicate that a single aggregation pathway dominated tau fibrillization kinetics under assay conditions and that it was operative at all assay concentrations (21).

FIGURE 2.

Time dependence of thiazine red-mediated tau fibrillization. A, recombinant full-length human tau (•, 0.4 μm; ○, 0.5 μm; ▪, 0.6 μm; □, 0.8 μm; ▴, 1 μm) was incubated at 37 °C in the presence of 100 μm thiazine red inducer, with aliquots removed and assayed for filament formation by electron microscopy. Each point represents the total length of all filaments per field (Γ_f) averaged from three negatives at the indicated incubation time, whereas the solid lines represent the best fit of all time series to an equilibrium nucleation model constrained so that n = 2, k_e+ = 9.5 × 10⁴ m^-1 s^-1, and k_e- = 0.019 s^-1 (see “Results” for details). B, demonstration of data collapse. The data from panel A were replotted with normalized axes Γ_f/Γ_∞ versus t/t₀, as described previously (21), except that the characteristic time, t₀, corresponded to the time when each series was 37% complete. C, the number of intermediate assembly stages of the nucleus, k, was estimated from the initial slopes of each time series shown in panel B by fitting the first 3–6 data points of each time series to a linear regression, then replotting the average slope of those lines (±S.E. of the estimate) against the number of data points examined (19). The solid line represents best fit of the data points to a linear regression, which was extrapolated to zero to yield 1.73 ± 0.19 as an estimate of k + 2. Therefore, k ∼ 0.

When aggregation is mediated by monomer addition, the initial slopes of the double-log normalized time series reflect k, the number of slow assembly steps in the pathway (21). Pathways mediated by small soluble aggregates, such as tubulin polymerization, initially proceed through multiple isodesmic steps (i.e. mediated by sequential, noncooperative addition of monomers (43)). Thus, k > 0 in these cases and double-log slopes, which are proportional to k + 2, are steep (21). When the slopes from Fig. 2B were plotted as shown in Fig. 2C (19) and subjected to linear regression, k + 2 was estimated as 1.73 ± 0.19. Thus, k ∼ 0 for the tau aggregation reaction, which is consistent with an equilibrium nucleation reaction (21) and inconsistent with a pathway that is purely isodesmic or mediated by small soluble aggregates.

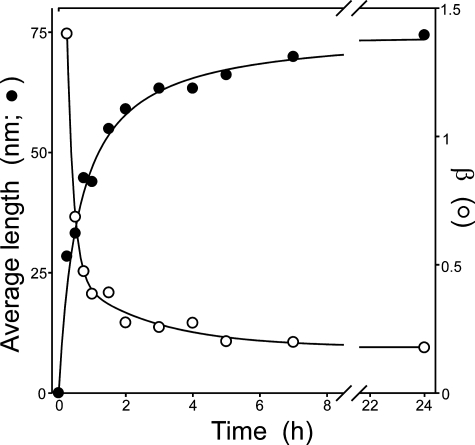
Linear aggregation reactions are characterized in part by a continuous increase in average filament length as the reaction approaches equilibrium (18, 43). However, this relationship breaks down under conditions where secondary reactions are rate-limiting, such as the secondary nucleation of aggregates along nascent hemoglobin S filaments (22). Therefore, to determine whether tau aggregation rate was limited by secondary nucleation, the average length of tau filaments was plotted as a function of time for each time series. The results showed that average filament length increased monotonically with time at all bulk tau concentrations (shown for 1 μm tau only; Fig. 3). However, electron microscopy methods cannot distinguish aggregates smaller than 10 nm in length and, therefore, underestimate filament number and overestimate average length. To avoid potential bias in average length measurements, the parameter β (Equation 1), which describes the exponential length distribution above the distribution mode (22), was estimated as well. Consistent with increasing average length, β decreases with time in equilibrium nucleation but not secondary nucleation reactions (22). Results showed that β decreased with time (shown for 1 μm tau only; Fig. 3), consistent with an equilibrium nucleation mechanism and contrary to the behavior of secondary nucleation. Overall, the initial characterization of reaction time series and filament length distributions were inconsistent with pathways mediated by small soluble aggregates or secondary nucleation, whereas the k value of ∼0 implicated an equilibrium nucleation mechanism.

FIGURE 3.

Filament length distributions. Average filament length (•) and β (the log-linear slope of the length distribution above the mode) (○) were determined for each time point in the 1 μm htau40 time series. Average length increased in a time-dependent manner with a concurrent decrease in β. The pattern is consistent with an equilibrium nucleation reaction but not secondary nucleation along filament lengths.

Model Constraints—The strategy for testing this hypothesis was to establish constraints for key rate parameters, to then derive estimates of rate constants by mathematical modeling of the time series, and finally to test the model by characterizing the evolution of filament length distribution as a function of time. The first reaction component examined was the nucleus, which represents the least stable species in the aggregation pathway (17). To estimate the nucleus cluster size, the exponential portion of each time series was replotted against t² and subjected to linear regression (Fig. 4A). This approach is appropriate for an equilibrium nucleation-elongation mechanism (17). The slopes of these fits were then plotted against protein concentration in double-log format as specified by Ferrone (17) (Equation 3) (Fig. 4B). The slope of this plot is proportional to n + 2, where n is the number of tau molecules in the nucleus. The calculated slope was 3.8 ± 0.2, indicating the nucleus consisted of 1.8 ± 0.2 tau molecules. These data suggest that the tau nucleus is a dimer.

FIGURE 4.

The tau nucleus is a dimer. A, the time series from Fig. 2A was replotted as a function of t². Each data point represents total filament length per field ±S.D. for the initial points of the time series, whereas each line represents best fit of the data points to a linear regression constrained to pass through the origin. B, the resultant slopes (±S.E. of the estimate) were then replotted as a function of bulk tau concentration in double-log format. The slope of this replot (3.8 ± 0.2) was taken as an estimate of n + 2, where n represents nucleus cluster size. The tau nucleus approximates a dimer.

Constraint of the elongation reaction began with estimation of the critical concentration (K_crit), a characteristic feature of nucleation-elongation reactions. It is defined as (36):

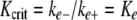(Eq. 13)

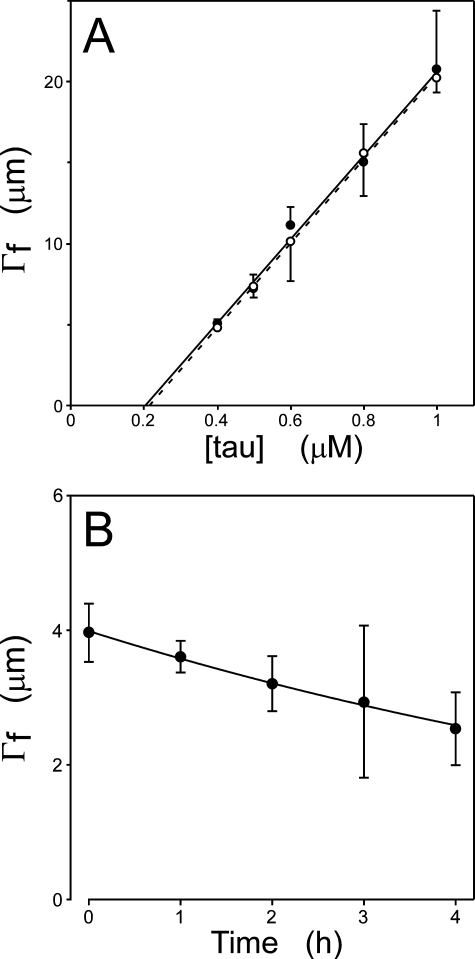
where K_crit is the critical concentration, and k_e- and k_e+ are the rate constants for protein monomer dissociation from and association with filament ends, respectively, assuming a simple reversible single step binding model. Therefore, K_crit approximates K_e, the equilibrium dissociation constant for filament elongation. Because K_crit also represents the highest protein monomer concentration that does not support aggregation (36), it can be estimated from the abscissa intercept of the tau concentration dependence of plateau fibrillization (Fig. 5A). Measurements at 7 h (0.21 ± 0.03) and 24 h (0.20 ± 0.02) were not significantly different (p < 0.05), suggesting that the reaction plateau was reached within 7 h and that the K_crit for tau aggregation in the presence of thiazine red was ∼200 nm.

FIGURE 5.

Estimation of K_crit and k_e-. A, plateau filament lengths from Fig. 2A were replotted as a function of bulk tau concentrations at 7 (○) and 24 h (•). Each data point represents total filament length per field ± S.D. (n = 3 observations), whereas each line (dashed, 7 h; solid, 24 h) represents linear regression of the data points. K_crit was estimated from the abscissa intercept of each regression line. B, tau filaments were prepared (1.6 μm htau40, 24 h at 37 °C), then diluted 10-fold into assembly buffer containing thiazine red. The resultant disaggregation was followed as a function of time by electron microscopy. Each data point represents total filament length per field ± S.D. (n = 3 observations), whereas the solid line represents best fit of the data points to an exponential decay function. The first order decay constant, k_app, was estimated as 3.0 ± 0.1 × 10^-5 s^-1.

To estimate k_e-, tau filaments assembled for 24 h were diluted 10-fold in assembly buffer containing thiazine red but no tau protein, and the time-dependent loss of filament length was measured by electron microscopy. Loss of filament length was first order as predicted for endwise depolymerization from a Poisson-like length distribution (33), with apparent first order rate constant (k_app) of 3.0 ± 0.1 × 10^-5 s^-1 (Fig. 5B). On the basis of the relationship between tau mass and filament length (Fig. 1), the dissociation elongation constant k_e- was then derived from k_app as 0.019 s^-1. On the basis of K_crit and Equation 13, k_e+ was calculated as ∼9.5 × 10⁴ m^-1s^-1.

Once k_e+ was estimated, a preliminary estimate of K_n was obtained from the slope and y intercept of Fig. 4B and Equation 4 as described previously for poly-Gln peptide Q₄₇ (15) and cellular retinoic acid-binding protein 1 (16) aggregation. The method is somewhat imprecise, however, because it involves extrapolation in double-log format. Upon conversion of lengths into c_p^*, the Fig. 4B slope of 3.8 ± 0.2 yielded a y intercept of 9.5 ± 1.5, which on the basis of Equation 4 corresponded to K_n values ranging from ∼10 to 1000 mm. This preliminary estimate indicates that K_n is 4–6 orders of magnitude larger than the equilibrium dissociation constant for elongation (approximated by K_crit; Fig. 5A). Together, the above estimates served to constrain n, K_n, k_e+, and k_e- for modeling studies.

Mathematical Simulation—Tau aggregation was simulated using the approximation of Wegner and Engel (37), which was explicitly derived for a dimeric nucleus and monomer addition. The model simplifies the family of differential equations (Equations 8, 9, 10, 11, 12) describing nucleation and extension to just two equations (Equations 6 and 7) relating c_p^* (tau protomer concentration) and c_p (tau filament concentration) to c_total (bulk tau concentration). Length measurements were converted to molar units by assuming all tau above K_crit was fibrillar and all tau below K_crit was a monomer having concentration c₁ (Fig. 2A). Parameter c_p^* was then calculated from c₁ and c_total at each assay point using Equation 5. The time series in molar units was then fit to Equations 5, 6, 7 using parameters constrained as established above except for K_n, which was allowed to vary between 10 and 1000 mm. The simulation converged at K_n = 12 mm and yielded the family of curves shown in Fig. 2A. These data show that the time series fit an equilibrium nucleation mechanism, a dimeric nucleus, and rate parameters estimated from direct experimentation. The final values for all parameters are summarized in Table 1.

TABLE 1.

Kinetic parameters in the presence of thiazine red

Parameter	Estimate
Nucleation reaction
n	1.8 ± 0.2
Kn (m)	1.2 × 10–2
Extension reactiona
Ke (m)	2.0 ± 0.2 × 10–7
ke– (s–1)	1.9 ± 0.2 × 10–2
ke+ (m–1 s–1)	9.5 ± 1.4 × 104
Thermodynamicsa
σ	1.7 × 10–5
ΔGσ (kcal/mol)	6.8

^aOverall constants reflecting events at both filament ends

The cooperativity of the reaction, σ, was quantified from K_e/K_n as ∼1.7 × 10^-5. Thus, the free energy difference between the nucleation and elongation reactions (ΔG_e - ΔG_n =ΔG_σ =-RTlnσ), which represents the stabilizing energy that accompanies contacts formed in the elongation step, was -6.8 Kcal/mol. These data are consistent with a cooperative reaction mechanism where elongation is strongly favored over nucleation.

Testing the model; Tau Fibrillization Dynamics—Although equilibrium length distribution depends on σ (18, 43), the rate at which the length distribution evolves is a function of the same rate constants that dictate the time-dependent formation of c_p^* (30). Therefore, analysis of length distribution can be used to check the consistency of rate constants established on the basis of c_p^* measurements alone (21). The distribution of filament lengths arising from equilibrium nucleation reactions evolves in three phases with distinct time scales (30). The first phase is distinguished by the rapid formation of a peaked length distribution, which is characterized by a mode. During this period, the concentration of seeds transiently reaches a maximum as the total filament concentration (c_p) is established. The second (propagation) phase is dominated by filament polymerization and is characterized by migration of the peaked distribution to longer lengths until the monomer pool is depleted (i.e. until c₁ ∼ K_crit). The final (distributive) phase involves the slow redistribution of monomers among filaments and results in the relative peak height of the distribution mode decreasing as the distribution broadens and skews toward longer lengths.

To simulate tau fibrillization dynamics, the experimental parameters summarized in Table 1 were incorporated into a family of differential equations describing mass-action kinetics for monomer addition and release (Equations 8, 9, 10, 11, 12). At 1 μm bulk tau concentration, the simulation predicted rapid formation of a peaked distribution skewed toward shorter lengths and a propagation phase that neared completion within 45 min (supplemental Movie 1). The time series was characterized by a gradual decrease in relative distribution mode height and increases in maximum filament lengths to >300 protomers/filament after 24 h of incubation (Fig. 6A). These dynamics corresponded to rapid equilibrium conditions and did not change substantially when K_n was held constant, whereas k_n+ and k_n- were varied in tandem above thresholds of 5 m^-1 s^-1 and 0.06 s^-1, respectively.

FIGURE 6.

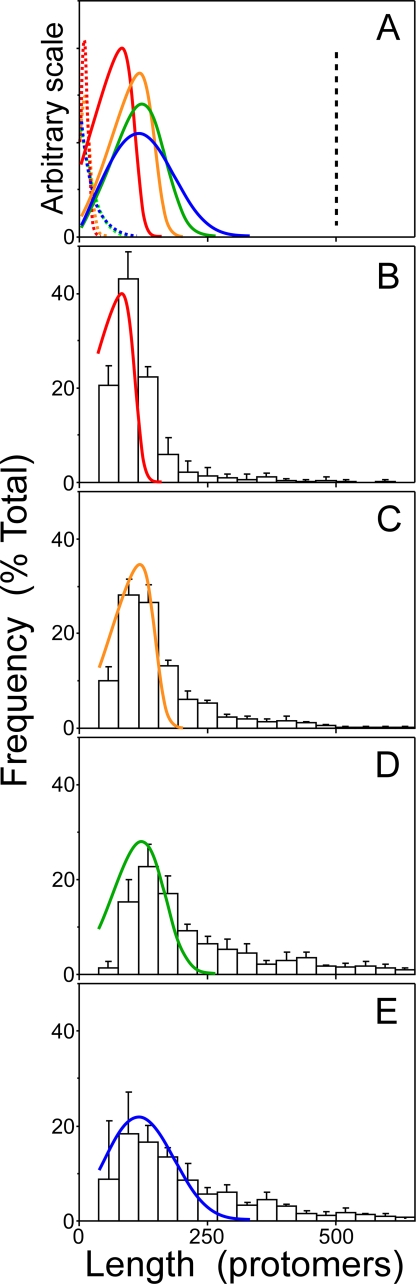
Tau filament length distributions. The time-dependent evolution of length distribution was calculated for 1 μm tau from the parameters in Table 1 in conjunction with Equations 8, 9, 10, 11, 12 (N = 500) as described under “Experimental Procedures.” A, two-dimensional slices through resultant time courses at 0.5 (red), 1 (orange), 7 (green), and 24 h (blue) are plotted, where each line represents relative frequency of filament length in units of protomers. For a nucleation-dependent mechanism where n = 2, calculated length distributions predicted rapid formation of a stable peaked distribution followed by monotonously decreasing relative mode height as a function of time (solid lines). Adjusting n above or below a value of 2 greatly modified the simulation. For example, under isodesmic conditions (no nucleation step, k_e- = 0.019 s^-1, k_e+ = 10⁶ m^-1 s^-1), length distributions shifted toward shorter lengths, so that no filament exceeded a length of 100 protomers (dotted lines). In contrast, increasing n to 3 (while using nucleation and elongation constants from Table 1) shifted the distribution so that all filaments aligned at the top limit of the calculated distribution range (N = 500), indicating that all filaments were at least 500 protomers in length at all time points between 0.5–24 h (shown as a single dashed line). The simulations predict that length distribution reflects aggregation mechanism. B–E, lengths of filaments >10 nm formed as function of time (B, 0.5 h; C, 1 h; D, 7 h; E, 24 h) from 1 μm tau were measured and segregated into 10-nm bins. The relative frequency of each bin relative to the total number of filaments in the sample was then calculated and superimposed on slices prepared from the calculated length distributions shown for n = 2 in panel A above. The calculated length distribution for this condition approximates experiment-derived mode and distribution skew.

To compare these predictions to experimental distributions, the lengths of all measured filaments at each point in the 1 μm tau time series were measured and segregated into 10-nm bins. The number of filaments in each bin was then determined, plotted in units of relative frequency (i.e. the number of filaments per bin divided by the total number of filaments in all bins), and finally overlaid with predicted length distributions calculated at 0.5-, 1-, 7-, and 14-h time points (Figs. 6, B–E). Results showed that the simulations approximated the experimental distribution mode, with frequency correctly skewed toward shorter lengths at early time points and toward longer lengths at 24 h. They also captured the monotonic decrease in relative mode height over time. Quantitatively, however, the simulations slightly underestimated experimental filament lengths, which were nearly exponential above the mode and also the duration of the propagation phase.

Two additional simulations were conducted to assess the sensitivity of filament length dynamics to aggregation mechanism. When the experimentally determined value of k_e- (Table 1) was introduced into a simple isodesmic reaction scheme (43), calculated length distributions (Fig. 6A) were skewed toward short filament lengths at all values of k_e+ approaching the diffusion limit (k_e+ = 10⁶ m^-1 s^-1). These data show that an isodesmic mechanism can accommodate the formation of small aggregates but is not compatible with experimentally determined length distributions. In contrast, simulations incorporating a trimeric nucleus (i.e. n = 3) predicted the formation of filaments far longer than those observed experimentally (Fig. 6A). These simulations show that length distribution is a sensitive test of aggregation mechanism and, when coupled with experimentally derived rate constraints, is capable of resolving differences in nucleus cluster size at least up to n = 3. Overall, simulations of length dynamics supported the hypothesis that thiazine red mediated tau aggregation proceeded through an equilibrium nucleation mechanism involving a dimeric nucleus and extension by monomer addition.

DISCUSSION

Although full-length recombinant tau protein resists aggregation under near physiological buffer conditions and submicromolar protein concentrations, it efficiently forms filaments with the mass-per-unit length of authentic PHF in the presence of thiazine red. As shown here, the induced aggregation pathway approximates equilibrium nucleation kinetics. This implies that thiazine red stabilizes amyloidogenic conformations of tau that are capable of spontaneous aggregation, as proposed previously for Congo red acting on immunoglobulin light-chain variable domains (28). If correct, then the conformational change must be rapid relative to the time course of aggregation and involve the majority of tau molecules in solution. The high molar ratio of thiazine red to tau protein used herein makes these assumptions reasonable. Once assembly-competent conformations are adopted, the rate-limiting step in the reaction becomes dimerization, with subsequent aggregate growth occurring through monomer addition.

This scheme is in qualitative accordance with the observed concentration dependence of the reaction and resultant length distributions despite methodological limitations. First, the electron microscopy-based assay method used here does not capture small filaments less than 10 nm in length. This introduces a systematic error that decreases in magnitude as filaments lengthen. For example, calculated length distributions for 1 μm tau predict that use of a 10-nm cutoff underestimates c_p^*by ∼28% at 15 min but by only ∼1% at 24 h. This error, which is common to assay methods based on size such as filtration (44) and ultracentrifugation (45), influences kinetic parameters and the quality of fit to time series data at early time points. Second, the equilibrium nucleation model does not include filament breakage or end-to-end annealing, both of which are required to rationalize experimental length distributions of actin polymers (46). End-to-end annealing of tau filaments, which has been observed to occur over a period of days under non-reducing conditions (47), would have the effect of biasing length distributions toward longer lengths. Although cross-β-sheet-containing filaments experience slow, length-dependent breakage in acidic solution (48), tau protofilaments incubated under near physiological conditions in the absence of agitation exhibit little detectable breakage over at least 19 h (49). To the extent that they occur, both annealing and breakage reactions are predicted to be slow. Third, the current model is based on the simple equilibrium nucleation scheme of Oosawa and Asakura (18), which was derived assuming that distinct pairs of rate constants govern the nucleation and extension reactions. More recent modeling of actin polymerization suggests the pathway is more accurately represented by three pairs of rate constants that reflect the intermediate characteristics of actin trimer (50). Energy calculations suggest that the early stages of amyloid formation may likewise be mediated by a gradient of rate constant pairs (51). Additional slow steps beyond dimerization would be expected to shift simulated length distributions toward longer lengths. Finally, the model neglects side reactions, such as the formation of species off the aggregation pathway. These would be expected to contribute to monomer depletion and, therefore, to change aggregation kinetics and filament length distributions. The simple nucleation-elongation scheme elaborated here is a starting point for incorporating these complications into the tau aggregation model.

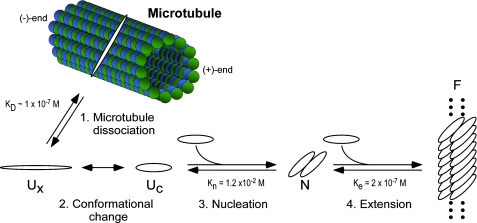
Implications for Tau Aggregation in Vivo—The aggregation pathway described above predicts that four principal steps mediate tau lesion formation in disease (Fig. 7). First, tau must dissociate from microtubules so that cytosolic concentration can exceed the minimal tau concentration necessary to support aggregation (i.e. K_crit). The binding affinity between full-length recombinant tau isoforms and tubulin polymer is in the 15-100 nm range (52, 53). In the presence of 20 μm intracellular tubulin dimer concentration (54), 1 μm tau would be expected to be >99% bound to tubulin, and free concentrations (<10 nm) would be inadequate to support aggregation. However, binding affinity is modulated by post-translational modifications such as phosphorylation (55, 56), which serves as a gatekeeper to control the amount of free tau available for aggregation. Tau phosphorylation inhibitors may decrease neuritic lesion formation in part by blocking this step (57).

FIGURE 7.

Hypothetical model of tau fibrillization in disease. Normal tau binds tightly to microtubules but dissociates upon phosphorylation to form free tau, which exists as a natively disordered, assembly incompetent monomer (U_x). A conformational change to an assembly competent state accelerates polymerization (U_c). Once assembly-competent species form, the rate-limiting step in tau fibrillization is the formation of dimer, which represents the thermodynamic nucleus (N). After nucleation, extension occurs through further addition of assembly competent monomers to the filament (F) ends. See “Discussion” for details.

High concentrations of free tau alone are not sufficient to support aggregation or seeding reactions in vitro, suggesting that tau needs to adopt aggregation-competent conformations before these reactions are triggered (Fig. 7). Thus, the second step involves overcoming this barrier. Here, it was surmounted by the addition of a small-molecule aggregation agonist, but it also can be overcome by exonic mutations, such as ΔK280 (58), post-translational truncation (59, 60), or by high stoichiometry phosphorylation (61). Without these modifications, expression of full-length tau isoforms in cells does not lead to efficient aggregation as predicted by the law of mass action even at supraphysiological tau concentrations (62).

Once aggregation-competent conformations are adopted, the rate-limiting step in fibrillization becomes dimerization, which is energetically disfavored at physiological tau concentrations and, therefore, a third key point of control (Fig. 7). The dimer may span the core of the tau filament, which adopts parallel, in register β-sheet conformation (5) and which is composed of ∼2 tau protomers per β-strand spacing (39). This organization is consistent with the β-spine structure deduced for Aβ_1–40 (63) and for peptides derived from the core regions of several different cross-β-sheet forming proteins, including tau (64). The β-spine model predicts that the interdigitation of hydrophobic side chains between two protomers lying perpendicular to the filament axis corresponds to the nucleation step in aggregate formation (65). Therefore, post-translational modifications that promote dimer formation may increase rates of fibrillization. For example, oxidative dimer formation is the rate-limiting step in α-synuclein fibrillization (66) and can also accelerate tau aggregation (67). But oxidative stress can induce dityrosine (68), disulfide, or other linkages in tau protein with isoform-specific effects. For example, the effects of disulfide bond formation depend on whether the tau isoform contains one (three-repeat tau) or two (four-repeat tau) Cys residues. In three-repeat tau, disulfides will necessarily form between monomers to form dimers, potentially driving filament nucleation. In contrast, four-repeat isoforms can form intramolecular disulfides that interfere with filament formation (69). Thus, the dimeric nucleus identified here may rationalize why certain rare tauopathies accumulate primarily three-repeat tau isoforms, whereas most others accumulate four-repeat isoforms (70). In addition to oxidation, dimer formation can be promoted by phosphorylation (71). Moreover, nucleation need not occur free in cytosol but in association with other cellular components. For example, the γ-tubulin ring complex can serve as a template for microtubule nucleation (72). In AD tissue, tau β-sheet structure first appears in association with membranes (73), and the ends of authentic PHFs associate with intracellular bodies (74). Thus, membranes may provide a surface that promotes tau conformational change and subsequent PHF nucleation.

The final aggregation step, filament elongation, is not rate-limiting but provides thermodynamic driving force for the reaction and establishes the minimum tau concentration necessary to sustain it. It too can be modulated by post-translational modification, with both glycation and pseudophosphorylation enhancing filament stability in vitro (27, 29). Elongation reaction identified herein is mediated by monomer addition. This observation along with identification of a dimeric nucleus implies that the small amounts of stable oligomers and dimers of tau found in vitro (75) and in situ (76) form separately from this fibrillization pathway. Together or individually, these four steps represent targets for the “multiple hits” implicated in sporadic AD pathogenesis (77).

Comparison with Previous Studies—Three other routes to PHF formation have been identified in vitro using supraphysiological concentrations of tau proteins. These are predicted to share steps 1 and 2 of Fig. 7 but differ in steps 3 and 4. First, PHFs can form from covalent tau dimers (26, 69). The reaction requires an exogenous inducer to trigger aggregation and then proceeds with positive cooperativity, potentially reflecting a nucleation dependent process (14). This pathway differs from the equilibrium nucleation scheme found here by the size of the nucleus cluster and by the elongation reaction being mediated by dimer addition. To mediate tau aggregation in disease, appreciable amounts of monomer would have to be replaced by dimer, so that the latter becomes favored to participate in both nucleation and extension reactions. The nucleation-dependent model described herein suggests that small amounts of dimer formation could support filament nucleation well before the dimer addition pathway becomes favored.

PHFs also form from recombinant tau monomers under reducing conditions in the presence of micelle-forming anionic surfactants such as arachidonic acid (78), vesicle-forming membrane lipids such as phosphatidylserine (13), and anionic microspheres (13). Under these conditions, the initial rate of formation of thioflavin S reactivity (a small molecule probe of cross-β-sheet structure (26)) is first order with respect to tau concentration, consistent with a rate-limiting, intramolecular folding reaction. The filamentous aggregates formed in the first 24 h have the morphology and mass-per-unit length of a PHF protofilament (6, 79). Therefore, these aggregates are predicted to contain ∼1 tau protomer/β-strand spacing and would be expected to lack the interdigitation of hydrophobic side chains that associate the two protofilaments of β-spine structures. Protofilament formation may, therefore, be isodesmic. In vitro, this pathway yields mature PHFs composed of two protofilaments only after >24 h of incubation (6, 79), suggesting their overall rate of production is limited by secondary nucleation along protofilament lengths, by protofilament annealing, or by disulfide bond formation fostered after exhaustion of reducing agent. The early stages of this pathway, which may also be active in AD, could serve as a physiological source of small soluble aggregates (Fig. 6A). Although PHF protofilaments have been purified out of AD tissue, their appearance has been ascribed to PHF breakage during isolation rather than to early-stage aggregation (80).

Finally, tau aggregates can form through a colloidal pathway in the presence of heparin inducer under non-reducing conditions (23, 81, 82). This pathway first forms granular aggregates containing ∼40–74 tau molecules, which then fuse to form filaments. The fusion reaction is reversible (81). Granular aggregates have been isolated from AD tissue in the presence of anionic detergents (82), but whether they represent small filaments or micellar aggregates is not clear from their morphology alone. Moreover, the disaggregation of mature filaments into granular units (81) suggests this pathway may yield filaments that differ from PHFs.

In summary, small-molecule-mediated induction of tau aggregation approximates nucleation-dependent kinetics. The pathway can operate at physiological tau concentrations in vitro and, on the basis of mass-per-unit length measurements, yields filaments consistent with the emerging β-spine structural model. The pathway supports a role for dimerization in filament formation but suggests that its significance lies at the step of nucleation.