The Stochastic Edge in Adaptive Evolution

Abstract

In a recent article, Desai and Fisher proposed that the speed of adaptation in an asexual population is determined by the dynamics of the stochastic edge of the population, that is, by the emergence and subsequent establishment of rare mutants that exceed the fitness of all sequences currently present in the population. Desai and Fisher perform an elaborate stochastic calculation of the mean time τ until a new class of mutants has been established and interpret 1/τ as the speed of adaptation. As they note, however, their calculations are valid only for moderate speeds. This limitation arises from their method to determine τ: Desai and Fisher back extrapolate the value of τ from the best-fit class's exponential growth at infinite time. This approach is not valid when the population adapts rapidly, because in this case the best-fit class grows nonexponentially during the relevant time interval. Here, we substantially extend Desai and Fisher's analysis of the stochastic edge. We show that we can apply Desai and Fisher's method to high speeds by either exponentially back extrapolating from finite time or using a nonexponential back extrapolation. Our results are compatible with predictions made using a different analytical approach (Rouzine et al.) and agree well with numerical simulations.

FOR small asexual populations and low mutation rates, the speed of adaptation is primarily limited by the availability of beneficial mutations: a mutation has the time to reach fixation before the next mutation occurs. Therefore, in this case the speed of adaptation increases linearly with population size and mutation rate. By contrast, for large asexual populations or high mutation rates, beneficial mutations are abundant. In this case, the main limit to adaptation is that many beneficial mutations are wasted: when arising on different genetic backgrounds, they cannot recombine and thus are in competition with each other. The theoretical prediction of the speed of adaptation in the latter case is a formidable challenge even for the simplest models. The earliest attempts to predict this speed go back to Crow and Kimura (1965) and Maynard Smith (1971). In recent years, several groups have improved upon and extended this work (Barton 1995; Tsimring et al. 1996; Kessler et al. 1997; Prügel-Bennett 1997; Gerrish and Lenski 1998; Orr 2000; Rouzine et al. 2003, 2008; Wilke 2004; Beerenwinkel et al. 2007; Desai and Fisher 2007). The recent works can be broadly subdivided into two classes: (i) so-called “clonal-interference models” (Gerrish and Lenski 1998; Orr 2000; Wilke 2004; Park and Krug 2007), which emphasize that different beneficial mutations have different-sized effects and that mutations with large beneficial effects tend to outcompete mutations with small beneficial effects, and (ii) models in which all mutations have the same effect s (Tsimring et al. 1996; Kessler et al. 1997; Rouzine et al. 2003, 2008; Beerenwinkel et al. 2007; Desai and Fisher 2007). The latter type of models emphasizes that in large populations, multiple beneficial mutations frequently occur in quick succession on the same genetic background. These models, however, neglect clonal-interference effects.

For the second class of models, where all mutations have the same fitness effect, each individual can be conveniently described by the number k of beneficial mutations it holds. The whole adapting population can then be seen as a traveling wave (Tsimring et al. 1996; Rouzine et al. 2003, 2008) moving with time through fitness space toward increasing values of k. In the traveling-wave approach, the bulk of the population, for which each k value is occupied by many individuals, can be accurately described using a deterministic partial differential equation. However, the partial differential equation breaks down for the rare mutants that have the highest fitness in the population, because these rare mutants are subject to substantial genetic drift and stochasticity. Therefore, the description of this stochastic edge must be approached differently and must be coupled with the description of the bulk of the population. Specifically, the deterministic equation admits a traveling-wave solution for any velocity. The high-fitness tail of that solution ends at a finite point, which is identified with the stochastic edge. To select one solution (and thus determine the wave speed), Rouzine et al. (2003, 2008) estimated the average size of the stochastic edge using a stochastic argument and matched this size to the solution of the deterministic equation.

Recently, Desai and Fisher (2007) proposed a new method to calculate the speed of adaptation for the same model. They mainly carry out an elaborate treatment of the stochastic edge, with little attention paid to the bulk of the population. The full-population model is effectively replaced with a two-class model consisting of the best-fit and the second-best-fit classes only; the best-fit class is treated stochastically, whereas the next-best class is assumed to increase exponentially in time due to selection. Beneficial mutations are neglected compared to the effect of selection, except for mutations into the best-fit class. At the very end of the derivation, the sizes of other fitness classes are estimated to provide a normalization condition.

Both Rouzine et al. (2003, 2008) and Desai and Fisher (2007) calculate the speed of adaptation once the evolutionary process has become stationary, that is, when the combined effects of mutation and selection maintain the shape of the traveling wave. The transient dynamics generally happen on a short timescale but are hard to quantify analytically (Tsimring et al. 1996; Desai and Fisher 2007).

Rouzine et al. (2003, 2008) define the speed of adaptation as the change of the population's mean number of mutations over time, 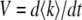. Desai and Fisher (2007) consider instead the change in the population's mean fitness, v = sV. Both approaches consider as an intermediate quantity the lead q, defined as the difference between the number of mutations of the best-fit individuals and the average number of mutations in the population, and write a relation between q and the mean establishment time τ = 1/V of a new fitness class at the stochastic edge of the population. (Note that Rouzine et al. 2003, 2008 write the lead as |x₀| rather than q and derive a relation between q and V rather than q and τ. Furthermore, k is in these articles the number of deleterious rather than beneficial mutations.) We would expect both approaches to make comparable predictions for V, and indeed they do when the speed of adaptation is moderate. For larger speeds, Desai and Fisher's (2007) derivation is no longer valid (M. M. Desai, personal communication), and their result gives a prediction that deviates strongly from the one obtained by Rouzine et al. (2008).

Here, our goal is to provide an extensive reanalysis of the approach of Desai and Fisher (2007) and to extend it to larger speeds. For completeness, we first rederive the relation between q and τ found by Desai and Fisher (2007) and point out the approximations made in the process. Then, we show in two different ways how we can extend their work to larger speeds of adaptation. With our modifications, the result of Desai and Fisher (2007) becomes compatible with the result of Rouzine et al. (2003, 2008). Finally, we substantiate our claims with numerical simulations.

MATERIALS AND METHODS

Model assumptions:

We consider exactly the same model as that of Desai and Fisher (2007). Briefly, we model a population of N sequences evolving in continuous time. A sequence with k beneficial mutations has fitness sk (which means we assume there is no epistasis); such a sequence reproduces with rate 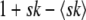, where 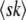is the average fitness in the population. The population size N is held constant at all times by removing one random sequence from the population for every reproduction event. All sequences are equally likely to be chosen for removal and thus have the same average death rate of 1. Mutation events are decoupled from replication events, and we assume that each sequence may independently undergo a mutation with a rate U_b: if a sequence has k beneficial mutations, it is removed with probability U_bdt and replaced by a sequence with k + 1 beneficial mutations. Since there are no differences in mutational effects in this model, all sequences with the same number of mutations k can be lumped together into one fitness class, and we refer to the number of sequences with k mutations at time t as n_k(t).

An evolutionary model in which mutation and replication events are decoupled is called a parallel mutation–selection model (Baake et al. 1997). This model has a long-standing tradition in theoretical population genetics (Crow and Kimura 1970). Even though the alternative model, in which mutation and selection are coupled, may be more appropriate for rapidly evolving viral populations, both models are biologically relevant. Furthermore, in the limit of small s and U_b, which we consider here, the mutation and selection terms decouple, and the two models become equivalent (see, e.g., Rouzine et al. 2003).

When the number n_k(t) of sequences with mutation number k is large enough, the evolution of n_k(t) becomes nearly deterministic:

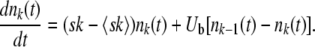(1)

Sequence classes that satisfy this condition and follow Equation 1 are called established. However, the best-fit sequences in the population are not numerous enough for a deterministic description, and stochasticity and genetic drift play an important role in their evolution. We make the approximation that we give the best-fit fitness class [the class corresponding to the largest k with n_k(t) > 0] a precise stochastic treatment, while we regard all other classes as established and treat them deterministically. The validity of this approximation has been discussed in detail (Rouzine et al. 2003, 2008; Desai and Fisher 2007); in particular, it was shown by Rouzine et al. (2008) that this approximation is valid if the speed of adaptation is much larger than U_b. Moreover, we check this approximation numerically in the present work. We refer to the one stochastic class as the stochastic edge and denote the value of k for that class by k₀.

Let 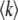be the mean number of mutations in the population. We define the lead q as q = k₀ − 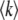. The lead is the distance from the stochastic edge to the population center. By the definition of fitness in the model, sequences at the stochastic edge have a fitness advantage of sq over the bulk of the population, and sequences in the first-established (i.e., second-best) class have a fitness advantage of s(q − 1). Following Desai and Fisher (2007), we make the approximation that the second-best class behaves deterministically according to Equation 1 and, neglecting incoming mutations from the third-best class and outgoing mutations to the best class, that it grows approximately exponentially with rate s(q − 1). (We discuss or check numerically the validity of these approximations later on.) While the second-best class is growing, any beneficial mutations that occur to sequences in this class feed the best class. Even though any individual mutant that arrives in the best class has a substantial probability of being lost to drift, the ongoing feeding of the best class guarantees that this class itself will become established at some point in time. At this point, the newly established fitness class becomes the second-best class (which, as we assumed, grows deterministically), a new stochastic edge develops at k₀ + 1, and the process repeats.

Note that during one cycle, the values of 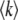and q change smoothly by 1 unit, but we ignore that change and assume that q remains constant from the creation of a new best class to its establishment. Therefore, the whole approach is valid only if q is large enough so that it makes sense to neglect a change of order 1 in q. We assume also that the stochastic edge becomes established when its size gets large enough compared to 1/(sq), which is a well-known stochastic threshold (Maynard Smith 1971; Barton 1995; Rouzine et al. 2001). This assumption makes sense only if 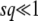. Finally, we assume that the stochastic edge does not produce any mutant until it is established, which implies 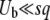. These conditions imply, of course, 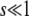. Note that q is not a parameter of the model, but a derived quantity. Therefore, all these assumptions must be checked a posteriori once q is computed as a function of the parameters N, s, and U_b.

Simulations:

We carried out three types of numeric simulations: fully stochastic whole-population simulations, semideterministic whole-population simulations, and stochastic-edge simulations. The first two ones are simulations of the whole population, whereas the third one is a simulation of the growth of the best-fit class only, assuming it is fed by an exponentially growing second-best-fit class. Details are given below. In all cases, we simulated continuous time by subdividing one generation into small time steps of length δt and updated the simulation after every such time step. In all results reported, δt was at most 0.01.

We used both the GNU Scientific Library (Galassi et al. 2006) and the library libRmath from the R project (R Development Core Team 2007) for generation of Poisson, multinomially, and hypergeometrically distributed random numbers. Source code to all simulations is available upon request from C. O. Wilke.

Fully stochastic whole-population simulations:

For each fitness class k, we kept track of a random variable n_k(t) representing the class size at time t. In each time step, we first calculated the number of offspring o_k in fitness class k. The o_k are Poisson random variables with mean 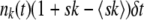. We then calculated the number of deaths d_k in each class. The total number of deaths 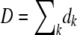in one time step equals the number of new offspring in that time step, 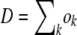. We generated the d_k's by drawing a single set of multinomially distributed random numbers with means 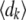= Dn_k(t)/N and 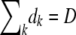. If we obtained one or more d_k with d_k > n_k(t), we redrew the entire set of d_k's. We then computed the state of the population after selection but before mutation as 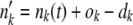. Next, we generated mutations. For each class k, we generated a binomially distributed random variable m_k with mean 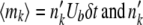trials. We then updated the population to .

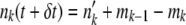The usage of the multinomial distribution to generate d_k's is an approximation, as the distribution of the d_k's is actually hypergeometric. [The hypergeometric distribution describes the probability p_hg(d, D; n, N − n) to obtain d white balls after D random draws from an urn containing n white and N − n black balls and is given by 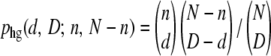. We also implemented hypergeometric sampling of deaths, by generating the random variables d_k one by one, going from the best-fit class to the worst-fit class with the probabilities 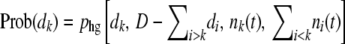. We found that the generation of hypergeometrically distributed random variables was much slower than multinomial sampling (up to a factor of 1000) and caused numeric instabilities at large 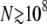, even when using an efficient numerical algorithm (Kachitvichyanukul and Schmeiser 1985). For N < 10⁸, simulation results with multinomial sampling of deaths and hypergeometric sampling of deaths were virtually identical.

We measure the speed of adaptation V for the stationary evolutionary process, when the population can be considered a traveling wave (Rouzine et al. 2003, 2008). We know of no good theory for predicting how long it takes for the population to reach stationarity, but simulations indicate that equilibration proceeds rapidly (see also Tsimring et al. 1996). In our simulations, we considered the population as equilibrated when at least 10 new fitness classes had been established. We then measured the time Δt it took the population to establish 40 additional fitness classes and calculated V as 40/Δt. We averaged V over 10 independent replicates.

Semideterministic simulations:

For each fitness class k, we kept track of a variable n_k(t) representing the class size at time t. We updated the size of the stochastic edge class 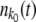stochastically and all other variables n_k(t) deterministically. As in the case of the fully stochastic simulations, in each time step we first calculated the number of offspring o_k in fitness class k. For k < k₀, o_k = n_k(t)(1 + sk − 〈sk〉)δt. At the stochastic edge, 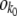is a Poisson-distributed random variable with mean 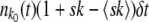. We then calculated the number of deaths d_k. The total number of deaths required is 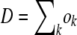. At the stochastic edge, 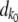is a Poisson-distributed random variable with mean 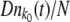. We set 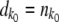if 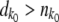. For k < k₀, we calculated 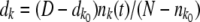. We then computed the state of the population after selection but before mutation as 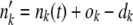. Next, we generated mutations. At the stochastic edge, 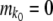(the stochastic edge does not produce beneficial mutations). For the second-best class, 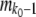is a Poisson-distributed random variable with mean 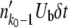. For all other k < k₀ − 1, m_k = 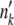U_bδt. We then updated the population to 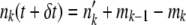. [In theory, this procedure can lead to a negative 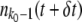. However, this extremely unlikely event never actually occurred in our simulations.] Finally, if 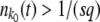, we designated the current stochastic edge class as established and set k₀ to k₀ + 1.

We measured the speed of adaptation as in the fully stochastic full-population simulations.

Stochastic-edge simulations:

We kept track of a single random variable n(t) representing the best-fit class in the population (the stochastic edge), which was set to zero at t = 0. Assuming that the population of the second-best-fit class was e^s(q−1)t/(sq), we generated at each time step three Poisson random variables o, d, and m, representing the number of offspring, deaths, and incoming mutations in the best-fit class, with means (1 + sq)n(t)δt, n(t)δt, and U_be^s(q−1)tδt/(sq), respectively, and updated n(t) as n(t + δt) = n(t) + o − d + m. All measures reported in results and discussion were obtained by averaging over 500 independent realizations of the simulation.

RESULTS AND DISCUSSION

Rederivation of the Desai–Fisher results:

In this section, we rederive the main results of Desai and Fisher (2007), using methods very similar to theirs, but with some simplifications. This section does not contain any new results; it is included here because we need to point out the various approximations made by Desai and Fisher (2007) before discussing them and also because we believe that an alternative presentation of their nontrivial results may be helpful to many readers.

Desai and Fisher (2007) define the establishment time τ as the time from the establishment of one new fitness class to the establishment of the next better fitness class. Their approach is based on an elaborate probabilistic calculation of the establishment time τ of a fitness class with advantage sq, given that this class is fed beneficial mutations from the exponentially growing second-best class. Since for large N every beneficial mutation that arrives in the best-fit class forms a clone that is independent of all other clones in the best-fit class, the growth (and potential establishment or extinction) of a single clone can be described using continuous-time branching theory. The treatment of a single clone is standard (Athreya and Ney 1972); the single clone follows a birth-and-death process with birth rate 1 + sq and death rate 1. The probability-generating function for the size m(t) of a clone at time t that had size 1 at time t = 0 is given by Athreya and Ney (1972):

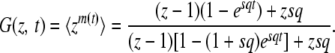(2)

Given this result for a stochastically growing individual clone, we now wish to study the size n(t) of the best-fit class at time t. This class grows by itself with a rate sq and is fed by the next-best class, which grows at a rate s(q − 1). We call f(t) the size of the next-best class, and we assume later on that

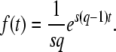(3)

Note that we assume a deterministic growth for this next-best class, and we neglect changes in f(t) due to both outflow of beneficial mutations from the second-best to the best-fit class and inflow of beneficial mutations from the third-best to the second-best class. We set the origin of time such that t = 0 when f(t) = 1/(sq), which is the well-known stochastic threshold for a clone with fitness advantage sq (Maynard Smith 1971; Barton 1995; Rouzine et al. 2001): a clone whose size far exceeds this threshold grows essentially deterministically, whereas a clone whose size falls far below this threshold is subject to genetic drift. The idea is that this second-best-fit class just got established at time t = 0 and was the previous stochastic best-fit class at times t < 0.

As the size n(t) of the best-fit class grows with rate sq, Desai and Fisher (2007) suggest to write for large t

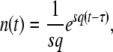(4)

where τ is some random variable. Intuitively, we might interpret τ as the time at which the new best-fit class appears to have reached the stochastic threshold, when sampled at later times when it is already deterministic. Of course, n(t) is really a random variable that in the t → ∞ limit converges to an exponential growth, and n(τ) has no reason to be equal to 1/(sq). But if n(t) had a deterministic exponential growth at all times, then τ would be the time for which n(t) had reached 1/(sq). In this case, it would take a (random) time τ to build a new established class from a class that had just crossed the stochastic threshold, the population would move by one fitness class during a time interval τ, and the speed of adaptation would be simply 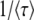, where 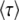is the average of τ. However, things are more complicated than this intuitive picture suggests. In Equation 4, the random variable τ has a distribution that depends on the time t at which n(t) is measured and we from now on write τ(t) rather than simply τ. When evaluating the speed of adaptation 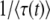, we have to choose a time t at which the average is taken. Desai and Fisher (2007) chose to take t = ∞ and, therefore, to define the establishment time as 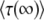. This choice of t is arbitrary, and we argue later on that it makes more sense to choose t on the order of 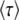. As we shall see, when q is large, 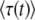converges quite slowly to 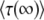, and the two expressions give different results. For this reason, Desai and Fisher (2007) considered only moderately large q, for which 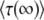is a good approximation of .

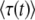We put aside for the moment the problem of choosing the best value of t in 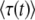and focus on calculating the cumulants of τ(t). We first calculate the probability-generating function 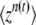of n(t), under the assumption that the best-fit class is fed by mutations from the second-best class, which itself has size f(t) at time t. In this calculation, we neglect beneficial mutations produced by the best-fit class, as mutations are rare and the number of sequences in this class is small. Assuming that the process starts at some time T₀ with n(T₀) = 0, we write 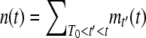, where m_t′(t) is the contribution at time t of a new clone if such a clone appeared at time t′. With a probability f(t′)U_bdt′, a clone actually appeared at time t′ and, according to Equation 2, we have 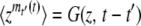. With a probability 1 − f(t′)U_bdt′, no clone appeared at time t′, we have m_t′(t) = 0, and, of course, 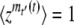. As all the m_t′(t) for a given t are independent random numbers, we can write 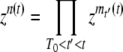and average independently all the terms in the product. We obtain

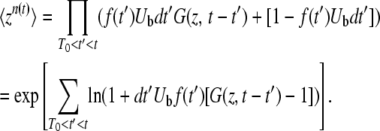(5)

As dt′ is infinitely small, we have ln(1 + dt′C) = dt′C, and we recognize that the summation is actualy an integral. Therefore,

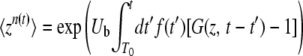(6)

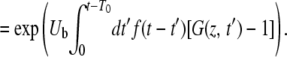(7)

This equation with T₀ = −∞ corresponds to Equation 24 of Desai and Fisher (2007).

In Equation 7, we use the G(z, t) given in Equation 2 and the f(t) given in Equation 3, change the variable of integration to v = (1 + sq)(1 − z)e^sqt′/[zsq − (1 − z)], and obtain

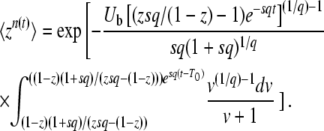(8)

(This equation corresponds to Equation 27 of Desai and Fisher 2007. Note that because of the way the change of variable was done, it is correct only for zsq > 1 − z.) To compute the cumulants of τ(t), it is easier to rewrite Equation 4 as

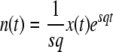(9)

with the random variable x(t) = e^−sqτ(t); the cumulants of ln x(t) differ from the cumulants of τ(t) only by a constant multiplicative factor. We obtain the generating function of x(t) from Equation 8 using 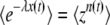for 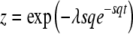. For now, we are interested only in the limit of infinite time. Making the substitution for z and taking the limit t → ∞ while holding λ constant, we find

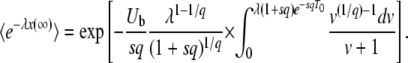(10)

In this expression, T₀ is the starting time at which the second-best class begins feeding the best-fit class. The second-best class can start producing mutants when its size is of order 1, which happens at large negative times. Unfortunately, Equation 10 is, strictly speaking, not valid if T₀ < 0, as we obtained it by using, in Equation 6, the expression Equation 3 for the size of the second-best-fit class, which is correct only for t > 0. However, as we assumed 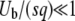, the mutation events from the second-best class at any negative time are very rare, so that we may expect that the final result will be dominated only by the events with t > 0 and that it will not depend much on the value of T₀, as long as T₀ is a negative number. One way to check the validity of this assumption is to verify that we reach the same results for T₀ = −∞ (equivalent to the assumption that Equation 3 is a good approximation for the size of the second-best class at negative times) and for T₀ = 0 (equivalent to the assumption that the second-best class is empty at negative times). Therefore, we first follow Desai and Fisher (2007) by taking the limit T₀ → −∞, and, at the end of this section, we consider briefly the case T₀ = 0 to validate this approximation. For T₀ = −∞, using 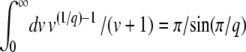, we obtain

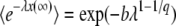(11)

with

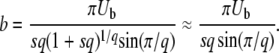(12)

(The first expression for b in Equation 12 is exact, but we use only the second, approximate expression in the rest of the article as we need 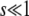anyway in the biological applications of that model. In fact, we often use b ≈ U_b/s when we suppose .)

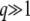Equation 11 is the generating function of x(∞), but we need the generating function of ln x(∞). For any random variable x, we can turn the former into the latter using the following identity, which is valid for μ < 0 and follows from the definition of the Gamma function:

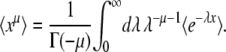(13)

(Actually, the equality holds without the averages.) Then, expanding ln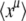 in powers of μ allows us to recover all the cumulants of ln x:

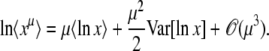(14)

Alternatively, if all we need is 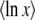, we can integrate by part λ^−μ−1 in Equation 13 (assuming that 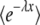goes to 0 for large λ) and expand directly to the first order in μ. We obtain

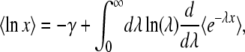(15)

where γ = − Γ′(1) ≈ 0.5772 is the Euler gamma constant. Applying this procedure to the random variable x(∞), we get from Equations 13 and 11

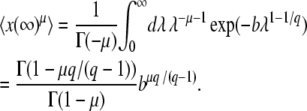(16)

Making use of the expansion 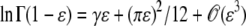, we obtain from Equation 14

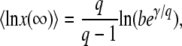(17)

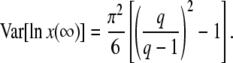(18)

Converting ln x(∞) back into τ(∞), we arrive at our final expressions

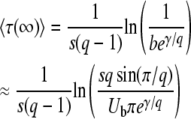(19)

and

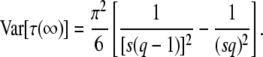(20)

We emphasize that these quantities were obtained in the limit t → ∞.

When we compare our results for mean and variance of τ(∞) to the results of Desai and Fisher (2007), we find that our expression for the variance agrees with their Equation 37. Our expression for 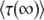is similar to their Equation 36, except that the factor q in the logarithm was accidently replaced by a factor q − 1 in Desai and Fisher (2007) (M. Desai, personal communication). As in Desai and Fisher (2007), we neglected the factor (1 + sq)^1/q in the expression (12) of b as we need 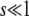in the context of the full biological model.

We now consider what happens if we use T₀ = 0 (and 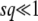) in Equation 10 instead of T₀ = −∞. Clearly, for large q, this integral is dominated by small v, so the value of the upper bound should not matter much to the final result. Indeed, if λ is not too small, we have

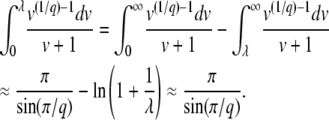(21)

We neglected v^1/q in the last integral, which is valid if λ is large enough, namely if either λ > 1 or 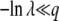. The same condition on λ allows the last simplification in Equation 21. Therefore, the generating function Equation 10 is identical for T₀ = 0 or T₀ = −∞, except for very small λ, and the probability distribution function of x(∞) does not depend on T₀ except for very large values of x(∞) such that 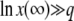. As it is easy to check from Equation 11 that Equation 15 is dominated by values of λ of order 1/b ≈ s/U_b, we finally obtain that the result for 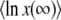and hence 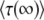is approximately the same for T₀ = 0 or T₀ = −∞ if either s/U_b > 1 or 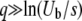. As Desai and Fisher (2007) assumed 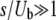in their work, their approximation of taking T₀ = −∞ is justified.

The stochastic threshold 1/(sq), which enters the calculation through Equations 3 and 4, is central to the entire approach of Desai and Fisher (2007). Yet it is not exactly true that all classes that exceed this threshold will behave purely deterministically. All we know for certain is that classes whose size is ≫1/(sq) will generally not show much stochasticity. Therefore, it is reasonable to ask what would happen if the true threshold were actually α/(sq), with some constant α ≠ 1. We find that replacing the threshold 1/(sq) in Equations 3 and 4 by α/(sq) results only in an additional factor α^−1/q inside the large logarithm in the final result for 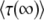, Equation 19. Because q is assumed to be large, the effect of that change is minor.

As a side matter, note that the generating function Equation 11 describes a distribution with a long tail; in particular, the average of x(∞) is infinite, which is not biologically possible and is an artifact of taking T₀ = −∞. If we were interested in the average of x(∞), we would need to keep T₀ finite and we would obtain, after some algebra, .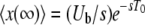

The case of large q:

In general, a weak selective pressure (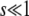) results in a broad fitness distribution, 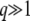. To gain better insight into the predictions of Equation 19 for this case, we consider the limit q large and s small. We find

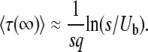(22)

By studying the deterministic evolution of the bulk of the population in the same limit, Rouzine et al. (2008) obtained in their Equation 39 a relation very similar to Equation 22. Using τ and q instead of the notations V = 1/τ and x₀ = −q of the cited work, we can write their result as

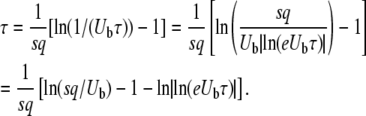(23)

Ignoring subleading corrections, we find that the main difference between Equation 22 and Equation 23 is a term q within the logarithm, which can become large in some situations.

We claim that when q is large, Equation 22 is not an accurate prediction for the mean establishment time. In particular, we obtain 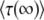< 0 for s < U_b. (Note that we assume throughout this work that 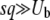, but unlike Desai and Fisher 2007, we do not require s > U_b.) This result is problematic, because the whole point of this calculation was to interpret 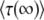as the mean time between the establishment of a best-fit class and the establishment of the next best-fit class in the full model describing a population of N sequences. Clearly, the establishment time in the full model cannot be negative, and this result would seem to suggest that the whole approach of approximating the full model by the sole behavior of its stochastic edge does not work for large values of q. However, we believe that the method can be fixed by replacing some of the assumptions that led to Equation 19 by improved and more accurate assumptions.

Approximations made in Desai and Fisher's approach:

Desai and Fisher (2007) made several approximations to obtain the relation Equation 19 between the establishment time and the lead q:

1. All the classes are evolving deterministically, except the stochastic edge.

2. The lead q does not vary in time between the creation and the establishment of a new mutant class.

3. The stochastic edge does not produce any mutant until it is established.

4. The second-best-fit class has an exactly exponential growth with a rate s(q − 1), as in Equation 3.

5. One can take the limit T₀ → −∞ when evaluating the mean establishment time.

6. At large times, the size n(t) of the stochastic edge is well fit by an exponential growth of rate sq, as in Equation 4 or Equation 9.

7. One can interpret the establishment time as 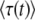for t → ∞.

Desai and Fisher (2007) discussed the validity of these approximations in the context of their parameter range of interest, i.e., for moderate q (see their Appendixes E–G). We reevaluate the approximations here in the context of large q.

Rouzine et al. (2003, 2008) gave detailed analytical arguments why approximation 1 is valid for 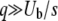. In our work, we verify this approximation numerically, using the semideterministic full-population simulation. Getting rid of this approximation and treating all classes stochastically is a formidable mathematical challenge that would be of limited interest because the approximation is quite good.

Approximations 2 and 3 are valid in, respectively, the limits 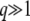and 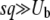, which we have assumed throughout. For more moderate values of q (between 2 and 5), Desai and Fisher (2007) discussed the validity of approximation 2 in their Appendix H.

Approximation 4 is more problematic. Saying that the second-best-fit class grows exponentially implies that we are ignoring the contribution from mutations originating in the third-best-fit class. On one hand the mutation rate U_b is supposed to be small compared to the effect of selection s(q − 1), but on the other hand the third-best-fit class is much larger than the second-best class. In appendix a, we present an argument indicating that approximation 4 is justified only at smaller times and is incorrect by a large factor for values of t close to the establishment time, which is unfortunately precisely the time at which most of the mutations occur. To what extent this deviation from approximation 4 affects our final result is difficult to assess at this point. Improving upon this approximation would require having a theory of at least the third-best-fit class.

We have already discussed the validity of approximation 5.

Approximations 6 and 7 are closely related: one can always decide to write Equation 4 for a well-chosen time-dependent random variable τ(t). But saying that n(t) is well fit by an exponential (approximation 6) is then equivalent to saying that τ(t) actually does not depend too much on time and that, consequently, one can choose any value of t to evaluate the establishment time, including t = ∞ (approximation 7). But, as we now argue, n(t) is not well fit by an exponential growth for large q. This implies that τ(t) has a strong t dependence and that choosing the best value of t when evaluating the establishment time is important; we argue that the proper value of t is of the order of the establishment time. Alternatively, one can get rid of approximation 6 and replace Equation 4 by a better fit of n(t). When carrying out this procedure, we find that the new random variable τ has indeed a weak time dependence and taking the limit t → ∞ makes sense. We presently explore both possible improvements.

Finite extrapolation time:

We are still fitting the best-fit class by an exponential, as in Equation 4 or Equation 9, but this time we try to evaluate 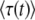for some finite time t. We go back to Equation 8, set T₀ = −∞, and substitute z = exp(−λsqe^−sqt) as before. However, this time we keep all terms to the first order in e^−sqt. We find

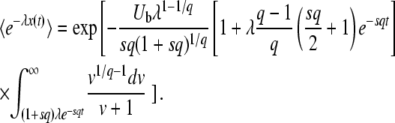(24)

For 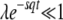, the integral assumes the value

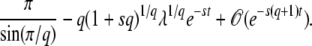(25)

Note that the small term appearing in the integral of Equation 24 is e^−sqt, but the first-order correction for finite time is actually proportional to e^−st, which is much larger. Compared to this correction, we neglect the term proportional to e^−sqt before the integral in Equation 24 and find

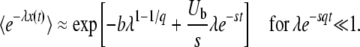(26)

(Desai and Fisher 2007 write a similar expression in their Equation G2, but do not exploit it.) When λe^−sqt is not small but q is large, we can obtain another expression by neglecting the v^(1/q) in Equation 8. Assuming sq small, we obtain after some algebra

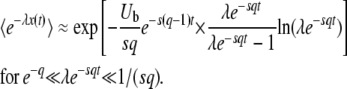(27)

Note that Equations 26 and 27 are both valid in the range .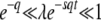

We want, as before, to compute 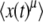by using Equation 26 into Equation 13. Expanding inside the integral in powers of the small parameter exp(−st), we would get

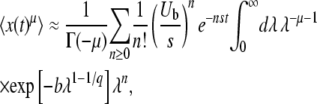(28)

but writing this equation is not justified a priori, because we may not use Equation 26 for arbitrarily large λ, and Equation 28 is actually a divergent series. We show, however, that the first terms of that series are nevertheless correct. Indeed, the integral in the nth order term of the series Equation 28 is mainly contributed from values of λ of order n/b ≈ ns/U_b. (This result is obtained by looking at the maximum of the integrand, in the limit of large q and large n.) Given the validity range of Equation 26, this means that the series Equation 28 is correct up to n = n_max with 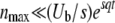. With this condition in mind, we compute the integrals and find

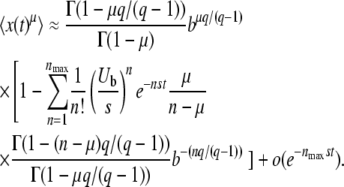(29)

Using 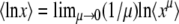as before (see Equation 14), we arrive at

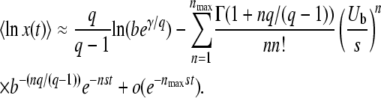(30)

The first term corresponds to the result for t → ∞, Equation 17, while the second term gives a correction for finite time. This expression can be simplified further for large q by using b ≈ U_b/s and 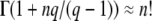, where the latter simplification is valid only if 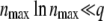. We recognize then the expansion of ln and obtain

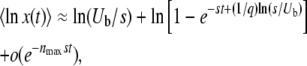(31)

where we recall that n_max is such that 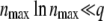and 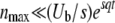. Furthermore, the 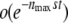is indeed a small correction only if 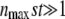. Therefore, Equation 31 is valid only if 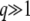(from the first condition above) and 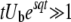(from the second and third conditions). [We made some simplifications using 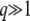to reach Equation 31, but as we will see, we need to keep the term 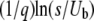given the relevant values of t.] In terms of τ(t), we finally get

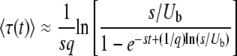(32)

for sufficiently large q and t.

Another way to reach Equation 32 is to use the integral expression Equation 15 to compute 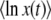. Making the change of variable y = λe^−sqt, we find

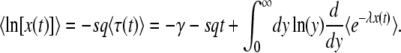(33)

We rewrite 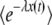from Equation 26 as a function of y,

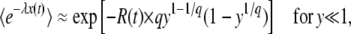with

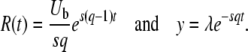(34)

(We assumed q large and used b ≈ U_b/s.) In fact, without any approximation, one can check that 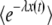can be written as exp[−R(t) × F(y)], where the function F(y) has no explicit dependency on λ or t. Clearly, as y is proportional to λ and 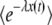decreases with λ, the function F(y) is an increasing function of y. [See, for instance, Equation 27, which shows how F(y) increases for 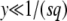.] Moreover, despite the presence of the large parameter q, this function varies neither slowly nor rapidly with y, so that the speed with which 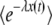changes with y depends only on the magnitude of R(t). When R(t) is large, 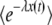interpolates very quickly between 1 and 0, and its derivative can be approximated by a delta function. This interpolation occurs at some value y_c of y that is very small; hence it is justified to use Equation 34 to compute y_c. Moreover, for R(t) large enough, 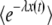becomes negligibly small within the range of validity of Equation 34 and will go on decreasing for larger values of y [because F(y) is an increasing function] so that values of y outside the validity range of Equation 34 do not contribute to the integral. All these remarks allow us to compute the integral in Equation 33; we find, for ,

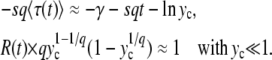(35)

Eliminating y_c in the previous equation gives

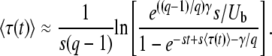(36)

Equation 36 is an equation for 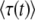; iterating it once and using q large, we recover Equation 32, up to some negligible terms. Note that the validity condition 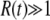is approximately the same as in the first method, as either one can be rewritten as 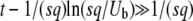. Numerical simulations (see Figure 1 confirm that our analytical argument is sound and that Equation 32 gives indeed a good numerical approximation of the measured 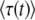in stochastic edge simulations for values of t larger (but not very much larger) than .

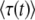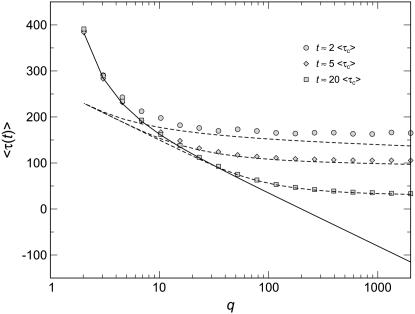
Figure 1.—

Numerical evaluation of the average 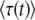in simulations of the stochastic edge, as a function of q, for U_b = 10⁻⁴ and sq = 0.02 held constant throughout. Points are simulation results; the standard error from the simulations is smaller than the symbol size. As measurement times t, we used three multiples of 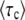and determined 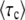from the approximation formula Equation 57. The dashed lines were calculated from Equation 32 (valid only for large q). The solid line represents 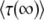(Equation 19, valid for all q).

We now exploit Equation 32 to test the validity of Desai and Fisher's (2007) result. The purpose of computing 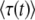is to compute the mean establishment time of a new class, which we call T in the remainder of this section. Desai and Fisher (2007) take T = 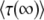. But, as we argue now, it makes more sense to take T ≈ 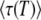. Indeed, the reason why τ(t) depends on t stems from the fact that fitting the growth of the new class by an exponential (see Equation 4) is not a perfect description of what is really happening, and the best value of the parameter τ in this fit depends on the range of values of t where we want this exponential fit to be the most precise. This range of values is precisely t of order T, because it is at this moment that the new class becomes the second-best-fit class, starts feeding an even newer class, and becomes approximated by a deterministic exponential growth (see Equation 3). The whole theory can be made self-consistent only if the value of the best-fit class just before it is established matches its value just after its establishment, which happens only if the size of the best-fit class is well described for t of the order of T. Consequently,

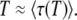(37)

We can try to solve Equation 37 directly from Equation 32; as the argument of the exponential in Equation 32 is small for t ≈ T, we may expand it and we obtain, ignoring subleading logarithmic terms inside the logarithm,

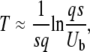(38)

which is quite different from the result of Equation 22 of Desai and Fisher (2007) and is rather closer to that of Equation 23. Note that in this procedure we are operating slightly outside the range of validity of Equation 32: we need to use this equation at t = T with T given in Equation 38, but we have shown it is valid only for 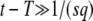, that is, for t slightly larger than T. As we use t ≈ T only in the argument of a large logarithm, we do not believe that this approximation should affect at all the final result of Equation 38 to the leading order. Our more precise method presented in the next section of this article confirms this claim.

Desai and Fisher's (2007) result in Equation 22 is obtained by making the approximation 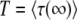, which is equivalent to neglecting the exponential in Equation 32. Clearly, this procedure is justified only when it gives a result compatible to that of Equation 38. This is the case only if

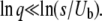(39)

[Note that Desai and Fisher 2007 stated the condition for the validity of their work incorrectly in their Appendix G (M. Desai, personal communication).]

Note that in this whole section, the derivation begins by assuming that the time T₀ at which the second-best class starts producing mutants is −∞. We now briefly check that this is a sound hypothesis by showing that we would have reached, to the leading order, the same final result in Equation 38 by taking T₀ = 0. As can be checked from Equations 34 and 35, the values of λ contributing most to the integral are ∼λ_c = y_ce^sqt ≈ 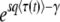. To reach Equation 38, we are interested in the time t ≈ T ≈ 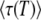, for which we obtain λ_c ≈ qs/U_b, which we assumed is large. Now, if T₀ = 0, the upper bound of the integral in Equation 24 should be λ (since we use 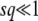, see Equation 10), which is large for the relevant values of λ. As in Equation 21, this means we need to subtract ln(1 + 1/λ) ≈ 1/λ, which is small, from the evaluation of this integral, Equation 25. But, within our working hypothesis 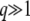and 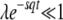, the value of that integral is large: it diverges logarithmically for large q and small ɛ = λe^−sqt; for q > 3 and ɛ < 0.1, it is >1, which is much larger than the small correction 1/λ. Therefore, considering T₀ = 0 instead of T₀ = −∞ does not change the final result in Equation 38 at the leading order.

When using a finite back-extrapolation time, we run into another difficulty that we have not mentioned yet. The mathematically exact value of 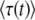for any finite t is −∞, because there is a nonzero probability p₀ that the size of the best-fit class is 0. For relevant values of t, the value of p₀ is incredibly small [one can show that 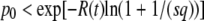, with R(t) given in Equation 35]. Of course, this event never occurred during all our simulations, and the only biologically observable quantity that makes sense is the average of τ(t) given that the new best-fit class is not empty. This quantity can be calculated in a precise way by replacing 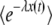everywhere in the previous derivation with (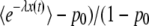). As a close inspection of our derivations would show, we use only the function 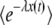in regions where it is much larger than p₀, so that nothing in our final result in Equation 32 should be changed because of that p₀. We now, however, present a better, more satisfying approach where none of these issues occurs.

A better back extrapolation:

In the previous subsection, we have seen that 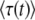depends strongly on t. At first glance, this result is somewhat unexpected. We intended the quantity τ to be the time at which the best-fit class crosses the stochastic threshold (i.e., the establishment time of a new fitness class), and this time should have a specific, well-defined value. Instead, we have found that the expected value 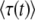decays as t increases; i.e., the longer we wait before we evaluate the system, the smaller the mean establishment time appears to be. This result indicates that τ(t), as defined above, is a poor method for getting an approximation of the mean establishment time.

We can understand the origin of the strong time dependence of 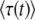from Equation 26. We rewrite this equation as

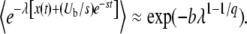(40)

In this form, we see that the variable x(t) (defined in Equation 9) has a deterministic part – (U_b/s)e^−st and that the fluctuations around that deterministic part have a nearly time-independent distribution described by the generating function on the right-hand side. The deterministic part has its origin in beneficial mutations fed into the best-fit class from the second-best class and can easily be understood by considering the deterministic approximation for the size n(t) of the best-fit class:

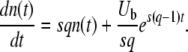(41)

[This equation follows from Equation 1 with n_k−1(t) given by Equation 3 and outgoing mutations neglected.] The origin of time is such that n_k−1(0) = 1/(sq), and we fix the integration constant by imposing that n(τ_c) = 1/(sq). This choice will allow us to interpret τ_c later on as the establishment time, that is the time it takes to move one notch in the periodic motion of the wave. We find

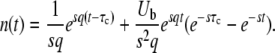(42)

Thus, because of incoming mutations, n(t) does not grow purely exponentially, even in the deterministic limit. If we try to approximate this deterministic n(t) or the stochastic n(t) by a pure exponential as in Equation 4, the optimal fit of the parameter (τ in the case of Equation 4) depends on the time at which we want a good fit. This deviation from pure exponential growth is the source of the strong time dependence in 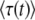. It makes more sense to fit the stochastic n(t) by Equation 42 but with τ_c now a random variable (see Figure 2. We may expect that in this way the distribution of τ_c will be largely independent of time. This is indeed the case. If we define x(t) = sqe^−sqtn(t) as before (see Equation 9), we obtain from Equation 42 the deterministic evolution of x(t):

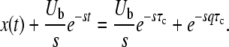(43)

Then, comparing this equation with Equation 40, we find that the deterministic component of x(t) in the probabilistic calculation corresponds exactly to the time-dependent part of x(t) in a fully deterministic model of the stochastic edge. Interpreting τ_c as a random variable, we see that the generating function of the right-hand side of Equation 43 is given by Equation 40 and is nearly time independent. (Only “nearly” because we neglected terms of order e^−sqt in the right-hand side of Equation 24 to reach Equations 26 and 40.)

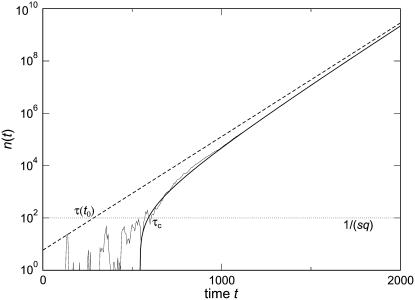
Figure 2.—

Stochastic-edge simulation and back extrapolation to obtain τ(t₀) and τ_c. The thin solid line represents the size n(t) of the best-fit class in a typical stochastic-edge simulation run for s = 0.001, U_b = 0.0001, and q = 10. The thick solid line is Equation 42 with τ_c = 590 and the dashed line is Equation 4 with τ(t₀) = 284. The values of τ_c and τ(t₀) have been determined at time t₀ = 10,000, which means that the stochastic value n(t₀) is indeed given by, respectively, Equations 42 and 4. For large times (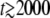), both fits are good but for intermediate times, the stochastic n(t) is best captured by the thick solid line. The time at which n(t) reaches the stochastic threshold 1/(sq) (represented as a horizontal dotted line) is much closer to τ_c than to τ(t₀). Moreover, the value of τ(t₀) would have depended much more on the choice of t₀. For instance, taking t₀ = 1000 would have given τ(t₀) = 380 and τ_c = 578.

To sum up, we write the stochastic size n(t) of the best-fit class as in Equation 42, where τ_c is a random variable. We equate the mean establishment time in the full population model with 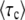. In our new approach, 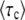does not depend much on time (the subscript “c” stands for constant) and we avoid the difficulty of Desai and Fisher's approach. From Equations 40 and 43 the distribution of τ_c is determined by

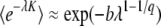(44)

with

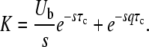(45)

The new difficulty, of course, is to obtain 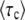from these two equations.

Scaling function for 〈τ_c〉:

The equations determining 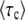are transcendental, and we have not been able to obtain a simple, closed-form expression for 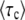. Nevertheless, we can gain substantial insight into how 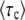depends on the parameter values s, U_b, and q. We make the change of variables

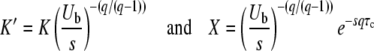(46)

and obtain, from Equations 45 and 46,

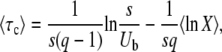(47)

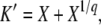(48)

and, from Equation 44,

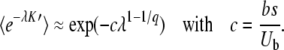(49)

The constant b is defined in Equation 12. Inserting this definition into c = bs/U_b, we obtain

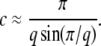(50)

We note that the constant c does not depend on U_b or on s. Therefore, 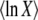does not depend on U_b or s, and Equation 47 fully captures the dependency of 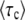both on U_b and on s. (Actually, using the most precise version of Equation 12, there is a very weak dependency on s in c, but for any biologically relevant case, s is small and this dependency can be neglected.) We can then write

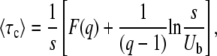(51)

where F(q) is a function depending only on q and given by

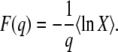(52)

In appendix b, we show that we can write 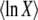as a single integral, see Equation B20, which can be easily numerically evaluated for any value of q. We obtain

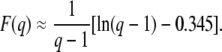(53)

The leading term comes from an analytical argument and the corrective term −0.345 is numerical. Figure 3 shows that the measured values of 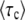in stochastic edge simulations can be reasonably well collapsed on the scaling function in Equation 53 for small values of s and U_b in a broad interval of q.

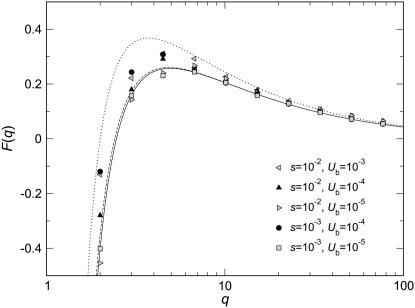
Figure 3.—

Measured values 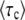collapse onto a single scaling function F(q). Data points are simulation results obtained from stochastic-edge simulations. For each parameter setting, we measured 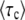and then plotted 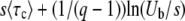as a function of q. The solid line represents a numerical evaluation of Equation 52 and the dashed line represents the approximate analytic expression Equation 53. The dotted line is the scaling function 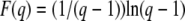derived from Equation 57.

Inserting Equation 53 into Equation 51, we obtain

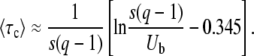(54)

Here again, the establishment time given by Equation 54 is very similar for large q to the result in Equation 23 obtained by Rouzine et al. (2003, 2008).

A simple approximation formula:

With Equation 54, we have a good approximation for 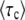, but the derivation of this approximation was quite tedious. We can alternatively derive a simple approximation formula for 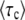on the basis of biological considerations. A similar derivation was first presented by Desai et al. (2007; Desai and Fisher 2007), and was also used by Rouzine et al. (2008) in the context of traveling-wave theory.

The average total number of mutations m(t) produced by the second-best class up to time t is

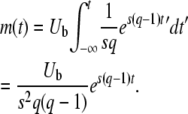(55)

Each of these mutations has a probability of going to fixation of sq/(1 + sq) ≈ sq (Lenski and Levin 1985). Since a single mutation that fixes is sufficient to establish a new fitness class, we have

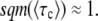(56)

We rearrange this equation and find

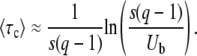(57)

Despite the simplicity of this argument, we find that this expression has good accuracy, in particular for large q. Equation 57 differs from Equation 54 only in the constant 0.345 subtracted from the logarithm.

In the remainder of this article, we do not use Equation 57. We included its derivation primarily to show that the edge treatment of Rouzine et al. (2008) is consistent with our derivation of .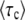

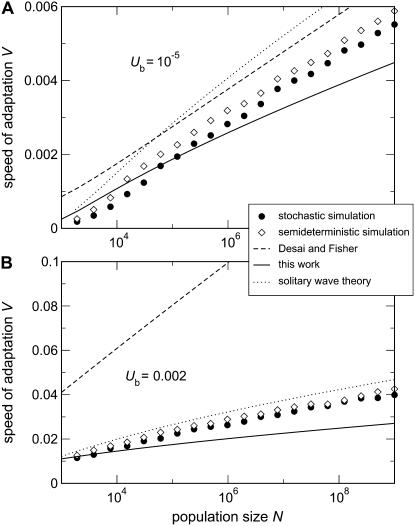
Predicting the speed of adaptation:

The goal of calculating 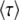in the previous subsections was to obtain the speed of adaptation V, which is approximately given by 1/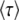. [Throughout this subsection, we mean 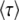to stand for eithe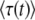r or 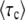.] Since 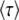depends on q, which is a derived property of the adapting population and not known in advance, we need a second, independent expression linking 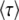and q. Desai and Fisher (2007) obtained this second expression from the normalization condition that the sum over all fitness classes has to yield the population size N. They argued that at the time of establishment of the best class, the size 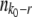of a fitness class r mutations away from the best class is given approximately by

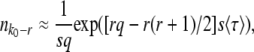(58)

because the second-best class has on average been growing exponentially at rate s(q − 1) for a time interval 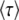, the third-best class has in addition been growing at rate s(q − 2) for an additional time interval 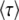, and so on. As the largest term in the sum arises for r ≈ q, Desai and Fisher (2007) simplified the normalization condition 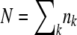to 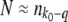, which yields

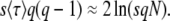(59)

Inserting the expression for 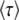from Desai and Fisher (2007) (their Equation 36) into this expression recovers their Equation 39, an expression that implicitly determines q as a function of s, U_b, and N. Note, however, that Equation 59 works only if s 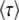is large; i.e., 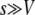. When s 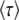is small, i.e., 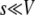, a better approximation to 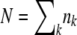is to replace the summation with an integral, 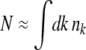which gives

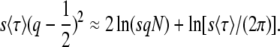(60)

Equations 59 and 60 correspond, respectively, to the two limits of a narrow wave and a broad wave discussed in Rouzine et al. (2008). Here, to better compare our results to Desai and Fisher's approach, we use only Equation 59 even for s < V as in Figure 4B. Using the more correct Equation 60 would have resulted in only a small correction of ∼5% at N = 10⁹ to <14% at N = 10⁴ for the parameter settings of Figure 4B (data not shown).

Figure 4.—

Speed of adaptation as a function of population size N. Points are simulation results: the solid circles come from stochastic simulations of the full model, while the open diamonds come from semideterministic simulations where only the best-fit class is stochastic. Dashed lines were obtained by numerically solving Equations 36 and 39 of Desai and Fisher (2007). Solid lines were obtained by numerically solving Equations 54 and 60 in the present work. Dotted lines are Equation 52 (for A) and Equation 51 (for B) from Rouzine et al. (2008). Parameters are s = 0.01 and U_b = 10⁻⁵ (A) and s = 0.01 and U_b = 0.002 (B). Note that our simulation results are in excellent agreement with simulation results reported by Desai and Fisher (2007).

To sum up, the final prediction in this model for the speed of adaptation V is

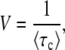(61)

where 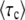as a function of N, s, and U_b is obtained by eliminating q in Equations 54 and 59. As we cannot analytically eliminate q, we have only two options: either to derive an approximate expression for q from these equations or to solve them numerically.

Desai and Fisher (2007) derived an approximate expression for q, neglecting some large logarithm inside of another logarithm (see their Equations 39 and 40). The final result shown in their Figure 5 agrees well with simulation results. However, when we compared this approximate expression to the corresponding exact numerical solution of their Equation 39, we found that the term Desai and Fisher (2007) neglected is not small in their parameter range and that, compared to the results of numerical simulations, the solution obtained by eliminating q numerically from Equations 54 and 59 performed worse than their approximate expression. Thus, the performance of the approximate expression is partly due to cancellation of errors, and we do not further consider this approximate expression here.

Figure 4 compares how the work of Desai and Fisher (2007) and the present work perform in predicting the speed of adaptation V. The dashed lines represent the exact numerical solution to the expression derived by Desai and Fisher (2007). This expression works reasonably well for low wave speeds [ln q < ln(s/U_b), Figure 4A], but performs poorly at high wave speeds [ln q > ln(s/U_b), Figure 4B], as expected. The poor performance at high wave speeds is caused by the breakdown of the 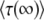approximation. If we instead use 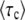, we get a significant improvement in the prediction accuracy at high wave speeds (solid lines in Figure 4). At low wave speeds, the two methods have comparable accuracies.

For comparison, we also plotted the predictions from traveling-wave theory (Figure 4, dotted lines), as derived by Rouzine et al. (2003, 2008). At low wave speeds (Figure 4A), traveling-wave theory performs approximately as well as both the original approach by Desai and Fisher (2007) and our revision of it. While all three methods show reasonable performance in this parameter region, none has excellent accuracy. At high wave speeds (Figure 4B), traveling-wave theory performs better than our revised version of the Desai-and-Fisher approach and comes close to the speed found in semideterministic simulations (see also next paragraph). Traveling-wave theory takes into account the effect of mutation pressure on intermediate fitness classes and thus incorporates their nonexponential growth. By contrast, we have neglected this effect in the present work, and have assumed that the second-best class grows purely exponentially (approximation 4). Certainly, the present work tends to underestimate the speed of adaptation because of approximation 4. It is less clear why traveling-wave theory always overestimates the wave speed. Possibly, the assumption made in traveling-wave theory that the wave speed is determined by the mean size of the stochastic edge might underestimate the drag exerted by the stochastic edge when it is very small.

We also carried out semideterministic simulations in which the best-fit class was treated stochastically and all other classes were treated deterministically. The semideterministic simulation tests the fundamental assumption, made both by Desai and Fisher (2007) and in traveling-wave theory (Rouzine et al. 2003, 2008), that only a single stochastic fitness class is necessary to describe an adapting population. Any analytical treatment of adaptive evolution based on this assumption can ever perform only as well as the semideterministic simulations. We found that the wave speed in the semideterministic simulations was close, but not exactly the same, as the true wave speed (Figure 4). In general, the semideterministic simulations tended to overestimate the wave speed, in particular for small wave speeds.

Conclusions:

The work by Desai and Fisher (2007) constitutes an interesting new approach to calculating the speed of adaptation. However, their work does not apply to high adaptation speeds, i.e., populations with large q. This limitation arises because the growth of the best-fit class cannot be described as a purely exponential growth times a random constant when the population evolves rapidly. Because the best-fit class is continuously being fed beneficial mutations from the second-best class, the random variable that modifies the exponential growth of the best-fit class is actually time dependent, and its mean changes with time.

Here, we have modified Desai and Fisher's method to handle correctly the nonexponential growth of the best-fit class. Our modification leads to a substantial improvement in the prediction of the speed of adaptation for rapidly adapting populations and agrees with predictions from traveling-wave theory. However, we have relied on an exponentially growing second-best class throughout this work, even though beneficial mutations from classes with lower fitness contribute significantly to the growth of the second-best class. A more accurate treatment of adaptive evolution than we have presented here will have to take this fact into account.

APPENDIX A: VALIDITY OF APPROXIMATION 4

The goal of this appendix is to test approximation 4, namely that the second-best-fit class grows exponentially with a rate s(q − 1):

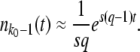(A1)

[Remember that k₀ was defined as the location of the stochastic edge, so that the second-best-fit class is at position k₀ − 1. The origin of time is when that class just got established: .]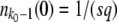

The size of any established class can be obtained from Equation 1, which reads for the second-best-fit class:

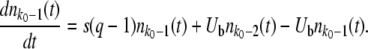(A2)

Equation A1 is the solution of Equation A2 only if the second and third terms on the right-hand side of Equation A2 are negligible. The third term is easily dealt with as we assumed throughout this work that 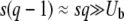. For the second term, we need to evaluate the size of the third-best class.

We proceed by assuming that the third-best class is described by a deterministic exponential formula, analogous to the equation used in the two-class model for the second-best class. Then, from Equation 58, we obtain for 0 ≤ t ≤ τ the expression

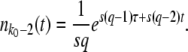(A3)

This expression is based on the assumptions that the class k₀ − 2 got established at time −τ when it reached the size 1/(sq), grew from time −τ to time 0 with rate s(q − 1), and grows from time 0 to time τ with rate s(q − 2).

Using the value of τ given in Equation 54, we find

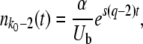(A4)

where α is of order 1. Using 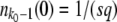and neglecting the third term on the right-hand side of Equation A2, we find as the solution to Equation A2

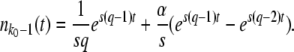(A5)

For moderate times such that 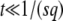, the second term in Equation A5 is negligible and we recover Equation A1. However, the most relevant time interval is when t is very close to τ, when most of the mutations from the second-best class to the not-yet-established best class occur (Rouzine et al. 2008). For t ∼ τ, further estimates depend on whether product sτ is small or large (i.e., whethe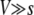r or 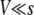). For 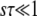, using exp[s(q − 2)t] ≈ (1 − st)exp[s(q − 1)t], we obtain

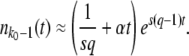(A6)

This expression deviates from Equation A1 due to the second term in parentheses. The deviation is by a factor of order 2 when t becomes of the order of 1/(sq), which happens early in a cycle, as 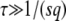from Equation 54. At the end of a cycle, t ∼ τ, the second term is larger than the first term by a factor of 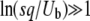. Therefore, approximation 4 is not valid, and the second-best-fit class cannot be described by Equation A1.

At 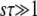and t ∼ τ, we can neglect the third exponential in Equation A5. Then, instead of Equation A6, we obtain

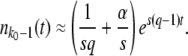(A7)

The first term in parentheses is negligible and the result differs from Equation A1 by the large factor 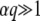. Therefore, approximation 4 is not valid in this case either.

Thus, taking into account the third-best class creates an additional large factor in the size of the second-best class at the most relevant times t ∼ τ. This factor is on the order of either q or ln(sq/U_b), whichever is smaller, and approximation 4 is not valid by itself. One could try to fix this issue by using Equation A5 instead of Equation A1 for the size of the second-best class, but it would make the derivation much more complicated. Note, however, that, as the effects of mutations enter the final result only through the logarithm of the mutation rate, it is plausible (but remains to be checked) that the large corrective factors of Equation A6 or Equation A7 will enter the final result as a logarithmic correction. On the other hand, there is no guarantee that taking into account the third-best class is sufficient, and it might be that one needs also to consider the effects of the fourth- or fifth-best class. In all cases, the replacement of the full-population model by a two-class model with an exponentially growing second-best class is problematic and deserves a more careful investigation.

APPENDIX B: CALCULATING 〈ln X〉

To calculate F(q), we have to calculate 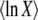, where X is the only positive root of

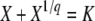(B1)

and we have written K instead of K′ for simplicity. The moment-generating function for K is (Equation 49)

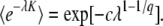(B2)

A first approach is to evaluate 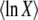numerically using an inverse Laplace transform. First, we calculate the density function p_K(y) of the probability distribution of K from the inverse Laplace transform of the moment-generating function of K,

(B3)

where 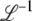can be written as an integral. In practice, this integral can be evaluated with efficient numerical algorithms (Valkó and Abate 2004; Abate and Valkó 2004). A transformation of variables gives us the density function p_X(y) of the probability distribution of X:

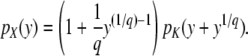(B4)

Finally, we integrate to obtain :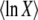

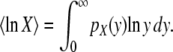(B5)

This method can be worked out, but it is delicate and computationally expensive to evaluate numerically with a good accuracy these not so well-behaved double integrals, especially for large values of q. We now present an alternative method that allows us to write 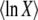as a simple integral, which is much easier to evaluate.

Writing ln X as a series:

Our first step is to invert Equation B1. By using Cauchy's integral formula from complex analysis, we can write for any analytical function f the quantity f(X) as

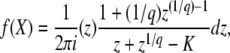(B6)

where the integration is on a contour surrounding the only positive root of Equation B1. We set f(z) = z^μ and make use of the Taylor series

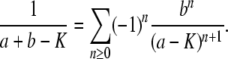(B7)

Setting a = z, b = z^1/q in the above expansion, we obtain

(B8)

(B9)

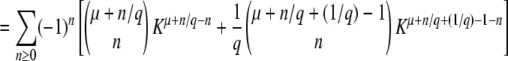(B10)

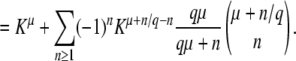(B11)

[We use the Binomial symbol for the x noninteger, with the convention that 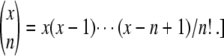Expanding both sides of the equation to first order in μ and comparing the coefficients of the linear term, we find

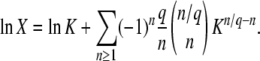(B12)

Taking the average:

We can now calculate 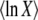by averaging Equation B12 term by term. Following the same steps as in the derivation of Equations 16 and 17 in the main text, we obtain from Equation B2

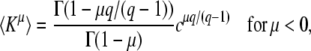(B13)

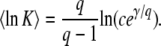(B14)

Using these two equations, we find

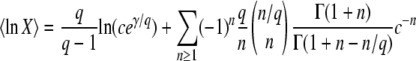(B15)

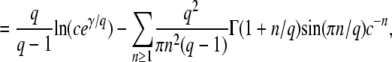(B16)

where we have made use of Euler's reflection formula Γ(x)Γ(1 − x) = π/sin(πx). The resulting series diverges. However, we treat it as a formal expansion of 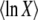and continue. We replace Γ(1 + n/q) by its integral representation, integrate by parts once, and obtain

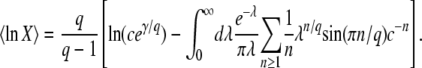(B17)

We now write sin(πn/q) as the imaginary part of e^iπn/q and note that the remaining sum is the Taylor expansion of the complex logarithm. Thus, we arrive at

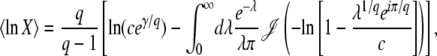(B18)

where 𝒥(z) indicates the imaginary part of z. Let ρ > 0 and φ be such that ρe^−iφ = 1 − λ^1/qe^iπ/q/c. Then, we have

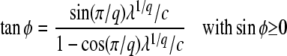(B19)

and

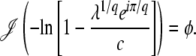(B20)

The angle φ is defined only up to a multiple of 2π, but the result must be φ = 0 when λ = 0 and the result must be a continuous function of λ. (While the sum converges only when λ^1/q/c < 1, we are considering here the analytical continuation of this function.) This reasoning implies that 0 ≤ φ ≤ π.

The final result is then

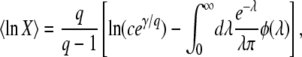(B20)

where

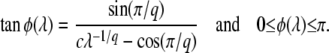(B21)

Note that

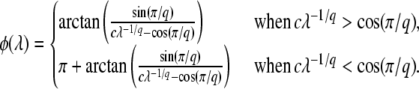(B22)

We evaluated both Equations B20 and B5 numerically and found excellent agreement between the two formulas.

Leading asymptotic of 〈ln X〉:

We now evaluate the integral in Equation B20 in the large q limit. For a fixed small λ and q → ∞, it is easy to see that

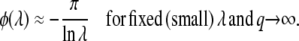(B23)

(Remember that c ≈ 1 for large q.) However, replacing φ(λ) by that expression leads to a diverging integral. What happens is that for a given large q, the approximation Equation B23 breaks for extremely small values of λ, and we obtain

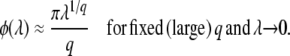(B24)

With the latter approximation, the integral converges. Looking more closely at the approximations made, we can check that Equation B23 is valid for 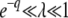and that Equation B24 is valid for .

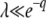Therefore, it makes sense to cut the integral into three parts: one for 0 < λ < e^−q, where we use Equation B24, one for e^−q < λ < ɛ, where we use Equation B23 and where ɛ is some fixed small number, and one for λ > ɛ. It is easy to check that the first and third parts give a number of order 1 (in other words, they do not diverge when q → ∞) and that the second part dominates the integral:

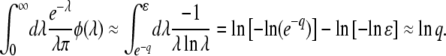(B25)

Once this leading term has been identified, we can evaluate numerically the integral for many values of q and extract an asymptotic expansion of the correction to the leading term. We found

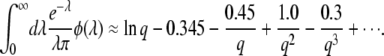(B26)

Another possibility is to write an expansion of the integral in powers of the variable q − 1:

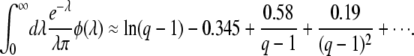(B27)

Both asymptotic expansions are, of course, equally good for large q, but it happens that truncated to its first terms, the second expansion is better than the first at approximating the integral for smaller q. Inserting the latter expansion into Equation B20 and using Equation 52, we recover Equation 53.

We have not been able to find a theory for the numerical coefficients of this asymptotic expansion, and this remains an interesting challenge. The expansion of Equation B27 is a very good approximation of the integral in the range q ∈ [2, ∞).