Size, foraging, and food web structure

Abstract

Understanding what structures ecological communities is vital to answering questions about extinctions, environmental change, trophic cascades, and ecosystem functioning. Optimal foraging theory was conceived to increase such understanding by providing a framework with which to predict species interactions and resulting community structure. Here, we use an optimal foraging model and allometries of foraging variables to predict the structure of real food webs. The qualitative structure of the resulting model provides a more mechanistic basis for the phenomenological rules of previous models. Quantitative analyses show that the model predicts up to 65% of the links in real food webs. The deterministic nature of the model allows analysis of the model's successes and failures in predicting particular interactions. Predacious and herbivorous feeding interactions are better predicted than pathogenic, parasitoid, and parasitic interactions. Results also indicate that accurate prediction and modeling of some food webs will require incorporating traits other than body size and diet choice models specific to different types of feeding interaction. The model results support the hypothesis that individual behavior, subject to natural selection, determines individual diets and that food web structure is the sum of these individual decisions.

Explaining and predicting community structure is a central part of ecological research. It is vital to answering questions about extinctions (1, 2), environmental change (3), trophic cascades (4), and ecosystem functioning (5, 6). We focus on one of the major components of community structure: the interactions between consumers and resources. Food webs represent communities in terms of species and the feeding links between them, and discovering what determines their structure is a major goal in ecology.

There are several different approaches to modeling food webs, each emphasizing different processes by which food web structure might be controlled. For example, dynamic models focus on how structure relates to population dynamics and community stability (2, 7–11). Evolutionary models incorporate the processes that control the formation and expansion of food webs (12, 13). Static models include rules that determine structural attributes of food webs (14–19). These models have developed our thinking about food webs in a number of ways, but they have limitations. The stochastic, and therefore generalized, nature of these models means that predicting the arrangement of links in a particular real food web is difficult. Here, we describe a new approach to modeling food webs that avoids some of these problems through use of the allometries of body size and foraging behavior of individual consumers.

The contingency model of optimal foraging predicts the diet that maximises a consumer's rate of energy intake (20). We have shown that this optimal foraging model can predict consumer diet breadths and food web connectance (21). This model of connectance [which we term the diet breadth model (DBM)] does not constrain the arrangement of trophic links in a food web and therefore cannot accurately predict food web structure. This is not surprising, because the DBM assumes that the four foraging traits in the model (energy content of resources, handling times, attack rates, and densities) are independent of each other. This is very unlikely, because body size is known to place constraints on many biological variables, including these four. Here, we link these foraging parameters through the effects of body size. We ask whether allometric foraging behavior predicts food web structure and thereby provides a mechanistic structural model of food webs. We term the model the allometric diet breadth model (ADBM).

Results

Qualitative Properties.

First, we describe how the phenomenological rules, which form the basis of previous static models, can be generated from the allometric optimal foraging framework (see Materials and Methods).

Rule 1.

There exists an ordering of species in which all species feed wholly, or largely on those lower than themselves in the ordering.

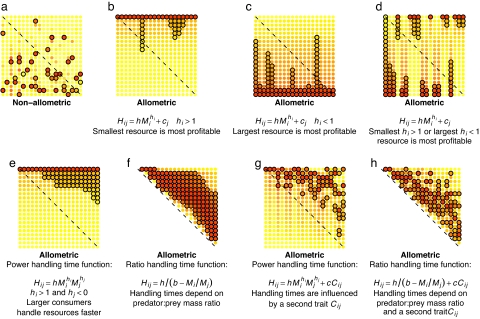
An ordered set (a ranking for each species) is absent if foraging behavior is independent of body size (Fig. 1a). An ordered set arises from allometric foraging for two reasons. First, body size is an axis along which species can be ordered independent of consumer identity (larger resources are larger, irrespective of their identity). Second, if the handling time function is similar for all consumers then profitabilities, P_ij = E_i/H_ij, will be similarly ranked among consumers. For example, if H_ij = hM_i^h_iM_j^h_j, P_i,j = eM_i^(1−h_i)(h M_j^h_j), and all consumers find the smallest (if h_i > 1; Fig. 1b) or largest (if h_i < 1; Fig. 1c) resource the most profitable. In contrast, if h_i < 1 for some consumers and h_i > 1 for others, the smallest resource will be the most profitable for some consumers, while the largest will be for others and there is no consistent feeding hierarchy across consumers (Fig. 1d).

Fig. 1.

Food web structures illustrated in predation matrices show the importance of allometry for structure. The allometric equation is given below the panel; parameter values are arbitrary and do not affect the qualitative patterns illustrated. Black circles indicate a realized feeding interaction. Body size increases from left to right and top to bottom, so that interactions in the upper-right triangle are for consumers feeding on resources smaller than themselves. Dashed diagonals lines indicate the position that cannibalistic interactions would take. Each element of the predation matrix is colored according to resource (row) profitability for the consumer (column) (yellow to red indicate low to high profitability, E_i/H_ij). In g and h, no color indicates zero profitability. In b, c, and d, variation in diet breadth is caused by the effect of consumer identity (c_j) on handling times; here, this effect is independent of consumer size.

All species only feed on those below themselves in the ordered set if we make the plausible assumption that larger consumers handle resources of a given size faster than smaller consumers. If so, λ̄·H̄, an important determinant of diet breadth (21), decreases with increasing consumer size, and diet breadth increases (Fig. 1 e and f).

Rule 2.

A consumer's resources occupy a contiguous section of niche space (15). This results from allometric foraging because a consumer j eats the most profitable k resources (where k is the number of species consumed), and these most profitable resources lie on a contiguous section of the body size axis (Fig. 1 b–f).

Rule 3.

Some consumers can feed a limited amount above themselves in the ordered set (15) (this is a relaxation of rule 2). The value of the allometric exponents determine whether and by how much species feed above themselves in the ordered set. For example, if handling time decreases very quickly with increasing consumer size, diet breadth increases very quickly with consumer size (Fig. 1 g). If diet breadth increases quickly enough, a consumer can feed on species above themselves in the ordered set.

Rule 4.

Consumer diets depend on their position in the ordered set. In some models this is will occur (although possibly weakly) as a statistical consequence of combinations of rules 1, 2, and 3 (e.g., cascade and niche models), whereas, in others, it is designed (16). If the axis in these previous models is taken to be body size, then consumers with similar body sizes tend to have more similar diets, and consumers that differ greatly in size have dissimilar diets. This rule is explicitly produced by allometric foraging, because handling times and encounter rates and, therefore, diet are a function of consumer body size (Fig. 1 e and f). This is not the case when variation in diet breadth is caused by an effect of consumer identity (c_j) that is independent of consumer size (e.g., Fig. 1 b–d).

Rule 5.

The section of niche space that a consumer feeds on may contain gaps (relaxation of rule 3) (16). This results from allometric foraging if a second resource trait influences handling time, e.g., H_ij = hM_i^h_iM_j^h_j + cC_i, where C_i is the second resource trait and c is a constant (19). If C_i and M_i are somewhat uncorrelated, handling time may be high, even though resource size (M_i) is optimal for a consumer, because C_i is large (Fig. 1 g and h). Note that we did not use a second trait in any of the analyses that follow.

The handling time function, in particular, has important effects on structure. We illustrate these with what we term the ratio handling time function and the power handling time function (see Materials and Methods for details). With the ratio handling time function, as the mass ratio between consumer and resource becomes small, handling time reduces to a constant (h/b), so that, no matter how small it is, a resource item will take time to handle. At first, a lower limit for handling times appears reasonable. This is intermediate between handling time increasing for very small resource items (e.g., ref. 22) or decreasing continuously (e.g., ref. 23). At a critical ratio (M_i/M_j = b), the handling time given by the ratio function becomes infinite as opposed to increasing continuously. An infinite handling time can be interpreted as complete inability to consume.

An influential consequence of these features is in the prediction of most profitable resource size. Maximum profitability max(P_ij) = max(E_i/H_ij) for the ratio handling time function is bM_j/2. Consequently, optimal resource size increases with consumer size, and minimum resource size may or may not (depending on exact parameter values) increase with increasing consumer size (Fig. 1f). For the power handling time, function max(P_ij) occurs at min(M_i) if h_i > 1 or max(M_i) if h_i < 1. Consequently, all consumers, regardless of their size, will consume the largest or smallest resource; here, minimum resource size cannot increase with consumer size (Fig. 1e). Some studies suggest that minimum prey size often increases, albeit only slowly, with predator size (e.g., refs. 24–29), although the pattern is not universal (e.g., refs. 24 and 30).

Quantitative Properties.

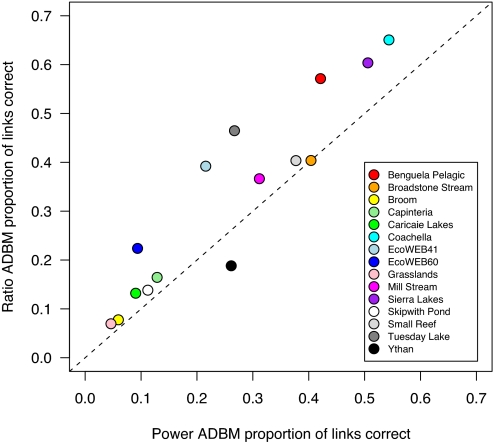
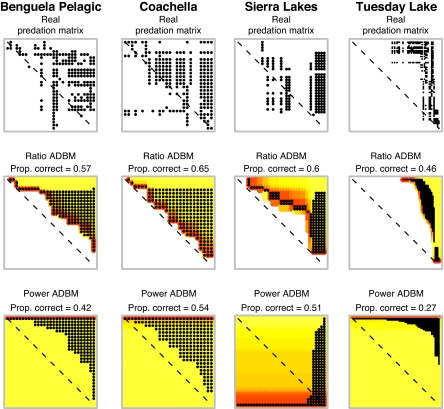
Across the real food webs, the proportion of links correctly predicted by the ADBM ranged from ≈0.05 to ≈0.65 and was generally greater for the ratio than the power handling time function (Fig. 2). The best predicted web was “Coachella Valley” (31), a food web of a desert ecosystem that includes plants, herbivores, and predators; here, 149 of 229 links were correctly predicted. The second best predicted was “Tuesday Lake” (32, 33), which contains phytoplankton, zooplankton, and fish (191 of 411 links correctly predicted). The two worst predicted were the “Grassland” food web (herbivores and parasitoids) and the “Broom” food web (herbivores, parasitoids, predators and pathogens) (8 of 115 and 8 of 103 links correctly predicted, respectively). Although it may be unsurprising that a size-based model fails to predict parasitoid interactions well, it is encouraging that it can predict well the links of both aquatic and terrestrial herbivores and predators. Indeed, the predicted predation matrices were often strikingly similar to the real food webs; for example, those for the food webs of the Benguela pelagic ecosystem, Coachella, Tuesday Lake, and Mill Stream [Fig. 3; all of the real and predicted predation matrices are given in supporting information (SI) Appendix].

Fig. 2.

Performance of the allometric diet breadth models (ADBM). Performance is measured as the proportion of correctly predicted feeding links. The ratio ADBM performs better than the power ADBM for 13 of the 15 modeled food webs. Paired t test: t = 3.6; df = 14; P = 0.003. The dashed line is the 1:1 relationship for reference.

Fig. 3.

Four real food webs and various models of them. Each predation matrix describes a food web, with resources in rows and consumers in columns. Body size increases from left to right and top to bottom. A black dot indicates the consumer in that column feeds upon the resource in that row. Hence, dots in the upper right triangle indicate feeding links where consumers are larger than their resources. The dashed diagonal line represents the position that cannibalistic links would occupy. Yellow to red indicate low to high resource profitability in the ADBM models. Here, consumer diets (columns of black dots) always include the darker red (most profitable) resources and extend by different amounts into yellows (less profitable resources). Ratio and power refer to the handling time allometries (see Materials and Methods). The predation matrices of all 15 real webs and their models are in SI Appendix.

We did not find that the complexity (i.e., number of parameters) of the ADBM was an important determinant of its performance (SI Appendix). Rather, the performance of the model results from its assumptions about the structural importance of size and foraging behavior in food webs. Nor did our use of allometry to estimate abundance appear flawed: Where in one case (Tuesday Lake) actual abundance data were available, using these rather than predicting abundance from body size produced only a small difference in performance (46% rather than 42% links correct).

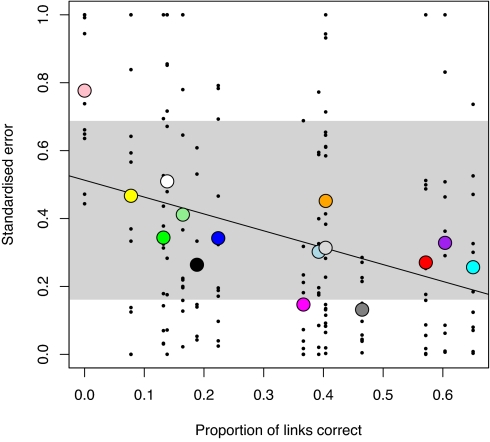
The ABDM predicted 12 structural properties of webs better when it predicted a greater proportion of the links correctly (Fig. 4). This confirms the intuitive idea that predicting a high proportion of links correctly will necessarily result in more accurate predictions of food web structure. Furthermore, the fit of the ADBM to these properties is similar to the range of fit given by the niche model (Fig. 4) (15).

Fig. 4.

Ability of the ADBM to predict food web structure. The standardized error in predicting 12 food web structural properties (listed in the SI Appendix) decreases with increases in the proportion of links correctly predicted. Large colored points are the mean standardized error of the ADBM for each web. Small black dots indicate the standardized error of each of the 12 properties for each web. Solid line is linear regression through the means (t = 3.0, df = 13, P = 0.01). The range of mean standardized error of the niche model (11) is shown by the vertical extent of the gray rectangle. The key in Fig. 2 applies.

The ADBM can predict well food webs in which observed diets are relatively contiguous along the body size axis. Conversely, it predicts less well the food webs in which diets of consumers are very noncontiguous along the size axis. This was confirmed by a strong positive relationship between the diet contiguity of real food webs (SI Appendix) and the performance of the ratio ADBM (r² = 0. 76, df = 13, P < 0.0001).

Some types of feeding interactions in the observed food webs were better predicted than others. Predacious and aquatic herbivore interactions were predicted better than parasitoid ones (across all food webs, predacious: 553/2,436 = 0.23; aquatic herbivory: 271/639 = 0.42; parasitoid: 8/124 = 0.06). Numbers of parasitic and pathogenic interactions were too rare (2 and 3, respectively) to warrant analyses. Note that these numbers are composed only of true-positive predictions and false-negative predictions, because information about types of trophic interaction was present only when a real feeding interaction occurred (and not for true-negative or false-positive predictions). There is potential value in comparison of the frequencies of false-positive and false-negative predictions. However, because observed and predicted connectance were equal, so was the number of false-positive and false-negative errors.

Discussion

For food webs that were well predicted, the success of ADBM can be explained by flexibility within general constraints. Allometric foraging places qualitative constraints on the diet of an individual consumer and on variation among the diets of consumers. An individual consumer only eats resources smaller than itself (given our handling time function) and does so for a contiguous range of the body size axis. Furthermore, the diets of consumers are related such that consumers with more similar body sizes have more similar diets than consumers with very different body sizes. Additionally, diet breadth increases, on average, with consumer size. This occurs at least because larger consumers can handle resources quicker than small ones and perhaps also because they encounter their prey more frequently (21). Within these general constraints, there is considerable flexibility in how links are distributed (Fig. 3). This flexibility is a function of the quantitative differences in the empirical body size distribution of the species in different webs, and the considerable influence on structure of the value of the allometric exponents. Studies of how these allometries differ between ecosystems, taxa, and feeding modes are now needed.

The greater performance of the ratio handling time function clearly derives from the potential for an increase in minimum resource size with increasing consumer size; this is not possible with the power handling time function. The increase in minimum resource size with consumer size can occur because there is a lower limit on handling times. Whether such a lower limit exists, whether it exists for some types of consumer and not others, and empirical estimates of it, are clearly important outstanding questions. At present, there appears to be insufficient information about the scaling of handling time with body size in the published literature to choose between these, or other types of function. Their importance for predicting who eats whom makes research into these scaling relationships a priority.

Currently, the parameterized ADBM necessarily predicts that each consumer feeds on a contiguous range of resource body sizes and predicts better webs where consumer's diet are more contiguous. Clearly, one development of the ADBM could be to include traits, other than size, that affect foraging variables (e.g., Fig. 1 g and h). For example, morphological or chemical defenses could alter handling times independent of body size. The effect of such defenses or other types of adaptation would be to allow noncontiguous diets along the size axis.

The more frequent correct prediction of predacious and aquatic herbivorous interactions supports the expectation that these better meet the assumptions of the contingency model of diet choice than parasitoid interactions and support work on the importance of feeding mode (e.g., parasitoid, parasite, pathogen, and predator) on food web structure (34–36). They also highlight the under representation of some types of links in food web data (pathogen and parasitic interactions). These findings also suggest that it would be interesting to explore the effect on the performance of the ADBM of incorporating consumer specific diet choice models (e.g., ref. 37) for parasites, pathogens, parasitoids, and probably terrestrial herbivores. Adaptive prey behavior (e.g., ref. 38) could also be incorporated, although each addition will come at the cost of increased model complexity.

We have avoided a detailed quantitative comparison between the performance of the ADBM and previous food web models, such as the cascade, niche, and nested hierarchy models (14–16). The only comparison that we make is between the approximate ranges of error in predicting aspects of food web structure (Fig. 4). This involves very few assumptions; in particular, it avoids assuming a size axis in niche model. Furthermore, although these previous models may make relatively good predictions of food web properties, they were never designed to predict the presence or absence of a particular feeding interaction, the arrangement of feeding interactions among a set of observed species, or the structure of a particular food web. Finally, the ADBM is also an entirely different type of model: It is deterministic, whereas the previous models are stochastic. These issues create significant questions over the utility of more detailed comparisons. We therefore restrict our comparison to the observation that the webs generated by the ADBM are equally good at predicting secondary structural properties (see 12 properties in Fig. 4) of the real webs as the most widely used phenomenological static model.

The ADBM models food webs by making explicit the individual-level mechanisms that determine diets. Web structure is an emergent consequence of these individual-level mechanisms, rather than of statistical rules about the distribution of links at the level of the whole food web. We believe the approach has considerable potential for answering longstanding questions about the determinants and drivers of food web structure. Apparent regularities in food web structures, such as food chain length, argue for robust, general mechanisms acting on all taxa. Foraging traits subject to natural selection provide such a general mechanism for the bounding of food web patterns. Our results support the idea that food webs are constrained in this way.

This perspective provides a simple yet robust conceptual framework for understanding the sometimes overwhelming complexity of ecological networks. It is a very different viewpoint, although not an exclusive one, to that in which the emergent properties of networks feedback and influence their structure, e.g., the idea that structure is constrained by stability (e.g., refs. 7 and 8). Although such theories are interesting, theoretically attractive and may play a part in structuring networks, our results suggest that building food webs from the bottom-up, by modeling the behavioral decisions of individuals, is a simple and promising alternative framework.

Materials and Methods

Model.

In the DBM (21), the contingency model of optimal foraging predicts the diet k of each consumer j that maximises rate of energy intake (20, 39),

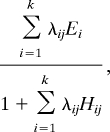where E_i is net energy gained by consumption of an individual of species i, H_ij is the time it takes for a consumer of species j to handle an individual of species i. The rate λ_ij at which individuals of species j encounter individuals of species i is the product of resource density N_i [dimensions of area⁻¹ or volume⁻¹] and attack rate A_ij [dimensions of area or volume time⁻¹]. In the ADBM we constrain the values of the parameters by scaling them with the body sizes of the consumers and resources.

If the mass of an individual of resource species i is M_i and of consumer species j is M_j, and lowercase letters are constants and exponents, the allometries we use are as follows: resource density, N_i = nM_i^n_i with n_i = −0.75 (ref. 40); energy content, E_i = eM_i; attack rate, A_i = aM_i^a_iM_j^a_j; ratio handling time function,

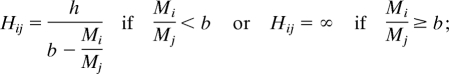and power handling time function, H_ij = hM_i^h_iM_j^h_j.

This scaling of density and body size is well established (25, 40), and the scaling of energetic content assumes a linear relation with body size. The allometry of attack rate was derived from ref. 41. Two simple and plausible handling time functions were used to illustrate their importance in predicting food web structure and because the literature contains inadequate information to chose one (SI Appendix).

Hereafter, terms that refer to the size of a species are generally shorthand for “the average size of an individual organisms of a species or life stage of a species.” The estimation of the species/life-stage sizes used in analyses of real food webs is detailed in Brose et al. (42).

Qualitative Model Properties.

First, we investigated how the mechanisms specified in the ADBM can reproduce the phenomenological rules used in previous static food web models and, therefore, might be expected to generate at least equally plausible food webs. The first rule (an ordered set and feeding depending on that order) is essential components of the cascade model and important components of later and more complex models (12, 14–16, 18). In the niche model (15), consumers feed on contiguous portion of the niche axis (Rule 2), and there is some scope for feeding on species higher in the niche axis (Rule 3). The nested hierarchy model (16) explicitly creates groups of consumers with similar diets (Rule 4) and allows gaps in consumers' otherwise contiguous resource niches (Rule 5). We also explore the qualitative importance of the handling time function for food web structure.

Quantitative Model Performance.

To assess the quantitative performance of the ADBM, we assembled data on the average body sizes of species (or life stages if a species is, for example, composed of larvae and adults of very different size) in 15 real food webs (SI Appendix). Because the literature does not contain empirical data for the allometries required in the model, we parameterized by optimisation, i.e., we held the number of links the same as observed in the real web and derived values of constants and exponents that maximized the number of links correctly predicted (SI Appendix). Our modeling effort therefore asks how well our model can predict the arrangement rather than the number of feeding links in food webs. This approach is akin to fitting a regression to data and then examining the quality of fit. We fit the ADBM separately to each of the 15 real food webs, because these differed greatly in ecosystem and taxa; exponents of allometric relationships can vary among these (25).

For each modeled food web, we counted the number of links predicted that were in the correct position, i.e., between a pair of species that consume each other in the real food web. This number of links correctly predicted was divided by the total number of predicted links. For example, if the model predicted 100 links, and 50 were between pairs of species connected by real feeding links, the performance was 50%. Because the number of predicted links (and therefore connectance) was constrained to be the same as that in real food webs, the model could not perform well simply because it predicted a food web with high connectance.

Few studies have used proportion of links predicted correctly as a measure of model fit; most have focused on how well a model predicts structural properties of food webs, such as food chain lengths and levels of omnivory. We calculated 12 structural properties for the real food webs and their models and summarized fit to each real food web as the mean standardized error (SI Appendix).

Trophic interactions were classified as either herbivorous, parasitic, parasitoid, pathogenic, or predacious in 9 of the 15 food webs. Across these nine webs, we counted the number of times each of these type of links was predicted correctly or incorrectly.