Abstract
Demographic stochasticity and heterogeneity in transmission of infection can affect the dynamics of host–vector disease systems in important ways. We discuss the use of analytic techniques to assess the impact of demographic stochasticity in both well-mixed and heterogeneous settings. Disease invasion probabilities can be calculated using branching process methodology. We review the use of this theory for host–vector infections and examine its use in the face of heterogeneous transmission. Situations in which there is a marked asymmetry in transmission between host and vector are seen to be of particular interest. For endemic infections, stochasticity leads to variation in prevalence about the endemic level. If these fluctuations are large enough, disease extinction can occur via endemic fade-out. We develop moment equations that quantify the impact of stochasticity, providing insight into the likelihood of stochastic extinction. We frame our discussion in terms of the simple Ross malaria model, but discuss extensions to more realistic host–vector models.
Keywords: vector-borne infection, multi-group model, heterogeneity, stochasticity, branching process, moment equations
1. Introduction
Many of the infections that have the greatest impact on human health, either in terms of mortality or morbidity, are vector borne. Mosquitoes are perhaps the best known disease vectors, with various species playing a role in the transmission of infections such as malaria, yellow fever, dengue fever and West Nile virus. Mathematical modelling has a long history of use in these settings, particularly in the case of malaria, with the Ross model (Ross 1910, 1911), later extended by Macdonald (1952), providing a simplified description of the transmission dynamics of malaria. This modelling framework has a broader applicability to other mosquito-borne infections and indeed to other host–vector infections.
Despite its simplicity, the Ross model has provided many insights into the spread of host–vector infections. Most notably, use of the model identified a threshold condition for the invasion and persistence of infection. These studies lead to the identification of perhaps the most important concept in mathematical epidemiology, the basic reproductive number of an infection. This quantity, written as R0, gives the average number of secondary infections that arise when a single infectious individual is introduced into an otherwise entirely susceptible population. If this basic reproductive number is greater than 1, then introduction of infection can lead to a disease outbreak.
Following the typical path of model development from a simple starting point through increasingly more complex forms, numerous refinements of the Ross model have been developed. These include models that include more realistic depictions of the transmission cycle of the infection and the demographics of both vector and host populations.
Heterogeneity in the transmission of vector-borne diseases has been well documented, both in observational and modelling studies. A striking result is that, for many infections, 20% of individuals are responsible for 80% of transmission—the so-called 20–80 rule (Woolhouse et al. 1997). As a result, models that ignore heterogeneity may be seriously misleading, importantly giving rise to inaccurate estimates of the likely success of disease control strategies.
Many of the models that have been employed in vector-borne settings have been deterministic, ignoring the possible importance of random effects. Some studies, however, have highlighted the effects that stochasticity can have on transmission (e.g. Bartlett 1964; Griffiths 1972; Dye & Hasibeder 1986). Random effects can exert a major impact whenever the prevalence of infection—in either the host or vector population, or both—is low. If there are few infectives, then it is possible for all of them to recover or die before passing on infection. Stochastic effects can be highly significant during the period immediately after the introduction of infection into a population: disease invasion is often highly stochastic. Random effects can also lead to extinction in endemic settings (Bartlett 1956). Whereas deterministic models often predict that the prevalence of infection will approach a stable equilibrium, random effects lead to the system being buffeted about this equilibrium. Stochasticity can lead to large departures from the equilibrium, potentially allowing the number of infectives to fall to low levels. Stochastic extinction, known as disease fade-out, can occur during such excursions.
In this study, we shall examine the impact of stochastic effects on the invasion and persistence of a vector-borne infection, both in well-mixed and in heterogeneous settings. This paper is organized as follows: following a brief review of the deterministic Ross model and its properties, we shall describe the corresponding stochastic formulation. We then examine the probability that disease invasion will occur following a given introduction. The impact of demographic stochasticity in the endemic setting is then discussed. After reviewing the way by which heterogeneity in transmission can be incorporated into the Ross framework, we assess the impact of stochasticity in heterogeneous settings.
2. The deterministic Ross model
The Ross model (Ross 1910, 1911) assumes that each host is, at any point in time, either susceptible to the infection or has the infection, in which case they are infectious. The host population size is assumed to be constant and its size is denoted by H. The number of hosts that are infectious is written as Y, which means that there are H−Y susceptibles. The fractions of the host population that are infectious and susceptible are given by Y/H and (H−Y)/H, respectively.
In a similar way, vectors are assumed to be either susceptible or infectious. We write the size of the vector population as V and the number of infectious vectors as I. It is assumed that the size of the vector population is constant: the rate at which vectors die balances the rate at which they are born. Newly born vectors are taken to be susceptible: it is assumed that no vertical transmission occurs.
A susceptible host can acquire infection by being bitten by an infected vector. A key assumption of the model is that the rate at which a given vector bites hosts is independent of the number of hosts that are present. For a mosquito-borne infection, this corresponds to assuming that each mosquito needs only a certain number of blood meals per unit time and there are sufficiently many hosts present for each mosquito to always be able to find a meal. Assuming that vectors do not have to compete for hosts on which to bite, the overall rate at which bites occur is proportional to the number of vectors but independent of the number of hosts. This asymmetry between hosts and vectors is a central feature of the model.
A single vector is taken to bite hosts at a rate of k bites per unit time. The probability of transmission occurring if an infectious vector bites a susceptible host once is written as p. This is the per-bite vector to host transmission probability. We denote the product kp by α. Once infected, a host remains infectious for an average of 1/ξ time units, after which they recover and are again susceptible.
The probability of transmission occurring if a susceptible vector bites an infectious host once is written as q, the per-bite host to vector transmission probability. We denote the product kq by β. Once infected, a vector remains infectious until it dies and it is assumed that infectious vectors live for an average of 1/δ time units.
With the above description, together with the assumptions of a constant recovery rate for hosts and a constant death rate for infective vectors, the model can be written as the following pair of differential equations:
| (2.1) |
| (2.2) |
2.1 The basic reproductive number, R0
The basic reproductive number gives the average number of secondary infections that would result from the introduction of a single infective individual into an entirely susceptible population. The two-step life cycle of the infection means that calculation of R0 involves looking at the two-step process: host to vector, then vector back to host (or vice versa).
Let be the average number of hosts directly infected by the introduction of a single infective vector into an entirely susceptible host population. Similarly, denote the average number of vectors that become directly infected upon the introduction of a single infectious host into an entirely susceptible vector population by . When the host population is entirely susceptible (Y=0), the transmission rate from the vector population to the host population is αI. Thus, the transmission rate per infective vector is α. Infective vectors live for an average of 1/δ time units, and so a single infective vector will give rise to an average of infective hosts. Employing a similar argument for an entirely susceptible vector population (I=0), we obtain .
Over the entire transmission cycle, one infective host gives rise to an average of
| (2.3) |
secondary infections in the host population. The same result is obtained if one looks at the average number of secondary infections in the vector population that results from the introduction of an infective vector.
Note that R0 is proportional to the size of the vector population but inversely proportional to the size of the host population. This results from the asymmetry in the dependence of the vector's biting rate on the sizes of the host and vector populations. Writing the term βα as k2pq, we obtain the well-known result that R0 depends on the square of the biting rate, since the transmission cycle involves two biting events.
For the deterministic Ross model, R0=1 defines a threshold condition for both invasion and persistence of infection. If the basic reproductive number is greater than 1, then the number of infectives will initially increase following the introduction of infection: the infection-free state is unstable. In the long term, the system will approach a stable endemic equilibrium, at which the numbers of infective vectors and hosts are positive. If the basic reproductive number is less than 1, then the infection will die out in the long term.
3. Demographic stochasticity in the Ross model
Rather than considering the average rates at which individuals move between classes, models with demographic stochasticity consider the discrete movements of individuals between classes (Bartlett 1956, 1960). The numbers in each class are no longer treated as continuously varying quantities; instead, the numbers in the stochastic model are taken to be integers. The rates that appear in the deterministic model are recast in terms of probabilities of the occurrence of each event (infection of host or vector, recovery and death) in a short time interval (table 1).
Table 1.
Events of the Ross model, their rates and probabilities of occurrence in a time interval of length dt.
| event | transition | rate at which event occurs | probability of transition in time interval [t, t+dt] |
|---|---|---|---|
| infection of host | Y→Y+1 | αI((H−Y)/H) | αI((H−Y)/H)dt |
| infection of vector | I→I+1 | β(V−I)(Y/H) | β(V−I)(Y/H)dt |
| recovery of host | Y→Y−1 | ξY | ξY dt |
| death of vector | I→I−1 | δI | δI dt |
An important possibility that this description raises is that the last infective can recover before infection is transmitted: the prevalence of infection can decrease to zero, following which the infection can only reoccur if it is reintroduced from outside the population. In contrast, many deterministic models have the weakness that infection can fall to very low levels—well below the point at which there is only one infective individual—only to rise up later. Thus, under some circumstances, persistence of infection in deterministic models can be an artefact of their allowing fractional numbers of infective ‘individuals’ (Mollison 1991).
3.1 Invasion probabilities
In the stochastic model, invasion of an infection into a naive population is not guaranteed by having R0 greater than 1: stochastic extinction can occur during the period immediately following introduction, when there are few infectives. Rather than the major outbreak that would be expected based on the behaviour of the deterministic model, only a minor outbreak might occur. During this early period after introduction, little depletion of susceptibles will have occurred and so invasion probabilities can be derived using the linear model that arises by assuming that the populations are entirely susceptible (Bartlett 1964; Griffiths 1972; Ball 1983). In the host–vector setting, these probabilities were first calculated by Bartlett (1964), using branching process theory (Athreya & Ney 1972; see also Ball 1983). Although the branching process approach is commonly used, it should be pointed out that it is not the only way to obtain these probabilities: Griffiths (1972), for example, used the backwards Kolmogorov equations.
Branching process theory tells us that the likelihood of invasion depends not only on the average number of secondary infections (i.e. R0), but also on their distribution about this average. The Ross model assumes a constant rate of recovery for the hosts and a constant death rate for infected vectors, leading to the duration of infection, for both hosts and vectors, being exponentially distributed. If secondary infections arise independently and at a constant rate over these infectious periods, the distributions of secondary infections both follow geometric distributions, with means and , respectively (e.g. Diekmann & Heesterbeek 2000). We remark that another description of infectious periods is sometimes deployed, namely that they are of fixed durations (for hosts and vectors, separately): this situation is discussed in the electronic supplementary material.
Extinction in the linear model is most likely to occur early in the process, so this corresponds to the occurrence of a minor outbreak in the nonlinear model, whereas non-extinction in the linear model corresponds to a major outbreak in the nonlinear model. The main result of branching process theory (Athreya & Ney 1972) can be used to calculate the probability of extinction in the linear model, following the introduction of a single infectious individual. This extinction probability, which we write as s, is found by calculating the smallest non-negative root of the equation
| (3.1) |
Here G(s) is the probability generating function of the distribution of secondary infections. The generating function is a mathematical way of summarizing the distribution of a discrete random variable, X, that can take non-negative integer values (e.g. Grimmett & Stirzaker 1992) and is given by the formula
| (3.2) |
Here P(X=k) stands for the probability that X takes the value k. It is straightforward to show that the generating function for a geometric distribution is given by
| (3.3) |
where μ is the average value. Once the extinction probability, s, is known, the probability of a major outbreak can be calculated as 1−s.
If the average number of secondary infections is greater than 1, then the relevant solution of (3.1) is less than 1, otherwise the solution will be equal to 1 (Athreya & Ney 1972). In the setting of a directly transmitted infection, this leads to the well-known result that the probability of a major outbreak, following the introduction of a single infective, i.e. the invasion probability, is equal to 1−1/R0 when R0 is greater than 1 (Bartlett 1960; Diekmann & Heesterbeek 2000).
When there is more than one type of individual, as in a host–vector model, multi-type branching process theory can be used to calculate extinction and invasion probabilities (Athreya & Ney 1972; see Becker & Marschner (1990) for a discussion in the context of a directly transmitted infection). When there are two types of individuals, which we label as 1 and 2, their distributions of secondary infections of each type can be summarized by the two generating functions,
| (3.4) |
Here, i is equal to 1 or 2 and Xij is the random variable giving the number of secondary infections of type j that arise from an individual of type i.
Extinction probabilities can be calculated by solving the pair of equations, G1(s1, s2)=s1 and G2(s1, s2)=s2. Then s1 gives the probability of extinction starting from a single individual of type 1, and s2 gives the corresponding probability for type 2. (As before, the probability of a major outbreak can be calculated as 1 minus the appropriate extinction probability.) The pair (s1, s2)=(1, 1) is always a solution. If R0≤1 it is the only solution, whereas if R0>1 there is another solution with both s1 and s2 being less than 1 (Athreya & Ney 1972). In other words, when R0 is less than or equal to 1, only minor outbreaks can occur, whereas when R0 is greater than 1, there is a positive probability of a major outbreak.
In the Ross model, for which we label the two types H and V, infective hosts only directly give rise to secondary infections in the vector population. Thus, we have that P(XHH=j, XHV=k) is equal to P(XHV=k) when j=0, and is zero otherwise. Consequently, the generating function GH(sH, sV) is a function of sV alone,
| (3.5) |
By the same argument, the generating function GV(sH, sV) has the form
| (3.6) |
Solving for the extinction probabilities gives the two equations,
| (3.7) |
and
| (3.8) |
We remark that the form of (3.7) and (3.8) should not be surprising, since we have a two-step life cycle from one type to the other and then back to the original, and it is well known that the generating function for such a two-step life cycle is the composition of the two single-step generating functions (e.g. Grimmett & Stirzaker 1992). An important observation is that the two extinction probabilities are not, in general, equal because the composition of functions typically depends on the order of composition.
Calculation of the extinction probability following the introduction of a single infectious vector (Bartlett 1964), under the assumptions of constant recovery and death rates, requires finding the smallest non-negative root of
| (3.9) |
It is easy to show that the relevant solution is the smaller of 1 and
| (3.10) |
Furthermore, expression (3.10) is smaller than 1, and hence is the relevant solution, if and only if the product is greater than 1. This condition is exactly that R0 is greater than 1. Consequently, when R0 is less than or equal to 1, the relevant solution is 1 and so a major outbreak can never happen. For R0>1, the probability of a major outbreak, following the introduction of a single infectious vector, is (Bartlett 1964)
| (3.11) |
The probability of a major outbreak following the introduction of a single infectious host is found by swapping the roles of and in the preceding argument. For R0>1, this probability is equal to
| (3.12) |
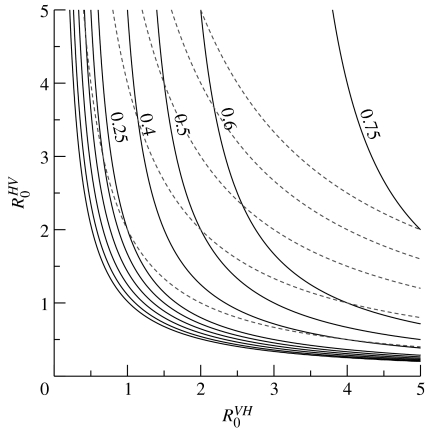
Figure 1 depicts the dependence of the probability of a major outbreak following the introduction of a single infective vector on and . Since the overall basic reproductive number is the product of these two quantities, invasion is possible even if one of these is less than 1. The asymmetric dependence of the invasion probability on these two single-step basic reproductive numbers is clear. Looking along the contour corresponding to an overall R0 value of 10 (the rightmost dashed curve in the figure), we see that the probability of a major outbreak is 0.75 if is 5 and is 2, whereas this probability falls to 0.6 if is 2 and is 5. Extinction is more likely to occur if the transmission step with the lower R0 comes first. We remark that one situation that can lead to such asymmetry is when there is a large disparity between the sizes of the host and vector populations, due to the appearance of the V/H term in the expression for .
Figure 1.
Invasion probabilities in the Ross model. The solid curves are contours in the plane along which the probability of a major outbreak, following the introduction of a single infective vector, is constant. From left to right, the contours are shown for invasion probabilities of 0.01, 0.05, 0.1, 0.15, 0.2, 0.25, 0.4, 0.5, 0.6 and 0.75. Where space permits, these probabilities are indicated to the right of the contours. The dashed curves denote contours along which the overall R0 (i.e. the product ) is constant. From left to right, these curves depict R0 values of 2, 4, 6, 8 and 10. As discussed in the text, the corresponding figure for the probabilities following the introduction of a single infective host can be obtained by switching the labels of the two axes.
3.2 Moment equations
For the deterministic model, repeated simulation, starting from the same initial conditions, always leads to the same outcome. This is not true for the stochastic model: random effects mean that the model realizations generated by such repeated simulation will typically follow different trajectories. The changing numbers of infectives over time must now be described in terms of a probability distribution. We write pt(y, i) to denote the probability of there being y infective hosts and i infective vectors at time t, starting from some specified initial condition. (Since the numbers of infectives can never be negative or exceed the appropriate population size, we define pt(y, i) to equal zero whenever y<0, i<0, y>H or i>V.)
Using the probabilities from table 1, the following expression can be derived for the probability that the system will have (y, i) infectives at time t+dt in terms of the state of the system at time t:
| (3.13) |
After rearranging, dividing through by dt and taking the limit as dt approaches zero, the following is obtained:
| (3.14) |
This set of (H+1)(V+1) differential equations, known as the Kolmogorov forward equations (Grimmett & Stirzaker 1992), describes how the probability distribution of the random variable pair (Y, I) changes over time. Noting that this set is linear in the pt(y, i), it can be written in the form
| (3.15) |
where A is a constant (H+1)(V+1)×(H+1)(V+1) matrix and p(t) is a vector that contains the pt(y, i), arranged in some suitable order. The matrix A is sparse: since there are at most four transitions by which a typical state can be departed, most of the entries of A are zero.
The Kolmogorov equations can be solved analytically in terms of matrix exponentials or by numerical integration. They can also be used to find stationary distribution(s) of the system: this involves finding a suitably normalized vector p such that Ap=0. (In other words, p is an eigenvector of A with eigenvalue zero.) The size of the equation set, however, limits the usefulness of the Kolmogorov equations for all but the smallest population sizes. Instead, numerical simulations of the stochastic model can be carried out using standard Monte Carlo techniques (Kendall 1950; Bartlett 1956, 1960), although these can be computationally expensive, particularly if large numbers of realizations are required or if the population sizes are large.
An alternative analytic approach involves consideration of the moments of the distribution of (Y, I). Starting from the Kolmogorov equations, the following equation for the time derivative of the expectation of a function of (Y, I), E(f(Y, I)), can be derived (e.g. Gardiner 1985):
| (3.16) |
Here j labels the four possible events (infection of host, infection of vector, recovery of host and death of vector); λj(Y, I) is the rate at which event j occurs; and (Δf(Y, I))j is the change in f(Y, I) that results when event j occurs.
Using this result, the following differential equations that describe how the first two moments of the (Y, I) distribution change over time can be derived:
| (3.17) |
| (3.18) |
| (3.19) |
| (3.20) |
| (3.21) |
The equations for the first-order moments—the averages E(Y) and E(I)—can be rewritten using the formula for the expectation of the product of random variables, E(YI)=E(Y)E(I)+cov(Y, I). Then replacing E(Y) by Y and E(I) by I gives a pair of equations that closely resembles the deterministic system (equations (2.1) and (2.2)), except for the presence of two terms, each of which is proportional to the covariance cov(Y, I). In general, the covariance of two random variables is non-zero, and so the deterministic model does not give an exact description of the average behaviour of the stochastic model. Instead, we can view the deterministic model as an approximation to the average behaviour if it is assumed that the covariance is zero, i.e. that the second-order central moment E({Y−E(Y)}{I−E(I)}) vanishes.
As we have just seen, the equations for the first-order moments involve second-order moments. Similarly, the equations for the second-order moments involve third-order moments. A corresponding result holds for the equations for the moments of each order. In order to obtain a finite set of moment equations, the set of equations must be truncated at some point. This involves making what is known as a moment closure assumption. We have seen that the deterministic model corresponds to assuming that second-order central moments are zero. To close our set at second order, we employ the multivariate normal approximation, which assumes that all third-order central moments vanish (Whittle 1957; Isham 1991; Lloyd 2004). For instance, we take E({Y−E(Y)}2{I−E(I)}) to equal zero. Multiplying out the brackets inside the expectation and simplifying using the linearity properties of the expectation operator, we see that the moment closure assumption applied to this term gives
| (3.22) |
This can be rearranged to give the third-order moment E(Y2I) in terms of lower-order moments,
| (3.23) |
Similarly, the moment closure approximation also gives
| (3.24) |
Substituting (3.23) and (3.24) into (3.17)–(3.21) yields a set of equations that are closed at the second order.
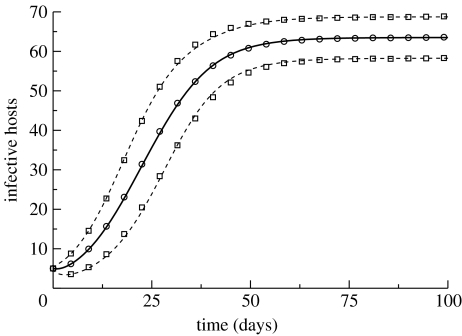
The closed set of second-order moment equations can be used to estimate the variability seen between realizations of the stochastic model at any point in time. It should be kept in mind that the moment equations are only an approximation to the variation exhibited by the system. Since we lack a good description of the adequacy of this approximation, their use is typically supplemented by the numerical simulation of the stochastic model. Such a comparison is made in figure 2, where the performance of the moment equations is compared with moments calculated over a collection of realizations obtained by simulation of the stochastic model.
Figure 2.
Moments of the stochastic model, shown as the mean number of infective hosts (solid curve) and mean ± s.d. (dashed curves), calculated using the moment equations. For comparison, numerical estimates of these quantities, obtained by averaging over 10 000 simulation runs of the stochastic model, are shown by the symbols. The initial condition has five infective hosts and five infective vectors. Parameter values are as follows: p=0.2; q=0.15; k=0.5; ξ=δ=1/7; H=100; and V=1000. The simulation-based estimates of moments are only calculated over realizations in which the infection has not undergone extinction by the time of interest (i.e. they are moments conditional on non-extinction). For the parameter values employed, extinction occurred in less than 2% of simulation runs.
We see that, at least for the set of parameter values and initial conditions used, the moment equations provide a fairly good approximation. It should be pointed out, however, that the moment equations perform less well, at least during the initial transient, if the initial numbers of infectives are small (below approx. five each, for the parameter set employed in the figure), although they do give the correct long-term values of the moments. This weakness of the moment equations is due to the higher probability of extinction if the system is started with few infectives and is a reflection of the moment equations' inability to capture the extinction events. (Extinction only occurred in 2% of the realizations underlying figure 2, whereas roughly 55% of realizations undergo extinction if the simulation is started with just one initial infective host and one initial infective vector.)
3.3 Variability about the endemic equilibrium
In the long run, the infection is guaranteed to go extinct: the only stationary state of the stochastic model has p(0, 0)=1 and all other p(y, i) equal to zero. Although it will eventually happen, extinction might only occur over a very long time scale. Over intermediate time scales, however, the system may appear to exhibit stationary behaviour, as described by the so-called quasi-stationary distribution (such behaviour is visible in figure 2 for t larger than approx. 80). This distribution can be found by examining the behaviour of the system conditional on non-extinction, as described by the probabilities qt(y, i), given by
| (3.25) |
for (y, i)≠(0, 0) (Darroch & Seneta 1967; Nåsell 1991). Here, the denominator gives the probability that extinction has not occurred by time t.
The quasi-stationary distribution captures the variability of realizations about the endemic equilibrium, providing a description of how far realizations wander away from the equilibrium as they are buffeted by demographic stochasticity. Assuming that the average prevalence of infection does not fall to low levels, extinction would be unlikely to occur if realizations remained very close to the average behaviour, whereas extinction would be much more likely if realizations wander over distances that are comparable to the average. Consequently, the coefficient of variation (the standard deviation divided by the mean) of the number of infectives has been suggested as a surrogate measure for the probability of extinction for directly transmitted infections (Keeling 2000; Lloyd 2004). In fact, making some additional assumptions, expressions for extinction probabilities can be written in terms of this quantity (Nåsell 1999). The situation is more delicate for a vector-borne infection since stochastic fade-out requires simultaneous extinction of infection in both host and vector populations: analogous expressions for extinction probabilities have yet to be developed for vector-borne infections. (The development of such expressions is beyond the scope of this study.)
The moment equations can be used to quantify the variability seen about the endemic equilibrium. Since the equations are an approximation, we assess their accuracy by comparison with a characterization of the quasi-stationary distribution obtained by Nåsell (1991) for a particular small population. Standard results (Darroch & Seneta 1967) show that, as with the stationary distribution, the quasi-stationary distribution can be found using an eigenvalue/eigenvector calculation. Removing the rows and columns of A that correspond to the state (0, 0) gives a matrix that we denote A′. The vector q is found as the appropriately normalized eigenvector corresponding to the largest eigenvalue of A′. Unless the system size is small, the size of the matrix A makes this calculation difficult, although the sparseness of A can be exploited. For the 50 host and 100 vector population employed by Nåsell (1991), A is a 5151 by 5151 matrix.
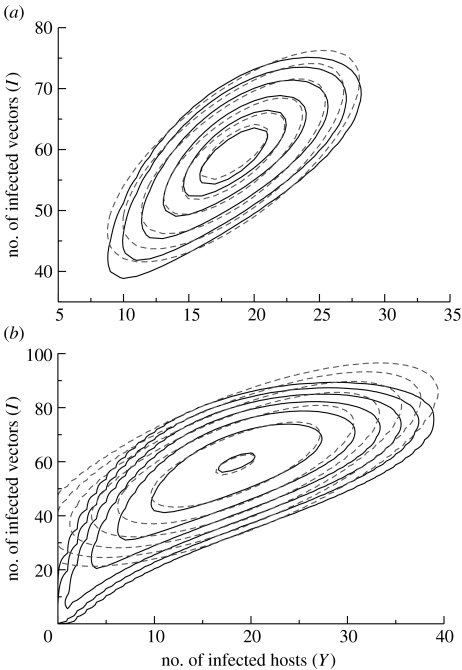
Figure 3 shows contours of the quasi-stationary probability density function, q(y, i), for various values of the density. For the bivariate normal distribution, these contours are ellipses (Grimmett & Stirzaker 1992). We see that the moment equations provide an excellent approximation for the main part of the distribution (figure 3a). The moment equations provide a relatively poor description of the tail of the distribution (figure 3b), which may well limit their use in providing a detailed quantitative description of extinction in the system.
Figure 3.
Quasi-stationary distribution of the numbers of infective hosts and infective vectors. The solid curves are contours of the probability density function calculated directly from the Kolmogorov equations. Dashed curves denote the corresponding contours calculated using the multivariate normal approximation. As discussed in the text, these contours are ellipses. (a) Contour heights are such that the ellipses of the multivariate normal distribution enclose 20, 40, 50, 80, 90 and 95% of the mass of the distribution. (b) Contour heights employed by Nåsell (1991) are used; his choice of contours emphasizes the tail of the distribution. Note that the scales on the axes differ between (a) and (b). The same set of parameter values is used for both (a) and (b) and is the set employed by Nåsell (1991), with α=0.05, β=4, ξ=0.1, δ=1, H=50 and V=100.
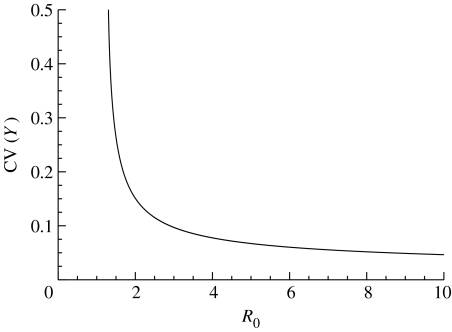
The variation seen about the endemic equilibrium depends on the parameter values of the model. Standard results (Kurtz 1971) show that, if the sizes of the host and vector populations are both taken to be proportional to N, then the variability, as measured by the coefficient of variation, scales as . In models for directly transmitted infections, it is well known that variability decreases as R0 is increased (Bartlett 1956; Nåsell 1996, 2002; Lloyd 2004). Figure 4, which shows the variability seen in the numbers of infective hosts in the quasi-stationary distribution about the endemic equilibrium, shows that this is also the case for the Ross model.
Figure 4.
Dependence of variability, as measured by the coefficient of variation and calculated using the moment equations, in the number of infective hosts seen about the endemic equilibrium as the basic reproductive number is varied. Parameter values are as follows: p=0.2; q=0.15; ξ=δ=1/7; H=100; and V=1000; and the biting rate, k, is varied to give the range of R0 values shown.
4. Multi-group extension
We now consider a situation in which there are m types of host and n types of vector (Barbour 1978; Dietz 1980; Dye & Hasibeder 1986). These types could signify, for instance, different classes based on genetic, behavioural or spatial distinctions.
Transmission parameters are allowed to differ between the types, and we label types by subscripts. Transmission from vector type i to host type j is described in terms of the transmission parameter αij. This αij is the product of the rate at which a vector of type i bites hosts of type j, kij, and the probability, pij, that such a bite would lead to transmission if the vector were infective and the host susceptible. In a similar way, transmission from host type i to vector type j is depicted in terms of the transmission parameter βij, which is the product of the biting rate kji and the transmission probability qij. (Note that the indices i and j are transposed in the biting rate when we consider transmission from host to vector.) The kij could be further decomposed: for instance, Dye & Hasibeder (1986) assume that vectors of each type have the same biting rate but that their bites are distributed differently across the different host types, writing kij=kγij, where .
We assume that αij and βij are such that there is the potential for the infection to spread between all pairs of types of individuals, although this could involve an infection chain that includes a number of intermediates. This assumption corresponds to the notion that the population cannot be subdivided into non-interacting groups. Finally, the host recovery rate ξi and the vector death rate δi can differ between the appropriate types.
Labelling H, V, I and Y according to their types, the model can be written as
| (4.1) |
| (4.2) |
Here the index j takes values from 1 to m, while l runs from 1 to n. The total numbers of hosts and vectors are written as H and V, respectively.
The earlier R0 calculation must be extended to account for the different types of hosts and vectors (Barbour 1978; Dietz 1980; Dye & Hasibeder 1986). Standard epidemiological theory tells us that the correct way to do this is to find the largest (dominant) eigenvalue of the so-called next generation matrix (Diekmann et al. 1990). The entries of this matrix, which we write as , tell us the average number of secondary infections that arise among hosts of type j when a host of type i is introduced into an entirely susceptible population. (Alternatively, and equivalently in terms of this calculation, one could work with the next generation matrix for vectors. We would write the entries of this matrix as .) An infective host of type i can give rise to a secondary infection of a host of type j by any one of n routes, involving the intermediate infection of one of the various vector types. Following the earlier argument, we have that
| (4.3) |
Here (respectively, ) gives the average number of secondary infections among vectors of type j (respectively, hosts of type i) that arise from a host of type i (respectively, a vector of type j)
The eigenvalues of the m×m next generation matrix can be found by solving a polynomial of degree m. We typically cannot find a simple formula for R0 in multi-group models unless some additional assumptions are made that lead to the matrix having some simple form. One well-studied setting (Diekmann & Heesterbeek 2000) involves separable next generation matrices, where takes the form aibj. In this case, the matrix is a rank 1 matrix; each column is a multiple of the vector a=(a1, a2, …, am)T. It is easy to see that a is an eigenvector of this matrix, with eigenvalue , and that all other eigenvalues equal zero. Hence, the basic reproductive number is equal to .
As a specific example, Dye & Hasibeder (1986) consider a setting in which vectors preferentially bite some people over others, employing a model in which there is one type of vector and m types of hosts. The vector biting rate is k, but these bites are allocated among the different types of hosts according to the fractions γi. The per-bite probability of transmission from an infected vector to a susceptible host of type i is written as pi and the per-bite probability of transmission from an infective host of type i to a susceptible vector as qi. If the lifespan of an infected vector is the same, regardless of its type, then the entries of the next generation matrix are k2γiγjqipjV/(δξHi). This matrix is of the separable form, and so we have
| (4.4) |
Further, Dye & Hasibeder (1986) assume that each pi is equal to p, and each qi is equal to q. If the fraction of hosts that are of type i is then written as hi, so that Hi=hiH, the expression for R0 becomes
| (4.5) |
This formula involves the sum of squares of the quantities γi/hi, weighted by hi. Using a result that relates the variance to the sums of squares and the square of the mean, often written in the form Var(X)=E(X2)−E(X)2, Dye and Hasibeder rewrite R0 as (k2pqV/δξH){1+Var(γi/hi,hi)}. The variance here is that of the quantities γi/hi, weighted by the fractions hi. Heterogeneity, which leads to this variance being greater than zero, inflates the value of R0 in a way that is familiar from a number of settings (Dietz 1980; Becker & Marschner 1990).
4.1 Invasion probabilities
The multi-type branching process described above can be extended in an obvious way to consider the m+n types of individuals of the multi-group model. The probabilities of the occurrence of major outbreaks, starting from a single individual of a given type, are found by solving the set of equations
| (4.6) |
| (4.7) |
Here, and give the extinction probabilities starting from one infectious host of type i or one infectious vector of type j, respectively. Using an obvious extension of the earlier notation, the generating functions and describe the distributions of the numbers of secondary infections of each type to which a host of type i and a vector of type j, respectively, give rise. As before, the lack of direct host to host and vector to vector transmission simplifies these equations: the do not depend on the and the do not depend on the .
These equations always have a solution with all and all . If R0 is greater than 1, there is also a solution with all the s strictly less than 1 (Athreya & Ney 1972): a major outbreak can occur. Invasion occurs with probability if a single infective type j vector is introduced, or with probability if a single infective type i host is introduced. If infection is introduced via a randomly selected individual, then the major outbreak probability is calculated as a weighted sum of the type-specific invasion probabilities (Becker & Marschner 1990). For instance, if infection is introduced via a host, with the probability that this host is of type i equalling πi, then the probability of a major outbreak is given by .
A further simplification of (4.6) and (4.7) occurs if the numbers of secondary infections of different types that arise from each individual are independent. In this case, the generating functions can be written as the products of simpler generating functions (Grimmett & Stirzaker 1992). This situation holds when infection is of fixed duration (see the electronic supplementary material for further discussion of this case). In general, however, the numbers of secondary infections are not independent. In particular, this is the case for the Ross model, with its exponential distributions of infectious periods. Although each individual is assumed to give rise to secondary infections of the different types independently and at constant rates over their infectious period, the distribution of infectious periods leads to non-independence. For example, an individual whose infectious period happens to be short will probably give rise to fewer secondary infections of each type than the typical individual. Similarly, if they happen to have a long infectious period, they will probably give rise to more than the average number of secondary infections of each type. Consequently, there will be some correlation between the numbers of secondary infections of the different types. (See Mollison & Kuulasmaa (1985) for a similar observation, made in a slightly different setting.)
Consideration of the joint probability distribution of the numbers of secondary infections of different types shows that the generating functions describing transmission in the multi-group Ross model are of the form (Griffiths 1972; Ball 1983)
| (4.8) |
Here is the average number of secondary infections of type i. (For further details of the calculation, see the electronic supplementary material.)
We illustrate the calculation of invasion probabilities by considering a two-host, one-vector model, for which equations (4.6) and (4.7) become
| (4.9) |
| (4.10) |
| (4.11) |
and so the invasion probabilities can be found in terms of the solution of
| (4.12) |
Using equations (3.5) and (4.8), this gives
| (4.13) |
Rearranging gives a cubic equation for sV, one solution of which is sV=1. The remaining solutions are found by solving the quadratic
| (4.14) |
To provide an example of the use of this equation, we consider a situation in which hosts differ only in terms of their attractiveness to vectors (so that pi=p and qi=q). We assume that there are 1000 hosts, of which one-fifth are of type 1 and the remainder are of type 2. As defined above, the parameter γ1 specifies the fraction of bites that are made on hosts of type 1. When γ1 is equal to 0.20, vectors have no preference between the two types of host, effectively returning us to the single-type (homogeneous) setting. Otherwise, there is heterogeneity in biting and hence transmission: vectors have a preference for hosts of type 1 (respectively, type 2) if γ1 is above (respectively, below) 0.2. Equation (4.4) shows that R0 is proportional to —a function with minimum at γ1=1/5, as expected from the preceding discussion.
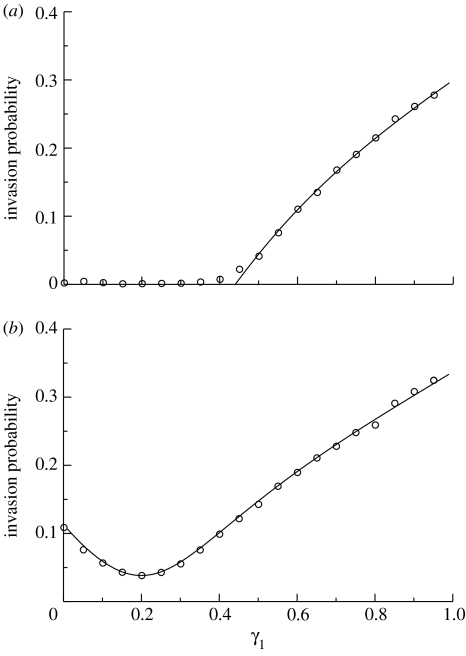
Invasion probabilities obtained from (4.13) are shown in figure 5, together with simulation-based results. Very good agreement is seen between the two sets of results in both cases. For the parameter values employed in figure 5a, the basic reproductive number is 3.7 if the vectors bite only hosts of type 1, while the corresponding basic reproductive number when vectors bite only hosts of type 2 is 0.92. Infection cannot invade the population if too many of the bites are made on hosts of type 2. Since there are 50% more vectors in the population depicted in figure 5b, these basic reproductive numbers are larger, having values 5.5 and 1.4, and invasion is possible for all values of γ1. We note that the invasion probability in figure 5b takes its lowest value when γ1=1/5.
Figure 5.
Major outbreak probability, following the introduction of infection with a single infective vector, in a two-host, one-vector model, as a function of the vector's preference for the first type of host. A fraction γ1 of bites are made on hosts of type 1 and γ2=1−γ1 are made on hosts of type 2. The solid curve denotes the invasion probability found by solving equation (4.13) and calculating 1−sV, and the symbols depict probabilities estimated from numerical simulation, using 10 000 realizations for each set of parameter values. Parameter values are as follows: p=0.2; q=0.15; k=0.5; ξ=δ=1/7; H1=200; and H2=800. (a) V=2000, and (b) V=3000.
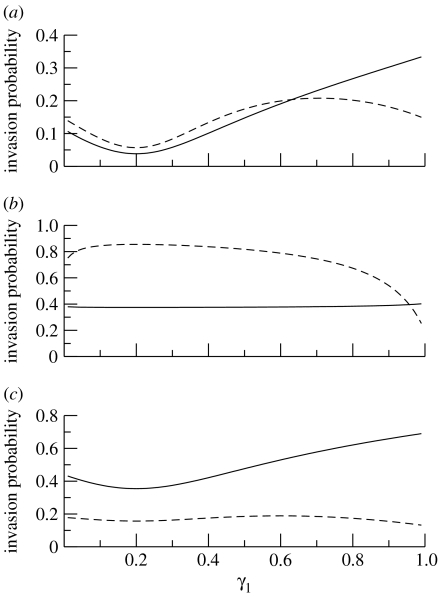
Changing the vector biting preference parameter, γ1, in the two-host, one-vector model can have dramatically different impacts on the probabilities of disease invasion starting from a single infective host or a single infective vector. This is illustrated in figure 6a–c, in each of which it should be noted that R0 takes a similar form, namely a quadratic with minimum at γ1=1/5. Changes in γ1 can lead to one invasion probability increasing while the other decreases, although they can also change together. In figure 6a, for example, there is a range of γ1 values for which the two invasion probabilities increase and decrease together as γ1 is varied, while they move in opposite directions over another range. In addition, the invasion probability need not be a monotonic function of R0, as shown by the decreasing invasion probability following the introduction of an infective host for values of γ1 above approximately 0.65.
Figure 6.
Major outbreak probability, following the introduction of infection with a single infective vector (solid curve) or a single infective host (dashed curve), in a two-host, one-vector model, as a function of the vector's preference for the first type of host. Invasion probabilities are calculated in terms of the solution of equation (4.13). As in the previous figure, a fraction γ1 of bites are made on hosts of type 1 and γ2=1−γ1 are made on hosts of type 2. In (a–c), γ=δ=1/7 and 20% of the host population is of type 1. Other parameter values are as follows: (a) p=0.2, q=0.15, k=0.5, H=1000 and V=3000. (b) As given in (a), except that V=30 000. (c) p=0.2, q=0.01, k=2.5, H=1000 and V=3000.
The magnitudes of the changes in the two invasion probabilities can also differ considerably, as witnessed in figure 6b,c. Such situations can arise when there is a large difference between the value of R0 from host to vector and its value from vector to host. In figure 6b, for example, the R0 value from vector to host is 0.7 and from host to vector (for a randomly chosen host) is 15.75. In figure 6c, the corresponding R0 values are 3.5 and 0.525. A fairly good estimate of the less variable invasion probability can be obtained using the formula for the well-mixed setting. (Recall that the well-mixed setting corresponds to γ1=0.2, and so, if the invasion probability is not changing much with γ1, its value at this point will be close to its value across the entire range.) For instance, for figure 6b, taking and in equation (3.11) gives an invasion probability starting from a single infective vector of 0.374: the value observed as γ1 is changed varies by less than approximately 8% of this. For figure 6c, the invasion probability starting from a single infective host differs by less than approximately 20% of the value 0.157 given by (3.12).
4.2 Moment equations
As before, a stochastic version of the multi-group model can be formulated by reinterpreting the rates that appear in the deterministic model. The Kolmogorov forward equations for this model consist of (H1+1)(H2+1)…(Hm+1)(V1+1)…(Vn+1) differential equations. The dimension of the moment equation set is significantly increased when compared with the corresponding set in the well-mixed model. There are m+n first-order moments, and the variance–covariance matrix has dimension (m+n)2, with (m+n)(m+n+1)/2 independent entries. (The variance–covariance matrix is symmetric since cov(X, Y)=cov(Y, X).) Consequently, there are (m+n)(m+n+3)/2 equations in our set of first- and second-order moment equations. Even for a two-host, two-vector model, this means we have 14 equations.
Generation of such a large set of moment equations by hand is a painstaking task, although this is somewhat reduced by the symmetry of the model. As an example, once one has an equation for the first-order moment E(I1), the corresponding equations for E(Ii), for i=2, …, m, follow by an appropriate change of indices. Rather than generating the set by hand, we employed an alternative approach that automates the process. The Kolmogorov forward equations can be used to formulate a partial differential equation for the generating function (or, alternatively, for the moment generating function) of the joint distribution of Y1, …, Ym, I1, …, In, (e.g. Bartlett 1956, 1960; Grimmett & Stirzaker 1992). The differential equations for the moments can be obtained by performing a series expansion of this equation. Finally, as discussed earlier, the set of equations must be closed using, for instance, the multivariate normal approximation. Each step of this process can be automated and so, using a symbolic algebra package (such as Maple or Mathematica), a computer can produce a set of moment equations (of any specified order), if given a description of the possible transitions of the model and the rates at which they occur (Root & Lloyd in preparation).
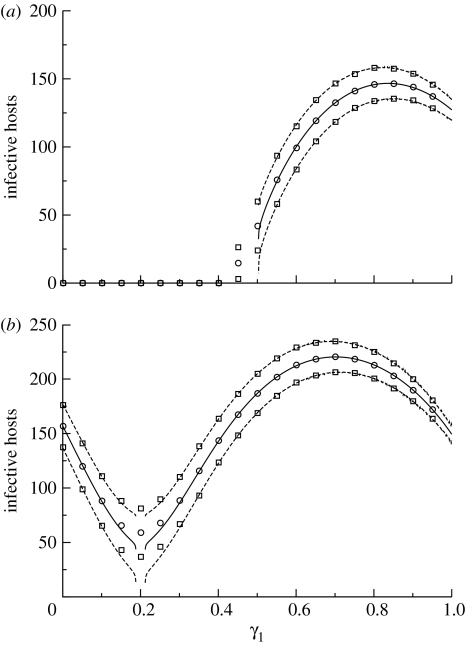
The moment equation set for the two-host, one-vector model discussed above comprises nine equations (we do not show these here). Figure 7 compares the estimates of moments obtained using these equations with estimates based on numerical simulation of the stochastic model. For the most part, excellent agreement is seen. This is not the case, however, near the R0=1 threshold in figure 7a, or near the point where R0 takes its minimum value in figure 7b. In fact, for the parameter set chosen in these examples, the moment equations were badly behaved in these regions. For example, they appeared not to converge at the minimum point in figure 7a. This may well be related to the more frequent occurrence of endemic fade-out in this regime: analogous problems have been noted in applications of moment equations closed by means of the multivariate normal approximation in the setting of an SIR model for a directly transmitted infection (Lloyd 2004). Use of an alternative moment closure approximation, such as the multivariate lognormal approximation (Keeling 2000), may lead to a better behaved system.
Figure 7.
Average behaviour and variation about the average in the two-host, one-vector model, in terms of the vector's preference for the first host. As in the previous figure, a fraction γ1 of bites are made on hosts of type 1 and γ2=1−γ1 are made on hosts of type 2. Solid curves denote the average total number of infective hosts, E (Y1+Y2). The variability of realizations about this average is indicated by the dashed curves, which depict mean±s.d. of the total number of infective hosts. The standard deviation is calculated as the square root of Var(Y1)+Var(Y2)+2cov(Y1, Y2). All curves are calculated using moment equations closed by means of the multivariate normal approximation. (The origin of the gaps in the curves is discussed in the text.) Symbols denote the corresponding quantities calculated from 1000 realizations of the stochastic model. All parameter values are the same as given in figure 5, with (a) depicting the model with V=2000 and (b) V=3000.
The total number of infective hosts is maximized when γ1 is below 1: even though the basic reproductive number is higher when γ1 equals 1, the smaller number of hosts of type 1 means that fewer infections arise when too many bites are concentrated on these hosts. Dye & Hasibeder (1986) discuss the possible shapes that this curve can take. An interesting observation is that the variability in the number of infective hosts decreases as γ1 is increased from its value at this maximum point to 1, even though the average number of infective hosts decreases.
5. Discussion
This paper has examined the use of two analytic tools that quantify the impact of stochasticity and heterogeneity in host–vector models. Results obtained using branching process methodology demonstrated that asymmetry between the disease transmission potentials from hosts to vectors and from vectors to hosts can have important consequences. For instance, the disease invasion probability starting from a single infective host and the invasion probability starting from a single infective vector can differ markedly, even though the overall basic reproductive number of the infection is the same in both cases. In heterogeneous settings, the two invasion probabilities can have a complex relationship with each other as model parameters are varied. In particular, we saw that the invasion probabilities need not have a monotonic relationship with the basic reproductive number of the infection, or with each other. Asymmetry between the transmission potentials can lead to one invasion probability having almost no variation as a model parameter is varied, while the other changes over a large range.
Moment equations were used to assess the impact of demographic stochasticity on the endemic behaviour of the Ross model. Even though the host and vector populations employed in the model simulations were by no means large (of the order of tens or hundreds in figure 3, or thousands in figure 7), the variation seen about the endemic equilibrium was typically not substantial. This is partly due to the Ross model being of SIS type: infected hosts become susceptible immediately upon recovery, and vectors that die are immediately replaced by newborns. The impact of demographic stochasticity is often much higher for infections against which hosts develop immunity, for which an SIR or SIRS description may be more appropriate. Immunity means that there can be a large number of recovered individuals that take no part in the infection process, leading to a reduction in the equilibrium number of infective hosts. This effect is most noticeable when the duration of immunity is long. A well-known example, albeit in a directly transmitted infection setting, is provided by measles in the pre-vaccination era (Bartlett 1956). Lifelong immunity following infection leads to a large separation of time scales between the infection process (with infection lasting on the order of a week and typical individuals acquiring infection within a few years of birth) and the demographic time scale on which the susceptible pool turns over (on the order of many decades). Consequently, demographic stochasticity exerts a major impact, with frequent disease extinction—due to endemic fade-out—occurring for all but the largest population centres.
The analyses discussed in this paper can easily be extended to consider a host–vector model for which the host acquires temporary immunity: the impact of immunity on variability about the endemic equilibrium is briefly explored using moment equations in the electronic supplementary material and it is indeed seen that host immunity increases the impact of demographic stochasticity.
The population dynamics of many vector populations has a sizeable seasonal component. Such effects can be incorporated within models such as the Ross model (Aron & May 1982). It is well known that seasonality can have a dramatic effect on the dynamics of infectious diseases, even within a deterministic framework. The interaction between the intrinsic predator–prey dynamics and external forcing can lead to sustained oscillations, or more complex dynamic behaviours, replacing the endemic equilibrium typically seen in unforced systems. In many instances, large swings in prevalence can result. Consequently, the impact of demographic stochasticity can be amplified in the presence of seasonality. Moment equations have been successfully deployed in seasonal settings (Lloyd 2004), providing estimates for the increased variability due to variations in transmission. This remains to be explored in the host–vector setting.
The complexity of stochastic models has often meant that model exploration is largely carried out by means of simulation approaches. Such simulation, however, can often prove to be time consuming, particularly when large number of realizations must be generated and large regions of parameter space are to be explored. Analytic approaches, such as those outlined here, can provide an attractive alternative, giving a rapid means to gain understanding of the dynamics of infections in the face of randomness.
Acknowledgments
We wish to thank Ingemar Nåsell for providing the Matlab code that was used to calculate the exact quasi-stationary distribution in figure 3 and an anonymous referee for helpful comments. This work was supported by the National Institutes of Health (grant number R01-AI54954-0IA2). A.M.R. holds a GAANN Fellowship (NCSU Scientific Computation programme funded under the US Department of Education award number P200A030277).
Footnotes
One contribution of 20 to a Theme Issue ‘Cross-scale influences on epidemiological dynamics: from genes to ecosystems’.
Supplementary Material
Additional details of some of the calculations from the text are given, together with discussion of the fixed duration of infection model and a model incorporating host immunity
References
- Aron J.L, May R.M. The population dynamics of malaria. In: Anderson R.M, editor. Population dynamics of infectious diseases. Chapman and Hall; London, UK: 1982. pp. 139–179. [Google Scholar]
- Athreya K.B, Ney P.E. Springer; Berlin, Germany: 1972. Branching processes. [Google Scholar]
- Ball F. The threshold behaviour of epidemic models. J. Appl. Prob. 1983;20:227–241. doi: 10.2307/3213797. [DOI] [Google Scholar]
- Barbour A.D. Macdonald's model and the transmission of bilharzia. Trans. Roy. Soc. Trop. Med. Hyg. 1978;72:6–15. doi: 10.1016/0035-9203(78)90290-0. [DOI] [PubMed] [Google Scholar]
- Bartlett M.S. Deterministic and stochastic models for recurrent epidemics. In: Neyman J, editor. Proc. Third Berkeley Symp. Mathematical statistics and probability. vol. 4. University of California Press; Berkeley, CA: 1956. pp. 81–109. [Google Scholar]
- Bartlett M.S. Methuen; London, UK: 1960. Stochastic population models. [Google Scholar]
- Bartlett M.S. The relevance of stochastic models for large-scale epidemiological phenomena. Appl. Stat. 1964;13:2–8. doi: 10.2307/2985217. [DOI] [Google Scholar]
- Becker N, Marschner I. The effect of heterogeneity on the spread of disease. In: Gabriel J.-P, Lefèvre C, Picard P, editors. Stochastic processes in epidemic theory. Lecture notes in biomathematics. vol. 86. Springer; Berlin, Germany: 1990. pp. 90–103. [Google Scholar]
- Darroch J.N, Seneta E. On quasi-stationary distributions in absorbing continuous-time finite Markov chains. J. Appl. Prob. 1967;4:192–196. doi: 10.2307/3212311. [DOI] [Google Scholar]
- Diekmann O, Heesterbeek J.A.P. Wiley; Chichester, UK: 2000. Mathematical epidemiology of infectious diseases. [Google Scholar]
- Diekmann O, Heesterbeek J.A.P, Metz J.A.J. On the definition and computation of the basic reproduction ratio R0 in models of infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- Dietz K. Models for vector-borne parasitic diseases. In: Barigozzi C, editor. Vito Volterra Symp. Mathematical models in biology. Lecture notes in biomathematics. vol. 39. Springer; Berlin, Germany: 1980. pp. 264–277. [Google Scholar]
- Dye C.M, Hasibeder G. Population dynamics of mosquito-borne disease: effects of flies which bite some people more frequently than others. Trans. Roy. Soc. Trop. Med. Hyg. 1986;83:69–77. doi: 10.1016/0035-9203(86)90199-9. [DOI] [PubMed] [Google Scholar]
- Gardiner C.W. Springer; Berlin, Germany: 1985. Handbook of stochastic methods. [Google Scholar]
- Griffiths D.A. A bivariate birth-death process which approximates to the spread of a disease involving a vector. J. Appl. Prob. 1972;9:65–75. doi: 10.2307/3212637. [DOI] [Google Scholar]
- Grimmett G.R, Stirzaker D.R. Oxford University Press; Oxford, UK: 1992. Probability and random processes. [Google Scholar]
- Isham V. Assessing the variability of stochastic epidemics. Math. Biosci. 1991;107:209–224. doi: 10.1016/0025-5564(91)90005-4. [DOI] [PubMed] [Google Scholar]
- Keeling M.J. Multiplicative moments and measures of persistence in ecology. J. Theor. Biol. 2000;205:269–281. doi: 10.1006/jtbi.2000.2066. [DOI] [PubMed] [Google Scholar]
- Kendall D.G. An artificial realisation of a simple “birth-and-death” process. J. R. Stat. Soc. B. 1950;12:116–119. [Google Scholar]
- Kurtz T.G. Limit theorems for sequences of jump Markov processes approximating ordinary differential equations. J. Appl. Prob. 1971;8:344–356. doi: 10.2307/3211904. [DOI] [Google Scholar]
- Lloyd A.L. Estimating variability in models for recurrent epidemics: assessing the use of moment closure techniques. Theor. Popul. Biol. 2004;65:49–65. doi: 10.1016/j.tpb.2003.07.002. [DOI] [PubMed] [Google Scholar]
- Macdonald G. The analysis of equilibrium in malaria. Trop. Dis. Bull. 1952;49:813–829. [PubMed] [Google Scholar]
- Mollison D. Dependence of epidemic and population velocities on basic parameters. Math. Biosci. 1991;107:255–287. doi: 10.1016/0025-5564(91)90009-8. [DOI] [PubMed] [Google Scholar]
- Mollison D, Kuulasmaa K. Spatial epidemic models: theory and simulations. In: Bacon P, editor. Population dynamics of rabies in wildlife. Academic Press; London, UK: 1985. pp. 291–309. [Google Scholar]
- Nåsell I. On the quasi-stationary distribution of the Ross malaria model. Math. Biosci. 1991;107:187–207. doi: 10.1016/0025-5564(91)90004-3. [DOI] [PubMed] [Google Scholar]
- Nåsell I. The quasi-stationary distribution of the closed endemic SIS model. Adv. Appl. Prob. 1996;28:895–932. doi: 10.2307/1428186. [DOI] [Google Scholar]
- Nåsell I. On the time to extinction in recurrent epidemics. J. R. Stat. Soc. B. 1999;61:309–330. doi: 10.1111/1467-9868.00178. [DOI] [Google Scholar]
- Nåsell I. Stochastic models of some endemic infections. Math. Biosci. 2002;179:1–19. doi: 10.1016/S0025-5564(02)00098-6. [DOI] [PubMed] [Google Scholar]
- Root, A. M. & Lloyd, A. L. In preparation. Computer-automated generation of moment equations for stochastic models.
- Ross R. J. Murray; London, UK: 1910. The prevention of malaria. [Google Scholar]
- Ross R. Some quantitative studies in epidemiology. Nature. 1911;87:466–467. [Google Scholar]
- Whittle P. On the use of normal approximation in the treatment of stochastic processes. J. R. Stat. Soc. B. 1957;19:268–281. [Google Scholar]
- Woolhouse M.E.J, et al. Heterogeneities in the transmission of infectious agents: implications for the design of control programs. Proc. Natl Acad. Sci. USA. 1997;94:338–342. doi: 10.1073/pnas.94.1.338. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional details of some of the calculations from the text are given, together with discussion of the fixed duration of infection model and a model incorporating host immunity