Ultrahigh-resolution crystallography and related electron density and electrostatic properties in proteins

Ultrahigh-resolution protein diffraction data allow valence electron density modelling and calculations of experimental electrostatic properties. Protein–ligand interaction energy may therefore be estimated.

Abstract

With an increasing number of biological macromolecular crystal structures measured at ultrahigh resolution (1 Å or better), it is necessary to extend to large systems the experimental valence electron density modelling that is applied to small molecules. A database of average multipole populations has been built, describing the electron density of chemical groups in all 20 amino acids found in proteins. It allows calculation of atomic aspherical scattering factors, which are the starting point for refinement of the protein electron density, using the MoPro software. It is shown that the use of non-spherical scattering factors has a major impact on crystallographic statistics and results in a more accurate crystal structure, notably in terms of thermal displacement parameters and bond distances involving H atoms. It is also possible to obtain a realistic valence electron density model, which is used in the calculation of the electrostatic potential and energetic properties of proteins.

The details observable in protein crystal structures depend on the experimental diffraction resolution. In X-ray diffraction (XRD), the experimental resolution (Å) is defined by d = λ/(2sinθ), where θ is the Bragg angle and λ is the wavelength. At the usual resolution for macromolecular crystallography, 1.6 < d < 3 Å, the number of Fourier components F(h, k, l) of the electron density (ED) as obtained by

is not high enough to estimate all the atomic parameters. In the ultrahigh-resolution case, we will show that bonding interactions and electrostatic properties may be quantified in relation to biological activity.

In contrast to the independent atom model (IAM), where all atoms are assumed to be neutral, spherical and independent, the crystal static valence electron density is modelled by a sum of multipolar pseudo-atom densities, 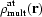, located at atomic centres (Hansen & Coppens, 1978 ▶), while the atomic core density, , remains unchanged,

where the term ρ_val represents the spherically averaged free atom Hartree Fock valence density. The third term of the summation describes the non-spherical part, in which the radial functions used are of Slater type: R _nl(r) = Nr ^nlexp(−ξr). The functions y _lm are spherical harmonics in real form; the (θ,ϕ) coordinates are expressed in an atom-centred local axis system, which facilitates the application of chemical similarity. The refinable parameters are the κ and κ′ coefficients, which describe the expansion–contraction of the perturbed valence ED (Coppens et al., 1979 ▶), and the population parameters P _val and P _lm.

To apply this formalism to ultrahigh-resolution protein diffraction data, we have proposed a multipolar parameters library (Pichon-Pesme et al., 1995 ▶; Zarychta et al., 2007 ▶). High-resolution XRD data have been collected at the Laboratoire de Cristallographie et de Modélization des Matériaux Minéraux et Biologiques (LCM³B, Nancy, France) on a large group of mono- or polypeptides to determine precisely the ED distribution of all natural amino acids (neutral or charged). Multipole refinement of the related structure factors allowed the building of an experimental database of multipolar parameters for each protein atom type in a given chemical environment (Jelsch et al., 1998 ▶), from which a specific atom-type nomenclature has been developed. The static electron deformation density,

can be calculated from the experimental database in all amino acids and natural peptides. The database parameters were shown to be transferable to the protein amino acids and permit the calculation of aspherical atomic scattering factors to be used for protein refinement.

The validity of these aspherical scattering factors was checked more than ten years ago (Jelsch et al., 1998 ▶) and has been confirmed since then by several studies. These factors have been successfully used to refine ultrahigh-resolution protein structures: a scorpion toxin (Housset et al., 2000 ▶), crambin (Jelsch et al., 2000 ▶) and hAR (Muzet et al., 2003 ▶). As shown in these papers, the use of aspherical scattering factors improves all least-squares statistical indices and, consequently, leads to more physically meaningful bond distances and thermal anisotropic displacement parameters. Aspherical features, such as, for instance, non-bonded density on a C=O O atom, are also taken into account.

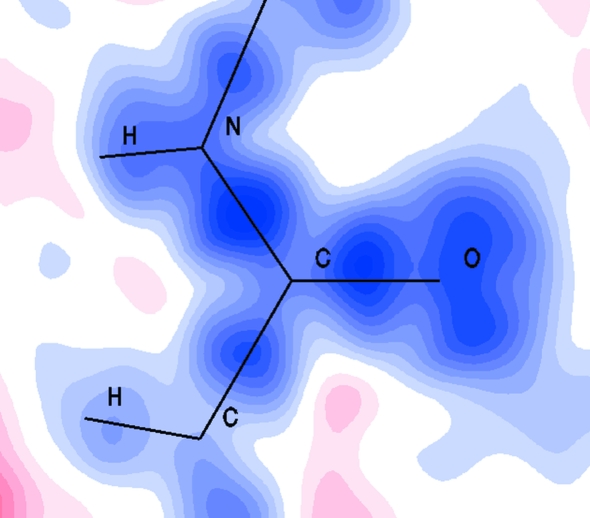
This finding led us to the development of the MoPro package of crystallographic programs (Guillot et al., 2001 ▶; Jelsch et al., 2005 ▶). In MoPro, for any chemical type of atom belonging to a protein-type molecule, automatic assignment of the corresponding aspherical scattering factor is performed, and these scattering factors can then be further used in the refinement process. Hence, a stereochemical and anisotropic thermal motion parameters refinement following the assignment of aspherical scattering factors can be performed on protein atoms, leading to the deconvolution of thermal motion and valence electron density deformation effects. This allows the computation of dynamical deformation valence electron density, smeared out by thermal vibrations, as routinely performed in small-molecule crystallography. Fig. 1 ▶ shows an example of a dynamical deformation electron density map computed in the plane of a well ordered peptide plane of the 0.62 Å structure of an eel pout type III antifreeze protein RD1 (Ko et al., 2003 ▶; Protein Data Bank code 1ucs). The bonding electron density features are clearly visible on each covalent bond, as well as electron density peak accumulation corresponding to the carbonyl O atom electron lone pairs.

Figure 1.

Dynamic valence electron density map computed in the Val5–Val6 peptide bond of the eel pout type III antifreeze protein RD1. Positive and negative electron density is, respectively, plotted in blue and red contours of ±0.08 e Å⁻³. Values between −0.08 and +0.08 e Å⁻³ are not represented (white colour).

Such a generalized refinement, which is not necessarily a charge density refinement as the aspherical scattering factors can be fixed parameters (as in the above example), should also be generalized to all small molecules and protein refinements in the future. Furthermore, as shown below, this atom transferability allows estimation of electrostatic properties at least as accurately as when usual force fields are used (Muzet et al., 2003 ▶).

Another approach, based on high-level theoretical calculations, was later proposed by Koritsanszky et al. (2002 ▶; SUNY Buffalo database). The aim of their theoretical database is different from ours because the also transferable multipolar parameters will be used to estimate properties such as protein–protein or protein–ligand interaction energies based on theoretical ED reconstruction, while our approach is based on experimental ultrahigh-resolution XRD data. A comparison between our experimental database and the SUNY Buffalo theoretical database is in progress (Pichon-Pesme et al., 2004 ▶) and will be published soon. A similar project has been proposed by Dittrich et al. (2004 ▶).

To summarize, we have at our disposal an experimental database that contains a set of transferable multipolar pseudo-atoms that can be used for protein refinement and electrostatic properties estimation. These transferable pseudo-atoms have their own topology and may therefore be considered as experimental topological atoms as defined by Bader (1990 ▶).