Quantitative Cardiac Perfusion: A Noninvasive Spin-labeling Method That Exploits Coronary Vessel Geometry¹

Abstract

PURPOSE:

To quantitate myocardial arterial perfusion with a noninvasive magnetic resonance (MR) imaging technique that exploits the geometry of coronary vessel anatomy.

MATERIALS AND METHODS:

MR imaging was performed with a spinlabeling method in six arrested rabbit hearts at 4.7 T. Selective inversion of magnetization in the short-axis imaging section along with all myocardium apical to that section produces signal enhancement from arterial perfusion. A linescan protocol was used for validation of flow enhancement. Flow was quantitated from two images and validated with spin-echo (SE) imaging. Regional perfusion defects were created by means of coronary artery ligation and delineated with gadolinium-enhanced imaging.

RESULTS:

Linescan estimates of T1 obtained at physiologic flows agreed with model predictions. Flow-induced signal enhancement measured on SE images also agreed with expected values. Finally, perfusion abnormalities created by means of coronary artery ligation were detected.

CONCLUSION:

This spin-labeling method provides quantitative estimates of myocardial arterial perfusion in this model and may hold promise for clinical applications.

Measurement of localized myocardial blood flow is an important tool in the assessment of myocardial function, coronary flow reserve, therapeutic intervention, and the physiologic importance of large vessel stenoses, in both the clinical and laboratory settings. There are currently several methods available for the measurement of perfusion. These include coronary catheterization by using radiopaque dyes with digital subtraction angiography or fluoroscopy and single photon emission computed tomography (CT) with thallium-201 and technetium-99m. These techniques, while valuable, involve ionizing radiation and offer measurement of only relative flow. Positron emission tomography (1-4) has been shown to provide quantitative flow information with use of oxygen-15 (5,6) and nitrogen-13 (7), albeit at low spatial resolution and with ionizing radiation. Invasive techniques such as injection of microspheres are suitable only for laboratory use. More recent developments in cardiac magnetic resonance (MR) imaging (1,3,8) and CT (1,9,10) rely on the use of exogenous contrast agents, and their mechanisms of signal modulation are poorly understood in vivo, making quantification of flow difficult.

Noninvasive MR techniques such as those exploiting the blood oxygenation level–dependent effect have been applied in the heart (11-14) and offer an indirect indication of perfusion through information on the oxygen status of the myocardium. Magnetization transfer contrast has been used to qualitatively delineate regions of ischemic or infarcted myocardium (15,16), although the mechanisms are incompletely understood (16,17).

Recently, several “spin-labeling” techniques have been introduced in an effort to measure tissue perfusion noninvasively. The echo-planar MR imaging and signal targeting with alternating radio frequency (EPISTAR) method has been applied to qualitatively measure perfusion in the brain (18) and is related to time-of-flight MR angiography (19). As well, qualitative flow estimates in the brain have been made using a nonselective/selective inversion method (20,21). Continuous, flow-induced adiabatic fast passage inversion has been used to create contrast for measuring perfusion in the brain (22-24), kidney (25-27), and heart (28). Currently, the adiabatic fast passage spin-inversion technique is the only spin-labeling method to permit quantitative myocardial arterial perfusion measurements.

The adiabatic fast passage spin-inversion technique (22) uses a lowamplitude, off-resonance radio-frequency (RF) pulse to invert arterial spins that are flowing into the imaging plane from a remote, proximal cannula. Mixing inverted inflowing spins with noninverted spins in the imaging section creates flow-dependent contrast. Although this technique has been shown to help quantitate perfusion in the isolated buffer-perfused rat heart (28), it has several limitations. Since the RF irradiation is applied continuously, there is substantial magnetization transfer to offresonance spins in the imaging section (29), necessitating the acquisition of a control image where the resonance offset of the RF irradiation has been flipped symmetrically about the imaging plane. Consequently, RF energy deposition is high owing to prolonged RF irradiation. The long, straight inflow tract required with this technique precludes its application in vivo, where turbulent blood enters the coronary ostia at the root of the aorta and descends toward the myocardium, with maximal coronary flow occurring during diastole. Since the site of spin inversion is removed from the imaging plane, there will be a distribution of transit times of spins into the imaged tissue, confounding attempts at quantitation. In addition, reports of quantification using this technique in the heart have been at superphysiologic flows (28).

The EPISTAR technique, introduced by Edelman et al (18), has been applied in the brain to create qualitative cerebral blood flow maps. This technique inverts all inflowing spins immediately proximal to the imaging plane. A 90° saturation pulse is then applied to the imaging plane to reduce spurious signal from side-lobe excitation of the initial inversion pulse, as well as to eliminate magnetization transfer effects. Although spin arrival times are uniform, saturation of the imaging plane reduces the contrast provided by the inflowing inverted spins by a factor of two. Conceivably, EPISTAR could be applied to myocardial perfusion measurements. However, it would be difficult to ensure that all arterial spins flowing into the imaging section are inverted, since coronary arterial flow is high at the base of the heart. Some initial work has been done toward quantification of EPISTAR perfusion measurements in the brain (30).

A method that inverts the spins within the imaging section can improve flow enhancement by mixing noninverted spins with inverted spins. Kwong et al (20) have demonstrated the use of this nonselective/selective inversion technique in the demonstration of qualitative flow deficits in the brain. In this method, a T1 image is acquired with a hard inversion pulse. A second T1 image is acquired with use of a selective inversion pulse, allowing for enhancement from inflowing noninverted spins. Subtraction of the two T1 images yields an estimate of perfusion. Estimation of two T1 maps is time consuming, computationally intensive, and typically provides poor signal-to-noise ratios (SNRs), making quantitative flow estimates difficult (20). Last, no distinction can be made between arterial and venous flow.

We propose an alternative noninvasive spin-labeling method that provides quantitative estimates of coronary arterial perfusion. As previously described (31), this technique relies on the unique geometry of the coronary vasculature. In the myocardium, arterial blood flows predominantly from base to apex (32,33). This is easily seen in Figure 1, an anterior view radiograph of the coronary arterial vasculature (34).

Figure 1.

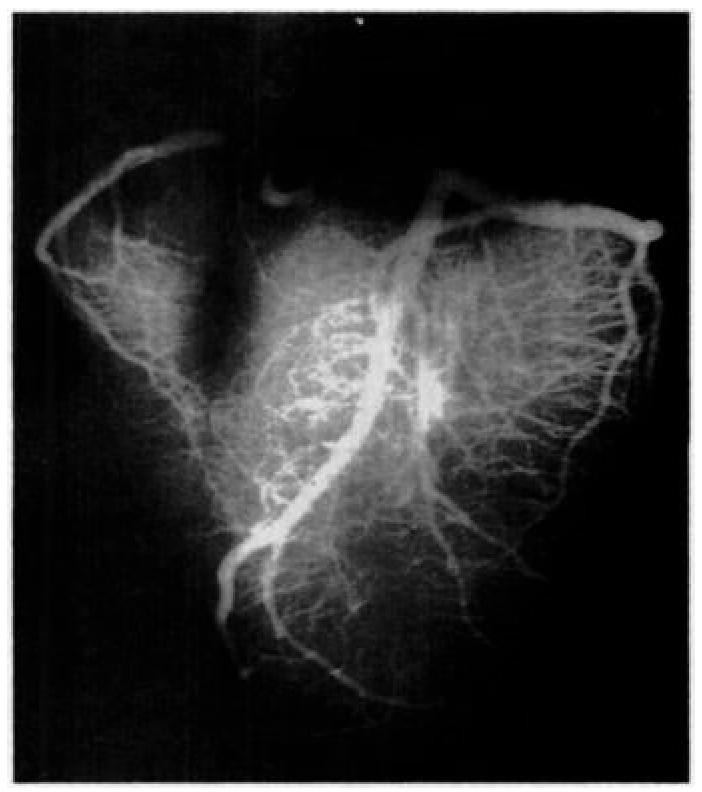
Anterior radiograph of a calf heart shows the geometry of the arterial vasculature. Notice the downward and horizontal direction of the arteries. (Image courtesy of Virginia Ferante, MS, The Johns Hopkins University School of Medicine, Baltimore, Md).

As diagrammed in Figure 2, coronary arteries descend from the root of the aorta on the epicardial surface and then dive into the myocardium toward the endocardium. Venous drainage runs parallel with the arteries, but flow is in the opposite direction. Selective inversion of the magnetization in the short-axis section of interest, along with all myocardium on its apical side, renders any flow-induced signal enhancement insensitive to venous flow, ensuring that only unlabeled arterial spins can act to enhance tissue signal. The following sections describe the application of this method.

Figure 2.

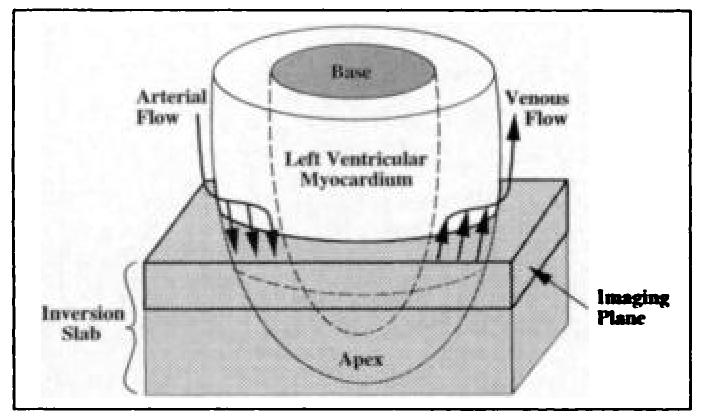
Diagram indicates the predominant directions of arterial and venous coronary flow. The imaging plane and inversion slab are also shown.

BACKGROUND

Bloch Equations

The Bloch equation for the tissue water longitudinal magnetization concentration (magnetization per gram of myocardium) M, including longitudinal relaxation and the effects of inflowing spins, is

$$\frac{\mathrm{d}M}{\mathrm{d}t}=\frac{M_o-M}{\mathrm{T}1}+f_a{M}_a-f_v{M}_v,$$ (1)

where M_o is the equilibrium magnetization concentration (magnetization per gram of myocardium), T1 the spin-lattice relaxation time in the absence of flow, f_a the arterial flow into the voxel in milliliters per minute per gram, f_v the venous flow out of the voxel in milliliters per minute per gram, M_a the arterial magnetization concentration (magnetization per milliliter of perfusate), and M_v the venous magnetization concentration (magnetization per milliliter of perfusate). With conservation of mass, f_a = f_v [unk] f at steady-state; f represents the true arterial flow. Assuming that water is freely diffusable and well mixed over the time scale of the experiment (1–2 seconds),

$$M_v=\frac{M}{\lambda },$$ (2)

where λ is the partition coefficient between tissue and perfusate defined as

$$\lambda =\frac{\text{milliters of water}}{\text{grams of myocardium}}.$$ (3)

The value of λ is relatively constant across mammalian species and is approximately 0.80 mL/g (35). Since the arterial magnetization remains unaffected by the initial selective inversion,

$$M_a=\frac{M_o}{\lambda }.$$ (4)

Substituting Equations (2) and (4) into Equation (1) and rearranging,

$$\frac{\mathrm{d}M}{\mathrm{d}t}=\frac{M_o-M}{\mathrm{T}{1}^{\mathit{app}}},$$ (5)

where the apparent T1, T1^app, is defined as follows:

$$\frac{1}{\mathrm{T}{1}^{\mathit{app}}}=\frac{1}{\mathrm{T}1}+\frac{f}{\lambda }.$$ (6)

Solving Equation (5) for M, at some measurement time τ,

$$\begin{array}{cc}\hfill M& =M_o(1-2{\mathit{We}}^{-\tau ∕\mathrm{T}{1}^{\mathit{app}}})\hfill \\ \hfill & =M_o(1-2{\mathit{We}}^{-\tau ∕\mathrm{T}1}{e}^{-f\tau ∕\lambda })\hfill \end{array}$$ (7)

and

$$W={}^1∕_2(1-\cos \alpha ),$$ (8)

where α is the effective tip angle in the inversion section and W the “inversion efficiency” equaling 1.0 for perfect 180° inversion. Because the value of fτ/λ is small for physiologic flow, a Taylor expansion can be used to simplify Equation (7), as follows:

$$\begin{array}{cc}\hfill S\left(f\right)\equiv \frac{M}{M_o}\approx & (1-2{\mathit{We}}^{-\tau ∕\mathrm{T}1})\hfill \\ \hfill & +\left(\frac{2\tau {\mathit{We}}^{-\tau ∕\mathrm{T}1}}{\lambda }\right)f.\hfill \end{array}$$ (9)

This equation shows that a linear relationship exists between normalized signal intensity, S(f), and arterial flow, f, for a fixed inversion delay τ at physiologic flows. The slope of this relationship determines the sensitivity of this method and should be optimized, as discussed below. The intercept of this relationship, which is determined by W, τ, T1, and λ, can be subtracted to yield a linear plot between normalized signal intensity and flow, although this adds no additional information. Inversion of Equation (9) provides the relationship for flow and normalized signal intensity, as follows:

$$\begin{array}{cc}\hfill f=& \frac{\lambda }{2\tau {\mathit{We}}^{-\tau ∕\mathrm{T}1}}\hfill \\ \hfill & \times \left(\frac{M}{M_o}+2{\mathit{We}}^{-\tau ∕\mathrm{T}1}-1\right).\hfill \end{array}$$ (10)

This can be used to make direct flow calculations from the normalized signal intensity.

Parameter Optimization for Quantitative Flow Measurements

A “perfusion” image acquired at a fixed τ after the selective inversion and a “magnitude” image with no preceding inversion will provide estimates of M and M_o, respectively, necessary to estimate flow from Equation (10). The optimum inversion delay, τ_opt, would occur when the signal difference for two different flows is maximized. For two flows f₁ and f₂, it can be shown that the optimum time delay after inversion is

$${\tau }_{\mathit{opt}}=\frac{\lambda }{f_2-f_1}\ln \left(\frac{\lambda +\mathrm{T}1f_2}{\lambda +\mathrm{T}1f_1}\right).$$ (11)

Since the argument of the logarithm is close to one for physiologic flows, a Taylor expansion for f₂ ≈ f₁ will simplify the above expression. It can be shown that for all flows of physiologic significance,

$${\tau }_{\mathit{opt}}\approx \frac{\lambda \mathrm{T}1}{\lambda +\mathrm{T}1f}.$$ (12)

Equation (12) can be used to determine an optimal delay between inversion and imaging for flows near f. Furthermore, if λ ≫ T1f, then τ_opt ≈ T1.

To determine an estimate of the flow differences that might be expected, consider the signal difference between two flows f₁ and f₂, as follows:

$$\delta \equiv S\left(f_1\right)-S\left(f_2\right)=\frac{2W\tau e^{-\tau ∕\mathrm{T}1}}{\lambda }\Delta f,$$ (13)

where Δf = f₂ − f₁. Normal physiologic perfusion is approximately 1 mL/min/g in myocardium. Under conditions of maximal vasodilatation, this may increase to 5–6 mL/min/g (36). Assuming λ = 0.8 mL/g and T1 = 2.3 seconds (2.3 seconds is the representative value of T1 we measured in the rabbit myocardium at 4.7 T and 39°C), then τ_opt = 2.1 seconds. Assuming an inversion efficiency of 0.81, the maximum signal difference seen would be 11.4%. Flow differences of 1 mL/min/g yield a 2.8% signal difference.

Assuming that image noise is Gaussian (37), the SNR per pixel is given as follows:

$$\mathrm{SNR}=\frac{M_o}{\sigma },$$ (14)

where σ is the standard deviation of the noise.

To claim that the signals are different with 95% certainty, the signal difference between two voxels must be greater than two standard deviations of the noise. Mathematically,

$$M_1-M_2=M_o\delta \ge \frac{2\sigma }{\sqrt{N}}$$ (15)

or, substituting in Equation (14),

$$\delta \ge \frac{2}{\mathrm{SNR}\sqrt{\mathrm{N}}},$$ (16)

where N is the number of pixels averaged together. Substituting Equation (13) into Equation (16) and rearranging,

$$\Delta f_{(P<.05)}\ge \frac{\lambda e^{\tau ∕\mathrm{T}1}}{\tau \mathrm{WSNR}\sqrt{N}}.$$ (17)

For two images acquired at different flows with SNRs of 100, T1 of 2.3 seconds, W of 0.81, τ of 2.1 seconds, and N of 1, the minimum flow difference that can be resolved is 0.7 mL/min/g for a single pixel. Averaging over a region of interest of 10 × 10 pixels improves this resolution to 0.7 mL/min/g.

MATERIALS AND METHODS

Isolation and Perfusion of the Rabbit Heart

As described previously (11-13), hearts from six New Zealand White male rabbits (2–4 kg) were isolated and attached to a Langendorff apparatus modified for MR imaging. An 8-mm-diameter intensity standard (20 mM CuSO₄) was inserted into the left ventricle via the mitral valve, along with a thin (outer diameter, 1 mm) plastic tube to serve as a vent, preventing distention of the left ventricle by Thebesian drainage. In addition, a section from a 60-mL syringe was fit over the heart before insertion into the coil to reduce translation and distention resulting from changes in perfusate pressure. With all hearts, a remote snare occluder was placed on the left anterior descending coronary artery, as previously described (13).

During attachment, perfusion pressure was maintained at 50–55 mm Hg, and coronary flow was continuously monitored by means of cannulation of the pulmonary artery (vena cavae ligated). Coronary flow was varied from approximately 0.5 to 6 mL/min/g during the course of an experiment by adjusting the height of a perfusate reservoir. Measurements of coronary flow were made by using an MR-compatible flow meter (Transonics, Ithaca, NY). Heart preparations that failed to maintain stable coronary flow were not used. Tissue and perfusate were maintained at 39°C by circulating warm water around the bathing chamber and the arterial inflow lines. It was important to operate at physiologic temperatures, as there is a temperature dependence on T1 (38).

Perfusate Composition

A modified Krebs-Henseleit buffer was used as the initial perfusate during the attachment of the heart to the Langendorff apparatus. This buffer contained 114.0 mmol/L NaCl, 0.4 mmol/L KH₂PO₄, 1.0 mmol/L MgSO₄, 28.0 mmol/L NaHCO₃, 3.5 mmol/L KCl, 1.5 mmol/L CaCl₂, and 5.6 mmol/L dextrose. The buffer was not recirculated.

After attachment, the perfusate was switched to a cardioplegic solution (modified St Thomas Hospital solution [39]) containing 110.0 mmol/L NaCl, 10.0 mmol/L NaHCO₃, 16.0 mmol/L KCl, 16.0 mmol/L MgCl₂, 1.2 mmol/L CaCl₂, and 1.0 mmol/L adenosine. Adenosine was included to maximally vasodilate the coronary bed, maximizing intravascular volume and minimizing time-varying flow heterogeneity. The cardioplegic solution was not recirculated.

Both buffer and cardioplegic solution perfusate were oxygenated with a 95% O₂, 5% CO₂ gas mixture.

MR Imaging

All imaging examinations were performed with an Omega CSI 4.7-T nuclear MR spectrometer (GE Medical Systems, Fremont, Calif) equipped with S-150 Accustar shielded gradients. A home-built loop-gap RF coil (31 mm in diameter) tuned to 200.08 MHz (proton resonance) was used for imaging. The coil was wrapped around a closed-end, cylindric acrylic bathing chamber in which the heart was suspended.

Inversion of myocardial water spins in the imaging section along with all myocardium on its apical side was achieved with a selective 180° pulse (Fig 3). High uniformity of the inversion section was achieved by using a symmetric sine RF pulse spanning 8π radians. The large number of sinc lobes created a sharp transition between the inverted and noninverted myocardium, reduced sidelobe excitation, and improved inversion efficiency.

Figure 3.

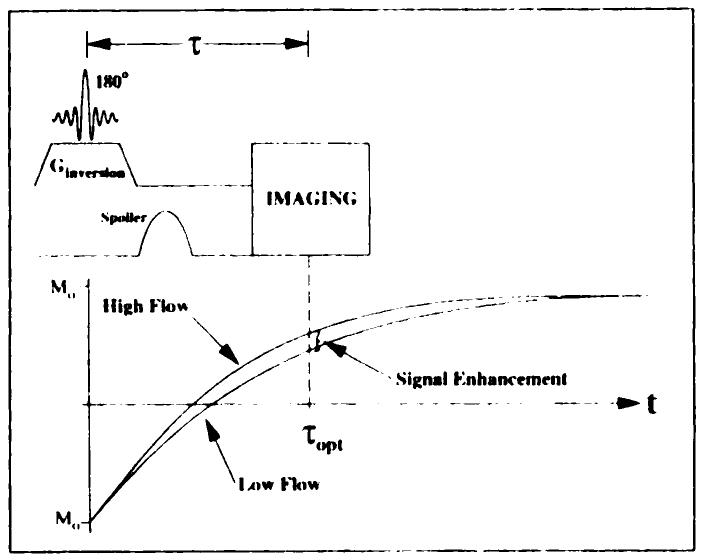
Pulse sequence timing. Imaging is preceeded by slab inversion and a τ_opt-second delay. The RF sinc spans 8π radians to create a selective inversion with a sharp transition and high inversion efficiency. Two T1^app recovery curves demonstrate the enhancement resulting from arterial flow. G_inversion = magnitude of inversion gradient, t = time, τ_opt = optimal inversion time.

Intensity profiles used for T1^app measurements were obtained along the length of a 5 × 5 × 31-mm rectangular volume contained within a short-axis plane, as previously described (12). Selective excitation was accomplished by means of a spin-echo (SE) sequence in which the section-selective pulses (90° and 180°) selected orthogonal planes, the intersection of which determined the refocused rectangular volume. The orientation of the linescan was prescribed from a short-axis image so that both left ventricular free wall and septum were clearly delineated in the profiles. The dimensions of the linescan were chosen so that the volume of sampled myocardium was large enough to provide sufficient signal, yet small enough to minimize partial voluming effects due to left ventricular wall curvature. When preceded by the selective inversion pulse and a variable delay, τ, this linescan protocol facilitated localized rapid acquisition of inversion-recovery T1^app data, with a good SNR.

In addition to the linescan protocol, standard SE imaging preceded by selective inversion was performed to obtain T1^app-weighted images. In this case, the inversion delay was fixed, and one phase-encoding step was acquired per inversion.

Experimental Protocol and Data Acquisition

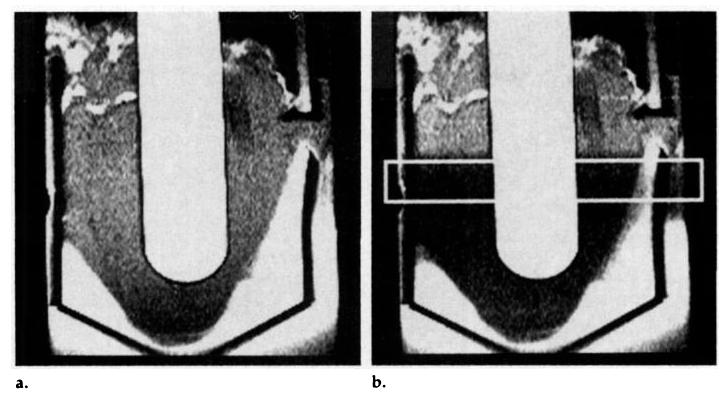
After isolation and attachment of the heart, the apparatus was inserted into the magnet and a short-axis, midventricular scout plane was chosen. The inversion slab was prescribed and optimized by using a long-axis profile that avoided the intensity standard and contained mostly myocardium. Figure 4 shows a typical long-axis image through the left ventricle and intensity standard without and with the preinversion pulse (a 90° saturation pulse and short delay were used to prevent enhancement from flow). This procedure was performed for all hearts studied.

Figure 4.

(a) Typical long-axis SE image through the intensity standard. (b) Long-axis image obtained in the same plane 20 msec after application of a 90° saturation pulse, which was used to prevent enhancement from flow. The short-axis imaging plane is indicated. The intensity standard appears bright because it has a T1 of less than 30 msec.

In three hearts, the linescan protocol was used to obtain data verifying the expression for T1^app given in Equation (6). Inversion times were varied from 120 msec to 10 seconds, echo time was 16 msec, a 10-second delay after each acquisition was used for T1 recovery, and two averages were performed. The image bandwidth was 40 kHz, the field of view was 60 mm, and 128 points were sampled for a resolution of 0.47 mm along the profile. Both imaging RF pulses were symmetric sinc pulses spanning 4π radians to minimize sidelobe excitation. Nineteen profiles were collected at approximately nine to 13 flow rates, ranging from 0.5 to 6 mL/min/g. Total time for one T1^app estimate was 8.5 minutes, and nine to 11 estimates were made at varied flow in each heart.

SE perfusion images were collected over a similar range of flows in three additional hearts in an effort to demonstrate a practical method of flow estimation, using Equation (9). In rabbit myocardium, λ has a value of 0.78–0.80 mL/g (35,40,41). Assuming λ = 0.8 mL/g, T1 = 2.3 seconds, f₁ = 1 mL/min/g, and f₂ = 5 mL/min/g, an optimal inversion delay of 2.1 seconds was calculated from Equation (11). Images were 128 × 64 pixels, with a 60-mm field of view and 5-mm section thickness, for voxel dimensions of 0.47 × 0.94 × 5 mm. No averaging was performed, repetition time was 12.1 seconds, and echo time was 12 msec, for a total acquisition time of approximately 13 minutes. Because of concerns regarding myocardial viability, hearts were not studied for more than 3 hours, allowing acquisition of only eight to nine images. In addition to the perfusion images, a magnitude image was acquired without a preinversion pulse to estimate M_o (Eq [9]).

In all experiments, a remote snare occluder was placed around a proximal branch of the left anterior descending coronary artery. After acquisition of several perfusion images and a magnitude image, the left anterior descending coronary artery was occluded. SE perfusion and magnitude images were acquired immediately after ligation, with no change in perfusion pressure. Only moderate (≈5%) reductions in total flow were seen after occlusion. Finally, a series of standard SE images were acquired (two averages) after injection of a 1-mL bolus of 500 mmol/L gadopentetate dimeglumine into the perfusate line. These images were used to qualitatively delineate regions of flow deficit.

RESULTS

T1^app Measurements

Signal from 4–10-pixel-wide regions in the linescan profile representing either the free wall or the septum were measured, and a least squares fitting algorithm was used to fit data with the parameters M_o, W, and 1/T1^app in Equation (7). The SNR of linescan profiles was approximately 20–30 with two averages. The fit value of W ranged from 0.82 to 0.84 ± 0.006, and the standard deviation of M_o was always less than 1%. The low variability of W and M_o suggested that this measurement technique was reproducible and precise. In Figure 5, measured 1/T1^app is plotted against total coronary flow (in milliliters per minute) for a typical experiment.

Figure 5.

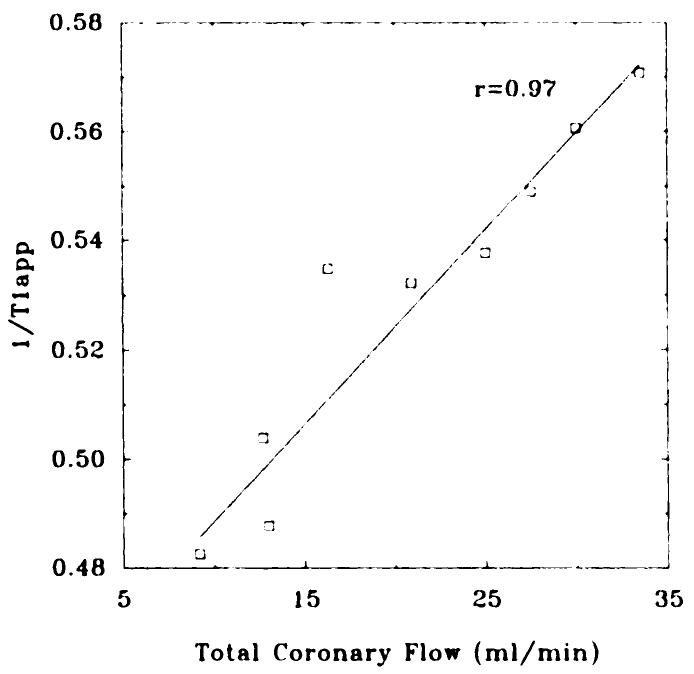
Graph shows 1/T1^app fit from linescan measurements, plotted against total coronary flow, for a typical experiment. The correlation coefficient (r) was .97 for this heart and .92 and .91 for the other hearts studied (data not shown).

A Monte Carlo simulation (42) was performed to estimate the uncertainty in the 1/T1^app fits. Briefly, the standard deviation, σ, of each linescan measurement was assumed constant in τ and calculated from the minimum total variance of the fit (σ²_tot), determined by the initial least squares fit

$$\sigma =\sqrt{\frac{{\sigma }_{\mathit{tot}}^2}{N}}.$$ (18)

The simulation added random Gaussian noise (standard deviation = σ) to each data point, and a new fit was performed. This process was repeated 20–30 times, and the standard deviation of the resulting list of 1/T1^app values was calculated as an estimate of the error associated with each 1/T1_app measurement. With this method, estimated errors for the 1/T1^app fits were less than ± 0.01 second⁻¹.

To make a comparison of the data presented in Figure 5 with Equation (6), the slope must be multiplied by the wet weight of the heart (7–10 g), measured at the conclusion of the experiment. Depending on the degree of ventricular drainage and surface blotting, the wet weight of the heart varied by 0.5–1.0 g, introducing additional error when comparing the theory with experiment.

The slopes of 1/T1^app against total coronary flow were multiplied by the wet weight of the heart to normalize flow in milliliters per minute per gram, and the results are shown in Table 1. The inverse of the slopes is also shown and represents estimates of λ. Variation of the intercepts indicated variability of the zero-flow T1.

Table 1.

Correlation Coefficient, Slope Multiplied by the Mass of Each Heart, Intercept, and Inverse of the Slope for the Three Hearts Studied with the Linescan Protocol

Heart	r	Slope (g/mL)	Intercept (sec−1)	Slope−1 (mL/g)*
1	.97	1.49 ± 0.27	0.456 ± 0.008	0.67 ± 0.09
2	.92	1.49 ± 0.19	0.453 ± 0.008	0.67 ± 0.12
3	.91	1.64 ± 0.38	0.448 ± 0.005	0.62 ± 0.24

^*Inverse of the slope represents an estimate of λ.

SE Images

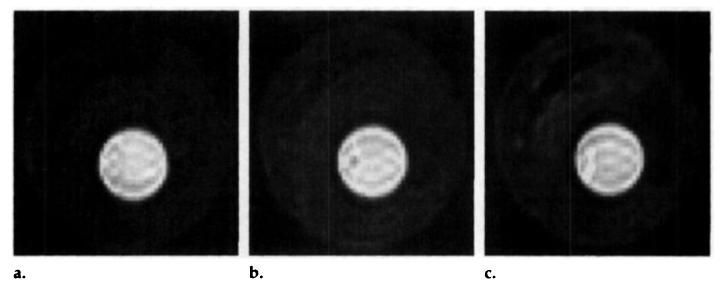
Representative short-axis SE images acquired 2.1 seconds after the selective inversion pulse are shown in Figure 6 for different coronary flows. Before the occlusion, several perfusion images were acquired at different flows, and a magnitude image was acquired as an estimate of M_o. A region of interest was drawn over the entire left ventricular myocardium (approximately 4,000 pixels), and the average intensity, normalized by the intensity from the magnitude image, was plotted against the total coronary flow in Figure 8.

Figure 6.

Representative short-axis SE images obtained 2.1 seconds after the selective inversion pulse. Coronary perfusion was approximately (a) 0.6 mL/min/g, (b) 1.8 mL/min/g, and (c) 5.4 mL/min/g.

Figure 8.

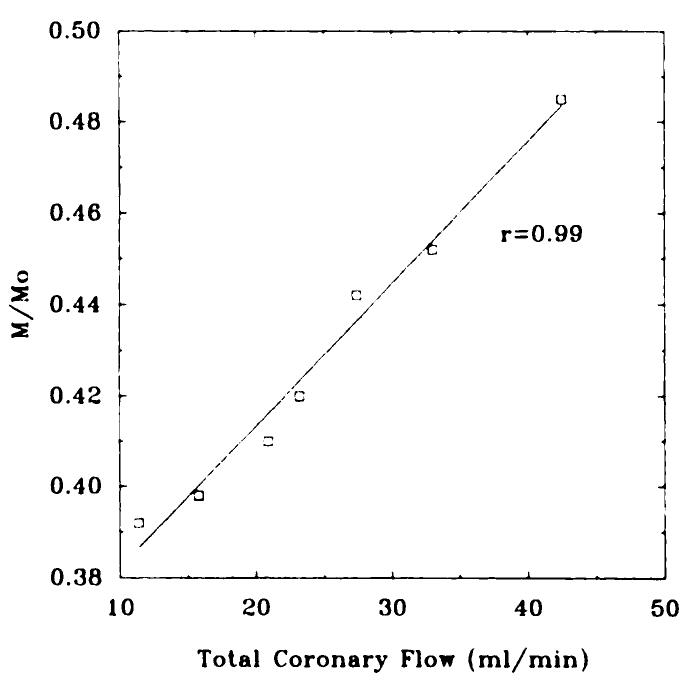
Intensity of the left ventricle normalized by the magnitude image plotted against total coronary arterial flow.

SNR in perfusion images was 160–180 in the three hearts that underwent SE imaging, and magnitude images had an SNR greater than 300. With high SNR and large regions of interest, the error of the estimation of the signal intensity is negligible when compared with the error on the total flow measurements, estimated as ±0.2 mL/min.

For all SE image data, the correlation coefficient, slope, and intercepts were calculated for the normalized magnetization against total coronary flow. The slopes were multiplied by the mass of the heart and the propagated errors calculated. The results of these calculations are shown in Table 2. The values of W and T1, determined from the linescan experiments performed before the SE experiments, were 0.82 and 2.25 seconds, respectively.

Table 2.

Correlation Coefficient, Slope, and Intercept for the Three Hearts Studied with SE Imaging

Heart	r	Slope (min · g)/mL	Intercept
1	.99	0.027 ± 0.0002	0.351 ± 0.005
2	.95	0.030 ± 0.004	0.380 ± 0.009
3	.88	0.025 ± 0.006	0.400 ± 0.02

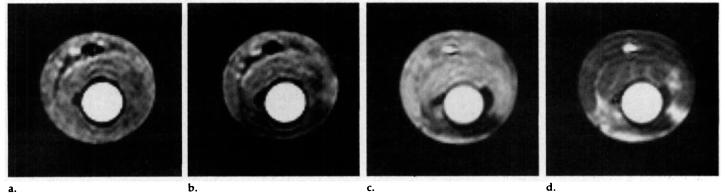
Figure 7b is an SE perfusion image acquired immediately after occlusion at the same perfusion pressure as the image in Figure 7a. Figure 7c and 7d are standard SE images acquired early and late, respectively, during the passage of a bolus of gadopentetate dimeglumine. Although different hearts exhibited different patterns of darkening on postocclusion images, all darkened regions accurately matched regions of flow deficit as indicated by the gadolinium-enhanced images.

Figure 7.

(a) Representative short-axis SE image obtained 2.1 seconds after the selective inversion pulse. Coronary perfusion was approximately 3 mL/min/g. (b) Image obtained with the same parameters as a after ligation of the left anterior descending coronary artery. Perfusion pressure was maintained constant before and after occlusion. (c) Conventional SE image (300/13, two signals acquired) obtained during the early phase after injection of a bolus of gadopentetate dimeglumine. (d) Image obtained with the same parameters as c, during the late phase after the same gadolinium bolus.

Regions of flow deficit, determined from the gadolinium-enhanced images, were used to measure the average signal intensity of the flow deficit region. In all cases where occlusion was indicated with gadopentetate dimeglumine, a substantial drop in signal intensity was observed. For the heart shown in Figure 7b, the signal intensity in the region of flow deficit was 24% less than that in the septal region. Before ligation, there was no significant difference in signal intensities between the septum and free wall. Magnitude images acquired after the occlusion showed no change in signal intensity in the flow deficit region, eliminating the possibility that changes in T2 or spin density were responsible for the signal change.

DISCUSSION

An alternative noninvasive spin-labeling method for quantitative measurement of myocardial arterial perfusion has been presented and its ability to quantitate flow has been demonstrated in the isolated, perfused arrested rabbit heart. This model is a simple biologic model that allows for fine control over many parameters, especially myocardial flow. Many of the problems associated with an in vivo, beating heart have been avoided.

With a selective slab that inverts magnetization in all spins in the imaging section and those apical to that section, this technique relies on the geometry of the coronary vasculature to ensure that signal enhancement results from nutritive, arterial flow. Except for adiabatic fast passage inversion, all other spin-labeling techniques are qualitative and do not help differentiate between arterial and venous flow. Differentiation of flow between venous and arterial sources is necessary to accurately assess and quantitate tissue perfusion. The use of an inversion slab that inverts venous spins flowing into the imaging section is an effective way to measure arterial flow.

With linescan techniques, accurate measurements of 1/T1^app were made to verify its relationship to flow. The inverse of the slopes measured in all hearts were in agreement with the value of λ, 0.78–0.80 mL/g. These data suggest that Equation (6) is valid within the accuracy of these experimental measurements.

Subsequent to the verification of the T1^app relationship, a method was investigated for quantitating flow on images, avoiding the lengthy process of determining accurate T1 and T1^app maps. Acquisition of a single image without preinversion, followed by image acquisition with selective preinversion can be used to determine estimates of relative flow. If T1, inversion efficiency, and tissue water partition coefficient (λ) are known, then a quantitative estimate of absolute flow can be made. If these values are not known, estimates of relative perfusion can still be made. This method was applied in three hearts, and a strong correlation was found between total coronary flow and image intensity. In addition, the slope and intercept of the data were compared with the theoretical values, and strong agreement was found between the two. According to Equation (9), the theoretical slope should be 0.0282 min g/mL with a T1 of 2.25 seconds, λ of 0.80 mL/g, τ of 2.1 seconds, and W of 0.82. The theoretical intercept with these parameters is 0.355. Clearly, from Table 2, strong agreement exists between the measured and predicted relationship for flow and magnetization within the experimental error.

In addition, ligation of the left anterior descending coronary artery produced regions of reduced signal intensity that were highly correlated with regions of flow deficit delineated on images acquired after gadopentetate dimeglumine bolus injection. Signal intensities measured in the region of flow deficit were heterogeneous, as were those measured on the gadolinium-enhanced images. On average, however, the decreased signal intensity suggested a drop in flow from 3 to 0.24 mL/min/g, representing a 92% flow reduction in the occluded zone. Magnitude images acquired before and after ligation exhibited no change in signal intensity, revealing that changes in signal intensity cannot be a result of T2 or spin-density changes.

There was an observable heterogeneity on the flow images, as seen in Figure 6, that was reproducible from image to image. The dispersion (standard deviation/mean) of flow was calculated on a pixel basis and was approximately 60%. This is consistent with findings by King et al (43) in the baboon, although the variation here was somewhat higher. The higher dispersion can be explained partially by the finer resolution available with the images, as there is a strong dependence of observed heterogeneity on voxel dimension (44). Regardless, the heterogeneity observed here appears to be a real effect with the possibility for further study.

Although SE imaging is acceptable for isolated heart preparations, the long acquisition time is unacceptable for potential clinical applications, precluding any attempts of breath-hold imaging, which is important for quantitative in vivo cardiac imaging (45). Ultrafast gradient-echo imaging has been applied to address this problem (31); however, gradient-echo imaging suffers from inherently poor SNR. In addition, the behavior of magnetization under repeated RF excitation makes a quantitative estimate of the magnetization during T1 recovery questionable (46). A multiecho fast imaging sequence such as interleaved SE, echo-planar imaging (47,48) or gradient-and SE imaging (GRASE) (49) would provide excellent SNRs with acquisition times compatible with clinical applications.

One of the underlying assumptions of all spin-labeling methods is that spins flowing into a voxel are well mixed before they exit the voxel. Although not conclusive, there is some evidence that suggests this is true in myocardium. The literature indicates that water exchange between intravascular and extravascular spaces in the myocardium is between 8 and 27 Hz (50,51). Functional capillary lengths are 500–1,000 μm (32), and flow velocities through capillaries can be calculated as approximately 1 mm/sec under normal flow. Accordingly, spins flowing through a voxel spend approximately 0.5–1 second in the capillary where the majority of water exchange occurs. With exchange rates of 8–27 Hz and assumed fast exchange between interstitial and intracellular water (50), one would expect good mixing. In addition, simulation results of Ma et al (52) suggest that for the velocity flow regime of capillaries, good mixing takes place on the second time scale. Finally, a linear relationship between signal intensity and coronary flow (r = .98) was measured at superphysiologic flows by Williams et al (28) by using spin inversion, suggesting that good mixing occurs even at high flows.

Incomplete mixing could result from poor exchange of water in large vessels and the interstitium. Since they total about 25% of the vascular volume, which is 22% at maximal vasodilatation (53), about 5% of the total tissue water could be inaccessible for mixing. This would reduce the effective value of λ by 5%, consistent with our measurements. Modeling of incomplete mixing is a second-order effect that could be accounted for by redefining λ as the volume of water available for free exchange per gram of myocardium.

The largest source of error in this method stems from the measurement of the wet weight of the hearts. An exact determination of wet weight was difficult, and these measurements varied considerably depending on the extent of surface drying and ventricular cavity drainage. Since there is close agreement on the water content of myocardium in the literature (35,40,41), a more accurate estimate of the wet weight could be made by measuring the dry weight of the heart and by using λ to calculate the wet weight. Errors of ±0.5–1.0 g were common.

Although the error on the measurement of coronary flow is small, the flow out of the pulmonary artery will underestimate flow resulting from Thebesian drainage into the left ventricle, which leaves through the small vent placed in the left ventricle. Thebesian drainage into the right ventricle still exits the pulmonary artery and will not contribute to coronary flow underestimation.

In the isolated heart, increased pressure often resulted in slight distention of the myocardium, which was evidenced on short-axis images. Although the heart is maximally vasodilated, the increase in pressure may increase the vascular volume and cause edema formation. Distention was rapidly reversible, however, suggesting that edema was not responsible for volume changes. In the beating canine heart it has been shown that intravascular volume increases with a square root dependence on flow (54). Regardless of mechanism, the apparent increase in volume could have two effects that could adversely affect quantitative flow estimates. First, the effective value of λ increases slightly as vascular volume increases. If the intravascular volume increases from 10% to 20%, then λ would increase from 0.80 to 0.82 mL/g, a modest increase reducing the sensitivity of this method by a small amount (Eq [9]). A larger effect is the increase in the wet weight of the heart. A 10% increase in the wet weight of the heart will result in a substantial error if coronary flow (in milliliters per gram per minute) is estimated from the total coronary flow divided by total weight of the heart, measured at zero flow and zero perfusion pressure. Measuring the changes in volume with images could be used to correct for this effect, although no attempt was made to do so here.

Although the prevailing direction of arterial flow is from base to apex, this assumption does not always hold. Retrograde flow is often observed in the presence of collateral flow in diseased states (55), as well as at the left ventricular apex (Fig 1). This would result in the inversion of some arterial spins apical to the imaging section. Under normal flow conditions, arterial blood volume is about 10% of the total blood volume (10%) (53). At a flow rate of 1 mL/min/g, the entire arterial volume should replace itself every 0.6 second, a time substantially shorter than the mixing time of 2.1 seconds. Under maximal vasodilatation, the replacement time would be 0.24 second, when the blood volume increases to 22% and the flow rate increases to 5 mL/min/g. Although retrograde flow would cause flow underestimation, there would still be substantial flow-induced enhancement.

A potential clinical application of this method is the identification of regions with flow abnormalities. Regions of myocardium that have critically stenosed arteries and little or no cardiac reserve could potentially be revealed after administration of a vasodilator such as dipyridamole, in the same fashion used in thallium-dipyridamole stress testing (56). At 1.5 T, the T1 of myocardium is approximately 870 msec (57), and assuming an inversion efficiency of 0.8 and λ of 0.8 mL/g, the optimal inversion delay would be 0.83 second. The maximal signal difference for a flow differential of 4 mL/min/g would be 4.3%. Fortuitously, an optimal inversion time of 0.83 second is ideal for gated imaging, where imaging follows inversion by approximately one RR interval. An SNR of 188 would be required to resolve flow differences of 1 mL/min/g with single pixel resolution. Effective SNR can be increased by reducing spatial resolution (58) or by averaging over regions of interest.

In conclusion, we have demonstrated a novel, noninvasive, spin-labeling method capable of perfusion quantification in the isolated arrested rabbit heart. This method has potential for in vivo clinical and investigational applications where relative or absolute flow quantification is required. The relationship between flow and signal enhancement with this method is linear, well understood, and avoids the need for exogenous contrast agents.

Abbreviations

EPISTAR

echo-planar MR imaging and signal targeting with alternating RF

RF

radio frequency

SE

spin echo

SNR

signal-to-noise ratio