Analysis of Self-Associating Proteins by Singular Value Decomposition of Solution Scattering Data

Abstract

We describe a method by which a single experiment can reveal both association model (pathway and constants) and low-resolution structures of a self-associating system. Small-angle scattering data are collected from solutions at a range of concentrations. These scattering data curves are mass-weighted linear combinations of the scattering from each oligomer. Singular value decomposition of the data yields a set of basis vectors from which the scattering curve for each oligomer is reconstructed using coefficients that depend on the association model. A search identifies the association pathway and constants that provide the best agreement between reconstructed and observed data. Using simulated data with realistic noise, our method finds the correct pathway and association constants. Depending on the simulation parameters, reconstructed curves for each oligomer differ from the ideal by 0.05–0.99% in median absolute relative deviation. The reconstructed scattering curves are fundamental to further analysis, including interatomic distance distribution calculation and low-resolution ab initio shape reconstruction of each oligomer in solution. This method can be applied to x-ray or neutron scattering data from small angles to moderate (or higher) resolution. Data can be taken under physiological conditions, or particular conditions (e.g., temperature) can be varied to extract fundamental association parameters (ΔH_ass, ΔS_ass).

INTRODUCTION

Protein-protein interactions play key roles in most biological processes. High-throughput proteomic techniques (1) have identified a large number of homo- and heterointeractions, up to 81,775 in yeast and 38,217 in humans (2). Such techniques are invaluable for building networks that reveal protein interactions (2,3), but they can only indicate the presence of an interaction. The function of a protein-protein complex, however, depends on both the stoichiometries and the strength of association between subunits, as well as on the structures of the subunits and complexes. The elucidation of protein interaction networks thus motivates the development of methods for rapidly determining interaction parameters and structures, particularly for the low-affinity transient interactions that are frequently revealed by high-throughput proteomics. Under experimental conditions, such low-affinity interactions typically yield heterogeneous systems containing multiple components.

Many techniques are available for determining the stoichiometry and/or strength of an interaction. They include hydrogen/deuterium exchange (4), analytical ultracentrifugation (5), titration calorimetry (6), composition gradient static light scattering (7,8), and surface plasmon resonance (9). In addition, classical separation tools such as size exclusion chromatography can be combined with other biochemical analyses to elucidate the nature of a protein-protein association. However, these techniques can provide only very limited structural information about the individual proteins or complexes.

Other techniques yield structures of varying resolution, yet each has limitations that prevent application to the broadest array of protein-protein complexes. Of the available methods, x-ray crystallography generally provides the highest resolution, but the weak and transient interactions of many protein-protein complexes prevent the growth of diffraction-quality crystals (10). Even in cases where the structure of a complex can be determined, only the final oligomeric state can be identified (and even that can be ambiguous depending on the observed crystal-packing interactions). Neither the pathway nor the strengths of association are revealed directly by a crystal structure. NMR spectroscopy has been used to determine the structures of protein-protein complexes. Although new techniques are being developed (11), the large molecular weight of many complexes hinders analysis. Consequently, only five NMR structures of protein-protein complexes in the Protein Data Bank (12) are for proteins of >200 residues (13). Like crystallography, an NMR structure reveals neither the pathway nor the strengths of association. Cryoelectron microscopy can provide structures of up to 5 Å resolution for complexes large enough to be accurately oriented (10) and is also capable of analyzing heterogeneous samples. Although it might be possible to infer the association model and constants of a protein-protein interaction from cryoelectron microscopy of equilibria trapped by rapid freezing, such measurements would require distinguishing oligomeric forms and tedious quantification (14). Thus, none of these tools readily provides both the association model and significant structural information from a single experiment.

Small-angle scattering (SAS) of either x-rays or neutrons allows low-resolution structural data to be collected from proteins that span a large range of molecular weights (15). Since SAS data are collected from solution, the measurements reflect the structure in solution, and conditions can be readily altered to reflect physiological changes. The lack of size restrictions, the absence of a requirement for crystallization, and rapidity of data collection in solution make SAS a potentially promising technique for the structural characterization of complexes identified by high-throughput proteomics assays. The complete analysis of SAS data has traditionally required a homogenous sample, however, making it unsuitable for weak-binding complexes.

Protein complexes can form either between different proteins (heteroassociation) or between identical proteins (homoassociation). Excluding random aggregation, homoassociation can proceed by either open or closed symmetry, distinguished by the relationship between the symmetry operators and the surface(s) of association. In closed (point-group) symmetry, no interaction surfaces are left unoccupied in the oligomers. As oligomers are formed, the association surfaces are sequestered within the complex, imposing an upper limit on the oligomeric state that can be achieved. Additional association (that is, more than two states in the association pathway) requires the use of additional interaction surfaces with different interaction energies and thus different affinities. Although some sets of affinities are favored in vivo (16), in principle, any relationship between successive association events is possible. In contrast, open symmetry (e.g., the helical association of actin) leaves an unoccupied interaction surface at each step and allows the formation of successively longer polymers, with each step using the same surface and occurring with the same energy.

In this article, we describe a method for analyzing SAS data from heterogeneous systems undergoing concentration-dependent association into closed-symmetry homooligomers. Our method discriminates between different association pathways, determines the association constants, and reconstructs the scattering curve of each oligomer from a concentration series of SAS data, which can be collected rapidly in a single experiment. The method employs singular value decomposition (SVD) to determine the set of linearly independent basis vectors and coefficients that best represent the set of observed SAS curves. These basis vectors and coefficients can be used (along with the mass fractions of each oligomer at each concentration) to reconstruct the scattering curve for each pure oligomer. The scattering curve of each pure oligomer and the same mass fractions can then be used to approximate the observed data. Since the mass fractions at each concentration are dependent on the association pathway and constants, a search over the feasible closed association pathways and constants determines the values that best approximate the observed data. Scattering curves of individual oligomers reconstructed by this analysis are available for the computation of interatomic distance distributions (P(r)), which provide the pairwise distances between all atoms in each oligomer. P(r) distributions in turn form the basis for computing low-resolution reconstructions of each oligomer through the application of ab initio shape reconstruction algorithms (17,18).

Concentration series of scattering data have previously been employed to fit the extrapolated forward scattering (I(0)), which is directly proportional to the molecular mass and concentration of the scattering particle, to association models. For example, this technique has been employed in multiple studies of the oligomerization of visual arrestin (19,20). Here, in effect, we extend such analyses to use the entire scattering curve via the SVD mechanism.

SVD itself has previously been applied to SAS data collected on protein solutions with varying concentrations of a chemical denaturant to identify, quantify, and characterize the partially folded intermediates of cytochrome c and lysozyme (21–23). In contrast, SVD of time-resolved scattering data has been used to determine that no stable intermediates exist when the HK97 bacteriophage capsid undergoes acid-induced maturation (24). In the closest precedent to our work, SVD was used to analyze SAS data collected on samples of the allosteric enzyme aspartate transcarbamylase where the relative amounts of the R and T states were altered by titration with the bisubstrate analog N-(phosphonacetyl)-L-aspartate (PALA) either alone or with allosteric effectors ATP or CTP (25). The absence of intermediate states was confirmed, and binding and allosteric parameters for PALA were found by fitting to the fractional amounts of each form. In this special case, when only two states are present and homogeneous samples are available for both states, the fractional amounts could be estimated directly from the coefficients of the decomposition. Other cases require restrained indirect estimation of the kind we describe here.

In all these examples, data from some samples that were homogenous (e.g., completely native or completely denatured protein) were available, easing the task of quantifying any intermediates. Our method removes that requirement; we show that a restrained SVD analysis (here restrained by self-association equations) does not require data from a homogeneous sample. We also show that fractional amounts and restraint parameters can be determined even when more than two forms are present. Accurate results can thus be obtained when associations of intermediate strength, including systems with multiple steps of association, cause heterogeneity at all experimental concentrations.

METHODS

Formulation of the oligomer reconstruction

We first represent a set of SAS data observed over M scattering angles from N concentrations of protein as an M × N matrix A. Since each scattering curve is a mass-weighted linear combination of the scattered intensities of all oligomers present,

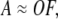(1)

where the SAS curves for each of the N_forms oligomers comprise the unknown M × N_forms matrix O, and the N_forms × N matrix F contains the unknown fractional mass of each oligomer at each concentration. Our goal is to reconstruct O from the data when the N concentrations in the data set exceed the N_forms number of oligomers while also determining the association model and constants reflected in F.

Singular value decomposition analysis

We chose to decompose the SAS data by SVD (Fig. 1 A) because it is robust and model-independent, allows an independent check on the number of oligomeric forms present, and seeks to separate noise from significant components (26). By SVD theory, any matrix A can be written as the product of three matrices,

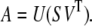(2)

Matrix U is M × N with columns forming a set of basis vectors that can be linearly combined to represent the scattering curves at the protein concentrations in the data set. Matrix SV^T is N × N with rows containing the amplitude vectors of coefficients applied to each basis vector to represent each observed scattering curve in A. The decomposition was implemented using the function svd in MATLAB (version 7.01, The MathWorks, Natick, MA).

FIGURE 1.

Schematic showing the flow of information during the analysis of scattering data. (A) Obtaining basis vectors, their associated weights, and amplitude vectors by SVD of the input data. (B) Reconstructing both the SAS curves of each oligomer and the set of observed data for a trial association pathway and constants using the fractional masses from the association model (in F) and the basis vectors (in U) and coefficients (in SV^T) from SVD.

Ideally, the number of significant basis vectors, N_sig, is thought to equal N_forms, the number of different oligomeric forms present in the mixture; additional basis vectors contain noise. During the initial analysis when N_forms is not known directly, N_sig can be estimated from the SVD by several criteria. The smoothness of the basis vectors in U (here a function of scattering angle) and the relative magnitude of the singular values (diagonal of matrix S) are well known criteria for this purpose. Since the basis vectors are the components of linear combinations that make smoothly varying contributions to the data curves, the amplitude vectors corresponding to significant basis vectors should also vary smoothly as the total protein concentration increases. As we demonstrate, though, estimation by these criteria is often unreliable in this application. In these cases, N_sig is set equal to N_forms of the trial association pathway (see below).

The value of N_sig allows the definition of submatrices containing the significant information, Ũ containing the first N_sig columns of U, 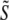containing the first N_sig rows and columns of the diagonal matrix S, and 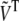containing the first N_sig rows of V^T. The SAS data set can then be approximated as the product of these submatrices,

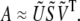(3)

Reconstruction of oligomer scattering curves

The matrix O of scattering curves for each oligomer can also be approximated in Ô as a linear combination of the same N_sig basis vectors in Ũ weighted by coefficients from a different (and unknown) N_sig × N_sig matrix B (Fig. 1 B),

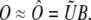(4)

To complete our reconstruction of the oligomer scattering curves in Ô we need to determine the best values of B. To solve for B, we note that the data in A can also be approximated by Â, which consists of the linear combination of the reconstructed individual oligomer curves in Ô with the mass fraction coefficients of each oligomer in F,

(5)

Substituting Eq. 4 into Eq. 5 and reassociating yields

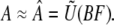(6)

Pairing the two different approximations of A in Eqs. 3 and 6 then allows us to solve for B in terms of F and the known 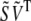by setting

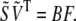(7)

We present below an algorithm for determining the best F and thus the best B by minimizing the difference between the reconstructed  and the experimental data A.

Determining the association model (pathway and constants)

Searching a set of trial association models

The fractional mass values in F are unknown before the experiment begins. However, these values can be determined directly from the association pathway and constants and the concentration of the samples. Different values in F alter the matrix B (Eq. 7), different values in B in turn alter the reconstructed scattering curves in Ô (Eq. 4), and F further affects the reconstructed data in  (Eq. 5). Variation in F thus alters the values in Ô and the agreement between  and the observed data in A. We quantify these effects in two scoring functions described below. We present an algorithm for determining the correct association pathway and constants that exploits these relationships by minimizing the scoring functions.

For each experiment we search a set of feasible association pathways. While the set of association pathways is in principle infinite, the principles of closed point group association and previous biological experience limit the association pathways to a smaller feasible set. Although the set can be changed depending on knowledge of the biological background, a standard set of the most common pathways is shown in Table 1.

TABLE 1.

Formulations of the equilibrium association constants for the feasible association pathways

Pathway	K12	K23	K34
1-2	[Dim]/[Mon]2	—	—
1-3	[Tri]/[Mon]3	—	—
1-4	[Tet]/[Mon]4	—	—
1-2-4	[Dim]/[Mon]2	[Tet]/[Dim]2	—
1-2-6	[Dim]/[Mon]2	[Hex]/[Dim]3	-
1-3-6	[Tri]/[Mon]3	[Hex]/[Tri]2	-
1-2-8	[Dim]/[Mon]2	[Oct]/[Dim]4	-
1-4-8	[Tet]/[Mon]4	[Oct]/[Tet]2	-
1-2-4-8	[Dim]/[Mon]2	[Tet]/[Dim]2	[Oct]/[Tet]2
1-2-6-12	[Dim]/[Mon]2	[Hex]/[Dim]3	[Dod]/[Hex]2
1-3-6-12	[Tri]/[Mon]3	[Hex]/[Tri]2	[Dod]/[Hex]2

The molar concentration ratios for computing the equilibrium association constants are listed. For example, for the monomer-trimer-hexamer (1-3-6) pathway, the association constant for the first-to-second-form equilibrium, K₁₂, equals [Trimer]/[Monomer]³, whereas the association constant for the second-to-third-form equilibrium, K₂₃, equals [Hexamer]/[Trimer]². Dim, dimer; mon, monomer; tri, trimer; tet, tetramer; hex, hexamer; oct, octamer; dod, dodecamer.

For each association pathway, we construct a grid with axes representing the association constants; the dimensions of this grid are thus one less than the number of forms in the pathway. For example, to consider a three-state association pathway, such as monomer-trimer-hexamer, the grid is two-dimensional, using as the axes the first-to-second-form (here monomer-trimer) equilibrium constant (K₁₂) and the second-to-third-form (here trimer-hexamer) equilibrium constant (K₂₃). In our computations, the range of each axis spans 32 orders of magnitude in association constants from 10⁻⁷ to 10²⁵, covering the range of feasible associations from very weak to extremely strong. Each axis contains 320 trial values at integer multiples of each power of 10 (e.g., 1 × 10⁻⁶, 2 × 10⁻⁶… 9 × 10⁻⁶). The grid is searched using an algorithm (Fig. 2) such that for each trial set of association constants, a trial F is calculated from the standard association equations (Table 1) and the known concentrations of the data. A trial B is then calculated with Eq. 7. Equations 4 and 5 then use this F and B to determine Ô and Â. The values of the scoring functions described below are then computed for each set of trial association constants (Fig. 1 B).

FIGURE 2.

The algorithm used to evaluate possible association constants for a trial association pathway.

It is likely that the true values of experimental association constants will not lie at the integer values in the coarse-grid search described above. We show, however, that the scoring functions are smooth, and the best scoring grid points from this coarse search bracket the best values of finer searches. Thus, using the results of the coarse search, we select dimensions for a new grid that bracket the best solution found on the coarse grid. The smaller dimensions of this grid allow it to be easily sampled as finely as 1/100 of the coarse-grid sampling. The use of coarse and fine-grid searches allows a better determination of the association constants within reasonable computation time while also allowing the accurate determination of a confidence interval (see below).

Since the reconstructed SAS curves in Ô are linear combinations of the N_forms basis vectors in Ũ (which can have both positive and negative values), it is mathematically possible for the reconstructed SAS curves to contain negative values even though scattering intensities are always nonnegative. Early testing showed that solutions with good scores under the scoring metrics (although not equal to the best) could be obtained for many association models disparate from the simulated system. Examination of these solutions revealed that they employed one or more oligomer scattering curves with significant negative values to compensate for the disagreement between the data and the combination of the other forms. We thus implemented a restraint against negative values in the reconstructed oligomer curves. Since negative values can appropriately arise in SAS data from statistical fluctuations around small scattering intensities and our current method for SVD does not provide for error propagation, we cannot directly assess the significance of any negative value. Thus, we have conservatively chosen to exclude an association model only if it yields an oligomer curve with a substantial number of negative values. In the simulations reported here, we exclude trial association models where >10% of the points in any oligomer curve are negative. The excluded solutions, which cover most of the coarse grid even for the correct pathway, are indicated as blank space in the coarse-grid search figures.

Evaluating the quality of the association model and constants

Quality score based on agreement with observed scattering intensities

The fit to the data arising from the reconstructed oligomer curves associated with a trial association model can be quantified through a normalized χ² comparison of the data in A and the reconstructed data in  using the estimated error σ(m,n) in each experimental data point,

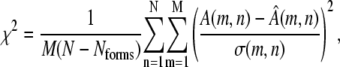(8)

where m sums over all M data points (scattering angles) in a SAS curve and n sums over all N scattering curves in the data set. The χ² values are calculated for M × N data points, but the number of degrees of freedom used for normalization is calculated by subtracting the degrees of freedom fixed by the N_forms basis vectors of the SVD, where N_forms is determined by the choice of association pathway to be evaluated. We show that in practice this score approximately equals 1 for the best fit to data with Gaussian simulated noise.

Quality score based on relative forward scattering

The intensity of scattering at zero angle (also called I(0) or forward scattering), which can be extrapolated from each oligomer scattering curve in Ô, should be directly proportional to the molecular weight of that oligomer. For example, I(0) values from the scattering curves of a monomer, dimer, and tetramer of a self-associating system should fit the ratio 1:2:4. We can thus evaluate an association model by a second quality score comparing the ratio of I(0)s that have been extrapolated from the reconstructed Ô to the ratio expected for each trial association pathway. The mean-squared mass ratio difference (MSMRD) score is summed over the N_forms in the postulated association model and normalized by the number of I(0) mass ratios,

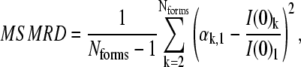(9)

where I(0)_k is the reconstructed forward scattering for the kth form and I(0)₁ the forward scattering for the first form (typically monomer), whereas α_k,1 is the expected ratio between I(0)_k and I(0)₁ (e.g., 3.0 for monomer/trimer). This score then equals zero for a perfect reconstruction. Note that this score is a generalization of methods used to determine association constants by fitting specific models to the change in I(0) with concentration (19,20).

For both simulated and experimental data the I(0) values can be estimated from Ô by the traditional Guinier plot analysis (27). For simulated data with excellent low-resolution intensities, we estimated the applicable q range for the Guinier analysis using a postulated radius of gyration (R_G) value significantly larger than that found for the highest-concentration simulated data curve and applying it to all the reconstructed oligomers. For experimental data the best q range may be determined by iterative estimation of R_G for the oligomeric form under consideration and may need to be modified based on the quality of the lowest-resolution data. Our results show that the MSMRD is useful as a supplementary metric in determining the correct association model.

Computing a confidence interval around the best association model

The values of χ² from the fine-grid search are also used to compute a confidence interval around the best association constants. Since we know the association constants must lie within the broad range that is searched and we demonstrate the small variation between scores at adjacent fine-grid points, the contribution of each grid point can be computed by converting the scores to a likelihood using and normalizing their total likelihood to 1. The normalized scores are ranked and summed to determine the desired confidence boundary. In all cases examined thus far, the confidence boundary encloses a single smooth and continuous surface.

Simulating scattering data from a self-associating monomer-dimer-tetramer system

We simulated small-angle x-ray scattering (SAXS) data from a closed symmetry self-association in a monomer-dimer-tetramer equilibrium using the homotetramer iron superoxide dismutase from Sulfolobus solfataricus (PDB id 1WB8) (28). After separating the homotetramer into a monomer (24 kDa), a hypothetical dimer, and intact tetramer components, theoretical x-ray scattering intensities for each component in solution (matrix O) were computed using x-ray scattering factors and a Fourier transform of the shape of the protein as implemented in the program CRYSOL (29). Calculated data was limited to a q_min of 0.015 and a q_max of either 0.05 (low resolution) or 0.14 (moderate resolution), where q = 4π*sin (θ)/λ. The fractional masses of each oligomer (matrix F) were computed at seven protein concentrations equally spaced in a geometric series from 0.25 to 16 mg/ml (0.25, 0.5, 1.0, 2.0, 4.0, 8.0, 16.0 mg/ml), using association constants of K₁₂ = 8.26 × 10³ M⁻¹ and K₂₃ = 2.83 × 10² M⁻¹. These concentrations are ones for which x-ray scattering data can readily be obtained at third-generation synchrotron sources. The simulated association constants are intentionally noninteger to test the ability of successive coarse- and fine-grid searches to find noninteger values such as those expected for real associations. Noiseless simulated scattering data (to make a noiseless version of matrix A) was then calculated by multiplying the simulated O times F.

Major sources of noise in experimental scattering data include counting error, parasitic scatter, and contaminating protein (including aggregates of the target protein and any fraction of the target protein not participating in the association). Not all of these are readily modeled, but adding a realistic Gaussian noise to each simulated SAXS curve simulates the contribution of counting error. Realistic Gaussian noise was calibrated using experimental x-ray scattering data (I_exp and its estimated error σ_exp) from a 1.0-mg/ml sample of a 21-kDa protein collected at the BioCAT undulator beamline 18-ID at the Advanced Photon Source (30) and fitted with a high-sensitivity CCD detector (31). The magnitude of the added noise as a function of resolution σ_sim(q) was then calculated and adjusted for concentration by

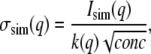(10)

where conc is the total protein concentration in units of mg/ml and k(q) is a resolution-dependent relative noise constant calculated from the experimental data by

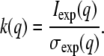(11)

A Gaussian distribution (as an approximation in large counts for Poisson counting statistics) of random values with width equal to σ_sim was generated using the randn function within MATLAB and added to the noiseless simulated intensities to produce the final simulated SAXS data. Examination of the simulated data reveals noise characteristics similar to the experimental standard and varying appropriately with concentration and resolution. We refer to this amount of added random noise as “standard noise”. To evaluate the reproducibility of our method in the presence of this realistic expected noise, 10 data sets with standard noise were generated and used as replicates for testing. An alternative minimal noise model was also employed in initial tests with ∼1/1000 of the standard noise.

Simulating scattering data from a self-associating monomer-trimer-hexamer system

The same procedure described above for the homotetramer was used to simulate SAXS data from a monomer-trimer-hexamer equilibrium using the hexameric Annexin XII from Homo sapiens (PDB id 1DM5) (32). Scattering intensities for the monomer (32 kDa), hypothetical trimer, and intact hexamer components were computed and combined into several simulated data sets to test the ability to detect oligomers present as only minor fractions. Several successive simulations were generated, with progressively larger values of the association constant K₁₂ to simulate smaller fractions of monomer at the concentration where the monomer is most common (that is, the lowest concentration). Ten data sets with realistic standard noise were generated from each simulation as described above and used as replicates for testing.

Simulating scattering data from a self-associating monomer-tetramer-octamer system

The same procedure was used to simulate SAXS data from a monomer-tetramer-octamer equilibrium using the octameric purE protein from E. coli (PDB id 1QCZ) (33). Scattering intensities for the monomer (17 kDa), hypothetical tetramer, and intact octamer components were computed and combined using simulated association constants of K₁₂ = 2.87 × 10¹² M⁻³ and K₂₃ = 1.29 × 10¹ M⁻¹.

Tests of the required data/parameter ratio and of the robustness of our method to both random and systematic noise were conducted with this system. To test the robustness to random noise, random noise at several levels was added to the simulated data as described previously, except that the σ_sim(q) of Eq. 10 was multiplied by 1, 2, or 4 before the generation of random noise. Five data sets were generated for each level of noise and used as replicates for testing. To test the robustness to systematic noise (e.g., the presence of aggregates), we constructed a simulated aggregate of this protein by building a model with six purE octamers packed together as in the crystal structure. Although not truly replicating the scattering seen with randomly aggregated protein, adding this protein to each simulated concentration at 0.5%, 1.0%, and 2.0% of the total protein and then calculating the expected scattering provides the opportunity to obtain an initial view of how decomposition could be affected by the kinds of systematic noise often seen in real systems.

To test the data/parameter ratio, additional data sets were simulated that contained scattering profiles from a smaller number of protein samples of varying protein concentration. Using the same range of concentrations for each test (0.25–16.0 mg/ml), we compared the data set with seven concentrations and standard noise already generated with smaller data sets of either five concentrations equally spaced in a geometric series (0.25, 0.71, 2.0, 5.66, and 16.0 mg/ml) or the theoretical minimum of three concentrations (0.25, 2.0, and 16.0 mg/ml) needed to determine basis vectors for three oligomeric forms. As described above, five replicates with standard noise were generated for these smaller data sets and used for testing.

Evaluating successful reconstruction of oligomeric curves

The association pathway and constants from the top scoring association model were used to recompute the best oligomer scattering curves in the matrix Ô_best. The quality of the final set of reconstructed scattering curves was evaluated by two methods. First, the scattering curves in matrix Ô_best were used to reconstruct the simulated scattering data as before, and the differences between the simulated and reconstructed scattering data were normalized by σ_sim(q) and examined for a random distribution of residuals. Second, the reconstructed scattering curves in Ô_best were directly compared to the scattering curves from the atomic structures in the simulated O, and the magnitude of their differences was evaluated by calculating the median of the absolute value of the relative deviation of each data point (MARD).

Implementation

Our simulation and analysis methods have been implemented as MATLAB scripts. Upon request, the software can be freely obtained for academic use from the authors. The most intensive calculations (the coarse- and fine-grid searches) require on the order of minutes to hours for each data set with three-state association models (two-dimensional searches) and on the order of days with four-state association models (three-dimensional searches) on a Pentium IV workstation.

RESULTS

Monomer-dimer-tetramer association pathway: Calculating and assessing simulated scattering data

We first investigated the ability of our method to determine the correct association pathway and constants for a sample self-associating system of closed symmetry. A monomer-dimer-tetramer equilibrium was selected as the first target of this study based on the frequent occurrence of this pathway (15). Scattering curves using x-ray scattering factors were computed from the atomic coordinates of monomer, dimer, and tetramer models from iron superoxide dismutase (Fig. 3 A). These curves display an increase in I(0) value corresponding to the relative molecular weight of each oligomer. The oligomer scattering curves were linearly combined according to the mass fractions generated from the standard chemical equilibrium equations (Table 1) to yield noise-free simulated data representing heterogeneous solutions of the associating protein at an experimentally reasonable set of concentrations. Simulated data with noise at the minimal and standard levels (Fig. 3 B) was calculated as described in Methods.

FIGURE 3.

Simulated SAXS data from two self-associating homooligomers. (A) SAXS curves computed from the atomic coordinates of the simulated monomer, dimer, and tetramer (dark to light curves, respectively) of PDB 1WB8. (B) SAXS curves from a heterogeneous mixture of monomer, dimer, and tetramer at association constants K₁₂ = 8.26 × 10³ M⁻¹ and K₂₃ = 2.83 × 10² M⁻¹, with standard noise. Curves are shaded from dark to light as the concentration increases. (C) SAXS curves computed from the atomic coordinates of the simulated monomer, trimer, and hexamer (dark to light curves, respectively) of PDB 1D5M. (D) SAXS curves from heterogeneous mixtures of the monomer, trimer, and hexamer with standard noise and using association constants adjusted to give a maximum monomer fraction of 45% at the lowest concentration (Table 4). Curves are shaded from dark to light as concentration increases.

The curves in Fig. 3, A and B, appear to have an isoscattering point at q ≈ 0.09, which would be characteristic of a system with only two states. Closer examination reveals that what appears to be an isoscattering point is only an artifact of all three curves crossing in close proximity. Examining the I(0) and R_G values computed by Guinier analysis from the simulated data (Table 2) shows that, as expected, the apparent I(0) of the mixtures is a linear combination of the I(0) values of the homogeneous oligomers times the fractional mass of each oligomer. Similarly, the squares of the apparent R_G values computed from the mixtures are approximated by the fractional mass-weighted linear combinations of the square of the R_G value of each oligomer.

TABLE 2.

Distribution of oligomers in the monomer-dimer-tetramer simulation and characteristics of the simulated data

	Fractional mass
	Monomer	Dimer	Tetramer	I(0)	RG (A)
Pure solutions
Oligomer
Monomer	100	—	—	9.9 × 106	19.8
Dimer	—	100	—	1.9 × 107	24.3
Tetramer	—	—	100	3.9 × 107	27.2
Heterogeneous solutions
Concentration (mg/ml)
0.25	0.858	0.142	0.000	1.13 × 107	20.7
0.5	0.751	0.248	0.000	1.24 × 107	21.4
1.0	0.594	0.403	0.003	1.40 × 107	22.3
2.0	0.417	0.565	0.018	1.62 × 107	23.3
4.0	0.246	0.670	0.085	1.93 × 107	24.4
8.0	0.108	0.590	0.302	2.50 × 107	25.8
16.0	0.029	0.318	0.653	3.31 × 107	27.0

Fractional masses are calculated from the standard association equations for K₁₂ = 8.26 × 10³ M⁻¹ and K₂₃ = 2.83 × 10² M⁻¹. The I(0) and radius of gyration (R_G) values are computed by Guinier analysis from the noise-free simulated data for each oligomer and from the standard noise simulations of the heterogeneous solutions at the indicated concentrations.

Monomer-dimer-tetramer association pathway: evaluating significant vectors in SVD

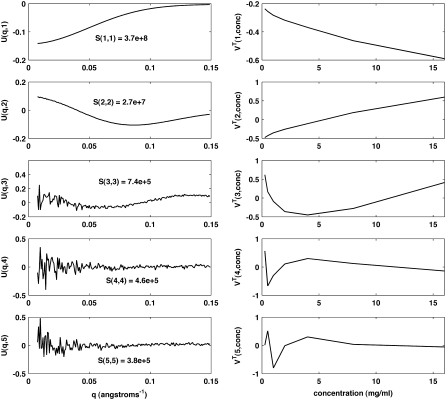
The simulated data were decomposed by SVD as detailed in Methods. Decomposition of simulated data either without noise or with minimal noise gave the theoretically expected results (not shown). With minimal noise, decomposition yielded three smooth basis vectors (columns of U), equal to the number of simulated oligomeric forms. The set of basis vectors showed visible noise only beginning with the fourth. Decomposition also showed a 4.2 × 10⁴-fold decrease between the third and fourth singular values (diagonal elements of S). The corresponding N_forms = 3 amplitude vectors (rows of V^T) varied smoothly with concentration, whereas all additional amplitude vectors displayed nonsmooth variation. The smooth variation in the amplitude vectors reflects both the fixed contribution of each basis vector to the scattering curve of each oligomer and the smooth variation in the distribution of oligomers with concentration (see Eq. 7).

Decomposition of simulated data with standard noise revealed that SVD analysis alone cannot remove all noise from experimentally realistic simulations. These effects can be seen (Fig. 4) by examining the first few basis vectors and associated coefficients. Here, the third basis vector shows noisy variations, although less than the fourth. The fourth singular value is also only 1.6-fold smaller than the third singular value, not enough to make an easy determination whether three or four basis vectors are significant. Smooth variation is seen for only the first three amplitude vectors, however, suggesting that the correct association pathway has three forms. Nonetheless, the difficulty in evaluating the basis vectors necessitates testing the set of feasible association pathways which contain two, three, and four forms (utilizing two, three, and four basis vectors, respectively), so that the additional restraints imposed by fitting an association model will reveal more definitively the number of basis vectors (oligomeric forms) that contribute to the scattering.

FIGURE 4.

SVD of the monomer-dimer-tetramer simulation. The first five basis vectors of the decomposition are shown (left column) along with the associated amplitude vectors from V^T (right column) and the singular values from S (insets). Due to the large range of coefficient S values, the values of the amplitude vectors do not accurately reflect their true relative contribution. Thus, the amplitude vectors are scaled solely to maximize visibility.

Monomer-dimer-tetramer association pathway: search over association pathways, coarse- and fine-grid searches with confidence intervals, and the effects of data-resolution range

Our search algorithm (Figs. 1 and 2) was used to find the association pathway and constants that best describe the simulated data. We evaluated a set of 10 trial association pathways containing two, three, and four states (Table 1) by searching a coarse grid of association constants, with the number of states (oligomeric forms) N_forms setting the value of N_sig (number of significant SVD basis vectors used).

The most effective decomposition requires that the shape of the scattering curves from the different oligomers (and not just their amplitudes) be distinct. Since differences in shape become more apparent at higher resolution, we conducted the same set of searches for a low-resolution data set simulated to a q_max = 0.05 and a moderate resolution data set with q_max = 0.14. As expected, the moderate-resolution data set performed better than the low-resolution one. The moderate-resolution data set yielded the correct monomer-dimer-tetramer association pathway with both scoring metrics (Table 3, bold values), whereas the low-resolution data gave more equivocal outcomes, showing a significant disagreement between the two metrics. Since accurate data with q_max = 0.14 are readily attainable with modern instruments and moderately concentrated samples, these results do not present any practical impediment to the application of our method. The results with the moderate-resolution data are described in more detail below.

TABLE 3.

Summary of coarse-grid evaluation of different association models against the simulated monomer-dimer-tetramer data at two resolution ranges

	χ2				MSMRD
Pathway	K12 ± SD*	K23 ± SD†	K34 ± SD‡	Score ± SD§	K12 ± SD	K23 ± SD	K34 ± SD	Score ± SD
Moderate resolution (qmax = 0.14 Å−1), K12 = 8.26 × 103, K23 = 2.83 × 102
1-2	2000 ± 0	—	—	2300 ± 4.2	3000 ± 0	—	—	4.1 ± 0.8
1-3	4e6 ± 0	—	—	780 ± 1.5	1.8e8 ± 1.5e8	—	—	0.0011 ± 6.9e-4
1-4	1e10 ± 0	—	—	1900 ± 2.7	9e13 ± 0	—	—	0.0032 ± 0.0038
1-2-4	8000 ± 0	300 ± 0	—	3.3 ± 0.8	8000 ± 310	300 ± 0	—	2.3e-4 ± 2.3e-4
1-2-6	4000 ± 0	9.4e5 ± 5.2e4	—	10.4 ± 1.4	5.7e5 ± 3.1e5	2.2e4 ± 2e4	—	0.3 ± 0.044
1-3-6	9e7 ± 8e6	9.4 ± 4.2	—	26.4 ± 1.8	7.3e9 ± 1.4e9	7.7 ± 0.9	—	0.038 ± 0.0017
1-2-8	3000 ± 0	4e9 ± 0	—	18.5 ± 0.6	6.7e5 ± 1.2e5	4.3e6 ± 1.6e6	—	1.6 ± 0.055
1-4-8	7e11 ± 0	40 ± 0	—	90.3 ± 1.8	6.9e14 ± 1.2e14	0.6 ± 0.2	—	0.031 ± 0.0081
1-2-4-8	8300 ± 670	310 ± 57	110 ± 67	3.5 ± 2.3	6.0e4 ± 0	290 ± 57	20 ± 0	0.21 ± 0.039
1-2-6-12	4000 ± 0	1.1e6 ± 4.8e5	3,400 ± 840	6.6 ± 2.2	6.9e4 ± 3200	9.9e4 ± 3200	2000 ± 0	1.6 ± 0.16
Low resolution (qmax = 0.05 Å−1), K12 = 8.26 × 103, K23 = 2.83 × 102
1-2	3e-4 ± 0	—	—	47 ± 0.88	3000 ± 0	—	—	4.1 ± 0.03
1-3	4e6 ± 0	—	—	1200 ± 3.6	3.0e8 ± 0	—	—	6.6e-4 ± 4.5e-4
1-4	1e10 ± 0	—	—	2900 ± 5.6	8.1e13	—	—	2.8e13
1-2-4	8,000 ± 0	300 ± 0	—	3.5 ± 0.40	8000 ± 0	300 ± 0	—	1.5e-4 ± 5.7e-5
1-2-6	4000 ± 0	1e6 ± 0	—	9.1 ± 0.41	5.4e5 ± 3.5e5	2.6e4 ± 2.2e4	—	0.35 ± 0.05
1-3-6	8e7 ± 0	100 ± 0	—	41 ± 0.12	7.5e9 ± 1.6e9	8 ± 1.1	—	0.04 ± 0.003
1-2-8	3,000 ± 0	4e9 ± 0	—	13 ± 0.46	4000 ± 0	9e6 ± 0	—	0.56 ± 0.01
1-4-8	7e11 ± 0	40 ± 0	—	160 ± 0.60	9.4e14 ± 7.3e14	0.92 ± 0.76	—	0.02 ± 0.002
1-2-4-8	7,900 ± 930	1030 ± 750	19 ± 40	2.0 ± 0.85	1.9e4 ± 1.1e4	240 ± 53	6.3 ± 2.8	0.0068 ± 0.004
1-2-6-12	6700 ± 480	1.4e7 ± 1.4e7	5200 ± 2000	1.7 ± 0.23	6100 ± 2,800	6.0e11 ± 1.3e12	1.7e4 ± 3.3e4	0.035 ± 0.022

Simulated data sets were constructed for the monomer-dimer-tetramer association with different maximum resolutions (q_max = 0.14 Å⁻¹ for moderate resolution and q_max=0.05 Å⁻¹ for low resolution). A coarse grid of association constants for each tested pathway was evaluated by χ² and MSMRD scoring for both resolution ranges. The expected best score when simulated association constants match the grid points exactly would be χ² = 1 and MSMRD = 0. The pathway with the best scoring association constants for each simulation and scoring method is indicated in bold.

^*Mean ± SD of the best first-association constant K₁₂ for that pathway over 10 simulated data sets.

^†Mean ± SD of the best second-association constant K₂₃ for that pathway over 10 simulated data sets.

^‡Mean ± SD of the best third-association constant K₃₄ for that pathway over 10 simulated data sets.

^§Mean ± SD of the score of the best set of association constants over 10 simulated data sets.

Of all the models evaluated using the moderate-resolution data, the χ² score of monomer-dimer-tetramer (the simulated pathway) at K₁₂ = 8 × 10³ M⁻¹ and K₂₃ = 3 × 10² M⁻¹ (compared with the simulated values of K₁₂ = 8.26 × 10³ M⁻¹ and K₂₃ = 2.83 × 10² M⁻¹) was substantially better than that for any grid point of any competing pathway for each of the ten data sets with different random noise. Averaged statistics are shown in Table 3. The second best scoring association pathway was monomer-dimer-tetramer-octamer with association constants of K₁₂ = 8.3 × 10³ M⁻¹, K₂₃ = 3.1 × 10² M⁻¹, and K₃₄ = 1.1 × 10² M⁻¹, and with a χ² very close to that of the top scoring model. Not unexpectedly, a monomer-dimer-tetramer model can be approximated by a monomer-dimer-tetramer-octamer model with a weak tetramer-octamer association. Expanding the association model to allow a fourth form, while not also explicitly restraining the additional scattering curve, to reflect a larger octameric oligomer allows additional freedom for fitting noise. The exact K₃₄ value may reflect mostly that freedom.

Plotting the results of the coarse-grid search for the monomer-dimer-tetramer pathway reveals a small set of neighboring grid points that score well in χ² (Fig. 5 A). The smoothness of the coarse grid search suggests that the best values lie near the integer grid point of K₁₂ = 8 × 10³ M⁻¹ and K₂₃ = 3 × 10² M⁻¹. Boundaries for a finer grid were set at K₁₂ = 5 × 10³ to 2 × 10⁴ M⁻¹ and K₂₃ = 2 × 10² to 4 × 10² M⁻¹ and searched with a spacing between adjacent grid points of 1/100 of the distance between the coarse-grid points (Fig. 5 B). The best solution from the finer grid is K₁₂ = 8.31 × 10³ ± 75 M⁻¹ and K₂₃ = 2.83 × 10² ± 4 M⁻¹ at a χ² of 2.99 ± 0.99 (mean ± SD from 10 simulated data sets). These values for the association constants are <1 SD from the simulated values. This finer search also shows smooth variation in χ², allowing the accurate evaluation of a confidence interval (Fig. 6). Even finer grid searches are not required because a small set of grid points around the minimum gives nearly identical scores. The smoothness of the scoring metric over both grid searches validates the successive grid search approach.

FIGURE 5.

Association constants for the monomer-dimer-tetramer simulation colored by quality of χ² score. The monomer-dimer-tetramer simulation described in the text and Table 2 was analyzed using the same association pathway and evaluated by the χ² agreement between reconstructed and simulated data (Eq. 8). (A) Coarse-grid search with spacing at integer values as described in Methods. Note that white space indicates a nonphysical reconstruction (>10% negative scattering intensities, as discussed in Methods), and that the large volume of the total search space not shown here also yielded nonphysical reconstructions. (B) Fine-grid search over the range of best coarse-grid χ² values with spacing between adjacent grid points set at 1/100 of the coarse-grid spacing.

FIGURE 6.

Confidence interval for the association constants of the monomer-dimer-tetramer simulation. The intervals for 75% (red), 90% (blue), and 95% (green) confidence calculated from the fine-grid search evaluated by χ² as described in Methods are indicated.

The MSMRD score based on the difference between the observed and expected forward scattering, I(0), values was also calculated over the coarse- and fine-grid searches. The best MSMRD score identified in the coarse-grid searches (Fig. 7 A) is the monomer-dimer-tetramer pathway with K₁₂ = 8 × 10³ M⁻¹ and K₂₃ = 3 × 10² M⁻¹, the same model selected as the best by χ². Evaluating the monomer-dimer-tetramer pathway with finer grid spacing (Fig. 7 B) gave a best solution of K₁₂ = 8.11 × 10³ ± 287 M⁻¹ and K₂₃ = 2.95 × 10² ± 4 M⁻¹, in close agreement with the best score by χ².

FIGURE 7.

Association constants in the monomer-dimer-tetramer grid search colored by quality of MSMRD score. The monomer-dimer-tetramer simulation described in the text and Table 2 was analyzed using the same association pathway and evaluated by the MSMRD agreement between reconstructed and expected forward scattering (Eq. 9). (A) Coarse-grid search with spacing at integer values, as described in Methods. Note that white space indicates a nonphysical reconstruction (>10% negative scattering intensities, as discussed in Methods), and that the large volume of the total search space not shown here also yielded nonphysical reconstructions. (B) Fine-grid search over the range of best coarse-grid MSMRD values with spacing between adjacent grid points set at 1/100 of the coarse-grid spacing.

The value of the two scoring functions was evaluated from these simulations (and those that follow). Examining the MSMRD score over the competing models (Table 3) reveals that the χ² score and the MSMRD score agree only when they both predict the correct model. The next best χ² scores (1-2-4-8 and 1-2-6-12) have relatively poor MSMRD scores, and the next best MSMRD scores (1-3 and 1-4) have poor χ² scores. At the same time, several simulations below will reveal situations that are less clear, where the χ² metric is generally (but not always) more accurate than the MSMRD when the two disagree. Thus, the MSMRD forms a valuable, but supplementary, metric for determining the correct model.

X-ray scattering curves for each oligomer were reconstructed from one standard noise data set under the selected monomer-dimer-tetramer association pathway with the best χ² search values of K₁₂ = 8.31 × 10³ M⁻¹ and K₂₃ = 2.83 × 10² M⁻¹. These reconstructions differ from SAXS curves computed from the atomic structure of each oligomer by 0.26% for monomer, 0.23% for dimer, and 0.12% for tetramer in MARD (Fig. 8 A).

FIGURE 8.

Reconstructed scattering curves for each oligomer (symbols) compared with scattering curves derived directly from the atomic structures (solid lines). The best grid point returned from the fine-grid association model search was used to reconstruct each oligomer scattering curve. (A) Monomer-dimer-tetramer simulation reconstructed with K₁₂ = 8.31 × 10³ M⁻¹ and K₂₃ = 2.83 × 10² M⁻¹. The MARDs from the scattering curves calculated from the atomic models are 0.26% for monomer (x), 0.23% for dimer (○), and 0.12% for tetramer (*). (B) Monomer-trimer-hexamer simulation (45% monomer) reconstructed with K₁₂ = 8.11 × 10⁹ M⁻² and K₂₃ = 5.36 × 10¹ M⁻¹. The MARDs from the scattering curves calculated from the atomic models are 0.99% for monomer (x), 0.13% for trimer (○), and 0.05% for hexamer (*).

To search for systematic errors in the reconstruction, residual values comparing the simulated scattering data (in matrix A) and reconstructed scattering data (in matrix Â) were examined (Fig. 9 A). Since the data spans a large range of intensity values, residual values were normalized by σ_sim(q). This plot of normalized differences reveals largely random fluctuations. The normalized residuals do increase slightly at higher concentrations and at higher scattering angle. The reasons for this distribution of residuals are being explored. A reconstruction using the exact simulated values of the association constants (K₁₂ = 8.26 × 10³ M⁻¹ and K₂₃ = 2.83 × 10² M⁻¹) was also generated, and the same trends were observed. Thus these trends are not due to any small errors in the association constants, but they may be related to unsuitable relative weightings within the SVD for the different scattering data points and/or the multiple data sets.

FIGURE 9.

Normalized residuals comparing  (scattering data reconstructed using the top scoring association model) to A (simulated data). (A) Normalized residuals for the monomer-dimer-tetramer simulation at protein concentrations of 0.25, 2.0, and 16.0 mg/ml (darkest to lightest, respectively). (B) Normalized residuals for the monomer-trimer-hexamer simulation (45% monomer) at protein concentrations of 0.25, 2.0, and 16.0 mg/ml (darkest to lightest, respectively).

Monomer-trimer-hexamer association pathway: further evaluating the search over association pathways, evaluating the minimum required amount of an oligomeric form

The detection of an oligomeric form by this method is clearly limited by the fractional presence of that form in the concentrations used for data collection. To test our method on another association pathway and to estimate the minimum amount of one form that can be detected, simulated monomer-trimer-hexamer association models (Table 4) were generated with a range of 2–55% fractional mass of monomer in the lowest protein concentration (that is, the one containing the greatest fraction of monomer). X-ray scattering curves were computed from atomic models of monomer, hypothetical trimer, and hexamer forms constructed from the structure of Annexin XII. These scattering curves were combined under the various models, and standard noise was added (Fig. 3 C). Nine alternative association pathways were compared with monomer-trimer-hexamer by coarse-grid searches for each of 10 data sets with random noise. The mean and standard deviation (SD) of the best grid point returned from each search by χ² and MSMRD was determined (Table 5).

TABLE 4.

Distribution of oligomers in simulations of a monomer-trimer-hexamer association with decreasing fractional mass of the monomer

	Fractional masses
Concentration (mg/ml)	Monomer	Trimer	Hexamer
55% Monomer, K12 = 5.53 × 109, K23 = 52.8
0.25	0.552	0.448	0.000
0.5	0.211	0.788	0.002
1.0	0.058	0.926	0.016
2.0	0.014	0.866	0.121
4.0	0.002	0.466	0.532
8.0	0.000	0.099	0.901
16.0	0.000	0.014	0.987
45% Monomer, K12 = 8.23 × 109, K23 = 52.8
0.25	0.453	0.547	0.000
0.5	0.152	0.845	0.003
1.0	0.040	0.936	0.024
2.0	0.009	0.821	0.170
4.0	0.001	0.370	0.629
8.0	0.000	0.069	0.931
16.0	0.000	0.009	0.991
35% Monomer, K12 = 1.25 × 1010, K23 = 52.8
0.25	0.352	0.647	0.000
0.5	0.106	0.890	0.004
1.0	0.026	0.937	0.037
2.0	0.005	0.757	0.238
4.0	0.000	0.279	0.720
8.0	0.000	0.046	0.954
16.0	0.000	0.006	0.994
10% Monomer, K12 = 5.88 × 1010, K23 = 52.8
0.25	0.103	0.895	0.002
0.5	0.024	0.956	0.020
1.0	0.005	0.840	0.155
2.0	0.001	0.403	0.596
4.0	0.000	0.076	0.924
8.0	0.000	0.010	0.990
16.0	0.000	0.001	0.999
2% Monomer, K12 = 2.94 × 1011, K23 = 52.8
0.25	0.022	0.967	0.010
0.5	0.005	0.901	0.094
1.0	0.001	0.519	0.480
2.0	0.000	0.119	0.881
4.0	0.000	0.016	0.984
8.0	0.000	0.002	0.998
16.0	0.000	0.000	1.000

Fractional masses are calculated from the standard association equations using successively stronger values of K₁₂ to decrease the fraction of monomer present at the lowest protein concentration.

TABLE 5.

Best coarse-grid points returned for simulations of a monomer-trimer-hexamer association with decreasing fractional mass of the monomer

	χ2				MSMRD
Pathway	K12 ± SD*	K23 ± SD†	K34 ± SD‡	Score ± SD§	K12 ± SD*	K23 ± SD†	K34 ± SD‡	Score ± SD§
55% Monomer, K12 = 5.53 × 109, K23 = 52.8
1-2 (3-6)	6,000 ± 0	—	—	1,800 ± 4.3	3,000 ± 0	—	—	4.0 ± 0.060
1-3	4.0e7 ± 0	—	—	610 ± 4.2	2.0e8 ± 0	—	—	0.0055 ± 0.0011
1-2-4	2,100 ± 320	1.9e4 ± 3,200	—	280 ± 26	5.6e4 ± 5,500	1,000 ± 0	—	0.014 ± 9.2e-4
1-2-6	6.0e4 ± 0	3e5 ± 0	—	170 ± 1.6	7.2e4 ± 4,500	2.0e6 ± 0	—	0.79 ± 0.031
1-3-6	6.0e9 ± 0	50 ± 0	—	4.4 ± 1.7	5.2e9 ± 2.5e9	51 ± 27	—	0.0030 ± 0.0025
1-2-8	3,000 ± 0	2.9e10 ± 5.8e9	—	340 ± 13	1.4e5 ± 8.9e4	3.8e9 ± 1.8e9	—	2.1 ± 0.11
1-4-8	1.0e14 ± 0	20 ± 0	—	200 ± 2.3	6.0e14 ± 3.7e14	3.4 ± 3.7	—	0.0036 ± 0.0023
1-2-4-8	9.1e4 ± 1.7e4	2,900 ± 1,700	97 ± 4.8	27 ± 5.2	8.0e4 ± 0	3,200 ± 420	20 ± 0	0.16 ± 7.7e-3
1-2-6-12	9.0e4 ± 0	8.8e4 ± 6,300	6,400 ± 1,100	21 ± 8.4	8.7e4 ± 8,200	5.2e8 ± 3.4e8	2.5e4 ± 5,300	1.9 ± 0.20
1-3-6-12	3.4e9 ± 5.5e8	72 ± 22	52 ± 4.5	14 ± 7.1	8.0e9 ± 0	100 ± 0	20 ± 0	0.52 ± 0.10
45% Monomer, K12 = 8.23 × 109, K23 = 52.8
1-2 (3-6)	7,000 ± 0	—	—	1,900 ± 4.0	3,000 ± 0	—	—	2.9 ± 0.058
1-3	5.0e7 ± 0	—	—	450 ± 2.07	3.0e8 ± 0	—	—	0.0024 ± 3.8e-4
1-2-4	2,000 ± 0	3.0e4 ± 0	—	170 ± 17	6.2e4 ± 4,500	880 ± 45	—	0.0043 ± 8.3e-4
1-2-6	6.2e4 ± 6,300	4.8e5 ± 6.3e4	—	110.0 ± 1.1	3.2e5 ± 8.4e4	4.8e5 ± 8.3e4	—	0.31 ± 0.047
1-3-6	7.2e9 ± 1.5e9	62± 0	—	5.3 ± 1.5	8.4e9 ± 5.5e8	54 ± 5.5	—	0.0055 ± 0.0034
1-2-8	3.0e4 ± 0	3.0e9 ± 0	—	400 ± 5.0	2.8e5 ± 8.4e4	5.6e9 ± 3.2e9	—	1.9 ± 0.27
1-4-8	6.0e13 ± 0	50 ± 0	—	140 ± 1.6	7.0e14 ± 2.2e14	1.6 ± 0.88	—	0.031 ± 0.0082
1-2-4-8	1.0e5 ± 0	3,000 ± 0	100 ± 0	39 ± 8.1	1.0e5 ± 0	7,500 ± 530	30 ± 0	0.40 ± 0.01
1-2-6-12	9.2e4 ± 1.7e4	1.4e5 ± 8.4e4	6,200 ± 420	27 ± 12	2.0e5 ± 0	8.2e7 ± 3.8e7	1.8e4 ± 4,600	2.1 ± 0.49
1-3-6-12	3.0e9 ± 0	90 ± 22	42 ± 18	21 ± 13	1.0e10 ± 0	980 ± 45	30 ± 0	1.9 ± 0.16
35% Monomer, K12 = 1.25 × 1010, K23 = 52.8
1-2 (3-6)	9,000 ± 0	—	—	2,000 ± 4.5	3,000 ± 0	—	—	2.0 ± 0.016
1-3	6.0e7 ± 0	—	—	340 ± 1.9	4.0e8 ± 0	—	—	7.5e-5 ± 7.1e-5
1-2-4	2,000 ± 0	6.3e4 ± 4,800	—	97 ± 11	7.6e4 ± 5,500	740 ± 55	—	0.0043 ± 0.0017
1-2-6	2.7e4 ± 1.3e4	5.2e6 ± 2.4e6	—	83 ± 5.5	4.0e5 ± 1.7e5	2.4e5 ± 8.9e4	—	0.37 ± 0.020
1-3-6	8.2e9 ± 6.3e8	79 ± 3.2	—	7.9 ± 6.6	8.6e9 ± 5.5e8	40 ± 0	—	0.019 ± 0.0053
1-2-8	7,400 ± 970	2.9e11 ± 1.4e11	—	230 ± 6.6	3.0e5 ± 2.2e5	4.6e8 ± 8.9e7	—	2.0 ± 0.11
1-4-8	1.0e13 ± 0	400 ± 0	—	110 ± 7.1	1.3e15 ± 9.3e14	4.8 ± 4.4	—	0.012 ± 0.014
1-2-4-8	8.9e4 ± 1.1e4	2,600 ± 530	200 ± 0	52 ± 9.4	3.0e5 ± 0	2,000 ± 0	20 ± 0	0.19 ± 0.10
1-2-6-12	5.7e4 ± 9,500	6.6e5 ± 2.0e5	8,600 ± 520	35 ± 10	2.6e5 ± 5.2e4	4.2e6 ± 1.0e6	1.0e4 ± 0	3.2 ± 0.46
1-3-6-12	2.0e9 ± 0	280 ± 45	66 ± 15	29 ± 8.0	2.0e10 ± 0	100 ± 0	20 ± 0	1.2 ± 0.73
10% Monomer, K12 = 5.88 × 1010, K23 = 52.8
1-2 (3-6)	2.0e4 ± 0	—	—	1,900 ± 6.0	3,000 ± 0	—	—	0.53 ± 0.0032
1-3	2.0e8 ± 0	—	—	480 ± 4.7	9.0e8 ± 0	—	—	8.2e-4 ± 3.6e-4
1-2-4	1,400 ± 600	1.3e6 ± 9.9e5	—	11 ± 1.0	4.0e5 ± 3.0e5	560 ± 400	—	0.028 ± 0.021
1-2-6	1.9e5 ± 3.8e4	9.4e5 ± 1.1e6	—	100 ± 0.8	7.2e5 ± 7.9e5	5.0e5 ± 4.1e5	—	0.62 ± 0.18
1-3-6	3e9 ± 0	1,000 ± 0	—	2.1 ± 0.5	5.0e10 ± 2.4e10	6.0 ± 12	—	0.025 ± 0.029
1-2-8	5,300 ± 480	4.4e11 ± 9.7e10	—	240 ± 1.0	9.8e5 ± 6.1e5	1.9e8 ± 1.9e8	—	2.0 ± 0.18
1-4-8	2.9e12 ± 3.2e11	1,900 ± 320	—	15 ± 1.8	4.0e15 ± 3.4e15	9.0 ± 1.4	—	0.12 ± 0.091
1-2-4-8	1,900 ± 410	8.6e5 ± 1.5e6	200 ± 630	13 ± 5.6	8.4e5 ± 1.3e5	1,900 ± 1,200	65 ± 15	0.71 ± 0.07
1-2-6-12	6,500 ± 1,100	8.7e8 ± 2.3e8	9.3e5 ± 8,200	8.5 ± 5.0	4.7e5 ± 3.5e5	6.3e5 ± 4.1e5	1.9e5 ± 8,800	6.9 ± 5.2
1-3-6-12	2.1e8 ± 1.4e8	2.2e4 ± 1.7e4	230 ± 270	10 ± 4.4	8.2e10 ± 1.1e10	580 ± 360	46 ± 8.9	1.6 ± 0.079
2% Monomer, K12 = 2.94 × 1011, K23 = 52.8
1-2 (3-6)	5.0e4 ± 0	—	—	1,300 ± 3.4	3,000 ± 0	—	—	0.048 ± 9.7e-4
1-3	5.0e8 ± 0	—	—	180 ± 0.72	1.0e9 ± 0	—	—	0.050 ± 0.0023
1-2-4	810 ± 240	1.7e7 ± 1.5e7	—	2.3 ± 0.32	2.6e5 ± 1.3e5	1,800 ± 490	—	0.018 ± 0.014
1-2-6	2.0e4 ± 0	2.0e8 ± 0	—	64 ± 0.48	6.8e5 ± 4.5e4	7.4e5 ± 8.9e4	—	0.65 ± 0.058
1-3-6	4.8e9 ± 6.3e8	3,200 ± 630	—	1.7 ± 0.15	2.6e10 ± 8.9e9	300 ± 0	—	0.22 ± 0.098
1-2-8	1.0e4 ± 0	6.4e12 ± 5.2e11	—	84 ± 3.7	5.0e5 ± 1.9e5	3.6e9 ± 2.9e9	—	2.5 ± 0.19
1-4-8	8.0e12 ± 0	12 ± 20	—	3.4 ± 1.2	4.4e15 ± 1.7e15	68 ± 4.5	—	0.11 ± 0.049
1-2-4-8	4.3e5 ± 2.7e5	1.1e5 ± 3.1e5	110 ± 120	2.6 ± 0.63	6.6e5 ± 1.5e5	6,400 ± 8,600	400 ± 300	1.3 ± 0.12
1-2-6-12	1.9e5 ± 1.9e5	4.5e9 ± 1.3e10	9.0e4 ± 1.2e5	3.9 ± 1.0	5.2e5 ± 1.6e5	2.7e6 ± 1.8e6	3.2e4 ± 6,300	6.2 ± 0.64
1-3-6-12	4.0e8 ± 0	3.9 ± 4.4	5.5e9 ± 3.5e9	100 ± 64	5.5e8 ± 2.1e8	3.4 ± 3.7	4.5e9 ± 2.1e9	32 ± 0.88

The pathway with the best scoring association constants for each simulation by χ² or MSMRD is indicated in bold.

^*Mean ± SD of the best first association constant K₁₂ for that pathway over 10 simulated data sets.

^†Mean ± SD of the best second association constant K₂₃ for that pathway over 10 simulated data sets.

^‡Mean ± SD of the best third association constant K₃₄ for that pathway over 10 simulated data sets.

^§Mean ± SD of the score of the best set of association constants over 10 simulated data sets.

Only the 55% monomer was unambiguously successful, with both scores indicating the monomer-trimer-hexamer model as the best and returning association constants at the coarse-grid values adjacent to the true values. Here again, the next best χ² scores have poor MSMRD scores and, the next best MSMRD scores have poor χ² scores. Not surprisingly, as the percentage of monomer decreases, it becomes progressively harder to determine the correct association model. Several of the most interesting comparisons are with the association pathways most similar to the monomer-trimer-hexamer pathway: monomer-trimer, trimer-hexamer (equivalent to monomer-dimer with a “monomer” of three times the sequence mass), monomer-dimer-hexamer, and monomer-trimer-hexamer-dodecamer. For example, the χ² score continues to return the correct pathway with fairly accurate association constants at 45% and 35% monomer, whereas the MSMRD score supports the monomer-trimer pathway. The χ² score continues to return the correct pathway (although with increasingly inaccurate association constants), even down to 2% monomer. This better performance of the χ² score in detecting the correct pathway to 2% and the correct pathway and constants to 35% forms one basis for our assigning the χ² a primary role in our method and the MSMRD a supplementary one. If this result can be generalized, detection of small amounts of an oligomeric form can be expected with the χ² metric, although greater amounts will be required to accurately determine the association constants.

To further evaluate the quality of the reconstruction with data containing limited amounts of monomer, one set of simulated data with standard noise produced for the 45% monomer simulation (Fig. 3 D) was analyzed further. This data set was evaluated with a fine-grid search (not shown) with dimensions of K₁₂ = 6 × 10⁹ to 8.5 × 10⁹ M⁻² and K₂₃ = 5 × 10¹ to 7 × 10¹ M⁻¹ with spacing 1/100 of the coarse grid. The best grid point returned by this search, K₁₂ = 8.11 × 10⁹ M⁻² and K₂₃ = 5.36 × 10¹ M⁻¹, compares well with the values of K₁₂ = 8.23 × 10⁹ M⁻² and K₂₃ = 5.28 × 10¹ M⁻¹ used for the simulation. Reconstructed oligomer scattering curves using the best grid search association constants differ from scattering curves computed from the atomic structure of each oligomer by 0.99% for monomer, 0.13% for trimer, and 0.05% for hexamer in MARD (Fig. 8 B). Not surprisingly, unlike the previous simulation where the forms were equally accurately reconstructed, the monomer is here significantly less accurately reconstructed than the other forms.

A normalized residual plot computed in the same manner as for the monomer-dimer-tetramer simulation showed no systematic deviations with scattering angle, but smaller than expected values for the lowest concentration and values that increase with concentration (Fig. 9 B). The reasons for this nonrandom distribution of residuals are presumably related to those in the first simulation.

The overall success of this reconstruction suggests an ability to detect and reconstruct minor oligomeric forms and to determine at least approximately correct association constants in situations where the minor form is present in as small as 45% fractional mass in the concentration most highly populated for that form. At the same time, a complete determination of the association model (both pathway and constants) requires the presence of a substantial fraction of each form in at least one sample concentration. Possible experimental strategies for ensuring this requirement by adjusting the experimental conditions are discussed below.

Monomer-tetramer-octamer association pathway: evaluating required data sets and random and systematic noise

Our second simulation provided strong evidence that, not surprisingly, the determination of the association pathway and constants is a significantly more difficult task than the determination of the correct association pathway alone. Although 45% fractional mass is required to determine the association constants reasonably accurately (to within one coarse-grid unit) (Table 5), the correct association pathway is found down to 2% fractional mass. This finding allowed us to conduct more extensive simulation studies of additional factors in less computation time by measuring success or failure against the more stringent standard of finding accurate association constants.

We desired to evaluate the effects of different levels of random and systematic noise arising from simulated counting error and the presence of a simulated protein aggregate, respectively. We also wanted to evaluate the requirement for number of data sets at different concentrations and to test the application of another association pathway to our method. We thus constructed a monomer-tetramer-octamer simulation using the purE protein. Simulated scattering data was calculated as before, and random or systematic noise was added at several levels, as described in Methods.

We found that random noise at any of these levels does not significantly impair the method's ability to determine the correct association constant through coarse- and fine-grid searches using either the χ² or MSMRD scores (Table 6). The best association constants do not change as a function of noise. Surprisingly, the χ² values do increase with additional random noise, whereas the MSMRD values do not. These effects are unexpected, since χ² is normalized by the noise level, whereas MSMRD is not. The insensitivity of the MSMRD perhaps arises from the fact that the MSMRD score depends on the least noisy, lowest-resolution data. In any case, our method seems to be quite robust to additional random noise.

TABLE 6.

Best coarse- and fine-grid points returned for simulations of a monomer-tetramer-octamer association

	χ2			MSMRD
Pathway	K12 ± SD*	K23 ± SD†	Score ± SD‡	K12 ± SD	K23 ± SD	Score ± SD
7 concentrations, 1 × Standard Noise, K12 = 2.87 × 1012, K23 = 12.9
1-4-8 (coarse)	4.0e12 ± 0	10 ± 0	76 ± 0.57	2.0e12 ± 0	8.0 ± 0	0.0091 ± 3.0e-4
1-4-8 (fine§)	2.9e12 ± 0	13 ± 0	1.2 ± 0.17	2.7e12 ± 2.9e10	14 ± 0.41	1.4e-6 ± 1.2e-6
7 concentrations, 2 × Standard Noise, K12 = 2.87 × 1012, K23 = 12.9
1-4-8 (coarse)	4.0e12 ± 0	10 ± 0	30 ± 11	2.0e12 ± 0	8.0 ± 0	0.0095 ± 8.3e-4
1-4-8 (fine§)	2.9e12 ± 1.0e10	13 ± 0.032	3.1 ± 1.5	2.8e12 ± 3.4e10	14 ± 0.67	1.1e-6 ± 1.0e-6
7 concentrations, 4 × Standard Noise, K12 = 2.87 × 1012, K23 = 12.9
1-4-8 (coarse)	4.0e12 ± 0	10 ± 0	14 ± 4.4	2.0e12 ± 0	7.8 ± 0.45	0.010 ± 8.8e-4
1-4-8 (fine§)	2.8e12 ± 2.7e10	13 ± 0.15	6.1 ± 2.9	2.7e12 ± 1.0e11	14 ± 0.62	5.3e-7 ± 6.3e-7
7 concentrations, 1 × Standard Noise, 0.5% Aggregate, K12 = 2.87 × 1012, K23 = 12.9
1-4-8 (coarse)	3.0e12 ± 0	10 ± 0	170 ± 1.1	9.0e10 ± 0	10 ± 0	0.0029 ± 4.0e-4
1-4-8 (fine§)	2.5e12 ± 4.5e9	11 ± 0.017	140 ± 0.77	5.5e10 ± 1.1e9	11 ± 0.71	9.2e-4 ± 1.1e-4
7 concentrations, 1 × Standard Noise, 1% Aggregate, K12 = 2.87 × 1012, K23 = 12.9
1-4-8 (coarse)	2.0e12 ± 0	10 ± 0	390 ± 0.73	7.0e10 ± 0	50 ± 0	0.0020 ± 7.8e-4
1-4-8 (fine§)	2.2e12 ± 0	11 ± 0.0084	330 ± 0.82	7.2e10 ± 6.6e8	48 ± 0.77	1.1e-7 ± 1.3e-7
7 concentrations, 1 × Standard Noise, 2% Aggregate, K12 = 2.87 × 1012, K23 = 12.9
1-4-8 (coarse)	2.0e12 ± 0	8.0 ± 0	980 ± 2.9	6.0e9 ± 0	2,000 ± 0	0.039 ± 0.0021
1-4-8 (fine§)	1.5e12 ± 1.5e9	9.9 ± 0.015	890 ± 2.6	1.0e10 ± 1.1e8	970 ± 11	1.1e-5 ± 8.1e-6
5 concentrations, 1 × Standard Noise, K12 = 2.87 × 1012, K23 = 12.9
1-4-8 (coarse)	4.0e12 ± 0	10 ± 0	160 ± 0.75	5.0e12 ± 0	40 ± 0	0.011 ± 7.3e-4
1-4-8 (fine§)	2.9e12 ± 0	13 ± 0	1.1 ± 0.16	2.7e12 ± 3.0e10	14 ± 0.18	1.6e-6 ± 1.3e-6
3 concentrations, 1 × Standard Noise, K12 = 2.87 × 1012, K23 = 12.9
1-4-8 (coarse)	NA¶	NA¶	NA¶	2.0e12 ± 0	7.4 ± 0.89	7.0e-4 ± 4.0e-4
1-4-8 (fine§)	NA¶	NA¶	NA¶	2.66e12 ± 6.57e10	20.16 ± 2.98	3.62e-8 ± 2.53e-8

The effects of increased noise, decreasing amount of data, and contamination by a large simulated aggregate of the protein were examined by varying the simulation conditions.

^*Mean ± SD of the best first-association constant K₁₂ for that pathway over five simulated data sets.

^†Mean ± SD of the best second-association constant K₂₃ for that pathway over five simulated data sets.

^‡Mean ± SD of the score of the best pair of association constants over five simulated data sets.

^§A fine grid was searched starting from the results of the coarse-grid search with a spacing between adjacent points 1/100 of the spacing of the coarse grid. In some cases, the range of the fine-grid search had to be extended beyond one coarse-grid point on either side of the best coarse-grid values to find the best fine-grid solution.

^¶Since three basis vectors are required for the three-state model, data curves at three concentrations are the theoretical minimum that can be employed, and are subject to increased numerical instability compared to the other situations, which are overdetermined. In this simulation, matrix inversion warnings were received, and unreasonable results were returned with the χ² metric, even though the MSMRD metric returned somewhat more reasonable results.

For the test of systematic noise, we constructed a simulated aggregate of this protein by building a model with six octamers packed together as in the crystal structure. Adding such an ordered form will not truly replicate the effect on scattering seen with randomly aggregated protein, but it does represent a large molecule contaminant of the same tertiary structure as the desired protein. Such contaminants could be both more difficult to remove experimentally and harder to extract from the data computationally (although see Discussion for potentially useful experimental and computational techniques). Simulations adding this contaminant at varying levels thus begin to test the response of our method to systematic errors similar to those most likely to occur. Additions of even 0.5% of this contaminant do affect the results (Table 6). The χ² scores increase greatly, although the effects on the determination of the best association constants by χ² are quite small. The MSMRD scores become quite variable and their best association constants are altered by 100-fold. Larger amounts of simulated aggregate have a correspondingly greater negative effect. Clearly our method is somewhat sensitive to the effects of such contaminants, but can still yield useful information with low contaminant levels. How large an impediment this actually is in practice will need to be evaluated in the future.

We also employed this system (with 1× standard random noise) to evaluate the relationship between the number of data sets at different protein concentrations (effectively the data/parameter ratio) and the quality of the analysis. Using the same range of protein concentrations for each test (0.25–16 mg/ml), we prepared data sets containing the seven concentrations employed thus far, which are twofold dilutions from 16 mg/ml to 0.25 mg/ml and form an equally spaced geometric series. We compared these data sets with smaller data sets of either five concentrations equally spaced in a geometric series or the theoretical minimum of three concentrations (also equally spaced) needed to determine basis vectors for three oligomeric forms (Table 6). The change from seven to five concentrations had little effect on the outcome. Reducing the number of concentrations to three led to numerical instabilities in matrix inversion. Although the MSMRD score does fairly well under this instability, the χ² returns meaningless results. We thus suggest that our method should always be employed with more data curves than oligomeric states. Although three oligomeric forms can be effectively reconstructed with as few as five scattering curves, as a practical matter we would recommend that experimenters collect as many scattering curves at different concentrations as practical, both to improve the data/parameter ratio and to cover the range of concentrations over which the various forms will be represented in significant amounts.

DISCUSSION

Current techniques for evaluating protein interactions generally provide either high-resolution, but static, structures of protein complexes (most easily those with large binding affinities), or a description of the stoichiometries and/or strength of the interactions. It has not previously been possible to obtain both association models and substantial structural information from a single biophysical experiment. Analysis of a concentration series of SAXS data as detailed in this article provides a biophysical tool capable of simultaneously elucidating equilibrium parameters from weakly associating systems, and allowing low-resolution reconstructions of each oligomer. Such a method is ideal for studying homo- and heterointeractions in weakly associating systems, without size restrictions or the need for crystallization.

Two scoring metrics have been developed for use with our method. We find that the most reliable results are achieved when χ² and MSMRD agree with each other. Some previous studies (19,20) have attempted to deduce association models solely from the extrapolated I(0) values. We propose that our decomposition method and employing both metrics may help avoid potential errors. When suboptimal conditions (low resolution, a low fraction of an oligomeric form, or systematic noise) occur, we have seen that the two metrics may not agree, with the χ² generally proving the better guide. We note that the MSMRD metric may be further developed through accurate experimental calibration of the forward scattering against standards of known concentration and molecular mass and then restraining the I(0) expected for the lowest-molecular-weight form to the sequence mass (for monomer) or a small multiple of it (for other oligomers).

Though we explore concentration-dependent association in this article, this technique can be applied to study association under the control of other experimental variables. Solution conditions such as temperature or the concentration of ions can also be varied in the SAS data set both to understand the physiological significance of these changes and to allow the extraction of the related thermodynamic parameters, including ΔH, ΔS, and SK_obs (34). Experimental conditions could also be varied to create an environment that either favors or disfavors association (e.g., addition of the same concentration of chaotropic or cosmotropic/crowding reagents to all samples). Varying these conditions potentially allows the collection of the most effective data for decomposition (e.g., >45% of each form in at least one data set, see Table 5) at the protein concentrations that are suitable for solution scattering.

Our method is currently described for homoassociations, but the extension to heteroassociations is direct (H. Chandola, T. E. Williamson, B. A. Craig, C. Bailey-Kellogg, and A. M. Friedman, unpublished). When used to study heteroassociations we expect even more robust performance, since the ability to control the amounts of the two components will provide a greater range of heterogeneous mixtures, and thus scattering curves, for decomposition. Furthermore, scattering from homogenous solutions of one or more of the individual components will generally also be available to aid the analysis.

To determine the association constants we have employed successively finer grid searches. We have chosen this method over direct determination of the constants or iterative refinement from initial values for ease of implementation and for the ability to directly evaluate and compare the quality of all feasible models. We demonstrate that successive grid searches are effective here where there are a limited number of variables and smooth surfaces for the scoring functions. A suitable future alternative is the use of iterative optimization, either directed (e.g., nonlinear least squares minimization) or stochastic (e.g., Monte Carlo), starting from the best values from an initial grid search. Such methods might become particularly suitable with the use of more complex models that require estimation of additional variables (e.g., an aggregated fraction).

Some methods for investigating self-associating systems either require or are aided by association/dissociation kinetics that are rapid (e.g., sedimentation velocity) or slow (e.g., separation of oligomers by size exclusion) over the time course of the experiment. Since the samples for scattering can be prepared at their final concentrations and allowed to reach equilibrium before data collection, the present method can be conducted on associations with any kinetics. In fact, our method also opens the possibility of collecting a time series of scattering data after rapid dilution of the sample, which could be decomposed and analyzed using equations that link fractional mass to time and the kinetic constants for dissociation. When combined with equilibrium measurements, this method could be used to determine the kinetic constants for both association and dissociation. This method would also help reveal the presence and structures of any kinetic intermediates, similar to the rapid scattering studies done to monitor protein refolding (35).

In the test cases shown here, we demonstrate that the scattering curves for individual oligomers can be reconstructed to an accuracy ranging from 0.05 to 0.99% in MARD. Preliminary studies (not described) show that errors at these levels have only small visible effects on estimation of the P(r) curve and three-dimensional reconstruction. The exact propagation of errors into the individual oligomer scattering curve, and then into the P(r) curve and three-dimensional reconstruction are matters for future investigation.

The proposed method has several potential limitations. However, the limitations are for the most part being alleviated with recent technology. The first limitation is the availability of samples that are suitable for scattering analysis. Aggregation, solubility, and sensitivity to radiation damage have traditionally limited the use of scattering for some proteins. We demonstrate that the presence of larger contaminants degrades our results, although aggregation can be alleviated by good sample preparation, filtration, or the use of size-exclusion chromatography in line with data collection (36). Size exclusion chromatography might be particularly useful with our method for any proteins that are in rapid equilibrium during and after the chromatography, although precise concentrations in the sample cell may then prove harder to control and monitor. Proteins of lower solubility can be investigated with stronger x-ray sources (30) and more sensitive detectors (31), and radiation damage can be limited by free radical scavengers and flowing sample past the beam during exposure (37). Access to facilities is another limitation that is improving and can be expected to improve further with the development of new x-ray and neutron sources. Finally, the amounts of purified protein required for a complete analysis are also being reduced by stronger sources, more sensitive detectors, and by sample cells better designed to exploit small beam sizes (30).

One system-specific feature limiting application of our method includes the sometimes small differences in scattering between different oligomers. The change in mass fractions must be large enough and each oligomer along an association pathway must be different enough in size and/or shape to yield scattering data curves with intensity differences significantly greater than the noise. This limitation was manifest when we attempted to apply the decomposition analysis to data simulated from actin, which undergoes open association to form successive larger linear oligomers. However, the small differences in scattering between successive actin oligomers (and thus across the concentration data series) resulted in accurate reconstruction only in the presence of exceedingly small amounts of noise. Such difficult self-associating systems not yet amenable to our method may yield to the formulation of additional restraints in the analysis. One intriguing additional restraint is enforcing the symmetry in real space that corresponds to the trial association model, perhaps by searching for the correct placement of symmetry axes around a fixed monomer (11). Such additional restraints may also aid those situations where low amounts of an oligomeric form (Table 5) or the presence of systematic noise (Table 6) weakens the ability to conduct the most accurate analysis.

Alleviating another system-specific problem, the presence of scattering components that do not participate in the association reactions (e.g., nonspecific aggregates and proteins denatured or damaged at the interaction surface), will require a more dynamic solution. Unlike sedimentation experiments, where the nonparticipating protein sediments differently from the participating protein, nonparticipating protein scatters just like the corresponding form of participating protein. Thus, adding a nonparticipating fraction parameter is not useful in our method; it serves only to change the protein available for association within the model, leading to a correction in the association constants, but not improving the agreement with the data. Therefore, it is impossible to actually fit the nonparticipating fraction from the data. As an alternative, changing conditions in the kinetic scattering experiment described above would lead to a change in protein association that would be different with different nonparticipating fractions. In this way the nonparticipating fraction and its form (monomer or oligomer) might be quantified.

Notwithstanding these limitations and areas for future development, the simulations described here demonstrate the feasibility of decomposing scattering data from heterogeneous self-associating systems to obtain accurate association constants and scattering curves for individual forms. Even though the “standard noise” data used here was simulated to accurately reflect the noise levels found in real data, further degradation of the signals by additional random or systematic noise still allows the extraction of useful information (Table 6), suggesting the potential for robust performance in practice. Work is proceeding on the evaluation of scattering data collected from suitable protein systems.