Abstract
The method of FRAP (fluorescence recovery after photobleaching), which has been broadly used to measure lateral mobility of fluorescent-labeled molecules in cell membranes, is formulated here in terms of continuous time random walks (CTRWs), which offer both analytical expressions and a scheme for numerical simulations. We propose an approach based on the CTRW and the corresponding fractional diffusion equation (FDE) to analyze FRAP results in the presence of anomalous subdiffusion. The FDE generalizes the simple diffusive picture, which has been applied to FRAP when assuming regular diffusion, to account for subdiffusion. We use a subordination relationship between the solutions of the fractional and normal diffusion equations to fit FRAP recovery curves obtained from CTRW simulations, and compare the fits to the commonly used approach based on the simple diffusion equation with a time dependent diffusion coefficient (TDDC). The CTRW and TDDC describe two different dynamical schemes, and although the CTRW formalism appears to be more complicated, it provides a physical description that underlies anomalous lateral diffusion.
INTRODUCTION
Protein mobility in cell membranes has been of great interest due to the essential role it plays in various biological functions on the cell level (1–4). This mobility has been measured by various techniques (5–8), one of which is the widely used fluorescence recovery after photobleaching (FRAP) (9), which measures the recovery of fluorescence at a certain spot on a membrane after photobleaching. The fluorescence recovery originates from fluorescently tagged proteins that move randomly in the membrane and cause the recovery of the fluorescence by replacing the bleached proteins. Several experimental approaches (in particular single particle tracking (SPT)), have shown that proteins in membranes might display non-Brownian motion (10–15) characterized by mean-squared displacements (MSDs) that do not grow linearly with time contrary to what is obtained for normal diffusion (16,17). In some cases, the MSDs follow the scaling 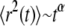 (
( ), meaning that conventional models such as the fluid mosaic model of Singer and Nicolson (18) do not provide a complete picture of protein movements in cell membranes. Observations made by SPT have demonstrated four different types of movement of proteins in cell membranes (19): Brownian motion (
), meaning that conventional models such as the fluid mosaic model of Singer and Nicolson (18) do not provide a complete picture of protein movements in cell membranes. Observations made by SPT have demonstrated four different types of movement of proteins in cell membranes (19): Brownian motion (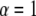 ), anomalous subdiffusion (
), anomalous subdiffusion (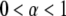 ), anomalous superdiffusion (
), anomalous superdiffusion (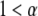 ), and spatial localization (immobile proteins;
), and spatial localization (immobile proteins; 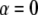 ). Although Brownian motion has a firm theoretical basis, the origins of the reported non-Brownian motions are not always clear and are still open to speculation. For instance, Ritchie et al. (10) claim that membranes might be divided into corrals by the cytoskeleton, and therefore the movements of proteins are assumed to occur by hopping from one corral to another.
). Although Brownian motion has a firm theoretical basis, the origins of the reported non-Brownian motions are not always clear and are still open to speculation. For instance, Ritchie et al. (10) claim that membranes might be divided into corrals by the cytoskeleton, and therefore the movements of proteins are assumed to occur by hopping from one corral to another.
The existence of anomalous diffusion raises the need for a theoretical framework that allows one to analyze recovery curves obtained using FRAP by taking into consideration the fact that proteins do not move by Brownian motion. Here we focus on subdiffusion (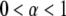 ) and use continuous time random walks (CTRWs) (20,21) to simulate the diffusional anomaly (22,23). The simulation results can then be fitted by a modified diffusion equation (24) that extends the diffusive picture to include subdiffusion (23,25). The article is organized as follows: the next section describes some aspects of anomalous diffusion and its characteristics. The third section introduces the fractional diffusion equation (FDE) and the time-dependent diffusion coefficient (TDDC), also referred to as fractional Brownian motion (FBM). The fourth section deals with how to handle FRAP recovery curves when anomalous diffusion occurs. In the fifth section, we describe the methods used to simulate and calculate FRAP curves. We then present results and compare the CTRW and TDDC approaches, and end with our conclusions.
) and use continuous time random walks (CTRWs) (20,21) to simulate the diffusional anomaly (22,23). The simulation results can then be fitted by a modified diffusion equation (24) that extends the diffusive picture to include subdiffusion (23,25). The article is organized as follows: the next section describes some aspects of anomalous diffusion and its characteristics. The third section introduces the fractional diffusion equation (FDE) and the time-dependent diffusion coefficient (TDDC), also referred to as fractional Brownian motion (FBM). The fourth section deals with how to handle FRAP recovery curves when anomalous diffusion occurs. In the fifth section, we describe the methods used to simulate and calculate FRAP curves. We then present results and compare the CTRW and TDDC approaches, and end with our conclusions.
ANOMALOUS DIFFUSION
A characteristic that distinguishes anomalous from regular diffusion is the time dependence of the MSD of a particle's trajectories. For normal diffusion, the MSD increases linearly with time:
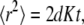 |
(1) |
where d is the spatial dimension and K is the diffusion coefficient [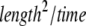 ]. In the anomalous subdiffusion case, the MSD does not grow linearly with time, but rather follows (23)
]. In the anomalous subdiffusion case, the MSD does not grow linearly with time, but rather follows (23)
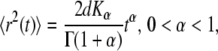 |
(2) |
where Kα is the anomalous diffusion coefficient of units [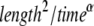 ] and α is the anomaly exponent. Γ(x) is the gamma function (26).
] and α is the anomaly exponent. Γ(x) is the gamma function (26).
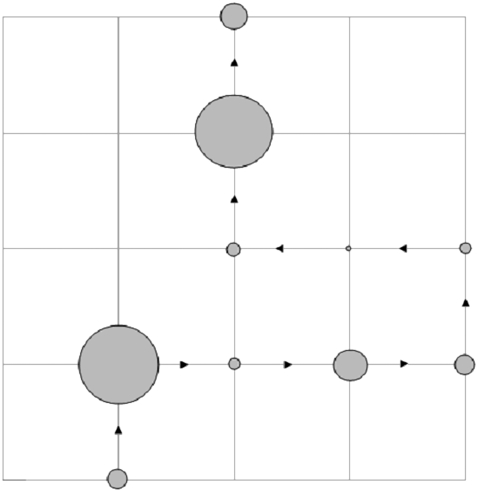
We assume that the CTRW describes the “microscopic dynamics” that underlies the observed anomalous diffusion in membranes. In systems modeled by CTRW, particles usually move randomly according to two independent probability density functions (pdfs): a pdf for choosing jump lengths and another pdf for choosing waiting times between jumps (27). In general, however, the jump lengths and waiting times can be coupled (28,29). Fig. 1 presents schematically a decoupled random walker on a two-dimensional grid. Here the jump lengths are fixed and the waiting time may vary from site to site and from visit to visit at a particular site.
FIGURE 1.
CTRW model on a two-dimensional lattice. The waiting times are symbolized by circles whose area is proportional to the waiting time a walker spends at a lattice point before the next jump event occurs. The jumps lengths are equidistant.
If the jump lengths' pdf and waiting times' pdf have finite second and first moments, respectively (variance and mean, respectively), the motion of the particles will always yield normal diffusion (23). This means that under these conditions, we encounter a behavior that can be described using Fick's diffusion equation. This normal behavior can be modified by choosing a waiting time pdf, 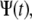 that does not possess a mean waiting time (23). Namely, there is no timescale in the problem and the particle is spatially trapped for extended periods of time. As an example, such a waiting time can be obtained in a closed form using the Mittag-Leffler function (30):
that does not possess a mean waiting time (23). Namely, there is no timescale in the problem and the particle is spatially trapped for extended periods of time. As an example, such a waiting time can be obtained in a closed form using the Mittag-Leffler function (30):
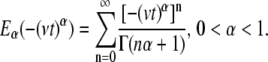 |
(3a) |
The Mittag-Leffler function is a generalization of the exponential function and reduces to it for 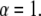 For
For 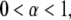 the short time behavior of the function is
the short time behavior of the function is
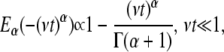 |
(3b) |
and the long time has the asymptotic power law behavior
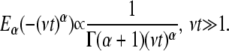 |
(3c) |
When taking the time derivative of the Mittag-Leffler function,
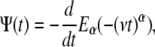 |
(4) |
we obtain a waiting time pdf whose asymptotic behavior is fat tailed that follows an inverse power law at large times, 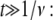
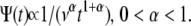 |
(5) |
Equation 5 displays a broad pdf with a slowly decaying tail that has a nonnegligible probability of very long waiting times. Such a fat-tailed pdf is characterized by a diverging mean, 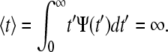 For α=1, Eq. 4 reads
For α=1, Eq. 4 reads 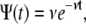 for which
for which 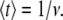
Equation 5 describes a situation in which there is a nonnegligible probability that a particle gets stuck in space for very long times (21). Particles that move randomly according to CTRW with a waiting time pdf as in Eq. 5 display an overall motion that is subdiffusive. Although Eq. 4 provides a closed form expression for fat-tailed waiting times, pdfs of waiting times can stem from different origins that lead to subdiffusion in a variety of systems. Examples include dispersive transport in amorphous semiconductors (27), dispersion of contaminates in underground water (31), and subdiffusion due to crowding in living cells (32). A model that might be relevant to the problem we are interested in, at least over some time window, is that of a system of local potential wells that act as momentary traps for particles, with a rate of leaving a trap being (33):
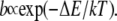 |
(6) |
Here 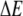 is the activation energy needed to leave the trap. Assuming that the depths of the potential wells are distributed exponentially,
is the activation energy needed to leave the trap. Assuming that the depths of the potential wells are distributed exponentially,
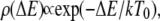 |
(7) |
where 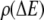 is the density of traps of depth
is the density of traps of depth 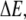 and
and 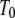 is an effective temperature that characterizes the trap distribution. In such systems, the waiting time pdf follows a power law (33) as in Eq. 5 with
is an effective temperature that characterizes the trap distribution. In such systems, the waiting time pdf follows a power law (33) as in Eq. 5 with
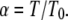 |
(8) |
The motion is therefore subdiffusive for 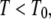 which corresponds to
which corresponds to 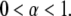 For temperatures
For temperatures 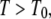 for which
for which 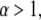 the waiting time pdf possesses a first moment, and regular diffusion is expected as observed in some amorphous semiconductors (27,33).
the waiting time pdf possesses a first moment, and regular diffusion is expected as observed in some amorphous semiconductors (27,33).
One can consider the movement of proteins in cell membranes with the above example in mind (34). If such energetic traps exist, anomalous behavior would arise. Traps can also be structural in nature as proposed by Ritchie et al. (10), where cytoskeleton fences confine the spatial motion of proteins, or due to dead ends along a structural backbone (8,10,35). In what follows, we use CTRW to describe the anomalous motion of proteins and how it shows up in FRAP experiments. This might help clarify recent debates about subdiffusion in SPT measurements (8,10,36).
THE FRACTIONAL DIFFUSION EQUATION
We proceed by using a generalization of the diffusion equation to account for anomalous subdiffusion. This generalization, known as the FDE, or the fractional Fokker-Planck equation (FFPE) (23,25), is expressed in terms of fractional calculus (noninteger order of differentiation). Instead of the regular diffusion equation usually assumed in FRAP analysis,
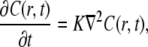 |
(9) |
where K is the diffusion coefficient (see Eq. 1), a fractional order equation is introduced:
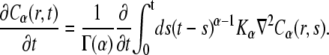 |
(10) |
Equation 10 is nonlocal in time and is characterized by a long-range kernel. It can be rewritten by using the Riemann-Liouville operator of noninteger order of differentiation:
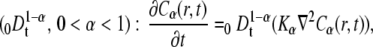 |
(11) |
where Kα is the anomalous diffusion coefficient (see Eq. 2).
We denote with the subscript 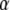 the concentration and diffusion coefficient in the case of anomalous diffusion (see Eq. 2). The Riemann-Liouville operator has the integral form
the concentration and diffusion coefficient in the case of anomalous diffusion (see Eq. 2). The Riemann-Liouville operator has the integral form
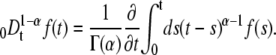 |
(12) |
Equations 10 and 11 reduce to the regular diffusion equation, Eq. 9, for 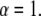 Note that in our example in Eq. 4, the waiting time is an exponential for
Note that in our example in Eq. 4, the waiting time is an exponential for 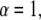 so that the anomaly disappears. Equation 10 has been derived from a CTRW model with the waiting time pdf as in Eq. 5. The derivation holds for long times and is based on the Kramers-Moyal expansion (24,37).
so that the anomaly disappears. Equation 10 has been derived from a CTRW model with the waiting time pdf as in Eq. 5. The derivation holds for long times and is based on the Kramers-Moyal expansion (24,37).
Whenever particles display anomalous subdiffusion that originates from a fat-tailed distribution of waiting times, Eq. 9 should be replaced by Eq. 11. The latter should be applied in the analysis of FRAP experiments in the presence of subdiffusion, bearing in mind that all proteins are assumed to move according to Eq. 5. In case of different protein populations, “distributed order” equations can be introduced (38), which add more parameters to the problem.
The solution of the FDE, Eq. 11, is given by a subordination relationship to the known solution 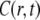 of the normal equation (23,39):
of the normal equation (23,39):
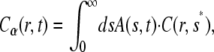 |
(13) |
where 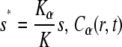 is the solution of the FDE, Eq. 11, which we are interested in, and
is the solution of the FDE, Eq. 11, which we are interested in, and 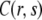 is the solution of the regular diffusion equation, Eq. 9, for the same initial and boundary conditions. The solutions are related through the integral in Eq. 13, where A(s,t) serves as a kernel function. A(s,t) is the modified one-sided Levy distribution function (23), which we discuss later on in more detail. The subordination accounts for the time cost of simple random walk steps introduced due to waiting times. It generally offers a translation of the number of steps into time (33). In the case of fat-tailed waiting times, the subordination takes the form of Eq. 13 with
is the solution of the regular diffusion equation, Eq. 9, for the same initial and boundary conditions. The solutions are related through the integral in Eq. 13, where A(s,t) serves as a kernel function. A(s,t) is the modified one-sided Levy distribution function (23), which we discuss later on in more detail. The subordination accounts for the time cost of simple random walk steps introduced due to waiting times. It generally offers a translation of the number of steps into time (33). In the case of fat-tailed waiting times, the subordination takes the form of Eq. 13 with 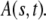 Solving Eq. 11 for the initial conditions of starting at the origin at time
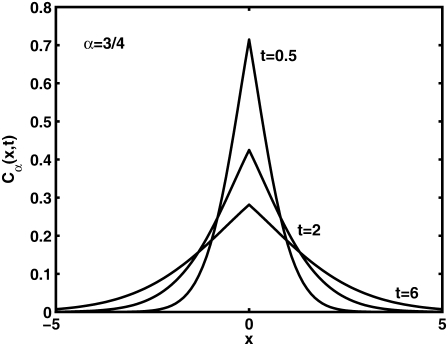
Solving Eq. 11 for the initial conditions of starting at the origin at time 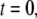 a non-Gaussian solution is obtained, which is characterized by a cusp at the origin (23) as shown in Fig. 2. Some evidence for the cusped behavior has been reported by Khan et al. (40), where single-particle tracking measurements were used to investigate Class I and II MHC proteins in the plasma membrane. Although this cannot be taken as a proof of a CTRW mechanism, it provides support to the role played by broadly distributed waiting times.
a non-Gaussian solution is obtained, which is characterized by a cusp at the origin (23) as shown in Fig. 2. Some evidence for the cusped behavior has been reported by Khan et al. (40), where single-particle tracking measurements were used to investigate Class I and II MHC proteins in the plasma membrane. Although this cannot be taken as a proof of a CTRW mechanism, it provides support to the role played by broadly distributed waiting times.
FIGURE 2.
Solution of Eq. 11, 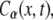 in one-dimension with the anomalous exponent
in one-dimension with the anomalous exponent 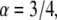 drawn for the consecutive time t = 0.5, 2, 6. The cusp shape of the pdf is distinct. See Metzler and Klafter (23).
drawn for the consecutive time t = 0.5, 2, 6. The cusp shape of the pdf is distinct. See Metzler and Klafter (23).
A few points to be noted:
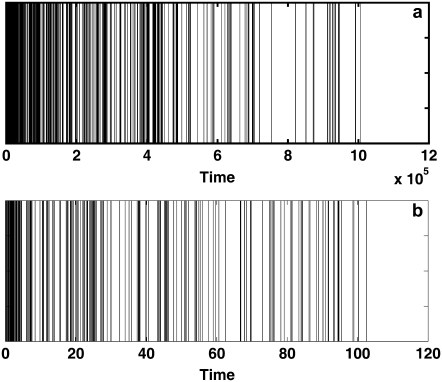
The process described by CTRW with the fat-tailed pdf in Eq. 5 is nonstationary and displays aging (41,42). Aging in CTRW systems with inverse power law waiting times pdf, Eq. 5, stems from the nonstationary nature of the process. As time evolves, less and less events occur per time interval, demonstrating the growing probability to get stuck for longer and longer times. This aspect of aging is shown in Fig. 3, where the occurrence of events is plotted as a function of time. As a result, experimental observations depend on the time of measurement relative to the starting times. Therefore, when solving the FDE, the initial conditions should be carefully dealt with. The starting time can be viewed from the CTRW point of view as the time when all particles start their random waiting period for the first jump. In FRAP experiments, the bleach time does not correspond to the starting time of the movement of the proteins. Here we assume a measurement that starts (bleaching time) at the same time that the system is prepared. In the more general case of subdiffusion, one should consider aging with care. Each protein may arrive at the membrane at some different time. However, in the case that cytoplasmic proteins exchange with proteins in the membrane, there is a possibility for a broad range of arrival (starting) times, and the aging treatment would be even more complicated (43).
- As mentioned, Eq. 11 is nonlocal in time, a property intimately related to the nonstationary nature of the CTRW with fat tails. Another commonly used generalization of the normal diffusion equation is the TDDC, which replaces the diffusion constant with a time-dependent diffusion coefficient:
Equation 14 is local in time in contrast to Eq. 11 and has a Gaussian type solution to be contrasted with the cusp shape solution of the FDE solution (Fig. 2). One should be aware that these two descriptions of anomalous behavior describe different physical processes. The CTRW description (or FDE) describes a particle moving among energetic or structural traps with time spent in each trap taken from a power law pdf, whereas the TDDC, Eq. 14, corresponds to a different mechanism of motion whose meaning is less obvious (16). Equation 14 is also referred to as fractional Brownian motion (FBM), since its solution gives the Gaussian FBM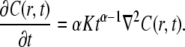
(14) 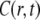 with a subdiffusive variance (44). Being local in time, the equation does not describe the long range temporal correlations typical of FBM (45).
with a subdiffusive variance (44). Being local in time, the equation does not describe the long range temporal correlations typical of FBM (45). In real systems, the power law in Eq. 5 might be truncated at long times, which would make the anomalous subdiffusion an intermediate behavior. Such truncation changes the process from nonstationary to stationary, eliminating the aging problem. Nevertheless, the description we present here is still valid for intermediate time windows depending on the system parameters (38). The truncated case can be dealt with in terms of the “distribution order” equation, as mentioned earlier.
FIGURE 3.
Characteristic of aging is the decreasing frequency of jumps as time evolves. CTRW with 100 independent particles was simulated and the number of jumps was detected for the same time interval at different times. A fat-tailed waiting time pdf was used with 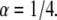 The decrease in the density of lines for larger times demonstrates a decrease in the number of events and therefore the aging concept. Note the different time scales in a and b.
The decrease in the density of lines for larger times demonstrates a decrease in the number of events and therefore the aging concept. Note the different time scales in a and b.
FRACTIONAL FRAP
We now continue by formulating FRAP experimental realizations in terms of CTRW and the corresponding FDE Eq. 11 and Eq. 13. CTRW for FRAP was first used by Nagle (21) for a one-dimensional case. Let us start by repeating the expression for fluorescence in the case of regular diffusion, where Eq. 9 holds. We recall that in FRAP experiments, one does not measure directly the concentration but rather the fluorescence given as (9)
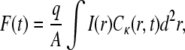 |
(15) |
where I(r) is the intensity of the laser beam, 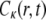 is the concentration of the fluorophore proteins (q and A are the products of the quantum efficiencies and attenuation factor, respectively) and
is the concentration of the fluorophore proteins (q and A are the products of the quantum efficiencies and attenuation factor, respectively) and 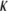 is a measure of the amount of the bleach that is connected to the initial conditions (not to be confused with K, the diffusion coefficient). In our calculations, we assumed a Gaussian laser beam. The temporal evolution of the fluorescence for simple diffusion and a Gaussian laser beam is then (9)
is a measure of the amount of the bleach that is connected to the initial conditions (not to be confused with K, the diffusion coefficient). In our calculations, we assumed a Gaussian laser beam. The temporal evolution of the fluorescence for simple diffusion and a Gaussian laser beam is then (9)
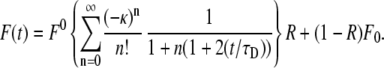 |
(16) |
Here, F0 is the fluorescence before photobleaching, F0 is the fluorescence immediately after the bleach, and R is the fraction of the mobile proteins.
If the proteins undergo anomalous subdiffusion in the membrane, we start from the FDE, Eq. 11, to describe their movement and make use, to obtain the fluorescence, of Eq. 13:
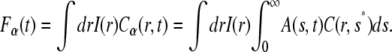 |
(17) |
Changing the order of integrations, we reach
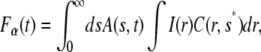 |
(18) |
and since the second integral on the right-hand side is just the fluorescence for normal diffusion, we can rewrite Eq. 18 as
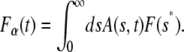 |
(19) |
which has the same form of Eq. 13 and is given explicitly by
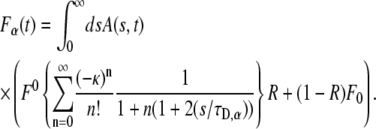 |
(20) |
Equation 20 is the central result in this article and provides an expression for fluorescence recovery in FRAP experiments for those systems in which the “microscopic dynamics” is well approximated by CTRW with fat tails. It provides a way to obtain the fluorescence in the subdiffusion case by integrating over the normal fluorescence recovery function multiplied by a modified one-sided Levy function (23). Using this method, we can derive anomalous fluorescence curves for a variety of experimental conditions as calculated earlier by Axelrod et al. (9). A word of caution: the FRAP method, which is usually applied for both membrane and bulk measurements, is not sensitive to the various types of motion of individual particles, but rather measures ensemble properties. This means that when obtaining FRAP curves, one sees only an average of the different individual behaviors and therefore an apparent diffusion behavior. This corresponds in the CTRW framework to a single waiting time  Equation 20 holds for those measurements that start at the same time that the fluorescent particles start diffusing.
Equation 20 holds for those measurements that start at the same time that the fluorescent particles start diffusing.
The one-sided Levy function 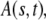 for a general
for a general 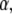 is given by the series
is given by the series
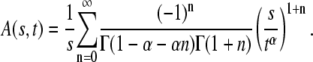 |
(21) |
This function, however, has a simple form only for a few special cases (23):
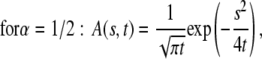 |
(22) |
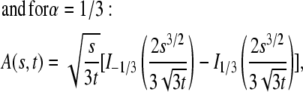 |
(23) |
where 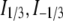 are the modified Bessel functions (26).
are the modified Bessel functions (26).
For 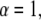 A(s,t) reduces to
A(s,t) reduces to 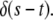 From Eqs. 21–23, we see that s has the dimensions of
From Eqs. 21–23, we see that s has the dimensions of 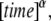 which means that the parameter
which means that the parameter 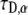 in Eq. 20 has the same fractional dimensions of time. When fitting Eq. 20 to experimental data, or to CTRW simulations in our case,
in Eq. 20 has the same fractional dimensions of time. When fitting Eq. 20 to experimental data, or to CTRW simulations in our case, 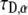 and
and 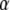 are the two informative fitting parameters.
are the two informative fitting parameters.
Starting from Eq. 14, we can also derive the fluorescence recovery curve that corresponds to the TDDC. Repeating the steps of Axelrod et al. (9), we reach the solution for a Gaussian laser beam profile and pure diffusion. In this case, the fluorescence as a function of time has the form of Eq. 14:
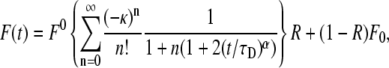 |
(24) |
where again F0 is the fluorescence before bleaching, F0 is the fluorescence immediately after the bleach, and R is the fraction of moving proteins. Equation 24 has a much simpler form than Eq. 20. It resembles Eq. 16 by replacing 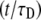 by
by 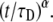 Both Eqs. 20 and 24 reduce to Eq. 16 when
Both Eqs. 20 and 24 reduce to Eq. 16 when 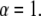 We believe, however, that the underlying process is better described by the CTRW and therefore by Eqs. 11 and 20.
We believe, however, that the underlying process is better described by the CTRW and therefore by Eqs. 11 and 20.
CTRW SIMULATIONS VERSUS THEORY
We simulated FRAP experiments for several cases as described below and performed calculations to be compared with these simulations. The simulations were based on the National Instruments CVI programming tool. The software we produced enabled us to simulate and visualize FRAP experiments for both normal and anomalous diffusion. All the calculations and simulations were done for the case of a Gaussian laser beam profile for which the normal fluorescence recovery is given by Eq. 16. In addition, we chose all the proteins to be mobile; namely, R = 1. We calculated the integral in Eq. 20 using Mathematica (Wolfram Research, Champaign, IL) software symbolic and numerical integration. We started with simulating FRAP experiment for normal diffusion for testing reasons. The curves obtained from the simulations were then fitted to the calculated ones with one fitting parameter, 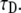 This parameter, which appears in Eq. 16, is presented in Axelrod et al. (9) as
This parameter, which appears in Eq. 16, is presented in Axelrod et al. (9) as
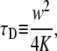 |
(25) |
where K is the diffusion coefficient and w is the half width at which the laser beam intensity is at 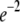 of its height at the origin. After fitting
of its height at the origin. After fitting 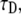 we easily calculated the diffusion coefficient. To check the validity of this coefficient, we used a different simulation of this same system that measured the MSD of an ensemble of particles as a function of time. The diffusion coefficient was calculated from Eq. 1 and was compared to the diffusion coefficient from the FRAP simulations. In comparing the two coefficients, we got an excellent agreement with a factor of <0.3% difference.
we easily calculated the diffusion coefficient. To check the validity of this coefficient, we used a different simulation of this same system that measured the MSD of an ensemble of particles as a function of time. The diffusion coefficient was calculated from Eq. 1 and was compared to the diffusion coefficient from the FRAP simulations. In comparing the two coefficients, we got an excellent agreement with a factor of <0.3% difference.
The next step was to simulate anomalous diffusion. This was done by assigning every protein a certain waiting time taken from a Levy α-stable distribution (46,47), whose fat tail is given by Eq. 5. We used the heap algorithm to arrange and sort the jumping times of proteins. A similar equation to the normal case holds also for the anomalous case:
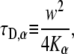 |
(26) |
and we recall that 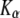 has the units
has the units 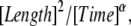 and
and 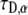 has the unit
has the unit 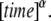 Our goal was first to find the
Our goal was first to find the 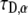 parameter when all the other parameters matched their simulation counterparts. The calculations were done for the case of
parameter when all the other parameters matched their simulation counterparts. The calculations were done for the case of 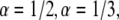 and
and 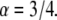 We started by obtaining the diffusion coefficient for each α by using the simulation measuring the MSD as a function of time for an ensemble of particles (over
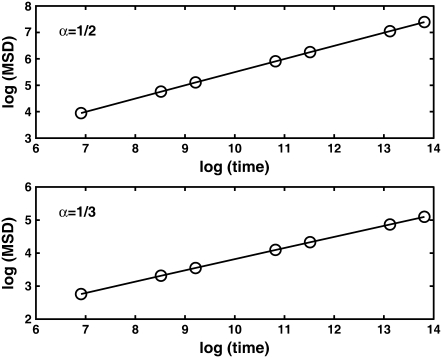
We started by obtaining the diffusion coefficient for each α by using the simulation measuring the MSD as a function of time for an ensemble of particles (over 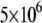 ) and fitting it to Eq. 2. Fig. 4 shows a log-log plot of this simulation. It is important to note that, as expected, the diffusion coefficients depend on the anomaly exponent (α), which means that two diffusion coefficients that have different exponents are not equal.
) and fitting it to Eq. 2. Fig. 4 shows a log-log plot of this simulation. It is important to note that, as expected, the diffusion coefficients depend on the anomaly exponent (α), which means that two diffusion coefficients that have different exponents are not equal.
FIGURE 4.
Log-log plot of the MSD versus time for 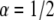 and
and 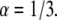 The diffusion coefficients
The diffusion coefficients 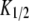 and
and 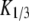 are calculated from the slopes of the fitted lines.
are calculated from the slopes of the fitted lines.
We then performed calculations of FRAP curves for anomalous diffusion. We first performed analytical and numerical calculations for 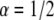 (using Mathematica software) to obtain the fluorescence recovery function for the corresponding anomalous case. We then fitted (a one parameter fit of
(using Mathematica software) to obtain the fluorescence recovery function for the corresponding anomalous case. We then fitted (a one parameter fit of 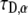 ) the simulated curve to this function numerically and calculated the diffusion coefficient by using Eq. 26. We compared the result with the coefficient of the simulated MSD. The comparison of the two diffusion coefficients gave us excellent agreement (within 0.6%). We followed the same procedure for
) the simulated curve to this function numerically and calculated the diffusion coefficient by using Eq. 26. We compared the result with the coefficient of the simulated MSD. The comparison of the two diffusion coefficients gave us excellent agreement (within 0.6%). We followed the same procedure for 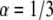 with a good match of the diffusion coefficients (a factor of <0.5%). In these fits, α was known and we therefore had to fit only a one-parameter fit (
with a good match of the diffusion coefficients (a factor of <0.5%). In these fits, α was known and we therefore had to fit only a one-parameter fit (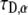 ). The mobile fraction of proteins (R), which serves as another fitting parameter in a FRAP experiment, is taken here to be unity, R = 1. The reason for this choice is that in anomalous subdiffusion due to CTRW, some proteins might get stuck for a considerable amount of time and are viewed therefore as immobile during the time of experiment. So being immobile is a matter of the observation time window. This is accounted for by the CTRW process with a single fat-tailed waiting time pdf as assumed in this article.
). The mobile fraction of proteins (R), which serves as another fitting parameter in a FRAP experiment, is taken here to be unity, R = 1. The reason for this choice is that in anomalous subdiffusion due to CTRW, some proteins might get stuck for a considerable amount of time and are viewed therefore as immobile during the time of experiment. So being immobile is a matter of the observation time window. This is accounted for by the CTRW process with a single fat-tailed waiting time pdf as assumed in this article.
The next step was to perform a two-parameter fit of both α and 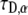 as is actually done in FRAP experiments using the programming tool of Mathematica software. To do so, we had to develop a special algorithm that could calculate FRAP curves for different α and
as is actually done in FRAP experiments using the programming tool of Mathematica software. To do so, we had to develop a special algorithm that could calculate FRAP curves for different α and 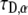 values using the series representation of the one-sided Levy function, Eq. 21. The fit was performed to a FRAP simulation for the case of
values using the series representation of the one-sided Levy function, Eq. 21. The fit was performed to a FRAP simulation for the case of 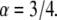 We obtained very good agreement for both parameters:
We obtained very good agreement for both parameters: 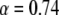 for the anomalous exponent and ∼10% difference for
for the anomalous exponent and ∼10% difference for 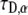 when compared to the simulation results. Both the simulation data and the calculated FRAP curve for these parameters are shown in Fig. 5.
when compared to the simulation results. Both the simulation data and the calculated FRAP curve for these parameters are shown in Fig. 5.
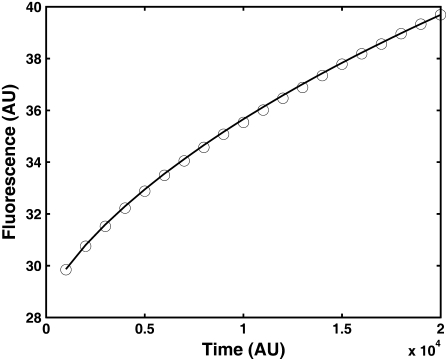
FIGURE 5.
Fitting simulation data of fluorescence recovery curves with parameters α and 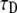 using the series representation of the one-sided Levy function, A(s,t). (Solid line) Calculated curve. (Open circles) Simulated curve. The fluorescence and time are in arbitrary units.
using the series representation of the one-sided Levy function, A(s,t). (Solid line) Calculated curve. (Open circles) Simulated curve. The fluorescence and time are in arbitrary units.
We also fitted the fluorescence function calculated from the TDDC/FBM equation to the simulated curve based on CTRW to compare the obtained anomalous diffusion coefficient with previous fit to the FDE. When fitting this function, however, we had again to deal with the question of how to treat the mobile fraction R. We examined a few fits for these fluorescence functions. Since we knew the correct parameters of the system, we could determine which fit best suited the system. We fitted the curves for two cases: 1), a three-parameter fit of 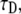 R, and α (see Eq. 24); and 2), a fit of
R, and α (see Eq. 24); and 2), a fit of 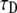 and
and 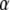 only, taking R = 1 as done for the FDE case. We calculated the
only, taking R = 1 as done for the FDE case. We calculated the 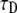 parameter in the following way:
parameter in the following way:
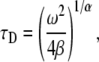 |
(27) |
where 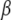 is the diffusion coefficient and
is the diffusion coefficient and 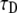 has the dimensions of [time]. The latter differs from the dimensions of
has the dimensions of [time]. The latter differs from the dimensions of 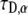 in the solution of the FDE. The MSD for the TDDC/FBM, Eq. 14, has the form
in the solution of the FDE. The MSD for the TDDC/FBM, Eq. 14, has the form
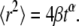 |
(28) |
When performing different fits, we observed different local minima that fitted almost equally well the curves. When fitting the two cases, 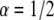 and
and 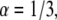 we reached local minima that did not suit well the simulation results. From these fits we obtained both the diffusion coefficient (
we reached local minima that did not suit well the simulation results. From these fits we obtained both the diffusion coefficient (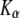 ) and the anomaly exponent (α). We obtained the anomaly exponent α from the FBM fit to the simulated
) and the anomaly exponent (α). We obtained the anomaly exponent α from the FBM fit to the simulated 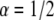 case with a factor of up to 3.5% difference and for
case with a factor of up to 3.5% difference and for 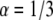 with a factor up to 9% difference. The diffusion coefficients that we obtained were less accurate. For the simulated
with a factor up to 9% difference. The diffusion coefficients that we obtained were less accurate. For the simulated 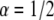 case, the difference was up to 40% difference and for
case, the difference was up to 40% difference and for 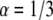 the difference was up to 70% difference. In all cases we obtained better results when taking R = 1. The diffusion coefficients were of the order of magnitude of the actual diffusion coefficient. When we fitted the curves with the suitable α (α = 1/2 or α = 1/3 and R = 1), the diffusion coefficients that we obtained were much more accurate. However, this approach is not applicable when fitting real FRAP experimental data, since one does not know a priori the α-value. When fitting the data with a value of R calculated using the fluorescence at the end of the experiment, as usually done, the fitting would lead to erroneous curves (α is >1) as can be seen in Fig. 6.
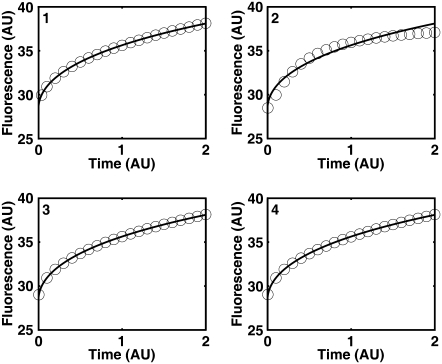
the difference was up to 70% difference. In all cases we obtained better results when taking R = 1. The diffusion coefficients were of the order of magnitude of the actual diffusion coefficient. When we fitted the curves with the suitable α (α = 1/2 or α = 1/3 and R = 1), the diffusion coefficients that we obtained were much more accurate. However, this approach is not applicable when fitting real FRAP experimental data, since one does not know a priori the α-value. When fitting the data with a value of R calculated using the fluorescence at the end of the experiment, as usually done, the fitting would lead to erroneous curves (α is >1) as can be seen in Fig. 6.
FIGURE 6.
Fitting simulation data with fluorescence functions for 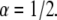 The fluorescence and time are in arbitrary units: 1), Fluorescence function obtained from the fractional diffusion equation. 2), Solution of TDDC/FBM with R evaluated from the fluorescence curve at the beginning and end of the simulation. 3), TDDC/FBM best fit for all three parameters, R,
The fluorescence and time are in arbitrary units: 1), Fluorescence function obtained from the fractional diffusion equation. 2), Solution of TDDC/FBM with R evaluated from the fluorescence curve at the beginning and end of the simulation. 3), TDDC/FBM best fit for all three parameters, R, 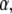 and
and 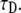 4), TDDC/FBM best fit for
4), TDDC/FBM best fit for 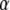 and
and 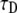 when taking R = 1.
when taking R = 1.
CONCLUSIONS
We presented what to our knowledge is a new method to model the fluorescent recovery curves that correspond to FRAP experiments in the case of anomalous diffusion. The method is based on the CTRW process with a fat-tailed waiting time pdf. We confronted CTRW and its corresponding FDE with the TDDC/FBM. Both the FDE and the TDDC better fit the “microscopic” CTRW modeling when all proteins are assumed mobile, R = 1.
The CTRW framework provides a reasonable way to describe analytically and numerically the diffusion of proteins in cell membranes. In the anomalous case, the FDE derived from CTRW allows a simple formal extension of the regular diffusion formulation of FRAP recovery curves.
Acknowledgments
The authors thank Yoav Henis for fruitful discussions. J.K. acknowledges the support of an Israel Science Foundation grant.
Editor: G. Barisas.
References
- 1.Zhang, F., G. M. Lee, and K. Jacobson. 1993. Protein lateral mobility as a reflection of membrane microstructure. Bioessays. 15:579–588. [DOI] [PubMed] [Google Scholar]
- 2.Henis, Y. I., B. Rotbalt, and Y. Kloog. 2006. Frap beam-size analysis to measure palmitoylation-dependent membrane association dynamics and microdomain partitioning of Ras proteins. Methods. 40:183–190. [DOI] [PubMed] [Google Scholar]
- 3.Niv, H., O. Gutman, Y. Kloog, and Y. I. Henis. 2002. Activated K-Ras and H-Ras display different interactions with saturable nonraft sites at the surface of live cells. J. Cell Biol. 157:865–872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ryan, T. A., S. J. Smith, and H. Reuter. 1996. The timing of synaptic vesicle endocytosis. Proc. Natl. Acad. Sci. USA. 93:5567–5571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Elson, E. L., and D. Magde. 1974. Fluorescence correlation spectroscopy. 1. conceptual basis and theory. Biopolymers. 13:1–27. [DOI] [PubMed] [Google Scholar]
- 6.Elson, E. L. 1985. Fluorescence correlation spectroscopy and photobleaching recovery. Annu. Rev. Phys. Chem. 36:379–406. [Google Scholar]
- 7.Ghosh, R. N., and W. W. Webb. 1994. Automated detection and tracking of individual and clustered cell-surface low-density-lipoprotein receptor molecules. Biophys. J. 66:1301–1318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kusumi, A., Y. Sako, and M. Yamamoto. 1993. Confined lateral diffusion of membrane- receptors as studied by single-particle tracking (nanovid microscopy)—effects of calcium-induced differentiation in cultured epithelial-cells. Biophys. J. 65:2021–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Axelrod, D., D. E. Koppel, J. Schlessinger, E. Elson, and W. W. Webb. 1976. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 16:1055–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ritchie, K., X. Y. Shan, J. Kondo, K. Iwasawa, T. Fujiwara, and A. Kusumi. 2005. Detection of non-Brownian diffusion in the cell membrane in single molecule tracking. Biophys. J. 88:2266–2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sheets, E. D., G. M. Lee, R. Simson, and K. Jacobson. 1997. Transient confinement of a glycosylphosphatidylinositol-anchored protein in the plasma. Biochemistry. 36:12449–12458. [DOI] [PubMed] [Google Scholar]
- 12.Schwille, P., U. Haupts, S. Maiti, and W. W. Webb. 1999. Molecular dynamics in living cells observed by fluorescence correlation spectroscopy with one- and two-photon excitation. Biophys. J. 77:2251–2265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schwille, P., J. Korlach, and W. W. Webb. 1999. Fluorescence correlation spectroscopy with single-molecule sensitivity on cell and model. Cytometry. 36:176–182. [DOI] [PubMed] [Google Scholar]
- 14.Weiss, M., H. Hashimoto, and T. Nilsson. 2003. Anomalous protein diffusion in living cells as seen by fluorescence correlation spectroscopy. Biophys. J. 84:4043–4052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Weiss, M., M. Elsner, F. Kartberg, and T. Nilsson. 2004. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 87:3518–3524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Saxton, M. J. 2001. Anomalous subdiffusion in fluorescence photobleaching recovery: a Monte Carlo study. Biophys. J. 81:2226–2240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Saxton, M. J. 2007. A biological interpretation of transient anomalous subdiffusion; I: qualitative model. Biophys. J. 92:1178–1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Singer, S. J., and G. L. Nicolson. 1972. Fluid mosaic model of structure of cell membranes. Science. 175:720–731. [DOI] [PubMed] [Google Scholar]
- 19.Feder, T. J., I. Brust-Mascher, J. P. Slattery, B. Baird, and W. W. Webb. 1996. Constrained diffusion or immobile fraction on cell surfaces: a new interpretation. Biophys. J. 70:2767–2773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Montroll, E. W., and G. H. Weiss. 1969. Random walks on lattices. II. J. Math. Phys. 6:167–181. [Google Scholar]
- 21.Nagle, J. F. 1992. Long tail kinetics in biophysics? Biophys. J. 63:366–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bouchaud, J. P., and A. Georges. 1990. Anomalous diffusion in disordered media—statistical mechanisms, models and physical applications. Phys. Rep. 195:127–293. [Google Scholar]
- 23.Metzler, R., and J. Klafter. 2000. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339:1–77. [Google Scholar]
- 24.Risken, H. 1989. The Fokker-Planck Equation, 2nd edition. Springer-Verlag, Berlin.
- 25.Barkai, E., R. Metzler, and J. Klafter. 2000. From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E. 61:132–138. [DOI] [PubMed] [Google Scholar]
- 26.Abramowitz, M., and I. A. Stegun. 1972, Handbook of Mathematical Functions. Dover Publications, New-York.
- 27.Scher, H., and E. W. Montroll. 1975. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B. 12:2455–2477. [Google Scholar]
- 28.Scher, H., and M. Lax. 1973. Stochastic transport in a disordered solid. 1. Theory. Phys. Rev. B. 7:4491–4502. [Google Scholar]
- 29.Klafter, J., and R. Silbey. 1980. Derivation of the continuous-time random-walk equation. Phys. Rev. Let. 44:55–58. [Google Scholar]
- 30.Goychuk, I., and P. Hänggi. 2004. Fractional diffusion modeling of ion channel gating. Phys. Rev. E. 70:051915-1–051915-9. [DOI] [PubMed] [Google Scholar]
- 31.Berkowitz, B., J. Klafter, R. Metzler, and H. Scher. 2002. Physical pictures of transport in heterogeneous media: advection-dispersion, random-walk, and fractional derivative formulations. Water Resour. Res. 38:1191–1202. [Google Scholar]
- 32.Golding, I., and E. C. Cox. 2006. Physical nature of bacterial cytoplasm. Phys. Rev. Let. 96:098102-1–09102-4. [DOI] [PubMed] [Google Scholar]
- 33.Blumen, A., J. Klafter, and G. Zumofen. 1986. Reactions in disordered media modeled by fractions. In Fractals in Physics. L. Pietronero, and E. Tosatti, editors. North Holland, Amsterdam. 399–408.
- 34.Lomholt, M. A., I. M. Zaid, and R. Metzler, 2007. Subdiffusion and weak ergodicity breaking in the presence of a reactive boundary. Phys. Rev. Let. 98:200603-1–200603-4. [DOI] [PubMed] [Google Scholar]
- 35.Scher, H., G. Margolin, R. Metzler, J. Klafter, and B. Berkowitz. 2002. The dynamical foundation of fractal stream chemistry: the origin of extremely long retention times. Geophys. Res. Lett. 29:1061. [Google Scholar]
- 36.Martin, D. S., M. B. Forstner, and J. A. Kas. 2002. Apparent subdiffusion inherent to single particle tracking. Biophys. J. 83:2109–2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Metzler, R., E. Barkai, and J. Klafter. 1999. Deriving fractional Fokker-Planck equations from a generalized master equation. Europhys. Lett. 46:431–436. [Google Scholar]
- 38.Sokolov, I. M., A. V. Chechkin, and J. Klafter. 2004. Fractional diffusion equation for a power-law-truncated Levy process. Physica A. 336:245–251. [Google Scholar]
- 39.Sokolov, I. M. 2002. Solutions of a class of non-Markovian Fokker-Planck equations. Phys. Rev. E Stat. 66:041101. [DOI] [PubMed] [Google Scholar]
- 40.Khan, S., A. M. Reynolds, I. G. Morrison, and R. J. Cherry. 2005. Stochastic modeling of protein motion within cell membranes. Phys. Rev. E. 71:041915-1–041915-7. [DOI] [PubMed] [Google Scholar]
- 41.Barkai, E. 2003. Aging in subdiffusion generated by a deterministic dynamical system. Phys. Rev. Let. 90:104101-1–104101-4. [DOI] [PubMed] [Google Scholar]
- 42.Barkai, E., and Y. C. Cheng. 2003. Aging continuous time random walk. J. Chem. Phys. 118:6167–6178. [Google Scholar]
- 43.Hornung, G., B. Berkowitz, and N. Barkai. 2005. Morphogen gradient formation in a complex environment: an anomalous diffusion model. Phys. Rev. E. 72:041916-1–041916-10. [DOI] [PubMed] [Google Scholar]
- 44.Lutz, E. 2001. Fractional Langevin equation. Phys. Rev. E. 64:051106-1–051106-4. [DOI] [PubMed] [Google Scholar]
- 45.Feder, J. 1998. Fractals. Plenum Press, New York.
- 46.Weron, R. 1996. On the Chambers-Mallows-Stuck method for simulating skewed stable random variables. Stat. Probab. Lett. 28:165–171. [Google Scholar]
- 47.Chambers, J. M., C. L. Mallows, and B. W. Stuck. 1976. Method for simulating stable random-variables. J. Am. Stat. Assoc. 71:340–344. [Google Scholar]