Differences in Internal Dynamics of Actin under Different Structural States Detected by Neutron Scattering

Abstract

F-actin, a helical polymer formed by polymerization of the monomers (G-actin), plays crucial roles in various aspects of cell motility. Flexibility of F-actin has been suggested to be important for such a variety of functions. Understanding the flexibility of F-actin requires characterization of a hierarchy of dynamical properties, from internal dynamics of the actin monomers through domain motions within the monomers and relative motions between the monomers within F-actin to large-scale motions of F-actin as a whole. As a first step toward this ultimate purpose, we carried out elastic incoherent neutron scattering experiments on powders of F-actin and G-actin hydrated with D₂O and characterized the internal dynamics of F-actin and G-actin. Well established techniques and analysis enabled the extraction of mean-square displacements and their temperature dependence in F-actin and in G-actin. An effective force constant analysis with a model consisting of three energy states showed that two dynamical transitions occur at ∼150 K and ∼245 K, the former of which corresponds to the onset of anharmonic motions and the latter of which couples with the transition of hydration water. It is shown that behavior of the mean-square displacements is different between G-actin and F-actin, such that G-actin is “softer” than F-actin. The differences in the internal dynamics are detected for the first time between the different structural states (the monomeric state and the polymerized state). The different behavior observed is ascribed to the differences in dynamical heterogeneity between F-actin and G-actin. Based on structural data, the assignment of the differences observed in the two samples to dynamics of specific loop regions involved in the polymerization of G-actin into F-actin is proposed.

INTRODUCTION

Actin is a highly ubiquitous protein that can be found in all eukaryotic cells. The actin monomers (G-actin) polymerize into a helical polymer (F-actin). This F-actin and the polymerization process itself, controlled through interactions with various actin-binding proteins, play crucial roles in a variety of functions related to cell motility and morphology including cell locomotion, cell division, and transport of intracellular organelles (1,2). F-actin also plays a central role in muscle contraction, as one of the major components in muscle. As various forces or loads can be exerted on F-actin during functioning, determining its mechanical properties is of central importance in understanding its functions. The mechanical properties of F-actin have been studied mainly in terms of the large-scale flexibility such as bending flexibility and torsional flexibility (3–13), and it has been suggested that controlled modulation of such large-scale flexibility is important in the expression of these functions (3,6,10).

F-actin is a two-start right-handed helix, in which each actin monomer is only in contact with its adjacent monomers. The large-scale flexibility of F-actin should therefore be the result of cumulative effects of local intermonomer interactions. The actin monomer itself consists of four subdomains (14), which could undergo different types of motions relative to one another (15,16). It has been shown that conformational changes of the actin monomer affect the flexibility of F-actin (6). Moreover, it is now well accepted that thermal fluctuations of atoms within a protein is crucial for conformational changes of the protein to occur and hence function (17). Thus, the thermal fluctuations of the atoms within the actin monomers (or the internal dynamics of the actin monomers) affect the dynamical properties at the level of the subdomain motions, which result in the conformational changes of the actin monomer. These conformational changes then affect the local intermonomer interactions, hence the large-scale flexibility of F-actin. Ultimate understanding of the flexibility of F-actin therefore requires characterizing the hierarchy of dynamics, which starts from the internal dynamics of the actin monomers on a picosecond timescale and an ångstrom length scale, through the slower relative motions of the subdomains within the monomers and those between the monomers within F-actin, to the large-scale motions of F-actin as a whole on a millisecond timescale and a μm length scale. As a first step toward this ultimate purpose, we have started investigation of the internal dynamics of the monomers within F-actin. Characterization of the internal dynamics of actin should provide a basis for elucidation of the hierarchy of the dynamics on different time and length scales.

Neutron scattering provides unique tools to directly measure the internal dynamics of biological macromolecules (18). The techniques including inelastic, quasi-elastic, and elastic incoherent neutron scattering have been applied to various proteins to investigate properties of their internal dynamics (18,19). In particular, elastic incoherent neutron scattering offers a method to obtain a quantitative measure of the flexibility of the proteins (17). The elastic incoherent neutron scattering experiment provides estimation of the atomic mean-square displacement that is principally of hydrogen atoms, the motions of which reflect those of the side chains and backbone atoms to which they are bound (18). Temperature dependence of this mean-square displacement provides a measure of the flexibility of the protein. We carried out the elastic incoherent neutron scattering experiments of F-actin and G-actin, and compared their dynamical properties. The results showed that behavior of the mean-square displacements is different between F-actin and G-actin. The differences in the dynamical behavior between the different structural states (the monomeric state and the polymerized state) of proteins are detected for the first time here. Analysis of the results obtained indicated that G-actin is “softer” than F-actin, and such differences in the dynamical properties arise from the differences in dynamical heterogeneity between F-actin and G-actin.

MATERIALS AND METHODS

Elastic incoherent neutron scattering

Neutron scattering experiments measure the so-called dynamic structure factor as a function of the momentum transfer and the energy transfer. The dynamic structure factor contains incoherent contributions arising from self-correlations in the atomic positions and coherent contributions arising from self- and cross-correlations of the atomic positions. Because hydrogen atoms are abundant in proteins and have incoherent scattering cross section more than one order of magnitude larger than most other atoms found in biological samples (mainly C, N, O, P, and S) including deuterium, D (= ²H), the contributions from the incoherent scattering of hydrogen nuclei are dominant in the observed scattering. Moreover, a quasi-uniform distribution of hydrogen atoms throughout a protein ensures that this incoherent scattering contains contributions from all the molecular motions of the hydrogen atoms. Because the motions of the hydrogen atoms reflect those of the side chains and backbone atoms to which they are bound (18), the incoherent scattering provides information on the global view of the protein dynamics. Elastic incoherent scattering, in particular, contains information on the distributions of the displacements arising from the motions of individual atoms within an accessible time window, defined by the energy resolution of the spectrometer used in the experiments (18). In the Gaussian approximation (20), the elastic incoherent structure factor, S(Q,0), can be described as:

(1)

where Q (= 4πsinθ/λ, where 2θ is the scattering angle, and λ the wavelength of the incident neutrons) is the amplitude of the momentum transfer, A is a constant, and 〈u²〉 is the mean-square displacement (18). This Gaussian approximation is valid under the condition where Q²〈u²〉 < ∼2 (21). Note that the definition of 〈u²〉 used here indicates the full amplitude of motions.

For the elastic incoherent neutron scattering experiments to measure S(Q,0), powder samples hydrated with D₂O are used. This is because the signals from the hydrogen atoms within the proteins should be maximized with minimal contributions from solvents, because ice formation during the measurements in low temperatures should be prevented, and because estimation of the mean-square displacement should be done with minimum contributions from translational and rotational movements of the proteins (19). The hydrated powder samples of F-actin and G-actin were therefore prepared.

Sample preparation

Actin was purified from acetone powder of chicken muscle according to the standard procedure (22). Polymerization was done by addition of KCl and MgCl₂ to the final concentrations of 60 mM and 2 mM, respectively, into the actin solution containing 2 mM Tris-HCl (pH 8.0), 0.2 mM ATP, and 0.1 mM CaCl₂ (G-buffer). For preparation of G-actin, the fluorescent probe tetramethyl-rhodamine-5-maleimide (TMR; Invitrogen, Carlsbad, CA) was attached to actin to inhibit polymerization (23). One TMR molecule was bound to one actin molecule. This TMR-labeled actin was used as G-actin. Labeling with TMR should not affect the results of the elastic incoherent neutron scattering experiments much because the number of nonexchangeable hydrogen atoms contained in TMR is 23 whereas one actin molecule (including one molecule of tightly bound ADP) contains 2273 nonexchangeable hydrogen atoms.

Purified F-actin and G-actin were suspended in D₂O by dialyzing against the appropriate solutions in D₂O (G-buffer + 60 mM KCl and 2 mM MgCl₂ for F-actin, and G-buffer for G-actin). For the preparation of the F-actin powder, the F-actin solution was centrifuged at 60,000 × g for 5 h. The concentration of F-actin in the pellet obtained was ∼60 mg/ml. This pellet was dried in a room atmosphere avoiding complete removal of hydration water, which could destroy structural integrity of F-actin; ∼200 mg of the dried pellet was then transferred into a square well (30 mm × 40 mm × 3 mm) of a rectangular aluminum sample holder, and equilibrated with D₂O atmosphere in a desiccator. After reaching the equilibrium, the holder was sealed with an aluminum cap fit into the well and indium wires so that the path length was 0.2 mm. The weight of the pellet within the sample holder was measured just after it was transferred to the sample holders and after the sample holder was sealed. The hydration ratio of the sample was calculated from the weights of the powders thus measured, using, as a reference, the weights of (a part of) the dried pellet that was not transferred to the sample holder measured before and after complete removal of hydration water by extensive incubation in vacuum. The hydration ratio of the F-actin powder was found to be 0.38 (g D₂O/g protein).

For the preparation of the G-actin powder, the G-actin solution was concentrated to be 38 mg/ml. The hydrated powder of G-actin was then prepared in a similar manner to the F-actin powder. The hydration ratio of the G-actin powder was found to be 0.36. The hydration ratios of the F-actin powder and the G-actin powder are thus very close to 0.4, which corresponds to the condition where the actin molecule is surrounded by one layer of hydration water (24). The powders prepared were checked by x-ray diffraction measurements, done at the small-angle scattering station BL-45XU-SAXS (25) at SPring-8, Harima, Japan. The pattern of the F-actin powders (data not shown) showed a peak at the Bragg spacing of ∼59 Å, which correspond to the position of the strong layer-line intensity in the fiber diffraction pattern of F-actin, indicating that the structural integrity of F-actin was maintained in this state as found in the dried “thin films” of F-actin (26). On the other hand, the patterns of G-actin powders did not show such peaks, indicating that polymerization did not occur on these samples.

In the powder samples thus prepared, the salts were highly concentrated. The concentration of F-actin in the pellet just before drying was ∼60 mg/ml, which corresponds to 1.4 mM on the assumption that the molecular weight of the actin molecule is 42,000. Because the molar ratios should be retained, the F-actin powder contains 1.4 Tris⁺, 0.07 Ca²⁺, 1.4 Mg²⁺, 43 K⁺, and ∼47 Cl⁻ per one actin molecule, assuming full dissociation into ions. The F-actin powder also contains ∼800 D₂O per one actin molecule (calculated from the hydration ratio of 0.38). On the other hand, because the concentration of G-actin in the solution just before starting drying corresponds to ∼0.9 mM, the G-actin powder contains 2.3 Tris⁺, 0.1 Ca²⁺, and 2.5 Cl⁻ per one actin molecule. It also contains ∼760 D₂O per one actin molecule. G-actin contains one high affinity cation-binding site and 5–10 low affinity cation-binding sites, and occupation of these sites induces the polymerization (27,28). The number of cations in the G-actin powder is therefore not enough to occupy these sites, thereby inducing polymerization.

Elastic incoherent neutron scattering experiments

Neutron scattering experiments on these samples were carried out on the backscattering spectrometer IN16 at the Institut Laue-Langevin, Grenoble, France, with an energy resolution of 0.9 μeV, which corresponds to the accessible time window of ∼730 ps, i.e., the accessible motions faster than 730 ps. An accessible Q-range of the instrumental setup used was between 0.5 and 1.9 Å⁻¹. This range corresponds to the Bragg spacing between 12.5 Å and 3.3 Å, indicating that the peak at 59 Å, which could be observed in the F-actin sample, is outside of the measured Q-range. Thus, the contribution of the coherent scattering that produces diffraction patterns is negligible compared to the incoherent scattering cross section of hydrogen atom. The data were collected during a linear increase in temperature from 20 K to 300 K. The heating rate was 0.4 K/min between 20 K and 150 K, and the rate was then decreased to 0.2 K/min between 150 K and 300 K, to increase the statistics in the high temperature range. It thus took ∼18 h to collect one set of the data. The data were corrected, at each Q-value, for scattering arising from the sample holder, and normalized by the intensity at the lowest temperature, T_std (the average intensity between 20 K and 50 K was used as a standard here). Logarithm of this normalized intensity was plotted against Q², and fit by a straight line, from the slope of which 〈u²〉 could be estimated (see Fig. 1 and its legend for the details of the fitting ranges). Because the intensities were normalized by that at T_std, the extracted value of 〈u²〉 at each temperature, T, corresponds to 〈u²(T)〉 − 〈u²(T_std)〉.

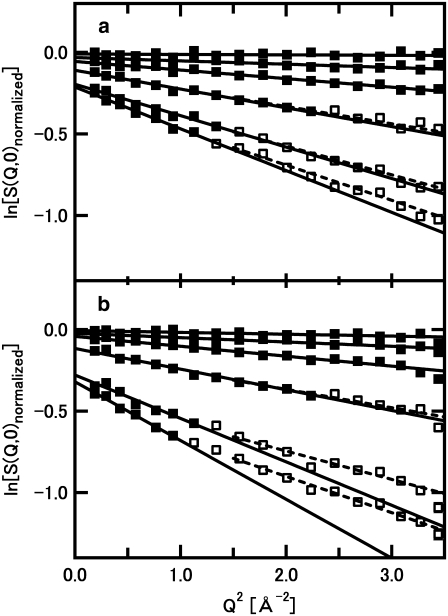
FIGURE 1.

Examples of the logarithm of the normalized intensity, S(Q,0), as a function of Q², of (a) F-actin, and (b) G-actin. (a) Variations of the intensity at 100 K, 155 K, 202 K, 249 K, 278 K, and 296 K, from top to bottom, respectively, are shown. (b) Variations of the intensity at 101 K, 147 K, 201 K, 249 K, 277 K, and 296 K, from top to bottom, respectively, are shown. Solid and open squares denote the data points, and solid lines denote the results of the linear fits. The data points used in the linear fits are shown by the solid squares. These points are within the region where the criterion for the Gaussian approximation (〈u²〉Q² < ∼2) strictly holds. 〈u²〉 of F-actin at 298 K, for example, was estimated to be 1.54 Ų, from the linear fit to the region of Q² smaller than 1.30 Å⁻², which holds the criterion for the Gaussian approximation because 1.54 × 1.30 = 2.00. The 〈u²〉 values and the maximum Q² values of the fitting regions of other data shown here are as follows: 1.16 Ų and 1.73 Å⁻² for F-actin at 278 K, 0.69 Ų and 2.89 Å⁻² for F-actin at 249 K, 2.16 Ų and 0.92 Å⁻² for G-actin at 296 K, 1.60 Ų and 1.25 Å⁻² for G-actin at 277 K, and 0.76 Ų and 2.63 Å⁻² for F-actin at 249 K. The whole measured Q² range was used in the fits to the data of F-actin and G-actin below 202 K, because the largest value of 〈u²〉 in these data was 0.36 Ų (G-actin at 202 K), thereby the maximum Q² values of the fitting regions being beyond the measured range. The results of the linear fits to the different region of Q², the data points between 1.5 Å⁻² and 3.73 Å⁻², are also shown as dashed lines. The 〈u²〉 values obtained from the fits to this region of higher Q² correspond to the motions with smaller amplitudes (see Discussion).

Analysis of the non-Gaussian behavior

In the plots of the normalized intensity against Q², deviations from the straight line may be observed in the high Q² region. One way to analyze such behavior is to use an equation in which deviations from the Gaussian behavior are incorporated. Such an equation has been developed without restricting the interpretation to a specific model (29) as:

(2)

This equation holds for the low Q-range as long as the deviation from the Gaussian behavior is small. To estimate a degree of the non-Gaussian behavior, this equation was applied to fit the variation of the normalized intensity over the whole measured Q-range. The parameter b in Eq. 2 represents a degree of deviations from the Gaussian, hence a measure of the non-Gaussian behavior.

RESULTS

Estimation of the mean-square displacements

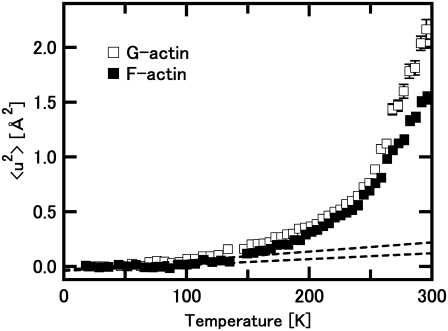
Fig. 1 shows examples of the natural logarithms of the normalized intensity, S(Q,0), plotted against Q². It also shows the results of the linear fits to the data within regions where the criterion for the Gaussian approximation strictly holds (solid lines). Up to ∼230 K, the whole measured Q-range is within this region. As the temperature increases, however, this region reduces to lower Q, corresponding to an increase in the values of the mean-square displacements 〈u²〉 (the data points used in the fits are represented by solid squares in Fig. 1, see the legend for the details). Fig. 2 shows the variations of 〈u²〉 as a function of temperature. Differences in behavior of 〈u²〉 between G-actin and F-actin are clearly observed. The values of 〈u²〉 of G-actin are consistently larger than those of F-actin, and the difference in the values is particularly significant above 250 K. This implies that G-actin is more flexible than F-actin, particularly above 250 K.

FIGURE 2.

Mean-square displacements, 〈u²〉, of F-actin and G-actin as a function of temperature. Solid squares denote the data of F-actin, and open squares denote those of G-actin. Dashed lines represent the behavior of the harmonic motions in the low temperature region. The lines were drawn using the force constant values of the state 1, which corresponds to the energy state at low temperature, in the model consisting of three energy states (see “Analysis of the temperature dependence of the mean-square displacements” in Results). Upper and lower lines represent the behavior of G-actin and that of F-actin, respectively. They are well fit to the data below 100 K, and the deviation from these lines above 150 K is evident. The change of the heating rate (see Materials and Methods for details) causes the loss of the few data points around 145 K. The transition around 150 K is, however, confirmed by the analysis in terms of force constant (see Fig. 4).

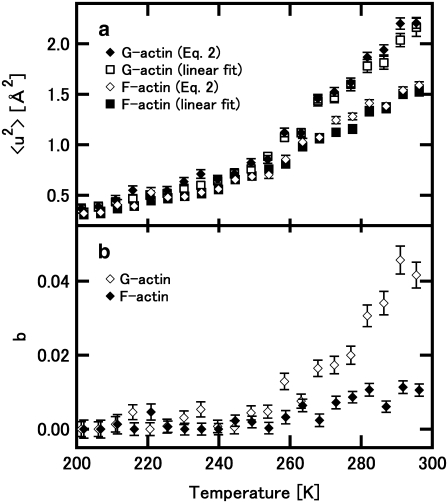
As shown in Fig. 1, deviations from the linear fits are observed in high Q-regions. These deviations increase as the temperature increases above 250 K. This deviation from the Gaussian approximation (the non-Gaussian behavior) is more significant in G-actin than in F-actin. To obtain a measure of such non-Gaussian behavior, fitting with Eq. 2 was carried out on the S(Q,0) curves above 200 K, which is well below the temperature at which the deviation from the linear fit can be observed. The parameter b could be regarded as a qualitative measure of the non-Gaussian behavior. Fig. 3, a and b, show the variations of 〈u²〉 and b, respectively, estimated using Eq. 2. Fig. 3 a also displays the values estimated from the linear fits shown in Fig. 2. The values from Eq. 2 and those from the linear fits are in good agreement, assuring validity of both the linear fits and Eq. 2 each other. Fig. 3 b clearly shows that the non-Gaussian behavior is introduced above 240 K and the degree of this behavior is more significant in G-actin than in F-actin.

FIGURE 3.

Variations of the parameter values in Eq. 2 as a function of temperature. (a) The variations of 〈u²〉 estimated using Eq. 2. Open and solid diamonds denote the values of 〈u²〉 estimated from Eq. 2 of F-actin and those of G-actin, respectively. Solid and open squares denote the values estimated from the linear fits (the data shown in Fig. 2) of F-actin and G-actin, respectively. (b) The values of b estimated using Eq. 2. Open and solid diamonds denote the values of G-actin and F-actin, respectively.

Analysis of the temperature dependence of the mean-square displacements

The temperature dependence of 〈u²〉 of the hydrated powders of the proteins often shows a dynamical transition where a linear increase in 〈u²〉 in low temperatures deviates upward at a point between 150 K and 250 K (21,30–38). This transition has been interpreted as a transition from the harmonic vibrational motions at low temperature to the onset of anharmonic diffusive motions (17). Here, an inspection of Fig. 2 shows that a deviation from a straight line at low temperature appears around 150 K, and a further bent appears around 250 K, suggesting that there are two dynamical transitions.

To characterize the temperature dependence of 〈u²〉, an effective force constant has been introduced (17). This has been defined as a slope of the increase in 〈u²〉 as a function of temperature, and is inversely related to the flexibility of the protein. Based on this concept of the effective force constant and a model describing two energy states as two concentric potentials with different depths and widths, Bicout and Zaccai developed a formalism that could describe the behavior of 〈u²〉 showing a dynamical transition (39). To analyze the behavior of 〈u²〉 showing two transitions, we have developed a formulation of a model consisting of three energy states, which is natural extension of the formalism by Bicout and Zaccai. Assuming that three energy states are termed the states 1, 2, and 3, and that fractions of the states 2 and 3 at the temperature T are φ₂(T) and φ₃(T), respectively, the free energy difference between the states 1 and 2, ΔG₁₂ (= ΔH₁₂ − TΔS₁₂), and that between the states 2 and 3, ΔG₂₃, (= ΔH₂₃ − TΔS₂₃) are described respectively as:

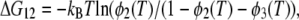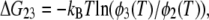where k_B is the Boltzmann constant, ΔH₁₂, ΔH₂₃, ΔS₁₂, ΔS₂₃, are the enthalpy difference between the states 1 and 2, that between the states 2 and 3, the entropy difference between the states 1 and 2, and that between the states 2 and 3, respectively. Rearrangement of these two equations gives

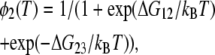(3a)

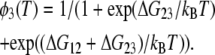(3b)

On the other hand, the mean-square displacement could be described as

where and are the mean-square displacements of the states 1, 2, and 3, respectively. Quasi-harmonic approximation of the force constant yields the mean-square displacement as

(4)

where k₁, k₂, and k₃ are the force constants of the states 1, 2, and 3, respectively. A factor of ½ is required here because of the definition of 〈u²〉 (see Materials and Methods). A fit of this equation to the temperature dependence of 〈u²〉 yields a set of the parameters, ΔH₁₂, ΔS₁₂, ΔH₂₃, ΔS₂₃, k₁, k₂, and k₃.

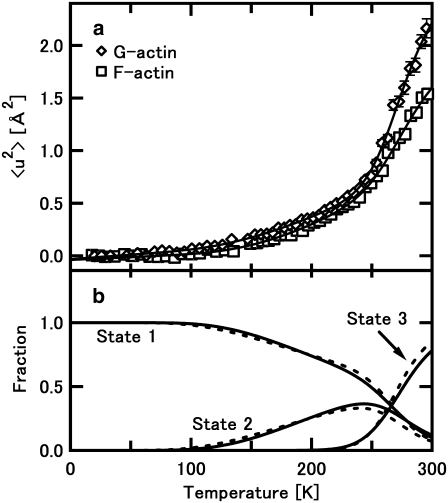
Fig. 4 a shows the results of the fit, and the values of the parameters obtained are listed in Table 1. The parameters describing the two transitions were estimated. The transition temperature from the state 1 to the state 2, and that from the state 2 to the state 3, were 153 K and 244 K for F-actin, and 144 K and 245 K for G-actin, respectively. An operative definition used by Bicout and Zaccai was used here, in which at the transition temperature, the fractions of the state 2 or the state 3 reach 10%. However, as shown in Fig. 4 b, the changes in the fraction of each state indicate that the transition to the state 2 starts at as low as 100 K, and the temperature range during which the transition from the state 1 to the state 2 occurs is very broad, suggesting that this transition is rather continuous. The transition from the state 2 to the state 3 also seems to be broad. Similar values in F-actin and G-actin were obtained for the enthalpy and entropy differences related to the free energy difference between these states. Main differences between F-actin and G-actin therefore seem to be in the values of the force constants: the force constants of G-actin are consistently lower than those of F-actin. This implies again that G-actin is more flexible than F-actin.

FIGURE 4.

Analysis of the temperature dependence of the mean-square displacement with Eqs. 3a, 3b, and 4. (a) The best fits to the data of F-actin and G-actin. Open squares and open diamonds denote the data of F-actin and G-actin, respectively, shown in Fig. 2. Solid lines denote the best fits to the data. (b) Fractions of the states 1, 2, and 3 as a function of temperature, calculated with Eqs. 3a and 3b, where the fraction of the state 1 is calculated as 1− φ₂(T) − φ₃(T). Solid lines denote the fractions of F-actin and dashed lines denote those of G-actin.

TABLE 1.

Summary of the parameters obtained from the best fits

Parameters	F-actin	G-actin
ΔH12 (kcal/mol)	1.47	1.14
ΔS12 (R)	2.67	1.81
ΔG12 (kcal/mol)	0.66	0.63
T12 (K)	153	144
ΔH23 (kcal/mol)	8.20	9.69
ΔS23 (R)	15.6	18.6
ΔG23 (kcal/mol)	0.62	0.56
T23 (K)	244	245
k1 (N/m)	5.18	3.30
k2 (N/m)	0.55	0.51
k3 (N/m)	0.45	0.33

ΔG (= ΔH − TΔS) was calculated as the free energy difference at the transition temperature. The transition temperatures were defined operationally as the temperatures at which the fraction of the state 2 (for the case of T₁₂) or the state 3 (for the case of T₂₃) is 10%.

DISCUSSION

We have carried out elastic incoherent neutron scattering experiments on the powder samples of F-actin and G-actin hydrated with D₂O, and characterized the internal dynamics of F-actin and G-actin on a picosecond timescale. The powder samples were also used in a study by solid-state NMR spectroscopy (40), in which motions of probes attached to the actin molecule were characterized, but the timescale of motions measured was of the order of nano- to microseconds. Although use of the powder samples is customary in the elastic incoherent neutron scattering experiments, the environment in which the proteins are placed might be different from the solution environment. However, the samples were prepared carefully so that the actin molecules kept having one layer of hydration (heavy) water, which is sufficient for the proteins to function (41), and that the hydration ratios were brought as close as possible in G-actin and F-actin. Considering this care in the sample preparation and structural integrity of F-actin that was retained in the powders, the differences between F-actin and G-actin observed were attributable to the differences in the structural states of the actin molecules.

There is, however, one difference in the sample environment between F-actin and G-actin: the composition of salts. At very high concentrations of salts, formation of the hydration structure around the salt ions could reduce the mobility of water molecules, thereby suppressing the dynamics of the protein (36). The F-actin powder contains rather high concentrations of K⁺ and Cl⁻ (see Materials and Methods). However, K⁺ is a chaotropic that breaks water structure (42), and Cl⁻ has little effects on the water structure (43). Thus, in the presence of K⁺ and Cl⁻, the mobility of water should be rather enhanced than suppressed. The translational diffusion coefficient of water in 3 M KCl has been indeed reported to be somewhat larger than that in pure water (44,45). It thus seems unlikely that the dynamics of F-actin was suppressed as a consequence of the reduced mobility of water by the ions. Direct binding of K⁺ to the actin molecule might have some effects. However, considering the fact that F-actin is always accompanied by the presence of high concentrations of cations, the state that cations are bound should be regarded as one of intrinsic properties of F-actin.

As shown in Fig. 1, the deviations from the linear fits in the curves of ln(S(Q,0)) increase with increasing temperature. Such non-Gaussian behavior arises either from the non-Gaussian behavior of single atoms, or from the dynamical heterogeneity, i.e., a distribution of the mean-square displacements. The non-Gaussian behavior has been analyzed by the equation including a higher order term in the expansion of an exponential. The parameter b in Eq. 2, representing a degree of deviations from the Gaussian, is a (qualitative) measure of the non-Gaussian behavior. The results of the fit with Eq. 2 showed clearly that the non-Gaussian behavior becomes significant above 240 K and the degree of this behavior is more significant in G-actin than in F-actin. Although it is not possible to unambiguously determine if such non-Gaussian behavior arises from the dynamics of single atoms or from the dynamical heterogeneity, several arguments favor the assumption of the dynamical heterogeneity. As shown by normal mode analysis (15,46), amino acid residues in different regions in a protein can fluctuate differently. NMR spectroscopy also detected heterogeneous motions of the amino acid residues within proteins (47–50). Existence of such dynamical heterogeneity has been shown in the neutron scattering study of bacteriorhodopsin (32). Furthermore, a recent molecular dynamics study showed that the dynamical heterogeneity is a major cause of the non-Gaussian behavior of globular proteins (51).

To gain insight into the dynamical heterogeneity of G-actin and F-actin, the linear fits to S(Q,0) in the high Q-region have been done. The values of 〈u²〉 estimated from different Q-regions correspond to the motions with different amplitudes (21,31,36). Because the deviations from the linear fits to the region where the Gaussian approximation holds occur at about Q² = 1.5 Å⁻², the region between 1.5 Å⁻² and 3.73 Å⁻² was used for the fits (dashed lines in Fig. 1). In analogy with small-angle scattering (52), estimation of 〈u²〉 from the region where the Gaussian approximation holds provides the average values of those arising from the motions with different amplitudes, whereas the values of 〈u²〉 from this high Q-region arise from population of atoms showing the motions with smaller amplitudes. Fractions of this population can be estimated from the ratio between the extrapolated value to Q² = 0 of the linear fit to the high Q-region and the extrapolated value from the fit to the region where the Gaussian approximation holds. They were found to be, for example, 95% and 87% for F-actin and G-actin at 296 K, respectively. High fractions of the atoms thus belong to the population showing the motions with the smaller amplitudes. Effects of the motions with large amplitudes on the S(Q,0) curves in the high Q-region are therefore considered to be small. Moreover, the values of Q²〈u²〉 obtained in the fits to the high Q-region stay near 2.0 (the values range from 2.0 to 4.9 even under the worst condition where 〈u²〉 of G-actin has the largest value at 296 K), which is reasonable for the Gaussian approximation (31). The values of 〈u²〉 obtained from the fits to the high Q-region should therefore be reasonable estimations.

Fig. 5 a shows the variations of 〈u²〉 estimated from the high Q-region. Here the differences are observed in the temperature below ∼240 K. On the other hand, 〈u²〉 above 240 K shows similar behavior in G-actin and F-actin. Fig. 5, b and c, compare the variations of 〈u²〉 from the high Q-region and those from the region where the Gaussian approximation holds (the low Q-region), of F-actin and of G-actin, respectively. These figures show that 〈u²〉 from the different Q-regions behave similarly at low temperature and differences become significant above 240 K. The similar behavior at low temperatures is natural because the whole measured Q-range is within the range where the Gaussian approximation is valid. However, the confrontation between the three figures shows that, above 240 K, 〈u²〉 from the high Q-region behaves similarly in F-actin and G-actin whereas 〈u²〉 from the low Q-region behaves differently in F-actin and G-actin. This implies that the actin molecule above 240 K has dynamical heterogeneity such that there are a “core” region and a “flexible” region: the core region shows similar dynamical behavior regardless of the structural states (F- or G-actin), whereas the flexible region undergoes larger amplitudes motions than the core region and shows significantly different dynamical behavior under the different structural states.

FIGURE 5.

Comparison of the mean-square displacements, 〈u²〉, estimated from the different Q-regions. (a) Variations of 〈u²〉 estimated from the linear fits to the data in the region where Q² is between 1.5 Å⁻² and 3.73 Å⁻² (the high Q-region). Solid squares denote the data of F-actin, and open squares denote those of G-actin. (b) Comparison of 〈u²〉 of F-actin estimated from the different regions. Solid squares denote the values estimated from the high Q-region. Open diamonds denote the value estimated from the region where the Gaussian approximation is valid (the low Q-region, these data were shown in Fig. 2). (c) Comparison of 〈u²〉 of G-actin estimated from the different regions. Open squares denote the values estimated from the high Q-region, and solid diamonds denote those from the low Q-region.

Crystal structures of actin show that the actin molecule has regions with high values of the isotropic temperature factor, B, which is a measure of dynamic and static disorder in crystallography, and related to the mean-square displacement by the equation 〈u²〉 = 2 × (B/8π²) (a factor of 2 is required because the definition of 〈u²〉 here is the full amplitude of the fluctuation). Inspection of the isotropic temperature factors of C_α atoms of the TMR-labeled actin (Protein Data Back code, 1J6Z; the G-actin sample we used), for example, shows that the residues having the isotropic temperature factor >1 SD larger than the average value include the residues 4–6, 39, 41, 44–52, 167, 194–197, 229–235, 237, 250, 288, 322–324, 350–351, and 362–372 (residues 4–6, the residues 39, 41, and 44–52, the residue 167, the residues 194–197, the residues 229–235 and 237, the residue 250, the residue 288, the residues 322–324, the residues 350 and 351, and the residues 362–372 are termed the regions A, B, C, D, E, F, G, H, I, and J, respectively, in Fig. 6). The region A is located in the N-terminal region that is labile (53) and related to myosin binding (14). The region B is located in and near the DNase I binding loop (residues 41–50) that is involved with intermonomer interaction in F-actin (54,55) in the subdomain 2. The regions C, D, G, and H are within the interface region between the monomers in F-actin (the residues 167, 288, and 322–324 in the subdomain 3 and the residues 194–197 in the subdomain 4 (54,55)). The regions E and F are within the region exposed to solvent in F-actin (residues 229–237) in the subdomain 4 (54,55). The regions I and J are located in the C-terminal region that is involved with interactions with many actin-binding proteins including gelsolin and profilin (56,57). About a half of the residues with the high isotropic temperature factors are thus related to the formation of F-actin. Thus, if it is assumed that these regions with the high isotropic temperature factors correspond to the flexible regions above, the differences in the dynamical properties of F-actin and G-actin can be ascribed to the dynamical behavior of these regions. The regions related to the formation of F-actin are likely to be less flexible in F-actin, thereby reducing the fraction of the flexible regions and/or differences in the dynamical properties between the flexible regions and the core regions. This results in the reduction of the dynamical heterogeneity in F-actin compared to G-actin.

FIGURE 6.

Regions with high 〈u²〉 values estimated from the isotropic temperature factors obtained by crystal structure analysis. (a) Variations of the estimated 〈u²〉 values as a function of the residue numbers. The 〈u²〉 value was calculated from the isotropic temperature factor of C_α atom in each residue, obtained from the PDB data (1J6Z). The black solid line denotes the average of the 〈u²〉 values of all residues, and the red solid line denotes the value 1 SD larger than the average. The regions having 〈u²〉 above this level are termed the regions A, B, C, D, E, F, G, H, I, and J (see text). (b) Ribbon diagram of the actin monomer drawn from 1J6Z. The diagram was drawn with SwissPdB Viewer (68). The residues with high 〈u²〉 values are highlighted by red or green. The residues with green are those related to intermonomer interactions in F-actin.

The temperature dependence of the mean-square displacements showed that two transitions occurred at ∼150 K and at ∼245 K. Occurrence of two transitions was also found in the study of bacteriorhodopsin (32), in which the transitions at 150 K and at 260 K were assigned as a dynamical transition and solvent effects, respectively. Similar behavior was also observed in lysozyme (38). The effective force constant analysis with a model with three energy states provided a set of parameters related to these transitions. The parameters related to the transition at ∼150 K, the enthalpy difference and the entropy difference between the state 1 and the state 2 shown in Table 1, are in concert with those found in other proteins (the hydrated powder of myoglobin; ΔH = 1.59 kcal/mol, ΔS = 1.80 R (39): the dry sample of bacteriorhodopsin; ΔH = 1.08 kcal/mol, ΔS = 1.30 R (39): the hydrated powder of lysozyme; ΔH = 0.72 kcal/mol, ΔS = 1.0 R (38)), describing the transition corresponding to the onset of anharmonic motions. Recent studies showed that the onset of contributions from anharmonic motions could be as low as 100 K (38,58,59), and these anharmonic motions have been interpreted as arising primarily from reorientational motions of methyl groups (38,50,59). This interpretation could be applied here as well: the transition observed might be apparent and due to the methyl group rotations entering the accessible time window at the transition temperature (29,60).

The enthalpy and the entropy differences related to the transition at 245 K have significantly higher values than those related to the transition at 150 K. Considering the enthalpy of hydrogen bonding to be 2–10 kcal/mol, the transition here seems to involve breaking of the hydrogen bonds. The large values of the entropy difference imply that this transition induces large diffusive motions that arise likely from local translational motions of the loops, in addition to vibrational motions with larger amplitudes, because the larger amplitudes of the local motions correspond to the larger numbers of the possible conformations. The values observed here are similar to those found in the hydrated samples of bacteriorhodopsin and ascribed to the solvent-exposed loops in bacteriorhodopsin (ΔH = 9.53 kcal/mol, ΔS = 14 R (39)). The transition temperature observed here is close to the temperature at which the dynamical transition of protein hydration water occurs (220–230 K) (61,62), above which the hydration water becomes more fluid (61). The dynamics of the protein is strongly coupled (even slaved) to those of hydration water or solvent (63–67). The transition of F- and G-actin observed here is thus interpreted as the onset of the diffusive motions including the local translational motions of the surface loops, corresponding to the onset of the large amplitude motions of the hydration water, which break hydrogen bond networks formed between the surface loops and the water molecules. The differences in the behavior of F-actin and G-actin are again attributable to the differences in the flexible regions. Because of the restricted motions of the region related to the formation of F-actin, the fraction of the surface loops showing large-amplitude diffusive motions is smaller in F-actin than in G-actin. This implies conversely that the surface loops that are involved with the polymerization are very flexible in G-actin. Thus, the flexibility of the loops itself might be important in the process of polymerization as it may involve induced fit of the interface regions.