Coordination of Kinesin Motors Pulling on Fluid Membranes

Abstract

Intracellular transport relies on the action of motor proteins, which work collectively to either carry small vesicles or pull membranes tubes along cytoskeletal filaments. Although the individual properties of kinesin-1 motors have been extensively studied, little is known on how several motors coordinate their action and spatially organize on the microtubule when pulling on fluid membranes. Here we address these questions by studying, both experimentally and numerically, the growth of membrane tubes pulled by molecular motors. Our in vitro setup allows us to simultaneously control the parameters monitoring tube growth and measure its characteristics. We perform numerical simulations of membrane tube growth, using the experimentally measured values of all parameters, and analyze the growth properties of the tube considering various motor cooperation schemes. The comparison of the numerical results and the experimental data shows that motors use simultaneously several protofilaments of a microtubule to pull a single tube, as motors moving along a single protofilament cannot generate the forces required for tube extraction. In our experimental conditions, we estimate the average number of motors pulling the tube to be approximately nine, distributed over three contiguous protofilaments. Our results also indicate that the motors pulling the tube do not step synchronously.

INTRODUCTION

Intracellular transport in living cells occurs either via the motion of small vesicles or by the formation of membrane tube networks spanning the cell (1–4). In both cases, motor proteins of the kinesin family are involved in the transport mechanism: they act collectively either to carry the vesicles or to pull membrane tubes. Several recent works are devoted to the coordination mechanism between motor proteins which collectively carry vesicles (5–7). They show that, to produce forces larger than the maximum force of a single motor, the motors are able to cluster. However, the mechanism by which motors coordinate their action to generate large forces is largely unknown. In particular, it remains unclear whether the observed steps in the motion of vesicles (8–10) result from the synchronized action of several motors or from individual motor stepping (11). Little is also known on the origin of the large forces generated by motors pulling on fluid membranes.

The properties of transported cargoes are essential to understand the collective behavior of motor proteins. Motors rigidly or elastically attached to a cargo can easily combine their action and develop forces substantially larger than that developed by a single motor (12,13). Examples are muscle contraction, chromosome motion, flagellar beating (14), and even the motion of microtubules in the in vitro gliding assays (15). In contrast to rigid and elastic cargoes, the fluid membrane of a transport vesicle or of a membrane tube does not resist tangential forces (16–18). The motors only pull the cargo at its leading edge, where they can apply forces normal to the membrane. We have previously shown that motors dynamically accumulate at the tip of growing membrane tubes as a consequence of the membrane in-plane fluidity (18). In these conditions, where motors contact each other frequently, the mutual motor interactions, the motor coordination, and their spatial distribution on the microtubule contribute to their collective behavior (19).

To better understand the collective force generation and coordination mechanism of kinesin motors pulling on fluid membranes, we present in this article a comparison between numerical simulations and experiments of the growth of membrane tubes pulled collectively by motor proteins. We first present briefly the experimental results obtained in experiments very similar to those of Leduc et al. (18). In particular, using fluorescence microscopy, we monitor the membrane tube formation along microtubules from a giant unilamellar vesicle partially coated with kinesin-1 motors (Fig. 1). The growth properties of individual membrane tubes are then compared quantitatively to the numerical results. As all parameters are known experimentally, this comparison allows for a determination of the kinesin organization when pulling a membrane tube. Our results suggest that the motors pulling the tube simultaneously use three protofilaments and that there is no synchronization in their motion. Finally, in view of our results, we propose a different picture of the function of motor processivity.

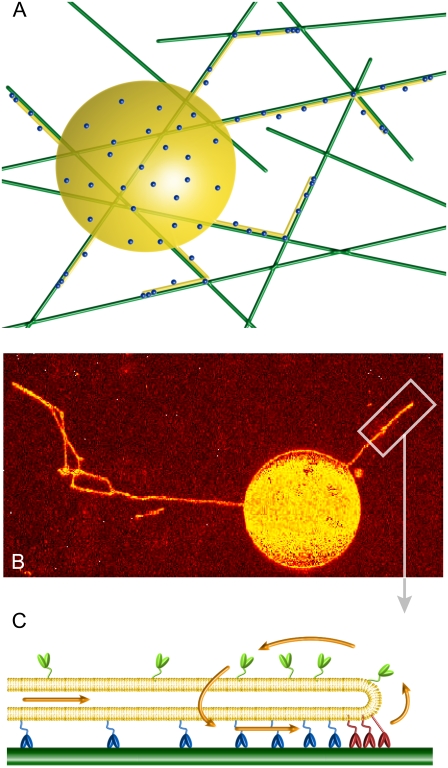
FIGURE 1.

System geometry. (A) Sketch of the experimental setup. A giant unilamellar vesicle (yellow), partially covered with kinesin-1 motors (dots), is placed over a network of microtubules (green) in presence of ATP. The motors bound to microtubules apply forces on the membrane and pull membrane tubes (yellow). (B) Confocal image of membrane tubes pulled by kinesin motors from a giant unilamellar vesicle. The image is a two-dimensional projection of the three-dimensional confocal reconstruction. The membrane was uniformly labeled with fluorescent lipids (TRITC-DHPE). The image is shown in false color to enhance contrast. Bar, 5 μm. (C) Sketch of the treadmilling mechanism for membrane tube extraction (in the membrane tube reference frame), where the motor fluxes are represented by arrows. The bound motors at the tip (red) move against the tube force F with velocity V and detach from the microtubule (dark green) at a rate k_u. The bound motors along the tube (blue) do not support any substantial force, move with velocity V₀ (motor velocity under vanishing load), and detach from the microtubule at a rate The motors not bound to the microtubule (unbound motors; light green) attach to the microtubule at a rate k_b. These unbound motors diffuse along the membrane tube (yellow) and are dragged by the membrane tube itself as it grows.

MATERIALS AND METHODS

All the reagents were purchased from Sigma (St. Louis, MO), except when specifically mentioned.

Giant unilamellar vesicles were prepared by electroformation as in Mathivet et al. (20) with the following compositions: 98.9% Egg phosphatidylcholine (EggPC), 0.1% 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-n-(cap-biotinyl) (DOPE-Cap-Biot), 1% n-6-tetramethylrhodamin-ethiocarbamoyl-1, 2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (TRITC-DHPE); or 98.99% EggPC, 0.01% DOPE-Cap-Biot, 1% TRITC-DHPE. The lipids EggPC and DOPE-Cap-Biot were purchased from Avanti Polar Lipids (Alabaster, AL) and TRITC-DHPE from Molecular Probes (Eugene, OR).

Kinesin KinBio401 motors were purified as in Surrey et al. (21). The plasmid was a kind gift of F. Nedelec (EMBL, Heidelberg, Germany).

Microtubules were obtained by polymerization of tubulin purified from pig brains and stabilized by taxol. See exact protocol in Leduc et al. (18).

Tubes were pulled from vesicles using the same protocol as in Leduc et al. (18).

Imaging

The tubes were observed either by fluorescence confocal microscopy (Axiovert 200; Carl Zeiss, Oberkochen, Germany) or mainly by fluorescence videomicroscopy (Axiovert 135; Carl Zeiss) thanks to the incorporation of 1 mol % fluorescent lipid TRITC-DHPE in the membrane. For the acquisition by videomicroscopy, we used a standard charge-coupled device camera (monochrome PULNiX 1/2” with an acquisition rate of 25 images/s; PULNiX, Sunnyvale, CA). Movies were recorded on video tapes and converted to .avi format with the ScionImage software (Scion, Frederick, MD).

Movies were analyzed using a tracking software kindly given by K. Zeldovitch (the same as in (18)) and average velocities of tube growth were obtained by linear fitting of the curve extension versus time.

Experiments on tube extraction

The experimental setup is similar to the one described in details in Leduc et al. (18). Giant unilamellar vesicles were partially biotinylated and coated with biotinylated truncated kinesin-1 motors through a streptavidin link (see Materials and Methods). The concentration ρ_∞ of motors on the surface of the vesicle was imposed by fixing the concentration of biotinylated lipids in the membrane. The protocol used ensured that only one motor was associated to each biotinylated lipid (18), allowing for a quantitative control of the motor density on the vesicle surface.

The kinesin-coated vesicles were put into contact with a network of taxol-stabilized microtubules fixed on a glass surface, in presence of 1 mM ATP (Fig. 1 A). Kinesins attached to microtubules, walked toward their plus ends, deformed the vesicle membrane and, if the motor density was large enough (see below), formed membrane tubes (Fig. 1, A and B).

The motors pulling a membrane tube sustain a force 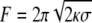(22), corresponding to the force required to extract a membrane tube from a vesicle of tension σ and bending modulus κ. To control the extraction force, F, we fixed the vesicle tension, σ, by imposing the osmotic pressure difference between the inside and the outside of the vesicle; in our experiments we estimated σ ≃ 2 10⁻⁴ mN/m, which leads to an extraction force of F ≃ 27.5 ± 2.5 pN (18). Note that this force is much larger than the stall force of a single kinesin-1 motor (6 pN), ensuring that motors must act collectively to pull the membrane tube. The growth of membrane tubes was then monitored over time (see Materials and Methods).

In Fig. 1 we sketch the experimental system and the mechanism of membrane tube formation (18). The motors are permanently attached to the membrane tube, but can be either attached to the microtubule (bound motors) or detached from it (unbound motors). We showed in Leduc et al. (18) that bound motors dynamically accumulate at the tip of the membrane tube. Indeed, bound motors far from the tip of the membrane tube move at their maximal velocity, V₀, because they do not sustain any substantial force, whereas the motors pulling the tube at the tip move more slowly because they sustain the tube force. At the same time, the bound motors at the tip detach faster than those along the tube, resulting in a larger density of unbound motors close to the tip. These unbound motors diffuse away from the tip, following the direction of decreasing unbound motor density, and eventually reattach to the microtubule. This constitutes a treadmilling mechanism with a closed circuit of motor flux in the vicinity of the tip (Fig. 1 C). Note that the length scale of the motor accumulation (≃ 1 μm (18)) is much larger than the length scale of the region where motors apply forces at the tip of the membrane tube (of approximately a few tens of nanometers).

Simulations of membrane tube growth

Kinesin motors walk along microtubules by a sequence of discrete steps (23,24). A single motor moves from a given tubulin dimer to the neighboring one at a fixed rate (25,26). Kinesin-1 motors are highly biased: at vanishing load, the rate at which they step forward to the next tubulin dimer is much larger than the rate at which they step backward. We adopt a discrete microscopic approach in the simulations and neglect the backward stepping of the motors.

We first consider a single microtubule protofilament and describe it as a one-dimensional lattice. The lattice spacing, ℓ, corresponds to the size of a tubulin dimer that gives the periodicity of the filament (Fig. 2). The membrane tube is discretized in N + 1 sites numbered from 0 at the left boundary to N at the very tip of the tube (Fig. 2). A motor at a given site can either be bound to or unbound from the microtubule. When bound, the motor can step forward to the next site, if empty, with a rate k_f or detach from the microtubule with a rate k_u. The unbound state represents motors attached to the membrane tube, but not to the microtubule, and therefore several motors can be placed in this state at a given site. The attachment rate of motors onto the microtubule is much larger than the detachment rate (see Table 1), so that most of the motors are attached to the microtubule. In the simulations, we find that the number of unbound motors at a given site hardly ever exceeds a few motors. This is much smaller than the maximum number of unbound motors at one site that we estimate to be ∼100 motors. We can therefore ignore interactions between unbound motors. Unbound motors diffuse along the membrane tube with a diffusion constant D and stochastically attach to the microtubule at a rate k_b if there is no bound motor at the binding site. In this discrete model, the diffusion of an unbound motor along the membrane tube is equivalent to a diffusion rate k_d = D/ℓ². Besides diffusion, unbound motors also move as a consequence of the membrane tube motion, as detailed below. The actual values of the motor transition rates depend on the forces exerted on the motor and they vary thus with the position along the membrane tube.

FIGURE 2.

Sketch of the vicinity of the tip of a growing membrane tube (top) and its coded representation in the simulations (bottom). The boxes along the microtubule (dark green) represent binding sites for motors. The membrane tube (yellow) is also discretized, using the same one-dimensional lattice as for the microtubule. The sites are labeled from 0 to N, with 0 and N corresponding respectively to the left boundary and to the position of the leading motor, which defines the position of the tip. In the coded representation, the number at each site corresponds to the number of motors occupying that site. Along the microtubule, the sites may be either empty or occupied by one bound motor (light blue and red) at most, which corresponds, respectively, to occupation numbers 0 and 1 in the code. Along the membrane tube, each site may be occupied by several unbound motors (light green), corresponding to an integer occupation number in the code. (A and B) Examples of the tube retraction dynamics (A.1 and A.2) and examples of the growth dynamics for each organization scheme (B.1–B.3). A portion of the tube in the vicinity of the tip is shown in the coded representation used in the simulations. For each case, the configurations before (top) and after (bottom) a particular motor transition (indicated by an orange arrow) are shown. The bound motors along the membrane tube do not change their positions upon tube motion (light green dashed box). Unbound motors are dragged by the membrane tube and change their positions accordingly upon tube motion (light blue dashed box). (A.1 and A.2) Tube retraction caused by the detachment of the leading motor. Two different motor configurations are shown. The membrane tube retracts up to the position of the closest bound motor. (B) Dynamics of tube growth for the three different organizations of motors pulling the membrane tube at the tip. Forward stepping of the leading motor for the three coordination schemes discussed in the main text: (B.1) cluster-tip, (B.2) variable-tip, and (B.3) fixed-tip.

TABLE 1.

Measured values for the parameters used in the simulations; article sources are indicated

ℓ	V0	fs	D	kb		a	κ
8 nm	0.6 μm s−1	6 pN	1 μm2 s−1	4.7 s−1	0.42 s−1	1.4 nm	10 KBT
(26)	(18)	(24)	(18)	(18)	(37)	(30)	(18)

The growing membrane tube is divided into three regions. The site numbered 0 corresponds to the left boundary and allows for motor fluxes in and out of the membrane tube. The tip is defined as the region where the motors apply forces to pull the membrane tube. Between these two boundaries, a bound motor moves forward with rate k_f = V₀/ℓ (V₀ being the velocity of the motor under vanishing force) and detaches at a rate 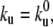corresponding to the rates at vanishing force. In the unbound state, the motors diffuse at a rate k_d = D/ℓ² and attach to the microtubule at a rate k_b. In Table 1 we detail the experimentally measured values of all parameters necessary to specify the rates.

Far from the tip region, both the average bound and unbound motor densities along the membrane tube, ρ_b and ρ_u, respectively, are homogeneous and constant (18). Detailed balance requires that 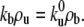When the membrane tube is pulled from a vesicle with initial surface density of motors ρ_∞, the continuity conditions for both the densities and fluxes in the bound and unbound states impose 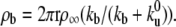The membrane tube radius r is related to the extraction force, F, by r = 2κ/F (22). In the laboratory reference frame, the fluxes of bound (J_b) and unbound motors (J_u) entering the membrane tube can be written as J_b = ρ_bV₀ and J_u = ρ_uV where V is the average growth velocity of the membrane tube. As the motor attachment rate is much larger than the detachment rate (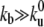; Table 1), ρ_b ≫ρ_u and the flux of unbound motors entering the membrane tube J_u can be neglected. This is consistent with the experimental observations of Leduc et al. (18). Note that unbound motors can leave the membrane tube either by diffusion or as a consequence of a tube retraction (Fig. 2 A).

There are general rules that can be established for the membrane tube dynamics, independently of the organization and cooperation mechanism of the motors in the tip region. When the leading bound motor at site N steps forward, the membrane tube grows by one site (N → N + 1), and if it detaches from the microtubule, there is no bound motor to sustain the membrane tube at the tip and the membrane tube instantaneously moves backward to the closest site containing a bound motor (Fig. 2 A). It is indeed legitimate to consider the tube retraction as instantaneous; the time needed for retraction over a few sites is ∼ ℓ/|V_R| ≃ 10⁻⁴ s (V_R being the retraction velocity, which has been measured to be |V_R| ∼ 100 μm s⁻¹ for a value of the vesicle tension similar to that of our experiments (27)), and it is much smaller than the time 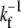for forward motor stepping (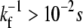; Table 1). When the membrane tube moves either forward or backward, the bound motors along the tube remain at their respective sites, since they are bound to the microtubule and the force applied on each one of them arising from the tube motion is negligible (Fig. 2). A bound motor is subject to the drag force that arises from the motion of the lipid to which it is attached in the fluid membrane. This force is of hydrodynamic origin and of order (K_BT/D)V_r, where V_r is the relative velocity between the bound motors and the membrane tube. Using the experimental values in Table 1, this drag force is <10⁻³ pN during membrane tube growth (V_r ∼ V₀) and smaller than 10⁻¹ pN during a retraction (V_r ∼ V_R). On the contrary, the unbound motors follow the tube motion because the viscosity of the membrane is larger than the bulk viscosity. Therefore, when the membrane tube moves forward or backward all the unbound motors along the tube move accordingly (Fig. 2).

As all values of the parameters are known experimentally (Table 1), we can explore the differences in membrane tube dynamics arising from differences in motor coordination schemes and organization at the tip. We propose three different coordination schemes for the motors at the tip, as follows.

Cluster-tip

In this scheme, we assume that the motors are fully synchronized and that they can transmit the forces when they are in contact in a rowlike configuration and that the first n_b consecutive bound motors ahead of the first empty site share the force to pull the membrane tube (Fig. 2 B.1). The distribution of the force among motors following each other is rather subtle and has been discussed in details in Campàs et al. (19). For simplicity, we consider here that the motors share the force equally: each motor sustains a force F/n_b. Synchronization between motors is taken into account by imposing that, when the first motor in the cluster (the leading motor, at site N) steps forward, the other motors in the cluster follow instantaneously (Fig. 2 B.1). The number of motors constituting the cluster, n_b, is a stochastic variable that depends on the motor kinetics.

The forward stepping rate, k_f, and detachment rate, k_u, of the motors in the cluster depend on the force, F/n_b, that each motor sustains and are given, respectively, by

(1)

where Θ(z) is the Heaviside step function. As a first approximation, we use a linear force-velocity relation to evaluate the forward stepping rate (28), and impose a vanishing forward rate when the force applied on the motor is larger than f_s to account for recent experimental observations on conventional kinesins (25,26). Following Kramer's rate theory (29), and in agreement with experimental observations (30), the detachment rate k_u increases exponentially with the force applied on the motor. The microscopic length a is associated to the position of the energy barrier against unbinding. As in Leduc et al. (18), we use the value a = 1.4 nm, which is in good agreement with experimental observations (30). The other rates, k_b and k_d, are the same as for the motors along the membrane tube (Table 1).

Variable-tip

In this scheme the motors transmit the forces when they are in contact, and there is no synchronization between motors. When the leading motor steps forward, the following motors do not follow instantaneously (Fig. 2 B.2). The detachment rate of the leading motor is increased because it sustains the total extraction force upon stepping. The tube retracts if the leading motor detaches before the second motor steps forward. As in the cluster-tip scheme, the first n_b consecutive bound motors share the force equally to pull the membrane tube (Fig. 2 B.2). The expressions for the rates k_f and k_u are given by Eq. 1.

Fixed-tip

In this scheme, only the motors which apply normal forces to the membrane can contribute to pull the tube and no synchronization exists between them. The curvature of the tip defines a region of fixed size L_tip ≡ ℓN_tip where the motors can apply normal forces to the membrane, independent of the fact of whether they are consecutive (Fig. 2 B.3). Typical values for the radius of curvature, r, of the tip suggest that N_tip is between 1 and 4, corresponding to a radius of curvature in the range r ≃ 8 − 32 nm. The number of bound motors, n_b, in the tip region is a stochastic variable that can vary in the range [1, N_tip]. Moreover, no synchronization between the motors exists, as in the variable-tip scheme.

Note that although the expression for the rates is the same for all schemes (Eq. 1), the dynamics of the stochastic variable n_b are different and, as a consequence, the membrane tube dynamics also differ significantly.

RESULTS AND DISCUSSION

We perform continuous time Monte Carlo simulations (see the Supplementary Material, Data S1 and Data S2) of the dynamics described above, and compare quantitatively the results to the experimental observations.

Conditions for membrane tube extraction

We first analyze the conditions in which molecular motors are able to extract membrane tubes. All the experiments were performed at the same surface tension, so that the extraction force, F ≃ 27.5 ± 2.5 pN, is the same in all cases. As shown in Leduc et al. (18), there exists a threshold motor density below which the motors cannot extract membrane tubes from the vesicle. The threshold density was determined experimentally as described in Leduc et al. (18) by varying the surface density of motors on the vesicle from which the membrane tube is pulled. For motor densities above ρ_∞ ≃ 200 μm⁻², membrane tubes were consistently observed. At a motor density ρ_∞ ≃ 100 μm⁻² no membrane tubes were observed, even 3 h after the injection of the kinesin-coated vesicles into the chamber. The actual value of the threshold density lies thus within the range 100–200 μm⁻². Note that the existence of a threshold motor density at a given extraction force F, means that at a constant motor density ρ_∞, the motors cannot pull a membrane tube if the extraction force is larger than a threshold force F_m.

Numerically, the threshold force F_m is determined as follows. For a given value of the surface density ρ_∞, the extraction force F is initially set to a very large value. The system is initialized with a certain number of consecutive bound motors, M_i, that ensures the initial membrane tube growth (with the initial length of the membrane tube, N_i, being N_i = M_i = 20). If the initial number of bound motors were too small, it could be more limiting than the value of the surface density of motors, and would lead to artifacts. Typically, the membrane tube initially grows (as it has enough bound motors at the tip) and, if the force is too large it retracts completely. We repeat this process 200 times for the same values of F and ρ_∞ and, if all membrane tubes retract we lower the force and repeat the process again for the same value of ρ_∞. As the force is progressively lowered, there exists a threshold value of the force F_m for which at least one membrane tube does not retract and grows with a finite average velocity. For the same value of ρ_∞ we repeat the whole process 20 times, and obtain several values of F_m that allow a statistical treatment of the data.

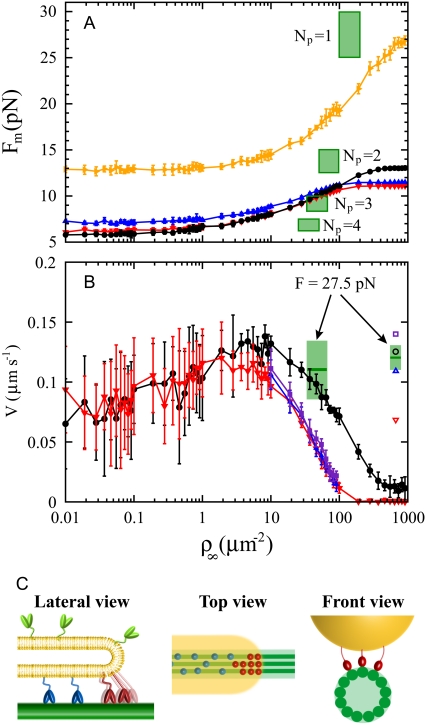
In Fig. 3 A we plot the numerically obtained value of the threshold force F_m as a function of ρ_∞ for the various motor coordination schemes. The force F_m saturates for large surface densities of motors independently of the scheme used, but the saturation value depends on the motor organization at the tip. One could expect this behavior for the fixed-tip scheme as there is an upper bound for the number of bound motors that pull the membrane tube. The force saturation for the two other schemes is a consequence of motor detachment events that prevent the formation of large clusters of consecutive motors at the tip and therefore the generation of large forces.

FIGURE 3.

Comparison between the numerical results and the experimental data. (A) Threshold force F_m for membrane tube extraction as a function of the surface motor density on the vesicle ρ_∞, for the various motor organization schemes at the tip: variable-tip (black circles), fixed-tip (N_tip = 2; red down-triangles), fixed-tip (N_tip = 3; blue up-triangles), and cluster-tip (orange right-triangles). The parameters of the simulations are those measured experimentally (Table 1). The experimentally measured values of the motor density and of the force (represented by a green rectangle due to the experimental uncertainty) must be rescaled by the number of protofilaments N_p to be compared to the simulations. (B) Average tube growth velocity V as a function of the motor density ρ_∞ when the extraction force is equal to its threshold value F_m(ρ_∞) for the various motor organization schemes at the tip: variable-tip (solid black circles) and fixed-tip (N_tip = 2, solid red down-triangles; N_tip = 3, solid blue up-triangles; N_tip = 4, solid violet squares). We also plot the membrane tube growth velocity V obtained in the simulations for a motor density ρ_∞ = 2000 μm⁻² and a force F = 27.5 pN in the variable-tip scheme (open black circle) and fixed-tip scheme (N_tip = 2, open red down-triangle; N_tip = 3, open blue up-triangle; N_tip = 4, open violet square). We consider that three protofilaments are simultaneously used by bound motors (N_p = 3), so that the force per protofilament is F/N_p = 9.2 pN. The experimentally measured values of the membrane tube velocity for the motor densities 200 μm⁻² and 2000 μm⁻² (at the same extraction force F = 27.5 ± 2.5 pN) are represented by green rectangles due to the experimental uncertainty. Note that these values have to be normalized to the number of protofilaments to be compared to the numerical results. (C) Schematic representation of the organization of motors pulling a membrane tube, using approximately the right proportions. Lateral, top, and front views are shown. Bound motors (blue and red) can use three different protofilaments (dark green) to pull the membrane tube (yellow). The motors applying the force to sustain the tube at the tip are shown in red, whereas the other bound motors are shown in blue.

The threshold force F_m is also constant for small values of ρ_∞ (Fig. 3 A). For such values of the motor density, the initial number of motors M_i is sufficient to extract the membrane tube and keep pulling it. Therefore, no matter how much the density ρ_∞ is lowered, the maximal force that the motors can sustain saturates because the initial number of motors is fixed to the same value in all cases. Reducing the initial number of motors M_i confirms this explanation as the saturation of F_m takes place at smaller values of ρ_∞ (data not shown). Note that at vanishing density ρ_∞, the flux of motors entering the membrane tube J_b strictly vanishes. However, membrane tubes can be extracted by the initially bound motors if the force is low enough.

In Leduc et al. (18), we studied membrane tube formation by molecular motors using a mean-field theory, which predicts a threshold force proportional to 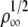but no saturation is found. Below saturation, the threshold force obtained here numerically also increases approximately as a power law, 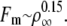The discrepancy between the mean-field theory and our numerical results could be due to the fact that the mean-field description does not account for the interaction between the motors and their organization at the tip.

The value of the threshold force F_m obtained in the simulations is lower than the experimental value F_m = 27.5 ± 2.5 pN for values of ρ_∞ in the range 100 μm⁻² < ρ_∞ < 200 μm⁻², in any motor organization scheme (Fig. 3 A). This implies that motors moving along a single protofilament cannot develop the forces required for membrane tube extraction. In the experiments, several protofilaments are likely to be used simultaneously by the motors. Although the membrane couples the motor dynamics between protofilaments at the tip, we assume, in a first approximation, that the motor dynamics on different protofilaments are independent. If bound motors use a number N_p of protofilaments when moving along the microtubule, the flux of motors entering the system is shared among these protofilaments, so that the motor fluxes per protofilament are J_b/N_p and J_u/N_p. As changes in the motor fluxes are only due to changes in ρ_∞, the experimental value of the motor density that must be compared to the numerical results is ρ_∞/N_p. Similarly, the extraction force F is shared between the protofilaments, so that the force that the motors pulling the membrane tube along a single protofilament must overcome is F/N_p.

If we consider that the motors use one, two, or more than three protofilaments (N_p = 1, N_p = 2 or N_p > 3), the numerical results do not agree with the measured value of the threshold force for any organization scheme (Fig. 3 A). It is only when bound motors use three protofilaments simultaneously that the threshold force F_m obtained in the simulations for the variable-tip and fixed-tip schemes (with N_tip = 2) agree with the measured value within the experimental uncertainty (Fig. 3 A). The values of the threshold forces obtained for the fixed-tip scheme with N_tip = 3 (Fig. 3 A) and N_tip = 4 (data not shown) are larger than those obtained for N_tip = 2, and do not fit the experimental data within error bars. For any number of protofilaments, the cluster-tip scheme does not fit the experimental data. As this is the only scheme that supposes synchronization between the motors, our results suggest that the motors pulling the membrane tube are not synchronized. However, this does not exclude some degree of coordination between the motors. We conclude that bound motors use three protofilaments simultaneously and step asynchronously to pull the membrane tube (Fig. 3 C). This is in agreement with naive geometric considerations presented in the Supplementary Material (Data S1 and Data S2) where we estimate that no more than three protofilaments can be used at the same time.

Based on the value of the threshold force F_m we cannot discriminate between the variable-tip and fixed-tip schemes. We now use the experimental average growth velocity, V, to select the most consistent organization scheme.

Growth velocity

For each motor surface density ρ_∞, we first determine the average growth velocity of the membrane tubes when the extraction force is just above the threshold value F_m shown in Fig. 3 A. Note that when the motor density ρ_∞ increases, the extraction force also increases and that the calculated velocity corresponds to membrane tubes pulled from vesicles with different tensions (and thus different extraction forces). In Fig. 3 B, we plot the numerically obtained velocity of membrane tubes pulled at the threshold force as a function of ρ_∞ for the two schemes variable-tip and fixed-tip with N_tip = 2 (N_tip = 3 and N_tip = 4 are also shown for a limited range of densities).

Below a surface motor density of about ρ_∞ ≃ 1 μm⁻², the two schemes give close velocities. For low motor densities (or low threshold forces) the two schemes should lead to a similar behavior as only a few consecutive bound motors are required to pull the membrane tube. At low densities, there are large fluctuations in the number of bound motors pulling the membrane tube as the average number is very small (n_b ≃ 1–2), leading to large fluctuations in the membrane tube velocity. For densities above ρ_∞ ∼10 μm⁻² (Fig. 3 B), the fluctuations are strongly reduced and the two schemes lead to clearly different average tube velocities. The velocity in variable-tip scheme is larger than in the fixed-tip scheme with N_tip = 2, N_tip = 3, and N_tip = 4. Indeed, in the fixed-tip scheme there is a limited number of sites where the motors can apply forces, whereas in the variable-tip scheme larger bound motor clusters can be stochastically created.

The average tube velocity has been determined experimentally in conditions close to the threshold for membrane tube extraction. The motor density on the surface of the vesicle was set to ρ_∞ ≃ 200 μm⁻², which is the closest value to threshold at an extraction force F ≃ 27.5 ± 2.5 pN. The average value, 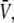of the tube velocity V measured for nine different membrane tubes, was 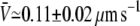(mean ± SD of the mean; Fig. 3 B). As the system is close to threshold, very few membrane tubes were observed; tubes were extracted only from ∼10% of the vesicles, whereas in conditions where the system is far above the threshold in membrane tube extraction, tubes were observed for nearly all vesicles. Only membrane tubes shorter than ∼10 μm were considered in the statistics, as for longer tubes the membrane tension may significantly increase during tube growth (31). The measured value of the average tube growth velocity is consistent with that obtained in the variable-tip scheme (Fig. 3 B). The smaller velocities for the fixed-tip scheme with N_tip = 2, N_tip = 3, and N_tip = 4 that result from its limited number of pulling motors, do not agree with the experimental data within the error bars (Fig. 3 B).

To further establish the variable-tip scheme as the most plausible one, we study the tube velocity at a motor density much larger than the measured threshold density. For the same force, F ≃ 27.5 ± 2.5 pN, the surface motor density was set to ρ_∞ ≃ 2000 μm⁻², i.e., 10 times larger than the threshold density at this value of the force. The average value of the tube velocity measured for 27 different membrane tubes was 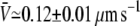(mean ± SD of the mean; Fig. 3 B). Using the same parameters as in these experiments, and only assuming that motors use three protofilaments to pull the membrane tube, the average tube velocity obtained in the simulations for 100 tubes is (Fig. 3 B): 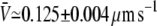for the variable-tip scheme, 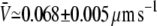for the fixed-tip scheme with N_tip = 2, 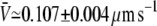for the fixed-tip scheme with N_tip = 3, and 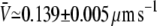for the fixed-tip scheme with N_tip = 4. The average membrane tube velocity for the variable-tip scheme is in good agreement with the experimentally measured value of the velocity (open circle in Fig. 3 B). In particular, it is closer to the experimentally measured velocity than the obtained velocities for the fixed-tip scheme with N_tip = 2, N_tip = 3, and N_tip = 4. This confirms the scheme variable-tip as the most plausible type of motor organization at the tip.

It is important to note that there are no fitting parameters in the velocity comparison: assuming that three protofilaments are simultaneously used by the motors, the variable-tip scheme reproduces all experimental measurements.

Motor distribution at the tip of the membrane tube

Due to the stochastic motor transitions, the number of motors pulling the membrane tube, n_b, is a stochastic variable that fluctuates during tube growth. We now study the distribution and average of the number n_b of consecutive motors at the tip.

We simulate the growth of a membrane tube in conditions far from the threshold for tube extraction, using the experimentally measured values of all parameters (Table 1). In particular, the force and surface motor density imposed in the simulations are, respectively, the force per protofilament, F/N_p ≃ 9.2 pN, and the motor density per protofilament, ρ_∞/N_p ≃ 300 μm⁻² (N_p = 3). Upon tube growth, we obtain the number of consecutive motors at the tip as a function of time, n_b(t). In Fig. 4 A we show the probability distribution of n_b, obtained using an ensemble average performed over 3000 independent simulated membrane tubes. The relaxation to the steady state takes place in less than ∼1 s and the probability distribution does not change over time after this. Although there is a finite probability that large motor clusters transiently form, the average number of pulling motors per protofilament, 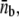is constant in time and small, 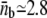(Fig. 4 B). As three protofilaments are used simultaneously and independently, we estimate the average number of motors pulling the membrane tube in the conditions specified to be ≃ 8.4. When the system is close to threshold (for ρ_∞/N_p ≃ 50 μm⁻²; N_p = 3), the average number of pulling motors is ≃ 6.3 (≃ 2.1 motors per protofilament), in agreement with the value predicted in Leduc et al. (18).

FIGURE 4.

(A) Numerically obtained probability distribution of the number of pulling motors. The inset shows the probability distribution in logarithmic scale, and suggests an exponential decay with n_b for n_b > 3. (B) Average number of motors pulling the membrane tube along a single protofilament, 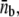as a function of time. The parameters in the simulations are those measured experimentally for a motor density much larger than the threshold density (Table 1 and F/N_p ≃ 9.2 pN, ρ_∞/N_p ≃ 300 μm⁻²; normalized to the number of protofilaments N_p used by bound motors, N_p = 3).

On each protofilament, there is thus a small cluster of consecutive motors that develops dynamically at the tip, which is determined by the balance of fluxes in this region and cannot develop arbitrarily large forces. Most importantly, even if a macroscopic high density phase of motors (traffic jam) exists upstream from the tip, the number of consecutive bound motors defining the tip region remains small due to their detachment events. This limits considerably the forces that motors moving along the same protofilament can exert when pulling on fluid membranes.

CONCLUSIONS

In this article, we investigated the mechanisms of force generation by motor proteins pulling collectively on a fluid membrane. The aim of our article was to directly compare in vitro experimental results on the growth of membrane tubes pulled by molecular motors to stochastic simulations with various organization schemes of the motors pulling the tube. As all physical parameters in our in vitro system are either measured or controlled experimentally, a quantitative analysis is possible and provides information on the organization of the motors pulling the membrane tube.

In a previous work (18), we showed that, to produce large-enough forces, motors must dynamically accumulate at the tip of growing membrane tubes to form a cluster. The comparison between experiments and numerical simulations suggests that motors clustering along a single protofilament cannot generate a large enough force to extract a membrane tube. Tube extraction requires therefore that the motors use several protofilaments simultaneously. Depending on the conditions, we find that the experimental results are best described if between six and nine motors, distributed over three contiguous protofilaments, contribute to pull the membrane tube. Our results also strongly suggest that the motors forming a cluster do not step synchronously since the cluster-tip organization scheme, where motors instantaneously follow the motion of the leading motor, does not describe correctly the experiments. If this result is general, as one can expect, it might imply that the observed steps of vesicles (e.g., peroxisomes, melanosomes, etc.) (8–9), where motors act in a very similar way as in membrane tubes, are a consequence of individual motor stepping rather than of the synchronous stepping of all the pulling motors. Our conclusions concerning the nonsynchronous motor stepping are in agreement with recent experimental evidence that, even when motors are attached rigidly, they do not step synchronously (32).

The maximal force that motors moving along a single protofilament can perform depends strongly on the attachment and detachment rates. Using typical values for kinesin-1 kinetics, we find that in our experimental conditions this maximal force is roughly 13 pN per protofilament. Interestingly, this result sets a clear limit to transport in vivo, and suggests that the regulation of motor binding/unbinding events may be essential for the force generation in intracellular transport. The importance of the attachment and detachment rates on the regulation of vesicle transport has recently been discussed in Gross et al. (2).

Our results also show that the collective behavior of motors pulling on fluid membranes is essentially different from that of rigidly or elastically coupled motors. We now briefly discuss the main differences between these two situations.

There are many biological contexts in which motor proteins are attached rigidly or elastically to a cargo that must be displaced, such as muscle contraction, chromosome movement, or flagellar beating. Another important example of rigidly bound motors is the motion of beads or filaments carried by multiple motors in the in vitro motility assays (33). In all these cases, the rigid/elastic attachment of the motors allows them to apply tangential forces to their cargo. The contributions to the exerted force of individual motors then add up and the stall force of a cargo with rigidly or elastically bound motors scales with the number of motors pulling it (34). In these conditions it is possible to estimate the number of motors pulling the cargo from its stall force (33).

On the contrary, motors attached to fluidlike cargoes, such as vesicles or membrane tubes, cannot apply tangential forces to their cargo. The motors must cluster at the leading edge of the tube or the vesicle, where they can apply normal forces to the membrane (18). Campàs et al. (19) and this study show that the effective stall force is not the product of the number of motors pulling the cargo times their individual stall force. Any estimation of the number of motors pulling a fluidlike cargo, such as a vesicle, from its measured stall force should therefore be considered with care.

The influence of the motor processivity on intracellular transport also strongly depends on the nature of the cargo. Processive motors are motors able to perform more than a single step without detaching from their filament. Rigid or elastic attachment of motors to a cargo leads to its processive motion, regardless of the processivity of individual motors. A larger processivity of each single motor merely increases the run length of the cargo along the filament, as shown, for example, theoretically in Klumpp and Lipowsky (34). Note that the collective action of purely nonprocessive motors (such as myosin-II) can also lead to the processive motion of a cargo if the number of attached motors is large enough (larger than the inverse of the so-called duty ratio, so that, on average, there is at least one motor bound to the cargo). It has also been shown, however, that a larger processivity of the motors may hinder the motion of the cargo because the presence of motors attached to the filament can prevent the motion of other motors (35), an effect known as protein-friction. Therefore, when motors are attached rigidly or elastically to cargoes, processivity is not essential and can even hinder the motion.

On the contrary, when motors are directly attached to the membrane of a fluidlike cargo, they can only apply substantial forces in the normal direction to the membrane. If the motors are nonprocessive, they cannot dynamically cluster and develop the necessary forces required for motion. In this case, an increase of the processivity of individual motors leads to an increase of the size of the motor cluster that generates the force, leading to a larger value of the maximal force that motors can sustain. It also enhances the processivity of the fluidlike cargo. Therefore, nonprocessive motors could only transport fluidlike cargos if previously clustered by other mechanisms, as suggested in Klopfenstein et al. (36).

We only discussed here the coordination of one particular type of motor protein acting collectively to pull a fluidlike cargo. The coordination of motors with opposing polarities (like dyneins and kinesins) attached to the same cargo constitutes a step further in the understanding of the coordination of motor proteins (2).