Characterisation of transition state structures for protein folding using ‘high’, ‘medium’ and ‘low’ Φ-values

Abstract

It has been suggested that Φ-values, which allow structural information about transition states (TSs) for protein folding to be obtained, are most reliably interpreted when divided into three classes (high, medium and low). High Φ-values indicate almost completely folded regions in the TS, intermediate Φ-values regions with a detectable amount of structure and low Φ-values indicate mostly unstructured regions. To explore the extent to which this classification can be used to characterise in detail the structure of TSs for protein folding, we used Φ-values divided into these classes as restraints in molecular dynamics simulations. This type of procedure is related to that used in NMR spectroscopy to define the structure of native proteins from the measurement of inter-proton distances derived from nuclear Overhauser effects. We illustrate this approach by determining the TS ensembles of five proteins and by showing that the results are similar to those obtained by using as restraints the actual numerical Φ-values measured experimentally. Our results indicate that the simultaneous consideration of a set of low-resolution Φ-values can provide sufficient information for characterising the architecture of a TS for folding of a protein.

Introduction

Φ-Value analysis is a powerful experimental method that provides information about transition states (TSs) for folding and unfolding at the level of individual residues (Fersht et al., 1992; Fersht, 1999). The Φ-value of a residue is defined as the ratio of the destabilisation of the TS, ΔΔG_D-TS, to that of the native state, ΔΔG_D-N, caused by its mutation

$${\Phi }^{\exp }=\frac{\Delta \Delta G_{\mathrm{D}-\mathrm{TS}}}{\Delta \Delta G_{\mathrm{D}-\mathrm{N}}}.$$ (1)

A Φ-value of 1.0 denotes the essentially complete formation of the local structure in the TS, whereas a Φ-value of 0 indicates that the residue is as unstructured in the TS as is in the unfolded state. Fractional Φ-values often arise from a partial formation of structure (Fersht et al., 1994) even if in principle they may reflect the presence of parallel pathways (Davis et al., 2002; Wright et al., 2003; Latzer et al., 2006).

In order to facilitate the structural analysis, it has been proposed that Φ-values should be grouped into classes (Fersht et al., 1994; Fersht, 1995; Daggett et al., 1996; Fersht and Sato, 2004; Garcia-Mira et al., 2004; Ferguson et al., 2005). This type of procedure is also used in NMR spectroscopy when distances derived from nuclear Overhauser effects (NOEs) are obtained (Wuthrich, 1989). NOE resonances are grouped into three classes according to their strength (‘strong’, ‘medium’ and ‘weak’), and molecular dynamics techniques are used to generate structures that are consistent with the NOE restraints (Brunger et al., 1998; Schwieters et al., 2006). It is generally believed that the success of NMR spectroscopy for the determination of protein structures is due to the simultaneous use of many restraints (Wuthrich, 1989). Although each individual restraint may be affected by a significant uncertainty, when considered together they define a structure with high accuracy. The similarity between the structural restraints that can be derived from NOE and Φ-value measurements has prompted this study.

Several approaches have been used to rationalise the results of experimental measurements of Φ-values and to characterise the ensembles of structures that represent the TS (the TS ensemble, TSE). In one approach, proteins are unfolded through high temperature simulations starting from their native states (Daggett, 2002). The TSE is identified by conformational clustering (Daggett, 2002) or by scanning the unfolding trajectories for structures that have the minimal deviation to experimental Φ-values (Gsponer and Caflisch, 2002). Comparison with experiments is done by defining Φ-values from the simulations in terms of the fraction of native contacts and the degree of formation of secondary structure (Daggett, 2002). Another computational approach to determine the TSE is to use the experimental Φ-values, interpreted as fractions of native contacts, as restraints in molecular dynamics simulations (Li and Shakhnovich, 2001; Vendruscolo et al., 2001; Paci et al., 2002; Paci et al., 2003; Geierhaas et al., 2004; Paci et al., 2004; Geierhaas et al., 2005; Best and Vendruscolo, 2006). The experimental restraints force the system towards regions of conformational space where the deviation from the experimental Φ-values is minimal (Vendruscolo and Paci, 2003). This approach has been applied to a number of proteins and was recently validated by using the resulting structures to predict the results of independent measurements (Salvatella et al., 2005). Although in principle both native and non-native interactions can be relevant in any given TS, in the implementation of the method that we have used here a Φ-value is defined in terms of number of native contacts formed in the TS compared with the total number of native contacts formed by the same residue in the native state.

In this work, Φ-values are classified as low, if they are measured to be less than 0.33, medium if their values are between 0.33 and 0.66 or high otherwise; we also show that the exact position of the boundaries between the classes is not critical. With this type of restraints, residues are forced to move towards regions of conformational space where they match the experimental Φ-values at low resolution. The resulting TSE structures are compared with those obtained from restrained simulations in which Φ-values are biased towards their experimental numerical value (Paci et al., 2002). We chose five proteins that are well characterised in vitro by Φ-value analysis: chymotrypsin inhibitor 2 (CI2) (Daggett et al., 1996), the third fibronectin type III domain from human tenascin (TNfn3) (Hamill et al., 2000), muscle acylphosphatase (mAcP) (Chiti et al., 1999), cold shock protein B (CspB) (Garcia-Mira et al., 2004) and the human titin immunoglobulin domain I27 (TI I27) (Fowler and Clarke, 2001; Wright et al., 2003). The relative compactness of the transition state can be determined using Beta-Tanford values (β_T) determined experimentally from the ratio of the folding m-value to the overall m-value. The β_T of these proteins range from 0.6 to 0.95; thus the TSs range from fairly disordered to very native-like, in terms of compactness.

In all cases, detailed comparisons show that the ensembles determined by the two types of simulations are very similar, suggesting that the proposed classification of Φ-values into classes (Fersht et al., 1994; Fersht, 1995; Daggett et al., 1996; Fersht and Sato, 2004; Garcia-Mira et al., 2004; Ferguson et al., 2005) provides reliable information about TSs and is sufficient to determine the overall topology.

Methods

Structure determination using Φ-value classes in restrained simulations

For a conformation of the protein at time t, we define the calculated Φ-value (Φ^cal) of residue i as (Vendruscolo et al., 2001; Paci et al., 2002)

$${\Phi }_i^{\mathrm{cal}}\left(t\right)=\frac{N_i\left(t\right)}{N_i^{\mathrm{nat}}},$$ (2)

where N_i(t) denotes the number of native contacts of residue i at time t and $N_i^{\mathrm{nat}}$ denotes the number of contacts in the native state. Experimental Φ-values are classified as low, medium or high, according to the following scheme

$$\begin{array}{ccc}\hfill \text{low}\hfill & \hfill \text{if}\hfill & \hfill 0.0\le {\Phi }^{\exp }<{\Phi }_{\mathrm{L}}\hfill \\ \hfill \text{medium}\hfill & \hfill \text{if}\hfill & \hfill {\Phi }_{\mathrm{L}}\le {\Phi }^{\exp }\le {\Phi }_{\mathrm{H}}\hfill \\ \hfill \text{high}\hfill & \hfill \text{if}\hfill & \hfill {\Phi }_{\mathrm{H}}<{\Phi }^{\exp }\le 1.0\hfill \end{array}.$$ (3)

At variance with the ‘specific simulations’ approach (Vendruscolo et al., 2001; Paci et al., 2002), Φ-values are not biased to achieve a specific value, but rather to remain within the range of values that characterises their class. A residue having a low Φ^exp-value, for example, is restrained to have a Φ^cal-value below Φ_L. For this purpose, we define the quantity

$$\rho =\frac{1}{N_{\Phi }}\sum _{i\in E}{\Lambda }_i^2,$$ (4)

where E is the list of N_Φ available experimental Φ-values and Λ is

$$\Lambda =\left[\begin{array}{cc}\hfill \text{low class}\hfill & \hfill \left\{\begin{array}{ccc}\hfill {\Phi }^{\mathrm{cal}}-{\Phi }_{\mathrm{L}}\hfill & \hfill \text{if}\hfill & \hfill {\Phi }^{\mathrm{cal}}>{\Phi }_{\mathrm{L}}\hfill \\ \hfill 0\hfill & \hfill \text{if}\hfill & \hfill {\Phi }^{\mathrm{cal}}\le {\Phi }_{\mathrm{L}}\hfill \end{array}\right\}\hfill \\ \hfill \text{medium class}\hfill & \hfill \left\{\begin{array}{ccc}\hfill {\Phi }^{\mathrm{cal}}-{\Phi }_{\mathrm{L}}\hfill & \hfill \text{if}\hfill & \hfill {\Phi }^{\mathrm{cal}}<{\Phi }_{\mathrm{L}}\hfill \\ \hfill 0\hfill & \hfill \text{if}\hfill & \hfill {\Phi }_{\mathrm{L}}\le {\Phi }^{\mathrm{cal}}\le {\Phi }_{\mathrm{H}}\hfill \\ \hfill {\Phi }^{\mathrm{cal}}-{\Phi }_{\mathrm{H}}\hfill & \hfill \text{if}\hfill & \hfill {\Phi }^{\mathrm{cal}}>{\Phi }_{\mathrm{H}}\hfill \end{array}\right\}\hfill \\ \hfill \text{high class}\hfill & \hfill \left\{\begin{array}{ccc}\hfill {\Phi }^{\mathrm{cal}}-{\Phi }_{\mathrm{H}}\hfill & \hfill \text{if}\hfill & \hfill {\Phi }^{\mathrm{cal}}<{\Phi }_{\mathrm{H}}\hfill \\ \hfill 0\hfill & \hfill \text{if}\hfill & \hfill {\Phi }^{\mathrm{cal}}\ge {\Phi }_{\mathrm{H}}\hfill \end{array}\right\}\hfill \end{array}\right].$$ (5)

In order to sample regions of phase space with low ρ, a biased molecular dynamics method is used (Paci and Karplus, 1999). The method adds a pseudo-energy bias to the energy function of the form

$$w(r,t)=\left\{\begin{array}{ccc}\hfill \alpha ∕2{(\rho -{\rho }_a)}^2\hfill & \hfill \text{if}\hfill & \hfill \rho \left(t\right)\ge {\rho }_a\hfill \\ \hfill 0\hfill & \hfill \text{if}\hfill & \hfill \rho \left(t\right)<{\rho }_a\hfill \end{array}\right\},$$ (6)

where

$${\rho }_a\left(t\right)=\underset{0\le \tau \le t}{\min }\rho \left(t\right).$$ (7)

Molecular dynamics simulations

All simulations were performed in the CHARMM19 force field with the EEF1 energy function as implicit solvent (Lazaridis and Karplus, 1999). The experimental native state structures were retrieved from the PDB database (Berman et al., 2000) and energy minimised to remove steric clashes (200 steps steepest descent). The following starting structures were selected: 1TIT (TI I27), 1TEN (TNfn3), 1APS (mAcP), 2CI2 (CI2) and 1NMG (CspB). The system was heated from 0 to 300 K during a period of 600 ps and then equilibrated for 2 ns. During equilibration, the proteins remained relatively close to their respective initial conformations. The resulting equilibrated structure was used as the starting one for the simulations to determine the TSE. As WT CspB is only marginally stable, Φ-value analysis was performed using the more stable E3L mutant (Garcia-Mira et al., 2004). We created the E3L mutant by changing the side chain of a minimised 1NMG structure (200 steps steepest descent) from Glu3 to Leu3 using the program MOLDEN (Schaftenaar and Noordik, 2000). The resulting molecule was again minimised with 400 steps steepest descent, and equilibrated as described above. The integration step was 2 fs in all the simulations. Temperature was kept constant using the Nose-Hoover thermostat.

The following numbers of experimental Φ-values have been used for the selected five proteins: 34 for CI2 from Daggett et al. (1996); 25 for Tnfn3 from Hamill et al. (2000), 22 for mAcP from Chiti et al. (1999), 17 for CspB from Garcia-Mira et al. (2004) and 22 for the native-like TS of TI I27 from Wright et al. (2003).

Determination of the structures of the TSE

For each protein, we performed a series of three different ‘classes simulations’ using three different combinations of values for Φ_L and Φ_H [Eq. (3) and Results section]. The parameter α in Eq. (6) was set to 10 000 initially, and then doubled every 400 ps to reach a final value of 160 000. In this procedure, the magnitude of the restraint term is comparable to that of the energy term. The simulations were carried out for a total of 6 ns. Then, in order to efficiently sample the conformational space in the region maximally compatible with the experimental Φ-values, a harmonic potential was applied in order to restrain ρ around zero, and a series of 1 ns simulations at six different temperatures were performed (300, 360, 430, 500, 640 and 780 K). It is important to note that these temperatures do not correspond to physical temperatures but to temperatures on the modified energy surface corresponding to the pseudo-energy that we used (Paci et al., 2002). The role of the different temperatures is to sample increasingly broad regions of conformational space compatible with the restraints (Paci et al., 2002).

For each protein, 6000 structures were generated in total (1000 for each temperature). The structures were then selected so that only structures that have a <Φ^cal> computed over all residues, measured or not, that falls between 70% and 100% of the mean Φ^exp are members of the TSE. A range for the SASA of the TS was estimated using the β_T value (Geierhaas et al., 2007). In a second step of the selection procedure, all structures that were not within the estimated range of SASA for the TS were removed.

Results

The choice of the class boundaries Φ_L and Φ_H

Three different sets of boundaries (Φ_L between ‘low’ and ‘medium’, and Φ_H between ‘medium’ and ‘high’) were used in the restrained simulations with restraints divided into classes (‘classes simulations’):

A: Φ_L = 0.33 and Φ_H = 0.66.

B: Φ_L = 0.30 and Φ_H = 0.60.

C: Φ_L = 0.21 and Φ_H = 0.70.

Set C was chosen as suggested by Garcia-Mira et al. (2004). These three series of simulations produced very similar results in all the five cases that we considered [CI2 (Daggett et al., 1996), TNfn3 (Hamill et al., 2000), mAcP (Chiti et al., 1999), CspB (Garcia-Mira et al., 2004) and TI I27 (Fowler and Clarke, 2001; Wright et al., 2003)], as will be demonstrated explicitly for CspB; the data presented for the remaining proteins are only those of the set A. We also discuss simulations of mAcP in detail; the simulations for CI2, TI I27 and TNfn3 are all described in the supplementary data available at PEDS online, and simply summarised in Table I.

Table I.

Structural properties of the TS ensembles determined for the five proteins considered in this work

Protein	MD type	NΦa	RMSDb (Å)	Rgc (Å)	ΔRgc (%)	Sd (Å2)	ΔSd (%)	<Φcal>e	<Φexp>f
CspB	‘specific’	17	5.8±0.7	11.6±0.4	+6	4700±400	+11	0.37	0.43g
CspB	‘classes’	17	6.3±1.1	11.8±0.4	+7	4900±300	+15	0.36	0.43g
CspB	‘classes21-70’h	17	5.2±1.2	11.9±0.5	+8	4900±300	+15	0.35	0.43g
CspB	‘classes30-60’i	17	5.3±1.0	11.8±0.4	+7	4900±300	+15	0.36	0.43g
CspB	‘specific’ ΔGj	17	6.8±1.5	12.0±1.0	+9	5000±700	+17	0.36	0.43g
mAcP	‘specific’	22	7.3±2.4	13.7±0.5	+4	6800±400	+19	0.27	0.30k
mAcP	‘classes’	22	5.9±1.1	13.8±0.4	+5	6900±400	+21	0.26	0.30k
mAcP	‘classes’	3l	7.4±1.4	14.2±0.4	+7	7200±400	26%	0.24	0.30k
CI2	‘specific’	34	10.1±2.4	14.7±1.2	+30	6600±500	+51	0.19	0.24m
CI2	‘classes’	34	10.6±2.0	14.4±1.1	+28	6300±400	+44	0.19	0.24m
TI I27	‘specific’	22	3.7±0.8	12.9±0.2	+0	5500±200	+8	0.50	0.57n
TI I27	‘classes’	22	3.5±0.6	12.8±0.2	-1	5400±300	+6	0.51	0.57n
TNfn3	‘specific’	25	6.9±2.0	13.7±0.6	+5	6500±500	+26	0.24	0.28o
TNfn3	‘classes’	25	5.9±2.4	13.6±0.8	+5	6300±400	+22	0.25	0.28o

Reported errors correspond to one standard deviation.

^aNumber of experimental Φ-values used as restraints.

^bRoot mean square distance from the native conformation.

^cAverage radius of gyration; difference in R_g between the TS and the native state.

^dSolvent accessible surface area; difference in S between the TS and the native state.

^eAverage calculated Φ-value computed from all the residues that have non-zero number of side-chain native contacts.

^fAverage experimental Φ-value.

^gData taken from Garcia-Mira et al. (2004).

^hλ₁ and λ₂ in Eq. (3) were set to 0.21 and 0.70, respectively.

ⁱλ₁ and λ₂ in Eq. (3) were set to 0.30 and 0.60, respectively.

^jThe generated structures are selected as defined by Eq. (9).

^kData taken from Chiti et al. (1999).

^lSimulation restrained using only the key residues Tyr11, Pro54 and Phe94.

^mData taken from Daggett et al. (1996).

ⁿData taken from Wright et al. (2003).

^oData taken from Hamill et al. (2000).

The TS ensemble of CspB

The native structure of the 67-residue protein CspB consists of a closed β-barrel structure formed by the combination of a three-stranded β-sheet (β1-3) and a two-stranded β-sheet (β4-5) (Schindelin et al., 1993; Schnuchel et al., 1993). The β_T is 0.9 (Garcia-Mira et al., 2004), indicating that the TS of this protein has a near-native compactness. Garcia-Mira et al. (2004) have performed an extensive Φ-value analysis to analyse the TS of this protein experimentally.

The results that we obtained for the TSE of CspB are summarised in Table I, both for the simulations with the actual numerical Φ-values obtained experimentally (‘specific simulations’) (TSEsp, Fig. 1A) and the ‘classes simulations’ (TSEcl, Fig. 1B) for the three sets of different boundaries. All measured quantities are the same, within statistical error. The average Cα-RMSD of the TSEs to the native state are 5.8 ± 0.7 Å and 6.3 ± 1.1 Å for TSEsp and TSEcl, respectively. The average radius of gyration (R_g) is also very similar, 11.6 ± 0.4 Å (an increase of 6% with respect to the native state) and 11.8 ± 0.4 Å (+7%) for TSEsp and TSEcl, respectively. The solvent accessible surface area (SASA) increases were +11% and +15% for TSEsp and TSEcl, respectively. This corresponds to total values of 4700 ± 400 Ų (TSEsp) and 4900 ± 300 Ų (TSEcl). The results of the ‘classes simulations’ using sets B and C of values for Φ_L and Φ_H are very similar to those obtained when set A is used (Table I).

Fig. 1.

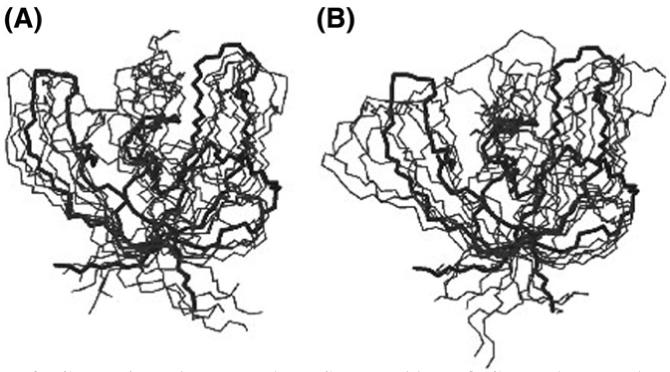
Comparison between the TS ensembles of CspB that we have determined in this work: (A) TSEsp (‘specific simulations’) and (B) TSEcl (‘classes simulations’).

The average <Φ^cal>, calculated over all residues, measured experimentally or not, is 0.37 for TSEsp and 0.36 for TSEcl. For comparison, the average over the residues measured experimentally is 0.43; this higher value reflects the bias in the choice of more core residues to probe the structure of the TS in correspondence to the likely folding nucleus. For sets B and C, <Φ^cal> was 0.36 and 0.35, respectively. The Φ-value profiles are shown in Fig. 2A. Diamonds represent the experimental Φ-values, the black curve data from TSEsp and the grey curve data from TSEcl. As required by the method, the coefficient of correlation between Φ^cal resulting from the ‘specific simulations’ and Φ^exp is 0.99. The agreement between Φ^cal from TSEsp and Φ^exp is also very close, with a coefficient of correlation of 0.92. Further, the calculated Φ-values from TSEsp match closely those obtained with TSEcl, with a coefficient of correlation of 0.92. The Φ-value profiles are almost identical, except for the loop region between strands β4 and β5. The Φ-value profile generated using set B of possible values for Φ_L and Φ_H is very similar to the one computed using set A or TSEsp. The coefficient of correlation to the Φ^exp values is 0.94 and to the full set of Φ^cal generated using TSEsp is 0.88. In the case of set C, the coefficient of correlation to Φ^exp is 0.93; the coefficient of correlation to Φ^cal generated using the ‘specific simulations’ is 0.84. These results indicate that the exact position of the boundaries Φ_L and Φ_H is not important.

Fig. 2.

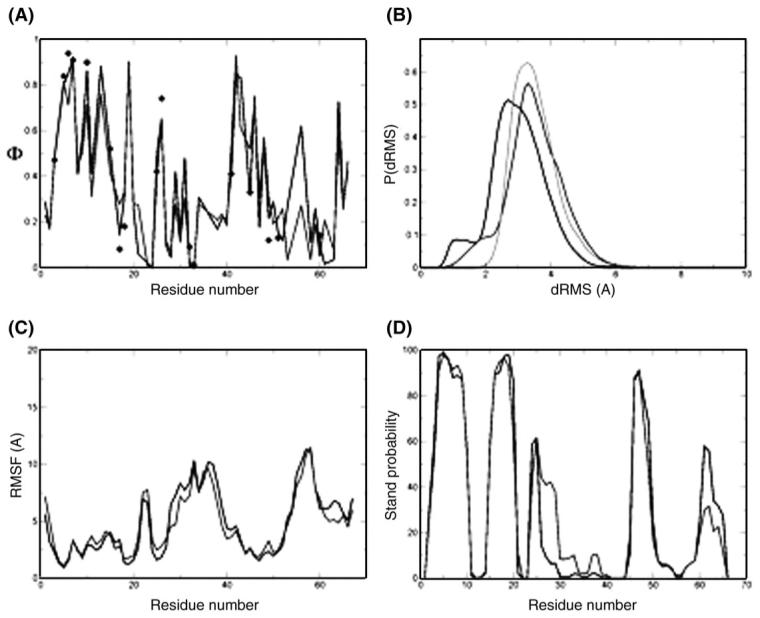
TS ensemble of CspB. (A) Φ-value profiles of the ‘specific simulations’ TSE (black curve) and the ‘classes simulations’ TSE (light gray curve); the experimental Φ-values are indicated by black diamonds. (B) Histogram of dRMS between all pairs of structures within each TSE and between the TSEs. The black line is the distribution of dRMS within the ‘specific simulations’ TSE and the light gray line the distribution of dRMS within the ‘classes simulations’ TSE. The dark gray line is the distribution of dRMS between the TSEs. (C) RMSD fluctuations per residue for the ‘specific simulations’ TSE (black curve) and the ‘classes simulations’ TSE (light gray curve). (D) Probability of β strand formation in the TSEs of CspB computed using the program DSSPcont (Carter et al., 2003). The ‘specific simulations’ TSE is represented by the black line and the ‘classes simulations’ TSE by the light gray line. The two methods generated structures of very similar secondary structure.

We determined 3089 structures to represent the TSE using the ‘specific simulations’ and 1632 for the ‘classes simulations’. To analyse the similarity between the two ensembles we calculated the C_α distance-based root mean square deviation (dRMS) between all pairs of structures within each ensemble and between the two ensembles. The distribution of pairwise dRMS between the two ensembles is very similar to the distribution within the ensembles (i.e. the light gray curve is very similar to the dark gray and black curve in Fig. 2B), indicating that the structures are very similar. In order to compare these two ensembles, structures were clustered with a 3 Å cut-off, so that all structures that are within 3 Å RMSD belong to the same cluster. This procedure yielded 53 main clusters for the ‘specific simulations’ and 45 main clusters for the ‘classes simulations’, indicating that the structural heterogeneity of the structures determined with the two methods is very similar. In order to analyse the behaviour of individual residues, the RMSD fluctuations per residue were calculated for both types of bias. The result is shown in Fig. 2C, the black and the light gray lines represent data for TSEsp and TSEcl, respectively. The data are again very similar, with a coefficient of correlation of 0.95.

The ‘specific’ and ‘classes simulations’ generate TSEs that are also very similar in terms of secondary structure elements and tertiary interactions. The secondary structure content of both ensembles was calculated using the program DSSPcont (Carter et al., 2003). The probability of β-strand formation is shown in Fig. 2D; the black line corresponds to TSEsp and the light gray line represents TSEcl. The results are remarkably similar for the β strands that have a very high probability of formation (β1, β2 and β4) as well as for those that have a low probability of formation (β3 and β5). In β3, the ‘classes simulations’ ensemble has a slightly larger probability of β-strand formation, whereas it is to some extent lower in β5 (compared with the ‘specific simulations’ ensemble).

The average side-chain interaction energy between pairs of residues was computed (Fig. 3). These energy maps are very similar, indicating that the native-like topology of the TS of CspB is well defined in both cases. Interactions between strands β1 and β2 are somewhat stronger in TSEcl, reflecting the slightly higher probability of formation of strand β2 in this ensemble. In contrast, interactions between strands β4 and β5 are stronger in TSEsp, which is explained by the lower probability of formation of β5 in TSEcl. Local as well as long-range interactions occurring in TSEsp are reproduced in TSEcl with remarkable precision. Although the restraints are more coarse-grained in the ‘classes simulations’, the interactions between individual residues are very similar to those arising from the ‘specific simulations’ ensemble.

Fig. 3.

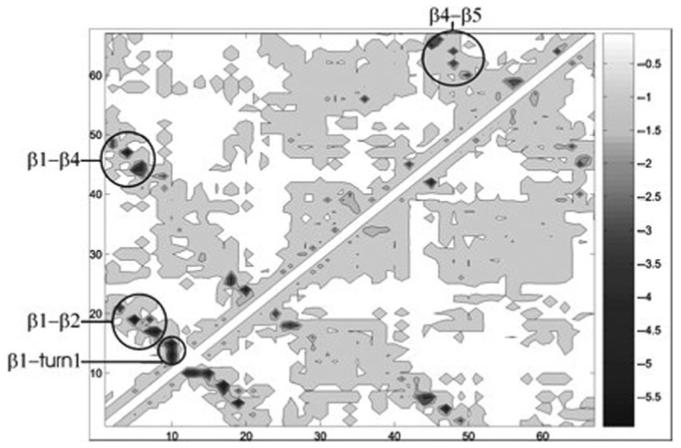
Energy maps of TSEsp (above the diagonal) and TSEcl (below the diagonal) of CspB. An energy map is a matrix representation of an ensemble of conformations in which the element i, j is the EEF1 (Lazaridis and Karplus, 1999) interaction energy between residues i and j, averaged in the ensemble. Energies are given in kcal/mol.

On the basis of the analysis of the experimental Φ-values, Garcia-Mira et al. (2004) have described several of the properties of the TS for folding of CspB. The restrained simulations generated using their experimental data enable us to verify their description in terms of the ensembles of structures that we determined.

Garcia-Mira et al. (2004) suggested that β1 is formed in the TS and that it has already established several long-range interactions with the segment of the sequence forming strand β4 in the native structure. This description is confirmed by our calculations; according to DSSPcont (Carter et al., 2003) (Fig. 2), both strands are fully formed and the interaction matrices (Fig. 3) reveal strong interactions between them. Val6 in β1, the residue with the highest Φ-values exhibits strong interactions with residues Leu41 to Gln45 at the C-terminal part of β4, as proposed by Garcia-Mira et al. (2004) Lys5, which also has a Φ-value close to 1.0, forms contacts with residues Gly44 to Ala46 in β4. As the side chains of Lys5 and Glu19 do not interact significantly in the native state crystal structure (PDB 1nmg), Garcia-Mira et al. (2004) suggested that this interaction is also absent in the TS. However, our equilibrium molecular dynamics simulations of the native state suggest that these side chains do interact when CspB is folded. In addition, we also found significant interactions between them in the TSE. The computed Φ-value for Glu19 is remarkably high (0.9±0.1 in both ensembles). All other Φ-values in strand β2 are below 0.5 in both ensembles (the Φ-value for Gly14 cannot be calculated in our model of native side-chain contacts). The Φ-value for Glu19 could not be measured experimentally with confidence because ΔΔG_D-N is only ∼0.3 kJ mol⁻¹. Here, simulations can help in estimating the Φ-value with a precision comparable to that of experiments (±0.1, as generally quoted for Φ-values). Interestingly, despite the only partial experimental Φ-values in β2, we find that this strand is fully formed in both TSEsp and in TSEcl.

Characterisation of the TS ensemble of mAcP

The ensembles of structures that we determined to represent the TS of mAcP are shown in Fig. 4 and their properties are reported in Table I. Within the statistical error, all the general properties are similar whether the classes or the specific method was used.

Fig. 4.

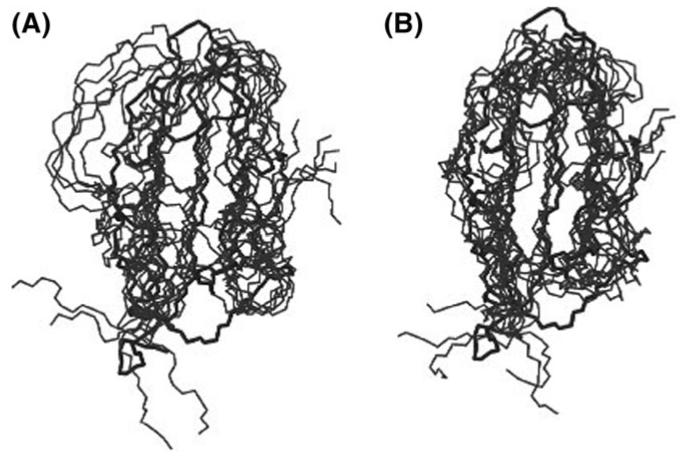
Comparison between the TS ensembles of mAcP that we have determined in this work: (A) TSEsp (‘specific simulations’) and (B) TSEcl (‘classes simulations’).

The Φ-value profile for mAcP is shown in Fig. 5A, where the diamonds indicate the experimental values and the black and light gray curves the Φ-values resulting from the restrained simulations, using either TSEsp or TSEcl, respectively. The Φ-values resulting from TSEcl are very similar to those of TSEsp with a coefficient of correlation of Φ^cal is 0.82.

Fig. 5.

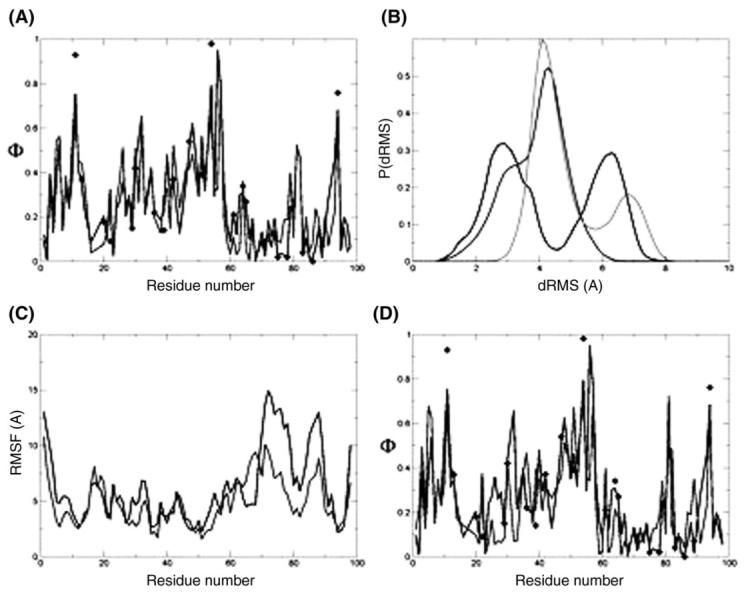
The TS ensemble of mAcP. (A) Φ-value profiles of the ‘specific simulations’ TSE (black curve) and the ‘classes simulations’ TSE (light gray curve); the experimental Φ-values are indicated by the black diamonds. (B) Histogram of dRMS between all pairs of structures within each TSE and between the TSEs. The black line is the distribution of dRMS within the ‘specific simulations’ TSE and the light gray line the distribution of dRMS within the ‘classes simulations’ TSE. The dark gray line is the distribution of dRMS between the TSEs. (C) RMSD fluctuations per residue for the ‘specific simulations’ TSE (black curve) and the ‘classes simulations’ TSE (light gray curve). (D) Φ-value profile of the ‘specific simulations’ TSE using all experimental Φ-values as restraints (black curve) and of the ‘key residue classes simulations’ TSE (light gray curve). The experimental Φ-values are indicated by the black diamonds.

Both ensembles (1144 structures from TSEsp and 1505 structures from TSEcl) were clustered (RMSD) using a 3 Å cut-off. This procedure yielded 43 main clusters for the TSE determined using TSEsp and 58 main clusters for TSEcl; the ensembles exhibit thus a similar structural homogeneity. Following to the procedure described for CspB, the TSEsp and TSEcl were also compared by computing sets of dRMS within and between them. Normalised histograms of the dRMS sets show that the TSEs are very similar (Fig. 5B). Interestingly, there is a bimodal distribution of structures within TSEsp. Even a RMSD clustering with a cut-off of 9 Å still yields two different groups of clusters. RMSD fluctuations per residue were also computed for each ensemble; the coefficient of correlation between the two data sets is 0.76 indicating significant similarity (Fig. 5C, the black and the light gray lines represent data from TSEsp and TSEcl, respectively).

We further tested the equivalence between the two types of bias by using them to define the key residues for folding, which are defined as those whose interactions alone are sufficient to establish the topology of the native state (Vendruscolo et al., 2001; Lindorff-Larsen et al., ​2004, ​2005). ‘Key residue simulations’ are restrained simulations that use as experimental input only a subset of residues (the key residues). These residues enable the determination of the TSE, as judged by the ability to reproduce the Φ-value profile, general properties and secondary and tertiary structure of the TS. Key residues have been identified for a number of proteins, including mAcP, TNfn3, TI I27 and the SH3 domains (Vendruscolo et al., 2001; Paci et al., ​2002, ​2003; Geierhaas et al., ​2004, ​2005; Lindorff-Larsen et al., 2004). The key residues in mAcP were identified as Tyr11, Pro54 and Phe94 (Vendruscolo et al., 2001). We performed restrained molecular dynamics simulations by requiring that these three residues have a Φ_high [‘key residue classes simulations’, see Eqs. (3) and (5)] resulting in the TSEkr ensemble. TSEkr and TSEsp were compared. The cross-correlated correlation coefficient between all Φ^exp and Φ^cal from TSEkr is 0.74, the correlation between the two sets of Φ^cal (i.e. using the whole set of 22 experimental Φ-values and only the key residues) is 0.77. These values are similar to those reported by Paci et al. (2002). Remarkably, for the ‘key residue classes simulations’, the correlation to the whole set of experimental Φ-values is 0.80. The correlation of Φ^cal from TSEkr to Φ^cal from the whole set of experimental Φ-values of TSEsp is 0.70. The data are shown in Fig. 5D, the black line is the ‘specific simulations’ with 22 experimental restraints and the light gray line represents the ‘key residue classes simulation’. Experimental Φ-values are indicated by diamonds.

Discussion

In the molecular dynamics simulations that we have presented, the Φ-values are interpreted in terms of approximate fractions of native contacts. This interpretation is based on the four conditions that should be considered in the Φ-value analysis to ensure that mutants create minimal perturbations to the folding process (Fersht et al., 1992), (i) mutations do not alter the pathway of folding, (ii) mutations do not significantly change the structure of the folded state, (iii) mutations do not perturb the structure of the unfolded state, (iv) refolding proceeds by the reverse route of folding.

The structural interpretation of Φ-values has an interesting analogy (Daggett et al., 1996) with that of inter-proton distances measured through NOEs in NMR spectroscopy (Wuthrich, 1989). The translation of individual NOE measurements into distances is potentially affected by a series of problems: if a molecule is not rigid, different protons will have different reorientational correlation times and therefore the corresponding NOE enhancements will not be comparable; in addition, the reorientation may be anisotropic; the dipole-dipole relaxation mechanism that gives rise to the NOE may involve also other neighbouring spins, for example in the case of equivalent spins (e.g. in methyl groups). This type of concern appeared initially so severe that the approach did not seem suitable for the determination of the structures of proteins (Wuthrich, 1989). However, it was soon realised that the availability of a large number of distance restraints allowed the use of distances information in a loose way and to determine structures at high resolution (Wuthrich, 1989). The approach that we present here also uses simultaneously the information obtained from several different measurements, in this case Φ-values. An important difference between NOEs and Φ-values is that one has several hundreds NOEs whereas only few Φ-values are normally available. However, NOEs provide individual pairwise distance restraints, whereas, in contrast, Φ-values yield multiple simultaneous restraints, so they impose severe conditions on the topology of the polypeptide chain (Vendruscolo et al., 2001; Lindorff-Larsen et al., ​2004, ​2005).

We note that this approach neglects the role that non-native interactions can play in stabilising TSs, and the contribution that non-native interactions may have in Φ-value analysis, which is based on energetic and kinetic measurements. Our results are fully consistent with the general assumptions of the Φ-value analysis, in particular with those about the relatively minor role played by non-native interactions in the TS. The interaction maps (Fig. 3) suggest that there are indeed a number of non-native interactions in the TSE, but these are generally significantly lower in energy than the native interactions observed. One, however, should remember that significant non-native interactions may be formed by specific residues, at least as long as they do not create significant free energy barriers between the TS and the native state. Where the role of non-native interactions is significant, this may be detected by non-classical Φ-values (>1 or <0), as has been seen, for example in the immunity proteins (Paci et al., 2004).

It has been shown for many proteins that the topology of the TSs is the same of the native states (Daggett et al., 1996; Vendruscolo et al., 2001; Daggett, 2002; Ferguson et al., 2005; Lindorff-Larsen et al., ​2004, ​2005). A significant problem in the structural interpretation of Φ-values is that equilibrium free energies and folding and unfolding rates are measured experimentally, so the interpretation of Φ-values in terms of contacts should be carefully tested. Indeed, concerns have been raised on this issue. Garcia-Mira et al. (2004) reported that since ‘Φ is the ratio of ΔΔG_TS-D and ΔΔG_N-D, it carries no information about the magnitude of these free energies or about the number of interactions provided by a particular residue’. Interesting examples are the Φ-values for K7A and L41 of CspB. The mutations destabilise the TS by a similar amount, but the Φ-values are very different, 0.9 and 0.4 for K7A and L41A, respectively, due to different destabilisations of the native state. We have performed restrained simulations, using both the ‘specific’ and the ‘classes simulations’, without restraining K7A and L41A; results are presented in Table II. The predicted Φ-values for K7A and L41A were 0.8 (0.9 experimental) and 0.5 (0.4 experimental), respectively. Thus these Φ-values are predicted with confidence using the assumption that Φ-values report on the degree of formation of native contacts in the TS.

Table II.

Prediction of Φ-values for K7A and L41 of CspB

Mutant	Φ exp	Φcal [Eq.(2)]a	Φcal FOLD-Xb
K7A	0.9	0.8	1.0
L41A	0.4	0.5	0.5

^aΦ-value calculated using the fraction of native contacts, see Eq. (2).

^bΦ-value calculated using Eq. (1). The values of ΔΔG_D-N and ΔΔG_D-TS are calculated using the program FOLD-X³⁶.

We have also examined the structures by following an approach by Lindorff-Larsen et al. (2003). The program FOLD-X (Guerois et al., 2002) was used to calculate the changes in stability resulting from the mutations in both the native state ensemble and the TS ensemble. This method allows us to calculate ΔΔG_D-TS, ΔΔG_D-N and thus to estimate the Φ-value (Lindorff-Larsen et al., 2003). It yielded Φ-values of 0.5 for L41A (0.4 experimental) and 1.0 for K7A (0.9 experimental). The values of ΔΔG_D-N and ΔΔG_D-TS in our simulations for K7A were both 4 kJ/mol and for L41A 13 and 7 kJ/mol, respectively. These values are close to the experimental values provided by Garcia-Mira et al. (2004), for K7A 5 and 4 kJ/mol for ΔΔG_D-N and ΔΔG_D-TS, respectively; for L41A, 11 and 4 kJ/mol for ΔΔG_D-N and ΔΔG_D-TS, respectively. Thus, in the case of CspB, the model of native contacts is a good approximation for Φ-values (Lindorff-Larsen et al., 2003). The predicted Φ-values are very close to the experimental values, independently from the definition of Φ-value that was used, i.e. by fraction of native contacts or by computing the values of ΔΔG_D-N and ΔΔG_D-TS using the program FOLD-X (Guerois et al., 2002).

We also used the method of calculating ΔΔG_D-TS of TS structures as a control of the filtering procedure that we used to select structures after the restrained simulations. For this purpose, we define the quantity

$${\rho }_{\Delta \Delta G}=\frac{1}{N_{\Phi }}\sum _{i\in E}\mid \Delta \Delta G_{\mathrm{D}-\mathrm{TS}}^{i,\mathrm{cal}}-\Delta \Delta G_{\mathrm{D}-\mathrm{TS}}^{i,\exp }\mid ,$$ (8)

where N_Δ is the number of experimental Φ-values and the index i represents the mutated residues. Six thousand structures are generated by the restrained simulation (see Methods section), in a following step ρΔΔG is calculated for each structure. Structures are accepted if ρΔΔG is lower or equal 2.0 kJ/mol.

The resulting ensemble for CspB has been analysed in detail, the general properties are presented in Table I. Within the statistical error, the values are the same than those of the ensemble that is generated using the filtering with an estimated range for SASA of the TS and the average Φ-value (as described in the Methods section). This result supports the method that we followed to define the TS.

Conclusions

We have shown that the simultaneous use of a large set of Φ-values divided into three classes (low, medium and high) as structural restraints in molecular dynamics simulations can provide sufficient information for characterising the architecture of the TS at the same level of accuracy obtainable by using the actual numerical values obtained experimentally. These results provide support to the idea that the combined use in structure determination approaches of multiple restraints that are individually of relatively low accuracy can result in conformations of relatively good quality.