Nuclear hourglass technique: An approach that detects electrically open nuclear pores in Xenopus laevis oocyte

Abstract

Nuclear pore complexes (NPCs) mediate both active transport and passive diffusion across the nuclear envelope (NE). Determination of NE electrical conductance, however, has been confounded by the lack of an appropriate technical approach. The nuclear patch clamp technique is restricted to preparations with electrically closed NPCs, and microelectrode techniques fail to resolve the extremely low input resistance of large oocyte nuclei. To address the problem, we have developed an approach for measuring the NE electrical conductance of Xenopus laevis oocyte nuclei. The method uses a tapered glass tube, which narrows in its middle part to 2/3 of the diameter of the nucleus. The isolated nucleus is sucked into the narrow part of the capillary by gentle fluid movement, while the resulting change in electrical resistance is monitored. NE electrical conductance was unexpectedly large (7.9 ± 0.34 S/cm²). Evaluation of NPC density by atomic force microscopy showed that this conductance corresponded to 3.7 × 10⁶ NPCs. In contrast to earlier conclusions drawn from nuclear patch clamp experiments, NPCs were in an electrically “open” state with a mean single NPC electrical conductance of 1.7 ± 0.07 nS. Enabling or blocking of active NPC transport (accomplished by the addition of cytosolic extracts or gp62-directed antibodies) revealed this large NPC conductance to be independent of the activation state of the transport machinery located in the center of NPCs. We conclude that peripheral channels, which are presumed to reside in the NPC subunits, establish a high ionic permeability that is virtually independent of the active protein transport mechanism.

Nuclear envelopes (NEs) of Xenopus laevis oocytes have been the favored preparation for evaluation of nuclear transport and for studies of nuclear pore complexes (NPCs) structure and function, but only limited data are available on the electrophysiological properties of this important barrier, mainly because of technical limitations.

Electrophysiological evaluation of NE started in the early sixties. Using two microelectrodes impaling the nucleus of a Drosophila salivary gland cell, Loewenstein and his coworkers (1) measured the electrical conductance of the NE. The conductance was much smaller than they had expected. At that time, NPCs were thought to be open gaps in the nuclear membrane with a diameter of at least 40 nm. From their electrical conductance measurements, Loewenstein and coworkers concluded that a protein structure must be present in these gaps that restricts the opening to less than 10 nm, resulting in an electrical conductance of about 1 nS per nuclear pore (2). This observation came very close to the view of the nuclear pore that has emerged as a result of much later studies, in which the diffusion of differently sized molecules was measured. According to this view, the NPC forms an aqueous channel of 8–12 nm in diameter and 40–50 nm in length (3). From this data, a NPC electrical conductance of 1–2 nS can be calculated (4).

In subsequent studies, the ontogenetic and phylogenetic variability of the NE conductance was evaluated. Interestingly, a remarkable effect of the steroid hormone ecdysone on the electrical conductance of the insect salivary gland nucleus could be shown (5). Significant differences were shown to exist between these nuclei and those of several marine oocytes (6). In particular, oocyte nuclei showed a significant higher electrical conductance than the gland cell nuclei (7). Although these experiments were based on solid technical grounds, electrophysiological work on NEs made slow progress over the next two decades. This lack of progress may in part have been caused by the lack of suitable experimental techniques to allow manipulation of nuclei.

Our current knowledge about the NE is, to a large extent, based on studies using large amphibian oocytes. Unfortunately, these nuclei cannot be investigated with the microelectrode technique for technical reasons (7, 8). To measure the conductance of NE with two microelectrodes, one of the electrodes is used to inject a current into the nucleus that induces a voltage drop across the NE. This voltage drop is measured with the second electrode. The amount of current needed to induce a measurable voltage drop directly depends on the NE surface area, which, in turn, increases proportionately with the second power of the nucleus’s diameter. As a consequence, there is a size limit on nuclei that can be studied with this technique, effectively excluding nuclei with a diameter of more than 70 μm (7, 8). Amphibian oocyte nuclei have diameters of up to 400 μm.

A possible way out of this dilemma could be the application of the patch clamp technique to the NE in a “nucleus attached” configuration (9–11). Here, only the limited membrane area inside the patch pipette is evaluated, and thus the size of the nucleus becomes irrelevant. However, application of the patch clamp technique to NE is still a subject of controversy. One serious concern is that in most cases the conductances measured with the patch clamp technique do not match the number of NPCs in the patch (12). The conclusion has been drawn that during patch clamp experiments most, if not all, of the NPCs are in a closed state (13). At present, it is not clear whether this closed state is a physiological property of NPCs or is a problem introduced by the method. Moreover, it is difficult to decide whether the remaining conductances originate from NPCs or from other ionic channels in the NE. In a recent study (12), we applied atomic force microscopy to demonstrate that membrane patches showing extremely low electrical conductances do not consist of a complete NE with nuclear pores, but rather consist of only either the outer nuclear membrane or endoplasmic reticulum. Patches consisting of complete NE revealed much larger conductances, but still not large enough to account for the number of pores in the patch. Therefore, direct proof is still lacking that NE patch clamping is a noninvasive approach that leaves NPCs in an operating, functional state. To address these problems we have developed the nuclear hourglass technique as an approach for measuring the NE electrical conductance of X. laevis oocyte nuclei.

Methods

Preparation of Nuclei.

Female X. laevis were anesthetized with 0.1% ethyl m-aminobenzoate methanesulfonate (Serva), and their ovaries were removed. Oocytes were dissected from ovary clusters and stored in modified Ringer’s solution (87 mM NaCl, 6.3 mM KCl, 1 mM MgCl₂, 1.5 mM CaCl₂, 10 mM Hepes, 5.5 mM glucose, pH 7.8) before use. For isolation, the oocytes were transferred into nuclear isolation medium (NIM) [90 mM KCl, 10 mM NaCl, 2 mM MgCl₂, 1.1 mM EGTA, 10 mM Hepes, 0.16 mM Ca²⁺ (corresponds to free Ca²⁺ of 10⁻⁸M because of presence of EGTA), polyvinylpyrrolidone (PVP, M_r = 40,000, 1.5%), pH 7.32]. The nuclei were isolated by piercing the oocyte with two pincers. The PVP was added to compensate for the lack of macromolecules in the NIM as compared with the intact cytosol. The presence of PVP is important to prevent the dramatic swelling of the cell nucleus, which occurs in pure electrolyte solution.

Cytosolic extracts and anti-gp62 antibodies were used to enable or block active protein transport across NPCs. Cytosolic extract was prepared from X. laevis oocytes as described in ref. 14. This extract was diluted with 50% NIM before using it in nuclear hourglass measurements. The polyclonal antibody directed against nucleoporin gp62 was a kind gift of G. Krohne (Biocentre, University of Würzburg, Germany) and is specific for X. laevis p62 (15, 16). For nuclear hourglass measurements, nuclei were incubated for 2 hr in NIM containing the antibody in 1:100 dilution.

Principle of the Measurement.

The main part of the setup is the buffer-filled capillary with the tapered part in its middle. At this site, the inner diameter of the capillary is about 2/3 of the diameter of the nucleus. A current of up to 1 mA is injected via two massive Ag/AgCl electrodes placed at the ends of the capillary. The voltage drop is measured with two conventional microelectrodes. The tips of these microelectrodes are placed near the narrow part of the capillary. Thus, only the electrical resistance of the fluid column between the electrode tips is measured, rather than the electrical resistance of the whole capillary. Because current and voltage are measured at the same time, the resistance can be calculated online and displayed during the measurements. By gravity, and a gentle downward flow of the buffered fluid, the nucleus is maneuvered into the tapered part of the capillary. Thus, the whole current now flows through the nucleus. The resulting rise in electrical resistance indicates the electrical resistance of the nucleus. To prevent electrical polarization of the nuclear membrane, the polarity of the current is continuously inverted at intervals of 1–2 sec.

The mechanical setup of the nuclear hourglass technique is simple. Because the tapered part of the capillary is fragile, the ends of the capillary have to be mechanically fixed, which is done by plugging the ends of the capillary into drilled holes of two acrylic blocks that are mounted on a bar. Short pieces of silicone tubing are fitted into these holes to ensure a leak-proof seal. The bar with the acrylic blocks is mounted on a rack so that the capillary is positioned with a vertical orientation. The acrylic blocks have additional holes drilled that make contact with the lumen of the capillary. One of the holes drilled in the lower acrylic block is used to supply fluid to the capillary, while the others allow access for current and voltage electrodes.

The capillary is filled with buffered fluid from one of several reservoirs through silicon tubing. Because the upper end of the capillary is open, the fluid level is balanced between the capillary and the reservoir. Mounted on a movable bar, the reservoirs can be raised or lowered a few millimeters to induce gentle fluid movements within the capillary. This mechanism is used to position the nucleus into the tapered part of the capillary. The position of the nucleus can be observed by means of a stereomicroscope.

Tapered capillaries are made from glass capillaries with 2 mm outer and 1.7 mm inner diameter (Servoprax, Wesel, Germany). The narrowing is introduced by using a vertical patch pipette puller (LM-3P-A, List Electronics, Darmstadt, Germany) and a modified pulling protocol. In a first step, heat and pulling force are applied to introduce an initial narrowing to about 50% of the initial outer diameter. In the second step, only heat and no pulling force is applied. Under these conditions, the walls of the narrowed part of the glass capillary become thickened, so that the inner diameter is reduced but the outer diameter remains essentially unchanged. After pulling, the capillaries are incubated for 1 hr in 1% BSA, which results in a coating that prevents adhesion of the nuclei to the glass walls during experiments.

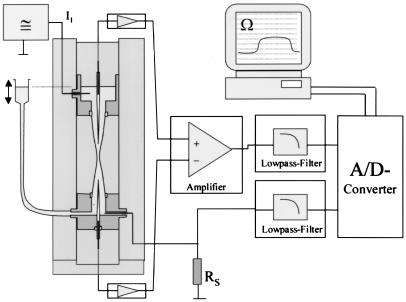
Fig. 1 shows the electrical circuitry of the setup. Two Ag/AgCl electrodes and a pulse generator are used to drive an alternating current of up to 1 mA through the capillary. Current is measured as a voltage drop over a series resistor of 100 Ω. This signal is recorded after filtering through a Bessel type low-pass filter. Two conventional KCl-filled microelectrodes are connected to a differential amplifier to measure the voltage drop across the center part of the capillary. The output of this amplifier also is filtered through a Bessel type low-pass filter before recording. For recording, a computer with a Digidata 2000 ADC board and pclamp7 software (Axon Instruments, Foster City, CA) is used. From current and voltage, the resistance is calculated online and displayed on the monitor.

Figure 1.

Electrical circuit of the nuclear hourglass technique. Two silver wires and a pulse generator are used to drive an alternating current of 1 mA through the capillary. Two conventional KCl-filled microelectrodes are connected to a differential amplifier to measure the voltage drop across the central part of the capillary. The resistance is calculated online from the applied current and measured voltage.

Analysis of Data.

The raw data obtained from the experiments represents the change in electrical resistance of the capillary, introduced by the whole nucleus that occludes the narrowing. This resistance of the whole nucleus, R_Nuc, is composed of three components: the electrical resistance of the upper and lower NE surface, R_NE1 and R_NE2, plus the electrical resistance of the nucleoplasm, R_Chromatin. From this, the electrical resistance of one single NE surface can be readily calculated:

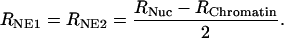1

However, it is convenient to use the reciprocal of the electrical resistance, the conductance G_NE:

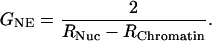2

To allow comparison of measurements from differently sized nuclei in differently sized capillaries the data are normalized by dividing by the area of the measured NE section. For simplicity, it is assumed that the area of the NE segment has a spherical shape. The following equation then can be used to calculate the area of the sphere segment:

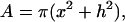3

where x is the radius and h the height of the sphere segment (see Fig. 2 for details). Then, electrical conductance per area, G̃_NE (S/cm²) of the NE is calculated by using the equation:

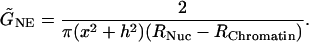4

Eq. 4 does not consider the possibility that a substantial amount of the current I could bypass the nucleus through the narrow gap between the inner wall of the capillary and the nucleus. This shunt would result in an underestimation of the nuclear resistance and an overestimation of the NE electrical conductance. This effect can be modeled by the introduction of a shunt resistance in the equivalent circuit (Fig. 2). To estimate the error introduced by R_Shunt, we can calculate its influence on the apparent value of R_Nuc:

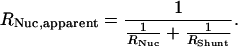5

A rough estimation for R_Shunt can be obtained by introducing a X. laevis oocyte of stage I into the capillary. These oocytes are approximately of the same size as compared with stage VI oocyte nuclei. Because the electrical conductance of the plasma membrane is extremely low compared with the NE, this measurement will be dominated by R_Shunt. Using this approach, we found that R_Shunt was always greater than 30,000 Ω. If a typical R_Nuc of 500 Ω is measured, the apparent resistance will be reduced by this R_Shunt to 492 Ω. The error introduced by shunt leakage is thus less than 2%.

Figure 2.

The nucleus inside the capillary and the resulting equivalent circuit. The electrical resistance detected by the nuclear hourglass technique is composed of the resistance of the two NE segments, R_NE1 and R_NE2, and the resistance of the interior of the nucleus, R_Chromatin, in series. The parallel resistor, R_shunt, models the possibility of a substantial amount of the current I bypassing the nucleus through the narrow gap between the inner wall of the capillary and the nucleus. The surface area of the NE segments corresponding to R_NE1 and R_NE2 is calculated by using the geometrical parameters r (the radius of a hypothetical sphere segment) and h (its height) as indicated.

Evaluation of R_Shunt using intact oocytes instead of isolated nuclei could be challenged by the argument that the R_Shunt of a nucleus could differ from that of an oocyte because of different surface properties. Therefore, we used another approach to obtain a minimum estimate of R_Shunt. This approach is based on the observation that R_Nuc can be increased by application of permanent direct current. In such experiments, instead of current pulses with alternating polarity, constant direct current of 100 μA was applied for several minutes. Under these conditions, the chromatin inside the nucleus slowly moves toward the inner (nucleoplasmic) NE surface adjacent to the positive electrode. This electrophoretic movement is accompanied by an increase in R_Nuc, which reaches a steady-state value of 6,900 ± 500 Ω after 90 ± 9 sec (n = 6). This dramatic increase in R_Nuc is most likely explained by a “plugging” of NPCs with charged nucleoplasmic macromolecules moved by the electric field. Macromolecules plugging the electrodiffusive pathways of NPCs would reduce electrical current flow through the NE and increase R_Nuc. On the basis of the observation that R_Nuc can be increased by such a maneuver, it must be concluded that R_shunt in these experiments is larger, or at least equal, to the maximum value of R_Nuc. Therefore, our minimum estimate of R_Shunt is 6.9 kΩ, which leads to a maximum estimate for the error introduced by shunt leakage of less than 6%. Thus, we usually made no attempt to make corrections for R_Shunt.

The conductance of a single NPC can be obtained by dividing through the number of pores per cm². The pore density was determined by using the atomic force microscopy technique as described in refs. 17 and 18. In brief, individual intact nuclei were picked up with a Pasteur pipette and transferred to a glass coverslip placed under a stereo microscope. Watching the nucleus carefully, the chromatin was removed by using sharp needles, and the NE was spread on glass, making sure that its nucleoplasmic side was facing downward. The specimens were washed with deionized water, dried briefly, and rehydrated in NIM before the scanning procedure. The drying step is necessary to improve the adhesion of the NE to the specimen support.

Results

The main reason for the development of the nuclear hourglass technique was that total electrical conductance of large amphibian oocytes is too large to be resolved by conventional microelectrode techniques (7). The maximal electrical conductance resolvable with the hourglass technique is 100 mS. The conductances of the X. laevis oocyte nuclei were in a range between 1 mS and 5 mS and thus could be resolved without problems.

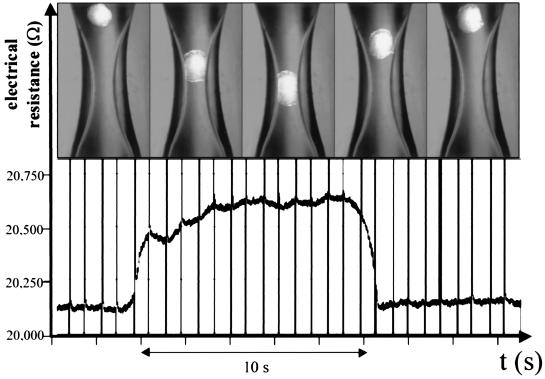
Fig. 3 shows an example of a single measurement. The sequence of pictures shows how the nucleus is positioned in the capillary by gentle fluid movement (see a movie that is available as supplemental material on the PNAS web site, www.pnas.org). For exact measurements it is necessary that the movement of the nucleus is slow, so that the nucleus rests in the narrowing for at least 5 sec. The single measurement is completed by a slow upward movement of the buffered fluid, which removes the nucleus from its occluding position, while the electrical resistance of the capillary returns to the baseline. This single measurement can be repeated with the same nucleus as often as desired. Between the single measurements, the nucleus hovers in the slowly upward-moving buffered fluid, which provides the possibility of changing the buffer fluid between single measurements and carrying out paired experiments with different buffers on the same nucleus.

Figure 3.

Example of a measurement. The oocyte nucleus is moved into the tapered part of the capillary by a gentle fluid movement. The resulting change in electrical resistance is shown below.

The experiment shown in Fig. 3 was carried out with 1.5% PVP in the buffer. We used this inert substance to mimic the osmotic pressure of the cytosol in our buffered solutions. As a consequence, the nuclei maintained their original size and did not osmotically swell. Under these conditions, nuclei had normal inner hydrostatic pressure and easily adapted their form to the capillary. They could be pushed through the narrowing of the capillary without application of significant hydrostatic pressure. As a result, the mechanical stress is negligible and measurements can be repeated as often as desired without damaging the nucleus. The adaptation of the nucleus to the shape of the capillary is at the same time a requirement for a good electrical seal between the nucleus and the capillary walls, which results in a high value for R_Shunt. In contrast, without PVP the nuclei were osmotically swollen, reflecting a high, nonphysiological hydrostatic pressure. This swelling made it impossible to use these nuclei for measurements because significant pressure had to be used to suck them into the narrowing, and they thus tended to burst.

NE electrical conductance was not altered by repetitive measurements. The average deviation of two consecutive measurements of the same nucleus was 2.8% (n = 22) and showed no obvious trend in any direction during 10 consecutive measurements. Thus, measurements with the nuclear hourglass technique are noninvasive and reproducible.

The parameter that is directly measured with the hourglass technique is the electrical resistance of the whole nucleus. In 37 experiments (see Table 1), using standard conditions, this resistance was 456 ± 13 Ω. A fraction of this resistance is caused by the electrical resistance of the chromatin. This resistance was determined in control experiments, where the NE was removed and only the compact cytoplasm of the nucleus was measured. In five experiments, the chromatin resistance was approximately 100 Ω. This value was used for R_Chromatin in all calculations using Eq. 3. The conductance per area of X. laevis oocyte NE was 7.9 ± 0.34 S/cm² (n = 37).

Table 1.

Electrical and structural data of NEs in X. laevis oocytes

Number of nuclei	37
Resistance of whole nuclei	456  ±  13 Ω
Conductance of single NE segments	6.2  ±  0.27 mS
Surface area of single NE segments	77,000 μm2
Number of NPCs of NE segments	3.7 × 106
NE electrical conductance per area	7.9  ±  0.35 S/cm2
Mean single NPC conductance	1.7  ±  0.07 nS

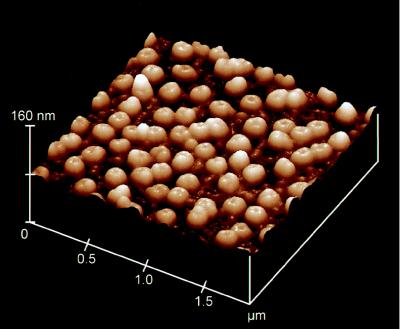
The density of NPCs per area NE was determined with the atomic force microscopy technique, as shown in Fig. 4. The average density of NPCs was 48 NPCs/μm². The average conductance of a single NPC was therefore 1.7 ± 0.07 nS. This value is in the same order of magnitude as expected from current structural models of the NPC, namely with the assumption of an aqueous channel of 9 nm in diameter and 15–30 nm in length (3). In contrast, this conductance is high, compared with published results obtained with the patch clamp technique. With this technique, usually only a few channels per μm² are observed. These channels frequently had conductances in the range of 0.2 to 0.5 nS (10, 11, 19–22). Only in some cases, single channel conductances of up to 1.7 nS have been observed (9, 23).

Figure 4.

Atomic force microscopy image of a X. laevis oocyte NE spread on mica. The mean density of NPCs is 48 pores/μm².

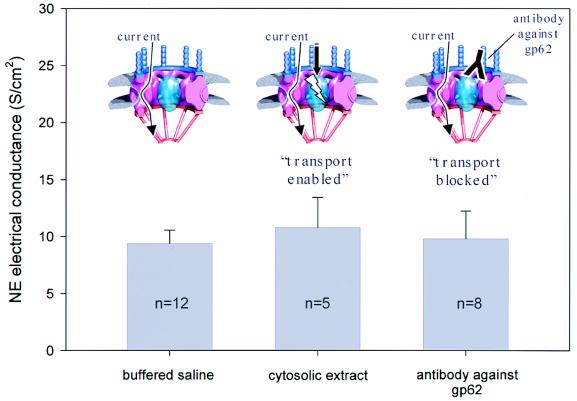
The NE electrical conductance value given above was measured in a buffered saline solution with cytosolic ion composition. However, NE electrical conductance may depend on the functional state of NPCs, namely on their ability to carry out active transport of karyophilic proteins. Active transport requires a set of cytosolic factors, which can be supplied by cytosolic extracts from X. laevis oocytes (14) and can be blocked by antibodies directed against the nucleporin gp62 (24). To investigate the dependence of NE electrical conductance on the “transport enabled” functional state of NPCs, measurements were carried out in a solution that contained 50% cytosolic extract from X. laevis oocytes. Fig. 5 shows that NE electrical conductance is essentially not altered when cytosolic factors are present to maintain a transport enabled functional state of the nuclear pores.

Figure 5.

Independence of NE electrical conductance from active protein transport. The functional state of NPCs is modulated by the addition of cytosolic oocyte extract (transport enabled) and by use of antibodies directed against the nucleoporin gp62 (transport blocked). The NE electrical conductance is virtually unaltered by these maneuvers. Insets show a consensus model of the NPC structure (modified from ref. 34). Although the centrally located transport machinery is in different functional states, the observed conductance may be the result of current flowing through peripheral channels as indicated by arrows.

Antibodies against the NPC glycoprotein gp62 already have been reported to block NE electrical conductance in patch clamp experiments (22, 25). We tested a polyclonal antibody against the X. laevis NPC glycoprotein gp62. The gp62 protein is located near the central channel of the NPC (26) and is thought to play a direct role in active protein transport through the NPC (24). Fig. 5 shows that the NE electrical conductance is not altered by the application of the antibody.

Discussion

The nuclear hourglass technique is an approach to measure biological membrane systems of large area and high conductance. More than 30 years ago, Loewenstein and coworkers (7, 8) found that their classical microelectrode approach was restricted to nuclei smaller than approximately 70 μm in diameter, excluding the much larger X. laevis oocyte nuclei from being investigated electrically. This situation did not change over the following two decades although Xenopus oocyte nuclei became a favorite tool for cell biologists in the field of NE and NPC research. In the last decade, the patch clamp technique has been proposed as a more suitable tool for investigating the electrical properties of NE. In the nucleus attached configuration, this technique can be used to investigate only a few μm² of the NE surface and is thus not restricted to small nuclei. However, one serious restriction of the patch clamp technique is its inability to resolve extremely large electrical conductances. Inferred from cell biological and electron microscopic data about the dimensions of NPCs, a conductance of 1 nS per NPC or more can be expected. In X. laevis oocyte nuclei, the NPC density is in the range of 50 NPC per μm². If the majority of the NPCs are in an electrically open state, this high density would result in a total conductance of the patched membrane that is in the range of a virtually open patch pipette. In this situation, it is nearly impossible to distinguish the membrane current from a leak current associated with an incomplete seal. Thus, the patch clamp technique is restricted to NEs with a lower density of NPCs or to conditions where a majority of the NPCs is in an electrical closed state. Such a closed state of most of the NPCs usually is experienced during nuclear patch clamp experiments (9, 10, 27–30). However, it is currently an issue for debate whether this is the normal, physiological state of the NPC. As a result, the inability of the patch clamp technique to characterize NEs with a high density of electrically open NPCs is a severe methodological restriction.

With the nuclear hourglass technique, the restrictions of both the classical microelectrode technique and the patch clamp technique are overcome. The method is able to resolve the NE electrical conductance of even the largest oocyte nuclei. In addition, the nuclear hourglass technique has the advantage to be noninvasive, because no impalement with electrodes is necessary.

Surprisingly, our experiments indicate an extraordinary high NE electrical conductance in the range of 8 S/cm² under all conditions tested so far. The simplest interpretation of these data is that all NPCs are in an electrically open state, with an electrical conductance of 1.7 nS per single NPC. This result is in good agreement with the expected electrical NPC conductance that can be calculated to range between 1 and 2 nS, based on published estimations of the physical NPC pore dimensions (4). The finding that the majority of the NPCs obviously are in an electrically open state with a high electrical conductance of 1.7 nS per NPC is in apparent contradiction to patch clamp experiments that show gigaseals lacking such large conductances (10). This striking differences cannot solely be explained by differences in the origin of the nuclei, because gigaseals lacking such large conductances also have been reported from the same type of nuclei preparation (17). The current view is that most of the NPCs are closed during patch clamp experiments (31). The reasons for the electrically silent NPCs that were observed during patch clamp experiments are still unknown.

Compared with the nuclear hourglass technique, the nuclear patch clamp technique offers the capability of single channel resolution of individual channel proteins in the NE. However, only a tiny fraction of the complete NE is evaluated during a patch clamp experiment. The investigator is inevitably biased to pick the experiments lacking a large number of electrically open NPCs, for the simple reason that the presence of many electrically open NPCs in the patched membrane will be indistinguishable from incomplete gigaseals. Thus, it is impossible to estimate the overall electrical conductance, and therefore the functional state, of a complete NE from patch clamp data. In contrast, the nuclear hourglass technique offers a noninvasive approach to evaluate the total NE electrical conductance.

Cytosolic factors did not alter the electrophysiological properties of the NE. In addition, the application of an antibody against the NPC protein gp62 failed to block NE electrical conductance. This protein is located near the central macromolecule translocation channel of the NPC (26) and plays a role in the active transport of macromolecules (24), which demonstrates that in the mature X. laevis oocyte NPCs are able to maintain a high ionic permeability independent of the functional state of the centrally located protein translocation machinery. This subject demands further investigation, because it is still likely that the electrical conductance of NPCs depends on the rate and size of macromolecules actually transported (32). To study the full impact of active macromolecular transport on NE electrical conductance, it will be necessary to supply both cytosolic factors and suitably large import substrates, like nucleoplasmin-coated gold particles.

A tempting speculation that provides another possible explanation for the independence of active transport and electrical conductance includes hypothetical peripheral channels of NPCs. These channels have been reported in three-dimensional models of the X. laevis oocyte NPC structure and are thought to reside in each of the eight subunits of the nuclear pore (33, 34). While their actual dimensions as well as their function are not yet known, they could contribute significantly to the electrical NPC conductance independent from the functional state of the macromolecule-transporting channel in the center of the NPC. The functional significance as well as the possible physiological regulation of such a transport-independent, peripheral NPC conductance has yet to be elucidated. The nuclear hourglass technique provides a tool to investigate this specific electrophysiological feature of the X. laevis oocyte NE.

Abbreviations

NPC

nuclear pore complex

NE

nuclear envelope

NIM

nuclear isolation medium

PVP

polyvinylpyrrolidone