Prime factors

Abstract

We use Voiculescu’s free probability theory to prove the existence of prime factors, hence answering a longstanding problem in the theory of von Neumann algebras.

In a series of papers, Murray and von Neumann (1–5) introduced and studied certain algebras of Hilbert space operators, also known as rings of operators. They are now known as “von Neumann algebras.”

A von Neumann algebra is a strong-operator closed self-adjoint subalgebra of the algebra of all bounded linear transformations on a Hilbert space. Factors are von Neumann algebras whose centers consist of scalar multiples of the identity. They are the building blocks from which all the von Neumann algebras are built. The most elementary factors, type I_n factors, are isomorphic to the algebra M_n of all n × n complex matrices. One of the basic constructions with factors (producing other factors) is that of forming the tensor product. For factors of type I_n, M_p ⊗ M_q is isomorphic to M_pq. Of course, no such tensor decomposition of M_p is possible precisely when p is a prime. The theory of tensor decompositions of factors of type I_n is little more than the theory of factoring integers into their prime components.

Murray and von Neumann (1) classified factors by means of a relative dimension function. Finite factors are those for which this dimension function has a finite range. For finite factors, this dimension function gives rise to a (unique, when normalized) tracial state. In general, a von Neumann algebra admitting a faithful normal trace is said to be finite. Infinite-dimensional finite factors are called factors of type II₁. They are “continuous” matrix algebras. Murray and von Neumann (2) spoke of “continuous dimensionality” in their factors of type II₁. In a parallel manner, when we study tensor products of factors of type II₁ and their tensor-product decompositions, we may speak of decomposition into “continuous primes.” Factors of type II₁ tensored with one another (as von Neumann algebras) produce, again, factors of type II₁. Each factor of type II₁ may be decomposed as the tensor product of M_n and a factor of type II₁ for each n in ℕ. In a sense, the “discrete primes” (that is, 2, 3, 5, …) are not significant in the theory of decomposition into “continuous primes.” The first question of the theory of such decompositions has to be that of the existence of a continuous prime: Is there a factor of type II₁ that is not (isomorphic to) the tensor product of two factors of type II₁? This problem and some related problems, concerning the basic structure of factors, have been asked and studied by many people (see, e.g., refs. 6 and 7, pp. 4.4.12 and 4.4.45). Popa (6) proves that there are prime factors of type II₁ with a nonseparable predual. The separable case remained open. In this paper, we shall answer this question affirmatively.

We describe below, briefly, a basic construction of factors of type II₁ by using regular representations of discrete groups. Our main result states that certain factors arising from free groups are prime. An outline of the proof follows the statement. We end with some open questions.

Main Result

There are two main classes of examples of von Neumann algebras introduced by Murray and von Neumann (1, 3). One is obtained from the “group-measure space construction”; the other is based on regular representations of a (discrete) group G (with unit e). The second class is the one needed in this paper. A brief description of that class follows.

The Hilbert space ℋ is l²(G) (with its usual inner product). We assume that G is countable so that ℋ is separable. For each g in G, let L_g denote the left translation of functions in l²(G) by g⁻¹. Then g → L_g is a faithful unitary representation of G on ℋ. Let ℒ_G be the von Neumann algebra generated by {L_g:g ∈ G}. Similarly, let R_g be the right translation by g on l²(G) and ℛ_G be the von Neumann algebra generated by {R_g:g ∈ G}. Then the commutant ℒ′_G of ℒ_G is equal to ℛ_G and ℛ′_G = ℒ_G. The function u_g that is 1 at the group element g and 0 elsewhere is a cyclic trace vector for ℒ_G (and ℛ_G). In general, ℒ_G and ℛ_G are finite von Neumann algebras. They are factors (of type II₁) precisely when each conjugacy class in G (other than that of e) is infinite. In this case, we say that G is an infinite conjugacy class (i.c.c.) group.

Specific examples of such II₁ factors result from choosing for G any of the free groups F_n on n generators (n ≥ 2), or the permutation group Π of integers ℤ (consisting of those permutations that leave fixed all but a finite subset of ℤ). Murray and von Neumann (3) prove that ℒ_Fn and ℒ_Π are not ∗ isomorphic to each other (a deep result). A factor is hyperfinite if it is the ultraweak closure of the ascending union of a family of finite-dimensional self-adjoint subalgebras. In fact, ℒ_Π is the unique hyperfinite factor of type II₁; it is contained in any factor of type II₁; and the tensor product of the hyperfinite II₁ factor with itself is ∗ isomorphic to itself. Now we state our main theorem.

Main Theorem.

The free group factor ℒ_Fn associated with the free group on n (≥2) generators is prime, i.e., it is not isomorphic to the tensor product of any two factors of type II₁.

We prove this result with the aid of Voiculescu’s free probability theory (8–10) (especially, his recently introduced concept of free entropy) and some geometrical methods for estimating free entropies. We refer to ref. 10 for the basics of free probability theory.

Let ℳ be a von Neumann algebra with a normal faithful trace τ, X₁, … , X_n be self-adjoint elements in ℳ. As analogues of classical entropy and of Fisher’s information measure, Voiculescu (8) introduced free entropy χ(X₁, … , X_n). Roughly speaking, χ(X₁, … , X_n) is the limit of certain normalized measurement of all self-adjoint matrices that approximate X₁, … , X_n in joint distributions as the dimension of the matrices tends to infinity. We list some properties of free entropy in the following lemma.

Lemma 1.

Let X₁, … , X_n, n ≥ 1, be self-adjoint elements in ℳ (with trace τ), C be τ(X₁² + ⋯ + X_n²)^1/2 and R₀ be max{∥X_j∥ : j = 1, … , n}. Then

(i) (ref. 8; p. 2.2) χ(X₁, … , X_n) ≤ n/2 log(2πeC²n⁻¹);

(ii) (ref. 8, p. 4.5) χ(X₁) = ∫∫ log|s − t|dμ₁(s)dμ₁(t) + 3/4 + 1/2 log 2π, where μ₁ is the (measure on the spectrum of X₁ corresponding to the) distribution of X₁;

(iii) (ref. 8; p. 5.4) χ(X₁, … , X_n) = χ(X₁) + ⋯ + χ(X_n) when X₁, … , X_n are free random variables.

From the above lemma, we know that there are self-adjoint elements X₁, … , X_n in ℒ_Fn with finite free entropy such that X₁, … , X_n generate ℒ_Fn as a von Neumann algebra. In the following, we shall prove that if ℳ is not prime and X₁, … , X_n, n ≥ 2, generate ℳ as a von Neumann algebra, then χ(X₁, … , X_n) = −∞. Hence, ℒ_Fn is prime. In fact, we prove a slightly stronger result in the following lemma.

Lemma 2.

Let ℳ be a factor of type II₁, ℛ₁ and ℛ₂ be mutually commuting hyperfinite subfactors of ℳ. Let P₁, P₂, … and Q₁, Q₂, … be projections in ℳ with trace 1/2 that generate ℳ as a von Neumann algebra. Suppose that P₁, P₂, … commute with ℛ₁, Q₁, Q₂, … commute with ℛ₂. If X₁, … , X_n are self-adjoint elements in ℳ that generate ℳ as a von Neumann algebra, then χ(X₁, … , X_n) = −∞.

We give an outline of the proof here. The detailed argument will appear elsewhere.

From the assumptions in Lemma 2, we know that, for any positive ω, there are projections P₁, … , P_p and Q₁, … , Q_q in ℳ, p, q ∈ ℕ, and self-adjoint polynomials ϕ₁, … , ϕ_n in the noncommutative ∗ polynomial ring ℂ〈x₁, … , x_p+q〉 such that

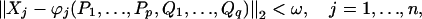where ∥ ∥₂ is the trace norm (∥X∥₂² = τ(X*X), X ∈ ℳ).

From the definition of free entropy (8), we shall estimate certain measurement of all (finite-dimensional) self-adjoint matrices that approximate X₁, … , X_n in joint distributions. For technical reasons, we use the notion of “modified” free entropy (9). More precisely, we estimate the free entropy of X₁, … , X_n in the presence of P₁, … , P_p and Q₁, … , Q_q. When self-adjoint elements A₁, … , A_n in M_k approximate X₁, … , X_n in joint distributions, there are projections E₁, … , E_p and F₁, … , F_q in M_k as well, corresponding to elements in certain Grassmann manifolds, that approximate projections P₁, … , P_p and Q₁, … , Q_q (in ℳ) in joint distributions. At the same time, A_j are close (in trace-norm) to ϕ_j(E₁, … , E_p, F₁, … , F_q).

From this observation, we are able to reduce the estimate of the free entropy of X₁, … , X_n to the volume estimate of the image of the cartesian product of the Grassmann manifolds under maps given by (noncommutative) polynomials ϕ₁, … , ϕ_n. Let k be the degree of the matrices that approximate X_j’s, D be an upper bound of the first derivatives of ϕ_j’s in the domain of the cartesian product of the Grassmann manifolds and d be the dimension of the manifolds. By using Szarek’s results (11) on nets in unitary groups and Grassmann manifolds, we have that

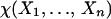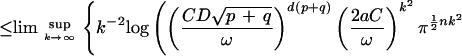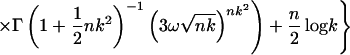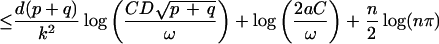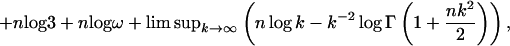where C is a universal constant, a = max{∥X_j∥₂ + 1 : 1 ≤ j ≤ n}, and Γ(·) is the classical Γ-function.

The assumptions that P₁, P₂, … commute with ℛ₁ and Q₁, Q₂, … commute with ℛ₂ give restrictions on the dimensions of the Grassmann manifolds. Hence, we can choose the dimension d so that d(p + q)/k² ≤ ω and d(p + q)/k²log(CD 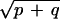) ≤ log(2C). From Stirling’s formula for the Γ-function, we have

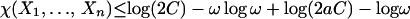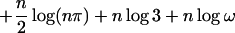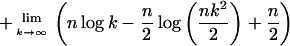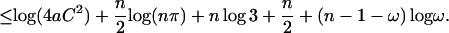Choosing ω arbitrarily small, we have χ(X₁, … , X_n) = −∞.

Using classical von Neumann algebra techniques, one can show that if ℳ is the tensor product of two factors of type II₁ (i.e., not prime), then ℳ satisfies all the hypotheses of Lemma 2.

Open Problems

Some questions about decompositions into continuous primes, analogous to simple facts about (discrete-)prime-factor decomposition, and about continuous primes, themselves, come instantly to mind:

 1. Are there infinitely many (nonisomorphic) prime factors of type II₁?

 2. Is ℒ_F2⊗̄ ℒ_F2 ∗ isomorphic to ℒ_F2⊗̄ ℒ_F2⊗̄ ℒ_F2 (“uniqueness” of prime decomposition)?

 3. With ℳ a factor of type II₁, let p(ℳ) be the set of integers n for which there are prime factors ℳ₁, … , M_n, n ∈ ℕ, of type II₁ such that ℳ ≅ ℳ₁⊗̄ ⋯ ⊗̄ ℳ_n. If there is no such n, let p(ℳ) be {∞}. Does p(ℳ) contain only one number?

Finally, we propose the project of classifying all von Neumann subalgebras of free group factors as an analogue of Connes’s classification of von Neumann subalgebras of the hyperfinite II₁ factor (12), and ask a question suggested by Lemma 2. Is the relative commutant of a nonatomic injective (or abelian) von Neumann subalgebra of ℒ_Fn in ℒ_Fn always injective?