Adaptive coevolutionary networks: a review

Abstract

Adaptive networks appear in many biological applications. They combine topological evolution of the network with dynamics in the network nodes. Recently, the dynamics of adaptive networks has been investigated in a number of parallel studies from different fields, ranging from genomics to game theory. Here we review these recent developments and show that they can be viewed from a unique angle. We demonstrate that all these studies are characterized by common themes, most prominently: complex dynamics and robust topological self-organization based on simple local rules.

1. Introduction

Complex networks are ubiquitous in nature. They occur in a large variety of real-world systems ranging from ecology and epidemiology to neuroscience, socio-economics and computer science (Albert & Barabasi 2002; Dorogovtsev & Mendes 2003; Newman 2003; Newman et al. 2006). While physics has for a long time been concerned with well-mixed systems, lattices and spatially explicit models, the investigation of complex networks has in recent years received a rapidly increasing amount of attention. In particular, the need to protect or optimize natural networks as well as the goal to create robust and efficient technical nets, prove to be strong incentives for research.

A network consists of a number of network nodes connected by links (see also box 1). The specific pattern of connections defines the network's topology. For many applications it is not necessary to capture the topology of a given real-world network exactly in a model. Rather, in many cases the processes of interest depend only on certain topological properties (Costa et al. 2007). The majority of recent studies revolve around two key questions corresponding to two distinct lines of research: what are the values of important topological properties of a network that is evolving in time? And, how does the functioning of the network depend on these properties?

Box 1. A brief network glossary.

Degree. The degree of a node is the number of nearest neighbours to which a node is connected. The mean degree of the network is the mean of the individual degrees of all nodes in the network.

Dynamics. Depending on the context, the term dynamics is used in the literature to refer to a temporal change of either the state or the topology of a network. In this paper, we use the term dynamics exclusively to describe a change in the state, while the term evolution is used to describe a change in the topology.

Evolution. Depending on the context the term evolution is used in the literature to refer to a temporal change of either the state or the topology of a network. In this paper, we use the term evolution exclusively to describe a change in the topology, while the term dynamics is used to describe a change in the state.

Frozen nodes. A node is said to be frozen if its state does not change over in the long-term behaviour of the network. In certain systems discussed here, the state of frozen nodes can change nevertheless on an even longer (topological) time scale.

Link. A link is a connection between two nodes in the networks. Links are also sometimes called edges or simply network connections.

Neighbours. Two nodes are said to be neighbours if they are connected by a link.

Node. The node is the principal unit of the network. A network consists of a number of nodes connected by links. Nodes are sometimes also called vertices.

Scale-free network. In scale-free networks, the distribution of node degrees follows a power law.

State of the network. Depending on the context, the state of a network is used either to describe the state of the network nodes or the state of the whole network including the nodes and the topology. In this review, we use the term state to refer exclusively to the collective state of the nodes. Thus, the state is a priori independent of the network topology.

Topology of the network. The topology of a network defines a specific pattern of connections between the network nodes.

The first line of research is concerned with the dynamics of networks. Here, the topology of the network itself is regarded as a dynamical system. It changes in time according to specific, often local, rules. Investigations in this area have revealed that certain evolution rules give rise to peculiar network topologies with special properties. Notable examples include the formation of small world (Watts & Strogatz 1998) and scale-free networks (Price 1965; Barabàsi & Albert 1999).

The second major line of network research focuses on the dynamics on networks. Here, each node of the network represents a dynamical system. The individual systems are coupled according to the network topology. Thus, the topology of the network remains static while the states of the nodes change dynamically. Important processes that are studied within this framework include synchronization of the individual dynamical systems (Barahona & Pecora 2002) and contact processes such as opinion formation and epidemic spreading (Kuperman & Abramson 2001; Pastor-Satorras & Vespignani 2001; May & Lloyd 2001; Newman 2002; Boguñá et al. 2003). These studies have made it clear that certain topological properties have a strong impact on the dynamics. For instance, it was shown that vaccination of a fraction of the nodes cannot stop epidemics on a scale-free network (May & Lloyd 2001; Pastor-Satorras & Vespignani 2001).

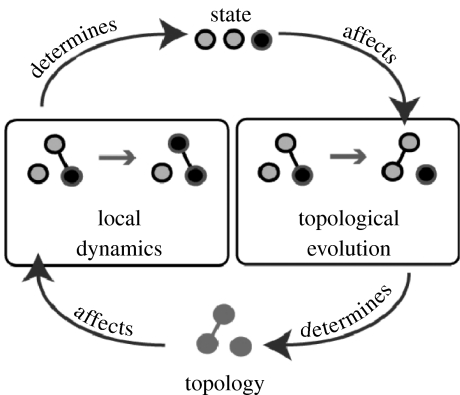
Until recently, the two lines of network research were pursued almost independently in the physical literature. While there was certainly a strong interaction and cross-fertilization, a given model would either describe the dynamics of a certain network or the dynamics on a certain network. Nevertheless, it is clear that in most real-world networks the evolution of the topology is invariably linked to the state of the network and vice versa. For instance, consider a road network. The topology of the network, that is the pattern of roads, influences the dynamic state, e.g. the flow and density of traffic. But if traffic congestions are common on a given road, it is probable that new roads will be built in order to decrease the load on the congested one. In this way a feedback loop between the state and topology of the network is formed. This feedback loop can give rise to a complicated mutual interaction between a time varying network topology and the nodes' dynamics. Networks which exhibit such a feedback loop are called coevolutionary or adaptive networks (figure 1).

Figure 1.

In an adaptive network, the evolution of the topology depends on the dynamics of the nodes. Thus, a feedback loop is created in which a dynamical exchange of information is possible.

Based on the successes of the two lines of research mentioned earlier, it is the next logical step to bring these strands back together and to investigate the dynamics of adaptive networks. Indeed, a number of papers on the dynamics of adaptive networks have recently appeared. Since adaptive networks occur over a large variety of scientific disciplines, they are currently investigated from many different directions. While the present studies can only be considered as a first step towards a theory of adaptive networks, they already crystallize certain general insights. Despite the thematic diversification, the reported results, considered together, show that certain dynamical phenomena repeatedly appear in adaptive networks: the formation of complex topologies; robust dynamical self-organization; spontaneous emergence of different classes of nodes from an initially inhomogeneous population; and complex mutual dynamics in state and topology. In §3–6, we argue that the mechanisms that give rise to these phenomena arise from the dynamical interplay between state and topology. They are therefore genuine adaptive network effects that cannot be observed in non-adaptive networks.

In this review, it is our aim to point out that many recent findings reported mainly in the physical literature describe generic dynamical properties of adaptive networks. These findings are, therefore, of potential importance in many fields of research. In particular we aim to make recent insights accessible to researchers in the biological sciences, where adaptive networks frequently appear and have been studied implicitly for a long time.

We start in §2 by discussing several examples that illustrate the abundance of adaptive networks in the real world and in applied models. Thereafter we proceed to the core of the review. In §3 adaptive Boolean networks are studied to explain how adaptive networks can self-organize towards dynamical criticality. Other less obvious, but no less intriguing forms of the self-organization are discussed in §4, while we review investigations of adaptive coupled map lattices. In particular, it is shown that a spontaneous ‘division of labour’ can be observed in which the nodes differentiate into separate classes, which play distinct functional roles in the network. Further examples of this functional differentiation of nodes are discussed in §5, which focuses on games on adaptive networks. Finally, in §6 we discuss the dynamics of the spreading of opinions and diseases on social networks, which shows that the adaptive networks can exhibit complex dynamics and can give rise to new phase transitions. We conclude this review in §7 with a summary, synthesis and outlook.

2. Ubiquity of adaptive networks across disciplines

Adaptive networks arise naturally in many different applications. Although studies that target the interplay between network state and topology have only recently begun to appear, models containing adaptive networks have a long tradition in several scientific disciplines. In §1, we have already mentioned the example of a road network that can be considered as a prototypical adaptive network. Certainly, the same holds for many other technical distribution networks such as power grids (Scirè et al. 2005), the mail network, the internet or wireless communication networks (Glauche et al. 2004; Krause et al. 2005; Lim et al. 2007). In all these systems a high load on a given component can cause component failures, e.g. traffic jams or electrical line failures, with the potential to cut links or remove nodes from the network. On a longer time scale, high load will be an incentive for the installation of additional connections to relieve this load. Further, in the engineering literature, games on adaptive networks, called network creation games, have recently become a hot topic. These are currently investigated in the context of evolutionary engineering (Scholz & Greiner 2007 and references therein).

Essentially the same mechanisms are known to arise in natural and biological distribution networks. For example, consider the vascular system. While the topology in the network of blood vessels directly controls the dynamics of blood flow, the blood flow also exhibits a dynamic feedback on the topology. One such process is arteriogenesis, where new arteries are formed to prevent a dangerous restriction in blood supply (ischemia) in neighbouring tissues (Schaper & Scholz 2003).

More examples of adaptive networks are found in information networks like neural or genetic networks. In the training of an artificial neuronal network, for example, it is obvious that the strength of connections and therefore the topology has to be modified depending on the state of the nodes. The changed topology then determines the dynamics of the state in the next trial. Also in biological neural and genetic networks some evidence suggests that the evolution of the topology depends on the dynamics of the nodes (Hopfield et al. 1983). An even more extreme example are immune networks, which have to restructure themselves in reaction to pathogens.

In the social sciences networks of relationships between individuals or groups of individuals have been studied for decades. On the one hand, important processes like the spreading of rumours, opinions and ideas take place on social networks and are influenced by the topological properties. On the other hand it is obvious that, say, political opinions or religious beliefs can in turn have an impact on the topology, when for instance conflicting views lead to the break-up of social contacts.

In game theory there is a long tradition to study the evolution of cooperation in simple agent-based models. In recent years spatial games that are played on social networks have become very popular. While most studies in this area so far focus on static networks, one can easily imagine that the willingness of an agent to cooperate has an impact on his social contacts. To our knowledge the huge potential of games on adaptive networks was first pointed out by Skyrms & Pemantle (2000).

Further examples of adaptive networks are found in chemistry and biology. A model of an adaptive chemical network is studied by Jain & Krishna (2001) and Seufert & Schweitzer (2007). In the model the nodes of the networks are chemicals which interact through catalytic reactions. Once the population dynamics has reached an attractor the species with the lowest concentration is replaced by a new species with randomly generated interactions. Although the topology of the evolving network is not studied in great detail, the papers show that the appearance of a topological feature, an autocatalytic loop, has a strong impact on the dynamics of both state and topology of the network.

While Jain & Krishna focus on the evolution of chemical species, their work is clearly inspired by models of biological evolution. In ecological research, models involving adaptive networks have a long tradition. A prominent area in which adaptive networks appear is food web evolution (Dieckmann & Doebeli 1999; Drossel et al. 2001; Dieckmann et al. 2004). Food webs describe communities of different populations that interact by predation. In almost all models the abundance of a species, i.e. the dynamic state, depends on the available prey as well as on the predation pressure, both of which depend, in turn, on topology of the network. If the population size drops below a certain threshold then the corresponding population goes extinct and the node is removed from the network. Therefore the dynamics of the topology depends on the state of the network.

The examples discussed above show that adaptive networks appear in a large variety of different contexts. However, the nature and dynamics of the adaptive feedback as such has to date only been investigated in a relatively small number of studies. In §§3–6, we focus on papers that specifically investigate the adaptive interplay of state and topology and illustrate the implications this interplay can have.

A prominent ancestor of adaptive network models was proposed by Christensen et al. (1998). In this work, a variant of the famous Bak–Sneppen model of macroevolution (Bak & Sneppen 1993) is discussed. The model describes the evolution of a number of populations, represented as nodes of a network in which the (undirected) links correspond to abstract ecological interactions. The state of each node is a scalar variable that denotes the population's evolutionary fitness. Initially this fitness is assigned randomly. Thereafter, the model is updated successively by replacing the population with the lowest fitness by a new species with random fitness. The replacement of a species is assumed to affect also the fitness of the other populations it is interacting with. Therefore, the fitness of all neighbouring species (i.e. species with direct links to the replaced one) is also set to random values. In the original model of Bak & Sneppen, the underlying network is a one-dimensional chain with periodic boundary conditions, so that every node has exactly two neighbouring nodes. In other words, the degree of each node is two. It is well known that this model gives rise to avalanches of species replacements which follow a scale-free size distribution (Bak & Sneppen 1993).

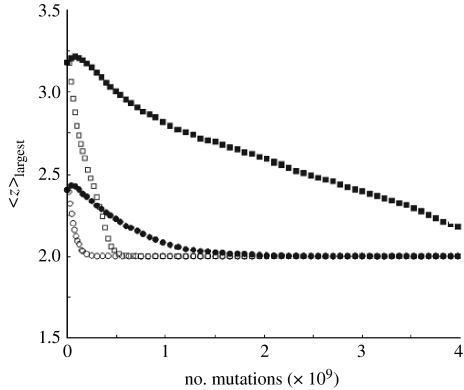
In Christensen et al. (1998), the simple topology of the Bak–Sneppen model is replaced by a random graph. The paper focuses mainly on the evolutionary dynamics on networks with static topology. However, in the second to last paragraph a model variant is studied in which the replacement of a population can affect the local topology. If the replaced population had a lower degree than the species in the neighbourhood, there is a small probability that a new link is added that connects to the replaced species. But if the replaced population had a higher degree than the species in the neighbourhood then one link that connects to the replaced species is removed with the same probability. This evolution rule effectively changes the mean degree, i.e. the average number of links connecting to a node. By numerical simulation, Christensen et al. find that the mean degree in the largest cluster of nodes approaches 2 (figure 2)—exactly the same mean degree as the linear chain used in the original Bak–Sneppen model. This finding is remarkable since it suggests that adaptive networks are capable of robust self-organization of their topology based on local rules. This observation triggered a number of subsequent studies which will be discussed in §3.

Figure 2.

For different initial conditions, the connectivity 〈z〉_largest of the largest connected cluster, of the adaptive Boolean network studied by Christensen et al. self-organizes towards the critical value of 2. Adapted from Christensen et al. (1998), fig. 3 (open circle, <z>=2, p=10⁻²; solid circle, <z>=2, p=10⁻³; open square, <z>=3, p=10⁻²; solid square, <z>=3, p=10⁻³).

3. Robust self-organization in Boolean networks

In order to understand the functioning of adaptive networks it is reasonable to focus on conceptually simple models. In Boolean networks the state of a given node is characterized by a single Boolean variable. Boolean networks with an underlying variable topology, offer a particularly simple and well-studied framework for the study of dynamical phenomena. Two prominent applications of Boolean networks are neural and gene regulatory nets, in which the state of a given node indicates whether a certain gene is being transcribed or whether a certain neuron is firing.

It is known that Boolean networks are capable of different types of dynamical behaviour, including chaotic and stationary (frozen) dynamics (Socolar & Kauffman 2003). At the boundary between stationarity and chaos, often lies a narrow transition region, where oscillatory dynamics can be observed and the density of frozen nodes exhibits power-law scaling. According to biological reasoning, neural as well as gene regulatory networks have to be close to or on this ‘edge of chaos’ to function properly (e.g. to code for different distinct cell types or allow meaningful information processing). A central question is how the networks manage to stay in this narrow parameter region while undergoing topological changes in the course of biological evolution and individual development. As we will show in the following it is probable that the adaptive nature of these networks plays a central role in the self-organization towards the critical oscillatory or quasi-periodic states.

Perhaps the simplest models for regulatory and neural nets are threshold networks. In these networks, the state of the Boolean variable indicates whether the corresponding node is active or inactive. Depending on the topology, active nodes may exert a promoting or an inhibiting influence on their direct neighbours in the network. If the inputs received by a node exceed a certain threshold, say if a node receives more promoting than inhibiting signals via its links, the node becomes active; otherwise it is inactive.

In order to study topological self-organization, Bornholdt & Rohlf (2000) used a Boolean threshold network in conjunction with an update rule for the topology: the time evolution of the system is simulated until a dynamical attractor, say a limit cycle, has been reached. Then a randomly chosen node is monitored for one period of the attractor or, in the case of chaotic dynamics, for a long fixed time. If the state of the node changes at least once during this time it loses a random link. However, if the state remains unchanged for the whole duration, a link from a randomly selected node is created. In short, ‘frozen’ nodes grow links, while ‘dynamical’ nodes lose links.

Note that adding links randomly can lead to the formation of, apparently non-local, long distance connections. However, since the targets of the links are randomly determined no distributed information is used. In this sense, topological evolution rules that add or remove random links can be considered as local rules.

By numerical simulation Bornholdt & Rohlf show that, independent of the initial state, a certain level of connectivity is approached. If the number of nodes N is changed, the emerging connectivity K follows the power law $K=2+12.4N^{-0.47}$. Therefore, in the case of large networks (N→∞), self-organization towards the critical connectivity K_c=2 can be observed. This is explained by further simulations which show that in large networks, a topological phase transition takes place at K=2. In this transition the fraction of frozen nodes drops from 1 to 0: before the transition all nodes change their state in one period of the attractor, while above the transition almost no node changes its state at all. This means that, in a large network, the proposed rewiring algorithm almost always adds links if K<2, but almost always removes links if K>2. In this way self-organization towards the dynamically critical state takes place. This form of self-organization is highly robust as it does not depend sensitively on the initial topology or the choice of parameters.

As pointed out by Bornholdt & Rohlf (2000), and later in a different context by Bornholdt & Röhl (2003), these results illustrate an important principle: dynamics on a network can make information about global topological properties locally accessible. In an adaptive network this information can feed back into the local dynamics of the topology. Therefore, the adaptive interplay between the network state and topology can give rise to a highly robust global self-organization based on simple local rules. Note that this genuine adaptive network effect can be observed in networks where topological evolution and dynamics of the states take place on separate time scales, as shown in the example presented by Bornholdt & Rohlf. These results inspired several subsequent investigations that extended the results (Bornholdt & Sneppen 1998, 2000; Luque et al. 2001; Kamp & Bornholdt 2002; Bornholdt & Röhl 2003; Liu & Bassler 2006; Rohlf 2007).

A natural generalization of the system of Bornholdt & Rohlf is to replace the threshold function by more general Boolean functions. In the Kauffman networks studied by Bornholdt & Sneppen (1998), Luque et al. (2001) and Liu & Bassler (2006), random Boolean functions are used, which are represented by randomly created lookup tables. Luque et al. (2001) create these lookup tables with a bias p so that a random input leads to activation with probability p and deactivation with probability 1−p. In this way, networks are created in which the critical connectivity can be tuned by changing p. Although a different rewiring rule is used, only allowing for disconnection, self-organization of the system towards the critical state (from above) is still observed.

The work described above shows that already very simple adaptive networks can exhibit complex dynamics. In order to find further examples of sets of interesting rules, an exhaustive search over a large class of adaptive network models is desirable. Indeed, first attempts in this direction for Boolean networks have been reported by Sayama (2007). In particular, a numbering scheme is proposed that allows us to enumerate all adaptive networks in a given class. A similar formal, cellular-automaton-inspired approach is also developed by Smith et al. (2007).

Finally, let us remark that beside the mechanism described by Bornholdt and others there exists an alternative mechanism for making information on the global state locally available, which again can be used to robustly self-organize the system. This ‘dual’ mechanism applies if the topology of the network changes much faster than the state. For illustration consider the following toy model: in a given network links are established randomly, but links between nodes of different states are instantaneously broken. These rules lead to a configuration in which every node of a given state is connected to all other nodes in the same state. This means that if a given node has, say, five links there are exactly five other nodes in the network that have the same state. Global information on the states has become locally available through the topology. This information can now feed back into the dynamics of the states on a slower time scale.

4. Leadership in coupled oscillator networks

In §3, we have discussed the adaptive interplay between state and topology as a dynamical feedback that can drive systems towards criticality. A similar feedback loop can, in a slightly different setting, guide the self-organization towards non-trivial topologies. One possible outcome is a spontaneous division of labour: the emergence of distinct classes of nodes from an initially homogeneous population. This phenomenon was first described by Ito & Kaneko (2002, 2003) in an adaptive network of coupled oscillators. It is remarkable that these authors state with great clarity, that their work was motivated by the new dynamical phenomena that can be expected in adaptive networks.

Ito & Kaneko study a directed network, in which each node represents a chaotic oscillator. The state of an oscillator is characterized by a continuous variable. Furthermore, every link in the network has an associated continuous variable that describes its weight, i.e. the strength of the connection. The states of the nodes and the weights of the links are updated in discrete time steps. In these updates, the new state of a given node is determined according to a logistic map (May 1976) which is coupled to the neighbouring oscillators via the network connections. The weights follow an update rule which increases the coupling between oscillators in similar states, while keeping the total weights of all inputs to each single oscillator constant.

The use of weighted networks is a convenient choice for the analysis of structural changes in adaptive networks. For example, they can be initialized with uniform weights and states plus minor fluctuations. Effectively that means that all oscillators are initially in almost identical states and are connected to all other oscillators with equal strength. In other words, initially the nodes form a homogeneous population. However, over the course of the simulation the weight of a large fraction of links approaches 0, so that a distinct network structure emerges. This structure can be visualized (and analysed) by only considering links above a certain weight and neglecting all others. In the model of Ito & Kaneko this network does not approach a frozen configuration, but remains evolving as links keep appearing and disappearing by gaining or losing weight.

Ito & Kaneko show that in a certain parameter region two distinct classes of nodes form that differ by their effective outgoing degree. Even a network in which some nodes are of high degree while other nodes are of low degree could still be considered to be homogeneous on average if every node has a high degree at certain times and a low outgoing degree at others. However, in the model of Ito & Kaneko this is not the case: despite the ongoing rewiring of individual links, a node that has a high/low outgoing degree at some point in time will generally have a high/low outgoing degree also later in time. Note that the outgoing degree indicates the impact that a given node has on the dynamics of others in the network. In this sense one could describe the findings of Ito & Kaneko as the emergence of a class of ‘leaders’ and a class of ‘followers’—or, to use a more neutral metaphor, of a spontaneous division of labour in which the nodes differentiate to assume distinct functional roles.

A similar division of labour was subsequently observed in a number of related systems which can be interpreted as simple models of neural networks (Bornholdt & Rohlf 2000; Gong & van Leeuwen 2004; van den Berg & van Leeuwen 2004). As a common theme, in all these models the topological change arises through a strengthening of connections between elements in a similar state—a rule that is for neural networks well motivated by empirical results (Paulsen & Sejnowski 2000). Even in systems in which no distinct classes of nodes emerge, the strengthening of connections between similar nodes often leads to strong heterogeneity in degree. A notable example is the formation of a scale-free topology reported by Fan & Chen (2004) and Fronczak et al. (2006).

From a technical point of view, the emergence of strong heterogeneity in degree is not always desirable. For instance, it is known that homogeneous networks, consisting of nodes with a similar degree, are easier to synchronize (Donetti et al. 2005). In an interesting paper, Zhou & Kurths (2006) study an adaptive network of coupled chaotic oscillators in which the connections between different nodes are strengthened. Note that this is exactly the opposite of the adaptation rule proposed by Ito & Kaneko. Consequently, the adaptive self-organization drives the network into the direction of a more homogeneous topology, ongoing with an enhanced ability for synchronization. Thereby, it is possible to synchronize networks that exceed by several orders of magnitude the size of the largest comparable random graph that is still synchronizable.

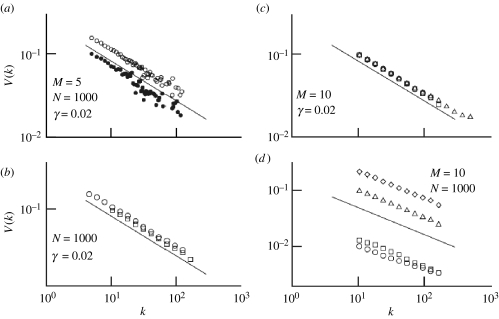
Another hallmark of adaptive networks that reappears in the work of Zhou & Kurths is the emergence of power laws. They show that in the synchronized state, the incoming connection weights V_i scale with the degree k of the corresponding node x_i as V(k)∼k^−θ, where θ=−0.48 is independent of the parameters in the model (figure 3). The authors point out that this universal behaviour arises owing to a hierarchical transition to synchronization. In this transition the nodes of the highest degree are synchronized first. Nodes of lower degree are synchronized later and therefore experience the increase in coupling strength for a longer time.

Figure 3.

The adaptive network of coupled oscillators studied by Zhou & Kurths organizes towards a topology in which the incoming weight V_i is a power law of the nodes degree k. The exponent θ=−0.48 is independent of (a) the specific type of oscillator under consideration, (b) the mean degree M (open circle, M=5; open square, M=10) (c) the size of the network (open circle, N=500; open square, N=1000; open triangle, N=10 000) and (d) the adaptation parameter γ (open circle, γ=10⁻⁴; open square, γ=10⁻³; open triangle, γ=10⁻²; open diamond, γ=10⁻¹). Adapted from Zhou & Kurths (2006), fig. 2.

Let us remark that the results reported in this section indicate that there could be a subtle connection to the mechanism described by Bornholdt & Rohlf (2000): the results of Ito & Kaneko show that there is a scale separation between the dynamics of the network (involving states and topology) and the time scale on which the emergent properties of the nodes change. In other words the turnover time for a node of high degree to become a node of low degree is many orders of magnitude larger than the time required for the rewiring of individual links. In contrast to other models, this time-scale separation is not evident in the rules of the system but emerges from the dynamics. One can suspect that the time-scale separation could arise owing to the presence of a phase transition at which the turnover time diverges. In the light of the findings described in §3, it is conceivable that an adaptive network could self-organize towards such a phase transition. However, more investigations in this direction are certainly necessary to verify that this is indeed the case.

5. Cooperation in games on adaptive networks

The term ‘division of labour’ used in §4 already suggests a socio-economic reading. Indeed, socio-economic models are perhaps the most fascinating application of adaptive networks so far. In this context, the nodes represent agents (individuals, companies, nations, etc.) while the links represent social contacts or, say, business relations. In contrast to other systems considered so far, agents are in general capable of introspection and planning. For this reason, the exploration of socio-economic systems is invariably linked to game theory.

One of the central questions in game theory is how cooperation arises in populations despite the fact that cooperative behaviour is often costly to the individual. A paradigmatic game which describes advantageous but costly cooperation is the Prisoner's Dilemma. In this game two players simultaneously choose between cooperation and defection. From the perspective of a single player choosing to defect always yields a higher pay-off regardless of the action of the opponent. However, the collective pay-off received by both players is the lowest if both players defect and the highest if both cooperate.

In models, the action a player takes is determined by its strategy, which comprises a lookup table that maps the information from a given number of previous steps to an action, as well as rules for the initial rounds where no such information is available. By updating the strategies of players according to a set of evolutionary rules, the evolution of cooperation can be studied.

Spatial games in which the players are arranged on a static network with links that represent possible games have been studied for some time (e.g. Novak & May 1992). More recently games on adaptive networks have come into focus. In these games the players can improve their topological position, for example by cutting links to defectors. The Prisoner's Dilemma game on adaptive networks has been studied by Ebel & Bornholdt (2002), Zimmermann et al. (2004), Eguíluz et al. (2005), Zimmermann & Eguíluz (2005) and Pacheco et al. (2006). An adaptive version of the closely related Snowdrift game was investigated by Ren et al. (2006) and a more realistic socio-economic model involving taxes and subsidies was discussed by Lugo & Jiménez (2006). In the results presented in these papers, the two common themes discussed above, namely the robust topological self-organization and the associated appearance of power laws, reappear and have been noted by many authors. For instance the formation of scale-free topologies, which exhibit a power-law degree distribution, is discussed in detail by Eguíluz et al. (2005) and Ren et al. (2006).

An effect that is reminiscent of the spontaneous division of labour and the emergence of social hierarchies was observed by Zimmermann et al. (2004), Eguíluz et al. (2005) and Zimmermann & Eguíluz (2005). However, in these papers, the adaptive interplay between the network state and topology stops at some point as the network freezes in a final configuration, a so-called network Nash equilibrium. It is therefore not clear whether the different social classes observed in the simulations arise owing to the same mechanism as in the model of Ito & Kaneko. As another possible explanation, the network could have reached an absorbing state, freezing the network and thus fixing local topological heterogeneities in some otherwise transient state.

An observation reported by Ebel & Bornholdt (2002) as well as Eguíluz et al. (2005) and Zimmermann & Eguíluz (2005) is that the approach to the final state is marked by large avalanches of strategy changes which exhibit power-law scaling. Such scaling behaviour is another indicator of self-organized critical behaviour.

From an applied perspective, it is interesting that elevated levels of cooperation are reported in all papers cited above. The mechanism that promotes cooperation in adaptive networks becomes apparent when one considers the interaction between the players and their neighbourhood. In all games on networks the local neighbourhood acts as an infrastructure or substrate from which pay-offs are extracted. The quality of this infrastructure depends on topological properties such as the degree or the number of cooperators in the neighbourhood. In an adaptive network a player can shape this neighbourhood by its own actions. Thereby, the neighbourhood becomes an important resource. The rules of the games are generally such that selfish behaviour degrades the quality of this resource as neighbours cut or rewire their links. This feedback may be regarded as a ‘topological punishment’ of the defecting player.

A rigorous investigation in the mechanism that promotes cooperation on adaptive networks is presented by Pacheco et al. (2006). In the limit in which topological dynamics is much faster than the evolution of strategies the authors show that the Prisoner's Dilemma on an adaptive network can be mapped to a game in a well-mixed population. However, this ‘renormalized’ game is not a Prisoner's Dilemma; the mapping effectively changes the rules of the game so that the Prisoner's Dilemma is transformed into a coordination game. This explains the elevated levels of cooperation since the cooperative behaviour is naturally favoured in the coordination game.

It is interesting to note that the adaptive nature of a network is not always apparent on the first glance. For instance, Paczuski et al. (2000) study the minority game on a fixed network. In this non-cooperative game, each agent makes a decision between two alternatives. The agents who decide for the alternative chosen by the minority of agents are rewarded. The decision of the agent depends on its own decision in the previous round as well as on the decision of its immediate neighbours in the network during that round. As in the Prisoner's Dilemma, the strategy of an individual agent can be described by a lookup table that is allowed to evolve in time to maximize success. Despite the fact that the game is seemingly played on a static network, Paczuski et al. observed all the hallmarks of adaptive networks described above, including the emergence of two distinct groups which differ in their success in the game. This enigma is resolved by noting that the evolution of the strategies in the lookup tables can effectively change the nature of the links in the network. In particular the lookup tables can evolve to such a state that the decision of certain neighbours in the network is ignored entirely (M. Paczuski 2007, personal communication). This means that even though the network itself is static, the effective degree, which is experienced by the nodes, can change over time. Therefore the network is after all adaptive.

While adaptive networks can add realism to previously studied games like the Prisoner's Dilemma, they also give rise to a new class of games. In these games the players do not try to maximize an abstract pay-off, but struggle to achieve an advantageous position on the network. For example, in a social network a position of high centrality is certainly desirable. The struggle for such a position is studied in models by Rosvall & Sneppen (2006a,b, 2007). The model describes the formation of a communication network between social agents. As an interesting feature of this model the communication provides the agents with meta information about the network structure.

In a related study by Holme & Ghoshal (2006) the agents attempt to achieve a position of high centrality while minimizing the number of contacts they have to maintain.

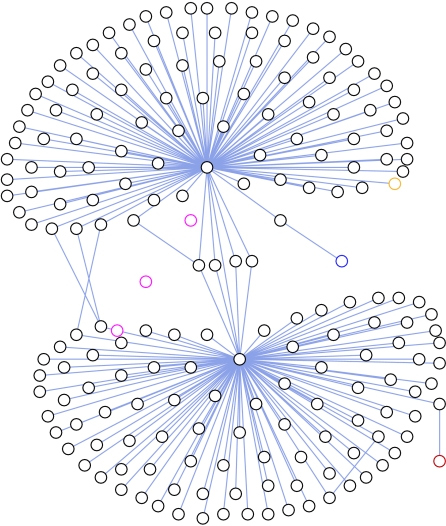
Holme & Ghoshal show in simulations that the system exhibits long periods of stability where one strategy is dominant. These are interrupted by sudden invasions of a different strategy. Apparently, no steady state is approached so that the successional replacement of the dominant strategy continues in the long-term behaviour. An interesting feature of the model is that it transiently gives rise to highly non-trivial topologies. Figure 4 shows an example of such a topology. The topology shown is complex in the sense that it is immediately evident that it is not random or regular, but possesses a distinct structure. Note that three distinct classes of nodes can be recognized in the figure. In particular, there is a class of agents who achieve the goal of being in a position of high centrality and low degree. However, while a spontaneous division of labour is evident, there is no de-mixing of classes: a node holding a position of low degree and high centrality at a certain time does not have an increased probability of holding such a position at a later time. Also note that the node's centrality that enters into the model is a global property. Therefore the emerging topologies are not organized based on local information alone.

Figure 4.

In the paper of Holme & Ghoshal, agents compete for a position of high centrality and low degree. This figure shows that complex global topologies are formed. In the figure three classes of nodes can be identified. Most nodes suffer a low centrality, while others gain high centrality at the cost of having to maintain a large number of links. Only a small class of ‘VIP’ nodes manage to achieve both high centrality and low degree. Adapted from Holme & Ghoshal (2006), fig. 2b.

6. Dynamics and phase transitions in opinion formation and epidemics

Above we have mainly been concerned with systems in which the state of the network changes much faster or much slower than the evolution of the topology. In systems that exhibit such a time-scale separation only, the averaged state of the fast variables can affect the dynamics of the slow variables and, therefore, the dynamical interplay between the time scales will, in general, be relatively weak. In contrast, new possibilities open up in systems in which the evolution of the topology takes place on the same time scale as the dynamics on the network. As dynamical variables and topological degrees of freedom are directly interacting, a strong dynamical interplay between the state and topology becomes possible. One might say that information on the dynamics of the state can be stored in and read from the topology and vice versa. In the study of this interplay we can no longer make use of the time-scale separation. Nevertheless it is still possible to analyse and understand the dynamics by using the tools of nonlinear dynamics and statistical physics. Depending on the language of description, the qualitative transitions in the dynamics and topology become apparent in the form of either bifurcations or phase transitions.

A simple framework in which the dynamical interplay can be studied is offered by contact processes, which describe the transmission of some property, e.g. information, political opinion, religious belief or epidemic infection along the network connections. One of the simplest models in this class is the epidemiological SIS model. This model describes a population of individuals forming a social network. Each individual is either susceptible (S) to the disease under consideration or infected (I). A susceptible individual in contact with an infected individual becomes infected with a fixed probability p per unit time. Infected individuals recover at a rate r immediately becoming susceptible again. If considered on a static network, the SIS model has at most one dynamical transition. Below the transition, only the disease-free state is stable, while above the transition the disease can invade the network and approaches an endemic state.

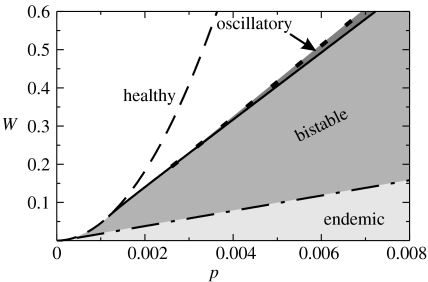
The spatial SIS model can be turned into an adaptive network if an additional process is taken into account: susceptible individuals can try to avoid contact with the infected. Such a scenario was studied by Gross et al. (2006). In their model, with probability w, a given susceptible individual breaks the link to an infected neighbour and forms a new link to another susceptible. This additional rule turns the SIS model into an adaptive network. As shown by Gross et al. (2006), even moderate rewiring probabilities change the dynamics of the system qualitatively. Sudden discontinuous transitions appear and a region of bistability emerges in which both the disease-free state and the epidemic state are stable (figure 5). Similar findings are also reported by Ehrhardt et al. (2006) who investigate the spreading of innovation and similar phenomena on an adaptive network.

Figure 5.

Two parameter bifurcation diagram of the adaptive epidemiological network studied by Gross et al. Bifurcations divide the parameter space in regions of qualitatively different dynamics. The dash-dotted line marks a transcritical bifurcation that corresponds to the threshold at which the epidemic can invade the disease-free system. The region in which an established epidemic can remain in the system is bounded by a saddle-node bifurcation (dashed), a Hopf bifurcation (straight) and a fold bifurcation of cycles (dotted). Adapted from Gross et al. (2006), fig. 4.

At high rewiring rates, the adaptive SIS model of Gross et al. (2006) can approach an oscillatory state in which the prevalence of the epidemic changes periodically. The oscillations are driven by two antagonistic effects of rewiring. On the one hand rewiring isolates the infected and thereby reduces the prevalence of the disease. On the other hand the rewiring leads to an accumulation of links between susceptibles and thereby forms a tightly connected cluster. At first the isolating effect dominates and the density of infected decreases. However, as the cluster of susceptibles becomes larger and tighter connected, a threshold is crossed at which the epidemic can spread through the cluster. This leads to a collapse of the susceptible cluster and an increased prevalence which completes the cycle. While this cycle exists only in a narrow region (figure 5) in the model described above, the parameter region in which the oscillations occur and the amplitude of the oscillations are enlarged if one takes into account that the rewiring rate can depend on the awareness of the population and therefore on the prevalence of the epidemic (Gross & Kevrekidis 2007).

In the adaptive SIS model the hallmarks of adaptive networks discussed above reappear; the isolation of infected and the emergence of a single tightly connected cluster of susceptibles is an example of the appearance of global structure from local rules. Moreover, the mechanism that drives the oscillations is reminiscent of the self-organization to criticality discussed in §3.

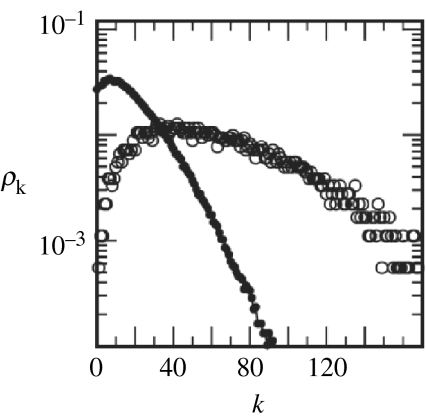
The rewiring rule that is used in the adaptive SIS model establishes connections between nodes in identical states and severs connections between different states. Stated in this way the rewiring rule reminds one of the model of Ito & Kaneko (see §4) in which connections between similar nodes are strengthened and others weakened. This analogy suggests that topologically different classes of nodes could emerge from the dynamics of the network. Indeed, figure 6 shows that two classes of nodes appear which are characterized by different degree distributions. In this case, we can identify the classes to consist of infected and susceptible nodes, respectively.

Figure 6.

In the model of Gross et al. (2006), two populations of nodes emerge that have distinct density distributions. These correspond to susceptibles (open circles) and infected (filled circles) and have low and high degree k, respectively.

In order to study the dynamics of the adaptive SIS model, Gross et al. (2006) and subsequently also Zanette (2007) apply a moment closure approximation. By means of this approximation, a low-dimensional system of ordinary differential equations can be derived that captures the dynamics of the network. The system of equations can then be studied with the tools of bifurcation theory (Kuznetsov 1989; Guckenheimer & Holmes 2000) which reveal the critical points in parameter space where qualitative transitions in the dynamics occur. In order to capture the dynamics of the adaptive SIS model, three dynamical variables are necessary, while the system-level dynamics of the standard (non-adaptive) SIS model can be captured by only one variable. This shows that in the adaptive model, two topological degrees of freedom communicate with the dynamics of the nodes.

Another approach to the dynamics of adaptive networks is offered by the tools of statistical physics, which can reveal critical points in the form of phase transitions. One example of such a phase transition is presented in a paper by Holme & Newman (2007), which focuses on opinion formation in populations. Specifically the paper considers the case of opinions, like religious belief, for which the number of possible choices is only limited by the size of the population. Disagreeing neighbours manage to convince each other with probability ϕ or rewire their connections with probability 1−ϕ. This ultimately leads to a consensus state in which the network is decomposed into disconnected components, each of which consists of individuals who hold a uniform opinion. For ϕ=0 opinions never change, so that the final distribution of opinions matches the initial distribution. For ϕ=1 no connections are rewired, so that the number of opinions in the consensus state cannot exceed the number of disconnected components that already existed in the initial network. Applying a finite-size scaling analysis, Newman & Holme are able to show that between these extremes a critical parameter value ϕ_c is located, at which a continuous phase transition takes place. At this transition a critical slowing down is observed, so that the network needs a particularly long time to reach the consensus state. In the consensus state the distribution of followers among the different beliefs approaches a power law.

The phase transition identified by Holme & Newman probably holds the key to the findings reported by Gil & Zanette (2006) and Zanette & Gil (2006). In these papers, the authors investigate a closely related model for the competition between two conflicting opinions. In this case, conflicts are settled by convincing neighbours or cutting links. It is shown that a critical point exists at which only very few links survive in the consensus state. Based on the previous results it can be suspected that this is a direct consequence of the critical slowing down close to the phase transition. In this region, the long relaxation time that is needed to settle to the consensus state might result in a very small number of surviving links.

7. Summary, synthesis and outlook

In this paper, we have reviewed a selection of recently proposed models for adaptive networks. These examples illustrate that adaptive networks arise in a large number of different areas including ecological and epidemiological systems; genetic, neuronal and immune networks; distribution and communication nets and social models. The functioning of adaptive networks is currently studied from very different perspectives including nonlinear dynamics, statistical physics, game theory and computer science.

Despite the diverse range of applications from which adaptive networks emerge, we have shown that there are a number of hallmarks of adaptive behaviour that recurrently appear.

1. Self-organization towards critical behaviour. Adaptive networks are capable of self-organizing towards dynamically critical states, like phase transitions. This frequently goes together with the appearance of power-law distributions. Unlike other forms of self-organized criticality this mechanism is highly robust (see §3).

2. Spontaneous division of labour. In adaptive networks, classes of topologically and functionally distinct nodes can arise from an initially homogeneous population. In certain models, a ‘de-mixing’ of these classes is observed, so that nodes that are in a given class generally remain in the class (see §4).

3. Formation of complex topologies. Even very basic models of adaptive networks that are based on very simple local rules can give rise to complex global topologies (see §5).

4. Complex system-level dynamics. Since information can be stored and read from the topology, the dynamics of adaptive networks involves local as well as topological degrees of freedom. Therefore, the dynamics of adaptive networks can be more complex than that of similar non-adaptive models (see §6).

In the context of biological applications, the hallmarks described above can be used as a working guideline: if one of these phenomena is observed in nature one should consider the possibility that it is caused by an (possibly so far unobserved or not recognized) adaptive network. As demonstrated in the example of Paczuski et al. (2000) the adaptive nature of a network may not always be obvious, but it can be revealed by a direct search. The reverse approach can also be rewarding: in systems which are known to contain an adaptive network it is promising to search for the hallmarks described above.

Given the evidence that is summarized in this review, we believe that adaptive networks could hold the key for addressing several current questions in many areas of research, but in particular in biology. Adaptive self-organization could explain how neural and genetic networks manage to exhibit dynamics that in many models appears only in critical states at the edge of chaos. Spontaneous division of labour could be important for many social phenomena, like leadership in simple societies, but also for developmental problems like cell differentiation in multicellular organisms. The capability of adaptive networks to form complex topologies has not been studied in much detail, but it seems to offer a highly elegant way to build up large-scale structures from simple building blocks. A biological example where this certainly plays the role is for instance the growth of vascular networks.

Many important processes have so far mainly been studied only on static networks. However, by doing so, important aspects of such systems may be overseen or neglected. For example, take the spread of infectious diseases. Currently huge efforts are made to determine the structure of real-world social networks. These are then used as input into complicated prediction models, which help to forecast the spread and dynamics of future epidemics (e.g. influenza). However, the most involved model or the best survey of the actual social network is in vain if it is not considered that people may radically change their behaviour and social contacts during a major epidemic.

We want to stress that answers to the questions outlined above would not only enhance our understanding of real-world systems comprising adaptive networks, but could also be exploited in bio-inspired technical applications that self-assemble or self-organize many subunits towards desired configurations. Such strategies are much sought for because many of these artificial systems will soon be too complicated to be easily designed by hand. Thus adaptive network structures may hold the key to provide novel, much-needed design principles and could well radically change the way in which future electrical circuits, production systems, interacting swarms of robots, or self-healing communication networks are operating (e.g. Kawamura et al. 1994).

From an applied point of view, it is desirable to compose an inventory of the types of microscopic dynamics that have been investigated in adaptive networks and their impact on system-level properties. Such an inventory could give researchers a guideline as to what kind of phenomena can be expected in natural systems where similar processes are at work. For instance, we have seen that ‘like-and-like’ processes which strengthen connections between similar nodes quite universally seem to give rise to heterogeneous topologies and global structures. A rough sketch of such an inventory based on the papers reviewed here is shown in box 2. In certain places the observations can be supplemented by mathematical insights. For instance, in every scale-separated system there has to be a discontinuous transition in the fast dynamics in order to maintain an adaptive interplay in the long-term evolution of the system. Otherwise the fast dynamics is simply slaved to the slow dynamics. Nevertheless much more information on the dynamics of adaptive networks is necessary to fill the inventory. This information will most likely come from automated numerical studies of large classes of adaptive networks.

Box 2. A first rough attempt at an inventory of dynamics of adaptive networks.

Activity disconnects. Rule: frozen nodes gain links, active nodes lose links. Outcome: self-organization towards percolation transition, active nodes scale as a power law. Examples: Bornholdt & Rohlf (2000) and Rohlf (2007).

Like-and-like. Rule: connections between nodes in similar states are strengthened. Outcome: heterogeneous topologies, possibly scale-free networks, emergence of topologically distinct classes of nodes. Examples: Bornholdt & Röhl (2003) and Ito & Kaneko (2002).

Differences attract. Rule: connections between nodes in different states are strengthened. Outcome: homogeneous topologies, power-law distributed link weights. Example: Zhou & Kurths (2006).

We note that the analysis of an adaptive network is not necessarily more involved than that of its static counterpart. While the nodes in static networks generally have different topological neighbourhoods, by contrast, the neighbourhood of nodes in adaptive networks changes over time. Owing to this mixing of local topologies the network as such becomes more amendable to mean field descriptions. However caution is in order, because naive mean field approximations can fail if a spontaneous division of labour occurs in the system and is not taken into account.

Apart from the investigation of more examples of adaptive networks, more fundamental work is certainly necessary. The works reviewed in this paper can only be considered as a first step towards a theory of adaptive networks. However, some important principles are already beginning to crystallize. The mechanism that drives the robust self-organization towards criticality is rather well understood: the dynamics on the network makes topological degrees of freedom accessible in every node. It thus spreads information on topological properties across the network. The local topological evolution can then react on this information and thus drive the topology to a topological phase transition at which the dynamics on the network is critical. Above we have conjectured that the observed division of labour could be driven by a similar mechanism, characterized by self-organization towards a phase transition at which the critical slowing down of the turnover times between emergent properties of nodes occurs. Moreover, the appearance of topologically distinct classes of nodes is certainly an important factor for the formation of complex topologies. Another factor is probably the dual mechanism described at the end of §3 by which global organization of the topology is possible. Finally, the investigations reported in §6 illustrate how topological degrees of freedom, acting as dynamical variables, can give rise to complex system-level dynamics. Thus, the four hallmarks described above seem after all to be connected. It is therefore not unlikely that all of these peculiar properties of adaptive networks can be explained by a single theory describing the transfer of information between state and topology of the network and the subtle interplay between different time scales.

Since adaptive networks appear in many different fields and are already implicitly contained in many models, a theory of adaptive networks can be expected to have a significant impact on several areas of active research. Future fundamental research in adaptive networks should focus on supplying and eventually assembling the building blocks for such a theory. While it has been shown that dynamics on the network can make global order parameters locally accessible, this mechanism has only been demonstrated for a few types of local dynamics. Except for these examples, it is not clear which set of local rules reveals what kind of global information. Another open question is how exactly the observed division of labour arises and how exactly non-trivial global topologies emerge from the local interactions. Finally, it is an interesting question, which topological properties are affected by a given set of evolution rules, so that they can act on topological degrees of freedom.

While the study of adaptive networks is presently only a minor offshoot, the results summarized above lead us to believe that it has the potential to become a major new direction in network research. In particular the prospect of a unifying theory and the widespread applications highlight adaptive networks as a promising area for future investigations.