Abstract
Gaining detailed understanding of the energetics of the proton-pumping process in cytochrome c oxidase (CcO) is one of the challenges of modern biophysics. Despite promising mechanistic proposals, most works have not related the activation barriers of the different assumed steps to the protein structure, and there has not been a physically consistent model that reproduced the barriers needed to create a working pump. This work reevaluates the activation barriers for the primary proton transfer (PT) steps by calculations that reflect all relevant free energy contributions, including the electrostatic energies of the generated charges, the energies of water insertion, and large structural rearrangements of the donor and acceptor. The calculations have reproduced barriers that account for the directionality and sequence of events in the primary PT in CcO. It has also been found that the PT from Glu-286 (E) to the propionate of heme a3 (Prd) provides a gate for an initial back leakage from the high pH side of the membrane. Interestingly, the rotation of E that brings it closer to Prd appears to provide a way for blocking competing pathways in the primary PT. Our study elucidates and quantifies the nature of the control of the directionality in the primary PT in CcO and provides instructive insight into the role of the water molecules in biological PT, showing that “bridges” of several water molecules in hydrophobic regions present a problem (rather than a solution) that is minimized in the primary PT.
Keywords: coupled electron transfer proton transfer, proton pumps, dielectric effects, free energy calculations, pKa in nonpolar regions
Cytochrome c oxidase (CcO) couples the four electron reduction of O2 to water and transmembrane proton transfer (e.g., refs. 1–4), which results in an electrochemical proton gradient that drives ATP synthesis. The elucidation of the structure of CcO (5, 6) and mutational (e.g., refs. 3 and 7–9) as well as other important studies (see refs. 3 and 4 for reviews) provided the opportunity to analyze coupled electron transfer/proton transfer on a molecular level in one of the most intriguing molecular machines. Unfortunately, the exact details of the action of CcO continue to present an extremely challenging problem (see below).
In trying to obtain a detailed structure–function correlation for CcO, it is important to understand the energetics and the time dependence of the pumping process. This challenge can be addressed by computer modeling approaches, and some elements of the CcO reaction have already been examined by simulation methods (10–14). However, the crucial relationship between protein structure and proton transfer (PT) energetics and directionality has not been established. That is, significant progress has been made in defining the conditions that would allow CcO to pump protons against a pH gradient (4, 15–17), in assessing the electrostatic energy of different possible intermediates (11, 12, 18–20), and in examining the energetics of the key water chains (10, 14) and of some PT steps (13). Furthermore, the actual examinations of the energetics of the overall pumping process have been performed by using a semimacroscopic model (17, 19, 20). However, we are not aware of studies that have actually generated a working pump by using the observed structure and well defined energy considerations. More specifically, theoretical evaluations of the pump features should determine the barriers for the PT steps while starting from the observed structure. At present, the only studies that explored the rate-determining barrier heights by molecular simulation approaches are those reported by our group (17, 19, 20). These exploratory studies, however, found that it is extremely hard to account even for the forward barriers, and that this could only be done by relaxing the constraint on reasonable dielectric constants. However, even in this case the resulting barriers led to back “leaking” and eventually to an unworkable pump (17).
Recent studies (see the next section) seem to strongly support the idea that the primary PT in CcO involves a PT from Glu-286 (E) to the Δ-propionic group on heme a3 (Prd or P−) instead of transfer to the iron-bound OH− (B−) of the binuclear center (Bn) or other alternative paths. However, accounting for this mechanism by clear molecular considerations is one of the most serious stumbling blocks for a detailed understanding of the action of CcO. It must be emphasized in this respect that it is quite simple to propose a pump with ad hoc barriers or with experimentally based barriers, but the problem is to obtain reasonable barriers by using the protein structure and consistent simulation approaches. Thus, it is essential to explore the gating problem by computational models that take into account all of the factors involved in the PT process.
This work revisits the primary PT, focusing on a systematic quantitative analysis of the competing paths for the relevant steps, as well as the early back reaction. This is done by more realistic calculations than those used in our previous studies, and considering all of the key energy contributions including the electrostatic contributions, the cost of inserting water molecules, and the cost of introducing significant structural deformations. Furthermore, the present calculations include the explicit effect of the membrane-induced dipoles. This additional effort has finally yielded reasonable kinetic control for the primary PT event and shed light on the control of the directionality in CcO.
Functional Constraints
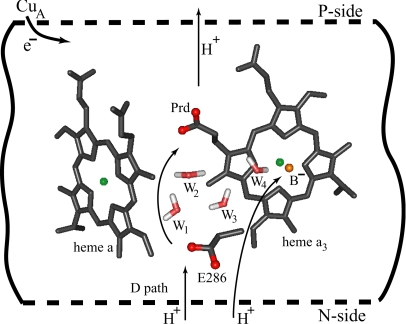
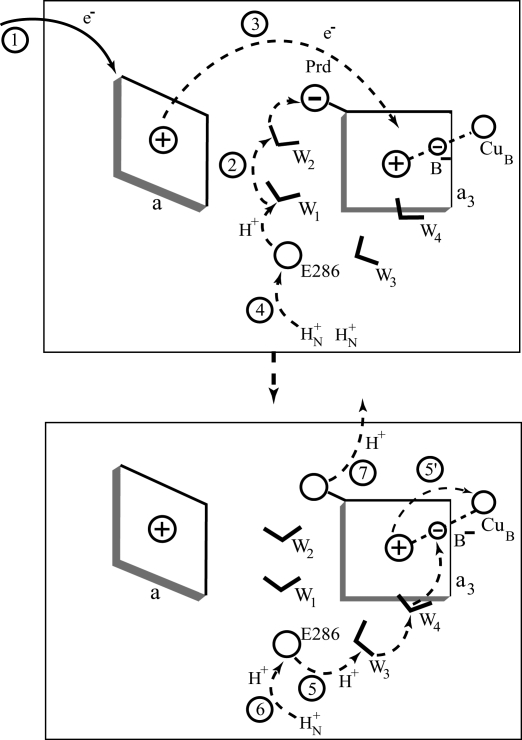
The parts of CcO that are relevant to this work are described in Fig. 1 (see also ref. 17), which also defines the notation that will be used here. The overall operation of CcO, described in ref. 17, goes through a four-step cyclic reaction, reducing one oxygen molecule to two water molecules, using four electrons and four protons. This reaction also pumps, on average, one proton per electron across the membrane. The sequence of electron transfer/proton transfer (ET/PT) events in each of the four steps can probably be described by the steps depicted in Fig. 2. This is the picture that emerged from an instructive recent study of the O to E step by Wikström and coworkers (15, 21), where some points about the proton donor and acceptor confirm the proposal of Brzezinski and coworkers (4) and also coincide with our recent theoretical and conceptual analyses (17). In this picture, the primary PT is triggered by ET to heme a, and it occurs most probably by transferring a proton from E286 to Prd. The problem, however, is to relate the corresponding kinetics to a detailed PT path and to obtain the relevant energetics from the available structural information. This challenge requires one to explain why the back PT is blocked, despite the fact that the proton concentration is higher at the so-called P side, and why the primary step does not involve a PT to B−. More specifically, it is extremely challenging to satisfy, in the aa3+B− configuration (oxidized heme is denoted by “+”), the relationship
where ΔG≠ designates an activation barrier, and the protonation states are written explicitly (e.g., E− designates deprotonated E). Here, the barrier (12.4 kcal/mol) is estimated according to transition state theory, from a corresponding rate constant (≈150 μs (15)). Furthermore, the leakage reaction of PT from the P side must be significantly slower than the forward reaction to ensure that the transfer of a proton from the P side to the N side is blocked. This requirement can be expressed as
Similarly, it is essential to satisfy the relationship
Otherwise, the proton will go first to B−, and the system will be trapped with the proton at Bn site (17, 20).
Fig. 1.
Schematic depiction of the main elements of CcO considered in this work.
Fig. 2.
Schematic diagram of the primary PT from E to P and the subsequent events. Because of space limitation, we do not draw each step separately; thus, the charges correspond to the first step in each figure. Here, we designate a reduced and oxidized heme by “a” and “a+,” respectively. We are not excluding here a possibility that the proton moves from Prd to another site after step 3.
Our previous works explored these conditions qualitatively by using the semimacroscopic version of the protein dipole–Langevin dipole (PDLD/S) method, combined with the linear response approximation (LRA) treatment (22) and the modified Marcus formula (17, 20), while assuming that water insertion occurs at a small cost and treating charge–charge interaction implicitly. This treatment identified the PT from E to P− (the EH P− → E− PH step) as the most likely primary PT (17) [in agreement with Wikström's recent study (15), which was not reported at that stage] but could not satisfy the above-mentioned conditions without assuming exceptionally low dielectric for the charge–charge interactions. This difficulty has not been widely appreciated because most workers have not tried to evaluate the energetics of forming protonated water molecules in the rate-limiting PT steps (see discussion in ref. 17 below in The Energetics of the Primary PT Paths). In particular, the use of low dielectric in macroscopic approaches will result in inconsistent energies in test cases for other proteins where the results are known (22), and the use of microscopic approaches leads to enormous convergence problems (see next section).
In this work, we apply our simulation approaches without a priori assumptions about the energetics of inserting water molecules or the dielectric for charge–charge interaction between the key elements of the system. This provides a less biased opportunity to explore the energetics of CcO.
Preliminary Validations
Reliable calculations of the energetics of PT steps in CcO are extremely challenging because they should deal with the formation of charges in protein interiors. Here, the selection of the optimal approach must be based on careful validation studies and on comparing microscopic and macroscopic approaches, which is rarely done. Because a proper validation is very important in the present case, we provide here a somewhat technical discussion of this issue. We examine the performance of different simulation approaches by evaluating the pKa of E286 [see supporting information (SI) Table S1] because this group is in a relatively nonpolar environment and its pKa is experimentally known (e.g., ref. 4). The results of our validation studies are summarized in SI Text together with similar calculations of the pKa of P−. This study demonstrates that the PDLD/S-LRA approach (see SI Text and ref. 22) reproduces the observed pKa values (calculated and observed pKa values are 10.3 and 9.4, respectively). On the other hand, the free energy perturbation adiabatic charging (FEP/AC) study (see Methods) overestimates the observed value even with the use of the polarizable ENZYMIX force field (see Methods) and the insertion of water molecules; the lowest calculated pKa was 13.6, and the pKa without water insertion and polarizable force field was ≈22 (see SI Text). Furthermore, even the use of our special approach of artificially overcharging the ionized group (to −2 and then back to −1) to induce water penetration (see ref. 22 for details) has not overcome this problem. At present, this is the only approach that reproduced by microscopic simulations the pKa of ionizable groups that were inserted in the interior of staphylococcal nuclease (see ref. 22 and references therein). This indicates that obtaining full convergence for the energetics of water penetration and local unfolding is very challenging (see SI Text).
The same problems encountered in the FEP/AC calculations also appear in most of the microscopic calculations that involve the primary PT step. Note that free energies obtained with the empirical valence bond (EVB) that represent the actual PT process and those obtained with the FEP charging are fully correlated (23). Thus, we adapted here a specialized approach using the regular EVB umbrella sampling (EVB/US) approach (see Methods) to generate the shape of the free energy surfaces but adjusting the PT free energies (by changing the so-called “EVB gas-phase shifts” discussed in Methods) to reproduce the PDLD/S-LRA estimates (see SI Text). At any rate, despite the convergence problems, we found it instructive to use microscopic calculations to estimate the lowest limit for the macroscopic effective dielectric constant for charge–charge interactions and for the evaluation of the energy of insertion of water molecules, and this is done in SI Text.
In general, the evaluation of the electrostatic energies in protein interiors is an extremely challenging task, but this issue is underappreciated because of the frequent omission of such interactions from critical test cases (see ref. 22). Macroscopic approaches that work well for the protein surface groups have to assume high and sometimes arbitrary dielectric for the internal groups because most of them do not consider the protein relaxation during the charging process (22) explicitly. This issue is treated consistently in our PDLD/S-LRA approach (see more in SI Text). On the other hand, microscopic models that are rigorous in principle involve enormous problems starting with major convergence difficulties and the frequent neglect of polarizability effects. Furthermore, popular long-range treatments of electrostatic effects by periodic boundary conditions are very problematic as reflected by the absence of systematic report of the dependence of calculated pKas on the size of the simulation systems (22). Finally, the use of brute-force potential of mean force (PMF) calculations suffers from major convergence problems (22).
The Energetics of the Primary PT Paths
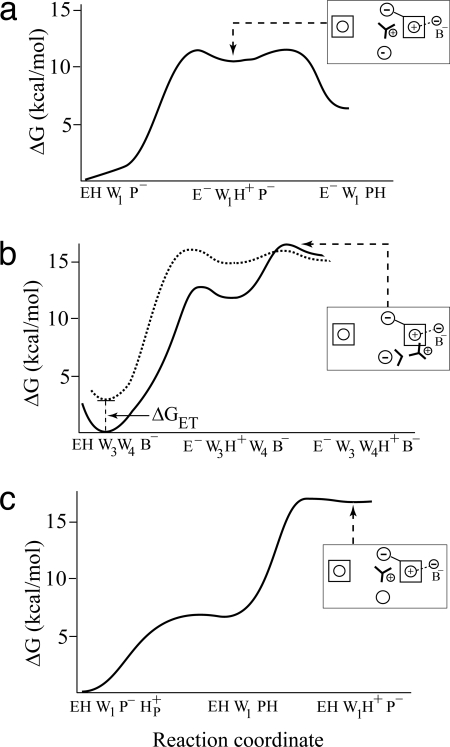
The energetics of the alternative paths were calculated by accounting for all of the relevant energy contributions (including water insertion and torsional deformations). The results are summarized in Table 1 and Fig. 3, and discussed below.
Table 1.
The energetics of the key transition states in the primary PT in CcO
| Label | State | ΔGw | (ΔΔGsol)np→pw→p | ΔG(w1)npw→p | (ΔG(wm)pow→p)* | ΔΔG(EHsol)po→npw→p | ΔGconf | (ΔG≠)p |
|---|---|---|---|---|---|---|---|---|
| (a) [PT from N, ″closed″] HN+ EH P− (W1)w → EH (W1H+) P− | 11 | 5 | −1 | — | — | 2 | 18 | |
| (b) [PT from N, ″open″] HN+WD EHP− (W1W2)w → (WDH+)E−(W1H+)W2P− | 11 + 4 | 13 | −1 | 3 | — | — | 31 | |
| (c) [E to P−, ″open″] EH P− (W1W2)w → E− (W1H+) W2 P− | 5 | 10 | −1 | 3 | −3 | — | 15 | |
| (d) [E to P−, ″closed″] EH P− (W1)w → E− (W1H+) P− | 5 | 8 | −1 | — | −3 | 2 | 12 | |
| (e) [PT from P, ″closed″] (back) EH P− (W1)w HP+ → EH (W1H+) P− | 9 | 5 | −1 | — | — | 2 | 16 | |
| (f) [PT to B−, ″closed″] EH B− (W3W4)w → E− (W3H+) W4 B− | 5 | 8 [6]† | 0 | 2 | −3 | 2 | 15 [13 + 3‡ = 16]† | |
| (g) [PT to B−, ″closed″] | EH B− (W3W4)w → E− W3 (W4H+) B− | 5 | 11 [7]† | 0 | 2 | −3 | 2 | 17 [13 + 3‡ = 16]† |
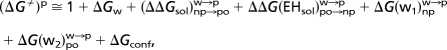 |
*wm designates 2 or 3 water molecules.
†The values in brackets correspond to the a+ a3 B− configuration.
‡The 3 kcal/mol represents the estimate of the ET energy.
Fig. 3.
Free energy profiles for the key competing paths on the primary event of CcO. (a) PT from E to P−. (b) PT from E to B−, where the dashed profile corresponds to a PT after ET from a to a3. (c) A leakage from the P side.
PT from the N Side Through the HN+ EH P− → EH W1H+ P− Path.
The starting point and the focus of our study is the forward PT path to P−. This path might look readily available until one tries to satisfy Eq. 1. Here, most of the options give extremely high barriers. This point is best appreciated by considering the energetics of protonating W1. If the protonation is done by a PT from the N side in a concerted path through E, we obtain (17)
where the first term represents the energy of protonating a water molecule in water, the ΔΔGsolw→p term represents the energy of moving the protonated water from the bulk solvent to the protein site, and ΔGins is the free energy of inserting water molecules in their sites. The main problem is that at pH 7, the first term already contributes ≈12 kcal/mol (17). With the additional terms, the barrier becomes much higher than the limit of Eq. 1 (see entry a in Table 1). The alternative path, considered in ref. 19 and entry b in Table 1, gives a much higher barrier.
The EH P− → E− PH Path.
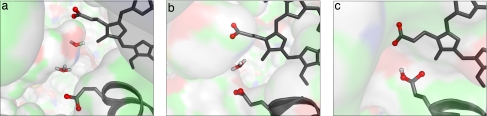
Probably the only option for getting a relatively low barrier for a PT to P− is the generation of the (E− W1H+) ion pair after the reduction of heme a (the energetics of this path is given by the thermodynamic cycle of Fig. S1). However, even with this option [where P− helps in stabilizing the ion pair (17)], it is hard to satisfy Eq. 1 without the use of an arbitrarily low effective dielectric for charge–charge interaction (low εeff). That is, starting with the x-ray structure (the open structure of Fig. 4a), we obtained ΔG≠ > 15 kcal/mol, when P− is included explicitly (Table 1, entry c). Assuming a low εeff for the (W1H+) (P−) interaction can reduce this barrier, but such an assumption must be based on microscopic analysis (see SI Text). The solution emerged from the considerations of the structural reorientation that brings E and P− close together. That is, a rotation of P− and E to the “closed” configuration shown in Fig. 4 b and c appears to be inexpensive. The problem is that, as a large rotation moves P− to the hydrophobic region, it involves a major desolvation penalty (≈8 kcal/mol increase in the ΔΔGsolw→p term). This is not a problem, however, for the uncharged EH. Thus, the generation of the configuration of Fig. 4b (see entry d in Table 1) already satisfies Eq. 1 with a reasonable ΔΔGsolw→p penalty and the insertion of just a single water molecule. Another exciting possibility is presented by the configuration of Fig. 4c. Here, we neither have to insert nor protonate any water molecule. The only penalty is the desolvation of P− and the larger torsional deformation.
Fig. 4.
Structures that can serve in the E → P PT process. (a) The open structure. (b) E turns in and promotes a PT through a single water molecule. (c) P− is brought closer to E and allows for a direct PT (paying, however, for moving P− to the nonpolar region).
Finally, an additional exotic possibility appears to be a PT from Glu-286 to Met-107 or Trp-172 (see SI Text) without inserting a water molecule. Interestingly, the E286D mutation still has significant activity (24) and obviously involves a somewhat larger distance between D286 and P−. However, even in this case, it was found that the distance is ≈7 Å, which can be reduced to ≈6 Å for a small price. Nevertheless, the E286A/I112E mutation (25) results in the shift of the primary donor further from P− (the closest distance between the E112 and Prd is 12 Å). This reduces the pumping and probably slows down the rate of the PT to P−. Thus, the PT barrier in this mutant is probably similar to that of the open configuration of the E286. Here, it seems that our approach overestimates the increase in the barrier for the open structure, and more careful simulation studies are clearly needed.
Avoiding the (EH B−) to (E− BH) Trap.
Another critical issue is the satisfaction of Eq. 3. Here, it is crucial to have a higher barrier for the PT from EH to B− than to P−. As seen from Table 1 (entries f and g), the constraint of Eq. 3 is mainly satisfied by two factors: the requirement of the insertion of more water molecules on the path to B− and the higher desolvation penalty for [E− W4H+] than that for [E− W1H+] in the aa3+B− configuration. Note that, in this case, we also have the option of PT occurring after an ET from heme a to heme a3. The PT barrier for such a process is lower, but the overall barrier should include the ET energy (see Table 1).
The difference in water insertion energies was not considered in our previous studies (17, 19, 20), and although this is a small effect, it is sufficient to tip the balance between the two paths. In this respect it is crucial to clarify that we are not dealing with the water orientation effect, which is rather trivial (see references in ref. 23) but rather with the free energy of inserting water molecules in the given PT path.
Blocking the E− PH HP+ → HN+ EH P− Back Reaction.
The next problem is the blockage of the back reaction involving a PT from the P side (Eq. 2). Here, the energy for the back reaction through the configurations of Fig. 4b is higher than the energy for the forward transfer through this configuration. Basically the free energy barrier is that of the [EH W1H+ P−] configuration but with 1.38(pHP-pKa(H3O+)) instead of 1.38(pHN-pKa(H3O+)) (see Table 1, entry e). Even alternative paths for the back reaction (e.g., starting with a PT from E to the N side) lead to higher barriers than that of ΔG1≠.
The importance of closing this back path has been recognized by Siegbahn and Blomberg (16), who proposed a barrier for moving from the P side to Prd. However, the molecular origin of this barrier has not been identified, and here we show that the [EH W1 P−] system can, by itself, provide the essential blockage of the back leakage.
Discussion and Analysis
One of the most serious challenges to the elucidation of the molecular mechanism of CcO is the rationalization of the directionality of the primary PT. To appreciate the origin of this problem, it is crucial to realize that the energy of generating an H3O+ in the bulk (pH 7) and moving it to hydrophobic sites is too high to be involved in the primary PT (see ref. 17). Similarly, even satisfying Eq. 1 by the more reasonable path of creating an [E−H3O+] ion pair is very challenging. Furthermore, accounting for the directionality and for the blockage of the back reaction (Eqs. 2 and 3) is another major challenge that has not been accomplished before by structure-based energy calculations (including our own). This problem has been a major stumbling block to any detailed analysis of the action of CcO. That is, a molecular model must reproduce the barriers in the system rather than assume these barriers arbitrarily. Of course, one can deduce the barriers experimentally, but at present it is not clear what the exact paths and configurations that correspond to the different barriers are.
The present work reproduces the correct order of the activation free energies (according to Eqs. 1–3) only after considering the energetics of water insertion and exploring different conformational states of the E and P groups. Remarkably, it was found that the closed configuration of Fig. 4b with one water molecule allows PT from E to P−, with a sufficiently low barrier. Furthermore, the same configuration blocks a PT from the P side; of course, this back reaction is not the microscopic reversal of the forward reaction, as is clear from Fig. 3. It was also found that the barrier for PT to the chemical site (the Bn center) is higher than the barrier for PT to the pump site because of the penalty of inserting water molecules. Our calculations still have an estimated error range of ≈2 kcal/mol, which may change the difference between the calculated barriers. However, the overall order of barriers is probably correct.
The idea that the conformational change of E plays an important role has been explored before (e.g., ref. 26), and it was found that such changes have a very small free energy cost. However, this idea was brought up in conjunction with the connectivity of EH to unprotonated water molecules. Here, in contrast, we explored the actual PT process, where the energetics of orienting water chains play only a minor part (27). In fact, the role of the conformational change appeared to be associated with minimizing the need for connecting water molecules. It is also interesting to point out that the present study concludes that the torsion of an uncharged P can be accomplished with a very small investment in torsional energy and that the main cost is associated with the movement of the charge of P− to the hydrophobic region. Thus, it would be interesting to use modified heme a3 with a shorter acidic chain instead of Prd.
Our finding that the barrier for the actual PT process becomes significantly smaller when E moves to the configuration of Fig. 4b is a major finding. This finding can be phenomenologically modeled by using a low dielectric for the P− WH+ interaction in the original open conformation. However, the origin of this low dielectric is far from obvious. That is, our previous studies (17, 19, 20) were forced to use smaller values of εeff than those found experimentally in most test cases (see ref. 22). Thus, the validation of these assumptions can provide a major guide in a qualitative assessment of the selection of different mechanisms. While exploring this issue, we found [by turning the explicit interaction between (P−) and (E− H3O+) on and off] that the dielectric for this interaction is in the range of 8–10 for the configuration of Fig. 4b (see Table S2). However, because the present study treats the torsional deformations of E and P− explicitly, the εeff that converts the electrostatic free energy in the [E− H3O+ P−] transition state in the original “open” x-ray structure to the actual free energy of this transition state in the “closed” configuration of Fig. 4b is quite low. In general, the effective dielectric cannot be used as a free parameter but should be deduced from explicit simulations of the relevant interactions and the response of the protein to these interactions. Here, the explicit considerations of torsional deformation and water insertion reduce the arbitrariness in the selection of εeff.
A very recent work (28), which appeared after the tentative acceptance of this article, reported calculations of the proton “translocations” from E to P. Although this treatment used basically our EVB method (29), it has not included E and P groups in the EVB calculations. This produced an almost barrierless PMF profile, but this PMF does not correspond to the E to P transfer (which should include the very large energy of deprotonating E) or to a transfer from the bulk water (17), because the energy of this process (≈12 kcal/mol) is not included. A similar problem appears in the study described in ref. 13.
The nature of the energetics elucidated in this work provides instructive clues about the design of a pumping system. That is, an arrangement with a group with a high pKa value in the location of E and a low pKa at the pump site satisfies the requirement for the initial directionality because the proton can only move from EH to P− to form the [E− H3O+ P−] configuration, whereas the motion of a proton from the P side to the N side leads to a [EH H3O+ P−] configuration with a higher energy (see Table 1).
It should be clarified here that the energetics of the PT steps is not determined directly by the connectivity of the water molecules or by the hydrogen-bonding between the unprotonated water molecules as implied by many works. When a water molecule serves as a site for the proton on the way between a donor and acceptor, the key issue is the energetics of placing this water at the specific site and, much more importantly, the energy of protonating it. These energy contributions cannot be determined by running long MD simulations (e.g., ref. 30) but can be evaluated by free energy calculations (see SI Text).
It is also important to note that the motions of the various structural elements (e.g., the loop motion mentioned in ref. 3) do not, by themselves, provide a gate for the PT process. The same is true for the various proposals that a large rearrangement of the water chain can provide a gate (e.g., see ref. 3). That is, any structural change during a PT process is completely defined by a free energy profile (the profile which describes the average of all structural fluctuations that occur along the reaction path), where the forward and backward barriers should satisfy the microscopic reversibility principle. For example, the energetics of the EH W ⇌ E− WH+ process is fully reversible, and it cannot provide a gate by itself; a gate must couple a given barrier with another process that will change this barrier (e.g., see refs. 17 and 19). The problem is, of course, to obtain the gating effect from actual molecular simulations that evaluate the forward and backward barriers in different states.
Mutational studies are essential for the elucidation of the action of CcO, but the interpretation of the corresponding results is not unique. For example, the finding that the N139D mutation blocks the [EH P− → E− PH] path was reproduced by the mechanism of ref. 19, where it was found that the barrier for a concerted PT increases by ≈1–2 kcal/mol because of the stabilization of the proton at a site before E. The same effect is also consistent with the current mechanism (see SI Text). Another example is provided by the W172F mutation (see SI Text). That is, interesting studies explored the role of Trp-172 by MD simulations that reproduced significant structural flexibility (3, 30, 31). However, the role of Trp-172 cannot be assessed without actual simulations of the energetics of the PT process. Our preliminary study indicated that the motion of Trp-172 brings its Cζ3 near EH, but a proton transfer to this site has a significant activation barrier. In contrast, a transfer to W2 and then to Nε1 (whose position is relatively fixed) may provide a viable path in the open structure.
The present work provides an instructive insight on the role of water molecules in biological PT processes. That is, there is a general tendency to assume that water molecules provide an excellent way for PT in proteins. However, this work demonstrates that the use of several water molecules to transfer a proton between acidic groups can be very expensive and that, in many cases, it may be better to avoid or reduce the number of bridging water molecules. This finding may have general implications in terms of the design of biological proton pumps.
Methods
The present work used models that were verified in previous studies of PT in proteins. These include the EVB and the FEP/AC microscopic models (both with a polarizable force field) and the PDLD/S-LRA semimacroscopic model, all of them described extensively elsewhere (e.g., refs. 29 and 32) and briefly in SI Text. The main twist of the present work is the adjustment of the EVB gas-phase shift to reproduce the PDLD/S-LRA free energies (see SI Text).
The simulation system was constructed by starting from the x-ray structure of CcO [Protein Data Bank entry code 1M56 (33)]. The protein was surrounded by a simplified polarizable membrane, as was done in ref. 23. Ionizable groups were kept at their ionization states in water, except for groups near the main simulation region, where we determined the relevant pKas by the PDLD/S-LRA approach.
The PDLD/S-LRA calculations involved two steps (e.g., references in ref. 22): first running MD to generate protein configurations for the charged and uncharged states, and then averaging the PDLD/S results for the generated configurations. The MD runs were performed with the polarizable ENZYMIX force field (34). All of the PDLD/S-LRA calculations were performed by the automated procedure of the MOLARIS program (34) where we generated 40 configurations for the charged and uncharged states using MD simulations of 1 ps, with a 1-fs time step for each configuration. The microscopic FEP and EVB/US calculations were performed by using the ENZYMIX force field (34), with the solute parameters described in refs. 19 and 23. The simulation included the use of 22 Å of the SCAAS spherical constraints and the local reaction field (LRF) long-range treatment (see ref. 34). The simulation system represented the membrane by a grid of induced dipoles (e.g., see ref. 23) that were treated explicitly in our polarizable model. The FEP/AC simulations were performed with 51 frames to transform the system between different charged states, where each frame included 80 ps of simulation with 1-fs time steps. The EVB/US simulations of some proton transfer steps were done with 31 frames, each with 30-ps forward and 30-ps backward runs. The results of the EVB calculations for PT between two acid groups “bridged” by a water molecule were also verified by quantum mechanical calculations (see SI Text and Fig. S2).
The free energies of inserting water molecules were evaluated as follows. In the first step, we placed a set of water molecules between the given donor/acceptor pair with weak distance constraints. Next, we mutated the water molecules (sequentially) to dummy atoms. The same procedure was then repeated for a water molecule in water. The thermodynamic cycle that is shown in Fig. S3 was then used to evaluate the water penetration free energy (including the restraint release energies).
The free energy of rotating E286 and P− groups was evaluated by creating a replica of the given side chain at the target geometry with dummy atoms instead of real atoms and then mutating the set of real atoms in the original position to dummy atoms and the dummy atoms in the new structure to real atoms. These calculations were done with FEP runs (≈1 ns) in both the forward and backward directions.
Supplementary Material
Acknowledgments.
We are grateful to Professors Peter Brzezinski, Marten Wikström and Per E. M. Siegbahn for many stimulating discussions. This work was supported by National Institutes of Health Grant R01 GM40283 and by computer time from the High Performance Computing and Communication Center at the University of Southern California.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0800580105/DCSupplemental.
References
- 1.Wikström MKF. Proton pump coupled to cytochrome-c oxidase in mitochondria. Nature. 1977;266:271–273. doi: 10.1038/266271a0. [DOI] [PubMed] [Google Scholar]
- 2.Michel H, Behr J, Harrenga A, Kannt A. Cytochrome c oxidase: Structure and spectroscopy. Annu Rev Biophys Biomol Struct. 1998;27:329–356. doi: 10.1146/annurev.biophys.27.1.329. [DOI] [PubMed] [Google Scholar]
- 3.Hosler JP, Ferguson-Miller S, Mills DA. Energy transduction: Proton transfer through the respiratory complexes. Annu Rev Biochem. 2006;75:165–187. doi: 10.1146/annurev.biochem.75.062003.101730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brzezinski P, Larsson G. Redox-driven proton pumping by heme-copper oxidases. Biochim Biophys Acta Bioenerg. 2003;1605:1–13. doi: 10.1016/s0005-2728(03)00079-3. [DOI] [PubMed] [Google Scholar]
- 5.Ostermeier C, Harrenga A, Ermler U, Michel H. Structure at 2.7 Å resolution of the Paracoccus denitrificans two-subunit cytochrome c oxidase complexed with an antibody FV fragment. Proc Natl Acad Sci USA. 1997;94:10547–10553. doi: 10.1073/pnas.94.20.10547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yoshikawa S, et al. Redox-coupled crystal structural changes in bovine heart cytochrome c oxidase. Science. 1998;280:1723–1729. doi: 10.1126/science.280.5370.1723. [DOI] [PubMed] [Google Scholar]
- 7.Pawate AS, et al. A mutation in subunit I of cytochrome oxidase from Rhodobacter sphaeroides results in an increase in steady-state activity but completely eliminates proton pumping. Biochemistry. 2002;41:13417–13423. doi: 10.1021/bi026582+. [DOI] [PubMed] [Google Scholar]
- 8.Pfitzner U, et al. Tracing the D-pathway in reconstituted site-directed mutants of cytochrome c oxidase from Paracoccus denitrificans. Biochemistry. 2000;39:6756–6762. doi: 10.1021/bi992235x. [DOI] [PubMed] [Google Scholar]
- 9.Han D, Morgan JE, Gennis RB. G204D, a mutation that blocks the proton-conducting D-channel of the aa3-type cytochrome c oxidase from Rhodobacter sphaeroides. Biochemistry. 2005;44:12767–12774. doi: 10.1021/bi051141m. [DOI] [PubMed] [Google Scholar]
- 10.Wikström M, Verkhovsky MI, Hummer G. Water-gated mechanism of proton translocation by cytochrome c oxidase. Biochim Biophys Acta Bioenerg. 2003;1604:61–65. doi: 10.1016/s0005-2728(03)00041-0. [DOI] [PubMed] [Google Scholar]
- 11.Olkhova E, Hutter MC, Lill MA, Helms V, Michel H. Dynamic water networks in cytochrome c oxidase from Paracoccus denitrificans investigated by molecular dynamics simulations. Biophys J. 2004;86:1873–1889. doi: 10.1016/S0006-3495(04)74254-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Song YF, Mao JJ, Gunner MR. Electrostatic environment of hemes in proteins: pKas of hydroxyl ligands. Biochemistry. 2006;45:7949–7958. doi: 10.1021/bi052182l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xu JC, Voth GA. Computer simulation of explicit proton translocation in cytochrome c oxidase: The D-pathway. Proc Natl Acad Sci USA. 2005;102:6795–6800. doi: 10.1073/pnas.0408117102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Popovic DM, Stuchebrukhov AA. Electrostatic study of the proton pumping mechanism in bovine heart cytochrome c oxidase. J Am Chem Soc. 2004;126:1858–1871. doi: 10.1021/ja038267w. [DOI] [PubMed] [Google Scholar]
- 15.Kim YC, Wikström M, Hummer G. Kinetic models of redox-coupled proton pumping. Proc Natl Acad Sci USA. 2007;104:2169–2174. doi: 10.1073/pnas.0611114104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Siegbahn PEM, Blomberg MRA. Energy diagrams and mechanism for proton pumping in cytochrome c oxidase. Biochim Biophys Acta Bioenerg. 2007;1767:1143–1156. doi: 10.1016/j.bbabio.2007.06.009. [DOI] [PubMed] [Google Scholar]
- 17.Olsson MHM, Siegbahn PEM, Blomberg MRA, Warshel A. Exploring pathways and barriers for coupled ET/PT in cytochrome c oxidase: A general framework for examining energetics and mechanistic alternatives. Biochim Biophys Acta Bioenerg. 2007;1767:244–260. doi: 10.1016/j.bbabio.2007.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Siegbahn PEM, Blomberg MRA, Blomberg ML. Theoretical study of the energetics of proton pumping and oxygen reduction in cytochrome oxidase. J Phys Chem B. 2003;107:10946–10955. [Google Scholar]
- 19.Olsson MHM, Sharma PK, Warshel A. Simulating redox coupled proton transfer in cytochrome c oxidase: Looking for the proton bottleneck. FEBS Lett. 2005;579:2026–2034. doi: 10.1016/j.febslet.2005.02.051. [DOI] [PubMed] [Google Scholar]
- 20.Olsson MHM, Warshel A. Monte Carlo simulations of proton pumps; On the working principles of the biological valve that controls proton pumping in cytochrome c oxidase. Proc Natl Acad Sci USA. 2006;103:6500–6505. doi: 10.1073/pnas.0510860103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gorbikova EA, Belevich NP, Wikström M, Verkhovsky MI. Time-resolved ATR-FTIR spectroscopy of the oxygen reaction in the D124N mutant of cytochrome C oxidase from Paracoccus denitrificans. Biochemistry. 2007;46:13141–13148. doi: 10.1021/bi701614w. [DOI] [PubMed] [Google Scholar]
- 22.Warshel A, Sharma PK, Kato M, Parson WW. Modeling electrostatic effects in proteins. Biochim Biophys Acta. 2006;1764:1647–1676. doi: 10.1016/j.bbapap.2006.08.007. [DOI] [PubMed] [Google Scholar]
- 23.Kato M, Pisliakov AV, Warshel A. The barrier for proton transport in aquaporins as a challenge for electrostatic models: The role of protein relaxation in mutational calculations. Proteins Struct Funct Bioinformatics. 2006;64:829–844. doi: 10.1002/prot.21012. [DOI] [PubMed] [Google Scholar]
- 24.Salomonsson L, Brändén G, Brzezinski P. Deuterium isotope effect of proton pumping in cytochrome c oxidase. Biochim Biophys Acta Bioenerg. 2008 doi: 10.1016/j.bbabio.2007.09.009. in press. [DOI] [PubMed] [Google Scholar]
- 25.Gilderson G, Aagaard A, Brzezinski P. Relocation of an internal proton donor in cytochrome c oxidase results in an altered pK(a) and a non-integer pumping stoichiometry. Biophys Chem. 2002;98:105–114. doi: 10.1016/s0301-4622(02)00088-1. [DOI] [PubMed] [Google Scholar]
- 26.Pomes R, Hummer G, Wikström M. Structure and dynamics of a proton shuttle in cytochrome c oxidase. Biochim Biophys Acta Bioenerg. 1998;1365:255–260. [Google Scholar]
- 27.Braun-Sand S, Burykin A, Chu ZT, Warshel A. Realistic simulations of proton transport along the gramicidin channel: Demonstrating the importance of solvation effects. J Phys Chem B. 2005;109:583–592. doi: 10.1021/jp0465783. [DOI] [PubMed] [Google Scholar]
- 28.Xu J, Voth GA. Redox-coupled proton pumping in cytochrome c oxidase: Further insights from computer simulation. Biochim Biophys Acta Bioenerg. 2008;1777:196–201. doi: 10.1016/j.bbabio.2007.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Aqvist J, Warshel A. Simulation of enzyme reactions using valence bond force fields and other hybrid quantum/classical approaches. Chem Rev. 1993;93:2523–2544. [Google Scholar]
- 30.Seibold SA, Mills DA, Ferguson-Miller S, Cukier RI. Water chain formation and possible proton pumping routes in Rhodobacter sphaeroides cytochrome c oxidase: A molecular dynamics comparison of the wild type and R481K mutant. Biochemistry. 2005;44:10475–10485. doi: 10.1021/bi0502902. [DOI] [PubMed] [Google Scholar]
- 31.Wikström M, et al. Gating of proton and water transfer in the respiratory enzyme cytochrome c oxidase. Proc Natl Acad Sci USA. 2005;102:10478–10481. doi: 10.1073/pnas.0502873102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kato M, Warshel A. Using a Charging Coordinate in Studies of Ionization Induced Partial Unfolding. J Phys Chem B. 2006;110:11566–11570. doi: 10.1021/jp061190o. [DOI] [PubMed] [Google Scholar]
- 33.Svensson-Ek M, et al. The X-ray crystal structures of wild-type and EQ(I-286) mutant cytochrome c oxidases from Rhodobacter sphaeroides. J Mol Biol. 2002;321:329–339. doi: 10.1016/s0022-2836(02)00619-8. [DOI] [PubMed] [Google Scholar]
- 34.Lee FS, Chu ZT, Warshel A. Microscopic and semimicroscopic calculations of electrostatic energies in proteins by the POLARIS and ENZYMIX programs. J Comput Chem. 1993;14:161–185. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.