Estimating the probability of initiated cell death before tumor induction

Abstract

The effects of cell toxicity are known to be inherent in carcinogenesis induced by radiation or chemical carcinogens. The event of cell death precludes tumor induction from occurring. A long standing problem is to estimate the proportion of initiated cells that die before tumor induction. No experimental techniques are currently available for directly gauging the rate of cell death over extended periods of time. The obstacle can be surmounted by newly developed theoretical methods of carcinogenesis modeling. In this paper, we apply such methods to published data on multiple lung tumors in mice receiving different schedules of urethane. Bioassays of this type play an important role in testing environmental chemicals for carcinogenic activity. Our estimates for urethane-induced carcinogenesis show that, unexpectedly, many initiated cells die early in the course of tumor promotion. We present numerical estimates for the probability of initiated cell death for different schedules (and doses) of urethane administration.

Section 1

As with many processes of carcinogenesis, the process of cell killing induced by a carcinogen is difficult to observe directly, and inferences rely on mathematical models. In a recent study (1), Moolgavkar et al. reported a statistical analysis of experimental data on enzyme-altered (ATPase-deficient) liver foci in rats induced by diethylnitrosamine. It is generally believed that these foci represent clones of initiated cells, and at least some of them eventually transform into malignant tumors. The authors used a two-stage birth–death–mutation model of carcinogenesis, usually referred to as the Moolgavkar–Venzon–Knudson model (2, 3), to estimate the extinction probability for clones of altered cells in initiation–promotion experiments. In the absence of a promoter, the estimated extinction probability was higher than 0.99, and its value tended to decrease when two different promoters were applied; this effect can be attributed to stimulation of cell proliferation.

The Moolgavkar–Venzon–Knudson model introduces the clonal expansion of initiated cells as the basic mechanism of tumor promotion. It is assumed that clonal growth begins immediately after initiation and can mathematically be described as a birth-and-death stochastic process. Under this model, the probability of a clone to become extinct is a natural summary characteristic of the susceptibility of initiated cells to death in the course of tumor development. However, there is experimental evidence that single initiated cells persist over an extended time period after the administration of a carcinogen. Using another biochemical marker (the placental form glutathione S-transferase) of cell initiation, Satoh et al. (4) have shown that single putative initiated cells (the placental form glutathione S-transferase-positive hepatocytes) and mini-foci consisting of such cells (2–10 cells) predominate in the preneoplastic liver within the first 12 weeks after a single exposure to diethylnitrosamine. Within 1 week after exposure, the enzyme-altered foci are almost entirely represented by single cells. Consistent with this evidence are early morphological effects of urethane on the lung tissue in mice (5, 6). It is well documented that microscopic foci of adenomatous tumor begin to appear in the alveolar epithelium not earlier than by 3 weeks after a single injection of urethane. It can be speculated that these foci are rapidly promoted clones of earlier initiated cells that escaped being killed by urethane.

From the above experimental observations, it may be deduced that an initiated cell remains dormant as long as it proceeds through the early stage of tumor promotion. During this stage, the event of cell killing caused by a carcinogen is of decisive importance in the future development of tumor. A stochastic model of carcinogenesis recently proposed by Yakovlev and Polig (7) allows for cell killing to compete with the process of tumor promotion at a single-cell level. Much like the Moolgavkar–Venzon–Knudson model, this model describes and explains a wide range of experimental findings documented in the literature, and its structure renders the associated statistical problems tractable. The phenomenon of cell death plays a key role in the dose–rate effects observed in carcinogenesis studies (7, 8). The model by Yakovlev and Polig provides a good description of various dose–rate effects in radiation and chemical carcinogenesis (9, 10) while keeping parametric assumptions to a minimum as far as the dependence of its parameters on dose rate is concerned. In the present paper, the potentialities of the Yakovlev–Polig model are exploited to estimate the contribution of cell death to the development of multiple pulmonary adenomas in mice receiving different schedules of urethane.

Section 2: The Model and Estimation Procedures

As applied to multiple tumorigenesis, the model describes the cumulative number of tumors produced within the time interval (0, t] as a Poisson random variable with the expected value given by

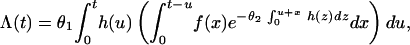1

where h(u) is the dose rate (the rate of administration of a carcinogen), f(x) is the promotion time distribution density, and θ₁ and θ₂ are parameters that describe the sensitivity of cells to carcinogenic and toxic (cell killing) modes of action, respectively. More specifically, θ₁h(t) is the mean number of initiated cells per unit time given the dose rate h(t). Similarly, the quantity θ₂h(t) represents the mean rate of formation of the lesions responsible for cell death, with the difference that θ₂ refers to intracellular lesions rather than altered cells. The derivation and biological substantiation of Eq. 1 are described at length by Yakovlev and Polig (7).

Suppose that the dose rate is kept constant over the exposure period T, which is a common practice in experiments with protracted exposures. Then the function h(t) is represented as

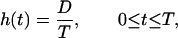2

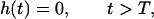where D is a total dose of carcinogen. In this special case, it follows from Eqs. 1 and 2 (see ref. 7 for derivation) that for t > T:

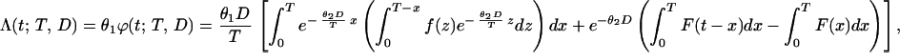3

where F(x) is the promotion time cumulative distribution function and f(x) stands for its density. In the context of urethane-induced carcinogenesis, Eq. 3 refers to situations in which animals are killed at times larger than the period of exposure to urethane. A modification of Eq. 3 can readily be derived for t ≤ T (7) but is of no use for our purposes.

Under the above model, the number of tumors at time t is thought of as a Poisson process with the integral intensity Λ(t; T, D). When analyzing the experimental data on urethane-induced pulmonary tumors reported by Shimkin et al. (5), we observed an over-dispersion effect that may be attributed to pronounced inter-individual variations in the tumor counts. Grosser and Whittemore (11) noted a similar effect in their analysis of the number and the size of lung tumors in mice receiving urethane in the drinking water. Our results of goodness-of-fit testing clearly indicate that a negative binomial distribution rather than a Poisson distribution of the number of tumors is consistent with the data of Shimkin et al. To obtain negative binomially distributed tumor counts under the model, we assume that the sensitivity parameter θ₁ (the mean number of initiated cells per unit dose) is a random variable that follows a Γ distribution, with a and 1/b standing for the shape and scale parameters of this distribution.

In this paper, we are concerned with experimental data on the formation of tumors, commonly referred to as adenomas, in the lungs of mice receiving different schedules of urethane. It is generally believed that the development of these benign tumors is irreversible and that some of them may progress to malignant carcinomas. The usual experimental practice is to count recognizable tumor foci in the lungs of mice killed at different time intervals from start of exposure. This and similar bioassays have been used for the testing of hundreds of environmental chemicals for carcinogenic potency (12). 0ne of the first stochastic models of carcinogenesis was intended for making inference from this type of data (13).

Let t_i, i = 1, … , n be the killing times, m_i, i = 1, … , n the number of animals killed at t_i, and k_ij, i = 1, … , n, j = 1, … , m_i the number of tumors observed in the jth animal killed at t_i. The likelihood function for these data is given by

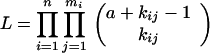4

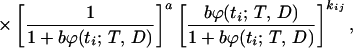where ϕ(t; T, D) is specified by Eq. 3. The parameter θ^*₁=ab represents the mean number of initiated cells per unit dose. The expected number of tumors developed by the time t is given by the formula: E{N(t; T, D)} = abϕ(t; T, D).

The promotion time distribution involved in Eq. 4 remains to be specified. To this end, the function f(u) in Eq. 3 was assumed to be a Γ distribution density with scale parameter α and shape parameter β because this distribution, quite simple as it is, provides a good fit to various experimental and clinical data when incorporated in stochastic models of tumor latency (9, 10, 14, 15). The formulas: τ = α/β and σ = 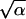/β can be used to calculate the mean and SD of the promotion time, respectively. To find the maximum likelihood estimates â, b̂, θ̂₂, α̂, and β̂ of the model parameters, the likelihood L = L(a,b,θ₂,α,β) was maximized numerically by computer using the flexible simplex algorithm (16). The maximum likelihood estimate of θ^*₁ is given by θ̂^*₁ = âb̂. To ensure stability of the estimation procedure, the search for estimates of the parameters a and α was limited to the set of positive integers. Comparisons of the parameter estimates pertaining to different groups of animals were based on asymptotic confidence intervals resulting from the likelihood ratio statistic.

Section 3: The Probability of Cell Death

Let q be the probability of initiated cell survival in the course of tumor promotion. The total expected number of initiated cells after exposure to dose D is equal to abD. It can be shown that the following intuitively appealing relation holds true:

5

To prove this assertion, let X be the initiation time and Y the length of the promotion stage of tumor development. According to the model presented in Section 2, the event of cell killing may occur during the random time U, where U = min(X + Y,T), and the conditional probability of this event given U is

The probability distribution density for X + Y can be written as

6

See ref. 15 for explanations. Therefore, the probability distribution density for U is of the form

where g(u) is given by Eq. 6, G(u) = ∫₀^u g(s)ds, I[0,T](u) is the indicator of [0,T], and δ(u) is the δ function. Thus, the unconditional survival probability q is given by

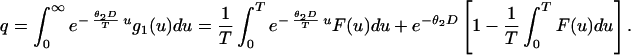7

On the other hand, from Eq. 3 we see that

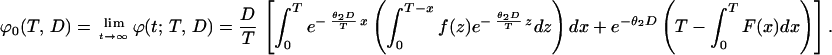8

Change variables in Eq. 8 by letting

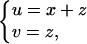then

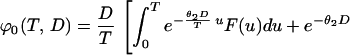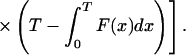Recalling Eq. 7, we conclude that q = 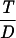ϕ₀(T, D). We will use Eq. 7 to estimate q from real data in the next section.

Section 4: Results of Data Analysis

We applied the model described in Section 2 to experimental data on urethane-induced lung tumors reported by White et al. (17). In these experiments, female strain A/J mice received injections of urethane according to different time and dose schedules, furnishing an opportunity to study the effect of dose rate on the tumor yield. With a fixed total dose, urethane was administered either once or in equal fractions every other day over periods of 8, 16, or 32 days. The animals were killed at 56, 84, 112, 140, and 168 days after the single or the first dose of urethane, and the number of pulmonary tumors was counted. At the time of killing, each group consisted of 10 animals. Three dose levels—0.5, 1, and 2 mg/g body weight—were selected for our analysis because the corresponding regimens of urethane administration for these doses were best matched to the constant dose rate assumption used in the derivation of Eq. 3. Using published data (18, 19) on the kinetics of urethane elimination from the body, we conducted numerical experiments to more realistically model the dose–rate variations with time. The results of our experiments strongly suggest that such a correction for urethane elimination has very little effect on the statistical inference based on Eq. 3.

First we maximized the likelihood Eq. 4 for each value of total dose and each exposure period separately. The estimated values of parameters indicate that dose rate does not exert any tangible effect on the parameter θ^*₁ = ab. The same is true for the mean promotion time τ = α/β as well as for the corresponding variation coefficient v = 1/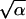. In view of this fact, the number of unknown parameters can be reduced. In doing so, we keep a, b (or a and θ^*₁), α, and β constant for all administration regimens at a fixed dose D. As an example, for D = 2 mg/g, two groups of animals characterized by different values of T (T = 16 and T = 32) were used to estimate the model parameters. When α, β, a, and b were kept equal for both groups of animals, the parameter estimates were as follows: α̂ = 3, β̂ = 0.04, (τ̂ = 74, σ̂ = 43), â = 35, b̂ = 17.8, θ̂₂ = 2.76 for T = 16, θ̂₂ = 2.94 for T = 32. Note that the value of θ̂₂ is also relatively insensitive to variations in the exposure period.

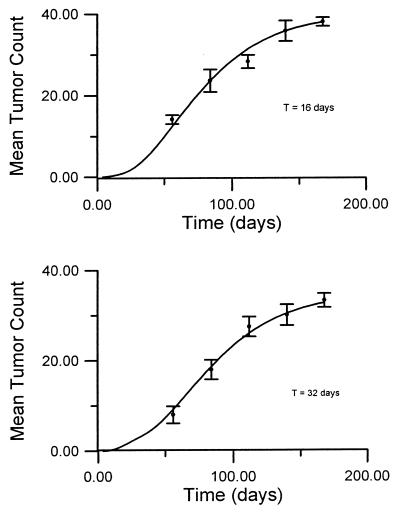
The model provides a good description of adenoma counts for all dose values included in the analysis. For D = 2 mg/g, the resulting fit is shown in Fig. 1. Depicted in this figure are the expected number of tumors per animal computed with the above values of the model parameters and the corresponding sample mean tumor counts at various times after the first injection of urethane.

Figure 1.

Expected number of tumors as a function of time for D = 2 and different exposure periods. Theoretical curves are shown with solid lines, experimental data are represented by the sample mean values. Bars indicate 1 SE for each experimental point.

An extensive discussion of biological effects of urethane in terms of the model parameters will be addressed in another paper (20). In the present communication, our focus is on estimation of the probability of initiated cell death P = 1 − q. Using the maximum likelihood estimates of the parameters incorporated into Eq. 7, we estimated the probability P for different values of D and T. The results are presented in Table 1. It is evident from Table 1 that a large proportion of initiated cells die in the course of tumor promotion, even at a dose as small as 0.5 mg/g body weight. The estimates of P appear to be robust to very large variations in the promotion time parameters. Shown in Table 2 are the values of P resulting from a numerical experiment in which the mean promotion time was substantially reduced whereas the other parameters, including the variation coefficient of the promotion time, were fixed at their estimated values. Comparing data in Table 1 and Table 2, we see that even a 3-fold decrease in the mean promotion time does not affect the estimated values of the probability of cell death. This suggests that a major part of initiated cells are killed by urethane in a very early stage of promotion, i.e., at a time when only single initiated cells are present in the alveolar epithelium. The estimates of P have proved to be fairly robust to perturbations in the promotion time variance as well. It should be noted that the target for urethane action is the population of stem cells; this explains why the lung tissue survives in the presence of that strong cell toxicity.

Table 1.

Estimated proportion of initiated cells killed in the course of tumor promotion

D = 0.5 mg, τ̂ = 133.3 days		D = 1 mg, τ̂ = 70.4 days		D = 2 mg, τ̂ = 74.4 days
T, days	Fraction killed, %	T, days	Fraction killed, %	T, days	Fraction killed, %
1	83.1	1	91.5	–	–
4	85.9	8	93.2	–	–
8	84.6	16	93.3	16	93.6
16	87.8	32	94.5	32	94.4

Table 2.

The probability of cell death with a reduced mean promotion time

D = 0.5 mg, τ = 40 days		D = 1 mg, τ = 23.5 days		D = 2 mg, τ = 24.8 days
T, days	Fraction killed, %	T, days	Fraction killed, %	T, days	Fraction killed, %
1	80.4	1	91.5	–	–
4	83.2	8	93.2	–	–
8	81.9	16	93.0	16	92.9
16	78.6	32	92.2	32	91.7

It is clear that the analysis of dose–effect relationships in chemical carcinogenesis is hampered by the fact that carcinogen-induced cell death contributes significantly to the observed carcinogenic effect of a given compound. In the case of urethane-induced carcinogenesis, this difficulty can be surmounted by invoking biologically meaningful endpoints other than tumor counts. One possibility is to use some of the model parameters for that purpose. In particular, we obtained the following estimates of the mean number of initiated cells as a function of dose: 85 for D = 0.5, 252 for D = 1, and 623 for D = 2. These estimates suggest that the dependence of the initiation rate on the dose of urethane is slightly super-linear. In terms of the probability of cell death, the dose–response relationship can be inferred from Table 1; it clearly reaches a plateau between 1 and 2 mg/g body weight. More data are necessary to perform an appropriate regression analysis of these relationships.