Network-based global inference of human disease genes

Abstract

Deciphering the genetic basis of human diseases is an important goal of biomedical research. On the basis of the assumption that phenotypically similar diseases are caused by functionally related genes, we propose a computational framework that integrates human protein–protein interactions, disease phenotype similarities, and known gene–phenotype associations to capture the complex relationships between phenotypes and genotypes. We develop a tool named CIPHER to predict and prioritize disease genes, and we show that the global concordance between the human protein network and the phenotype network reliably predicts disease genes. Our method is applicable to genetically uncharacterized phenotypes, effective in the genome-wide scan of disease genes, and also extendable to explore gene cooperativity in complex diseases. The predicted genetic landscape of over 1000 human phenotypes, which reveals the global modular organization of phenotype–genotype relationships. The genome-wide prioritization of candidate genes for over 5000 human phenotypes, including those with under-characterized disease loci or even those lacking known association, is publicly released to facilitate future discovery of disease genes.

Introduction

The identification of genes responsible for specific diseases has long been one of the major tasks in the study of human genetics. Traditional gene-mapping approaches, such as linkage analysis and association studies (Botstein and Risch, 2003), have been demonstrating remarkable success in this field. Family-based linkage analysis is able to associate diseases with specific genomic regions. These regions are often large, containing tens or even hundreds of genes, for which experimental examination of causative mutations are expensive and laborious. In contrast, candidate association studies work well when applied to a set of carefully selected functional candidate genes that have clear biological relation to the disease. However, the selection of functional candidates is not straightforward and is often limited by the scope of experts. Indeed, the prioritization of positional candidates from linkage analysis and the selection of functional candidates for association studies have been translated into a need for computational methods to assess the susceptibility of genes to diseases on the basis of functions of genes.

With the fast accumulation of functional genomics data, computational methods based on gene functions have augmented or even supplanted traditional gene-mapping approaches (Botstein and Risch, 2003; McCarthy et al, 2003). These computational methods are largely based on the similarity of characteristics of disease genes, including sequence features (Adie et al, 2005; Aerts et al, 2006), expression patterns (van Driel et al, 2003; Aerts et al, 2006; Franke et al, 2006), functional annotations (Freudenberg and Propping, 2002; Perez-Iratxeta et al, 2002; Turner et al, 2003; Aerts et al, 2006; Franke et al, 2006), literature descriptions (van Driel et al, 2003; Aerts et al, 2006; Li et al, 2006; Gaulton et al, 2007), physical interactions (Aerts et al, 2006; Franke et al, 2006; Oti et al, 2006), and many others (see review of Oti and Brunner, 2007).

Typically, with these features available, a method for prioritizing disease genes computes a score quantifying the association between a gene and a disease, and then uses the computed scores to rank the candidates and select plausible susceptibility genes. However, various factors, such as the pleiotropy of genes, the interactions among genes, the genetic heterogeneity of diseases, and the ambiguous boundary between different diseases, as well as the incompleteness and false-positive data sources, might prevent the direct inference of single gene–disease association (van Heyningen and Yeyati, 2004).

With the development of systems biology, studies have shown that phenotypically similar diseases are often caused by functionally related genes, being referred to as the modular nature of human genetic diseases (Oti and Brunner, 2007; Oti et al, 2008). This modularity, as recently supported by various reports (Brunner and van Driel, 2004; Gandhi et al, 2006; Lim et al, 2006; van Driel et al, 2006; Goh et al, 2007; Lage et al, 2007; Wagner et al, 2007; Wood et al, 2007), suggests that causative genes for the same or phenotypically similar diseases may generally reside in the same biological module, either a protein complex (Lage et al, 2007), a pathway (Wood et al, 2007), or a subnetwork of protein interactions (Lim et al, 2006). Aside from human disease, recent large-scale studies in yeast (Fraser and Plotkin, 2007; McGary et al, 2007) and worm (Lee et al, 2008) also support the idea that genes sharing mutant phenotype are tightly linked in the network.

With this understanding, we reason that this modular nature implies a positive correlation between gene–gene relatedness and phenotype–phenotype similarity. It is interesting to see whether this second-order association between gene and phenotype can be quantified for predicting disease genes. On the basis of this notion, we build a regression model that can explain phenotype similarity by gene closeness (topological proximity in molecular interaction network). We show that the correlation between phenotype similarities and gene closeness, defined by the concordance score, is a strong and robust predictor of disease genes. With the use of this score, we propose a new method, CIPHER (Correlating protein Interaction network and PHEnotype network to pRedict disease genes), to prioritize candidate genes and to explore gene cooperative behavior in human disease. Our method successfully ranks known disease genes at top 1 in 709 out of 1444 linkage intervals, and we demonstrate its effectiveness in prioritizing candidate genes for diseases without known genetic basis by genome-wide scan of disease genes. The high accuracy of our method and its ability to perform genome-wide scan has enabled us to predict a comprehensive genetic landscape of more than 5000 human phenotypes.

Results

Principles of CIPHER

CIPHER assumes that two genes closer to each other in a molecular interaction network may often lead to more similar phenotypes. The assumption is formulated into a regression model from which we derive a score to assess how likely a gene may be involved in a specific phenotype. The score, called the concordance score, is calculated across the entire phenotype network and protein network, measuring the general concordance between the phenotype similarities and the functional genetic relatedness of disease genes.

To build such a regression model, ideally one needs (1) a complete set of standardized phenotypes and the quantified similarities between those phenotypes, (2) a reliable and complete set of physical interactions between proteins of human genes, and (3) a complete list of known disease gene–phenotype associations. In this study, a disease-related phenotype can be operationally interpreted as a textual description of a disease's detectable outward manifestations, and for our study, we use the text records from the OMIM database (McKusick, 2007). Similarity between two phenotypes quantifies the overlap of their OMIM descriptions and is calculated through text mining (van Driel et al, 2006). Protein–protein interactions (PPIs) are collected from a manually curated PPI database called HPRD (Peri et al, 2003). Disease gene–phenotype associations are obtained from the OMIM database. Although none of the data sets are currently complete, they are comprehensive enough as will be shown below.

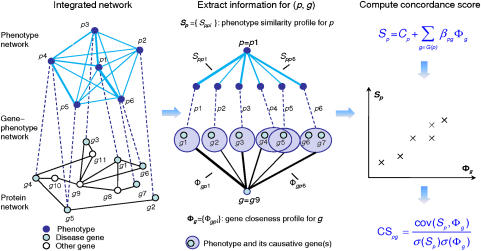
The scoring scheme of CIPHER is illustrated in Figure 1. Given a query phenotype and a set of candidate genes, CIPHER first assembles human phenotype network, gene–phenotype network, and protein network into a single network. Then, the phenotype similarity scores between the query phenotype and all phenotypes are extracted directly from the phenotype network, forming the similarity profile of the query phenotype, and the topological distances from the candidate gene to all known disease genes in the protein network are calculated and grouped according to phenotypes they belong to, composing the closeness profile of the candidate gene. Third, with the use of a linear regression model, the correlation between the closeness profile and similarity profile is calculated and assigned as the concordance score for each candidate gene. Finally, all candidates are ranked on the basis of the scores received.

Figure 1.

Scoring scheme of CIPHER. First, the human phenotype network, protein network, and gene–phenotype network are assembled into an integrated network. Then, to score a particular phenotype–gene pair (p, g), the phenotype similarity profile for p is extracted and the gene closeness profile for g is computed from the integrated network. Finally, the linear correlation of the two profiles is calculated and assigned as the concordance score between the phenotype p and the gene g.

We explore two definitions of topological distance on the basis of two different neighborhood systems: shortest path (SP) and direct neighbor (DN). The two versions of CIPHER are termed CIPHER-SP and CIPHER-DN, respectively. See the section of Materials and methods for more details of the data sources and the model.

Performance of CIPHER

To examine how well the concordance score reflects the biological truth, we assess CIPHER's ability to uncover known disease genes. Each of the known gene–phenotype association is taken as one test case, and for each case we generate a set of genes as the negative control (note that some of them may be true disease genes yet to be discovered). We then calculate the concordance score for each test gene, and rank the test genes according to the score. If the known disease gene is ranked as top 1, we consider it a successful prediction, and we define the precision as the proportion of successful predictions among all predictions. We set a threshold and only make prediction when the highest score of all test genes in a case is no less than it, and define recall as the fraction of true disease genes predicted among all disease genes. An equivalent definition has been used before (Lage et al, 2007).

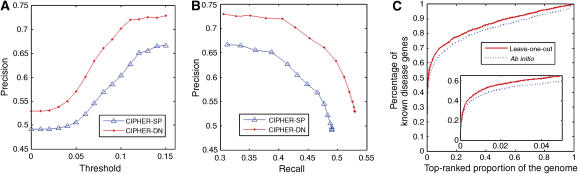
We test our method on three types of control sets: artificial linkage interval, random control, and the whole genome. To simulate the real-life situation in which one or more susceptible linkage interval(s) rather than specific genes have been identified by linkage analysis, a benchmark test on artificial linkage intervals around the known disease genes is generally adopted (Perez-Iratxeta et al, 2002; Franke et al, 2006; Lage et al, 2007). We take a total of 108 genes upstream and downstream of the known disease gene as controls, to simulate the average size of linkage intervals in OMIM morbidmap (Lage et al, 2007). A large-scale leave-one-out cross-validation (see Materials and methods) shows CIPHER-SP can at least rank known disease genes as top 1 in 709 out of 1444 test cases, achieving a precision of 0.49 and a recall of 0.49. For high-scoring candidates, the precision can approach 0.67 while maintaining a high recall of 0.31 (Figure 2). For CIPHER-DN, the precision is even higher, varying from 0.53 to 0.73.

Figure 2.

Performance of CIPHER on linkage intervals and the whole genome. (A) Score threshold plotted against precision. (B) The precision-recall curve when score threshold varies. (C) The percentage of known disease genes contained in the top-ranked proportion of genes in the ranked genome. The zoom-in plot shows details of the curve in top 5% of the ranked genome.

It should be noticed that such a benchmarking might be artificially biased toward better characterized genes, because test genes without PPIs at the moment will be ranked at the tail. To better assess the prediction power, we conduct a cross-validation on random control. In total, 99 genes are sampled from the protein network with equal probability to simulate a fully characterized interval in which all genes have PPIs in the protein network. The leave-one-out cross-validation shows that CIPHER-SP successfully ranks 643 causative genes at top 1, yielding a precision of 0.445. These results show that the performance of CIPHER on random control is only slightly lower than that on artificial intervals, revealing that CIPHER is not biased toward better characterized genes.

We also examine the performance of CIPHER on genome-wide scan of disease genes, which can be used to guide the selection of candidates for association studies without any prior knowledge. This is done by using the whole genome as the test set. Note that the concordance score can only be computed for genes in the protein network, which we termed the ranked genome. We first use the leave-one-out cross-validation, and then check the power of the model to detect disease genes ab initio, i.e. without any known disease genes for the query phenotype (see Materials and methods). This is of great importance because no causative genes have been identified for half of the OMIM phenotypes (McKusick, 2007). In terms of the leave-one-out cross-validation, in 153 of 1444 cases CIPHER-SP successfully predicts the known disease genes from the 8919 genes in the protein network, with a precision of 0.106. In terms of the ab initio prediction, CIPHER-SP successfully predicts 140 cases, yielding a precision of 0.097. The decrease in precision is small (8%), indicating that our model does not rely on known disease genes of the same phenotype very much and is effective in predicting disease genes for phenotypes without any known genetic origins. For CIPHER-DN, precisions are even higher (0.114 and 0.109, respectively). The curve in Figure 2C summarizes CIPHER-SP's ability to enrich disease genes within top-ranked candidates. Specifically, for the leave-one-out cross-validation, our model correctly ranks 88.8, 71.5, and 50% of the known disease genes within top 50, 10, and 1% of the ranked genome, respectively.

These benchmark tests show that CIPHER-DN generally achieves higher precision than CIPHER-SP, but later (in Case study section) we will see that it is less powerful in detecting novel plausible susceptibility genes, potentially because non-disease proteins are less likely to interact with disease proteins. Moreover, we find that most (52%) of the genes in the ranked genome do not have a DN involved in any disease, thus no concordance score can be calculated by CIPHER-DN. On the other hand, by taking indirect connections into consideration, CIPHER-SP can uncover potential susceptibility genes that are less studied. Therefore, we will mainly focus on CIPHER-SP in the following sections.

Comparison with other methods

Various methods (Perez-Iratxeta et al, 2002; Turner et al, 2003; van Driel et al, 2003; Adie et al, 2005; Aerts et al, 2006; Franke et al, 2006; Oti et al, 2006; Lage et al, 2007) have been proposed for prioritizing candidate genes, but few of them have reported the precision within their publications. Traditionally, the power of these methods is measured by their ability to enrich known disease genes over random selection, say, fold enrichment. Lage et al (2007) shows that previous methods for prioritizing candidate genes in linkage interval generally achieve average fold enrichment between 3.8 and 23.1, while our method yields 53.5-fold enrichment. For genome-wide prediction, only two other methods (Freudenberg and Propping, 2002; Gaulton et al, 2007) have been applied to the whole genome, achieving the fold enrichment of 14.7 and 67, respectively. In contrast, CIPHER-SP can approach average enrichment of 954.4 and 864.7 for the leave-one-out cross-validation and the ab initio prediction, respectively. For CIPHER-DN, the enrichment are 1016.8 and 972.2, respectively. Therefore, CIPHER significantly outperforms all these methods in terms of the fold enrichment, both in linkage intervals and the whole genome.

Of these methods, the Bayesian predictor developed by Lage et al (2007) uses the same types of input (phenotype similarity and molecular interaction) as CIPHER, and it prioritizes candidate genes by using similar phenotypes associated with the first neighbors. It achieves a precision of 0.45 and a recall of 0.21 at the default score threshold of 0.1, leading to a fold enrichment of 23.1 (Lage et al, 2007). Only part of the benchmark cases can be obtained, which contains 218 gene–phenotype associations overlapped with our benchmark data. CIPHER correctly identifies 133 of the 218 associations, yielding a precision of 61.01%, significantly outperforming the Bayesian predictor (45%). Further, a comparison for the precision-recall curve of the Bayesian predictor (Figure 2a in Lage et al, 2007) with that of CIPHER (Figure 2B) again shows that CIPHER is superior over the Bayesian predictor, especially for high recall rate, suggesting that CIPHER can achieve higher accuracy and can be applied to many more diseases.

Another method of particular interest is ENDEAVOUR (Aerts et al, 2006), which integrates more than 10 types of genomic data, including Gene Ontology (GO), PPIs, gene expression, literature, and even disease probability predicted from other prioritizing methods. One may expect that by integrating many more types of data sources, ENDEAVOUR would yield better performance than CIPHER. However, the leave-one-out cross-validation for 83 causative genes involved in 12 complex diseases indicates that CIPHER has comparable performance with ENDEAVOUR (0.542 versus 0.530), despite using much less data sources. Further, we reason that the use of literature evidence in this benchmark test would unfairly improve ENDEAVOUR's performance because these literatures may include direct evidence that reports the association between the gene and the disease. After removing literature evidence, the precision of ENDEAVOUR lowers to 0.434.

Confounding factor, bias, and robustness

One possible concern is the potential confounding factor in the benchmarking procedure. For genes associated with more than one phenotype (796 out of 1444 genes in this study), it is relatively easy for the leave-one-out cross-validation to identify the correct gene. Situation where a known causative gene is later found to be associated with other phenotypes is quite possible, as suggested in the OMIM database, in which on average a gene is related to 1.7 phenotypes (McKusick, 2007). Nonetheless, to assess the possible loss of power in identifying novel genes undiscovered in any other phenotype before, we completely remove all other phenotypes sharing the same causative gene under benchmarking. The same leave-one-out cross-validation yields a precision of 0.3179. Though decreased, it represents a 34.6-fold enrichment over random selection, still much better than other methods (a 50% increase over the second best method discussed in this article).

Moreover, it is argued that the protein network we used might be biased toward disease proteins (Oti et al, 2006; Xu and Li, 2006). An examination of the HPRD database shows that indeed disease proteins have more interaction partners than other proteins (10.28 compared to 7.30). However, it is difficult to show conclusively whether this bias is due to investigators' preferential interest in disease-related proteins, or the intrinsic property of disease proteins (see discussion in Oti et al, 2006; Xu and Li, 2006; Fraser and Plotkin, 2007). Nonetheless, to assess whether CIPHER critically relies on this bias, we import about 12 000 additional interactions among non-disease proteins from OPHID (Brown and Jurisica, 2005) to eliminate the bias. PPIs in OPHID are predicted from high-throughput screen results of model organisms, thus are less biased toward human disease. Benchmark test on artificial loci using the denser protein network yields a precision of 0.4521 for CIPHER-SP, only slightly lower than the original precision 0.491. Therefore, though current protein network might be biased toward disease proteins, our model does not rely on such bias to predict disease genes.

The above test of bias shows that CIPHER may be robust to the noise in PPIs data set—the importing of ∼1/3 less reliable interactions does not undermine the power much. We further test this hypothesis by substituting HPRD with the entire OPHID data set, whose size is comparable to HPRD (see Materials and methods). Using the leave-one-out cross-validation on random control, CIPHER-SP achieves a comparable precision of 0.33. Although slightly lower than the performance on HPRD (0.445), the precision is still much higher (at least 43% higher in terms of the fold enrichment) than those of most other disease gene prioritization methods and the random selection. Therefore, we have shown our method can accurately identify disease genes using noisy data that are not specifically generated for the purpose of investigating human diseases.

We also find that our method is robust to noise in the phenotype similarity data. We introduce noise into the phenotype similarity score to assess the robustness of our method to the potential imprecision of phenotype scores. Results (Supplementary Figure S1) show that our method achieves a precision above 0.35 even if the phenotype score contains up to 30% noise, indicating that our method is relatively insensitive to noise in phenotype score.

Case study: breast cancer

To demonstrate CIPHER's ability in uncovering known disease genes and predicting novel susceptibility candidates, we present a case study for breast cancer, which is the most commonly occurring cancer among women and accounts for 22% of all female cancers. Known susceptibility genes, including BRCA1 (Miki et al, 1994) and BRCA2 (Wooster et al, 1995), can only explain less than 5% of the total breast cancer incidence and less than 25% of the familial risk, suggesting that many susceptibility genes remain to be discovered (Oldenburg et al, 2007). The overview section of breast cancer (MIM 114480) in OMIM gives a list of 22 susceptibility genes (May, 2007), 16 of which are characterized in the protein network data. We first examine the results of the genome-wide ab initio prioritization. For CIPHER-SP, it assigns high ranks to most of the known breast cancer causative genes, with 10 out of these 16 genes ranked in top 300 of the ranked genome (Table I). This is statistically significant compared to uniform distribution of disease gene ranks (P=1.0 × 10⁻¹¹, Fisher's exact test, one sided) and 300 is a reasonable number to be included in a high-resolution single nucleotide polymorphism (SNP) association study for a complex disease in human population (Gaulton et al, 2007). CIPHER-DN performs even better on these 10 genes, all ranked within top 49.

Table 1.

The ranks and percentages of known breast cancer susceptibility genes in genome-wide ab initio prioritization

Known disease gene	Rank in 8919 candidates
	CIPHER-SP	%	CIPHER-DN	%
BRCA1	1	0.01	2	0.02
AR	3	0.03	3	0.03
ATM	19	0.21	4	0.04
CHEK2	66	0.74	19	0.21
BRCA2	139	1.56	49	0.54
STK11	150	1.69	21	0.23
RAD51	174	2.00	36	0.40
PTEN	188	2.10	24	0.26
BARD1	196	2.20	41	0.45
TP53	287	3.22	45	0.50
RB1CC1	798	8.95	6360	71.30
NCOA3	973	10.91	343	3.84
PIK3CA	1644	18.43	367	4.11
PPM1D	1946	21.82	7318	82.04
CASP8	4978	55.81	2397	26.87
TGF1	7116	79.78	3502	39.26

Next we checked whether our method can predict novel susceptibility genes that were identified recently. We find that 15 genes suggested as novel breast cancer susceptibility genes by literatures are ranked relatively high (top 10%) in a total of 8919 candidates by CIPHER-SP ab initio (Supplementary Table S2). Eight of them (GGA1, CENTG1, NCOA6, ADAM12, GAB1, ITGA9, MAP3K6, and MYOD1) are reported to mutate at significant frequencies in breast cancer cells and are likely to be responsible for driving the initiation, progression, or maintenance of the tumor (Sjoblom et al, 2006; Wood et al, 2007). The protein kinase AKT1, ranked at 27, is a novel oncogene, and recently a transforming mutation was identified in human breast, colorectal, and ovarian cancers (Carpten et al, 2007). The cell cycle checkpoint gene RAD9, ranked at 130, is a novel oncogene activated by 11q13 amplification and DNA methylation in breast cancer (Cheng et al, 2005). MDM2, ranked at 182, has a SNP in promoter region that was found to accelerate breast and ovarian carcinogenesis in BRCA1 and BRCA2 carriers of Jewish Ashkenazi descent (Yarden et al, 2007). Eestrogen receptor beta (ESR2), ranked at 336, was recently suggested to be associated with increased risk in sporadic breast cancer patient by haplotype analysis (Maguire et al, 2005). WRN, ranked at 340, is a Werner Syndrome causative gene recently found to be associated with breast tumorigenesis (Ding et al, 2007). IKBKE, ranked at 793, is identified by integrative genomic approaches as a breast cancer oncogene (Boehm et al, 2007). RAD50, ranked at 799, is suggested to have effect on genomic integrity and susceptibility to breast cancer (Heikkinen et al, 2006). CIPHER-DN fails to assign ranks to some of these genes.

Further, we examine gene function and pathway enrichment among the top 100 breast cancer-related genes. This is carried out using DAVID (Dennis et al, 2003), by analyzing enrichment of GO Biological Process terms (Supplementary Table S3), and BIOCARTA pathways (Supplementary Table S4). Results show that those genes are enriched in cell cycle and its regulation, DNA damage and repair, cell growth/cell death and their regulation, and estrogen receptor regulation, which agree well with current knowledge on breast cancer (Oldenburg et al, 2007).

A predicted genetic landscape of human diseases

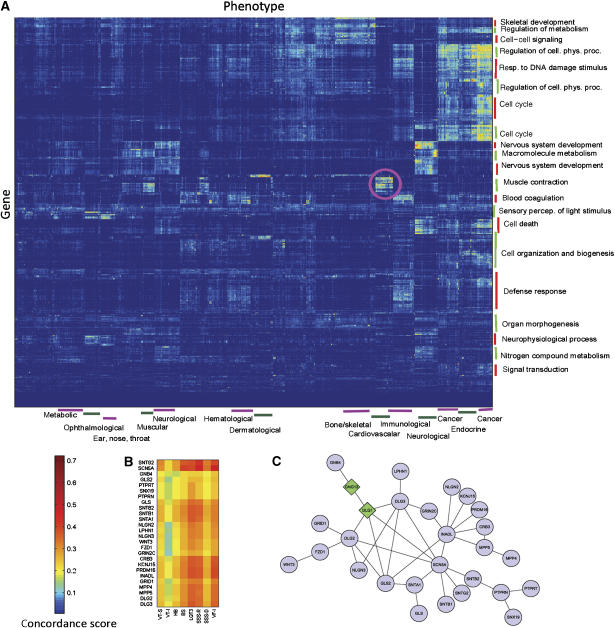
We use CIPHER to infer genome-wide molecular basis for all human phenotypes defined in the phenotype network, to chart a genetic landscape of human diseases. We first compute the concordance scores between all the 1126 phenotypes and 8919 genes within our data, yielding a matrix of more than 10 million elements. A two-way hierarchical clustering (Eisen et al, 1998) is then performed to reveal the modular organization of human genotype–phenotype relationships (Figure 3A). Phenotypes clustered together generally have similar molecular basis, or share significant genetic overlaps. Phenotype clusters are manually inspected and annotated with enriched disease categories on the basis of manual classification concerning the physiological system affected (Goh et al, 2007), and gene clusters are annotated with the most enriched biological process terms of GO, according to DAVID (Dennis et al, 2003).

Figure 3.

Modular organization of the predicted genetic landscape of human diseases. (A) Hierarchical clustering of the concordance scores between 8919 genes and 1126 phenotypes. The color of each cell represents the concordance score of a phenotype (column) and a gene (row), where red/blue indicates high/low concordance score. Phenotype clusters are annotated with enriched disease categories (bottom) and gene clusters are annotated with the most enriched biological process terms of GO (right). The pink circled region indicates a module composed of a gene set of muscle contraction involving in a set of cardiovascular diseases. (B) Zoom-in plot of part of the pink circled region, involving 8 cardiovascular diseases and 26 highly related genes. VT-S: ventricular tachycardia, stress-induced polymorphic [MIM 604772]; VT-I: ventricular tachycardia, idiopathic [MIM 192605]; HB: heart block, non-progressive [MIM 11390]; BS: Brugada syndrome [MIM 601144]; LQT3: long QT syndrome-3 [MIM 603830]; SSS-R: sick sinus syndrome, autosomal recessive [MIM 608567]; SSS-D: sick sinus syndrome, autosomal dominant [MIM 163800]; VF-I: ventricular fibrillation, idiopathic [MIM:603829]. (C) Protein interaction network of the 26 genes (circles) and 2 other genes (diamond) linking GNB4 to the main component.

The modularity of disease landscape is manifested as many isolated and highly scored blocks or modules, each comprising a set of functionally related genes implicated in a set of genetically overlapped phenotypes. For example, the pink circled region in Figure 3A indicates a module composed of a gene set enriched with function of muscle contraction involving in a set of cardiovascular diseases. Figure 3B shows a continuous part of this region, in which 8 cardiovascular diseases are highly related to 26 genes, nearly all of which are within a subnetwork connected by PPIs between themselves (Figure 3C). Another interesting module comprises a set of ophthalmological diseases and genes with function of sensory perception of light stimulus. As shown in Figure 3A, one disease set may be related to several gene sets, e.g. immunological diseases are related to genes with function enriched in blood coagulation and defense response. On the other hand, one gene set may be related to several disease sets, e.g. muscle contraction genes are also highly related to muscular diseases, apart from cardiovascular diseases.

It is hoped that various analyzing methods devised for gene expression profile can also be used to extract useful information from this predicted disease landscape, for example, the identification of differentially expressed genes (Hatfield et al, 2003), and gene set enrichment analysis (Subramanian et al, 2005).

We further chart a much more comprehensive landscape for human diseases, involving more than 14 000 human proteins and more than 5000 phenotypes. The extended human protein network with more than 70 000 interactions is assembled from three curated databases (see Materials and methods). On the basis of this protein network, genome-wide prioritization is carried out for existing phenotypes within the phenotype network, including those without known genetic basis at the moment. All these data are publicly available online (http://bioinfo.au.tsinghua.edu.cn/cipher, also see Supplementary dataset S5 for results of top 100 genes). We hope that the predicted genetic landscape will facilitate future discovery of disease genes. To find out true causative genes from the prioritized list, one can select high-rank genes and test their causality using appropriate experimental protocols. For example, one can sequence the putative causative genes and check for DNA mutations in sufficient size of patient samples (Carpten et al, 2007). Or, for confirmation of putative oncogenes, one can seek for mutations or amplification/translocation of the genes in primary tumors, and also gather experimental evidences that demonstrate critical roles of the putative genes for cancer cell's viability or proliferation (Boehm et al, 2007).

Exploring gene cooperativity

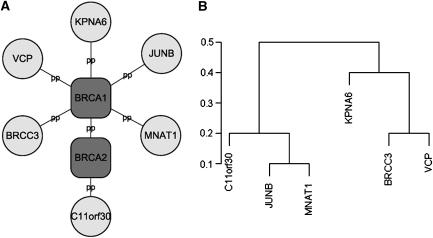
Most genes underlying common (or complex) diseases are non-Mendelian. These genes show very little effects independently but may interact with each other and behave cooperatively to predispose to disease. Various sophisticated algorithms are proposed to uncover these joint effects in population association studies (Ritchie et al, 2001; Zhang and Liu, 2007). Here, we show that CIPHER provides another interesting way to address this issue. Note that the basic assumption of our model parallels the regression model in transcription factor-binding motif discovery from gene expression data, which assumes additivity of the contributions from different transcription factors to target gene expressions (Bussemaker et al, 2001). The model fits the expression data using motif occurrence counts in gene promoter regions, which has the same form as equation (3). Various methods have been proposed to address the problem of cooperativity between transcription factors such as MARSMotif (Das et al, 2004), which builds response function in terms of nonlinear component functions and their products. It is able to identify known functional motifs and their cooperative combinations. Assuming the same nonlinear behavior exists among genes in terms of causing complex disease, we run MARSMotif on top 100 breast cancer-related genes of ab initio genome-wide scoring, and identify 3 significant gene pairs that best explain the variation of the phenotype similarities (Supplementary Table S6). Interestingly, though none of the three pairs of genes interact directly with each other, all of them are linked to each other through BRCA1 and/or BRCA2 by PPIs, and form a star-like subnetwork (Figure 4A). All the six genes are recorded in OMIM, and most of them have already been related to breast cancer. For example, BRCC3 [MIM 300617] is the third subunit of BRCA1/BRCA2-contained complex BRCC (Dong et al, 2003), an ubiquitin E3 ligase that enhances cellular survival following DNA damage. JUNB [MIM 165161], suggested by MARSMotif to cooperate with BRCC3, is an oncogene recently discovered to play important role in biological behavior of breast cancer (Langer et al, 2006). The biological interpretation for their cooperativity is unclear. One possible explanation is the between-pathway hypothesis (Kelley and Ideker, 2005) that the two genes within an interacting pair come from different pathways compensating each other, with BRCA1 as the communication center, or the pivot node (Ulitsky and Shamir, 2007). Interestingly, we find indeed these six genes are clustered into two groups with interacting genes being separated in different groups. (Figure 4B; clustering is based on similarities of GO annotations calculated by GOstats package in Bioconductor; Gentleman et al, 2004).

Figure 4.

BRCA1 subnetwork. (A) Six genes found to participate in three interacting pairs by MARSMotif are linked to BRCA1/BRCA2 by protein–protein (pp) interactions. (B) Hierarchical clustering of the six genes according to their similarity of function (Gene Ontology Biological Process annotation).

Discussion

The success of this model, CIPHER, can be attributed to a combination of several aspects. First, we take the advantage of large-scale phenotype similarity information. Second, and may be more importantly, our model exploits the modularity of genetic diseases more comprehensively. For each candidate gene–phenotype association, the concordance score makes sufficient use of the information implicated in the entire protein network and phenotype network, rather than merely the local environment. In contrast, both ENDEAVOUR and the Bayesian predictor consider only direct interacting proteins and phenotypes associated with them. The global nature of the concordance score makes CIPHER robust to the imprecision of phenotype similarity scores and suffer less from the false positives and false negatives in the current protein network.

There are three potential applications of the predicted genetic landscape of human diseases. First, for candidate association studies, our results can be used to guide the selection of candidate genes in a less biased manner. Previously, the selection of candidate genes suffers from the poor prior knowledge about the biology of the disease, and is limited by the scope of experts. The global nature of our method suffers less from such limitation, and candidates are selected in the context of protein interaction network, which would facilitate the interpretation of the results. Second, the genome-wide prioritization results can also be integrated into weighted/hierarchical genome-wide association studies by mapping concordance scores to SNPs according to their genomic locations. Recent studies (Chen and Witte, 2007; Ionita-Laza et al, 2007) show that by quantitatively incorporating prior information about SNPs, one may clearly distinguish true causal variants from noise. Third, the predicted disease landscape provides a preliminary but systematic view of genetic overlaps between different disease phenotypes, which has immediate practical implications for the design of gene-mapping studies (Rzhetsky et al, 2007; Oti et al, 2008). The need for large sample size and the high cost in collecting patient samples have long been a great challenge for genome-wide gene-mapping studies (Hirschhorn and Daly, 2005). Sample pooling strategy, which combines case–control from several genetically overlapped complex diseases, is promising to handle this problem. Here, the disease landscape moves one step forward to show specifically on which parts of the genome they may overlap, suggesting possible hypothesis on pathogenesis of syndrome.

Certainly, our approach can be improved in the following directions. First, our method is limited to genes with known protein interactions (about one-third of the entire human genome). Further expanding the protein network to embrace less reliable protein interactions (such as the OPHID network) or non-physical functional associations (Franke et al, 2006) may increase the power to detect less-studied disease genes in practice, as suggested in the study of yeast mutant phenotypes (McGary et al, 2007). Second, our method suffers from the imprecision and subjectiveness in quantifying phenotype similarity. The continuing endeavor for standardizing and quantifying phenotypic description would further enhance our method (Biesecker, 2005). Third, like other methods for disease gene finding, our method cannot tell where the causative genetic variants are in high-rank genes. With the recent progress in the prioritization of candidate genetic variants for human diseases (Jiang et al, 2007), it is expected that by prioritizing candidate genes and genetic variants at the same time, the two may benefit each other and facilitate the discovery of disease genes and causative genetic variants therein.

Our method illustrates well the power of the integration of different types of networks. We suggest that the ongoing large-scale mapping of human interaction networks (Aloy, 2007) and systematic collection of human phenotypic data (Freimer and Sabatti, 2003) are valuable for biomedical research, and the increasing coverage and quality of human interaction network, as well as more standardized and objective phenotype descriptions will facilitate the discovery of new disease genes. We also believe that the global concordance analysis may provide ways to better understand the association of different diseases, a holistic rule is also held in traditional Chinese medicine (Li et al, 2007). Taken together, our preliminary study on modeling rules connecting phenotype and genotype networks is one step further toward the emerging field of ‘network medicine' (Barabasi, 2007).

Materials and methods

Data sources

We obtain 34 364 manually curated PPIs between 8919 human proteins from the HPRD database (Peri et al, 2003). We also obtain 33 049 predicted human PPIs between 7185 (4116 are absent from HPRD) proteins from the OPHID database (Brown and Jurisica, 2005), which is built by mapping PPIs from high-throughput screen of model organisms to human. The extended protein network combines HPRD, OPHID and two other curated PPI databases: BIND (Bader et al, 2003) and MINT (Chatr-aryamontri et al, 2007), yielding a network of 72 431 unique pairwise binary interactions between 14 433 human proteins.

We use the phenotype defined in OMIM database (McKusick, 2007). The phenotype similarity scores are obtained from van Driel et al (2006), calculated by text mining of OMIM phenotype records using Medical Subject Headings (MeSH) terms (Lowe and Barnett, 1994). Each phenotype is characterized by a vector of standardized and weighted phenotypic feature terms mapped from corresponding OMIM records (full text and clinical synopsis fields) using MeSH terms (the anatomy (A) and disease (C) sections). The similarity score between two phenotypes is determined by the cosine of their feature vector angle (Brunner and van Driel, 2004). The reliability of the phenotype similarity score has been tested (van Driel et al, 2006), showing that these phenotype similarities are positively correlated with a number of measures of gene functions. The final phenotype network contains pairwise similarity scores for 5080 OMIM phenotypes, covering the majority of recorded human phenotypes.

The gene–phenotype associations are defined in OMIM and are automatically extracted from BioMART (previously known as EnsMart; Kasprzyk et al, 2004). We filter out phenotypes that are not included in our phenotype network, as well as phenotypes having no causative genes in our protein network. In total, we collect 1444 cases (validated gene–phenotype associations) involving 1126 phenotypes in HPRD network, and 2002 cases involving 1421 phenotypes in the extended protein network. All these data sources are downloaded in May, 2007.

Regression model and the concordance score

Our model assumes the additivity of the contribution to phenotype similarity from different disease genes and is defined as

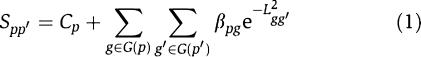Here, S_pp′ is the similarity score between a query phenotype p and another phenotype p′, and L_gg′ is the topological distance between genes g and g′ on the protein network. G(p) denotes all disease genes belonging to the phenotype p. The Gaussian kernel e^−L2_gg′ is used to transfer gene–gene distance to gene–gene closeness. C_p is a constant, and β_pg is the coefficient of this regression model, respectively. C_p could be explained as the basal similarity between p and other phenotypes whose causative genes are not connected to those of p in the protein network, and β_pg represents the level of the gene g contributing to the similarity of the phenotype p to any other phenotype p′. For practical consideration, we simply assume that this coefficient is independent of p′ and g′. In summary, this model assumes that the similarity of two phenotypes can be explained as the result of the linear contribution of their disease gene closeness in PPI networks.

We consider two types of neighborhood systems to define the topological distance L_gg′, depending on how indirect interaction is considered: (i) SP, in which L_gg′ is the graph theory SP length between genes g and g′ in the protein network and (ii) DN, a modified version of SP, in which L_gg′=∞ for indirect neighbor.

To quantify the association between a phenotype and a gene, we define the closeness of gene g to phenotype p′ as the summation of gene–gene closeness from gene g to all disease genes of phenotype p′, as

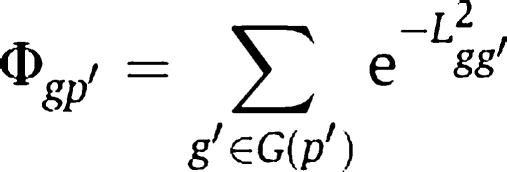Thus equation (1) can be rewritten as

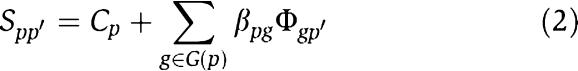The similarities between the query phenotype p and all n phenotypes and the closeness between gene g and all n phenotypes are defined as the phenotype similarity profile and the gene closeness profile, respectively, and are denoted as vectors S_p=(S_pp1, S_pp2, …, S_ppn) and Φ_g=(Φ_gp1, Φ_gp2, …, Φ_gpn). Thus, we can extend equation (2) to the form of

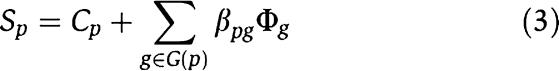In this linear regression model, we define the Pearson linear correlation coefficient as the concordance score

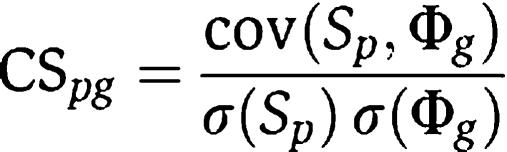where cov and σ mean covariance and standard deviation, respectively. This concordance score measures the consistency between the position of gene g in the protein network and the variations of phenotype similarity for phenotype p in the whole phenotype network. It is then used to rank all the candidate genes for a specific phenotype. Note that in CIPHER-DN, for genes that do not link to any disease genes directly, Φ_g=0, and thus σ(Φ_g)=0 and the CS_pg cannot be computed. In such scenario, we set CS_pg=−1, and these genes will be ranked at the tail.

Benchmark tests

A leave-one-out cross-validation procedure is used to assess the performance of CIPHER. In this procedure, we remove the direct link between true disease gene g and phenotype p, and see if the method can recover this link (rank gene g at the top of the N test genes). This is carried out by taking known disease gene g as unknown when calculating Φ_gip, the closeness from test gene g_i to query phenotype p. Specifically, we compute a gene–gene distance matrix, together with a gene–phenotype closeness matrix before the benchmark test. For a test case involving phenotype p, causative gene g and N–1 control genes g₁, g₂, …, g_N−1, we modify the gene–phenotype closeness from all N test genes to phenotype p, by subtracting the closeness between gene g and all N test genes (including gene g itself). This is equivalent to taking gene g as a non-causative gene when calculating the gene–phenotype closeness matrix. For ab initio prediction, we use leave-k-out cross-validation done in a similar way, where k denotes the number of known disease genes for the query phenotype. For phenotypes with more than one known causative genes, we modified the definition of a successful prediction: for a test case (p, g) in which p has k known disease genes, if gene g is among the top k-ranked genes, we consider it a successful prediction.

Fold enrichment

If a method successfully ranks known disease genes in the top m% of all candidate genes in n% of the linkage intervals, there is a n/m-fold enrichment on average. For example, when testing on artificial interval, our method successfully ranks known disease genes in the top 0.917% (top 1 of 109) of all test genes in 49.1% (709 of 1444) test cases, achieving a fold enrichment of 53.5 on average.

Comparison with ENDEAVOUR

ENDEAVOUR (version 1.39) is downloaded from the website: http://homes.esat.kuleuven.be/~bioiuser/endeavour/endeavour.php. We run it on our data set. To provide sufficient training for ENDEAVOUR, we include phenotype with at least six causative genes from CIPHER's benchmark set. After automated mapping of identifiers, 83 genes involved in 12 phenotypes are recognized by ENDEAVOUR. For each disease gene, other genes from the same phenotype are used to construct the training set. The test set consists of the causative gene and 108 flanking genes, as used by CIPHER. ENDEAVOUR is trained and benchmarked by leave-one-out cross-validation on the training and test sets, and then the resulting ranks are compared with CIPHER.

Eliminating bias in the protein network

The average degree of disease proteins and others in current protein network are 10.28 and 7.30, respectively. To eliminate this bias, we import additional interactions among non-disease proteins from OPHID to elevate the average degree of non-disease proteins, while maintaining the size of the protein network. In total, about 12 000 PPIs are extracted, which increase the average degree of non-disease proteins to 10.30, hence eliminating the bias.

Assessing the influence of noise in phenotype similarity score

New phenotype scores are generated by combining the original score with noise:

where the noise score_noise is generated from a uniform distribution U(0,1), and α is a coefficient ranging from 0 to 1, indicating the proportion of noise in the combined score. The curve showing how the precision of CIPHER (tested on random control) changes when α varies from 0 to 1 can be found in Supplementary Figure S1.

Supplementary Material

Supplementary Figure S1

Supplementary Information 1

Supplementary Information 2

Supplementary Table S2

Supplementary Table S3

Supplementary Table S4

Supplementary Table S6