A gene–culture coevolutionary model for brother–sister mating

Abstract

We present a gene–culture coevolutionary model for brother–sister mating in the human. It is shown that cultural—as opposed to innate—determination of mate preference may evolve, provided the inbreeding depression is sufficiently high. At this coevolutionary equilibrium, sib mating is avoided because of cultural pressures.

Westermarck (1) proposed that “there is an innate aversion to sexual intercourse between persons living closely together from early youth” (italics added). In particular, sibs reared together are expected to avoid mating with one another. Studies on the Chinese custom of sim-pua (adoption of a future daughter-in-law) (2) and on marriage patterns among adults reared together as children in Israeli kibbutzim (3) seem to support Westermarck’s proposition.

Throughout the vertebrate, invertebrate, and plant kingdoms, the propensity to inbreed varies widely (4). In plants, both self-fertilization and self-incompatibility are widely represented. From simple population genetic models, an allele that increases the level of selfing may succeed if the depression of fitness that results from inbreeding is less than 50% (5–9). In animals and birds, experiments designed to detect inbreeding avoidance have produced mixed results (10). In Japanese quail, for example, females reared with siblings chose the company of first cousins over that of both sibs and third cousins (11). Such kin recognition mechanisms would permit inbreeding to be avoided without the necessity of dispersal, which is commonly evoked as a major means of inbreeding avoidance in many mammals.

An “innate” behavior is understood as one that has the same expression across the normal range of environments, so that within the species, there is little variation. Humans, however, are subject to an extraordinarily wide array of social environments, partly as a result of cultural differences among ethnic groups. Whereas sib mating has been banned in most societies that we know about, past and present, it was institutionalized in some (12, 13). Cousin mating, a milder form of inbreeding, is often preferred over complete outbreeding (14).

In the case of institutionalized sib mating in Roman Egypt, the innate avoidance mechanism postulated by Westermarck was readily overridden. Wolf’s studies (15, 16) of minor marriage in Taiwan are usually regarded as providing evidence for the Westermarck effect. But matings between the foster sibs did in fact occur.

Archaeological demonstration of lithic traditions suggests that cultural transmission has been an important determinant of behavior in hominids for more than two million years. In a cultural species, it is more appropriate to frame the discussion in terms of a “norm of reaction” rather than narrowly innate behavior. Thus, a genotype may respond quite differently depending on the cultural pressures its carrier experiences. For example, whether the parents are sibs or unrelated may directly affect the probability that their offspring mate with one another.

Here we present a coevolutionary model in which the probability of sib mating is determined by an individual’s genotype and also by whether or not its parents were sibs. Analysis of this model yields the particularly interesting result that a wide norm of reaction may be evolutionarily stable (see qualification below). When gene–culture coevolution has resulted in fixation of a genotype with a wide norm of reaction, avoidance of sib mating will not be innate. Nevertheless, the evolved biases in cultural transmission and the selective disadvantage of inbred offspring will cause sib mating to be eliminated from the population. At this coevolutionary equilibrium, individuals are genetically capable of mating with sibs, but do not because of cultural pressure.

Model

With genetic determination of the inbreeding rate, it is well known that there is an evolutionary trade-off between the transmission of genes identical by descent to inbred offspring and the inbreeding depression suffered by those offspring. In the case of sib mating in an outbreeding population, the relatedness of a parent to inbred and outbred offspring is in the ratio of 3:2. Hence, using an inclusive fitness argument, if the inbreeding depression is d, sib mating will invade if 3 (1 − d) > 2 or d < 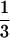. This was also observed in a formal dynamical analysis (7). This argument holds under both diploidy and haploidy. For mathematical simplicity, we assume haploidy in what follows. Specifically, we posit two haploid genotypes A₁ and A₂.

Experimental data suggest that mate choice is more strongly exercised by the female of a species. Therefore, we posit that the occurrence of sib mating is dependent on female choice. If she is of genotype A_i and her parents are sibs, the probability she will want to mate with her brother is b_is, whereas if her parents are unrelated, the corresponding probability is b_ir. In this context we should note, however, that marital dissatisfaction in the marriages studied by Wolf is not necessarily expressed more strongly in the sim-pua (i.e., wife).

Mating is conditional on survival to reproductive age. Each individual, male or female, whose parents are sibs has a viability of 1 − d relative to an individual with unrelated parents. One girl and one boy are born in each family, and deaths occur independently. A surviving female may want to mate with her brother, but can only do so if he also survives. If he dies, she mates with an unrelated male with probability h. The remaining fraction 1 − h of incestuous females who have lost their brothers refrain from mating.

Define S_ij to be the frequency of ordered sib matings between an A_i female and an A_j male, with R_ij the corresponding frequency of random matings between an A_i female and an A_j male. Among the newborns of the next generation, let X_ij be the frequency of ordered sibships, comprising an A_i sister and an A_j brother and derived from a sib mating. Similarly, Y_ij is the frequency of ordered sibships of the same composition but derived from unrelated parents. In this haploid model,

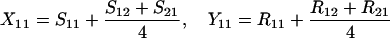1

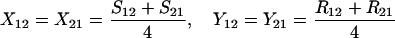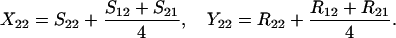Finally, let z_i be the frequency of genotype A_i among the random mating males. We assume that all males, whether mated to their sisters or not, compete equally for random mating females. Hence

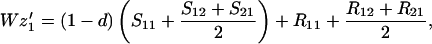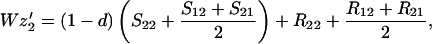2

where a prime indicates adults of the next generation and

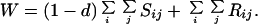3

Our assumptions imply the following recursions in the basic variables S_ij and R_ij, where all summations are over 1 and 2:

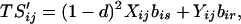4a

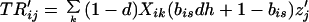4b

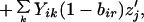where

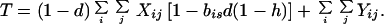4c

Genetic Monomorphism in A₁

Assume that the genotype A₁ is fixed. Dynamics of the frequency of sib matings, S₁₁ (and of random matings, R₁₁ = 1 − S₁₁) are then determined by the vertical transmission rates, b_1s and b_1r, and by natural selection against inbred offspring, d.

The equilibrium frequency of sib matings, Ŝ₁₁, satisfies

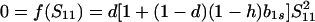5

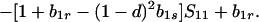Because b_1r ≥ 0 and f(1) = −(1 − d)[1 − (1 − hd) b_1s] ≤ 0, there is only one valid equilibrium if 1 − (1 − hd) b_1s > 0 (d > 0 is assumed). If 1 − (1 − hd) b_1s = 0, Eq. 5 factors to yield

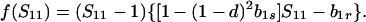6

Hence, two valid equilibria, Ŝ₁₁ = b_1r/[1 − (1 − d)²b_1s ] and Ŝ₁₁ = 1, exist if b_1r < 1 − (1 − d)²b_1s, but Ŝ₁₁ = 1 is the only valid equilibrium when this inequality is reversed.

For small perturbations from the equilibrium, Ŝ₁₁, stability is governed by the eigenvalue

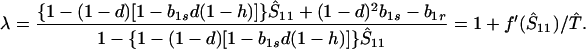7

(Here we are still assuming fixation on the genotype A₁. Stability to introduction of the allele A₂ will be considered later.) Clearly, λ > −1. Hence, the equilibrium Ŝ₁₁ is stable if f′ (Ŝ₁₁) < 0—i.e., when Ŝ₁₁ is the smaller root of f(S₁₁) = 0, and Ŝ₁₁ is unstable when f′ (Ŝ₁₁) > 0. Thus, when there is only one valid equilibrium, it is always stable, and when there are two, the smaller is stable.

Stability to Introduction of New Allele A₂

We next consider stability of the genetic monomorphism in A₁ derived above to introduction of a new allele A₂. Standard linear stability analysis shows that the nonzero eigenvalues are given by the roots of the characteristic polynomial

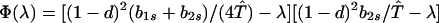8a

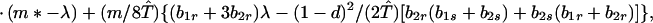where

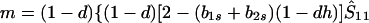8b

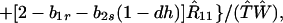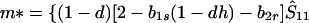8c

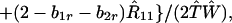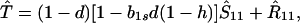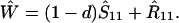8d

Φ(λ) is a cubic of the form

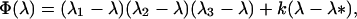9

where we may assume λ₁ ≤ λ₂ ≤ λ₃. In Appendix 1 we show that, provided λ* ≤ λ₃, the monomorphic equilibrium is locally stable if Φ(1) < 0 and locally unstable if Φ(1) > 0.

Norms of Reaction and Evolutionarily Stable Strategies (ESS)

Each genotype A_i is defined by its norm of reaction specified by b_ir, b_is. A genetic monomorphism in A₁ will be evolutionarily stable (17, 18) if the parameters b_1r and b_1s are such that A₂ cannot invade whatever the values of b_2r and b_2s.

Our first major result is that a fully internal norm of reaction—i.e., 0 < b_1r, b_1s < 1—cannot be an ESS. The proof, which is detailed in Appendix 2, relies on small perturbations of the parameters. Set b_2r = b_1r + ξ and b_2s = b_1s + η, where ξ and η are small. Then λ* < λ₃ in which case linear stability is assured if and only if Φ(1) < 0. In general, the expansion of Φ(1) will take the form

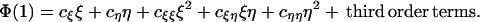10

For a fully internal norm of reaction to be an ESS, we require the linear terms c_ξ = c_η = 0 and the quadratic form to be negative definite. However, as shown in Appendix 2, c_ξξ = 0, whence c_ξξc_ηη − (c_ξη/2)² ≤ 0 and, even if c_ξ = c_η = 0, the quadratic form is not negative definite.

Thus, for any norm of reaction with 0 < b_1r, b_1s < 1, there is always another norm of reaction b_2r, b_2s that can invade. Under the reasonable assumption that b_1r ≤ b_1s, an evolutionarily stable norm of reaction entails b_1r = 0 and/or b_1s = 1.

Norms of Reaction with b_1r = 0

In view of the often-made claim that avoidance of sib mating is innate, the case b_1r = 0 deserves special attention. When b_1r = 0, we have Ŝ₁₁ = 0 and T̂ = Ŵ = 1 at the genetic monomorphism. (If, in addition, h = 0 and b_1s = 1, the unstable equilibrium Ŝ₁₁ = 1 also exists.) From Eqs. 8a and 8c, because λ* = (1 − d)²(b_1s + 2b_2s)/6 < 1/2 and m* = (2 − b_2r)/2 ≥ 1/2, we have λ* < λ₃. Hence, linear stability of Ŝ₁₁ = 0 to invasion by A₂ is determined by the sign of

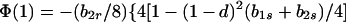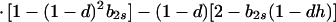11

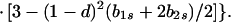Notice first that b_2r does not affect stability provided it is positive. Here we assume b_2r > 0, reserving the analysis of the case b_2r = 0 for the next section. Second, a norm of reaction of the form b_1r = 0, b_1s ≥ 0 will be an ESS only if Φ(1) < 0 for all b_2s. Rewrite Eq. 11 as

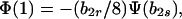12

where

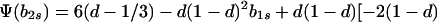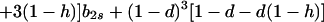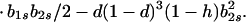12a

Hence, Ψ(b_2s) is linear in b_2s if h = 1 and takes the form of a quadratic that is convex upward if 0 ≤ h < 1. In either case, Ψ(b_2s) > 0 [Φ(1) < 0] for 0 ≤ b_2s ≤ 1 if and only if Ψ(0) > 0 and Ψ(1) > 0.

In particular, from the requirement that Ψ(0) > 0, a necessary condition for evolutionary stability of b_1r = 0 is

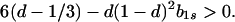13

Hence, for a given value of d > 1/3, inequality 13 is more likely to be satisfied the smaller is the value of b_1s, i.e., the narrower is the norm of reaction.

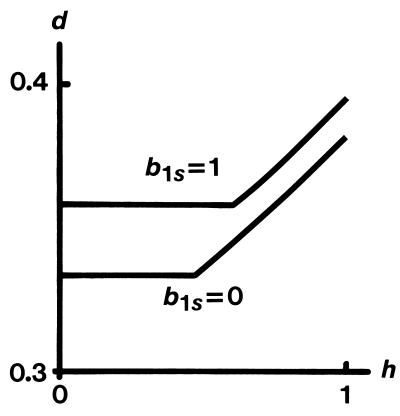
In Fig. 1 we graph the minimum values for d for which the two extreme cases, b_1r = b_1s = 0 and b_1r = 0 with b_1s = 1, will be evolutionarily stable (subject to the condition b_2r > 0). The horizontal axis measures h. For intermediate values of b_1s we have a family of nonintersecting curves that lie between these two curves. The dependence on h and b_1s is not pronounced, and we see that the norm of reaction b_1r = 0 with b_1s = 1 can be an ESS if d > 0.4. If the inbreeding depression from sib matings in humans has consistently exceeded 40%, then a wide norm of reaction, i.e., a large difference (b_1s − b_1r), may have evolved. Based on Seemanová’s study (19) of nuclear family incest, Durham (20) estimates the inbreeding depression resulting from death plus major defect to be about 45%.

Figure 1.

The curves labeled b_1s = 0 and b_1s = 1 give the minimum values of the inbreeding depression, d, for which the two norms of reaction b_1r = b_1s = 0 and b_1r = 0 with b_1s = 1 will be evolutionarily stable against all alternatives that satisfy b_2r > 0. The horizontal axis measures the probability, h, that an incestuous female mates with an unrelated male when her brother dies. For intermediate values of b_1s, there is a family of nonintersecting curves that lie between these two curves. The curve labeled b_1s = 0 meets the d axis at 1/3.

Case of b_1r = b_2r = 0

Recall that the norm of reaction we consider in this paper is defined by the pair of probabilities, b_ir and b_is. We showed in the previous section that any norm of reaction with b_1r = 0 can be stable against all alternatives that satisfy the restriction b_2r > 0. To complete the analysis, let us consider the fate of mutants with b_2r = 0. In other words, when two strategies are both characterized by b_ir = 0 differing only in b_is, which will do better?

From Eq. 11 we expect that the dominant eigenvalue will be one, necessitating a second order analysis. This is outlined in Appendix 3. Applying the method of Nagylaki (21), we obtain the interesting result that, even to second order, the genetic monomorphism in A₁ is neutrally stable. Hence, natural selection on the alternative norms will be very weak, and transitions may occur by random drift. In particular, a wide norm of reaction is just as likely to evolve as a narrow one.

Norms of Reaction with b_1s = 1

A norm of reaction with b_1r = 0 implies no sib matings at equilibrium. However, sibling incest is in fact observed at low, but nonnegligible, frequencies in modern human societies. Because sibling incest is rare, we should consider the evolutionary stability of norms of reaction with b_1r small. To this end, expand the characteristic polynomial Eq. 8b evaluated at λ = 1 in powers of b_1r, giving

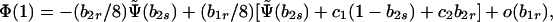14

where Ψ̃(b_2s) is given by Eq. 12b with b_1s set equal to 1, and c₁ and c₂ are functions of the parameters.

Evolutionarily stability obtains when Φ(1) < 0 for all b_2r and b_2s. However, from Eq. 14 this cannot occur: If Ψ̃(b_2s) < 0 for some b_2s, then Φ(1) > 0 for sufficiently large b_2r. If Ψ̃(b_2s) > 0 for all b_2s, then Φ(1) > 0 when b_2r = 0 and b_2s = 1. From Eq. 12b, we see that Ψ(b_2s) can vanish at most twice for b_2s in [0,1]. Hence, we conclude that a strategy with b_1r small and b_1s = 1 cannot be an ESS.

On the other hand, numerical work suggests that a norm of reaction where b_1r is large can be evolutionarily stable to all alternative strategies that satisfy b_2s < 1. When b_2s = 1, this norm of reaction is neutrally stable to second order. An example of such a norm of reaction is b_1r = 0.5 and b_1s = 1 when d = 0.2 and h = 0. However, in this case the frequency of sib matings at equilibrium is predicted to be one, which is unrealistically high.

Discussion

In our model, if b_ir = b_is the female’s mating preference is completely determined by her genotype. The particular case b_ir = b_is = 0 corresponds to innate avoidance of brother–sister mating. On the other hand, if b_ir < b_is parental mating behavior directly affects mate choice by their daughter. In particular, if b_ir = 0 and b_is = 1 then we can say that mate choice is culturally determined.

A norm of reaction provides for phenotypic plasticity of a genotype in a range of environments. Sensitivity to variation in parental mating type may then be regarded as a norm of reaction mediated by cultural transmission. In our model the norm of reaction for genotype A_i is defined by the pair b_ir, b_is. It is natural to refer to the difference b_is − b_ir as the width of this norm.

We have attempted to identify parameter sets b_1r, b_1s that are unbeatable by any alternative set b_2r, b_2s. Although there are no norms of reaction that are truly evolutionarily stable, the approach has proved informative. First we showed that a fully internal norm of reaction 0 < b_1r, b_1s < 1 cannot be an ESS. On the reasonable assumption b_1r ≤ b_1s (otherwise a daughter is more likely to be incestuous when her parents are unrelated than when they are themselves incestuous), evolutionary stability entails b_1r = 0 and/or b_1s = 1. Next we showed that a norm of reaction where b_1r is positive and small with b_1s = 1 can also be rejected. Hence, the remaining candidates for an unbeatable parameter set are (i) b_1r = 0 with b_1s arbitrary; and (ii) b_1r positive and large with b_1s = 1.

Concerning alternative ii, numerical work suggests that the norm of reaction b_1r positive and large with b_1s = 1 may be evolutionarily stable. However, the only cases we have been able to identify entail an equilibrium frequency of one for sib matings. Even if we introduce forms of cultural transmission other than the vertical (parent–offspring) assumed here (22), it would seem difficult to reduce the predicted frequency to the low levels observed in most societies past and present.

A norm of reaction where b_1r = 0 may be evolutionarily stable against all alternatives that satisfy b_2r > 0. Here, the other parameter defining the norm, b_1s, may take any value between 0 and 1. In Fig. 1 we graph the minimum values of the inbreeding depression, d, for which the two extreme cases, b_1r = b_1s = 0 and b_1r = 0 with b_1s = 1, are evolutionarily stable. For intermediate values of b_1s, we have a family of nonintersecting curves that lie between these two curves.

When d is sufficiently large and h is relatively small—e.g., if d > 0.358 and h < 0.617, any such norm of reaction will be evolutionarily stable (subject to the condition b_2r > 0). For smaller d or larger h, Fig. 1 shows that a small value of b_1s is more likely to produce evolutionary stability. Note that a norm of reaction where b_1r = 0 and b_1s is small involves relatively strong genetic determination of inbreeding avoidance, whereas if b_1r = 0 and b_1s is large, there is a significant cultural component in the determination of the daughter’s preference. There is no theoretical reason to prefer one norm over the other on the basis of our model, although the latter norm seems more realistic because human mate choice is sensitive to cultural pressures. That the former will evolve in a larger region of the space of parameters d and h is consistent with the proposal of Cavalli-Sforza and Feldman (23) that genetic determination will usually prevail over the cultural.

With this norm of reaction, regardless of the value of b_1s, the frequency of sib mating will converge to zero at the gene–culture coevolutionary equilibrium. In particular, if b_1s > 0, individuals are genetically capable of sib mating, but do not because of cultural pressures.

An interesting relation exists between the two norms of reaction b_1r,b_1s, and b_2r,b_2s, where b_1r = b_2r = 0 but b_1s and b_2s differ. Both are neutrally stable to second order to invasion by the other. In fact, numerical iteration of Eq. 4a reveals that the subspace R₁₁ + R₁₂ + R₂₁ + R₂₂ = 1 is neutrally stable. Hence, two such norms of reaction may coexist, implying a genetic polymorphism in the probability that a daughter from a brother–sister union will herself be incestuous. Moreover, in a finite population transitions between the two norms may occur by random drift.

We now argue that the norm of reaction, b_1r = 0 with b_1s > 0, may be consistent with the known facts and suggest a way in which this may be tested. First, in apparent contradiction, sib matings are observed at low, but nonnegligible, frequencies in modern societies. However, nuclear family incest often involves the mentally retarded (19), so that this is unlikely to be an evolved response. Second, about one-sixth of all marriages in one region of Roman Egypt were between full sibs (13). These socially recognized unions were recorded in the census documents and persisted for several centuries before the custom eventually disappeared. Hence, the institution is best regarded a transient phenomenon, initiated by forces extraneous to our model. We may be able to test our prediction of b_1s > 0 (or, for example, that incest results from being homozygous for a recessive gene) if sufficient trans-generational data are available. If b_1s > 0, brother–sister marriages should occur recurrently in the descendants of an incestuous pair. What is transmitted vertically may not be an “inbreeding meme,” but rather economic circumstances that favor sib mating. However, the result will be the same. If b_1s = 0, on the other hand, occurrence of sib mating should be sporadic. Third, the norm of reaction b_1r = 0 with b_1s > 0 cannot be an ESS unless the inbreeding depression, d, exceeds 1/3. As noted above, Durham’s (20) estimate of d based on Seemanová’s (19) data is about 45%. However, this estimate combines the effects of mortality and morbidity, on the assumption that serious abnormalities are the equivalent of death. The inbreeding depression as computed from differential mortality alone is about 10%.

Ralls et al. (24) estimated inbreeding depression in 38 captive species of mammals. As measured by survivorship to a specified age, the average inbreeding depression for sib matings is 33%. They suggest that, under natural as opposed to captive conditions, the cost of inbreeding may be exacerbated. In the case of humans, it is arguable whether inbreeding depression would have been more severe without modern medical care. Although this seems likely, reproductive compensation coupled with selective infanticide of malformed children would partly reduce the disparity in the number of surviving children. We conclude that the inbreeding depression for sib matings may have been about 45% during most of history and prehistory, if serious congential abnormalities resulted in death, infertility, or the inability to mate.

Finally, a few words on the incest taboo. Why sex and marriage within the nuclear family are prohibited by custom, rule, or law is a major conundrum that continues to puzzle anthropologists, and even some jurists (ref. 25; see also ref. 20 for a recent review). The present paper only scratches the surface of the problem, but we believe that it suggests one direction in which a solution may be sought. In the context of a gene–culture coevolutionary model, the establishment of an incest taboo may be equated with the spread of an “outbreeding meme.” The meme spreads in our model because of evolved biases in cultural transmission and natural selection against inbred offspring. There is no need to invoke rational choice based on a realization of the deleterious consequences of inbreeding.

ABBREVIATION

ESS

evolutionarily stable strategies

Appendix

Our demonstration assumes that in Eq. 9 we have the strict inequalities 0 < λ₁ < λ₂ < λ₃, but the proof can be generalized. From Eq. 8d, T̂ ≥ (1 − d)². Hence, two of the λ_i’s have the bounds

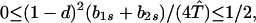A1-1

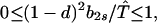A1-2

and λ* has the bounds

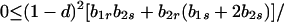A1-3

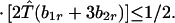We wish to prove that the dominant eigenvalue, which is positive, is less than unity if Φ(1) < 0, and is greater than unity if Φ(1) > 0. Consider three cases. First assume λ* ≤ λ₁. Then Φ(λ) > 0 in the interval λ₂ ≤ λ ≤ λ₃, where λ₂ ≤ 1 from Eqs. A1-1 and A1-2. Moreover, Φ"(λ) = 2 [(λ_{1 −} λ) + (λ_{2 −} λ) + (λ_{3 −} λ)] < 0 for λ ≥ λ₃. Hence, Φ(λ) intersects the λ-axis only once when λ > λ₃. Next, if λ₁ < λ* ≤ λ₂, then Φ(λ₁) < 0 ≤ Φ(λ₂) and we also have λ₁ < λ₂ ≤ 1. Similarly, if λ₂ < λ* ≤ λ₃, then Φ(λ₁) < 0 ≤ Φ(λ*) where λ₁ < λ* ≤ 1/2. In all cases, therefore, if λ* ≤ λ₃, then the largest root of Φ(λ) is less than unity if Φ(1) < 0 and greater than unity if Φ(1) > 0. It is clear that if λ* > λ₃ and Φ(1) > 0, the largest eigenvalue is greater than unity.

Appendix

Set

A2-1

where ξ and η are small. Then λ* ≈ (1 − d)²b_1s/(2T̂) < (1 − d)²b_1s/T̂ ≈ (1 − d)²b_2s/T̂, which implies λ* < λ₃. Substitution of Eq. A2-1 and λ = 1 in Eq. 8b yields

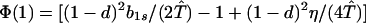A2-2

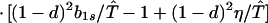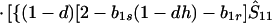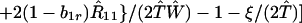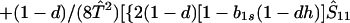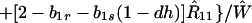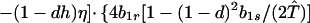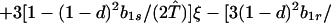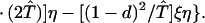Expanding Eq. A2-2 in ξ and η, there is no ξ² term. Hence, c_ξξ = 0 in Eq. 10.

Appendix

Expansion of Eq. 4a in the small variables S₁₁, S₁₂ + S₂₁, S₁₂ − S₂₁, S₂₂, R₁₂ + R₂₁, R₁₂ − R₂₁, and R₂₂ yields the local stability matrix:

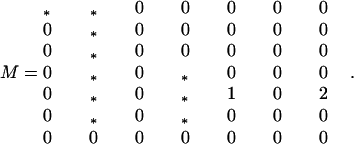A3-1

The asterisks indicate nonnegative terms. In particular, the three diagonal asterisks are less than unity, whence the dominant eigenvalue one is nondegenerate.

The right eigenvector corresponding to this dominant eigenvalue (0,0,0,0,1,0,0)^T, where T denotes the transpose. Hence, according to the method of Nagylaki (21) we need consider only the terms in (R₁₂ + R₂₁)² among the second-order terms. Such terms appear in the expansions of (R₁₂ + R₂₁)′ and R₂₂^′, where they contribute −(R₁₂ + R₂₁)²/2 and (R₁₂ + R₂₁)²/4, respectively.

Next, the left eigenvector corresponding to the eigenvalue one is

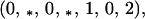A3-2

where the asterisks here indicate positive terms. Then the product of the vector of second order terms and Eq. A3-2 vanishes. Thus, if b_1r = b_2r = 0, then to second order, the genetic monomorphism in A₁ is neutrally stable to the introduction of A₂.