Load and P_i Control Flux through the Branched Kinetic Cycle of Myosin V^,

Abstract

Myosin V is a processive actin-based motor protein that takes multiple 36-nm steps to deliver intracellular cargo to its destination. In the laser trap, applied load slows myosin V heavy meromyosin stepping and increases the probability of backsteps. In the presence of 40 mm phosphate (P_i), both forward and backward steps become less load-dependent. From these data, we infer that P_i release commits myosin V to undergo a highly load-dependent transition from a state in which ADP is bound to both heads and its lead head trapped in a pre-powerstroke conformation. Increasing the residence time in this state by applying load increases the probability of backstepping or detachment. The kinetics of detachment indicate that myosin V can detach from actin at two distinct points in the cycle, one of which is turned off by the presence of P_i. We propose a branched kinetic model to explain these data. Our model includes P_i release prior to the most load-dependent step in the cycle, implying that P_i release and load both act as checkpoints that control the flux through two parallel pathways.

Myosin V is a cargo-carrying molecular motor that converts chemical energy from ATP hydrolysis into 36-nm hand-over-hand strides, as it moves processively along actin tracks (1). A striking feature of the molecule is its long α-helical neck domain, which binds six calmodulins in series (2) and acts as a lever arm (3–6). Beyond the neck, the two heavy chains form a predominantly α-helical coiled-coil that ends in a globular cargo-binding domain, which is also involved in regulating the activity of the molecule (7, 8).

For myosin V to travel processively over long, 1–2-μm distances, the ATPase activity and motion generation of the individual heads must be coordinated so that one head remains bound to actin as the other head steps forward (9). This coordination requires the heads to communicate, presumably through intramolecular strain that develops as the leading head attempts to swing its lever arm forward but is resisted by the strongly bound trailing head (5, 9–11). This internal resistive load may slow the release of ATP hydrolysis products (i.e. ADP and/or P_i) from the active site of the leading head, whereas the positive strain experienced by the trailing head may accelerate their release (10–14). The specific biochemical and mechanical states that each head transitions through during its processive run is far from certain, but we and others have proposed that myosin V proceeds through a branched kinetic scheme (15, 16), potentially offering the myosin V molecule alternate processive pathways as it negotiates the crowded cytoskeletal network of the cell (17) and the loads that this meshwork may present.

To characterize the kinetic pathways of myosin V and the specific states that are sensitive to load, we have used the single molecule laser trap assay to examine the stepping kinetics of expressed double-headed myosin V heavy meromyosin in response to load. With increasing load, the attached lifetime following a forward step was significantly prolonged. At high forces, a dynamic equilibrium was reached where the probability of myosin V taking a forward or backward step was equal. Additional insight into the kinetic pathways taken by myosin V under load was obtained through changes in inorganic phosphate (P_i) concentration, because P_i release may be linked to the powerstroke and potentially reversed in the presence of P_i (18, 19). The presence of P_i significantly reduced the load sensitivity of the stepping kinetics of myosin V. Both the effects of load and P_i were interpreted as further evidence that myosin V can utilize multiple kinetic pathways and that within each pathway one or more transitions are sensitive to load.

EXPERIMENTAL PROCEDURES

Protein Engineering, Expression, and Purification—Double-headed murine brain heavy meromyosin Va (hereafter called myosin V) with an N-terminal biotin tag and a C-terminal yellow fluorescent protein was expressed in Sf9 cells as described previously (15). This construct, previously used by our laboratory, had properties indistinguishable from expressed wild-type murine myosin Va heavy meromyosin (20). The biotin tag is amino acids Met⁷⁰–Glu¹⁵⁶ from the Escherichia coli biotin carboxyl carrier protein, which is biotinated at a single lysine during expression in Sf9 cells (21, 22). Actin was purified from chicken pectoralis as described previously (23). The filamentous actin was labeled with TRITC3 phalloidin.

Standard Laser Trap Assay Buffers—The assay buffer used contained: 100 μm ATP, 25 mm KCl, 1 mm EGTA, 10 mm dithiothreitol, 4 mm MgCl₂, >25 μg ml^-1 Δall-calmodulin (a constitutively active non-Ca²⁺-binding mutant of calmodulin (24)), 0.25 μg ml^-1 glucose oxidase, 45 μg ml^-1 catalase, 5.75 μg ml^-1 glucose, and 25 mm imidazole, pH 7.4. The buffer was supplemented with either 40 mm sodium phosphate when stated (boiled for >10mins prior to use to remove contaminating pyrophosphate) or 92 mm KCl (to compensate for ionic strength change with P_i). All of the experiments were performed at ∼20 °C.

Laser Trap and Actin Velocity Measurements—The laser trap assay was conducted using the experimental setup described previously (25). To construct the three bead assay, latex beads (diameter, 1.4 μm; Interfacial Dynamics, Or) were coated with N-ethylmaleimide (NEM)-myosin by incubating overnight at room temperature in 1.4 mg/ml NEM-myosin solution. Flow-cells were constructed as outlined previously (25, 26), except myosin V was attached to the surface using an antibody to its C-terminal YFP. Solutions were added to the flowcell in the following order: 1) 20 μl of 50 μg ml^-1 anti-YFP 3e6 antibody (Invitrogen) for 2 min; 2) 100 μl of 0.5 mg ml^-1 bovine serum albumin (Sigma-Aldrich) for >6 min; 3) 40 μl of myosin V (between 0.4 and 0.1 μg ml^-1 to ensure only a single myosin molecule interacts with the actin filament) for 2 min; 4) 100 μl of assay buffer with 1 μl of sonicated NEM-myosin-coated beads and 1 μl of 10 nm TRITC phalloidin-labeled actin. Two traps were created, and a single NEM-myosin-coated latex bead was captured in each trap. With actin filaments floating in solution, the microscope stage was then maneuvered so that the free ends of the actin filament were attached to the beads within the traps. The actin was then pretensioned to at least 4 pN by adjusting the separation between traps. This bead-actin-bead assembly was lowered onto a bead that was fixed to the flowcell surface and sparsely coated with myosin V. We observed activity on less than 10% of the surface beads visited, confirming that only single molecules were being interrogated. The data in this study were obtained from a total of 11 molecules, five without added P_i and the remainder with P_i. Each molecule was sampled for an extended period, allowing hundreds of steps to be recorded from each.

We found that extremely low trap stiffnesses were necessary to observe processive motion, likely because of the low stall forces that characterize this motor. To reduce the stiffness of the laser traps, a partial force clamp was used (27). In brief, a 20-kHz closed loop feedback system was applied by linking the bead and laser trap positions via acoustic optical deflectors (28). The feedback frequency response is in excess of the corner frequency obtained from the Lorentzian form power spectrum of the trapped bead displacement in solution (<500 Hz (29)). Therefore, the feedback system was not limited by the closed loop response time. The feedback was offset by a desired fraction of the bead position, effectively reducing the restoring force of the laser trap without compromising its stability. The final combined stiffness of the laser traps was ∼0.004 pN/nm. The linear range of the photodiode detectors (up to 900 nm) was determined for each set of myosin runs by stepping the bead and thus its image across the detector. A processive run was not analyzed if it went beyond the linear range of the detector or if all of the steps were not distinguishable.

Data Analysis—Myosin V stepping was measured by observing the position of the bead that was being pulled away from its trap center. The data were filtered at 2 kHz and digitally sampled at 4 kHz. Step transitions were determined manually using Clampfit 9.0 (Molecular Devices) and guided by changes in bead position variance, calculated with a sliding boxcar of 15 ms (see Fig. 1d). The steps were then idealized by recording start position, end position, and mean displacement for a dwell period. Force lifetime relationships were constructed by averaging dwell times in successive 0.2-pN force bins; the average force in the 0.2-pN bin was used as the abscissa for plotting histograms. This approach of calculating lifetimes was found to provide an accurate estimate for dwell time and confirmed by using a Monte Carlo-generated data set to compare estimates using average dwell times to the expected value (data not shown). Backsteps were defined as steps between 0 and -50 nm and were seen at all loads but less frequently at low loads (see Fig. 4). Detachments were classified as backsteps larger than 50 nm because forward steps rarely exceeded this value (<7%; see Fig. 2, a and c). At high loads, detachments did not necessarily return to the base line prior to reattachment, suggesting that the myosin V molecule can bind to actin rapidly. This is consistent with the fast ATP hydrolysis rate (∼750 s^-1) (10). At low loads backward steps and detachments were similar in character; therefore variance was used to identify backwards steps that resulted in a return to base line with an increase in variance (which occurs upon detachment of myosin V from actin). Pairwise analyses were carried out as described under “Results,” the step size of a backstep was subtracted from its corresponding preceding or forward step, and these data were then plotted as histograms. All of the data were fit using the least squares Marquardt method to the equations shown in the results or figure legends.

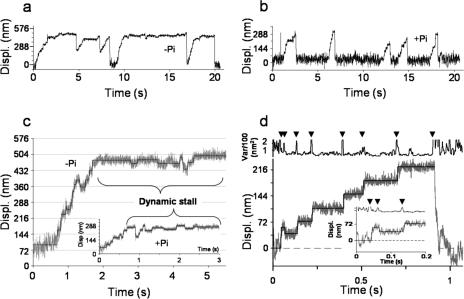
FIGURE 1.

Myosin V processivity with and without 40 mm P_i. a, an example displacement (Displ.) trace generated by a single myosin V molecule moving against the load of the laser trap. As myosin V moves further from the trap center, its velocity slows because of the increased load. b, in the presence of P_i, the displacement of a single myosin V molecule does not appreciably slow at high loads. c, examples of dynamic stall. Displacement is presented in gray for raw data in the absence and presence (inset) of P_i. The idealized form of these data is shown as a solid line (see “Experimental Procedures”). Backsteps occur more frequently as the load increases (greater displacement from base line), until very high loads where an equal probability of forward and backward steps is seen, resulting in a net zero velocity. Also seen in these data traces are backwards steps with magnitudes greater than -50 nm; such backsteps are classified as detachments. d, an expanded trace of myosin V taking a backwards step in the presence of P_i at a low load (data in gray, idealization shown as solid line). The displacement variance (calculated using 15-ms boxcar) was used as a guide to identify the beginning and end of a step. The inset is an expanded view of a low force backstep (∼0.2 pN). The continued reduced variance after the backstep confirms this is not base-line drift or a detachment.

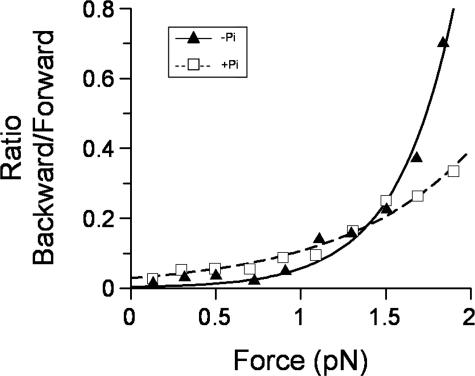
FIGURE 4.

Equilibrium distribution of backsteps versus load. The ratio of the number of backward-forward steps was plotted against the mean force, binned at 0.2 pN. In the absence of P_i (triangles), the data were very load-dependent and best fit to a single load-dependent process (Equation 2) yielding K₀ = 0.003 ± 0.001 and x = 12 ± 1 nm. With P_i present (squares), a decrease in load dependence is seen, as well as a greater ordinate axis offset, indicating P_i induces backstepping in the absence of load. A fit to Equation 2 yielded K₀ = 0.03 ± 0.005 and x = 5.2 ± 0.4 nm. No error bars are shown because these data are absolute counts for the entire data set from multiple single molecules.

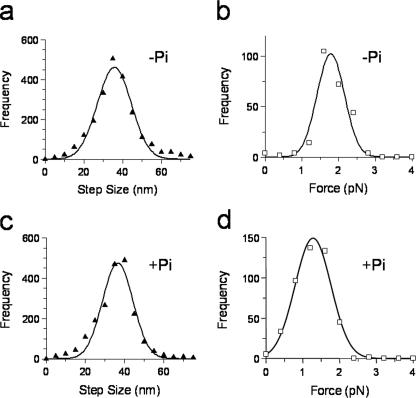
FIGURE 2.

Step size and maximum force histograms in the presence (+P_i) and absence (-P_i) of 40 mm P_i. a, step size histogram for all forward steps, the data are fit to a Gaussian distribution with mean 36 ± 9 nm. b, maximum force histogram, the force experienced by myosin V in the last step before detachment. The data were fit to a Gaussian distribution with mean force of 1.8 ± 0.4 pN, n = 450. c, same as a but with P_i and a fit of 37 ± 8 nm. d, same as b but with P_i and a fit of 1.3 ± 0.5 pN, n = 249. Frequency equals the number of observed steps.

RESULTS

To further define the mechanochemical pathway used by myosin V during a processive run, the attached lifetimes of forward and backward steps, ratio of backwards to forward steps, and detachment kinetics were determined under load in the presence and absence of P_i.

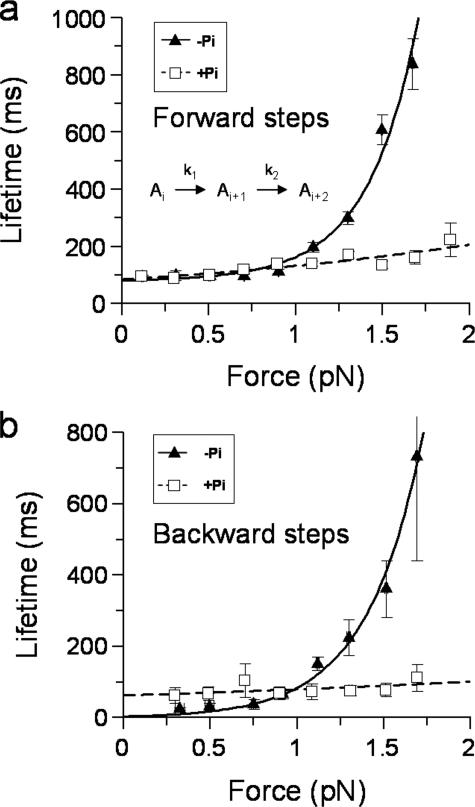
Forward Stepping Kinetics—Single myosin V molecules take successive 36 ± 9-nm steps against the linear elasticity of the laser trap (Figs. 1, a and c, and 2a). As the motor steps forward against loads >1pN (total displacements >250 nm at ∼0.004 pN/nm typical trap stiffness), the attached lifetime following a step increases, suggesting that the stepping kinetics are load-sensitive (Fig. 3a, triangles). The load dependence of the forward step lifetimes was best fit by a modified Arrhenius/Eyring formula (30) containing two sequential load-dependent processes (Fig. 3a),

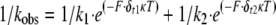(Eq. 1)

where the attached lifetime equals 1/k_obs; k₁ and k₂ are the rates for the load-dependent processes at zero load; δ_t1 and δ_t2 are the distances to the transition state; F is the load; κ is the Boltzmann constant; and T is temperature in Kelvin. The fit to this equation yielded k₁ = 13 s^-1, δ_t1 = 0.4 nm, k₂ = 426 s^-1, and δ_t2 = 14 nm.

FIGURE 3.

Effect of load and P_i on the attached lifetime following forward and backward steps. a, forward step lifetimes were averaged and binned as described under “Experimental Procedures.” In the presence of P_i (squares), the data are only slightly load-dependent and fit well to the first term of Equation 1 yielding 1/k_f(+Pi) = 84 ± 9 ms, δ_tf(+Pi) = 1.8 ± 0.3 nm and n = 2,368 steps. In the absence of P_i (triangles), the lifetimes slow considerably as the motor experiences load. The data do not fit well to a single load-dependent process and are therefore fit to both terms in equation 1. The fit yields 1/k₁ = 79 ± 32 ms, δ_t1 = 0.4 ± 2.6 nm, 1/k₂ = 2.3 ± 1.1 ms, and δ_t2 = 14 ± 1 nm, n = 2,199 steps. The lifetimes were calculated as means for measured dwell times (described under “Experimental Procedures”), and the error bars represent the standard errors of the means for both force and lifetime. A minimal kinetic scheme for a linear sequential model described by Equation 1 is shown on the graph. The transit time through the pathway is given by the sum of the dwell times for each step (1/k_x). Under load, the step that contributes most to the transit time shifts from k₁ to k₂ (see main text). b, lifetimes of backsteps were averaged as described under “Experimental Procedures.” In the absence of P_i (triangles) the data were best fit to a single term of Equation 1 yielding 1/k_b = 4 ± 1.3 ms, δ_tb = 12 ± 0.9 nm, and n = 230 steps. With P_i present (squares), the number of backsteps versus load was reduced but was still well described by a single load-dependent relationship yielding 1/k_b(+Pi) = 63 ± 12 s^-1, δ_tb(+Pi) = 1 ± 0.6 nm and n = 212 steps.

The addition of high concentrations of phosphate reverses phosphate-dependent transitions within the actomyosin ATPase cycle. In the presence of 40 mm P_i, with total ionic strength held equal to that in the absence of P_i, myosin V moved processively with multiple 37 ± 8-nm steps (Figs. 1, b and d, and 2c); however, the maximum force prior to detachment occurred at significantly (t test p < 0.0001) lower loads 1.3 ± 0.5 pN (Fig. 2d) compared with that in the absence of phosphate 1.8 ± 0.4 pN (Fig. 2b). The maximum detachment force was independent of laser trap stiffness (data not shown), indicating that the detachment force was not limited by the inherent run length of the motor as defined under unloaded conditions (15).

Strikingly, in the presence of phosphate processive runs proceeded at a nearly constant rate and did not slow considerably with load as observed in the absence of P_i (Fig. 1, compare a and b). The load dependence of the attached life-times was best described by a single process (equivalent to the first term of equation 1) with a rate at zero load, k_f(+Pi) = 12 s^-1, and a δ_tf(+Pi) = 2 nm (Fig. 3a, squares). Thus the presence of P_i eliminated the faster, more load-sensitive process that normally exists for forward steps in the absence of P_i.

Kinetics and Thermodynamics of Backsteps—Backsteps could be observed at all loads (Fig. 1), and the mean attached lifetimes following a backstep showed load-dependent kinetics (Fig. 3b, triangles). The data were best fit by a single load-dependent process (equivalent to the second term of equation 1), yielding k_b = 263 s^-1 and δ_tb = 12 nm. These values are comparable with the fast (k₂), highly load-dependent (δ_t2) process associated with forward steps, suggesting that these two processes may share the same rate-limiting step.

The ratio of backward to forward steps increased exponentially with load (Fig. 4, triangles). At ∼2 pN, myosin V reaches a dynamic stall where the probability of taking a step forwards or backwards is approximately equal, as evidenced by the similarity to the measured maximum detachment force (Fig. 2b). The ratio of backward to forward steps defines an equilibrium constant for directional stepping that showed load dependence and therefore was fit to the following relationship,

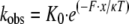(Eq. 2)

where k_obs is the observed equilibrium; K₀ is the equilibrium in the absence of load; F is the applied load; x is the change in the equilibrium position of the myosin V molecule as a result of a backstep; κ is the Boltzmann constant; and T is temperature in Kelvin. Based on the fit (Fig. 4, triangles), the equilibrium position of the motor shifts by x = 12 nm during a backstep. At zero load k_obs = K₀ = 0.003, indicating that only one in 333 steps will be a backstep.

As with the forward steps, the presence of P_i transformed a fast and highly load-sensitive attached lifetime following a backstep (Fig. 3b, triangles) to a slower (k_b(+Pi) = 16 s^-1) and less load-dependent (δ_tb(+Pi) = 1 nm) process (Fig. 3b, squares). The load dependence for forward and backwards steps in the presence of P_i was similar, suggesting that the attached lifetime following either a forward or backwards step is limited by the same transition in the processive cycle. The ratio of backwards to forwards steps decreased relative to those in the absence of P_i. With P_i, the data were well described by Equation 2 (Fig. 4, squares), yielding values of K₀ = 0.03 and x = 5 nm. These parameters indicate that the probability of a backstep has increased ∼10-fold at zero load, but the process of undergoing a backstep is not as sensitive to load as in the absence of P_i. Furthermore unlike in the absence of P_i, with phosphate present runs rarely reach dynamic stall, indicating that the rate of detachment is elevated in the presence of P_i.

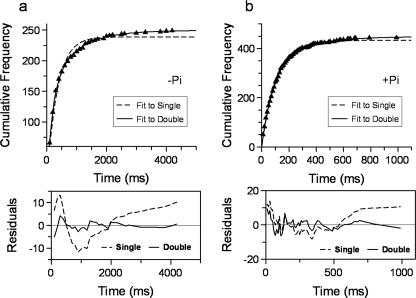
Kinetics of Run Termination—Information about the detachment kinetics of myosin V from actin can be derived from the attached lifetimes of the last step prior to detachment across all loads. These data were plotted in the absence of P_i as cumulative frequencies (Fig. 5a), which provide a robust bin width-independent analysis (31, 32), and were best fit by a double exponential with rate constants of 5 and 1 s^-1. These data indicate that myosin V may detach from actin via two independent routes. In the presence of P_i, the attached lifetimes of the step prior to termination of a processive run were well fit by a single exponential with a rate of 9 s^-1 (Fig. 5b), suggesting that P_i has eliminated one of the two detachment paths that normally exist in the absence of P_i.

FIGURE 5.

Termination of a processive run. Lifetimes of the last step prior to detachment as defined under “Experimental Procedures” were plotted, discarding empty bins, as cumulative frequencies (a) in the absence of P_i. These data were fit to a single exponential relationship as defined by: N·(1 - e^-t·k)/(1 - e^-tmax·k), where N is the number of observations, t is time, k is the rate constant, and t_max is the fixed maximum bin width. However, the fit as shown by the dotted line has residuals (bottom panel) that deviate characteristically from the data, suggesting a more complex relationship. A fit to the sum of two exponential terms (solid line) produced a better fit (see residuals in bottom panel), yielding: N₁ = 153 ± 9, k₁ = 5.1 ± 0.3 s^-1, N₂ = 95 ± 9, k₂ = 1.1 ± 0.1 s^-1, and t_max was fixed to 4200 ms; actual number of observations = 249. b, with P_i present, the cumulative frequency plot is well fit by just a single exponential (dotted line) with residuals as shown in the panel beneath the plot. The fit to the data yielded n = 433 ± 1, k = 9.2 ± 0.1 s^-1, and t_max was fixed to 1000 ms; actual number of observations = 444. When fit to a double exponential (solid line) the fit was only improved for the last two points. Furthermore, the noise at shorter time scales appears the same as in the single exponential residuals and does not have the characteristic shape associated with a fit of a single to a double exponential, as seen in the residuals in a. Thus the marginal improvement provided by a double exponential fit was not warranted.

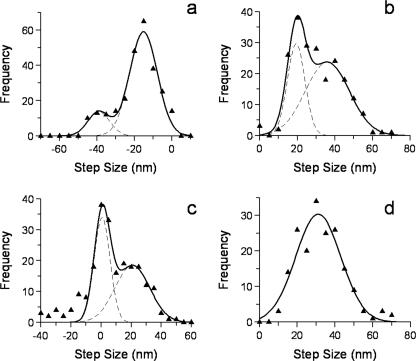
Amplitude of the Backstep in the Absence of P_i—The amplitudes of backsteps observed at all loads were best described by two populations centered on -15 ± 7 and -39 ± 6 nm (Fig. 6a). To understand the origin of these backsteps, the size of the preceding forward steps were also examined. Steps prior to a backstep consisted of two populations with amplitudes of 19 ± 5 and 36 ± 12 nm (Fig. 6b), corresponding to a partial or full forward step, respectively. Taking advantage of the single-molecule approach in this study, we were able to use pairwise analysis; where the size of a backstep is subtracted from the preceding forward step for each individual backstep detected. We found two populations (Fig. 6c). The predominant population was centered on 0.7 ± 5 nm consistent with myosin V backstepping to its original position, in both the case of a 19- and 36-nm preceding forward step. The second population was centered on 21 ± 12 nm and likely originates as a result of a 15-nm backstep after a 36-nm preceding forward step (see “Discussion” and Fig. 8). Following a backstep, myosin V steps forward again with a mean amplitude of 31 ± 12 nm (Fig. 6d). The large standard deviation and shorter than 36-nm step size may indicate that this step originates from a combination of steps with differing mean values, a point that is addressed in the discussion.

FIGURE 6.

Step size analysis associated with backsteps. a, backstep size histogram (without P_i) was fit to the sum of two Gaussian distributions; mean₁ = -15 ± 7 nm, amplitude₁ = 60, mean₂ =-39 ± 6 nm, amplitude₂ = 13. b, step size histogram for steps preceding a backstep (without P_i); two populations were evident and were fitted to the sum of two Gaussian distributions; mean₁ = 19 ± 5 nm, amplitude₁ = 30, mean₂ = 36 ± 12 nm, amplitude₂ = 24. c, pairwise histogram in the absence of P_i. For each backward step the preceding step size is subtracted and plotted as a histogram. Two populations are evident and were fitted to the sum of two Gaussian distributions; mean₁ = 0.7 ± 5 nm, amplitude₁ = 34, mean₂ = 21 ± 12 nm, amplitude₂ = 18. d, histogram of step amplitudes following a backstep (without P_i). These data were fit to a single Gaussian; mean₁ = 31 ± 12 nm.

FIGURE 8.

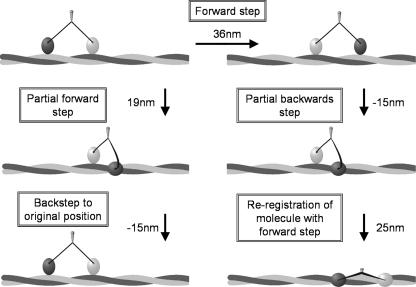
A cartoon depiction of the origin and consequences of backsteps. Our data suggest that the majority of backsteps return the motor to its original position on actin as a result of a partial forward step (see Fig. 6, b and c). This process is illustrated on the left side of this figure; under load myosin V steps forward short of the next actin pseudo-repeat; therefore, the center of the molecule only travels ∼19 nm. The lead head detaches and with the reversal of the powerstroke of the trail head, steps backwards to the preceding actin pseudo-repeat; returning the molecule to its original position. The 21-nm peak in Fig. 6c is accounted for by a full 36-nm forward step (left to right, upper two states) followed by a partial backstep of 15 nm (right side of figure). Following this partial backstep, the rear head steps to the actin pseudo-repeat in register with the lead head, resulting in a shorter forward step (∼25 nm) and a spiral around the actin filament.

DISCUSSION

Our study demonstrates that the forward stepping kinetics of myosin V are defined by two load-dependent processes, consistent with previous measurements (16, 33, 34). One process is 10-fold faster and 10-fold more load-dependent than the other, resulting in longer attached lifetimes under resistive loads (Fig. 3a, triangles). The probability of backsteps increases dramatically with load until stall (Fig. 4), where the probability of taking a forward or a backward step is approximately equal, similar to observations of dynamic stall made for kinesin and dynein (35–37), but previously unseen for myosin V. Because load slows myosin V and increases the probability of backsteps, the net motor velocity slows, as reported previously (38). Following a backstep, the load dependence for the attached lifetime is described only by the faster and more load-sensitive process observed for forward stepping (Fig. 3b, triangles).

To gain further insight into the identity of the load-dependent steps, high concentrations of phosphate were added to prevent progression through steps that involved phosphate release. The mechanochemical coupling of the motor was markedly altered by phosphate. The most striking difference was that both forward steps (Fig. 3a, squares) and steps following a backstep (Fig. 3b, squares) could be best described by a single process with little load sensitivity, similar to the slower process seen for forward steps in the absence of P_i (Fig. 3a, triangles). We use these results to provide additional support, as well as to provide constraints for a branched kinetic model of myosin V processivity.

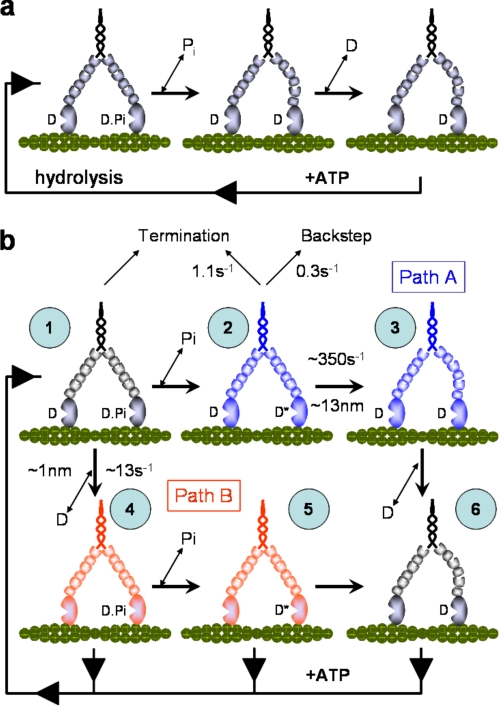
Forward Stepping—The load-dependent kinetics for forward stepping were well described by a linear reaction scheme consisting of two sequential transitions (Fig. 3a). Given the ATPase cycle of myosin V, these transitions might reflect P_i release from the leading head followed by ADP release from the trailing head (Fig. 7a). Although this simple kinetic scheme has been proposed previously (12, 14, 33, 39), other studies required more complex branched kinetic models to describe myosin V processivity (15, 16). Independent of our earlier work (15), the stepping kinetics in the present study once again require that a branched kinetic model be considered. If we begin by assuming the linear scheme in Fig. 7a, the addition of P_i should have halted or at least slowed the rate of forward stepping at low loads. This was not the case, suggesting that rebinding of P_i (state 1) shunts the motor along an alternate path (Fig. 7b, Path B) that has only a single load-dependent transition (Fig. 3a). With the remaining load-dependent rate of 12–16 s^-1 at zero load similar to measured ADP release rates obtained both in solution and the laser trap (9, 10, 12), we propose that the alternate path (Fig. 7b, Path B) begins with ADP being released from the trailing head (state 1 → state 4) prior to P_i release from the leading head (state 4 → state 5). In addition to the ADP release rate being similar, so is its sensitivity to load as reported for a myosin V S1 construct (13). Although our figure (δ_t = 0.4–2 nm) is less than the reported 4.3 nm, the double-headed structure of our heavy meromyosin construct may allow the imposed load of the trap to be distributed between the heads, resulting in a reduction of the load experienced by the trailing head relative to single-headed constructs (39).

FIGURE 7.

Models for myosin V processivity. a, simplified linear model for the processive biochemistry of myosin V. In this model the release of P_i from the lead head is coupled with rotation of the lever arm. This generates internal strain favoring the release of ADP from the rear head. ATP subsequently binds to the nucleotide free rear head permitting the center of the molecule to step forwards 36 nm. b, a six-state branched model for myosin V processivity under loaded conditions (see text for discussion and details). All of the rate constants and load sensitivities shown are the averages for the range of values obtained in this study. The blue states form Path A with red forming Path B, and black are states common to both pathways. Under load and without P_i, we propose that state 2 is the predominantly populated because load directs flux to Path A as the rate of ADP release from the rear head slows, and P_i release from the lead head of state 1 is essentially irreversible. Furthermore, state 2 precedes the loaded rate-limiting transition of Path A (state 2 → state 3). With P_i present, the rate-limiting step becomes the ADP release step of Path B (state 1 → state 4), therefore state 1 becomes the steady-state complex because flux is diverted from state 2. Termination occurs at state 1 for both Paths A and B and at state 2 for Path A only; the latter effectively protects myosin V from populating a strongly bound dead end complex.

The loss of the highly load-dependent transition in the presence of P_i also suggests that normally the motor can travel along Path A, where an additional state following P_i release must exist that is highly load-dependent (state 2; Fig. 7b). This state would have ADP bound to both heads, with the leading head still in the pre-powerstroke conformation. Such a state has been characterized biochemically and by single-molecule experiments (10–12) and has potentially been observed by electron microscopy (40). The transition out of state 2 requires the leading head to rotate its lever arm against the combined resistance of the trailing head and the external load, thus accounting for the high load dependence. We propose that this transition (state 2 → state 3), leads to the “telemark” conformation of the motor (state 3) (41). In summary, flux through Path A is guaranteed by the essentially irreversible release of P_i from state 1, committing the motor to attempt the highly load-dependent state 2 to state 3 transition. Although a similar transition exists in Path B (state 5 → state 6), it may not be as load-dependent at the loads studied here, because of a reduction in the internal strain within the motor as a consequence of the rear lever arm rotation upon ADP release (state 1 → state 4) (13). Furthermore, ATP binding to the trailing head in state 4 or 5 would release it from actin, resulting in the forward transition occurring unimpeded by internal strain or more likely terminating the run as both heads would be in a weak binding state. This might explain why the motor no longer reaches dynamic stall in the presence of P_i (Figs. 1b and 4).

Run Termination—Processive runs terminated at relatively low forces (1.3–1.8 pN), consistent with more recent observations (38) but lower than earlier estimates (9, 33). The differences may be due to the manner in which the loads are imposed or the myosin V constructs used; both are matters for speculation. Examination of the attached lifetimes for the last step prior to termination suggests that myosin detaches from actin by either of two processes, one at a slow rate of 1 s^-1 and a second at 5 s^-1 (Fig. 5a). Because the slower termination is eliminated in the presence of P_i, we expect it occurs along Path A, subsequent to P_i release. Although run termination can occur at all loads, its probability is highest at high loads (Fig. 2), where the motor presumably resides in state 2. Therefore, detachment and run termination occur from this state at 1 s^-1, consistent with detachment rates proposed from a comparable state with a strongly bound rear head and a less tightly bound lead head (32).

Because of its insensitivity to P_i, the faster detachment rate of 5s^-1 must occur from a state common to Paths A and B (i.e. state 1). Termination from state 1 was proposed in our earlier model under unloaded conditions (15), where competition between the rates of detachment and stepping forward determine the probability of run termination. The fact that this rate increases to 9 s^-1 in the presence of P_i is predicted by P_i shunting the flux through Path B where the cycling rate is less load-dependent and ranges between 12 s^-1 under unloaded conditions to 5 s^-1 at the highest loads (Fig. 3a, squares). Thus the faster detachment rate in both the presence and absence of P_i merely reflects the overall cycling rate of the motor. Termination from state 1 will only occur as fast as the motor can return to this state, which is determined by the cycling rate. These termination data provide further evidence for a branched kinetic model. By having a second termination point in Path A from a state that predominates under high loads, the motor avoids entrapment in a strongly bound state.

Backsteps—The size, occurrence, and kinetics of backsteps offer further evidence for a branched kinetic mechanism as well as providing insight into the structural states that the motor adopts during its processive run.

Backstep sizes were found to be predominantly distributed about -15 nm with a smaller population at -39 nm, which we consider to be equivalent to a full -36-nm backstep (Fig. 6a). This bimodal distribution suggests different origins in the biochemical cycle, which was investigated by examining the sizes of steps preceding and following a backstep. We found the preceding forward step was not always a full 36-nm step; instead there was a substantial 19-nm component (Fig. 6b) and that when this occurred there was an increased chance of a backstep (data not shown). Pairwise analysis (Fig. 6c) exploits our single molecule approach to find correlations between the size of a backstep and its preceding forward step. This analysis indicates that backsteps either return myosin to its original position (zero nm peak) or short of this (21-nm peak). The 0-nm peak in the pairwise histogram is likely generated by 36-nm backsteps from 36-nm forward steps, and also by 15-nm backsteps after truncated 19-nm forward steps (Fig. 8, left side). To explain the second peak, a ∼15-nm backstep from a complete preceding 36-nm forward step generates a 21-nm peak in the analysis (Fig. 8, right side).

What are the implications of myosin V backstepping against a load? Backsteps either return myosin V to its position before taking a backstep or only partially back. In the case of a partial return (Fig. 8, right side), the lead head releases and then rebinds actin short of its pseudo-repeat, bringing the heads closer together than 36 nm. This foreshortened step results in the lead head binding azimuthally to F-actin, relative to the trailing head. The subsequent forward step brings the trailing head into the new longitudinal register of the leading head by docking onto the next actin pseudo-repeat. During this transaction the centroid moves forwards 25 nm, and the interhead spacing is returned to 36 nm. This suggests that under load, myosin V may take shorter forward steps and spiral around the actin filament (42). Analysis of the steps following a backstep indicates that the subsequent forward step is ∼31 nm (Fig. 6d), consistent with a combination of full 36-nm and partial 25-nm steps. The resultant increase in spiraling may provide another mechanism for guiding cargo around cellular obstacles (43).

From which specific mechanochemical state(s) within the cycle do backsteps originate? The load dependence for attached lifetimes following a backstep is described by a fast (263 s^-1), highly load-dependent process (δ_tb = 12 nm) (Fig. 3b, triangles), similar to the faster of the two processes that comprise the load dependence of forward stepping. Thus after the motor steps back, it steps forward again through the same highly load-dependent rate-limiting step that all forward steps transition through along Path A (i.e. state 2 → state 3). Additionally, the backstep itself likely occurs from state 2, because the lifetime of steps preceding a backstep are indistinguishable from those preceding normal forward steps at the same load (data not shown). Therefore, both the step size and kinetic data suggest that load, for most cases, induces a foreshortened 19-nm step (Figs. 6b and 8, left side). We propose that as the motor attempts the state 2 to state 3 transition from this position on actin the following occurs: 1) resistive load detaches the lead head; 2) the trailing head is then pulled backwards, reversing its powerstroke; and 3) the detached lead head switches its role and reattaches as the trailing head, one actin pseudo-repeat (i.e. 36 nm) distal to the new leading head (Fig. 8, left side). This scenario would result in the shorter backsteps of 15 nm that are observed most frequently and returns the motor to state 2, the state occupied predominantly under load. In the presence of P_i the same pattern of backstep amplitudes and pairwise histograms were seen. However, the relative contributions were changed perhaps reflecting different origins compared with that in the absence of P_i (see supplemental Fig. 1S).

What evidence exists to support load-induced detachment for backsteps? We observe the frequency of backsteps to increase dramatically with load, from one step in 333 under unloaded conditions to one step in two at stall (Fig. 4). This load-dependent equilibrium constant, K, for backward to forward steps enables us to estimate the backward stepping rate (k_back) as a function of load assuming K = k_back/k_f, where k_f is the reciprocal of the attached lifetimes in Fig. 3a (triangles). This simple calculation suggests that k_back = 0.3 s^-1 with a slight load dependence of δ_tback = ∼1.3 nm (data not shown). The rate and load dependence of this process is similar to that observed for load-induced backstepping in the absence of ATP (32) and detachments of single heads (11). Therefore, it is likely that resistive loads forcibly detach the lead head from a prepowerstroke conformation.

Conclusions—In this study, we have used both load and P_i to perturb the mechanochemical cycle of myosin V. Our data support a model in which myosin V can transit through two pathways in a branched cycle (Fig. 7b) and that the flux through these pathways is modulated by load and P_i. The flux through these pathways will be determined by the rate of P_i release from the leading head (state 1 → state 2) relative to the rate of ADP release (state 1 → state 4) from the trailing head. The present data do not address this question, but an earlier study suggested that P_i release along Path A is slow under unloaded conditions (15), allowing flux through Path B. The fast rate of P_i release (>200 s^-1) measured in solution for both single- and double-headed myosin V constructs (10, 12) suggests the contrary, with minimal flux through Path B. However, neither of these biochemical studies directly probed the rate of P_i release from the leading head when the trailing head is strongly bound to actin with ADP in the active site, i.e. the state 1 → state 2 transition. Until this rate is determined, the significance of this alternate pathway will be a matter of debate.

At high loads, the occurrence of backsteps increases dramatically, consistent with load rupturing the attachment of the lead head from actin. These backsteps may permit myosin V to try multiple times to negotiate cellular obstacles and even rotate around the helix of actin to find alternate routes. Although myosin V structurally appears simply as two independent motors, a remarkable feedback system exists between the heads so that myosin V can effectively deliver its cargo while negotiating the challenges presented to it by the cytoskeletal meshwork.