Abstract
Recombinant inbred lines derived from an advanced intercross, in which multiple generations of mating have increased the density of recombination breakpoints, are powerful tools for mapping the loci underlying complex traits. We investigated the effects of intercross breeding designs on the utility of such lines for mapping. The simplest design, random pair mating with each pair contributing exactly two offspring to the next generation, performed as well as the most extreme inbreeding avoidance scheme at expanding the genetic map, increasing fine-mapping resolution, and controlling genetic drift. Circular mating designs offer negligible advantages for controlling drift and exhibit greatly reduced map expansion. Random-mating designs with variance in offspring number are also poor at increasing mapping resolution. Given equal contributions of each parent to the next generation, the constraint of monogamy has no impact on the qualities of the final population of inbred lines. We find that the easiest crosses to perform are well suited to the task of generating populations of highly recombinant inbred lines.
DESPITE decades of effort, the molecular variants that underlie complex trait variation have largely eluded detection. Quantitative genetics has mapped these fundamental units of the genotype–phenotype relationship to broad chromosomal regions and quantitative trait loci (QTL), but dissecting QTL into their constituent quantitative trait nucleotides (QTNs) has been challenging. Historically, a major impediment to QTL mapping was the development of molecular markers, but as the time and cost of marker development and genotyping have declined, the bottleneck in QTN discovery has shifted to the mapping resolution permitted by a finite number of meiotic recombination events. Simple, practical methods for increasing mapping resolution will help break the QTN logjam. We investigated aspects of inbred line cross designs to identify such simple, practical methods.
Many techniques increase the number of informative meioses contributing to a mapping population derived from a cross between inbred strains. The simplest technique is merely to increase the number of individuals sampled in an F2 or backcross (BC) population. A more appealing approach is to increase the number of meioses per individual, which increases the mapping resolution without increasing the number of individuals to be phenotyped and genotyped and permits the separation of linked QTL. The production of recombinant inbred lines (RILs), derived from an F2 population by generations of sib mating or selfing (Bailey 1971; Soller and Beckman 1990), allows for the accumulation of recombination breakpoints during the inbreeding phase, increasing their number by twofold in the case of selfing and fourfold in the case of sib mating (Haldane and Waddington 1931).
The accumulation of breakpoints in RILs is limited by the fact that each generation of inbreeding makes the recombining chromosomes more similar to one another, so that meiosis ceases to generate new recombinant haplotypes. As an alternative to RILs, Darvasi and Soller (1995) proposed randomly mating the F2 progeny of a cross between inbred founders and using successive generations of random mating (RM) to promote the accumulation of recombination breakpoints in the resulting advanced intercross lines (AILs). Linkage disequilibrium decays each generation as sex does the work of producing new haplotypes. A trivial extension of the AIL design preserves the diversity in the intercross population by inbreeding to yield highly recombinant inbred lines, as Darvasi and Soller (1995) noted. Such a design had previously been employed by Ebert et al. (1993). This recombinant inbred advanced intercross line design has obvious appeal in its union of the advantages of both AILs and RILs and has been employed in the production of mapping populations in several species (Ebert et al. 1993; Liu et al. 1996; Lee et al. 2002; Peirce et al. 2004).
The inbred lines derived by inbreeding from an advanced intercross population have many names in the literature, including intermated recombinant inbred populations (IRIP; Liu et al. 1996) or intermated recombinant inbred lines (IRIL; Sharopova et al. 2002). These names risk confusion with recombinant inbred intercross populations (Zou et al. 2005), which are populations of heterozygotes derived by intermating recombinant inbred lines. IRIP also implies that the population is inbred, although in fact it is the individual lines that are inbred. The term advanced recombinant inbreds (ARI) (Peirce et al. 2004) also fosters confusion with RILs in an advanced stage of inbreeding. We therefore use the simplest abbreviation, combining the RILs with AILs: RIAILs, or recombinant inbred advanced intercross lines (Valdar et al. 2006).
RIAILs have become increasingly popular for QTL mapping, but one aspect of the approach seldom addressed is the mating design best suited to the intercrossing phase of RIAIL production. Analytical studies have generally assumed random mating in an infinite population. In practice, finite populations suffer relative to the ideal case because of genetic drift and because of the reduced effective recombination rate that results from mating among relatives (Darvasi and Soller 1995; Teuscher and Broman 2007). Moreover, the exact pattern of mating among relatives has consequences for the rate of loss of heterozygosity within individuals and populations, as worked out by Sewall Wright (1921). We investigated the practical consequences of mating pattern, including regular-mating schemes and variations on random mating, on the utility of RIAILs for fine mapping.
In regular-mating schemes, each individual mates with a specified relative each generation, so that the pedigree is independent of the generation. Selfing and sibmating are examples of regular mating in which the population is subdivided into separate lines that do not cross with one another, but many regular-mating systems involve intermating among an entire population. Wright (1921) described schemes for the “least possible inbreeding” in finite populations, where all mates are necessarily related. In a population of size 4, for example, the scheme calls for matings between individuals that are first cousins twice over; they share no parents, but necessarily share all grandparents. Matings involve quadruple second cousins in populations of size 8, octuple third cousins in populations of 16, and so forth.
Although Wright's inbreeding avoidance (IA) design eliminates drift resulting from variance in parental contributions to subsequent generations, it increases the drift due to segregation in heterozygotes because it maximizes the frequency of heterozygotes. Alternative regular-mating schemes that force matings among close relatives increase inbreeding in the short term but, by decreasing segregation drift, may reduce allele-frequency drift at the population level. Kimura and Crow (1963) introduced two simple mating designs, circular mating (CM) and circular pair mating (CPM), whose reliance on matings among relatives preserves more diversity in a population than Wright's (1921) scheme. The unintuitive relationship between inbreeding and diversity is illustrated by the fact that optimal designs for maintaining diversity in a population are those that eliminate intermating and instead divide the population into independent highly inbred lineages by, for example, selfing (Robertson 1964). Among regular breeding systems that do not subdivide the population, including all systems that would be useful for RIAIL construction, the optimal design for retaining diversity is unknown (Boucher and Cotterman 1990).
In addition to the extreme forms of regular inbreeding defined by Wright's (1921) inbreeding avoidance scheme and Kimura and Crow's (1963) circular designs, variations on the theme of random mating may also alter the outcome of RIAIL production. Moreover, regular inbreeding designs may be difficult to carry out in practice. The formal designs require a truly constant population size. The loss of individuals due to accident or to segregating sterility, for example, would prevent the application of the scheme, unlike a random scheme where losses merely shrink the population. One modification of random mating is the imposition of monogamy in which each mate has offspring with only a single partner. This is often a practical necessity, but it might also have consequences for the relatedness of mates in subsequent generations. A second possible modification of random mating is to equalize the contributions of each individual to the next generation. Eliminating the variance in offspring number, by permitting exactly two offspring per parent, has the effect of doubling the effective population size relative to the truly random case, which exhibits Poisson variance in offspring number (Crow and Kimura 1970).
METHODS
We simulated populations of recombinant inbred advanced intercross autosomes generated under a variety of breeding designs. Additional variables were the number of generations of intercrossing, which ranged from 2 (for RILs derived from an F2 population) to 20 (for RIAILs derived from an F20 population), and the population size (N), which ranged from 8 to 512 by doublings. The final number of RIAILs derived from an intercross of size N is N/2, as each mating pair in the final generation of the intercross yields a single RIAIL. Motivated by an interest in Caenorhabditis elegans, we considered an androdioecious population with males and self-fertile hermaphrodites. Hermaphrodites behave solely as outcrossing females during the intercross phase of our simulations, but self during the inbreeding phase. The model is directly applicable to any system with both outcrossing and selfing. Chromosomes were also modeled to resemble those of C. elegans, with a single obligate crossover event at each meiosis, yielding one breakpoint or none in each gametic chromosome. This meiotic mechanism corresponds to 50-cM chromosomes with total interference. Each chromosome was tracked as a string of 10,000 markers, all differing between the parental lines. To generate F2 individuals, we simulated meiosis in F1 individuals heterozygous for the 10,000 markers and drew two gametes randomly. We then considered eight breeding designs, illustrated in Figure 1, as well as a backcross population, in which each individual was represented by a chromosome drawn at random from a simulated F2 genome. We used the backcross rather than an F2 population as a baseline for our results because it has, like an inbred line population, only two genotypes per marker. Every cross design was simulated 1000 times to yield distributions of evaluation statistics.
Figure 1.—
Mating schemes. Each mating scheme is represented in the M-matrix format of Boucher and Nagylaki (1988) and as a three-generation pedigree. In the M matrix, each row represents a progeny of the parental generation represented by the columns. Entry mij is the number of gametes from individual j contributing to the zygote of individual i. Row totals are always 2. In the regular-mating schemes (left), the matrix is fixed from generation to generation, while in random schemes (right) it is a random realization each generation. Some schemes have zero variance in offspring number (equal contributions), so that column totals are also constrained to equal 2. In the pair mating schemes, each column must share all entries with another. In the pedigrees, hermaphrodites are circles, males are squares, and the lines depict parent–offspring relationships. For the random-mating schemes, the M matrix corresponds to the relationships depicted in the first two generations of the pedigree.
Breeding designs:
We confine our attention to breeding designs with discrete, nonoverlapping generations and constant population size. We simulated the following eight breeding designs.
RIL: Recombinant inbred lines by selfing. Each F2 individual capable of selfing (i.e., hermaphrodites, N/2 individuals) produced two gametes by independent meioses and these two chromosomes formed the genotype of an F3 individual. We simulated 10 generations of selfing and considered chromosomes from the final generation. This inbreeding phase is shared by all the RIAIL breeding designs below.
CM–RIAIL: Circular mating. F2 males and hermaphrodites alternate around a circle, and each individual mates with each of its neighbors, according to Kimura and Crow's (1963) scheme. The F3 individuals assume their parents' place in the circle and mate with their neighbors, which are their half-siblings.
CPM–RIAIL: Circular pair mating. Individuals are paired and the pairs are arranged in a circle, according to Kimura and Crow's (1963) scheme. Each pair produces one male and one hermaphrodite, and the pairings in the next generation shift by one individual around the circle.
IA–RIAIL: Inbreeding avoidance. Wright's (1921) design for “maximum possible avoidance of consanguineous mating.” In a population of size 2m, with equal numbers of males and hermaphrodites, mates share no ancestors in the previous m − 1 generations.
RM–RIAIL: Random mating. F3 individuals were formed by randomly drawing independent gametes from the F2 population, one from a male and one from a hermaphrodite, and subsequent generations were formed similarly.
RMEC–RIAIL: Random mating with equal contributions of each parent to the next generation. That is, variance in offspring number is zero. For each generation, males were formed by drawing gametes sequentially from randomly ordered lists of males and hermaphrodites in the previous generation. The lists were then randomly reordered, and gametes to form hermaphrodites drawn in turn. Each parental individual thereby contributes gametes to a single male and a single hermaphrodite in the next generation.
RPM–RIAIL: Random pair mating. F2 males and hermaphrodites were randomly paired and F3 individuals drew gametes independently from a random parental pair. Mating pairs were chosen randomly in each generation. Pair mating is equivalent to a requirement for monogamy.
RPMEC–RIAIL: Random pair mating with equal contributions. F2 individuals were paired randomly. Each pair then generated gametes to form one male and one hermaphrodite for the F3 population.
Evaluation statistics:
Map expansion:
The accumulation of breakpoints during intercrossing or inbreeding results in an increase in the recombination fraction between markers and consequently an apparent expansion of the genetic map (Haldane and Waddington 1931; Darvasi and Soller 1995; Teuscher and Broman 2007). Teuscher et al. (2005) provided a simple formula for the expected map expansion in a RIAIL population in the infinite population, random-mating case. For lines derived by selfing for i generations, starting from an advanced intercross population after t generations of intercrossing, the expected genetic map expands by a factor of t/2 + (2i − 1)/2i, approaching t/2 + 1 with inbreeding to fixation. In finite populations, both allele-frequency drift and matings between relatives diminish the map expansion.
We compared the observed map expansion for each simulation to that expected in the infinite population, random-mating case. Our simulations feature a map length of 0.5 M and a final population size of N/2, so the expected number of breakpoints after a single meiosis, N/4 (0.5 M × N/2 chromosomes), provides a simple relation between the count of breakpoints and the map size. After t generations of intercrossing and 10 generations of selfing, the expected number of breakpoints in the ideal case is (N/4)(t/2 + [210 − 1]/210). We measured the observed number of chromosomal breakpoints present in the final population at the end of each simulation. Breakpoints were recognized as switches in the parental origin of markers in sequence along each chromosome. The ratio of observed-to-expected number of breakpoints is our statistic for the approach of each simulation to the ideal map expansion.
Expected bin size:
Map expansion is a useful guide to the improved resolution achievable under different crossing designs. However, the cross design of a RIAIL population, unlike that of a BC, F2, or RIL population, partly uncouples mapping resolution from map expansion. Because each recombination breakpoint arising during the intercross phase of RIAIL construction can be inherited by multiple descendant lines, replicated breakpoints can increase the map expansion without improving mapping resolution. The limiting resolution is determined by the spacing of independent breakpoints, which we can assess from the distribution of bin sizes (Vision et al. 2000). A bin is an interval within which there are no recombination breakpoints in the sampled population and whose ends are defined by the presence of a breakpoint in any individual in the sample or by the end of the chromosome. A bin is thus the smallest interval to which a Mendelian trait could be mapped in the population on which the bins are defined. Following Vision et al. (2000), we focus on the expectation of the size of a QTL-containing bin. This expected bin size incorporates aspects of both the mean and the variance of bin size. On a chromosome of length L with n bins with lengths li, a random marker (or QTL) falls in bin i with probability li/L. The expectation for bin size is the sum over the n bins of the product of the probability that a marker falls within the bin (li/L) and the bin length, li. The expected bin size is thus the sum of the squares of the bin lengths (SSBL, Vision et al. 2000) divided by the chromosome length L, 1/L Σli2, with the summation over the n bins. This expected bin size is larger than the average bin size because a randomly chosen marker is more likely to fall into a larger bin; this phenomenon is known as length-biased sampling or the waiting-time paradox. In fact, standard results from renewal theory show that the expected QTL-containing bin size can be approximated by M + V/M, where M is the average bin size and V is the variance of bin size, and the approximation is increasingly accurate for a larger number n of bins (Cooper et al. 1998).
We measured the bin lengths for each simulated population by first identifying each pair of markers between which a chromosome in the population exhibits a breakpoint and then counting the markers between pairs of breakpoints or between breakpoints and chromosome ends. The number of bins and their sizes are constrained by the number of markers tracked in the simulations (recall that the 10,000 markers are spaced uniformly every 0.005 cM). We then converted the expected bin lengths from marker units into centimorgans using the physical–genetic distance ratio of 200 markers/cM. We also found the largest bin for each population of simulated chromosomes. This statistic is highly correlated with the expected bin size (supplemental Table 1).
Allele-frequency drift:
The power to detect a QTL is strongly influenced by the allele frequencies at the QTL, and genetic drift during intercrossing permits the alleles to depart from the expected 0.5 frequency. For each simulated population, we found the minor allele frequency of a single arbitrary marker and calculated its absolute departure from 0.5. We also calculated the allele frequency at each marker along the chromosome and found the marker exhibiting the most extreme departure from 0.5. We used the expected single-locus departure and expected extreme departure from 0.5 as summary statistics to assess the influence of cross design on drift.
RESULTS
Map expansion:
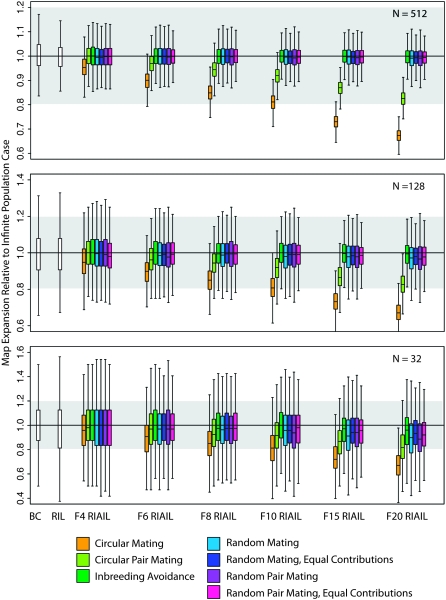
At large population sizes, with ≥256 individuals, random-mating designs and inbreeding avoidance all achieve close approximation to the infinite-population case, averaging >98% of the ideal map expansion even with 20 generations of intercrossing (Figure 2, supplemental Table 1), with small variance. The circular mating schemes exhibit much less map expansion, just 67% in the case of circular mating for 20 generations and 83% for circular pair mating. The loss of map expansion in the circular designs is nearly independent of population size but highly sensitive to the number of generations of intercrossing.
Figure 2.—
The realized map expansion, relative to the infinite population expectation. Given a map size for the BC population, the expected map expansion factor is 2 for RILs, and ∼t/2 + 1 for Ft RIAILs. Although population size has an obvious influence on how well a cross approximates the infinite population case and on the variance among realizations, the loss of map expansion in the circular mating designs is the dominant pattern. The scale of the y-axis varies among the panels due to the higher variances at smaller population sizes. The shading indicates the range of outcomes within 20% of the expected expansion. The box plots indicate medians and interquartile ranges, with the whiskers encompassing all points within 1.5 times the interquartile range. Outliers are not plotted.
At modest population sizes, inbreeding avoidance exhibits slightly greater map expansion than the other designs, and IA, RMEC, and RPMEC exhibit slightly lower variance in map expansion than the random-mating (RM and RPM) designs. These effects are negligible, particularly given the large variances in map expansion for each design at small population sizes. For N ≥ 64, all but the circular designs achieve roughly the expected level of map expansion.
Expected bin size:
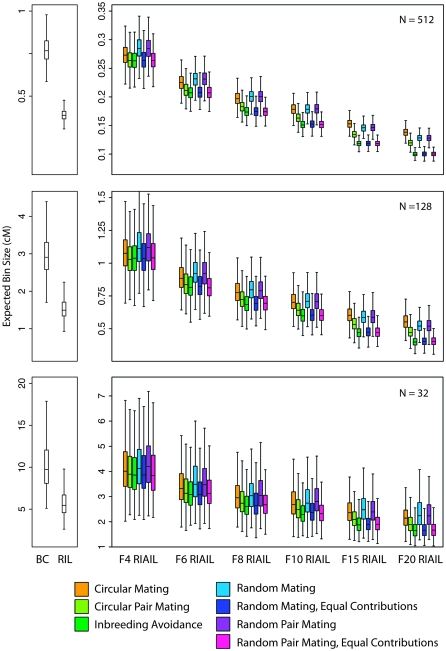
Inbreeding avoidance and random mating with equal contributions, with or without monogamy, are indistinguishable from one another and are superior to the other designs at reducing expected bin size (Figure 3, supplemental Table 1). At large population sizes, circular pair mating is next best, although significantly worse, and random mating is the worst design for <10 generations of intercrossing. After 10 generations, circular mating is even worse than random mating. In the largest population that we considered, with 512 individuals, 15 generations of intercrossing with circular mating yields the same expected bin size (0.153 cM) as just 10 generations of intercrossing with RPMEC, RMEC, and IA designs. At smaller population sizes, random mating is uniformly the worst design for reducing expected bin size, and at very low population sizes (<32), random-mating designs actually lose mapping resolution with additional generations of intercrossing because unique breakpoints are lost as a single recombinant chromosome drifts to fixation.
Figure 3.—
Expected bin size in centimorgans. Inbreeding avoidance and random-mating schemes with equal contributions are superior (produce the smallest bins) to the other designs. The scale of the y-axis varies among the panels. The box plots indicate medians and interquartile ranges, with the whiskers encompassing all points within 1.5 times the interquartile range. Outliers are not plotted.
Allele-frequency drift:
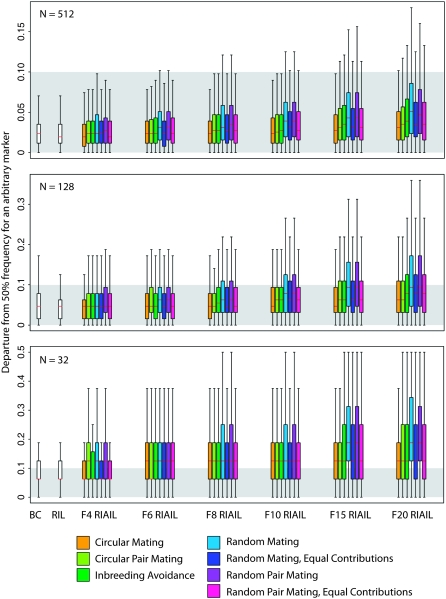
Naturally, population size has a dominant effect on genetic drift, as illustrated by the expected departure from allele-frequency equity in the BC or RIL populations, in which a single generation of segregation is its only cause (Figure 4, supplemental Table 1). In this case, the expected departure is 0.185 for N = 8, but only 0.025 for N = 512 (i.e., the expected minor allele frequency at a QTL is 0.315 in the former case and 0.475 in the latter). The BC and RIL expected departures place a lower bound on the possible allele-frequency departure in a population of recombinant inbred advanced intercross lines.
Figure 4.—
Allele-frequency drift, as measured by the departure from 50% frequency of an arbitrary marker. The influence of population size swamps the effects of breeding design. The scale of the y-axis varies among the panels. The shading indicates the range of outcomes with a <10 percentage point departure from allele-frequency balance. The box plots indicate medians and interquartile ranges, with the whiskers encompassing all points within 1.5 times the interquartile range. Outliers are not plotted. The blockiness of the plots is due to the discrete nature of the possible allele frequencies, particularly at low population sizes.
Within each population size, the two random-mating designs with variance in offspring number are significantly worse than other designs, as expected; eliminating variance in family size doubles the effective population size with respect to genetic drift (Crow and Kimura 1970). Also in keeping with expectation, circular mating is better than the others at preventing drift. However, the differences among the designs are modest, particularly at larger population sizes. In a population of 512, the expected departure is 0.036 after 20 generations of CM intercrossing and 10 of selfing vs. 0.043 in the same cross with RMEC intercrossing and 0.058 for RM. In each case, these departures are acceptably close to the baseline 0.025. Only when the population drops to 128 does any design yield an expected departure of 0.1, and then only for RM and RPM and only in the case of ≥15 generations of intercrossing. For smaller populations, although CM is substantially better than other designs, it is still inadequate for preventing significant drift. In a population of 64, the BC baseline in our simulations has an expected departure of 0.072. After 10 generations of intercrossing, CM holds the departure down to 0.088 vs. 0.096 for RPMEC and 0.127 for RPM.
The dominant influence of population size is also seen in the extremes of the allele-frequency departures. We found the point on each chromosome with the most extreme allele frequency in each simulation. This point is the locus at which QTL detection power will be most compromised by genetic drift. In populations of 512, with ≤10 generations of intercrossing, the expected extreme departure for all designs with equal parental contributions is <0.1 (supplemental Table 1). That is, on average, no marker will have a minor allele frequency <0.4. For smaller populations, extreme allele frequencies like these are the norm; for N = 256, the expected extreme departure exceeds 0.1 for every design with intercrossing past F4; in such a population, the baseline expected extreme departure, in a BC population, is already 0.074. Circular mating retains its advantages in the context of extreme departures, but again they are small; for a 10-generation intercross in a population of 64, the expected extreme departure is 0.218 for CM, 0.250 for RPMEC, 0.254 for IA, and 0.295 for RPM.
DISCUSSION
The three measures of RIAIL quality—map expansion, bin size reduction, and drift minimization—reflect different aspects of the utility of a mapping population. Map expansion is important for separating closely linked QTL, bin size reduction is critical for localizing QTL, and drift minimization is necessary to preserve detection power. The crossing designs vary in their effects on each of these qualities, but some designs are clearly worse and others better across the spectrum. Most importantly, our study suggests that one of the simplest and most practical designs—random pair mating with equal contributions of each parent to the next generation—is an effective way to generate RIAILs for high-resolution mapping.
The simulation results make clear that a clever cross design is no substitute for a large population. In any population large enough to be useful for mapping (intercross N ≥ 128, yielding ≥64 RIAILs), the effects of genetic drift are modest for all designs with equal parental contributions. Although circular designs are slightly better than the others at reducing drift, the differences are negligible and the magnitude of drift not a serious impediment to mapping. In a panel of 64 RIAILs, for example, the typical QTL will be present at an allelic ratio of 28:36 in F20 CM–RIAILs and 27:37 in F20 RPMEC–RIAILs. The importance of drift diminishes to irrelevance in larger intercross populations.
Differences among designs are more substantial for map expansion and expected bin size. Circular designs are dramatically worse than others at map expansion, and they join random-mating designs with variance in offspring number in their inadequacy in reducing bin size. The best designs are the inbreeding avoidance scheme and the random-mating designs with equal contributions. Surprisingly, these designs are indistinguishable in their efficacy for reducing bin size and expanding the genetic map. Although random-mating designs include some matings among close relatives, they also include matings among very distantly related individuals. Inbreeding avoidance, on the other hand, while avoiding matings among close relatives, has a lower limit on the level of relatedness among mates, determined by population size. Apparently, inbreeding avoidance excludes matings among very close relatives at the cost of excluding matings among very distant relatives.
Monogamy is a practical necessity for performing crosses in many species, and although multiple mates per individual may seem intuitively to provide more opportunities for effective recombination, monogamy incurs no cost in RIAIL construction for any of the measures considered.
Although most analytical and simulation studies have considered designs that we find undesirable, particularly random mating (Darvasi and Soller 1995; Teuscher et al. 2005) or circular mating (Valdar et al. 2006), few experimentalists have employed these approaches (e.g., Ebert et al. 1993; Yu et al. 2006). Instead, the most common experimental design for AILs and RIAILs is an intuitively appealing blend of random mating with equal contributions and inbreeding avoidance (Liu et al. 1996; Lee et al. 2002; Peirce et al. 2004). However, many articles provide ambiguous accounts of the variance in offspring number. Our results suggest that, given equal parental contributions, special effort to avoid matings between relatives are neither necessary nor harmful.
We have considered only a few of the possible designs for RIAIL construction. Peirce et al. (2004) proposed a scheme for constructing RIAILs one strain at a time, a method that removes the possibility that breakpoints will be inherited by multiple strains. The design completely eliminates shared ancestry among mates, so that each inbred strain derived from an Ft intercross would require a separate initial population of 2t−1. The approach requires a radically larger number of individuals than the approach of building RIAILs from a population, but the crosses can be done sequentially rather than simultaneously, eliminating the constraints imposed by labor and space costs. Given the close approximation of large population RIAILs to the infinite-population case, the slight benefits of the one-at-a-time scheme in terms of eliminating breakpoints shared by descent is unlikely to justify the exceptional outlay of resources required for each strain. For example, construction of 256 F10 population-derived RIAILs requires 10 rounds of mating, each entailing 256 crosses. The equivalent number of F10 one-at-a-time RIAILs would require 256 rounds of mating entailing 256 crosses each, plus 256 rounds of mating entailing 128 crosses each, and so forth. The ultimate difference is between 2560 crosses for population-derived RIAILs and 130,836 crosses for the one-at-a-time RIAILs.
An alternative approach is marker-assisted selection, which can be used to apply balancing selection at every marker in the genome (Wang and Hill 2000). For a finite number of strains, this is even better than RIAIL construction in a intercross population of infinite size because heterozygosity in the final, finite RIAIL panel can exceed the binomial sampling expectation. Of course, marker-assisted selection is currently labor- and cost-intensive because it requires genotyping at each generation. The added expense may be justified in the case of long-lived or commercial species or species in which selection is likely to drive strong departures from allele-frequency balance during intercrossing. An economical alternative to marker-assisted selection is selective phenotyping, in which a larger-than-necessary mapping population is culled according to genotype to maximize the mapping potential of a given number of individuals (Vision et al. 2000; Jin et al. 2004; Jannink 2005; Xu et al. 2005). In this case, only a single generation of genotyping is required.
Two concerns for any experimental RIAIL population are mutation and selection, forces neglected in our simulations. Although all cross designs that employ many generations of breeding, including RILs, provide opportunity for selection to alter allele frequencies and for spontaneous mutations to arise, RIAILs are particularly at risk. In recombinant inbred lines, any new mutation is confined to a single line and at worst inflates the nonadditive phenotypic variance. Because a mutation can be inherited by multiple lines in an RIAIL population, it can be actively misleading for efforts to map segregating variants present in the parental strains. Each additional generation of intercrossing also permits the population to respond to selection, with the potential to exacerbate allele-frequency skews due to segregation distortion and unintentional directional selection.
Breeding designs for RIAILs have different consequences for mutation and selection. Equal contribution designs conform to the middle-class neighborhood model for mutation accumulation (Shabalina et al. 1997), in which the absence of selection among families permits mutations that would otherwise be deleterious to behave as though neutral. As a result, selection on standing variation is minimized (only genotypes causing sterility or lethality are eliminated), but the potential for spontaneous mutations to spread is increased. Experimental results on the impact of mutation accumulation in middle-class neighborhood populations are equivocal but suggest that the effects are modest (Shabalina et al. 1997; Keightley et al. 1998; Fernandez and Caballero 2001; Reed and Bryant 2001; Rodriguez-Ramilo et al. 2006). Designs with variance in family size avoid mutation accumulation at the expense of exposure to selection-driven allele-frequency skew. Because allele-frequency skews are extremely common even in F2 populations (segregation distortion), the loss of mapping power due to selection is likely to be a more serious concern for RIAIL populations than mutation accumulation, and consequently the best equal contribution designs (IA, RMEC, and RPMEC) remain preferable to the alternatives.
Our results suggest that the most effective designs for RIAIL construction are inbreeding avoidance and random mating with equal contributions of each parent to the next generation. These results are encouraging, as random pair mating with equal contributions is likely to be the most practical and convenient design for most organisms.
Acknowledgments
We thank Daniel Promislow for drawing our attention to relevant literature. M.V.R. is supported by a Jane Coffin Childs Fellowship and L.K. by the National Institutes of Health (grants R37 MH059520 and R01 HG004321) and a James S. McDonnell Foundation Centennial Fellowship.
References
- Bailey, D. W., 1971. Recombinant-inbred strains: an aid to finding identity, linkage, and function of histocompatibility and other genes. Transplantation 11 325–327. [DOI] [PubMed] [Google Scholar]
- Boucher, W., and C. W. Cotterman, 1990. On the classification of regular systems of inbreeding. J. Math. Biol. 28 293–305. [DOI] [PubMed] [Google Scholar]
- Boucher, W., and T. Nagylaki, 1988. Regular systems of inbreeding. J. Math. Biol. 26 121–142. [DOI] [PubMed] [Google Scholar]
- Cooper, R. B., S.-C. Niu and M. M. Srinivasan, 1998. Some reflections on the renewal-theory paradox in queueing theory. J. Appl. Math. Stochastic Anal. 11 355–368. [Google Scholar]
- Crow, J. F., and M. Kimura, 1970. An Introduction to Population Genetics Theory. Harper & Row, New York.
- Darvasi, A., and M. Soller, 1995. Advanced intercross lines, an experimental population for fine genetic mapping. Genetics 141 1199–1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebert, R. H., II, V. A. Cherkasova, R. A. Dennis, J. H. Wu, S. Ruggles et al., 1993. Longevity-determining genes in Caenorhabditis elegans: chromosomal mapping of multiple noninteractive loci. Genetics 135 1003–1010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez, J., and A. Caballero, 2001. Accumulation of deleterious mutations and equalization of parental contributions in the conservation of genetic resources. Heredity 86 480–488. [DOI] [PubMed] [Google Scholar]
- Haldane, J. B. S., and C. H. Waddington, 1931. Inbreeding and linkage. Genetics 16 357–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jannink, J.-L., 2005. Selective phenotyping to accurately map quantitative trait loci. Crop Sci. 45 901–908. [Google Scholar]
- Jin, C., H. Lan, A. D. Attie, G. A. Churchill, D. Bulutuglo et al., 2004. Selective phenotyping for increased efficiency in genetic mapping studies. Genetics 168 2285–2293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley, P. D., A. Caballero and A. Garcia-Dorado, 1998. Population genetics: surviving under mutation pressure. Curr. Biol. 8 R235–R237. [DOI] [PubMed] [Google Scholar]
- Kimura, M., and J. F. Crow, 1963. On the maximum avoidance of inbreeding. Genet. Res. 4 399–415. [Google Scholar]
- Lee, M., N. Sharopova, W. D. Beavis, D. Grant, M. Katt et al., 2002. Expanding the genetic map of maize with the intermated B73 × Mo17 (IBM) population. Plant Mol. Biol. 48 453–461. [DOI] [PubMed] [Google Scholar]
- Liu, S. C., S. P. Kowalski, T. H. Lan, K. A. Feldmann and A. H. Paterson, 1996. Genome-wide high-resolution mapping by recurrent intermating using Arabidopsis thaliana as a model. Genetics 142 247–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirce, J. L., L. Lu, J. Gu, L. M. Silver and R. W. Williams, 2004. A new set of BXD recombinant inbred lines from advanced intercross populations in mice. BMC Genet. 5 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed, D. H., and E. H. Bryant, 2001. Relative effects of mutation accumulation versus inbreeding depression on fitness in experimental populations of the housefly. Zoo Biol. 20 145–156. [Google Scholar]
- Robertson, A., 1964. The effect of non-random mating within inbred lines on the rate of inbreeding. Genet. Res. 5 164–167. [Google Scholar]
- Rodriguez-Ramilo, S. T., P. Moran and A. Caballero, 2006. Relaxation of selection with equalization of parental contributions in conservation programs: an experimental test with Drosophila melanogaster. Genetics 172 1043–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shabalina, S. A., L. Yampolsky and A. S. Kondrashov, 1997. Rapid decline of fitness in panmictic populations of Drosophila melanogaster maintained under relaxed natural selection. Proc. Natl. Acad. Sci. USA 94 13034–13039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharopova, N., M. D. McMullen, L. Schultz, S. Schroeder, H. Sanchez-Villeda et al., 2002. Development and mapping of SSR markers for maize. Plant Mol. Biol. 48 463–481. [DOI] [PubMed] [Google Scholar]
- Soller, M., and J. Beckman, 1990. Marker-based mapping of quantitative trait loci using replicated progenies. Theor. Appl. Genet. 80 205–208. [DOI] [PubMed] [Google Scholar]
- Teuscher, F., and K. W. Broman, 2007. Haplotype probabilities for multiple-strain recombinant inbred lines. Genetics 175 1267–1274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teuscher, F., V. Guiard, P. E. Rudolph and G. A. Brockmann, 2005. The map expansion obtained with recombinant inbred strains and intermated recombinant inbred populations for finite generation designs. Genetics 170 875–879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdar, W., J. Flint and R. Mott, 2006. Simulating the collaborative cross: power of quantitative trait loci detection and mapping resolution in large sets of recombinant inbred strains of mice. Genetics 172 1783–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vision, T. J., D. G. Brown, D. B. Shmoys, R. T. Durrett and S. D. Tanksley, 2000. Selective mapping: a strategy for optimizing the construction of high-density linkage maps. Genetics 155 407–420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, J., and W. G. Hill, 2000. Marker-assisted selection to increase effective population size by reducing Mendelian segregation variance. Genetics 154 475–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, S., 1921. Systems of mating. II. The effects of inbreeding on the genetic composition of a population. Genetics 6 124–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, Z., F. Zou and T. J. Vision, 2005. Improving quantitative trait loci mapping resolution in experimental crosses by the use of genotypically selected samples. Genetics 170 401–408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu, X., K. Bauer, P. Wernhoff, D. Koczan, S. Moller et al., 2006. Fine mapping of collagen-induced arthritis quantitative trait loci in an advanced intercross line. J. Immunol. 177 7042–7049. [DOI] [PubMed] [Google Scholar]
- Zou, F., J. A. Gelfond, D. C. Airey, L. Lu, K. F. Manly et al., 2005. Quantitative trait locus analysis using recombinant inbred intercrosses: theoretical and empirical considerations. Genetics 170 1299–1311. [DOI] [PMC free article] [PubMed] [Google Scholar]