When Parameters in Dynamic Models Become Phenotypes: A Case Study on Flesh Pigmentation in the Chinook Salmon (Oncorhynchus tshawytscha)

Abstract

The Pacific chinook salmon occurs as both white- and red-fleshed populations, with the flesh color type (red or white) seemingly under strong genetic influence. Previously published data on crosses between red- and white-fleshed individuals cannot be reconciled with a simple Mendelian two-locus, two-allele model, pointing to either a more complex inheritance pattern or the existence of gene interactions. Here we show that a standard single-locus, three-allele model can fully explain these data. Moreover, by implementing the single-locus model at the parameter level of a previously developed mathematical model describing carotenoid dynamics in salmon, we show that variation at a single gene involved in the muscle uptake of carotenoids is able to explain the available data. This illustrates how such a combined approach can generate biological understanding that would not be possible in a classical population genetic explanatory structure. An additional asset of this approach is that by allowing parameters to become phenotypes obeying a given genetic model, biological interpretations of mechanisms involved at a resolution level far beyond what is built into the original dynamic model are made possible. These insights can in turn be exploited in experimental studies as well as in construction of more detailed models.

A comprehensive understanding of how genetic variation causes phenotypic variation of a complex trait is a long-term disciplinary goal of genetics. It is hard to see how we are to fulfill this goal unless we succeed in making mathematical conceptualizations demonstrating how genetic variation becomes manifested in phenotypic variation at various systemic levels up to the whole-organism level. Compared to the broader class of mathematical models describing how complex biological phenotypes arise from the interactions of lower level systemic entities, these models can be distinguished by having an articulated relationship to the individual's genotype. They seek to account for the effects of genetic variation through a description of the proximal processes linking the two domains in terms of regulatory principles and mechanisms such that phenotypic values are emergent properties of lower-level processes. We call these types of models causally cohesive genotype phenotype (cGP) models. As the adjective “cohesive” means “causing to cohere” (Merriam-Webster 2008), we think the cGP concept quite appropriately describes models that at some given level of resolution have the quality of causing components involved in a genotype–phenotype relation to cohere in a logically consistent and ordered way. In short, cGP models stick genotypes and phenotypes causally together. This is in contrast to standard population genetic models where phenotypic values are assigned directly to genotypes without involving any intermediate processes. During the past decade a number of groups (Omholt et al. 2000; Peccoud et al. 2004; Welch et al. 2005) have pointed to the importance of integrating quantitative genetics with systems theory. The importance of such a combined theory for practical breeding and QTL mapping in the future is underlined by three recent articles on plants (Yin et al. 2004 ; Hammer et al. 2006; Genard et al. 2007), where QTL information is linked to dynamic models making this a powerful way to study gene–environment interactions and narrow the genotype–phenotype gap.

Building upon a previously developed dynamic ordinary differential equations (ODE) model of carotenoid metabolism capable of predicting muscle pigment levels in salmonids (Rajasingh et al. 2006), in this article we develop a cGP model to account for >20-year-old genetic data on the Pacific chinook salmon (Oncorhynchus tshawytscha), which still lack a consistent explanatory genetic model. Certain subpopulations of chinook exhibit no or very little flesh pigmentation and are known as white-fleshed chinook, in contrast to the more abundant red-fleshed variety (Milne 1964). The color dichotomy is highly heritable (Withler 1986). Withler (1986) reported the outcome of a crossing study between red- and white-fleshed chinook from the Quesnel River in British Columbia. A genetic model that invoked two genetic loci, each with two alleles, was proposed to explain the inheritance of flesh color in the 16 seapen-reared families. The anomalous red:white ratios among the progeny of one red male parent could not be accounted for by the model. Assuming that the actual discrepancy is real, we sought to explain the observed inheritance patterns within a cGP model framework. The cGP framework combines genetics with a mathematical conceptualization of what we currently know about carotenoid metabolism in vertebrates in terms of carotenoid uptake, transport, and delivery and its close association with lipid metabolism.

During maturation the eggs and skin of the white-fleshed chinook variety do contain pigments, though in smaller amounts than in the mature red-fleshed one (Hard et al. 1989; Ando et al. 1992). Due to a negative nutrient and energy budget during sexual maturation, partly caused by reduced or ceased feeding, salmon species like several other fish species seem particularly prone to heavily exploit white muscle tissue to support development of gonads, eggs, and for the formation of secondary sexual characteristics (Mommsen 1998, 2004). The reduced coloration of eggs in the white-fleshed chinook may thus be explained by lack of release of carotenoids into the blood stream during the targeted muscle degradation. The flesh does also contain low levels of pigmentation in a large proportion of cases (Ando et al. 1992). This suggests that the “white” subpopulations metabolize and utilize carotenoids much the same way as the “red” ones, but that the ability to accumulate carotenoids in muscle is substantially reduced. This is in accordance with the fact that a sensitivity analysis of the model published by Rajasingh et al. (2006) identified the muscle membrane uptake processes as a potent site for genetic variation.

Guided by the above considerations we set out to identify a minimalistic classical genetic model in terms of the number of loci and alleles that could explain the results obtained by Withler (1986) and that in addition could be reconciled with the dynamic model reflecting our current understanding of carotenoid metabolism in pigmented salmonids.

MATERIALS AND METHODS

Simulated populations:

Simulated red- and white-fleshed chinook populations were generated by means of a previously developed framework for combining genotype–phenotype representations with genetic maps (Hayes et al. 2006; Gjuvsland et al. 2007). Genetic maps describe the structure of the genome for each individual in the populations, in terms of the number of chromosomes, the number and position of genes/markers on these chromosomes, and the probability of recombination between adjacent genes/markers during meiosis. Using such a framework a population of 100 individuals containing two chromosomes of 3 cM each was simulated. One gene was placed on each chromosome and for each individual the genotype at a given locus was determined by sampling alleles at equal probability (one-half for the biallelic cases, one-third for the triallelic). To transform the genetic variation in the members of these populations to quantitative phenotypes (i.e., muscle pigment concentrations), either one or both of the two genes on the two different chromosomes were assumed to be genes underlying the trait (see below for the two different models used for generating genotypic values). The phenotypes were then obtained as the sum of the genotypic and environmental values.

On the basis of the phenotypic values, the population was separated into red- and white-fleshed fish, with white individuals being classified as having a muscle carotenoid concentration <1 mg/kg. Two pairs were randomly picked from each group, a red male and female and a white male and female. They were then used to obtain four full-sib families of 100 individuals each by performing the following crosses (female × male): red × red (R × R), red × white (R × W), white × red (W × R), and white × white (W × W). Phenotypes were generated for offspring in each cross. This set of four crosses was repeated 1000 times by picking different parental pairs from the original population.

Population genetic GP model:

The genotypic values were generated by randomly sampling from gamma distribution (shape k = 2, scale σ = 0.5) values which lay within the range of chinook carotenoid content values observed by Withler (1986). To this was added the environmental deviation, obtained by sampling from a normal distribution N ∼ (0, σ), with the standard deviation σ being chosen so as to get a broad-sense heritability (H²) value of ∼0.8. This value was the mean of the sire and dam component binomial heritability estimates (Withler 1986).

Dynamic cGP model:

The genetic framework was subsequently linked with the previously mentioned dynamic ODE model (Rajasingh et al. 2006) simulating the carotenoid uptake and deposition in salmonids. The muscle carotenoid levels obtained by running the model were taken as the genotypic values. The carotenoid uptake into the muscle from the blood is a saturable process, represented in the model by an uptake rate and a sigmoid function. The threshold of saturation θ_ma and the relative uptake rate R_ma were assigned as heritable parameter values to a single gene. For each allele segregating at that particular gene, values for the heritable parameters were sampled from a uniform distribution ranging between 3 and 10% of the values used in Rajasingh et al. (2006) for R_ma and θ_ma. Such a range was chosen to obtain muscle carotenoid levels resembling the observations of Withler (1986) in chinook. For a two-locus situation, the second gene was used to represent the locus controlling the carotenoid uptake into the blood from the intestine and the bioavailable fraction r_c was set as the heritable parameter for it. Given the lack of data on the weight range of the experimental population, the weight of simulated individuals was kept constant over the population. An environmental effect was added to the genetic effect in a similar manner as for the population genetic model.

Pattern search:

The phenotypic patterns of the simulated crosses among the 1000 sets that gave red–white offspring ratios similar to the experimental crosses of Withler (1986) were examined for each genetic model. A chi-square goodness-of-fit test at the 0.05 significance level was performed between the red–white offspring ratios obtained by Withler and those of the best-fitting crosses that were simulated for each type of genetic model.

The simulations and analysis were performed using MATLAB.

RESULTS

Population genetic modeling:

To shorten the search for the interaction pattern responsible for the required offspring ratios, the genetic framework was first simulated with random phenotype values without making use of the dynamic model, i.e., a standard population genetic approach. A population of red- and white-fleshed individuals was generated and crosses between pairs of red- and white-fleshed males and females in accordance with the design of the red- and white-fleshed chinook experiment were performed (Withler 1986).

We first tested the genetic model suggested by Withler (1986), i.e., two alleles segregating at each of the two loci where the red-determining allele was dominant, which was the simplest Mendelian model consistent with most of the observed offspring ratios in the experimental setup. As had been noted by Withler (1986), the crosses obtained in these simulations were not able to produce the aberrant white-offspring frequencies for red male fathers (data not shown). The population genetic model was then modified to allow the segregation of three alleles at each of the two loci and new populations were simulated. The offspring in these sets of crosses also failed to display excessive white-fleshed offspring ratios, although there was greater variance in the red–white ratios as can be expected with increased allele number (data not shown).

Tetrasomic inheritance (Wright et al. 1983; Allendorf and Thorgaard 1984) was introduced in the male fish for the two- and three-allele setup and populations generated. Pseudolinkage of homeologous chromosomes was implemented in male fish according to the secondary tetrasomic model of inheritance (Wright et al. 1983; Allendorf and Danzmann 1997). Here homologous chromosomes pair and recombine first at regions close to the centromere followed by homeologous pairing and recombination at the distal end of the chromosome, which is where tetrasomy is found to occur (Wright et al. 1983; Gharbi et al. 2006). Preferential pairing between the homeologous chromosomes depending upon degree of similarity (such as whether the homeologs were derived from the same population or not) would give rise to males with different frequency of tetrasomic segregation (Allendorf and Danzmann 1997). This also did not produce the observed abnormal offspring ratios.

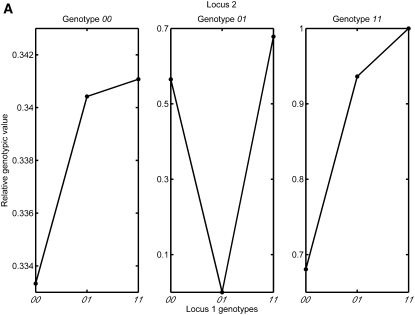
We then introduced intralocus overdominance at the two loci without tetrasomic inheritance. The crosses produced showed no irregular offspring ratios for red fathers although red- and white-fleshed offspring ratios change with different d values as can be expected (data not shown). However, crosses with phenotypic patterns producing the desired offspring ratios emerged when we introduced a dominance-by-dominance type of interaction between the two loci (Figure 1A). Thus a two-locus model involving epistasis is capable of explaining Withler's chinook experiment, as was alluded to by Withler herself (Withler 1986).

Figure 1.—

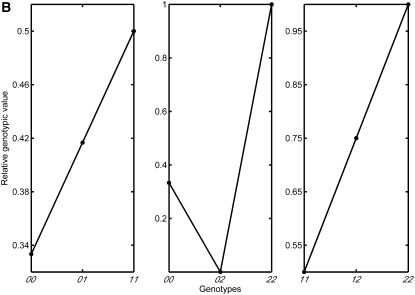
The relative genotypic values for the two-locus and single-locus genetic models. (A) Two-locus, two-allele model. The relative genotypic value (phenotypic value minus the environmental effect) is plotted against the three possible genotypes at locus 1, with respect to different genotypes at locus 2. The two loci exhibit a dominance-by-dominance type of epistasis, as can be seen from the low genotypic value of the double heterozygote. (B) Single-locus, three-allele model. The genotypic value is plotted against the genotypes for all three possible combinations of allele pairs (01, 02, and 12) at the single locus. Underdominance is introduced for the allele pair 02.

Applying Occam's razor, we asked whether the experimental data could be reconciled with a single-locus model with three alleles possessing an overdominance relationship of some sort between the alleles. It turned out that a single-locus, three-allele model in which one of the allele pairs exhibited overdominance was capable of accounting for the data (Figure 1B). As there is of course no way to decide with the current data whether a single-locus, a two-locus or some other genetic model is the correct one, we decided to go further with the single-locus one for reasons of simplicity and see how far this could bring us.

cGP modeling:

Considering that muscle membrane uptake is a likely site of genetic variation we linked the three-allele single-locus genetic model with the muscle uptake parameters of the dynamic carotenoid model. These parameters are the maximal uptake rate of carotenoids over the muscle membrane and the threshold parameter defining at which concentration level of carotenoids in the blood the uptake rate is 50% of the maximal rate (see Rajasingh et al. 2006 for further details). Apart from the muscle uptake parameters no other parameter values from the original model were modified. The simulation of the experimental design was performed the same way as for the population genetic model (see above) and red- and white-fleshed populations were generated.

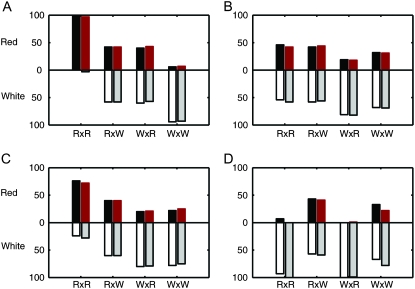
The phenotypic patterns produced by the offspring of the four crosses for the different sets were examined as in previous cases. Certain sets of crosses were seen to have offspring ratios identical to those of all the four experimental crosses, including the abnormal W × R cross. A goodness-of-fit test at the 0.05 significance level was performed between offspring ratios of the experimental crosses and those of the simulated crosses that seemed to give a good fit visually. Four crosses having red–white offspring ratios that gave the smallest chi-square values were chosen (Figure 2). Differences between simulated and experimental offspring ratios for sets A, B, and C were statistically insignificant at the 0.05 significance level. Given the low number of red offspring in the R × R and W × R crosses for set D, the differences were statistically significant here. However, as the chi-square goodness-of-fit test is unsuitable for small frequency values (Snedecor and Cochran 1989) and as the visual fit was good, the simulated cross was accepted.

Figure 2.—

Experimental (first bar) and simulated (second bar) crosses between red- and white-fleshed chinook salmon. The progeny from four sets of crosses between red- and white-fleshed chinook salmon performed by Withler (1986) are shown together with similar simulated results (A–D). The number of offspring in each experimental data set was rescaled to percentages. The four simulated results were chosen from crosses generated by a single-locus, three-allele model that gave offspring ratios having a good fit to the experimental sets.

A cGP model based on the two-locus population genetic model with epistasis was also able to account for the data. One locus was then associated with the muscle uptake parameters and one locus was associated with a parameter describing the uptake rate of carotenoid from the intestine (see Rajasingh et al. 2006 for further details). The epistasis structure consisted of a negative interlocus dominance-by-dominance interaction, similar to the previously described population genetic model. As predicted, crosses having red–white offspring ratios similar to the experimental ratios were obtained in this case as well. The current model resolution did not allow for the introduction of a genetic model with two loci together influencing the muscle membrane uptake.

DISCUSSION

Assets of the cGP model approach:

In this specific case, three major aspects distinguish the cGP model approach from a pure population genetic model approach, which we think are valid in general.

First, even a simple dynamic model describing a complex trait may be instrumental for suggesting potent sites for genetic variation through a sensitivity analysis of the parameters in the model. The sensitivity analysis of the original model of the carotenoid system clearly identified the uptake rate over the muscle membrane as a process where genetic variation influencing this rate would cause substantial phenotypic variation in flesh pigment level (Rajasingh et al. 2006). In contrast, identifying possible sites of genetic variation would be beyond the capabilities of a standard population genetic model.

Second, a standard population genetic model is totally unconstrained in defining organismal-level phenotypic values for the various genotypes, while a cGP model in many cases will be considerably constrained. This is illustrated by the fact that the muscle membrane uptake appears to be a more probable site for the crucial chinook variation than the intestine or other processes belonging to basic carotenoid metabolism, as previously shown by sensitivity analysis of the dynamic model (see Introduction). By following this lead we were in principle forced to target the muscle uptake parameters as sites for genetic variation. If the dynamic model had not been sensitive to variation in these parameters we would not have been able to generate organismal-level phenotypes with empirically relevant pigment levels.

Third, a simple cGP model of a complex trait can have considerable explanatory power in terms of regulatory principles and mechanisms beyond the actual resolution level of the model. Implementation of a genetic model via the parameters of the dynamic model enables us to say something about underlying processes that are not part of the model and provides the ground for generation of specific hypotheses on mechanisms that can explain the genetic interactions. In our case, a single-locus model with overdominance as well as a two-locus model with epistasis attached to the muscle membrane uptake can explain the Withler (1986) data. In the first case we will be guided toward suggesting possible mechanisms by which a single receptor can display an overdominance structure (see below). In the other case we will be forced to make a more detailed dynamic representation of uptake of carotenoids over the muscle membrane and then show how epistasis can emerge in this more refined setting.

cGP models as a source for hypothesis generation:

To illustrate how one can use a cGP result as a basis for generating hypotheses about high-resolution mechanisms not built into the original model, we show in the following how one can make biological sense of the single-locus model results in terms of what we know about carotenoid metabolism. The close association between carotenoid and fatty acid transport in salmonids (Clevidence and Bieri 1993; Parker 1996; Aas et al. 2000) and the saturation effect seen in the muscle (March and Macmillan 1996) suggests that a modified fatty acid uptake system is responsible for the intake of carotenoids over the muscle membrane. The mutation causing the white chinook phenotype can then be structural in the sense that it negatively affects function of the uptake system or regulatory in the sense that it negatively affects the density of uptake sites, or it can influence both.

A negative overdominance phenomenon implies that the heterozygote performs less well than both homozygotes on one of the allele pairs. It also implies that an interaction of some sort is required to take place between the two gene products. It is premature to take these speculations further beyond noting how a cGP model may induce investigations involving experts on fatty acid uptake processes seeking to come up with possible mechanistic scenarios capable of accounting for the existence of overdominance phenomena.

Conclusion:

Even though it may turn out that the causative mutation(s) responsible for the chinook dichotomy is not associated with the muscle membrane uptake, the results still demonstrate that a significant increase in understanding of a genetic phenomenon associated with a complex trait may be obtained by integrating even a simple mathematical model of a biological system with a genetic framework. They also demonstrate how useful a cGP model approach is to guide the formulation of new hypotheses about biological mechanisms that can be tested experimentally. Needless to say, there are currently many complex traits where it may be quite challenging to formulate realistic explanatory models of even low resolution level. However, with the pace systems biology is developing we are quite confident that cGP models will relatively soon become an integral part of the geneticist's toolbox.