Abstract
Although protein evolution can be approximated as a “molecular evolutionary clock,” it is well known that sequence change departs from a clock-like Poisson expectation. Through studying the deviations from a molecular clock, insight can be gained into the forces shaping evolution at the level of proteins. Generally, substitution patterns that show greater variance than the Poisson expectation are said to be “overdispersed.” Overdispersion of sequence change may result from temporal variation in the rate at which amino acid substitutions occur on a phylogeny. By comparing the genomes of four species of yeast, five species of Drosophila, and five species of mammals, we show that the extent of overdispersion shows a strong negative correlation with the effective population size of these organisms. Yeast proteins show very little overdispersion, while mammalian proteins show substantial overdispersion. Additionally, X-linked genes, which have reduced effective population size, have gene products that show increased overdispersion in both Drosophila and mammals. Our research suggests that mutational robustness is more pervasive in organisms with large population sizes and that robustness acts to stabilize the molecular evolutionary clock of sequence change.
PROTEIN sequence divergence is often approximated as a “molecular evolutionary clock” (Zuckerkandl and Pauling 1965), where the accumulation of amino acid substitutions is proportional to the time separating the sequences. In the absence of temporal variation, the distribution of substitution counts across a protein's phylogeny is expected to follow a Poisson distribution, where both the mean and the variance of substitution counts are equal to the rate (intensity) parameter λ (Ohta and Kimura 1971). As the mean and variance of the Poisson distribution are both equal to λ, substitution counts should show a ratio of the variance to the mean, known as the index of dispersion [R(t)], of 1. However, temporal variation in the rate of substitution influences the statistical character of substitution counts occurring over time. If substitution rate varies over time, then substitution counts of evolving proteins are expected to be “overdispersed” with R(t) > 1 (Cutler 2000). It is now abundantly clear that the accumulation of amino acid sequence change in both mammals (Gillespie 1989; Smith and Eyre-Walker 2003) and Drosophila (Zeng et al. 1998; Kern et al. 2004; Bedford and Hartl 2008) is overdispersed. Additionally, the index of dispersion shows a linear correlation with the mean per-branch substitution count (M) in Drosophila, suggesting that substitution counts are better described by a negative binomial distribution rather than a Poisson distribution (Bedford and Hartl 2008). Such a negative binomial distribution is consistent with rate variation occurring over time across individual protein phylogenies.
Although, historically, the index of dispersion has been used as a test of the neutral theory (Ohta and Kimura 1971; Gillespie 1989), findings of R(t) > 1 do not necessarily imply evidence of selection. Simple models of adaptive evolution suggest that substitutions fixed through positive selection may themselves be Poisson distributed. Additionally, more complex models of neutral evolution incorporating epistasis suggest that purely neutral substitutions may show significant overdispersion. Thus, the index of dispersion represents a test of the extent of heterogeneity of sequence evolution rather than a test of the selective forces at work.
There have been multiple studies of the index of dispersion of sequence evolution using lattice protein simulations (Bastolla et al. 2000; Wilke 2004; Bloom et al. 2007a). Although lattice protein models are heavily abstracted from the real proteins they seek to emulate, they do incorporate some important details of protein evolution. For instance, such lattice models give rise to a many-to-one mapping of genotypes to phenotypes, in which multiple sequences result in the same structure. Results from such lattice protein simulations show that evolution under purifying selection for a specific protein structure results in overdispersion of the substitution process (Bastolla et al. 2000). Interestingly, these simulations also show that the effective population size at which lattice proteins evolve significantly affects the resulting indexes of dispersion. Populations of lattice proteins evolving under small population sizes show high levels of overdispersion, whereas those proteins evolving under large population sizes show low levels of overdispersion (Wilke 2004; Bloom et al. 2007a). At present, it is unknown whether real proteins show a similar pattern. By analyzing substitution counts occurring among orthologous proteins in four species of yeast, five species of Drosophila, and five species of mammals (Figure 1), we find that effective population size strongly dictates the degree of randomness in the molecular clock, with large effective population sizes buffering stochastic variation in evolutionary rate. This result is consistent with the evolution of increased mutational robustness in proteins evolving under large population sizes.
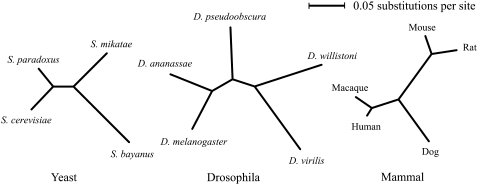
Figure 1.—
Unrooted phylogenies of yeast, Drosophila, and mammalian species. Branch lengths shown are proportional to evolutionary distance, as determined by analysis of concatenated protein data sets. These distances were used to correct for lineage effects influencing substitution counts in individual proteins (see methods).
METHODS
Ortholog prediction and alignment:
Annotated Saccharomyces cerevisiae, S. paradoxus, S. mikatae, and S. bayanus protein sequences were obtained from the Saccharomyces Genome Database (accessed January 2008; http://www.yeastgenome.org/) (Goffeau et al. 1996; Kellis et al. 2003). Protein sequences from Drosophila species (Drosophila ananassae, D. melanogaster, D. pseudoobscura, D. virilis, and D. willistoni) were obtained from the AAAWiki (accessed January 2008; http://rana.lbl.gov/drosophila/wiki/index.php/) (Adams et al. 2000; Drosophila12 Genomes Consortium 2007). Mammalian protein sequences from dogs, humans, macaques, mice, and rats were procured from Ensembl (accessed January 2008; http://www.ensembl.org/) (MouseGenome Sequencing Consortium 2002; International Human Genome Sequencing Consortium 2004; Rat Genome Sequencing Project Consortium 2004; Lindblad-Toh et al. 2005; Rhesus Macaque Genome Sequencing and Analysis Consortium 2007).
Orthology assignments within yeast, Drosophila, and mammals were obtained using the SYNERGY algorithm (Wapinski et al. 2007). Briefly, SYNERGY performs a bottom-up traversal of a species tree, identifying orthologs between the species below each ancestral species in the tree. SYNERGY uses sequence similarity and gene order to generate putative orthology assignments and employs a modified neighbor-joining procedure to reconstruct gene tree topologies at each intermediate stage of the algorithm. It refines orthology assignments according to the resulting tree structure. This method generates a genomewide catalog of orthology assignments and their corresponding gene trees. To avoid complications caused by gene duplication and gene loss, only those genes that maintain a 1:1 orthologous relationship among all species were analyzed. This pruning left 3788 yeast, 10,032 Drosophila, and 11,136 mammalian proteins.
Orthologous protein sequences were aligned using MUSCLE v3.6 (Edgar 2004). To control for sequence annotation errors, alignment errors, and spurious ortholog predictions, we eliminated all alignments in which gaps accounted for >25% of total alignment length, leaving 3081 yeast, 7174 Drosophila, and 8065 mammalian proteins.
Estimation of substitution counts:
Substitution counts were estimated under maximum likelihood using the AAML package of PAML v3.14 (Yang 1997). Substitution rate was kept constant across sites within sequences (α = 0), but was allowed to vary freely across branches of the phylogeny. Amino acid substitution rate was constrained to be proportional to the frequency of the target amino acid, with frequencies based upon genomic averages. Analyses using substitution matrices based upon empirical substitution rates observed among our orthologous proteins, as well as those using PAM matrices (Dayhoff et al. 1978), show similar, but slightly larger, values of R(t) (data not shown). Additionally, estimating α as a free parameter for each gene results in similar, though slightly larger, values of R(t) (data not shown). Generally, more detailed likelihood models result in larger values of R(t), so that our relatively simple models provide conservative estimates.
Estimation of index of dispersion:
Indexes of dispersion were calculated following Gillespie (1989) and Bedford and Hartl (2008). This approach uses standard statistical techniques for calculating the mean and variance of weighted samples. The branch weights for a given n-branched species tree are obtained via a concatenated set of all available protein sequences (Figure 1), where the length of branch i on the concatenated tree is Ti. The weight of branch i is then
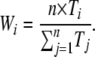 |
Such a weighting scheme eliminates lineage effects that are present throughout a genome, so that variance in substitution counts must be specific to a particular gene and not due to effects of branch length differences present in the species tree. The sample mean (M) and sample variance (S2) of substitution counts occurring on a particular protein tree are calculated as
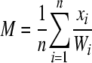 |
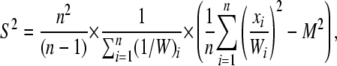 |
where xi represents the number of substitutions occurring on branch i of the protein tree. R(t) is estimated as the ratio of the sample variance to the sample mean.
Statistical analysis by maximum likelihood:
The likelihood of the observed substitution counts was compared between Poisson and negative binomial models. The probability of observing k substitutions drawn from a Poisson distribution with rate parameter λ is given by
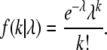 |
The probability of observing k substitutions drawn from a negative binomial distribution with rate parameter λ and dispersion parameter ω is
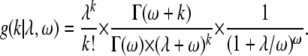 |
The Poisson model is nested within the negative binomial model, such that as ω approaches infinity the negative binomial density reduces to the Poisson density; i.e., g(k, λ, ∞) reduces to f(k, λ). In both models, the rate parameter λ was estimated via maximum likelihood separately for each protein, taking into account the relative weightings of each branch (see above and Figure 1). A single dispersion parameter ω was estimated across proteins. The log likelihood for the Poisson model, with k substitutions on branch i of protein j, is
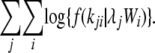 |
The log likelihood for the negative binomial model, with k substitutions on branch i of protein j, is
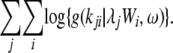 |
Additionally, estimates of λ and ω were made for each protein individually using a similar approach.
RESULTS
On average, proteins from yeast, Drosophila, and mammals all show greater variance in substitution counts than would be expected if sequence evolution were a simple Poisson process [Table 1; in all three cases R(t) > 1, P < 10−15, Wilcoxon's signed-rank test]. Differences in average per-branch substitution count M may result from variation in evolutionary time, variation in evolutionary rate, or a combination of the two. Variation in protein evolutionary rate is evident in comparisons of M between proteins sharing the same species phylogeny. Such variation arises due to differences in the per-site rate of evolution and to differences in protein length. It is easy to see that longer proteins or faster evolving proteins will have more substitution events than shorter proteins or more slowly evolving proteins. Variation in M between yeast, Drosophila, and mammals is due to variation in the rate of protein evolution and also to differing amounts of evolutionary time separating species.
TABLE 1.
Mean per-branch substitution count (M) and mean index of dispersion [R(t)] of amino acid sequences in closely related species of yeast, Drosophila, and mammals
| n | mean M | mean R(t) | |
|---|---|---|---|
| Yeast | 3081 | 30.0133 | 2.0993 |
| Drosophila | 7174 | 40.7729 | 4.1892 |
| Mammals | 8065 | 20.6350 | 6.4790 |
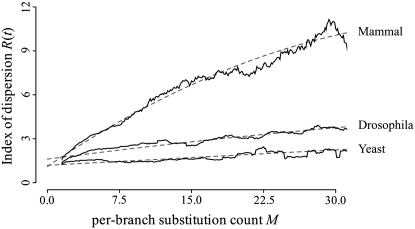
Unexpectedly, we find that proteins from yeast, Drosophila, and mammals all show a positive correlation between M and the index of dispersion R(t) (Figure 2). Regression analysis shows that, in all three cases, the intercept lies close to 1, and for both Drosophila and mammalian proteins there is a highly significant linear term (Table 2). In yeast and Drosophila, adding a quadratic term to the regression does not significantly improve the regression fit, while mammalian proteins show a relatively weak but significant quadratic term. This indicates that the relationship between M and R(t) can be adequately explained as nearly linear. A linear relationship between M and R(t) is expected if substitution counts follow a negative binomial distribution (Bedford and Hartl 2008). Often used in cases of overdispersion, a negative binomial distribution predicts that R(t) = 1 + λ/ω, where λ represents the rate parameter and ω represents the dispersion parameter of the negative binomial distribution. It is the ω-parameter rather than R(t) that gives the degree of departure from Poisson. When ω = ∞, the negative binomial density reduces to the Poisson density. Proteins with values of ω close to 0 have less “stable” molecular clocks than proteins with large values of ω.
Figure 2.—
Relationship between per-branch substitution count (M) and index of dispersion [R(t)] among yeast, Drosophila, and mammalian proteins. Variation in M is due to differences in per-site rate of evolution, differences in sequence length, and differences in evolutionary time. Values of R(t) > 1 indicate departure from a Poisson molecular clock. Solid lines represent a sliding-window analysis of mean R(t) values (window size ±1.5M). Dashed lines represent regressions of R(t) ∼ aM2 + bM + c. Best-fit parameters for these regressions are shown in Table 2.
TABLE 2.
Linear regression of mean substitution count (M) vs. index of dispersion [R(t)] for yeast, Drosophila, and mammalian proteins
| Coefficient | 95% C.I. | t-value | Pr(>|t|) | |
|---|---|---|---|---|
| Yeast | ||||
| Intercept | 1.1891 | 0.7662, 1.6119 | 5.5142 | 3.9e-8 |
| M | 0.0353 | −0.0085, 0.0791 | 1.5811 | 0.1140 |
| M2 | −0.0000 | −0.0009, 0.0009 | −0.0225 | 0.9820 |
| Drosophila | ||||
| Intercept | 1.6117 | 1.3468, 1.8766 | 11.9272 | <1.0e-15 |
| M | 0.0858 | 0.0600, 0.1117 | 6.5076 | 8.4e-11 |
| M2 | −0.0005 | −0.0010, 0.0000 | −1.7941 | 0.0729 |
| Mammalian | ||||
| Intercept | 1.1059 | 0.6151, 1.5966 | 4.4169 | <1.0e-15 |
| M | 0.4453 | 0.3852, 0.5054 | 14.5237 | <1.0e-15 |
| M2 | −0.0049 | −0.0063, −0.0035 | −6.8337 | 8.9e-12 |
Values of λ and ω can be estimated through numerical optimization of the likelihood function (see methods). By holding ω constant across proteins, but allowing λ to vary, we estimate a global ω for yeast, Drosophila, and mammals (Table 3). In all three cases, we find that a negative binomial distribution gives a substantially better fit than a Poisson distribution (P < 10−15 in each case, LRT with d.f. = 1). Maximum likelihood allows levels of overdispersion to be rigorously compared between species. We find that estimated values of ω are significantly smaller in mammals compared to yeast and Drosophila, and that values of ω are significantly smaller in Drosophila than in yeast (Table 3).
TABLE 3.
Maximum-likelihood estimation of protein-specific rate (λ) and genomewide dispersion (ω) parameters using Poisson and negative binomial models of substitution counts in yeast, Drosophila, and mammalian proteins
| d.f. | l.l. | Estimated ω | 95% C.I. | |
|---|---|---|---|---|
| Yeast | ||||
| Poisson (λ) | 3081 | −49,712.9 | — | — |
| Negative binomial (λ, ω) | 3082 | −47,140.9 | 37.037 | 35.088, 39.216 |
| Drosophila | ||||
| Poisson (λ) | 7174 | −214,166.5 | — | — |
| Negative binomial (λ, ω) | 7175 | −178,263.0 | 13.699 | 13.423, 13.986 |
| Mammals | ||||
| Poisson (λ) | 8065 | −256,628.0 | — | — |
| Negative binomial (λ, ω) | 8066 | −179,484.9 | 3.494 | 3.435, 3.554 |
l.l., log likelihood.
In accordance with results from lattice protein simulations, there appears to be a strong effect of population size on the extent to which sequence evolution departs from its Poisson expectation. Standard estimates of effective populations sizes are ∼104–105 for mammals, 106 for Drosophila, and 107–108 for microorganisms. Yeast, with a large effective population size, shows a large value of ω; mammals, with a relatively small effective population size, show a small value of ω; whereas Drosophila is intermediate for both effective population size and ω. Thus, it appears that population size and the dispersion of the molecular clock are tightly coupled. Evolution under large population sizes results in relatively little overdispersion, whereas evolution under small population sizes results in a great deal of overdispersion.
The apparent negative correlation observed between population size and index of dispersion across different organisms is borne out in comparisons between X-linked and autosomal protein-coding genes within Drosophila and within mammals. In a species with an equal sex ratio, there will be a 0.75:1.00 ratio of X chromosomes to autosomes within the population, so that proteins encoded on the X are expected to evolve with a smaller effective population size than proteins on the autosomes. Accordingly, we observe that estimates of the dispersion parameter ω are significantly smaller in proteins encoded on the X than on the autosomes in both Drosophila and mammals (Table 4). X-linked protein-coding genes were taken as those currently on the X chromosome of D. melanogaster and humans. Although there is expected to be some limited evolutionary variation in which genes are X-linked, this variation will add noise without biasing our results. Interestingly, Drosophila shows a 28% decrease in the estimated ω of X-linked protein-coding genes, while mammals show a very similar 27% decrease in the estimated ω of X-linked protein-coding genes.
TABLE 4.
Maximum-likelihood estimation of protein-specific rate (λ) and genomewide dispersion (ω) parameters using Poisson and negative binomial models of substitution counts in proteins encoded on the X vs. proteins encoded on the autosomes
| d.f. | l.l. | Estimated ω | 95% C.I. | |
|---|---|---|---|---|
| Drosophila autosomal | ||||
| Poisson (λ) | 6129 | −180,292.6 | — | — |
| Negative binomial (λ, ω) | 6130 | −151,850.1 | 14.265 | 13.928, 14.556 |
| Drosophila X-linked | ||||
| Poisson (λ) | 1015 | −32,805.1 | — | — |
| Negative binomial (λ, ω) | 1016 | −25,598.4 | 11.136 | 10.582, 11.723 |
| Mammalian autosomal | ||||
| Poisson (λ) | 7776 | −247127.9 | — | — |
| Negative binomial (λ, ω) | 7777 | −173,185.4 | 3.527 | 3.469, 3.589 |
| Mammalian X-linked | ||||
| Poisson (λ) | 259 | −8383.0 | — | — |
| Negative binomial (λ, ω) | 260 | −5584.6 | 2.775 | 2.525, 3.048 |
l.l., log likelihood.
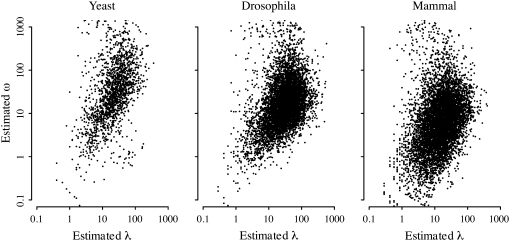
Additionally, we find that per-protein estimates of rate parameter λ and dispersion parameter ω show a weak positive correlation across proteins in yeast, Drosophila, and mammals (Figure 3; corY = 0.133, corD = 0.183, corM = 0.133, P < 10−15 in all three cases, Spearman's rank correlation). This is perhaps surprising, as the naïve expectation might be that fast-evolving proteins show a greater deviation from Poisson evolution than slow-evolving proteins. We observe the opposite: proteins that accumulate substitutions quickly do so with a more regular clock than proteins that accumulate substitutions slowly. This may seem at first paradoxical, as the index of dispersion R(t) shows a strong positive correlation with the mean per-branch substitution count M (Figure 2). However, under a negative binomial distribution, R(t) is expected to show a strong positive correlation with λ, simply due to the summary statistics inherent to the negative binomial. Thus, even if λ and ω share a weak negative correlation, λ and R(t) will still show a positive correlation. To confirm this scenario, we sampled substitution counts from a negative binomial distribution using as parameters the per-protein estimates of λ and ω. We find that the randomly sampled substitution counts show a statistically similar relationship between M and R(t) to that of the biological data (supplemental Table 1).
Figure 3.—
Relationship between per-gene estimates of rate parameter λ and dispersion parameter ω among yeast, Drosophila, and mammalian proteins. Proteins with small values of ω accumulate substitution in a less clock-like fashion. Parameters were estimated via maximum likelihood by fitting substitution counts to a negative binomial distribution (see methods). λ and ω show a weak positive correlation in all three species (corY = 0.133, corD = 0.183, corM = 0.133, P < 10−15 in all three cases, Spearman's rank correlation).
DISCUSSION
We find that the mean index of dispersion [R(t)] is significantly >1 for yeast, Drosophila, and mammalian proteins (Table 1; P < 10−15 in all three cases, Wilcoxon's signed-rank test). These results are consistent with previous findings regarding overdispersion in both Drosophila (Zeng et al. 1998; Kern et al. 2004; Bedford and Hartl 2008) and mammals (Gillespie 1989; Smith and Eyre-Walker 2003; Kim and Yi 2008). This study is the first to report on overdispersion in yeast. We emphasize here that, although our interpretations may be different, the findings of the present study are highly compatible with the findings of Kim and Yi (2008). Kim and Yi find, through similar methodology, that mammalian nonsynonymous substitutions show a mean R(t) of 4.94. Poisson evolution predicts that mean R(t) = 1. Additionally, Kim and Yi report that, in 33% of mammalian proteins, Poisson evolution can be rejected at the 5% level. We interpret these results as indicative of non-Poisson evolution; although a Poisson model can explain the R(t) values of a subset of the genome, such a model fails to explain genomewide patterns of overdispersion. We also emphasize that the finding of overdispersion does not necessarily imply positive selection or adaptive evolution; overdispersion is compatible with nearly neutral evolution occurring in a heterogeneous fashion. The specific mechanisms creating overdispersion remain unclear, as many different biological scenarios may result in heterogeneous substitution rates (for further discussion see Bedford and Hartl 2008).
We find significantly reduced indexes of dispersion in proteins experiencing evolution under large effective population sizes. The negative correlation between overdispersion and effective population size is seen across both organisms (Figure 2; Tables 2 and 3) and chromosomes (Table 4). Correspondence between organismal comparisons and chromosomal comparisons suggests that the observed negative correlation is a general population genetic phenomenon and not due to the specifics of X chromosomes or of multicellularity. Still, with only three groups of organisms, it is possible, although unparsimonious, that the observed patterns of overdispersion may result from other factors besides effective population size. There exist many differences in the biology of these organisms that could possibly contribute to variation in the overdispersion of the molecular clock. Similarly, there exist differences between X chromosomes and autosomes other than differences in effective population size. As comparative genomic data become increasingly extensive, the population size hypothesis can tested further.
Theory predicts that evolution under large population sizes should result in selection for increased robustness to random mutation (van Nimwegen et al. 1999). This would explain our findings, as well as computer simulations of lattice proteins referred to in the Introduction. Although it has previously been shown that proteins possess significant robustness to random amino acid change (Guo et al. 2004; Bloom et al. 2006), it has not been clear whether such tolerance is due to selection for increased robustness or whether such tolerance is an innate characteristic of functional protein sequences. Our results strongly suggest that selection for increased mutational robustness has occurred in yeast and to a lesser extent in Drosophila proteins relative to mammalian proteins. Selection for mutational robustness has previously been demonstrated in an RNA virus (Montville et al. 2005), as well as in large in vitro populations of cytochrome P450 proteins (Bloom et al. 2007b). However, the present study is the first to show that selection for increased mutational robustness may be active in the proteins of higher organisms.
The argument favoring selection for mutational robustness requires very little in the way of assumptions regarding protein evolution. The presence of nearly neutral networks permeating sequence space has been inferred from theoretical models of RNA and protein folding (Fontana et al. 1993; Schuster et al. 1994; Depristo et al. 2005) as well as from recent PCR mutagenesis experiments (Guo et al. 2004; Bloom et al. 2006). Such nearly neutral networks are expected to arise from the many-to-one mapping of genotypes onto fitness combined with the compactness (high dimensionality) of genotype space. In such scenarios, a single-amino-acid substitution in a protein sequence often has little or no effect on fitness; however, this substitution may alter the fitness effects of subsequent substitutions at other sites in the protein. Thus, as sequences evolve they move across nearly neutral networks, sometimes acquiring robust conformations in which many mutations result in functionally nearly equivalent sequences and sometimes acquiring fragile conformations in which most mutations result in reduced fitness.
Interestingly, when the product of the effective population size and the nearly neutral mutation rate (4Nμ in diploid organisms) is significantly >1, then proteins evolve to preferentially acquire robust conformations even though these conformations have the same immediate fitness as their more fragile neighbors in sequence space (van Nimwegen et al. 1999). Increased mutational robustness arises from the presence of multiple competing sequences existing within the population simultaneously (extensive polymorphism); equilibrating incoming and outgoing mutations results in a preference for robust conformations. However, when 4Nμ ≪ 1, then at any given point in time the population is most likely to have converged on a single sequence and its evolution across the nearly neutral network follows a blind random walk, testing random mutations and sometimes accepting mutations if they lie on the nearly neutral network. In this case, the population spends equal amounts of time employing each sequence in the nearly neutral network, and no additional mutational robustness is evolved.
Mutational robustness may also arise as a byproduct of selection for phenotypic robustness (Meiklejohn and Hartl 2002). In this case the same relationship between robustness and population size is expected to be preserved, because the effective strength of selection (2Ns in diploid organisms) is greater in large populations than in small populations. Indeed, theoretical work has shown that selection for robustness against errors in protein translation, a specific type of phenotypic robustness, is significantly more effective in large populations than in small populations (Wilke and Drummond 2006).
A protein's substitution rate is expected to vary over time as it moves between fragile and robust conformations. Substitution away from a robust sequence will be faster than substitution away from a fragile sequence, simply because a greater percentage of mutations in robust sequences result in functionally nearly equivalent proteins. Variation in substitution rate will result in overdispersion of substitution counts across a phylogeny. However, selection for mutational robustness acts to buffer rate variation, thereby reducing overdispersion of substitution counts.
Theory predicts that the extent of mutational robustness will increase with 4Nμ, so that both the effective population size of the species and the effective nearly neutral mutation rate of the protein are important. Thus, in addition to a negative correlation between non-Poisson behavior and population size, we expect a negative correlation between the extent of non-Poisson behavior and the rate at which substitutions accumulate in a protein. Fast-evolving proteins should possess, on average, more polymorphism than slow-evolving proteins. This polymorphism is what drives selection for mutational robustness. We find exactly this: fast-evolving proteins, although showing larger values of R(t), show patterns of evolution closer to Poisson than do slow-evolving proteins (Figure 3). This suggests that individual proteins vary in their extent of mutational robustness and that fast-evolving proteins have, on average, greater robustness than slow-evolving proteins.
Recent whole-genome sequencing efforts have found per-site nonsynonymous nucleotide diversity (π) to be 0.0180 for autosomes in D. simulans (Begun et al. 2007). Assuming polymorphisms segregate neutrally, π provides an estimate of 4Nμ. Taking the average number of nonsynonymous sites in a protein as 1000, we estimate per-protein 4Nμ to be 2.6 for Drosophila species. This estimate is consistent with our findings regarding overdispersion, as theory predicts that some degree of mutational robustness should evolve when 4Nμ > 1 (van Nimwegen et al. 1999). As expected, estimates of 4Nμ for X-linked protein-coding genes are significantly lower, with 1.8 as the D. simulans average (Begun et al. 2007). Estimates of nucleotide diversity in S. cerevisiae (Ruderfer et al. 2006) and S. paradoxus (Johnson et al. 2004) are significantly lower than estimates in Drosophila, despite the difference in effective population size. However, because the yeast species studied here rarely undergo sexual recombination in nature, background selection and hitchhiking may significantly reduce global levels of polymorphism (Ruderfer et al. 2006). These effects make direct comparison of Drosophila with yeast difficult. In contrast, population genetic estimates from mammals should be more comparable to those from Drosophila. Taking the average per-site nonsynonymous diversity in humans (Cargill et al. 1999) and an average length of 1000 nonsynonymous sites per protein, we arrive at an approximate average per-protein estimate of 4Nμ = 0.3. Similar to Drosophila, human X-linked genes show reduced levels of polymorphism (International SNP Map Working Group 2001). Estimated values of 4Nμ suggest that there should exist substantially more robustness in Drosophila proteins compared to mammalian proteins and in X-linked proteins compared to autosomal proteins. This prediction is consistent with our findings regarding overdispersion of these sequences.
When 4Nμ ≫ 1, the population dynamics of multiple simultaneously segregating alleles within a protein are expected to affect the index of the dispersion of substitution events. In this case, genetic variation cosegregates within a protein, forcing substitutions to occur in clusters of multiple fixations, although these grouped fixation events may tend to occur at regularly spaced intervals (Gillespie 1994). The net effect of such clustered fixations is to increase the index of dispersion of the substitution process. In this model, population dynamics predict a positive correlation between R(t) and population size, rather than the negative correlation we observe between R(t) and population size. Additionally, the effect of 4Nμ ≫ 1 on the fixation process is expected to be diminished by recombination. It has been shown that regions of the Drosophila genome with reduced recombination show very similar values of R(t) as those regions with high recombination (Bedford and Hartl 2008), further suggesting that population dynamics plays a minor role in accounting for our results.
Our findings suggest that mammalian proteins are more susceptible to the effects of random mutation than proteins in yeast and Drosophila. This hypothesis leads to a strong prediction: that in vitro screens using PCR mutagenesis will show that random amino acid replacements are more likely to disrupt function in mammalian orthologs of yeast or Drosophila proteins. It has been shown that protein stability mediates tolerance of protein folding to random sequence change, so that extra stability beyond what is needed for function can buffer the negative effects of random mutations. Thus, we predict that the buffer provided by extra stability will be smaller in mammalian proteins relative to yeast or Drosophila orthologs.
It seems reasonable to expect that selection for mutational robustness should also occur in response to mutations other than amino acid changes. Each type of mutation will have a particular rate of occurrence μ, and only those types of mutation where 4Nμ is significant are expected to show selection for mutational robustness. For example, if whole-gene deletions occur with high enough frequency, then robustness to such deletions may be selected for. Genomic screens have shown that 83% of yeast proteins may be deleted while still maintaining viability in rich medium (Winzeler et al. 1999), suggesting widespread robustness. If Drosophila or mice have lower values of 4Nμ for whole-gene deletion events as seems reasonable, then we expect that screens of deletion mutants in Drosophila or mice will show significantly higher levels of essential genes. Through contrasting orthologous proteins and genetic networks in yeast and higher organisms, we may be able to elucidate the mechanisms by which mutational robustness evolves.
Acknowledgments
We thank members of the Hartl lab for thoughtful discussion, two anonymous reviewers for helpful comments, and the FAS Center for Systems Biology at Harvard University for computational resources. This work was supported by a National Science Foundation Predoctoral Fellowship (to T.B.) and by National Institutes of Health grant GM079536 to D.L.H.
References
- Adams, M. D., S. E. Celniker, R. A. Holt, C. A. Evans, J. D. Gocayne et al., 2000. The genome sequence of Drosophila melanogaster. Science 287 2185–2195. [DOI] [PubMed] [Google Scholar]
- Bastolla, U., M. Vendruscolo and H. E. Roman, 2000. Structurally constrained protein evolution: results from a lattice simulation. Eur. Phys. J. B 15 385–397. [Google Scholar]
- Bedford, T., and D. L. Hartl, 2008. Overdispersion of the molecular clock: temporal variation of gene-specific substitution rates in Drosophila. Mol. Biol. Evol. (in press). [DOI] [PMC free article] [PubMed]
- Begun, D. J., A. K. Holloway, K. Stevens, L. W. Hillier, Y.-P. Poh et al., 2007. Population genomics: whole-genome analysis of polymorphism and divergence in Drosophila simulans. PLoS Biol. 5 e310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom, J. D., J. J. Silberg, C. O. Wilke, D. A. Drummond, C. Adami et al., 2005. Thermodynamic prediction of protein neutrality. Proc. Natl. Acad. Sci. USA 102 606–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom, J. D., S. T. Labthavikul, C. R. Otey and F. H. Arnold, 2006. Protein stability promotes evolvability. Proc. Natl. Acad. Sci. USA 103 5869–5874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom, J. D., A. Raval and C. O. Wilke, 2007. a Thermodynamics of neutral protein evolution. Genetics 175 255–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom, J. D., Z. Lu, D. Chen, A. Raval, O. S. Venturelli et al., 2007. b Evolution favors protein mutational robustness in sufficiently large populations. BMC Biol. 5 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cargill, M., D. Altshuler, J. Ireland, P. Sklar, K. Ardlie et al., 1999. Characterization of single-nucleotide polymorphisms in coding regions of human genes. Nat. Genet. 22 231–238. [DOI] [PubMed] [Google Scholar]
- Cutler, D. J., 2000. Understanding the overdispersed molecular clock. Genetics 154 1403–1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayhoff, M. O., R. M. Schwartz and D. C. Orcutt, 1978. A model of evolutionary change in proteins, pp. 35–352 in Atlas of Protein Sequence and Structure, Vol. 5, Suppl. 3, edited by M. O. Dayhoff. National Biomedical Research Foundation, Washington, DC.
- DePristo, M. A., D. M. Weinreich and D. L. Hartl, 2005. Missense meanderings in sequence space: a biophysical view of protein evolution. Nat. Rev. Genet. 6 678–687. [DOI] [PubMed] [Google Scholar]
- Drosophila 12 Genomes Consortium, 2007. Evolution of genes and genomes on the Drosophila phylogeny. Nature 450 203–218. [DOI] [PubMed] [Google Scholar]
- Edgar, R. C., 2004. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 32 1792–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontana, W., P. F. Stadler, E. G. Bornberg-Bauer, T. Griesmacher, I. L. Hofacker et al., 1993. RNA folding and combinatory landscapes. Phys. Rev. E 47 2083–2099. [DOI] [PubMed] [Google Scholar]
- Gillespie, J. H., 1989. Lineage effects and the index of dispersion of molecular evolution. Mol. Biol. Evol. 6 636–647. [DOI] [PubMed] [Google Scholar]
- Gillespie, J. H., 1994. Substitution processes in molecular evolution. II. Exchangeable models from population genetics. Evolution 48 1101–1113. [DOI] [PubMed] [Google Scholar]
- Goffeau, A., B. G. Barrell, H. Bussey, R. W. Davis, B. Dujon et al., 1996. Life with 6000 genes. Science 274 546–567. [DOI] [PubMed] [Google Scholar]
- Guo, H. H., J. Choe and L. A. Loeb, 2004. Protein tolerance to random amino acid change. Proc. Natl. Acad. Sci. USA 101 9205–9210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Human Genome Sequencing Consortium, 2004. Finishing the euchromatic sequence of the human genome. Nature 431 931–945. [DOI] [PubMed] [Google Scholar]
- International SNP Map Working Group, 2001. A map of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature 409 928–933. [DOI] [PubMed] [Google Scholar]
- Johnson, L. J., V. Koufopanou, M. R. Goddard, R. Hetherington, S. M. Schäfer et al., 2004. Population genetics of the wild yeast Saccharomyces paradoxus. Genetics 166 43–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellis, M., N. Patterson, M. Endrizzi, B. Birren and E. S. Lander, 2003. Sequencing and comparison of yeast species to identify genes and regulatory elements. Nature 423 241–254. [DOI] [PubMed] [Google Scholar]
- Kern, A. D., C. D. Jones and D. J. Begun, 2004. Molecular population genetics of male accessory gland proteins in the Drosophila simulans complex. Genetics 167 725–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, S.-H., and S. V. Yi, 2008. Mammalian nonsynonymous sites are not overdispersed: comparative genomic analysis of index of dispersion of mammalian proteins. Mol. Biol. Evol. 25 634–642. [DOI] [PubMed] [Google Scholar]
- Lindblad-Toh, K., C. M. Wade, T. S. Mikkelsen, E. K. Karlsson, D. B. Jaffe et al., 2005. Genome sequence, comparative analysis and haplotype structure of the domestic dog. Nature 438 803–819. [DOI] [PubMed] [Google Scholar]
- Meiklejohn, C. D., and D. L. Hartl, 2002. A single mode of canalization. Trends Ecol. Evol. 17 468–473. [Google Scholar]
- Montville, R., R. Froissart, S. K. Remold, O. Tanaillon and P. E. Turner, 2005. Evolution of mutational robustness in an RNA virus. PLoS Biol. 3 e381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mouse Genome Sequencing Consortium, 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420 520–562. [DOI] [PubMed] [Google Scholar]
- Ohta, T., and M. Kimura, 1971. On the constancy of the evolutionary rate of cistrons. J. Mol. Evol. 1 18–25. [DOI] [PubMed] [Google Scholar]
- Rat Genome Sequencing Project Consortium, 2004. Genome sequence of the Brown Norway rat yields insights into mammalian evolution. Nature 428 493–521. [DOI] [PubMed] [Google Scholar]
- Rhesus Macaque Genome Sequencing and Analysis Consortium, 2007. Evolutionary and biomedical insights from the rhesus macaque genome. Science 316 222–234. [DOI] [PubMed] [Google Scholar]
- Ruderfer, D. M., S. C. Pratt, H. S. Seidel and L. Kruglyak, 2006. Population genomic analysis of outcrossing and recombination in yeast. Nat. Genet. 38 1077–1081. [DOI] [PubMed] [Google Scholar]
- Schuster, P., W. Fontana, P. F. Stadler and I. L. Hofacker, 1994. From sequences to shapes and back: a case study in RNA secondary structures. Proc. R. Soc. Lond. Ser. B 255 279–284. [DOI] [PubMed] [Google Scholar]
- Smith, N. G. C., and A. Eyre-Walker, 2003. Partitioning the variation in mammalian substitution rates. Mol. Biol. Evol. 20 10–17. [DOI] [PubMed] [Google Scholar]
- van Nimwegen, E., J. P. Crutchfield and M. Huynen, 1999. Neutral evolution of mutational robustness. Proc. Natl. Acad. Sci. USA 96 9716–9720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wapinski, I., A. Pfeffer, N. Friedman and A. Regev, 2007. Automatic genome-wide reconstruction of phylogenetic gene trees. Bioinformatics 23 i549–i558. [DOI] [PubMed] [Google Scholar]
- Wilke, C. O., 2004. Molecular clock in neutral protein evolution. BMC Genet. 5 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke, C. O., and D. A. Drummond, 2006. Population genetics of translational robustness. Genetics 173 473–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winzeler, E. A., D. D. Shoemaker, A. Astromoff, H. Liang, K. Anderson et al., 1999. Functional characterization of the S. cerevisiae genome by gene deletion and parallel analysis. Science 285 901–906. [DOI] [PubMed] [Google Scholar]
- Yang, Z., 1997. PAML: a program package for phylogenetic analysis by maximum likelihood. Comput. Appl. Biosci. 13 555–556. [DOI] [PubMed] [Google Scholar]
- Zeng, L.-W., J. M. Comeron, B. Chen and M. Kreitman, 1998. The molecular clock revisited: the rate of synonymous vs. replacement change in Drosophila. Genetica 102/103 369–382. [PubMed] [Google Scholar]
- Zuckerkandl, E., and L. Pauling, 1965. Evolutionary divergence and convergence in proteins, pp. 97–166 in Evolving Genes and Proteins, edited by V. Bryson and H. J. Vogel. Academic Press, New York.