Localized and extended deformations of elastic shells

Abstract

The dried raisin, the crushed soda can, and the collapsed bicycle inner tube exemplify the nonlinear mechanical response of naturally curved elastic surfaces with different intrinsic curvatures to a variety of different external loads. To understand the formation and evolution of these features in a minimal setting, we consider a simple assay: the response of curved surfaces to point indentation. We find that for surfaces with zero or positive Gauss curvature, a common feature of the response is the appearance of faceted structures that are organized in intricate localized patterns, with hysteretic transitions between multiple metastable states. In contrast, for surfaces with negative Gauss curvature the surface deforms nonlocally along characteristic lines that extend through the entire system. These different responses may be understood quantitatively by using numerical simulations and classified qualitatively by using simple geometric ideas. Our ideas have implications for the behavior of small-scale structures.

Thin naturally curved shells arise on a range of length scales: from nanometer-sized viruses (1) to carbon nanotubes (2), from the micrometer-sized cell wall (3) to bubbles with colloidal armor (4), and from architectural domes (5) to the megameter-scale earth's crust (6). In each of these examples, the underlying curved geometry of the object leads to enhanced mechanical stability relative to that of naturally flat sheets. In particular, whereas a naturally flat sheet can almost always be bent weakly without stretching, almost any deformation of a curved shell causes its mid-surface to bend and stretch simultaneously. This fact is a simple consequence of a far-reaching concept from differential geometry, Gauss's Theorema Egregium and its application to determine the conditions for the isometric deformation of a surface (7). Indeed, our everyday experience playing with thin flat and curved sheets of similar materials such as sheets of plastic suggests that the natural geometry of the surface dominates its mechanical response: a surface with positive Gauss curvature (e.g., an empty plastic bottle) has a qualitatively different response from that of a surface that is either flat (e.g., a plastic sheet) or has negative Gauss curvature. To understand this we must combine the geometry of idealized surfaces and the effects of a small but finite thickness on the mechanical response of these slender structures.

We do this by using a simple indentation assay, the method of choice to probe the properties of solid interfaces at various length scales (8, 9) and connect geometry to mechanics. The nonlinear character of the governing equations that arises from the effects of large deformations precludes the use of purely analytical techniques to solve them. It is nevertheless possible to get a qualitative view of the mechanical response of a doubly curved thin shell (thickness t, radii of curvature R₁, R₂; R = min[R₁, R₂]; ε = t/R ≪ 1) subjected to a point indentation load by a consideration of the linearized equations of equilibrium. For such a shallow shell, where we may use the Cartesian coordinates (x, y) to describe any material point on the shell rather than any more elaborate intrinsic coordinate system, these are given by (10, 11):

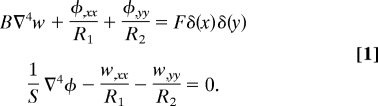Here, w = w(x, y) is the deflection of the shell relative to its naturally curved state, φ = φ(x, y) is the Airy stress function (whose derivatives yield the components of the depth-integrated in-plane stresses), and (.)_{, x} = ∂(.)/∂x, etc. Futhermore R₁ and R₂ are (the possibly inhomogeneous) principal radii of curvature of the shell, B = Et³/12(1 − ν²) and S = Et are the bending and stretching stiffness of the curved surface made of material with Young's modulus E and Poisson ratio ν, respectively, and F is the applied localized indentation load. A complete formulation of the problem additionally requires the specification of boundary conditions on the displacements and stresses associated with support or lack thereof along a boundary curve. The Eqs. 1 are globally elliptic, i.e., following the usual classification of linear partial differential equations, they have imaginary characteristics and thus require the prescription of conditions along all boundaries. However as we shall see, they nevertheless can exhibit behaviors associated with hyperbolic or parabolic systems because of the fact that, when scaled appropriately, the term with highest derivative in the first equation in 1 is in general very small.

Because of the localized nature of the indentation load, the behavior of the shell is expected to be quite different in the neighborhood of the point of indentation than far from it. To see this we define our dimensionless variables to be x̄ = x/t; ȳ = y/t; w̄ = w/t; φ̄ = φ/Ft, where the Airy stress function is scaled so that bending stresses dominate the strongly localized response of the shell in a linearized setting, i.e., we have assumed that F ∼ σt², with the nominal stress σ ∼ O(E) near the localized indentation. Then, we may write the dimensionless form of the above equations, on dropping the bars, as

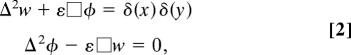where Δ = ∇² = (.),_xx + (.),_yy is the Laplacian operator, □ = (1/R₁)(.),_xx + (1/R₂)(.),_yy is the generalized d'Alembertian wave operator, and ε = (B/SR²)^1/2 = h/R ≪ 1 is a dimensionless parameter. Further analysis requires the consideration of a region close to the indentation region where the Eqs. 2 break down owing to the dominance of nonlinear effects (12–14). However, the mechanical response of the shell over this localized zone is not relevant on distances large compared to the thickness of the shell, where there is a different far-field solution that is dominated by the almost inextensional bending response (10–14) of the shell. Because we are interested in scales that are comparable to the lateral extent of the shell, we define our dimensionless variables to be x′ = x/R; y′ = y/R; w′ = wB/FR²; φ′ = φt²/FR³. Here the Airy stress function is scaled differently so that bending stresses continue to dominate the almost inextensional response of the shell in a linearized setting. Then, we may write the dimensionless form of the above equations, on dropping the primes, as

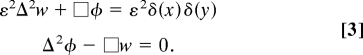On eliminating the Airy stress function φ by substituting the second equation in 4 into the first, we get

which is a singularly perturbed linear partial differential equation, whose domain of validity is limited to regions far from the point of indentation. Substituting the perturbation expansion w(x, y) = w₀(x, y) + ε²w₁(x, y) + O(ε⁴) into 3 yields, at leading order, □w₀ = 0. Thus, we see that for very thin shells the far-field response to point indentation depends in a fundamental way on the geometry of the underlying shell (7, 10–12, 15), because the generalized d'Alembertian operator □ is elliptic for an ellipsoidal surface (with Gauss curvature R₁R₂ > 0), it is parabolic for a singly curved surface (with Gauss curvature R₁R₂ = 0), and it is hyperbolic for a saddle-shaped surface (the Gauss curvature R₁R₂ < 0). Of course, the complete solution is determined only when the exterior solution to 4 is matched with the interior solution to 2 in the neighborhood of the localized load and further matched with the boundary-layer solution that inevitably exists in the neighborhood of the curve of support (13, 14).

For a spherical cap shell that is clamped along its edge, the underlying positive Gauss curvature implies that the deformation is localized in the neighborhood of the indentation but decays isotropically away from it, and earlier results (12–14) show that once the sphere is weakly deformed near the localized load, it flattens before eventually becoming partly inverted. Even larger indentations lead to a faceting behavior of the spherical shell as seen when a plastic bottle is poked with a pen (Fig. 1A). For a cylinder that has zero Gauss curvature, the behavior under indentation loads is more complex and subtle owing to the anisotropy in initial curvature along and perpendicular to the principal axis. Previous work (16) has shown that both the location of the indentation and the nature of the boundary conditions are crucial in determining the cylindrical shell's response. For a long free cylinder that is pinched at an edge, the deformations persist over many diameters owing to the dominant role of nearly inextensible deformations. In contrast, for a cylinder that is clamped along its later edges, the deformation is strongly localized near the point of indentation, but decays anisotropically away from it, slowly along the axis but much more rapidly in the direction perpendicular to it, eventually leading to the formation of localized structures that themselves bifurcate (17). Finally, for a shell with negative Gauss curvature such as the inner part of a toroidal shell (15), the leading order solution is wave-like with characteristics making an angle ${\tan }^{-1}(\sqrt{R_1{R}_2})$ with the principal axes of the shell, so that the deformation is nonlocal and extends all of the way to the shell boundary or up to the intersection of the nodal lines of zero Gauss curvature with these characteristics. Indeed, for this last case, the indentation problem is the spatial analogue of the Cauchy initial-value problem for wave propagation, although there are important differences caused by the presence of boundary layers near the point of indentation and along the nodal lines.

Fig. 1.

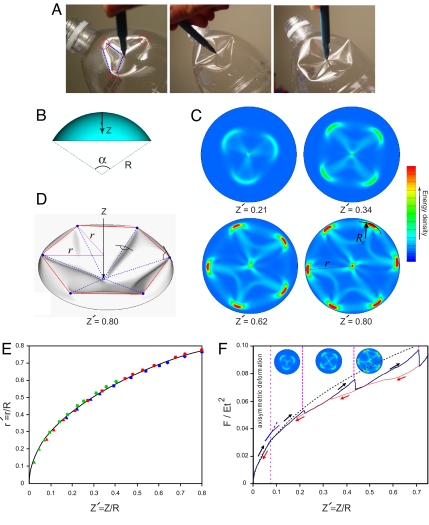
Indentation of a spherical cap. (A) Localization of deformation in a plastic bottle indented by a sharp pen. The deformation is localized approximately along a polyhedron with a triangular base (Left). As the indentation increases, one of the vertices bifurcates, leading to a polyhedral pattern with a square base (Center). Further indentation leads to further symmetry breaking (Right). (B) Schematic diagram of a clamped spherical cap with natural curvature R, indented at its center. (C) Elastic energy density in the elastic shell (t/R = 0.005) for various normalized indentations Z′ (see also Movie S1). The localization of deformation at the vertices is characterized by the localized region of radius R_c (see Fig. S1). (D) Typical deformed configuration of the elastic shell (t/R = 0.005 for a normalized indentation Z′ = Z/R = 0.8). The vertices lie approximately on a circle of r(Z). (E) The scaled radius r′ = r/R, versus the normalized center indentation, Z′. The solid line is given by 5, which for small indentations simplifies to $\mathrm{r\prime }\sim \sqrt{\mathrm{Z\prime }}$. The results from numerical simulations for different t/R (green: t/R = 0.001; red: t/R = 0.005; blue: t/R = 0.01), where filled triangles, squares, pentagons, and hexagons correspond to deformed configurations with 3, 4, 5, and 6 vertices, respectively. (F) Force–indentation response of an elastic shell with t/R = 0.005. Localization of deformation, which leads to formation of a pattern with three vertices, occurs at Z′ ∼ 0.076. The slopes of the response are shown at this indentation, which indicates ∼30% reduction in the apparent stiffness of the elastic shell as the asymmetric buckling pattern emerges, which is consistent with the analytical predictions (17, 18) as well as the approximate solution based on estimating the energy in the rim of the dimple. The dashed line is an approximate solution derived for axisymmetric deformations (14), and it compares qualitatively with the numerical simulations; however, as expected, it overestimates the forces relative to those for the faceted shell. All of the simulations were carried out for a cap with an opening angle α = 120°.

The above approximate analysis is valid only for small deformation because of the limitations posed by the asymptotic analysis of the linearized equations and cannot be easily extended to explain the rich behavior afforded by poking a plastic bottle with the point of a pen, as shown in Fig. 1A. This simple experiment shows that as the indentation displacement is increased, the bottle first deforms to form a circular dimple, which then loses symmetry to a polygonal shape with three vertices attached by ridges to each other as well as to the indentation point. Further indentation leads to the formation of additional vertices and ridges. To understand the formation of these faceted structures, we use detailed numerical simulations based on the finite element method. We restrict our material choice to that of an isotropic linear elastic material for two reasons: simplicity and generality. The computations were carried out by using ABAQUS (Dassault Systèmes), a commercial finite element package, with the following material parameter values: Young's modulus E = 1 GPa and Poisson ratio ν = 0.3. Four-node shell elements with reduced integration were used in all calculations. A single element spanned the thickness and no initial geometric or material imperfection was included in the computational model. To follow the postbuckling response of the structure, we used a stabilizing mechanism based on automatic addition of volume-proportional damping, which was decreased systematically to ensure that the response is insensitive to this change.

Our first numerical experiments explored the point indentation of a segment of a spherical shell with thickness t and natural curvature R (here we considered the range 0.0005 ≤ t/R ≤ 0.01) that is clamped at its boundary, shown in Fig. 1B. This simulation qualitatively mimics the simple experiment of indenting a plastic bottle shown in Fig. 1A. Because the spherical cap has positive Gauss curvature it responds initially by deforming axisymmetrically with an approximately linear force–indentation response (Fig. 1E), but once the deformation is of the order of the thickness of the shell, the response becomes nonlinear. Further indentation leads to the appearance of an axisymmetric dimple with a strongly localized region of deformation along a circular ridge, about which the cap is approximately mirror-symmetric relative to its original shape, so that this mode of deformation is sometimes termed mirror-buckling (13, 14). When the indentation is increased even farther, this dimpled axisymmetric mode loses stability to an asymmetric mode (17–19), which starts out with threefold symmetry and then through a series of transitions moves through polyhedral shapes with a varying number of vertices, as shown in Fig. 1C [see also supporting information (SI) Movie S1]. Each of these transitions is marked by the bifurcation of a single vertex defect into two, which then move apart just as when a cylindrical shell is indented along an edge (20).

Qualitatively, these faceted polyhedral forms arise because inextensible or almost-inextensible deformations are energetically preferred by the shell when the axisymmetric mirror-buckled form loses stability; a polyhedron involves stretching only in the neighborhood of a few points and lines rather than uniform deformations that would require stretching over large areas. The polyhedral shape can be approximated by a regular n-gonal pyramid with its polygon apex located at the indentation point (see Fig. 1D for n = 6). A simple geometrical argument for the position of the vertices follows by equating the length of a ridge that connects a vertex of the pyramid to its apex and the length of the corresponding spherical arc in the undeformed shape and yields

where Z′ = Z/R is the normalized indentation and r′ = r/R is the scaled radius of the circle on which the vertices lie. The expression 5 describes the results of our detailed simulations very well (Fig. 1E). In Fig. 1F, we show the force–displacement curve associated with increasing and decreasing indentation, along with a curve that corresponds to an analytical approximation assuming axisymmetric deformations (14).

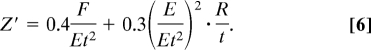The appearance of the asymmetric mode with three vertices is accompanied by a reduction in the apparent stiffness of the spherical cap, but is reversible with no hysteresis. In contrast, the appearance and disappearance of the modes with a larger number of vertices shows hysteresis, which here is due to the inherent geometric nonlinearity rather than any material nonlinearities, which are absent in our system. As in other hysteretic systems, the presence of heterogeneities is crucial in determining the system response; indeed, this is well known in elastic shell theory (21, 22). A closer look at the vertices shows that they are “rounded off”; this is due to the small but finite thickness of the shell, which leads to localized stretching and prevents divergent curvatures. Indeed, the balance between bending and local stretching yields a characteristic size of the vertices (see SI Text); however, the size of the vertices is only weakly dependent on their number and indentation amplitude, in contrast with observations of localized structures in naturally flat sheets such as developable cones (23, 24).

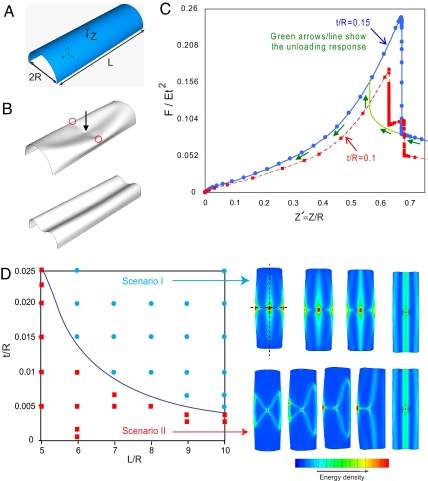
To contrast the behavior of spherical shells, which have positive Gauss curvature, with that of other curved shells, we now turn to the indentation of a segment of a cylindrical shell, which has zero Gauss curvature and is clamped along its lateral edges. Indenting the shell (length L, thickness t, radius R) shown in Fig. 2A at its center leads to the formation of two vertices; further indentation eventually leads to a final configuration that is a simple deformed developable surface (16). However, the intermediate configurations leading to the final developable state depend on the geometrical parameters L/R and t/R. We find two generic scenarios: (I) the shell never breaks symmetry in the span-wise or longitudinal directions of the cylinder; and (II) the shell breaks symmetry in both the span-wise and the longitudinal directions. A phase diagram characterizing the parameter regime for these scenarios is shown in Fig. 2C; shells with large t/R and L/R always follow scenario I, whereas those with small t/R and intermediate L/R follow scenario II. For shells with very small L/R the behavior is like that of a planar elastica, which also deforms symmetrically. In Fig. 2D, we show the detailed indentation response in each of these scenarios: in scenario I we see a single jump in the force when the cylinder snaps through to the final configuration, whereas in scenario II, we see multiple jumps corresponding to the different metastable states (which are dependent on t/R) that lie between the initial and final configurations. As one might expect, these transitions are also strongly hysteretic (Fig. 2C).

Fig. 2.

Indentation of a cylindrical shell. (A) Schematic of a semicylindrical shell with radius R and length L, clamped along the lateral edges with free ends. The ends of the shell are free to displace and rotate and the shell is indented at its center. (B) The deformed configuration of the shell (L/R = 6, t/R = 0.15) shows an abrupt transition from a complex deformation pattern to a simple planar deformation mode as the indentation is increased from Z′ = Z/R = 0.67 (Upper) to Z′ = 0.68 (Lower). (C) Force–indentation response of a semicylindrical elastic shell with L/R = 6. For the shell with t/R = 0.15, both loading and unloading responses are plotted, and are again hysteretic. (D) Two possible transition pathways from a semicylindrical shell to the final developable surface. The results are for shells with L/R = 6 and t/R = 0.15 (Upper Right) and t/R = 0.1 (Lower Right), the latter of which has been observed experimentally (16).

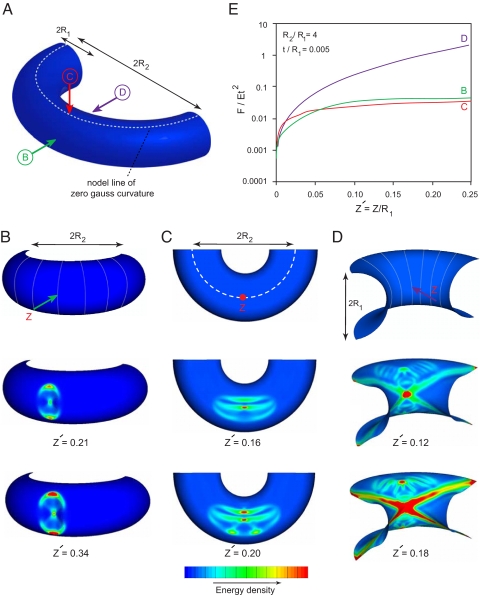
We finally turn to the case of the indentation of a segment of a toroidal shell clamped along its edges, as shown in Fig. 3A. This scenario is geometrically (and thus physically) interesting because the outer (inner) halves of toroidal shells have positive (negative) Gauss curvature, with two nodal lines of vanishing Gauss curvature that separate these regions. In Fig. 3B, we show the response of the toroidal shell as it is indented at a point along the line with positive Gauss curvature. The response qualitatively has the same features as the response of the spherical shell studied in Fig. 1. In Fig. 3C, we show the response of the shell when indented at a point on its nodal line of vanishing Gauss curvature. For small deformations, localized vertices form on either side of the nodal line. Increasing the indentation causes the deformation in the outer half of the shell, which has positive Gauss curvature, to remain localized, whereas in the inner part of the toroidal shell the deformation extends along a narrow zone all of the way to the two nodal lines of zero Gauss curvature along characteristics as suggested by our linearized analysis.

Fig. 3.

Indentation of a toroidal shell. (A) Schematic of a segment of a toroidal shell with radii R₁ and R₂. Three different parts of the shell are subject to point indentation. For all of the calculations, the shells with t/R₁ = 0.005, R₂/R₁ = 4 were clamped along the lateral edges. The other ends of the shells are free to displace and rotate. (B) Deformation caused by normal indentation of the outer surface, which has positive Gauss curvature. (C) Deformation caused by normal indentation along the nodal line, which has zero Gauss curvature. (D) Deformation caused by normal indentation of the inner surface, which has negative Gauss curvature. (E) Force–indentation response of the three shells under indentation. The inner part of the half-toroidal shell shows a much stiffer response under indentation compared with the other two shells, consistent with an extended region along which the deformation is felt. The normalized force is plotted on a logarithmic scale.

Our study shows that the mechanical behavior of naturally curved thin shell structures, which are soft by virtue of their geometry, is very rich. The indentation response of these objects generally leads to multifaceted multistable polyhedral structures, but the extent of these deformations depends on the underlying geometry of the surface. Our analysis has been restricted to purely elastic shells, i.e., systems where there are no irreversible effects. This is not as restrictive as might seem, because on small length scales, in polymersomes, nanotubes, virus shells, graphene sheets, and other thin shell structures inelastic effects are often relatively unimportant. Therefore, these symmetry-breaking elastic bifurcations that lead to polyhedral localized structures should be easily realizable in them. Furthermore, our studies might provide a stimulus to the design of mesoscopic structural materials with geometry-dominated responses that can serve as mechanical memories (using the geometrically determined multistability of the shape that the shells can take), exhibit long-range force transmission (using toroidal shells), and form the basis for surfaces with controllable frictional, wetting, and adhesion properties.