Hierarchical Bayesian Methods for Estimation of Parameters in a Longitudinal HIV Dynamic System

Summary

HIV dynamics studies have significantly contributed to the understanding of HIV infection and antiviral treatment strategies. But most studies are limited to short-term viral dynamics due to the difficulty of establishing a relationship of antiviral response with multiple treatment factors such as drug exposure and drug susceptibility during long-term treatment. In this article, a mechanism-based dynamic model is proposed for characterizing long-term viral dynamics with antiretroviral therapy, described by a set of nonlinear differential equations without closed-form solutions. In this model we directly incorporate drug concentration, adherence, and drug susceptibility into a function of treatment efficacy, defined as an inhibition rate of virus replication. We investigate a Bayesian approach under the framework of hierarchical Bayesian (mixed-effects) models for estimating unknown dynamic parameters. In particular, interest focuses on estimating individual dynamic parameters. The proposed methods not only help to alleviate the difficulty in parameter identifiability, but also flexibly deal with sparse and unbalanced longitudinal data from individual subjects. For illustration purposes, we present one simulation example to implement the proposed approach and apply the methodology to a data set from an AIDS clinical trial. The basic concept of the longitudinal HIV dynamic systems and the proposed methodologies are generally applicable to any other biomedical dynamic systems.

1. Introduction

Treatment of human immunodeficiency virus type 1 (HIV-1)-infected patients with highly active antiretroviral therapies (HAART), consisting of reverse transcriptase inhibitor (RTI) drugs and protease inhibitor (PI) drugs, results in several orders of magnitude of viral load reduction. The rapid decay in viral load can be observed in the relative short term (Perelson et al., 1997; Wu et al., 1998), and it either can be sustained or followed by a resurgence of virus within months (Nowak and May, 2000). The resurgence of virus may be caused by drug resistance, noncompliance, pharmacokinetics problems, and other factors during therapy. Mathematical models, describing the dynamics of HIV and its host cells, have been important in understanding the biological mechanisms of HIV infection, the pathogenesis of AIDS progression, and the role of clinical factors in antiviral activities.

Dynamic models have been introduced into various biomedical fields such as cancer (Goldie and Coldman, 1979) and AIDS. Many HIV dynamic models have been proposed by AIDS researchers (Perelson et al., 1996; Wu et al., 1998; Perelson and Nelson, 1999; Huang, Rosenkranz, and Wu, 2003) in the last decade to provide theoretical principles in guiding the development of treatment strategies for HIV-infected patients, and have been used to quantify short-term dynamics. Unfortunately, these models are of limited utility in interpreting long-term HIV dynamic data from clinical trials. The main reason is that many of the model parameters cannot be uniquely estimated from the viral load data. As a result, simplified and linearized models have often been used to characterize the viral dynamics based on the observed viral load data (Ho et al., 1995; Perelson et al., 1996; Perelson and Nelson, 1999). Although these models are useful and convenient to quantify short-term viral dynamics, they cannot characterize more complex long-term viral load trajectories. In this article, we utilize a set of relatively simplified models, which is a system of differential equations with time-varying coefficients, to characterize long-term viral dynamics. In our models we consider many factors related to the resurgence of viral load, such as pharmacokinetic properties, treatment compliance, and drug susceptibility. Thus our models are flexible to quantify long-term HIV dynamics.

Data from viral dynamic studies usually consist of repeated viral load measurements taken over time for each subject. Because the viral dynamic processes share certain similar patterns between patients while still having distinct individual characteristics, the hierarchical nonlinear mixed-effects (NLME) models appear to be reasonable for modeling HIV dynamics. The NLME model fitting can be implemented using standard statistical software, such as the function nlme() in S-plus and the procedure NLMIXED in SAS. In practice, the difficulty of using these standard packages in fitting NLME models arises when the closed form of the nonlinear function is not available. For example, our viral dynamics model is a system of nonlinear ordinary differential equations, which does not have a closed form. In this case the standard packages cannot be used directly, and we must rely on the numerical solution to fit the mixed-effects models.

Bayesian statistics has made great strides in recent years. For various models, including the hierarchical NLME, parameter estimation and statistical inference are carried out via the Markov chain Monte Carlo (MCMC) procedures (Gelfand et al., 1990; Wakefield, 1996). The MCMC methods were introduced in NLME models with applications in pharmacokinetic/pharmacodynamic (PK/PD) modeling in the mid-1990s (Wakefield, 1996; Lunn et al., 2002). Although a Bayesian analysis for a population HIV dynamic model was investigated by Han, Chaloner, and Perelson (2002) and Putter et al. (2002), they only used short-term viral load data to estimate the parameters, and they also assumed that the drug efficacy was constant over time.

We combine a Bayesian approach with mixed-effects modeling techniques to estimate both population and individual dynamic parameters under a framework of the hierarchical Bayesian nonlinear (mixed-effects) model. The advantages of the proposed approach include: (i) we model the population viral dynamics and the within-subject and between-subject variations via a hierarchical model framework; (ii) our models are flexible in dealing with both sparse and unbalanced longitudinal data from individual subjects by borrowing information from all subjects; (iii) the MCMC methods can be easily employed for computation, and thus closed-form solutions to the model (a system of nonlinear differential equations with time-varying coefficients) are not required; and (iv) because the posterior distributions for the unknown parameters can be obtained, it is easy to conduct statistical inferences.

This article is organized as follows. We introduce the HIV dynamic system and propose a simplified viral dynamic model with time-varying drug efficacy, which incorporates the effects of PK variation, drug resistance, and adherence in Section 2. A Bayesian approach implemented using MCMC techniques is employed to estimate dynamic parameters in Section 3. The simulation study is used to illustrate our methodologies in Section 4. The data for pharmacokinetics, drug resistance, and adherence as well as the viral load data from an AIDS clinical trial are described and the proposed methodology is applied to estimate the dynamic parameters in Section 5. Finally, the article is concluded with some discussions in Section 6.

2. The Models for Long-Term HIV Dynamics

2.1 Antiviral Drug Efficacy Model

Recent treatment strategies usually include genotype or phenotype testing in order to determine an individual’s susceptibility to antiretroviral agents before a treatment regimen is selected. Here we use the phenotype marker IC₅₀ (Molla et al., 1996), which represents the drug concentration necessary to inhibit viral replication by 50%, to quantify agent-specific drug sensitivity. Herein, we refer to this quantity as the median inhibitory concentration. To model the within-host changes over time in IC₅₀ due to the emergence of new drug-resistant mutations, we used the following function (Huang et al., 2003)

$$I{C}_{50}(t)=\{\begin{array}{cc}{I}_0+\frac{I_r-I_0}{t_r}t& \text{for\hspace{0.17em}}0<t<t_r,\\ I_r& \text{for\hspace{0.17em}}t\ge t_r,\end{array}$$ (1)

where I₀ and I_r are respective values of IC₅₀(t) at baseline and time point t_r . In clinical studies, such as the one to be introduced in Section 5, it is common to measure IC₅₀ values only at baseline and failure time (Molla et al., 1996). Thus this simplified function of IC₅₀(t) may serve as a good approximation.

Poor adherence to a treatment regimen is one of the major causes for treatment failure (Besch, 1995). Patients may occasionally miss doses for various reasons. The deviation from prescribed dosing affects drug exposure in predictable ways. For a time interval T_k < t ≤ T_k+1, the effect of adherence can be defined as follows.

$$A(t)=\{\begin{array}{cc}1& \text{if\hspace{0.17em}all}\hspace{0.17em}\text{doses\hspace{0.17em}are\hspace{0.17em}taken\hspace{0.17em}in\hspace{0.17em}}(T_k,T_{k+1}],\\ R_k& \text{if\hspace{0.17em}}100R_k\%\hspace{0.17em}\text{doses\hspace{0.17em}are\hspace{0.17em}taken\hspace{0.17em}in\hspace{0.17em}}(T_k,T_{k+1}],\end{array}$$ (2)

where 0 ≤ R_k < 1 with R_k indicating the adherence rate for drugs. T_k denotes the adherence evaluation time at the kth clinical visit.

In recent years, antiretroviral drugs have been developed rapidly. In most previous viral dynamic studies, investigators assumed that either drug efficacy was constant over treatment time (Perelson and Nelson, 1999; Ding and Wu, 2001) or drugs had perfect effect in blocking viral replication (Ho et al., 1995; Perelson et al., 1997; Putter et al., 2002). However, the drug efficacy may change as concentrations of antiretroviral drugs and other factors (e.g., drug resistance) vary during treatment (Perelson and Nelson, 1999), and thus the drugs may not be perfectly effective. To model the relationship of drug exposure and resistance with antiviral efficacy, we employ the following modified E_max model (Huang et al., 2003) to represent the time-varying drug efficacy for two antiretroviral agents within a class (e.g., the two PI drugs IDV and RTV in our clinical study introduced in Section 5),

$$\gamma (t)=\frac{I{Q}_1(t)A_1(t)+I{Q}_2(t)A_2(t)}{\phi +I{Q}_1(t)A_1(t)+I{Q}_2(t)A_2(t)},$$ (3)

where $I{Q}_i(t)=C_{12h}^i/I{C}_{50}^i(t)$ (i = 1, 2) denotes the inhibitory quotient (IQ) (Hsu et al., 2000); $C_{12h}^i$ and $I{C}_{50}^i$ (i = 1, 2) are the trough levels of drug concentration in plasma (measured after 12 hours from doses taken) and the median inhibitory concentrations for the two agents, respectively. Note that C_12h could be replaced by other PK parameters such as the area under the plasma concentration-time curve (AUC). Although IC₅₀(t) can be measured by phenotype assays in vitro, it may not be equivalent to the IC₅₀(t) in vivo. Parameter f is used to quantify the conversion between in vitro and in vivo IC₅₀ that can be estimated from clinical data. γ(t) ranges from 0 to 1. If γ(t) = 1, the drug is 100% effective, whereas if γ(t) = 0, the drug has no effect. Note that, if $C_{12h}^i$, A_i (t), and $I{C}_{50}^i(t)$ are measured from a clinical study and φ can be estimated from clinical data, then drug efficacy γ(t) can be estimated during the course of antiretroviral treatment. Similarly, we can model the combined drug efficacy of HAART regimen with both PI and RTI agents.

2.2 HIV Dynamic Model

Basic models of viral dynamics describe the interaction between cells susceptible to infection (target cells), infected cells, and free virus. The mathematical details of this model have been presented elsewhere (Nowak and May, 2000). In practice, we will need to make a trade-off between the model’s complexity and the identifiability of parameters based on available measurements from clinical trials. If a model has too many components, it may be difficult to analyze; many of the variables in the model may not be measurable and parameters may not be identifiable. If a model is too simple, the model parameters can be identified and estimated; however, some important clinical factors, such as pharmacokinetics, drug adherence and resistance, and other biological mechanisms of HIV infection, cannot be incorporated. In order to consider clinical factors and biological mechanisms of HIV infection, and to flexibly address data analysis and parameter identifiability issues, we propose an extended antiviral response model. Although our model includes the interaction of target uninfected cells (T), infected cells that actively produce viruses (T*), and free virus (V ), it differs from previous developed models in that it includes a time-varying parameter γ(t), which quantifies the antiviral drug efficacy. The model is expressed in terms of the following system of differential equations under the effect of an antiretroviral treatment

$$\begin{array}{l}\frac{d}{dt}T=\lambda -\rho T-[1-\gamma (t)]kTV,\\ \frac{d}{dt}{T}^{\ast }=[1-\gamma (t)]kTV-\delta T^{\ast },\\ \frac{d}{dt}V=N\delta T^{\ast }-cV,\end{array}$$ (4)

where λ represents the rate at which new T cells are created from sources within the body, such as the thymus, ρ is the death rate of T cells, k is the infection rate of T cells infected by virus, δ is the death rate for infected cells, N is the number of new virions produced from each of the infected cells during their lifetime, and c is the clearance rate of free virions. The time-varying parameter γ(t) denotes the antiviral drug efficacy as defined in the formula (3). If the regimen is not 100% effective (not perfect inhibition), the system of ordinary differential equations cannot be solved analytically. The solutions to equation (4) then have to be evaluated numerically. Let β = (φ, c, δ, λ, ρ, N, k)^T denote a vector of parameters, and log₁₀V_ij (β, t) denote the common logarithm of the numerical solution of V(t) for the ith individual at time t_j , which is the viral load measured in plasma and will be used for parameter estimation.

As shown by Huang et al. (2003), if γ(t) > e_c (e_c = 1 − cρ/kN λ is a threshold of drug efficacy) for all t, virus will be eventually eradicated. Otherwise, viral load may rebound before the viral eradication (due to drug resistance, for example). Thus, the efficacy threshold e_c may reflect the ability of a patient’s immune system to control viral replication, and it is important to estimate e_c for each patient based on the clinical data.

3. Bayesian Approach for Parameter Estimation

In order to apply the proposed mathematical models to study long-term HIV dynamics and model viral responses, we need to resolve two important statistical problems: (i) how to estimate the unknown parameters in HIV dynamic models and (ii) how to conduct inference and handle the identifiability issue of model parameters. It is challenging to resolve these problems for a system of nonlinear differential equations with time-varying parameters, because there is no closed-form solution, and there are too many unknown parameters. In addition, among the components involved in viral dynamics we usually only have viral load data, whereas the CD4⁺ T cell count data are considered too noisy to be used in dynamic parameter estimation. It is possible that we may not be able to identify all the unknown parameters in model (4). To deal with the identifiability problem of parameter estimation, mathematicians usually substitute some of the unknown parameters with their estimates from previous studies (Perelson et al., 1997). Here we investigate a Bayesian approach to tackle this difficulty. In Bayesian terminology, the information from previous studies is regarded as prior knowledge, which is combined with clinical data to perform the statistical inference on unknown parameters. A detailed description of the methodology is given below.

3.1 Hierarchical Bayesian Modeling Approach

Under the longitudinal dynamic system framework, the hierarchical Bayesian approach can be used to incorporate a prior at the population level to estimate the dynamic parameters. We denote the number of subjects by n and the number of measurements on the ith subject by m_i. For notational convenience, let μ = (log φ, log c, log δ, log λ, log ρ, log N, log k)^T, θ_i = (log φ_i, log c_i , log δ_i, log λ_i, log ρ_i, log N_i , log k_i )^T , Θ = {θ_i, i = 1, …, n}, Θ_{i} = {θ_l, l ≠ i}, and Y = {y_ij, i = 1, …, n; j = 1, …, m_i}. Let f_ij (θ_i, t_j) = log₁₀V_ij(θ_i, t_j), where V_ij(θ_i, t_j) denotes the numerical solution of V(t) in the differential equation (4) for the ith subject at time t_j.y_ij (t_j) and e_i(t_j) denote the repeated measurements of common logarithmic viral load and measurement error with mean zero for the ith subject at times t_j (j = 1, 2, …, m_i), respectively. Note that the log transformation of dynamic parameters and viral load is used to ensure positive estimates of dynamic parameters and to help stabilize the variance, respectively. Then the Bayesian nonlinear mixed-effects (BNLME) model can be written as the following three stages (Davidian and Giltinan, 1995).

Stage 1

Within-subject variation: y_i = f_i(θ_i) + e_i, [e_i ∣ σ², θ_i] ~ 𝒩 (0, σ²Im_i), where y_i = (y_i1(t₁), …, y_imi(t_mi))^T, f_i(θ_i) = (f_i1(θ_i, t₁), …, f_imi (θ_i, t_mi))^T, e_i = (e_i(t₁), …, e_i(t_mi))^T, and the bracket notation [A ∣ B] denotes the conditional distribution of A given B.

Stage 2

Between-subject variation: θ_i = μ + b_i, [b_i ∣ Σ] ~ 𝒩 (0, Σ).

Stage 3

Hyper-prior distributions: σ⁻² ~ Ga(a, b), μ ~ 𝒩 (η, Λ), Σ⁻¹ ~ Wi(Ω, ν), where the mutually independent Gamma (Ga), Normal (𝒩), and Wishart (Wi) prior distributions are chosen to facilitate computations (Gelfand et al., 1990; Davidian and Giltinan, 1995). Note that the parameterization of the Gamma and Wishart distributions is such that Ga(a, b) has mean ab and Wi(Ω, ν) has mean matrix νΩ. The hyper-parameters a, b, η, Λ, Ω, and ν are known.

Following the studies in Davidian and Giltinan (1995) and Gelfand et al. (1990), it is shown from the BNLME model that the full conditional distributions for the parameters σ⁻², μ, and Σ⁻¹ can be written explicitly as

$$\begin{array}{l}[{\sigma }^{-2}\mid \mathit{\mu },{\mathbf{\Sigma }}^{-1},\mathbf{\Theta },\mathbf{Y}]\sim Ga\left(a+\frac{{\mathrm{\Sigma }}_{i=1}^n{m}_i}{2},{\mathit{A}}^{-1}\right),\\ [\mathit{\mu }\mid {\sigma }^{-2},{\mathbf{\Sigma }}^{-1},\mathbf{\Theta },\mathbf{Y}]\sim \mathcal{N}({\mathit{B}}^{-1}\mathit{C},{\mathit{B}}^{-1}),\\ [{\mathbf{\Sigma }}^{-1}\mid {\sigma }^{-2},\mathit{\mu },\mathbf{\Theta },\mathbf{Y}]\sim Wi({\mathit{D}}^{-1},n+\nu ),\end{array}$$ (5)

where $\mathit{A}=b^{-1}+\frac{1}{2}{\mathrm{\Sigma }}_{i=1}^n{\mathrm{\Sigma }}_{j=1}^{m_i}{[y_{ij}-f_{ij}({\mathit{\theta }}_i,t_j)]}^2$, B = nΣ⁻¹ + Λ⁻¹, $\mathit{C}={\mathbf{\Sigma }}^{-1}{\mathrm{\Sigma }}_{i=1}^n{\mathit{\theta }}_i+{\mathbf{\Lambda }}^{-1}\mathit{\eta }$, and $\mathit{D}={\mathbf{\Omega }}^{-1}+{\mathrm{\Sigma }}_{i=1}^n({\mathit{\theta }}_i-\mathit{\mu })\times {({\mathit{\theta }}_i-\mathit{\mu })}^T$. The full conditional distribution of each θ_i, given the remaining parameters and the data, cannot be written explicitly, but it can be seen that the density function of the conditional distribution of [θ_i ∣ σ⁻², μ, Σ⁻¹, Θ_{i}, Y] is proportional to

$$\begin{array}{l}exp\{\frac{-{\sigma }^{-2}}{2}{\mathrm{\Sigma }}_{j=1}^{m_i}{[y_{ij}-f_{ij}({\mathit{\theta }}_i,t_j)]}^2\\ -\frac{1}{2}{({\mathit{\theta }}_i-\mathit{\mu })}^T{\mathbf{\Sigma }}^{-1}({\mathit{\theta }}_i-\mathit{\mu })\}.\end{array}$$ (6)

3.2 MCMC Implementation

To carry out the Bayesian inference, we need to specify the values of the hyper-parameters in the prior distributions. In the Bayesian approach, we only need to specify the priors at the population level, which are easy to obtain from previous studies or reference literature and usually are accurate and reliable.

In principle, if we have reliable prior information for some of the parameters, then strong priors with small variances may be used for these parameters. For other parameters such as φ, where not enough prior information is available and where we intend to use the available clinical data to determine them, then a noninformative prior with a large variance may be given for these parameters. Generally, one usually chooses noninformative prior distributions for the parameters of interest (Carlin and Louis, 1996).

After we specify the model for the observed data and the prior distributions for the unknown parameters, we can draw statistical inference for the unknown parameters based on their posterior distributions. In the above Bayesian modeling approach, evaluation of the required posterior distributions in a closed-form solution is prohibitive. However, as indicated in Section 3.1, it is relatively straightforward to derive either full conditional distributions for some parameters or explicit expressions, which are proportional to the corresponding full conditional distributions for other parameters.

Under the Bayesian framework, MCMC methods enable us to draw samples from the target distributions of interest or the posterior distributions of unknown parameters. In this article we combine both the Gibbs sampler and the Metropolis–Hastings (M–H) algorithm to carry out the MCMC procedure. See Gelfand et al. (1990) and Lunn et al. (2002) for more detailed discussion of these specific MCMC algorithms. In our approach, the Gibbs sampling steps update σ⁻², μ, and Σ⁻¹, while the M–H algorithm updates θ_i, i = 1, …, n. After collecting the final MCMC samples, we are able to draw statistical inference for the unknown parameters. In particular, we are interested in the posterior means and quantiles.

To implement the M–H algorithm, it is necessary to specify a suitable proposal density. Several possible proposal density choices are discussed in the literature, and a popular choice is the multivariate normal distribution, which results in the random-walk M–H algorithm (Roberts, 1996). In our implementation, the proposal density is chosen to be a multivariate normal distribution centered at the current value of θ_i, as it can be easily sampled and is symmetric (Roberts, 1996; Wakefield, 1996). An important issue regarding the random-walk M–H algorithm is the choice of the dispersion of the proposal density. If the variance of the proposed density is too large, then a large proportion of proposed moves will be rejected, and the Markov chain will, therefore, produce many repeats and will result in inefficiency of the algorithm. On the other hand, if the variance of the proposed density is too small, then the chain will have a high acceptance rate but will move around the parameter space slowly, again leading to inefficiency (Carlin and Louis, 1996; Roberts, 1996). We consider this issue in the MCMC implementation.

As suggested in Carlin and Louis (1996), one long run may be more efficient when considering the following two points: (i) a number of initial “burn-in” simulations are discarded and (ii) one may only save every kth (k being an integer) simulation samples to reduce the dependence among samples used for parameter estimation. We use this strategy in our MCMC implementation. See Huang, Liu, and Wu (2004) for the details of the iterative MCMC algorithm including discussions of selecting the proposal density and other issues.

When the MCMC implementation is applied to the simulation study data and the actual clinical data, an informal check of convergence is conducted based on graphical techniques according to the suggestion of Gelfand and Smith (1990). An example of the graphical results will be displayed in Section 4. Based on the results, we propose that, after an initial number of 30,000 burn-in iterations, every fifth MCMC sample was retained from the next 120,000 samples. Thus, we obtained 24,000 samples of targeted posterior distributions of the unknown parameters.

4. Simulation Study

In this section, we present one simulated numerical example to illustrate the introduced Bayesian approach. The scenario we consider is as follows. We simulate a clinical trial with 20 HIV-infected patients receiving long-term antiviral treatment. For each patient, we assume that measurements of viral load are taken at 25 time points ranging from day 0 to day 200 of follow-up. The design of this experiment is similar to an actual AIDS clinical trial that we will describe in detail.

A potential advantage of a Bayesian analysis over a likelihood method is that if an informative prior is available, then Bayesian inferences can be obtained despite the fact that a model is not identifiable from the perspective of the likelihood (Rannala, 2002). Based on this consideration, we designed the following example to illustrate our approach in order to handle the problems of parameter identifiability. In our model, it can be shown that the two parameters log c and log δ can be identified (see Figure 1(a)) if we assume that the other five parameters (log φ, log λ, log ρ, log N, log k) are constant. Because the classic methods of identifiability (Audoly et al., 2001) for a system of nonlinear differential equations cannot be used, and the exact identifiability checks for nonlinear differential equation models are unfortunately not available (Audoly et al., 2001), an informal check of parameter identifiability based on graphical techniques can be used by studying samples drawn from the MCMC sampling scheme for each parameter. We can check the k-lag serial correlation of the samples for each parameter. If the model is unidentifiable and the prior distribution is not informative, the k-lag serial correlation tends to be large even for a large k. In this case, the trace plot usually lacks randomness, that is, the consecutive samples move toward one direction. In practice, one can use these facts to check the identifiability of parameters by carefully studying the samples drawn from the MCMC scheme (Gelfand and Sahu, 1999). The sampling-based series correlation check can not only detect the possible unidentifiability, but can also shed some light on the relationship among unidentifiable parameters. We thus designed a simulation experiment to only estimate the two parameters log c and log δ that are identifiable in our model, and assume that the other five parameters are given as constants whose values are (log φ, log λ, log ρ, log N, log k) = (2.5, 4.6, −2.3, 6.9, −11.0). These values were chosen from previous studies in the literature (Perelson and Nelson, 1999; Nowak and May, 2000; Ding and Wu, 2001). Based on the discussion in Section 3.2, the prior distribution for μ = (log c, log δ)^T was assumed to be $\mathcal{N}(\mathit{\eta },\mathbf{\Lambda })$ with Λ being a diagonal matrix. The details of the prior construction for unknown parameters are discussed in Huang et al. (2004). Thus, the values of hyper-parameters are chosen as follows

Figure 1.

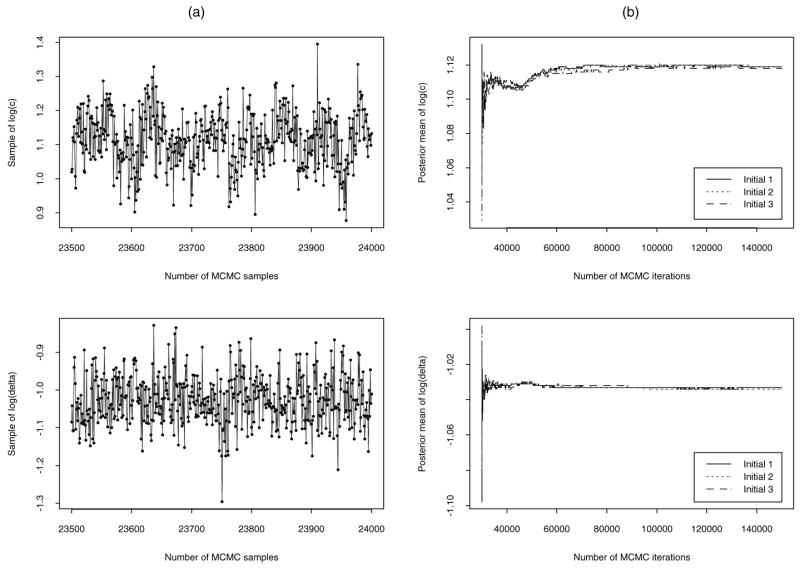
(a) Trace plot to informally check parameter identifiability based on the last 500 samples drawn from the MCMC sampling scheme (left panels). (b) Convergence diagnostics with respect to three different initial values (right panels) in simulation example.

$$\begin{array}{l}a=4.5,\hspace{0.17em}b=9.0,\hspace{0.17em}\nu =5.0,\eta ={(1.1,-1.0)}^T,\\ \mathbf{\Lambda }=\text{diag}(1000,\hspace{0.17em}1000),\mathbf{\Omega }=\text{diag}(2.5,\hspace{0.17em}2.5).\end{array}$$

Note that the noninformative priors are chosen for both log c and log δ. The values of the hyper-parameters were determined based on several studies in the literature (Perelson et al., 1996; Han et al., 2002). In addition, the data for the pharmacokinetic factor (C_12h), phenotype marker (baseline and failure IC₅₀’s), adherence, and the baseline viral load (V₀) were taken from an AIDS clinical trial study (Section 5). The true individual dynamic parameters, log c_i and log δ_i, are generated by log c_i = log c + b_1i and log δ_i = log δ + b_2i, where log c = 1.1 and log δ = −1.0 are the true values of population parameters, and both b_1i and b_2i are random effects following a normal distribution with mean 0 and standard deviation of 0.2.

Based on generated true parameters, known parameters, and data (C_12h, IC₅₀, and A(t)), the observations y_ij (the common logarithm of total viral load) are generated by perturbing the solution of the differential equation (4) with a within-subject measurement error, that is, y_ij = log₁₀V_ij + e_i , where V_ij is the numerical solution of viral load to the differential equation (4) for the ith subject at time t_j . It is assumed that the within-subject measurement error e_i is normally distributed with $\mathcal{N}$(0, 0.15²).

We apply the introduced Bayesian approach to estimate the dynamic parameters via implementing the MCMC procedure using FORTRAN code that calls a differential equation subroutine solver (DIVPRK) in IMSL Math/Library (1994), which uses the Runge–Kutta–Verner fifth-order method. As discussed previously, the graphical check of the parameter identifiability, based on the last 500 samples drawn from MCMC sampling scheme for both parameters log c and log δ, is presented in Figure 1(a). It can be seen that the consecutive samples move randomly toward different directions, which indicates that the MCMC sampler is not “sticky” and the two parameters are regarded as identifiable.

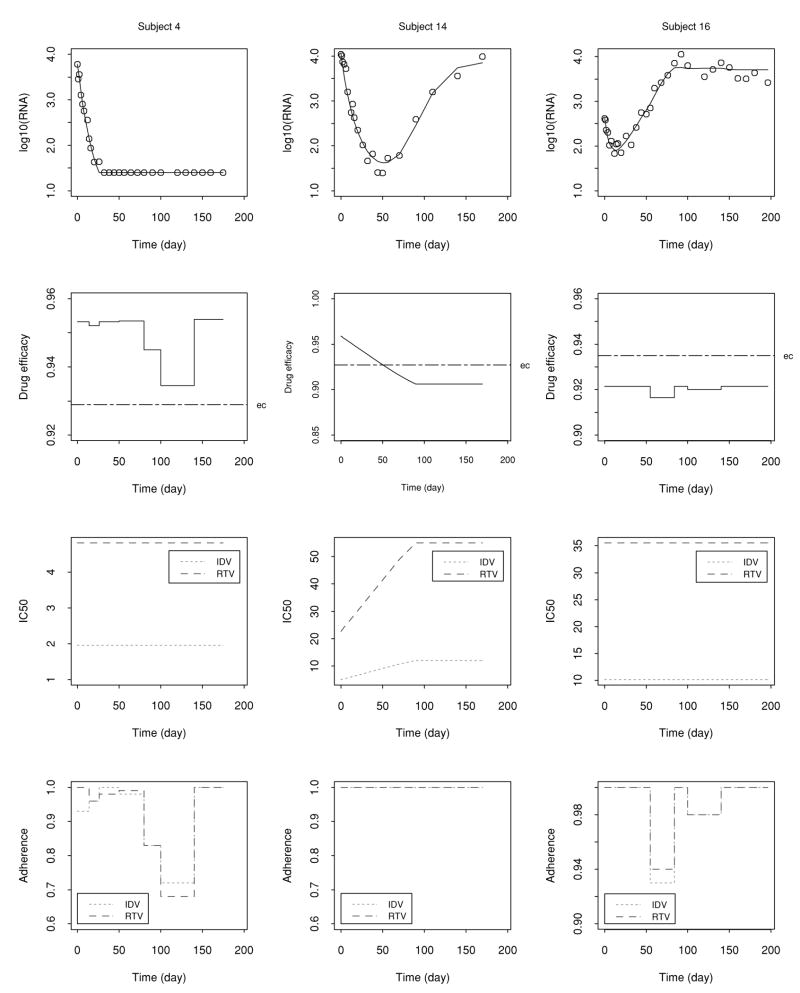
Figure 2 displays the three representative individual fitted curves with generated viral load data on log₁₀ scale, the estimated drug efficacy $(\widehat{\gamma }(t))$ with threshold (e_c), as well as observed IC₅₀(t) and adherence of the two PI drugs. It can be seen that the models provide a good fit to the generated data. Notably, by comparing the plots of fitted curves and estimated drug efficacy $\widehat{\gamma }(t)$, it can be seen that if $\widehat{\gamma }(t)$ falls below the threshold e_c, viral load rebounds, and in contrast, if $\widehat{\gamma }(t)$ is above e_c, the corresponding viral load does not rebound, which is consistent with our theoretical analysis of the dynamic models (Huang et al., 2003). It is also important that we can estimate the threshold of the drug efficacy (e_c). The efficacy threshold may represent how well the immune system of a patient can control viral replication. Thus, the efficacy threshold (e_c) is important for individual patients.

Figure 2.

Individual fitted curves with generated viral load data in log₁₀ scale, drug efficacy with threshold (e_c), as well as IC₅₀(t) and adherence of the two PI drugs (IDV and RTV) for the three representative subjects from the simulation example.

In Table 1, we summarize the generated true values of parameters (log c and log δ) and the mean estimates with 40 replications for the 20 subjects, as well as the corresponding bias, which is the difference between the mean estimate and the true value of parameters, and the standard error (SE), defined as the square root of mean squared error. The percentage is based on the absolute value of the true parameter. It can be seen from Table 1 that both the bias and SE for population parameter estimates are very small. For individual parameter estimates, the bias is also small, ranging from 0.001 to 0.243, and the SE (%) ranges from 0.6 to 25.7.

Table 1.

The true values and mean estimates of population (Pop) and individual dynamic parameters with 40 replications as well as the corresponding bias and standard error (SE), defined as the square root of mean squared error. The percentage of SE is based on the absolute value of the true parameter.

	True value		Mean estimate		Bias		SE (%)
	log c	log δ	log c	log δ	log c	log δ	log c	log δ
Pop	1.100	−1.000	1.107	−1.006	0.007	−0.006	3.02	3.00
Sub1	0.658	−0.778	0.684	−0.767	0.026	0.011	17.1	21.6
Sub2	0.851	−1.216	0.865	−1.125	0.014	0.091	22.4	22.3
Sub3	1.287	−0.833	1.153	−0.778	−0.134	0.055	12.8	9.6
Sub4	1.244	−0.875	1.303	−0.922	0.059	−0.047	10.4	17.0
Sub5	1.004	−0.704	1.206	−0.890	0.202	−0.186	27.1	12.0
Sub6	1.046	−1.095	1.056	−1.077	0.010	0.018	4.8	10.1
Sub7	1.032	−1.173	1.144	−1.117	0.112	0.056	12.6	19.2
Sub8	1.038	−1.332	1.126	−1.397	0.088	−0.065	19.9	15.0
Sub9	1.534	−0.848	1.523	−0.806	−0.011	0.042	2.3	34.5
Sub10	1.073	−1.037	1.077	−1.040	0.004	−0.003	4.7	25.7
Sub11	1.295	−1.080	1.152	−0.997	−0.143	0.083	13.4	14.1
Sub12	1.064	−1.101	1.115	−1.127	0.051	−0.026	7.2	10.5
Sub13	1.048	−0.928	1.054	−1.008	0.006	−0.080	6.1	17.8
Sub14	1.35	−0.934	1.352	−0.935	0.002	−0.001	0.6	6.3
Sub15	1.201	−1.101	1.197	−1.078	−0.004	0.023	7.5	15.4
Sub16	1.235	−0.855	1.230	−0.908	−0.005	−0.053	1.4	17.5
Sub17	0.853	−1.135	1.096	−1.210	0.243	−0.075	20.7	18.3
Sub18	1.024	−1.251	1.042	−1.131	0.018	0.120	6.3	18.4
Sub19	1.196	−0.962	1.144	−0.930	−0.052	0.032	7.6	16.9
Sub20	1.171	−0.834	1.165	−0.899	−0.006	−0.065	2.1	20.0

A common concern with Bayesian methods is their dependence on various aspects of the modeling process. Possible sources of uncertainty include the prior distributions and the initial values. The basic tool for investigating model uncertainty is the sensitivity analysis. That is, we simply make reasonable modifications to the assumptions in question, recompute the posterior quantities of interest, and see whether they have changed in a way that significantly affects the resulting interpretations or conclusions. If the results are robust against the suspected assumptions, we can report the results with confidence and our conclusions will be solid. However, if the results are sensitive to the assumptions, we choose to communicate the sensitivity results and interpret the results with caution (Carlin and Louis, 1996). In order to examine the dependence of dynamic parameter estimates on the prior distributions and initial values, we carried out a sensitivity analysis. As an example, we followed the method proposed by Raftery and Lewis (1992) to implement the MCMC sampling scheme and monitor several independent MCMC runs, starting from different initial values. Those runs exhibited similar and stable behavior. An informal check of convergence diagnostics based on graphical techniques suggested by Gelfand and Smith (1990) was investigated. As an example, the number of MCMC iterations and convergence with regard to three different initial values are displayed in Figure 1(b). We summarize the sensitivity analysis results as follows: (i) The estimated dynamic parameters were not sensitive to the priors and/or the initial values, and the results were reasonable and robust. (ii) When different priors and/or different initial values were used, the results were similar to those presented in Figure 2 and Table 1.

5. Application to an AIDS Clinical Trial Study

We apply the proposed methodology to the data from an AIDS clinical trial study. This study was a Phase I/II, randomized, open-label, 24-week comparative study of the PK, tolerability, and antiretroviral effects of two regimens of IDV and RTV on HIV-1-infected subjects failing PI-containing antiretroviral therapies (Acosta et al., 2004). The 44 subjects were randomly assigned to two treatments: Arm A (IDV 800 mg q12h + RTV 200 mg q12h) and Arm B (IDV 400 mg q12h + RTV 400 mg q12h). Out of the 44 subjects, 42 subjects are included in the analysis; the remaining two subjects were excluded from the analysis because the PK and IC₅₀ data were not obtained. Plasma HIV-1 RNA (viral load) measurements were taken at days 0, 7, 14, 28, 56, 84, 112, 140, and 168 of follow-up. The study data for PK parameters (C_12h), phenotype marker (baseline and failure IC₅₀’s), and adherence were also used in our modeling. Adherence was determined by pill count data. A more detailed description of this study can be found in Acosta et al. (2004).

Similar to the simulation example, the prior distribution for μ = (log φ, log c, log δ, log λ, log ρ, log N, log k)^T is assumed to be $\mathcal{N}(\mathbf{\eta },\mathbf{\Lambda })$ with Λ being a diagonal matrix. We chose the values of the hyper-parameters (Perelson et al., 1996; Nowak and May, 2000; Ding and Wu, 2001; Han et al., 2002) as follows:

$$\begin{array}{l}a=4.5,\hspace{0.17em}b=9.0,\hspace{0.17em}\nu =8.0,\\ \mathbf{\Lambda }=\text{diag}(1000.0,\hspace{0.17em}0.0025,\hspace{0.17em}0.0025,\hspace{0.17em}0.0025,\hspace{0.17em}0.0025,\hspace{0.17em}0.0025,\hspace{0.17em}0.001),\\ \mathit{\eta }={(2.5,\hspace{0.17em}1.1,\hspace{0.17em}-1.0,\hspace{0.17em}4.6,\hspace{0.17em}-2.5,\hspace{0.17em}6.9,\hspace{0.17em}-11.0)}^T,\\ \mathbf{\Omega }=\text{diag}(1.25,\hspace{0.17em}2.5,\hspace{0.17em}2.5,\hspace{0.17em}2.0,\hspace{0.17em}2.0,\hspace{0.17em}2.0,\hspace{0.17em}2.0).\end{array}$$

The MCMC techniques consisting of a series of Gibbs sampling and M–H algorithms were used to obtain the results as presented in Huang et al. (2004). We found that the model provided a good fit to the observed data for most of the subjects. In terms of the dynamic parameter estimates, a large between-subject variation in the estimates of all individual dynamic parameters was observed (data not shown here). The population posterior means and the corresponding 95% equal-tail credible intervals for the seven parameters are summarized in Table 2. As shown, the population estimates are 3.06 and 0.37 for c and δ, respectively, which are the most important parameters in understanding viral dynamics. In comparison with previous studies, our population estimate of c (3.06) is almost equal to the mean estimate of c, 3.07 in Perelson et al. (1996), and our population estimate of δ is consistent with the mean value of δ, 0.37 in Klenerman et al. (1996). However, our population estimate of c is slightly less than the mean estimate of c, 3.1 in Perelson and Nelson (1999) and is greater than the population estimate of c, 2.81 obtained by Han et al. (2002). On the other hand, our population estimate of δ (0.37) is less than the first-phase decay rate of 0.43 (Nowak and May, 2000), 0.49 (Perelson et al., 1996), and 0.5 (Perelson and Nelson, 1999). In addition, in two separate studies by Markowitz et al. (2003) and Perelson et al. (1997), the mean values of 1.0 and 0.7 for δ were obtained by holding the clearance rate c as constant with values of 23 and 3, respectively, and these two values are substantially greater than our population estimate of 0.37 for δ. These differences may be due to various reasons. For example, the analysis of those studies assumed that viral replication was completely stopped by the treatment, and/or they used short-term viral load data to fit their models. In addition, the first-phase decay rate, estimated from a biexponential viral dynamic model (Ho et al., 1995; Perelson et al., 1996; Ding and Wu, 2001) under perfect treatment assumption, is not the true death rate of infected cells (δ) because the current antiretroviral therapy cannot completely block viral replication (Perelson and Nelson, 1999). In this study, we estimated the death rate of infected cells (δ) directly by accounting for the nonperfect treatment with time-varying drug efficacy. Note that we are unable to validate our results of the other parameter estimates, as no conclusive or comparable estimates have been published to date.

Table 2.

A summary of the estimated posterior means (PM) of population parameters and the corresponding 95% equal-tail credible intervals, where L_CI and R_CI denote the left and right credible limits of 95% credible intervals

	φ	c	δ	λ	ρ	N	k
PM	24.9	3.06	0.37	98.1	0.081	975.6	0.000017
LCI	10.6	2.79	0.33	89.1	0.073	886.3	0.000016
RCI	57.7	3.37	0.41	107.9	0.089	1074.2	0.000018

6. Discussion

In this article, we proposed a concept of longitudinal dynamic system, in particular for modeling HIV dynamics. Our models are simplified with the main goals of retaining crucial features of HIV-1 dynamics and, at the same time, guaranteeing their applicability to typical clinical data, in particular long-term viral load measurements. We investigated a hierarchical Bayesian (mixed-effects) modeling approach to estimate dynamic parameters in the proposed mathematical model for long-term HIV dynamics. Fitting of mathematical models using a Bayesian approach is a powerful way to analyze data from studies of viral dynamics. First, Bayesian modeling involves specifying prior distributions of model parameters to perform the analysis. Thus, it cannot only incorporate the estimates of dynamic parameters from previous studies, but also handle the parameter identifiability problems. Second, the Bayesian approach allows the fitting of complex models and is more flexible than other methods such as the nonlinear least squares (NLS) method. Third, the graphical output of simulation-based Bayesian algorithms provides both informative diagnostic aids and easily understood inferential summaries.

We have presented a simulation example and an actual AIDS clinical trial study to illustrate how the Bayesian procedures can be applied to HIV dynamic studies. Both the population and individual dynamic parameters can be estimated from the hierarchical Bayesian modeling approach. For the simulation study, it was seen that the models provided a good fit to the data. The bias estimates for both population and individual dynamic parameters were very small, and the corresponding SEs (%) of the estimates were reasonable. Under this setup, one thus might claim that both population and individual parameters would be identifiable by only providing the population prior information under a framework of the hierarchical Bayesian model based on our simulation study. For the actual AIDS clinical trial data set, the proposed model fitted the clinical data reasonably well for most subjects in our study, although the fitting for a few subjects (less than 10%) was not completely satisfactory due to unusual viral load response patterns, inaccurate measurements of drug exposure, and/or adherence for these subjects. For example, self-reported pill count measurements may not reliably reflect actual adherence profiles for some subjects.

Most of the previous studies have assumed perfect drug effect (Ho et al., 1995; Perelson et al., 1996; Wu et al., 1998; Markowitz et al., 2003) or imperfect constant drug effect (Perelson and Nelson, 1999; Ding and Wu, 2001) to estimate dynamic parameters with short-term viral load data. These assumptions contributed to the limitations of those studies which might result in inaccuracy of dynamic parameter estimation. Compared with those studies, our model proposed in this article has the following features: (i) considers time-varying drug efficacy during long-term treatment; (ii) provides more reasonable biological interpretation; (iii) incorporates drug concentration, adherence, and resistance in the model; and (iv) provides a good fit to the observed long-term viral load data (whole data). Thus, based on this model, the results of estimated dynamic parameters should be more reliable and reasonable in the interpretation of long-term HIV dynamics.

Although the analysis presented here used a simplified model, which appeared to perform well in capturing and explaining the observed patterns and characterizing the biological mechanisms of HIV infection under relatively complex clinical situations, our model is however limited in several ways. Our mathematical model (4) is a simplified model among many variations of viral dynamic models (Perelson and Nelson, 1999; Nowak and May, 2000). We did not consider the compartments of productively infected cells, long-lived, and latently infected cells separately (Perelson et al., 1997). Instead we pooled all the infected cell populations together. The virus compartment was not further decomposed into infectious virions and noninfectious virions as in Perelson et al. (1996). Thus, different mechanisms of nucleoside reverse transcriptase inhibitor (NRTI) and PI drug effects were not modeled. In fact, we only considered the PI drug effects in the drug efficacy model (3) because the information on NRTI drugs was not collected in our study and the effect of NRTI drugs was considered less important compared to the PI drugs. We modeled drug resistance using the phenotype IC₅₀ values instead of modeling viral genotype species separately (Nowak and May, 2000). One of the main reasons is that genotypic assay results are hard to interpret due to the large number of mutations that lead to resistance of antiretroviral drugs. Although more elaborate models with consideration of more infected cell and virus compartments, more detailed drug effects, and specific drug-resistant viral species may provide more accurate descriptions for long-term HIV dynamics, they may give rise to the identifiability problems of model parameters due to the complexity of the models, and thus limit the usefulness of these models. The trade-off between the complexity and applicability of HIV dynamic models should be considered, and further studies on this issue are definitely needed. Nevertheless, these limitations would not offset the major findings from our modeling approach.

We assumed that the distribution of the random effects b_i is normal. However, due to the nature of AIDS clinical data, it is possible that the data may contain outlying individuals and, thus, may result in a skewed distribution of individual parameters, that is, the random effects may not follow a normal distribution. As Wakefield (1996) suggested, a t distribution may be used, which is more robust to outlying individuals than the normal distribution. We plan to address this issue and report the results in future studies.

In summary, the mechanism-based dynamic model is powerful and efficient in establishing the relationship between antiviral response and drug exposure/drug susceptibility, although some biological assumptions have to be made. The fitting of a model specified as a set of differential equations is routinely done in many fields (in particular pharmacokinetics and pharmacodynamics, which are closely associated with the analysis of clinical data considered in this article). Our hope is that this work might stimulate the investigation of more realistic models to analyze data from AIDS clinical trials with antiviral treatment which, in turn, would help to better understand the biological mechanism of HIV infection, to study the pathogenesis of AIDS progression, to guide the development of antiviral treatment strategies, and to take into account the roles of clinical factors in antiviral activities. We also expect that the proposed longitudinal dynamic system concept can be applied to other biological processes.