Hyperpolarization-activated graded persistent activity in the prefrontal cortex

Abstract

We describe a phenomenon of hyperpolarization-activated graded persistent activity (HAGPA) in prefrontal cortex neurons. Successive hyperpolarizing pulses induced increasingly higher rates of tonic firing that remained stable for tens of seconds, allowing the neuron to retain a memory of the previous history of stimulation. This phenomenon occurred at the cellular level and in the absence of neuromodulators. Neurons with HAGPA had a sag during hyperpolarization, and blocking h-current eliminated the sag and prevented HAGPA, suggesting that the activation of this hyperpolarization-activated cationic current was necessary for the occurrence of the phenomenon. A single-neuron biophysical model including h-current modulation by intracellular calcium was able to display HAGPA. This form of neuronal memory not only allows the transformation of inhibition into an increase of firing rate, but also endows neurons with a mechanism to compute the properties of successive inputs into persistent activity, thus solving a difficult computational problem.

Persistent activity refers to the firing of a neuron or neural circuit that exceeds the duration of a stimulus, persisting after the stimulus has terminated (1–3). Persistent firing can emerge from a reverberatory neural network with recurrent connections (4–7), or be achieved by cellular, intrinsic mechanisms without the involvement of the network (8–10). These mechanisms should be able to constantly maintain a certain level of activity, and they are crucial to generate functions such are working memory (6, 11) or ocular movements (12, 13). A more sophisticated system should also regulate the rate of persistent activity depending on the quantitative and qualitative characteristics of the preceding stimulation, therefore supporting complex mnemonic processes. An example of intrinsically generated graded persistent activity has been described in enthorinal (9) and amygdalar (14) neurons, its occurrence requiring the presence of cholinergic agonists (9, 15). In that case, neurons maintain a constant firing rate that gradually increases with the repetition of depolarizing pulses, therefore maintaining different levels of activity depending on the number of previous stimuli.

In this study, we demonstrate that a different kind of graded persistent activity rooted in cellular mechanisms occurs in neurons of the prefrontal cortex in the absence of neuromodulators.

Results

Hyperpolarization-Activated Graded Persistent Activity in Prefrontal Neurons.

One hundred and sixty-five neurons intracellularly recorded from ferret (n = 40), rat (n = 120), and guinea-pig (n = 5) prefrontal cortex were included in this study. All neurons had overshooting action potentials, resting membrane potentials between −65 and −75 mV, and an average input resistance of 41.3 ± 2.4 MΩ.

While recording from neurons with tonic discharge, we observed that some neurons would increase their tonic firing frequency after being hyperpolarized for a few seconds. This increase was progressive for successive pulses, a phenomenon we called hyperpolarization-activated graded persistent activity (HAGPA). To test systematically for HAGPA, neurons were injected with a continuous depolarizing current (0.3 ± 0.03 nA) if required (two of the neurons fired spontaneously), such that their membrane potential would be depolarized just enough to evoke a tonic firing of 1.5–5 Hz (3.3 ± 0.5 Hz). Next, hyperpolarizing pulses of amplitudes between −0.2 and −0.8 nA and 2–4 s duration were injected, interleaved with intervals of 12–40 s in between pulses (Fig. 1A and B; see supporting information (SI) Movie S1).

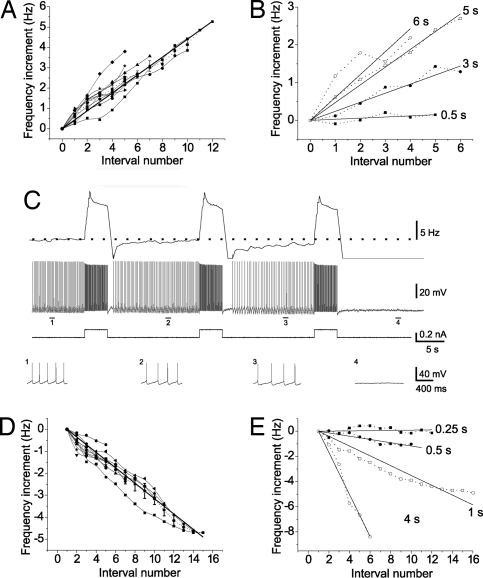
Fig. 1.

Graded persistent activity induced by successive hyperpolarizing pulses (HAGPA). (A) Consecutive, equal amplitude hyperpolarizing pulses (−0.4 nA, 4 s) induced a graded increase in the firing rate that was stably maintained throughout the intervals in between the pulses. Rate of spike frequency (Top) (bins = 1 s), membrane voltage (Middle) and intracellularly injected current (Bottom). At the lowest part of A, the action potentials corresponding to the underlined sections (1–5) have been expanded. The firing frequency value at the starting point was 1.7 Hz. Shown are recordings from guinea pig infragranular neuron. (B) Another example of HAGPA (supragranular neuron from guinea pig) to further illustrate the stability of the firing rate during the intervals between hyperpolarizing pulses (−0.3 nA and 3 s). The first nine displayed intervals lasted 17 s; then, the stability of the firing was tested for 78 s. Subsequent pulses further increased this stable firing rate. The intervals in between the last two pulses were of 27 s each. The firing frequency value at the starting point (first interval on the left) was 5 Hz.

Criteria for Hyperpolarization-Activated Graded Persistent Activity.

To classify a neuron as one with HAGPA a minimum of four hyperpolarizing pulses was injected. The phenomenon consisted in an increase in the firing frequency after each of the hyperpolarizing pulses (Fig. 1 A and B). The criterion for HAGPA was a minimum increase of 0.2 Hz in firing frequency after each of four hyperpolarizing pulses. Each increase would determine the new persistent firing frequency of the neuron and it should remain constant at the new value for a minimum time of 10 s (starting at least 2 s after the end of the hyperpolarizing pulse to exclude the initial rebound and subsequent adaptation). However, in almost every neuron that showed HAGPA, longer intervals were tested to assure the stability of the firing for tens of seconds and (when tested) even for minutes (Fig. 1B, note the 78-s interval, also in Movie S1). After an interval of 10–40 s, a subsequent hyperpolarizing pulse of the same amplitude and duration was injected, and a further increase in the tonic firing rate of the neuron was evoked.

HAGPA was observed in 39 of 165 neurons (23.6%), revealing that in the frequency of tonic firing of these neurons there was information referring to the previous history of membrane voltage transitions. All neurons that displayed HAGPA were classified as regular spiking (16). Of 126 neurons recorded from supragranular layers, 24.6% showed HAGPA, whereas 20.5% did in infragranular layers (8 of 39).

HAGPA was observed only if, at the beginning of the protocol, and before the first hyperpolarizing pulse was given, the neuron was already firing tonically even if at low frequencies. Only in four neurons was the same mechanism of HAGPA enough to bring the neuron from a silent subthreshold membrane value to a suprathreshold tonic firing state (Fig. S1 A and B). Neurons that did not fire tonically with depolarization, e.g., because their response had a strong adaptation enough to silence the neuron, could not show HAGPA (this strong adaptation occurred in 56 of 126 neurons without HAGPA). The remaining 70 neurons (of 126 without HAGPA) did maintain tonic frequency firing and still did not fulfill the criteria for HAGPA (Fig. S1C).

To verify that the increase in the firing was directly related to the preceding hyperpolarizing pulses and to rule out any nonspecific slow depolarization, the stability of firing for every neuron was tested for long periods of time (tens of seconds to minutes). Only neurons that maintained stable firing frequency before and during the intervals in between hyperpolarizing pulses were included. A certain degree of spike frequency adaptation could often be observed during the intervals (Fig. 1). This adaptation was generally well fitted by a single exponential and the average time constant was 0.7 ± 0.05 s (n = 36). Measurements to estimate the firing frequency increase during HAGPA were obtained from the average frequency during the last 5 s in the interval. Adaptation would have no role in the genesis of HAGPA given that it would tend to decrease rather than enhance the phenomenon. Long intervals in between pulses illustrate that once the slow adaptation is finished, the firing is stable (Fig. 1B and Figs. S2 and S3).

Possible changes in the action potential threshold were also taken into account. In all HAGPA(+) neurons, the threshold for action potential firing was determined before and at the end of the HAGPA protocol (while the firing frequency was increased). Of 39 neurons, 35 did not display changes in the firing threshold (average value of 48.5 ± 0.9 mV). The remaining 4 neurons displayed a certain change in threshold, two of them showing an increase (1 mV) and two of them showing a decrease (2–3 mV), the difference being nonsignificant.

A total of 39 neurons with HAGPA were injected with series of hyperpolarizing pulses (4–15 pulses as described above). The starting tonic firing rate was on average 3.3 ± 0.5 Hz. Each additional hyperpolarizing pulse induced an increase in the firing rate of an average of 0.4 ± 0.1 Hz. When the firing frequency increment after each hyperpolarizing pulse was plotted against the interval number, a linear increase in the firing frequency was observed (R² = 0.8; P < 0.0001). The slope of the linear increase was similar when neurons with similar injection protocols were selected (Fig. 2A). A maximum firing frequency or plateau was eventually reached, and after 5–15 pulses (average 6.7 hyperpolarizing pulses, n = 27) the average plateau firing frequency was 6.3 Hz (Fig. S4). Some neurons did not reach a plateau, even when firing tonically at 14 Hz (n = 8, Fig. S4A).

Fig. 2.

Linearity of the increase in the firing rate. (A) Spike frequency during the interval versus interval number in 10 neurons during a similar HAGPA protocol (3- to 5-s pulse, −0.3 to −0.5 nA amplitude). Only the linear zone was represented, because with longer number of pulses a plateau was reached (see Results). All neurons had a similar slope firing rate increase; average slope, 0.48 ± 0.02 Hz per interval (n = 10). (B) Changes in the slope depending on the duration of the hyperpolarizing (−0.3 nA) pulses. The duration of the pulses is displayed next to each linear fitting. (C) Depolarizing pulses (0.2 nA, 4s) after induction of HAGPA in this neuron (for complete protocol see Fig. S5). The progressive increase in firing frequency previously induced by the HAGPA protocol was reversed by the inverse protocol (DSGPA), such that the firing went from 6 Hz to complete silence after four consecutive depolarizing pulses. (Top to Bottom) Rate of spike frequency (bin = 1s; Top), membrane voltage and intracellular injected current, expanded traces of membrane potential corresponding to the indicated time periods (1–4). Neuron recorded from infragranular layers of ferret prefrontal cortex. (D) Decrease in tonic firing frequency as a result of the injection of consecutive depolarizing pulses. Spike frequency during the interval in between depolarizing pulses (0.2–04 nA; 2–4 s) versus interval number (n = 10 neurons). Average slope, −0.35 ± 0.01 Hz per interval. (E) Changes in the slope of firing frequency decrease with successive depolarizing pulses for pulses of different duration. The duration of the pulses is displayed next to each linear fitting. A, B, D, and E include neurons from either rat, ferret, or guinea pig prefrontal cortex.

The slope of the firing frequency versus interval number depended on the duration of the hyperpolarizing pulses, longer hyperpolarizing pulses inducing higher firing frequencies, and thus increasing the slope of the linear relation (Fig. 2B). There was an inherent stability of the neuronal firing frequency, and a minimum hyperpolarizing pulse duration (generally >0.5 s; Fig. 2B) was necessary to induce HAGPA. Shorter pulses (either hyperpolarizing or depolarizing) usually did not alter the firing rate (Fig. S2), suggesting a nonlinear threshold for HAGPA generation.

In 18 of 39 neurons that showed HAGPA, the hyperpolarizing current injected during the pulses was later switched to depolarizing pulses. The same duration (2–4 s) and amplitude (0.3–0.5 nA) were maintained. In 9 of these 18 neurons, this reversed HAGPA (Fig. 2C and Fig. S5), inducing a gradual decrease of the persistent firing frequency that followed a similar rate to the increase (Fig. 2D and Movie S2). Therefore, every additional pulse would further decrease the frequency of firing until the neuron was eventually silenced (Fig. 2C and Figs. S5 and S6). We will refer to this phenomenon as depolarization-suppressed graded persistent activity (DSGPA).

The graded decrease in tonic firing rate during DSGPA was also linear with the number of depolarizing pulses and had a similar slope (of opposite sign) to the previously described increase in firing rate (−0.35 ± 0.01 Hz per pulse; R² = 0.92; P < 0.001; Fig. 2D). This slope was also sensitive to the duration of the depolarizing pulses, and longer depolarizing pulses induced steeper decreases in firing frequency than shorter pulses (Fig. 2E). Pulses of duration <0.5 s had little effect on the firing frequency (Fig. 2E and Fig. S2C).

HAGPA was studied in slices without spontaneous network activity, and it persisted in the presence of synaptic blockers [6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) 20 μM; 2-amino-5-phosphonovaleric acid (APV) 50 μM; bicuculline methiodide (BMI) 10 μM] in the bath whenever tested (n = 7). Because synaptic activity was not implicated in the genesis of HAGPA, we conclude that that is unlikely to be a network phenomenon but a cellular one, depending on neuronal intrinsic properties.

H-Current Blocker, ZD7288, also Blocks HAGPA.

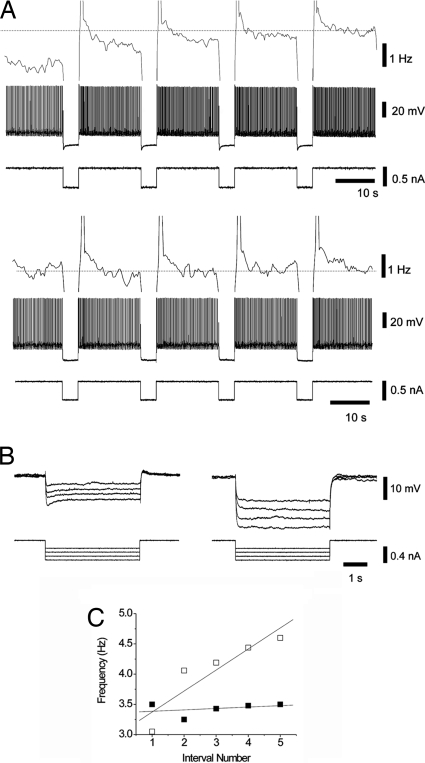
The dependence of HAGPA on hyperpolarization suggested that a hyperpolarization-activated current could be involved. A sag voltage was observed during the hyperpolarizing pulses in 37 of the 39 neurons that showed HAGPA (Fig. 3). A specific h-current blocker, ZD7288 (17, 18) (250–500 μM), was locally applied to 17 neurons displaying HAGPA and always resulted in the blockade of the sag (Fig. 3). When tested (n = 13), ZD7288 application not only blocked the sag but also blocked HAGPA, totally (n = 8; Fig. 3 A and C) or partially (n = 4), except in one neuron. These results suggest that h-current activation is a key mechanism underlying HAGPA. Although h-current activation seems to be necessary for HAGPA, the existence of I_h is not enough to induce it. Six cortical neurons with a sag during hyperpolarization that was later blocked by ZD7288 were recorded, but HAGPA could not be induced in them. In four cases, we recorded from thalamocortical neurons from the lateral geniculate nucleus, known to have a prominent h-current (19, 20). HAGPA was not obvious in these neurons, although they had a sag voltage during hyperpolarizing pulses that was blocked by ZD7288. We conclude that the activation of I_h is necessary but not sufficient to induce HAGPA.

Fig. 3.

ZD7288, an h-current blocker, prevents the occurrence of hyperpolarization-activated graded persistent activity. (A) HAGPA (Top) was blocked by local application of ZD7288 (500 μM) (Bottom). Shown are firing frequency (Top trace), membrane voltage (Middle trace), and injected current (Lower trace). Note the blockade of the sag typical of h-current activation by ZD7288. (B) Detail of the hyperpolarization-activated sag blocked by ZD7288 for pulses of different amplitude (−0.2 to −0.5 nA) in the same neuron, the input resistance increasing from 24.25 to 50.7 MΩ. Recording was from an supragranular neuron in rat cortex. (C) Increment in firing frequency during the intervals in between pulses versus interval number before (□) and after (■) ZD7288 application for the neuron in A).

Modeling HAGPA.

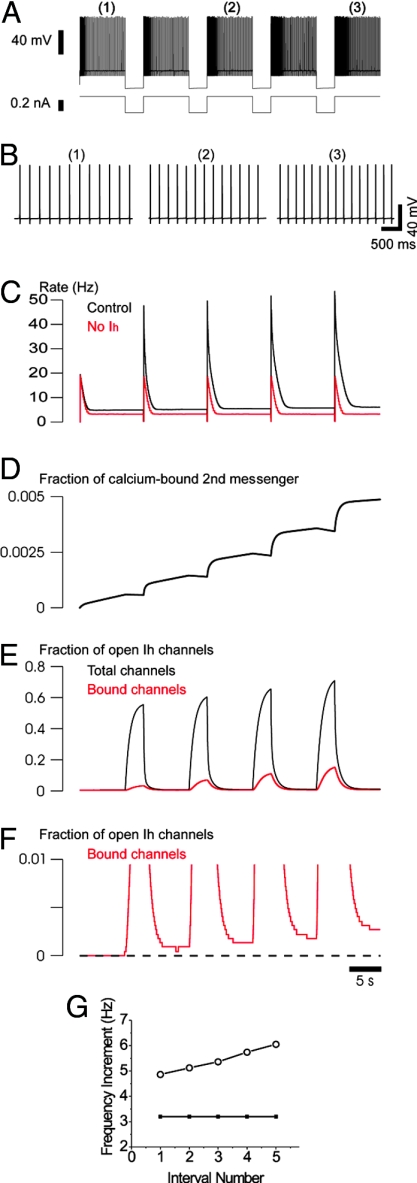
The role of I_h activation in the generation of HAGPA was further studied by using a computational model of prefrontal cortical neurons created in the NEURON environment (see Methods and SI Experimental Procedures for details and demo). This biophysical model comprised the minimal set of ionic currents to account for this phenomenon. After injection of successive hyperpolarizing pulses riding on a depolarizing holding current, the model reproduced the experimental observations (Fig. 4 A and B). The mechanism was based on I_h regulation by [Ca²⁺]_i, a process that has been demonstrated in thalamic neurons (21). In this process, calcium stimulates the production of another second messenger, which binds to the open state of the channel (21, 22). This binding to the open state enables I_h channel activation to be sensitive to the previous level of firing activity: the second messenger is produced during the firing through calcium entry via the high-threshold Ca²⁺ current; during the hyperpolarizing pulse, I_h activates while the intracellular medium is still highly concentrated in second messenger (Fig. 4D), resulting in a strong activation of I_h because of second messenger binding to the open state. During subsequent pulses, I_h activates to successively higher levels (Fig. 4 E and F), owing to the slow unbinding of second messenger from I_h channels (which was here of the order of 10 s) (21). The parameters of the binding of [Ca²⁺]_i ions to the second messenger can determine the increase in firing rate with consecutive pulses and the saturation or not of the effect, as illustrated in Fig. S7. The elimination of I_h from the model prevents the occurrence of HAGPA (Fig. 4 C and G) reproducing the experimental observations (Fig. 3).

Fig. 4.

Biophysical model of HAGPA. (A) HAGPA in a model comprising several voltage- and calcium-dependent currents (Na⁺ and K⁺ currents for action potentials; high-threshold Ca²⁺ current, the hyperpolarization-activated current I_h and its modulation by Ca²⁺). HAGPA after successive hyperpolarizing current pulses (−0.3 nA; 3-s duration; 10-s inter-pulse period; holding current, 0.23 nA). (B) Details of the increased firing rate after each current pulse corresponding to the periods underlined in A. (C) Neuronal firing rate (Hz) during the protocol in the control situation (as in A) and in the absence of I_h (red line). Note that, in the absence of I_h, there is no progressive increase in the firing rate with successive pulses. (D) Fraction of calcium-bound second messenger. (E) Fraction of open I_h channels (total channels, black) and fraction of open I_h channels (calcium-bound channels, red) showing the accumulation of activation of I_h current. Calcium entry during action potentials boosted the activation of I_h in a step-like fashion at the offset of each hyperpolarizing pulse. (F) Zoom of the calcium-bound channels in F illustrating the fine structure of the accumulation of bound channels with successive hyperpolarizations. (G) Increment in spike frequency during the steady state in the interval versus interval number in the HAGPA protocol in A (○) and during the same protocol but in the absence of I_h (●).

Thus, experiments and models point to the conclusion that a continuum of states of persistent firing activity is accessible to these neurons, with the following properties: (i) different levels of elevated firing activity, lasting for seconds, can be evoked by the same input; (ii) the level of firing depends on prior hyperpolarization; (iii) it depends on the I_h current; (iv) calcium regulation of I_h, previously identified in heart (23) and thalamic cells (21, 24), can explain this phenomenon. Interestingly, calcium-activated second messengers are markers of the level of firing of the cell. The fact that these messengers bind to open I_h channels (with very slow unbinding rate) enables I_h to activate in a manner proportional to the prior level of firing. Because I_h activation in turn modulates the firing of the cell, this mechanism can implement the ability of the cell to produce different responses to the same input, according to input history. In particular, inhibition would be expected here to play a major role by activating I_h in physiological conditions (Fig. S8). Thus, two elements commonly observed in cortical neurons, strong inhibition (25–27) and I_h current (28, 29), combined with calcium regulation of I_h, can potentially implement mechanisms for integration of input history over periods of several seconds.

Discussion

In this study we have shown that a single prefrontal neuron can modify its tonic firing frequency for long periods of time depending on the quantity (shown as number of pulses) and characteristics (illustrated for polarity and duration of the pulses) of the previous inputs. Persistent activity has been shown to participate in different tasks such as parametric working memory (30), decision making (31, 32), or oculomotor control (12, 13, 33).

Cellular mechanisms of graded persistent activity have also been previously described in entorhinal (9, 15) and amygdalar neurons (14); however, the phenomenon described here is radically different: (i) it occurs in prefrontal neurons, an area that has been directly implicated in mnemonic processes; (ii) no neuromodulators are required [muscarinic agonists in (9, 13, 14)]; and (iii) the phenomenon is of opposite sign to the one previously described [graded increase in tonic firing with depolarizing pulses in (9, 14)] and therefore the underlying ionic mechanisms are distinct.

Increased excitability because of intrinsic mechanisms and after hyperpolarization or inhibition has also been described in a different system (vestibular nucleus) (8). However, apart from the general description, the phenomena are totally different in terms of (i) the underlying mechanisms (BK channels in vestibular neurons versus I_h-current in HAGPA); (ii) the time course in which they work (for vestibular neurons, 5 min of hyperpolarization/inhibition are required and the increased firing lasts up to 30 min; HAGPA increases excitability after 2–6 s of hyperpolarization); and (iii) vestibular neurons do not display graded increases in excitability, but one increase in excitability after a period of hyperpolarization/inhibition that is not bidirectional or reversible. In HAGPA, the increase of excitability is related to hyperpolarization duration, providing the neuron with a mechanism to code for the duration of previous stimuli. That HAGPA provides neurons with a memory of both the qualitative and quantitative history of stimulation grants the phenomenon a larger versatility.

To ensure that graded persistent activity described here was specific and not some kind of deterioration or drift was a major concern when HAGPA was first observed. The changes in firing frequency were not unidirectional, supporting specificity. More than half of the neurons in which pulses were inverted presented HAGPA and DSGPA (Fig. 2C and Fig. S5), and in every case the tonic firing was stable for long periods of time. Furthermore, the recordings were very stable, as demonstrated by the constancy of action potential amplitude throughout them (see Movie S1).

Temporal integration memory processes in which slow intrinsic currents are implicated have been described in several systems (10, 34, 35). I_h is a hyperpolarization-activated cationic current that generates a characteristic sag potential during hyperpolarization. Its modulation by intracellular calcium and slow kinetics (21) make I_h suitable to play a role in temporal integration. Our experiments revealed that 94% of neurons with HAGPA also had a sag during hyperpolarization of the membrane potential, and application of an I_h blocker (ZD7288) removed the sag and prevented HAGPA. Our relatively simple biophysical model could generate HAGPA in a robust way based on calcium modulation of I_h through a second messenger (22). Therefore, both, our experimental and modeling results suggest that I_h is necessary for the generation of HAGPA. However, the presence of I_h in a neuron is not sufficient: i.e., thalamocortical neurons from the ferret LGN, known to have a prominent h-current (19, 20), did not display HAGPA (see Results). One difference is that, in thalamic neurons, I_h and the low-threshold calcium current I_T were proposed to interact (21, 22) whereas we emphasize here the high-threshold current I_L. Other conditions for HAGPA could also include codistribution of I_h and other ionic channels as well as the lack of ionic currents supporting spike frequency adaptation that would preclude the persistency of the firing.

I_h channels are located in different regions of the neocortex, as is the prefrontal cortex (36). Persistent activity in prefrontal neurons has been associated with working memory, e.g., in delayed response visual tasks, in which neurons from the dorsolateral prefrontal cortex maintain a mnemonic activity during the period between a visual cue and a delayed behavioral response (2), and in somatosensory discrimination tasks, in which prefrontal neurons firing reveals a parametric representation of the memorized stimulus (30). Even if it had not been the objective of this work to study the cellular basis of working memory, the fact that HAGPA exists in 23.6% of the recorded prefrontal neurons would indicate that it participates in the firing modulation during different processes occurring in the prefrontal cortex. However, it is important to remark that HAGPA is a cellular mechanism, and that the functional implications of integrating it in the active network have not yet been explored. To our knowledge, I_h has not been specifically characterized in monkey prefrontal cortex, although it has been identified in monkey pulvinar (37), and h-channels are present in the human brain (38), consistent with I_h and HAGPA also being present in primate prefrontal cortex. Although we cannot provide statistical information at this stage, we have occasionally recorded HAGPA in somatosensory and visual cortex. The existence of I_h and HAGPA in other cortical areas could implicate this mechanism in processes such as addition and subtraction involved in perceptual discrimination (39).

Activation of HAGPA requires hyperpolarization or inhibition. Strong inhibition is prevalent in neocortical neurons (25–27, 40), and presenting sensory stimuli to awake behaving monkeys while recording from various areas of the cortex (including prefrontal cortex) often results in an inhibition of neuronal firing (30). Furthermore, increased persistent firing with successive stimuli during working memory tasks (“climbing delay activity”) does not always follow excitation by the stimulus but also stimulus-induced suppression (41). HAGPA in in vitro prefrontal neurons described here could be the cellular counterpart of such behaviorally relevant and previously seemingly paradoxical phenomena.

Methods

For further details see SI Experimental Procedures.

Slice Preparation.

The methods for preparing cortical slices were similar to those described in ref. 5. Cortical slices (400 μm) were prepared from prefrontal cortex of adult ferrets, rats, or guinea-pigs of either sex that had been deeply anesthetized with sodium pentobarbital (40 mg/kg) and decapitated. Slices were placed in an interface-style recording chamber and bathed in artificial cerebrospinal fluid (ACSF) containing 124 mM NaCl, 2.5 mM KCl, 2 mM MgSO_4, 1.25 mM NaHPO_4, 2 mMCaCl_2, 26 mM NaHCO_3, and 10 mM dextrose, aerated with 95% O₂, 5% CO₂ to a final pH of 7.4. Bath temperature was maintained at 34°C–35°C. Recordings were initiated after 2 h of recovery.

Electrophysiological Recordings.

Sharp intracellular recording electrodes were beveled to final resistances of 50–100 MΩ and filled with 2 M KAc.

Biophysical Model.

The model consisted of a single-compartment neuron described by the following membrane equation:

where V is the membrane potential, C_m = 1 μF/cm² is the specific capacitance of the membrane, g_L = 1 mS/cm² is the leakage conductance, E_L = −70 mV, and is the leakage reversal potential. I_Na and I_Kd are the sodium and potassium currents responsible for action potentials, I_KM is a slow voltage-dependent potassium current, I_CaL is a high-threshold calcium current and I_h is the hyperpolarization-activated cationic current. These voltage-dependent currents are variants of the same generic equation:

where the current I_j is expressed as the product of the maximal conductance, g_j, activation (m), inactivation (h), and the difference between the membrane potential V and the reversal potential E_j. The gating of the channel is derived from the following first order kinetic scheme:

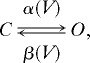where O and C are the open and closed states of the gate. The variables m and h represent the fraction of independent gates in the open state, following the convention introduced by ref. 42. The steady-state activation and the time constant are, respectively, given by m_∞ = α/(α + β) and τ_m = 1/(α + β), and similarly for h. For details on each voltage-dependent current see SI Experimental Procedures.

Hyperpolarization-Activated Current and Calcium Regulation.

I_h current was described by using a kinetic model including calcium regulation (22, 24). The voltage dependence of I_h was modeled with a single-variable kinetic scheme (m formalism) based on previous models for the dependence of its activation on voltage and intracellular Ca²⁺. I_h voltage dependence was based on voltage-clamp data of this current in thalamic neurons (19), and the rate constants used were identical to those in ref. 43.

The regulation of I_h by intracellular Ca²⁺ was based on voltage-clamp data from the hyperpolarization-activated current in sino-atrial cells (23). Ca²⁺ may not bind directly to the channel (21, 44). This Ca²⁺ dependence was incorporated in different models, first by using direct binding of Ca²⁺ ions to the open form of the channel (24), and subsequently through indirect binding of Ca²⁺ to a second messenger (P), which itself binds to the open form of the channel (22). This latter model was used here because it is consistent with experimental data, best explained by the direct binding of cAMP to the open channel (21). A similar model was also proposed for the H-type current in the heart, in which cAMP allosterically modulates the channel (45, 46). In this case, the modulation arose from the fact that cAMP has a much higher affinity to the open state, which is very similar to the present model, in which we postulate that there is no binding at all to the closed state.

The full kinetic scheme was:

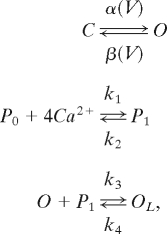where the first reaction represents the voltage-dependent transitions of I_h channels between closed (C) and open (O) forms, with α and β as transition rates. The second one represents the binding of Ca²⁺_i ions to a second messenger (P₀ for unbound and P₁ for bound) with four binding sites for Ca²⁺ and rates of k₁ = 7,716 mM⁻⁴·ms⁻¹ and k₂ = 10⁻⁵·ms⁻¹ (half-activation of 0.006 mM Ca²⁺). The Ca²⁺-activated form P₁ associates with the open state of the channel, leading to a “locked” open state O_L, with rates of k₃ = 10 ms⁻¹ and k₄ = 0.001 ms⁻¹.

The current is then proportional to the relative concentration of open channels:

with a maximal conductance of g_h = 0.02 mS/cm² and a reversal potential of E_h = −40 mV. Because of the factor g_inc = 2, the conductance of the calcium-bound open state of I_h channels is twice that of the unbound open state. This mechanism produces an augmentation of conductance after the binding of Ca²⁺, as observed in sino-atrial cells (23).

The robustness of the HAGPA model is discussed in the SI Experimental Procedures.