Packaging Double-Helical DNA into Viral Capsids: Structures, Forces, and Energetics

Abstract

Small, icosahedral double-stranded DNA bacteriophage pack their genomes tightly into preformed protein capsids using an ATP-driven motor. Coarse-grain molecular-mechanics models provide a detailed picture of DNA packaging in bacteriophage, revealing how conformation depends on capsid size and shape, and the presence or absence of a protein core. The forces that oppose packaging have large contributions from both electrostatic repulsions and the entropic penalty of confining the DNA into the capsid, whereas elastic deformations make only a modest contribution. The elastic deformation energy is very sensitive to the final conformation, whereas the electrostatic and entropic penalties are not, so the packaged DNA favors conformations that minimize the bending energy.

INTRODUCTION

Bacteriophage carry double-helical DNA genomes surrounded by protein capsids. The capsids of the smallest bacteriophage, with genomes of ∼10–50 kbp, are icosahedral, or nearly so. At one vertex of the capsid there is a group of proteins that are responsible for driving the DNA into the capsid and holding it there while the tail proteins are attached, finishing the viral assembly.

Early x-ray diffraction studies showed that the DNA inside viruses has some order, leading to the suggestion that it is arranged in a series of coaxially spooled layers (1,2). This model has two potential problems. First, coils near the center of the spooling axis would be strongly bent. Second, the highly ordered coaxial spool model ignores entropic contributions that would favor disorder at physiological temperatures. Flow dichroism experiments showed that DNA is not as ordered as predicted by the coaxial spool model (3). Early electron microscopy (EM) images of elongated bacteriophage suggested that the DNA resembles a twisted toroid (4). Other proposals include the ball-of-string model (5), models with kinks in the DNA (5,6), and the folded-toroid model (7).

Packaging of viral DNA into the capsid is driven by a motor within the portal. Energy is required to force the DNA into this small space because of elastic deformations of DNA bending, electrostatic DNA-DNA repulsions, and the entropic penalty of the reduced conformational space. Single-molecule experiments found that the φ29 motor can generate forces in excess of 50 pN (8), and thus is stronger than the myosin and kinesin motors. The total free-energy change is ∼12,000 kcal/mol, and the motor has an efficiency of ∼30% (8). More recent measurements have suggested that the forces can exceed 100 pN (9). Similar experiments have examined the effects of ionic strength and the concentrations of polyvalent cations on packaging forces (10).

Here we review recent advances in theoretical and modeling studies on DNA packaging. We describe the approaches used, discuss how well they reproduce the experimental data, and close with a discussion of current challenges and open problems. The reader is referred to reviews by Jardine and Anderson (11) and by Johnson and Chiu (12) for excellent coverage of recent experimental work.

SURVEY OF MODELING APPROACHES

There are two principal methods for modeling DNAs the size of bacteriophage chromosomes (i.e., ∼10–100 kbp in length): continuum-elastic models and molecular-mechanics models.

The continuum-elastic approximation requires the presupposition of a conformation for the final structure. In the most detailed studies (13–15), the structure was assumed to be globally arranged as a coaxial spool and locally hexagonally close-packed. The DNA-DNA interaction potential was based on a potential of mean force measured by Rau and Parsegian (16,17), who used osmotic pressure to compress DNA to densities typical of those found in viruses. Entropic contributions to the packaging free energy were assumed to be negligible. The resulting curves for the force as a function of the percent DNA packed (13,14) strongly resembled those observed in the single-molecule packaging experiments (8), and quantitative agreement was obtained with the adjustment of two free-fitting parameters (15).

Theoretical studies using continuum-elastic models have had considerable success in investigating ejection of the DNA from mature viruses (13,15,18–23), in large part because they have been so tightly coupled to experiment. Among the most significant contributions of these works are a deep understanding of the role of osmotic pressure in packaging and ejection (13,15,18,20–23), and the demonstration that binding of host cell proteins accelerates ejection through ratcheting and entropic effects (19).

The second method for modeling viral packaging is based on molecular-mechanics approaches. The level of detail in all-atom models (24) precludes their use for problems as large as viral DNA packaging. Coarse-grain models treat double-helical DNA as a string of beads connected by springs parameterized to mimic the elastic moduli of the real molecule (18,25–36), and the DNA is driven into the capsid using various algorithms. This approach allows one to examine the forces, thermodynamics, and kinetics of packaging, along with the range of packaged structures. As we will see, the molecular-mechanics studies cast doubt on two critical assumptions of the continuum-elastic approach: DNA conformations are not coaxially spooled in all capsids, and the entropic cost of packaging is not negligible.

Coarse-grain DNA models contain beads ∼25 Å in diameter that represent 5–10 basepairs (bp). Successive beads are connected by harmonic springs whose stiffness matches the Young's modulus for DNA stretching. The angular springs connecting successive triplets of beads are parameterized to match the persistence length. All of the studies reviewed here used similar parameters for these degrees of freedom. Only two of these studies included DNA torsional stiffness (29,36). Volume exclusion terms keep regions of DNA that are far apart in the primary structure from passing through one another. Most use a semiharmonic “soft sphere” repulsion or the repulsive part of a van der Waals potential. Some purely elastic models (25–28,30–32) do not include long-range electrostatic repulsions. Other models do (18,29,33–35). They use a variety of functional forms for long-range DNA-DNA interactions, but all are parameterized to match the Rau-Parsegian potentials of mean force (16,17).

The simplest approach for modeling a capsid is to treat it as a sphere of radius R and penalize any DNA bead at radius r > R. The energy can depend either quadratically (25,26,31,32) or as the fourth power of (r-R) (18,29). Spherical (27,28) and ellipsoidal restraints (28) have been modeled with a Weeks-Chandler-Anderson potential (37). Repulsive planes can be used to define an icosahedral capsid (30). We model capsids of arbitrary shape with pseudoatomic representations (33–36).

A recent coarse-grain model uses a density functional approach that formulates the Helmhotz free energy as a functional of DNA and ion density profiles (38). This model examines osmotic pressure inside capsids and reveals radial DNA density profiles at different packing densities. Packaging forces have not been determined, and the absence of a bending stiffness term precludes prediction of specific conformations.

Model DNAs can be packaged without assuming a final geometry by pushing successive DNA pseudoatoms into the capsid one at a time and equilibrating the structure at each step. A variety of equilibration algorithms have been used, including molecular dynamics (MD) (26,31–35), Brownian dynamics (BD) (18,29), and Langevin dynamics (LD) (30). MD without solvent damping allows equilibration of genomes as large as 40 kB, but the absence of viscous effects means that kinetic questions cannot be addressed. BD and LD allow the determination of kinetic parameters, but the slow rate of equilibration limits them to DNAs containing ∼6 kbp (30) to ∼8 kbp (18). Stochastic rotation dynamics is a variation of MD in which the polymer is immersed in a coarse-grained solvent model (39). Ali et al. (27,28) used this algorithm to examine the packaging of models with <800 bp of DNA and a persistence length ∼¼ that of B-DNA. It remains to be seen whether this algorithm can be used to study more realistic models of bacteriophage DNA.

THE STRUCTURE OF DOUBLE-HELICAL DNA IN BACTERIOPHAGE

Cryo-electron microscopy (cryo-EM) provides a high-resolution view of the average organization of bacteriophage DNA. Simulations yield individual DNA conformations, and one can assess the accuracy of these by calculating the average densities from multiple simulations and comparing them with the cryo-EM results. The average (ideal) conformation of bacteriophage DNA depends on the capsid size and shape, and the presence or absence of core proteins that help to organize the DNA (35), but the simulations reveal substantial particle-to-particle variation in conformation.

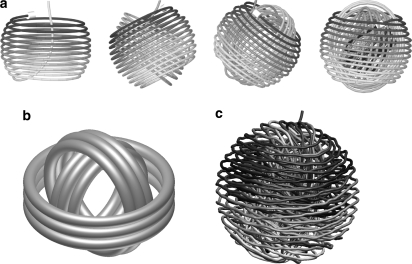
DNA conformations in spherical and icosahedral capsids lacking large core structures favor a concentrically spooled structure (26,31,35) (Fig. 1). Hall and Schellman (3) proposed concentric spooling as a possibility 25 years ago. Brownian-dynamics simulations gave similar structures (18), but only when the DNA-DNA interaction included an attractive component.

FIGURE 1.

Concentric spools. (a) Sequence of energy-minimized structures for DNA packed into a spherical capsid with no core (26). (b) Idealized representation. (c) DNA packaged in a spherical capsid with no core at T = 300 K (35).

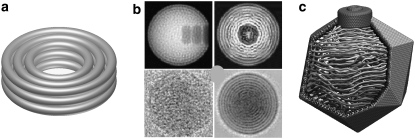
The overall organization is a coaxial spool if the virus has a large core and is spherical or icosahedral in shape (30,32,34,35) (Figs. 2 and 3). Two-dimensional cryo-EM images of T7 showed concentric ring patterns that clearly suggested coaxial spooling (40). Pronounced rings are obtained from coarse-grained models if a single projected density pattern is azimuthally averaged (30), or if densities from several particles are averaged and then reconvolved with the EM contrast transfer function (32) (Fig. 2 b). Fig. 3 shows that three-dimensional density maps from models closely resemble those obtained from cryo-EM (41–44). There is substantial variation in the DNA conformations in different packaging runs.

FIGURE 2.

Coaxial spools. (a) Idealized representation. (b) Simulated (32) (upper two panels) and experimental (40) (lower two panels) transmission EM density maps for T7 DNA. Projections of single particles along an axis perpendicular to the axis of packaging give a punctate pattern (left two panels), whereas projections along the axis of packaging give concentric rings when multiple images are averaged (right two panels): 10 independent packaging trajectories for the simulations, and 70 independent particles for the experiments. (c) Cutaway view of a single coaxially spooled conformation for a model of ɛ15 (34). To permit a clearer view of the DNA organization, the graphical diameter of the DNA strands is ∼8 Å (much less than the DNA-DNA contact distance of 25 Å).

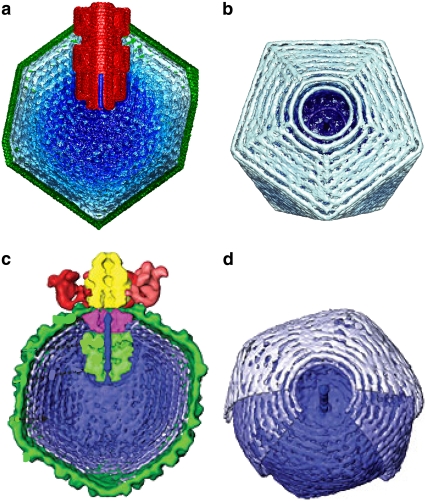
FIGURE 3.

Single-particle reconstructions of electron density maps for ɛ15 from simulations (34) (panels a and b) and experiment (41) (panels c and d). The complete capsid and core are shown in the transverse cutaway views (a and c), whereas only the DNA density is shown in the views down the packaging axis (b and d). The central closed circular ring of density in views b and d is a consequence of averaging over many conformations (40 independent packaging trajectories in the simulations, and ∼15,000 particles in the experimental reconstruction). The ring of density is due to the groove in the core protein, which, from very early in the packaging trajectory, has high DNA density. Build-up of pressure in this groove is believed to drive a conformational switch in the portal protein, signaling that the capsid is full (43).

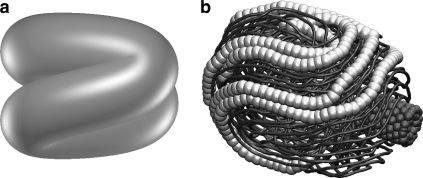
The φ29 virus has an elongated capsid with an axial ratio of ∼5:4, and it has almost no core. The favored conformation is a folded toroid (Fig. 4), which closely resembles the structure first proposed by Hud (7). It is interesting that Forrey and Muthukumar (30) found a folded toroidal conformation in a model DNA packed into an icosahedral capsid with no core, but only with an attractive DNA-DNA interaction potential. Spakowitz and Wang (29) found folded toroids in a spherical capsid, but only when they did not relieve torsional stresses by rotating the DNA as they packed it (the folded conformation is produced when twisting stress is converted to writhe, which is more favored energetically).

FIGURE 4.

Folded toroidal conformation. (a) Idealized structure proposed by Hud (7). (b) Simulation of DNA packed into the slightly elongated capsid of φ29, which has a very short core (33). Individual pseudoatoms (6 bp) are shown in some regions to facilitate recognition of the characteristic pattern, which resembles the seams on a baseball.

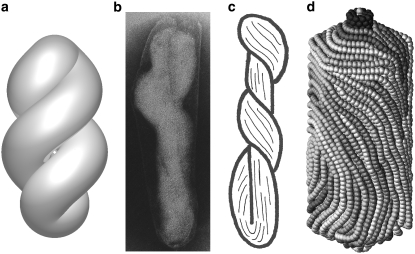
In elongated capsids with axial ratios of 2:1–3:1, twisted toroidal conformations are favored (Fig. 5), as suggested by Earnshaw et al. (4). This balances the penalties of elastic deformations (which would favor longitudinal DNA packaging) against the entropic penalty associated with ordered longitudinal conformations.

FIGURE 5.

Twisted toroidal conformation. (a) Idealized structure. (b) Electron micrograph of a partially disrupted giant T4 phage (4), which led to (c) the original model of Earnshaw et al. (4). (d) Simulation of 39.7 kbp of DNA packed into an elongated icosahedral capsid with an axial ratio of ∼3:1 (35).

We recently examined models with torsional stiffness in which the entering end of the DNA is unconstrained. We confirm the earlier report of Spakowitz and Wang (29) that inclusion of torsional stiffness has no effect on the energetic cost of packaging. In contrast to their study, we find no effect of torsional stiffness on conformation, whether the model is rotated as it enters the capsid or not. Both ends of the DNA were constrained in their model, preventing the complete relief of torsional stresses. These stresses are easily relieved at each step of packaging in our model.

Collectively, these studies have clarified the circumstances under which different DNA conformations are favored. All of these descriptions, however, are idealizations, and the conformations generated in all simulations are distributed widely about these ideal forms (18,28–34).

FORCES, THERMODYNAMICS, AND KINETICS OF DNA PACKAGING IN BACTERIOPHAGE

In molecular-mechanics simulations, the packaging force can be directly calculated during DNA packing (18,27–34). The simulation is stopped at regular intervals, and a separate simulation is carried out while the end of the DNA is held fixed at the portal. The average force required to keep the DNA from leaving the capsid is an equilibrium value, because the net packing velocity is zero during the measurement. Integrating the F versus d curve along the packaging trajectory gives the change in Helmholtz free-energy, ΔA. The molecular-mechanics energy is an internal energy, so the entropic penalty is obtained by subtraction: −TΔS = ΔA − ΔU. The energy function also gives separate values for the elastic and electrostatic components of ΔU.

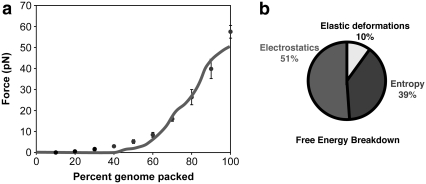
Our simulations on φ29 (33) yielded packaging F versus d curves with an excellent match to the original results from the single-molecule experiments (8). Fig. 6 shows the results of these simulations, along with the decomposition of the packaging free energy into its principal components. Electrostatic repulsions contribute most of the enthalpic penalty, whereas the elastic cost of bending is modest. The entropic penalty makes up ∼½ of the total free-energy cost, invalidating the assumption of theoretical studies (13–15) that the −TΔS term is negligible. The φ29 genome has a radius of gyration of ∼340 nm free in solution and ∼15 nm inside the virus, so it undergoes a volume compression of ∼10,000-fold on packaging. It would be surprising if there were no entropic penalty for such a reduction of conformational space.

FIGURE 6.

Energetics of packaging. (a) Force versus distance curve for the packaging of DNA into φ29, as determined in single-molecule pulling experiments (red line) (8), and as measured in a simulation (points) (33). Error bars are ±1 SD. (b) About 39% of the free-energy cost of packaging DNA into the viral capsid is due to the entropic penalty of confinement. The remainder of the cost is due to the change in internal energy, including electrostatic repulsions (51%) and elastic bending deformations (10%). The contributions from DNA stretching, DNA-DNA hard-core repulsions (volume exclusion), and DNA-capsid volume exclusion repulsions are all negligible.

SUMMARY AND CHALLENGES

Coarse-grained modeling studies have revealed how the ideal conformation of viral DNA depends on the capsid size and shape, and the presence or absence of core proteins, and that individual conformations vary widely around those ideal conformations. Electrostatic repulsions and entropic penalties are the dominant components of the free-energy costs of DNA packaging. The bending-energy cost, though small, is the dominant factor in defining the optimal conformation because it is more sensitive to conformation than the electrostatic energy, which depends almost entirely on the packaging density.

Such modeling studies still face significant challenges, however. Methods are needed for treating very large genomes (above 50 kbp) and examining kinetic issues in DNAs larger than the current limits (∼10 kbp). Models are needed that can accurately treat DNA kinking, a possibility that was suggested long ago (5,6) and has been proposed to explain unexpectedly high rates of cyclization of small closed-circular DNAs (45). Simulations should be carried out to investigate the distributions of knots found in tailless mutants of bacteriophages P2 and P4 (46–49).