Nanoparticles as Fluorescence Labels: Is Size All that Matters?

Abstract

Fluorescent labels are often used in bioassays as a means to detect and characterize ligand-receptor binding. This is due in part to the inherently high sensitivity of fluorescence-based technology and the relative accessibility of the technique. There is often little concern raised as to whether or not the fluorescent label itself affects the ligand-receptor binding dynamics and equilibrium. This may be particularly important when considering nanoparticle labels. In this study, we examine the affects of nanoparticle (quantum dots and polymer nanospheres) fluorescent labels on the streptavidin-biotin binding system. Since the nanoparticle labels are larger than the species they tag, one could anticipate significant perturbation of the binding equilibrium. We demonstrate, using fluorescence cross-correlation spectroscopy, that although the binding equilibria do change, the relative changes are largely predictable. We suggest that the nanoparticles' mesoscopic size and surface tension effects can be used to explain changes in streptavidin-biotin binding.

INTRODUCTION

The quantification of ligand-receptor binding interactions is at the heart of understanding signal transduction in biological systems. Moreover, membrane-bound receptor proteins comprise more than 50% of potential targets and available prescription pharmaceuticals (1). For reasons of convenience, history, and accessibility, the majority of binding/kinetic information is derived from radiolabeling and/or fluorescence assays. Although tagging ligands with fluorescent labels provides a convenient method for monitoring both equilibria and dynamics in solution, the impact of labeling on the very property being measured may be significant. Therefore, one needs to ensure that the ligand binding information being extracted remains physiologically relevant.

We examine to what extent the natural equilibrium of the biotin-streptavidin model system is affected by the conjugation to bulky fluorescent nanoparticle labels. Furthermore, we wish to determine whether or not any observed changes in the native equilibrium can be correlated to the mesoscopic property of label size. In doing so, we hope to gain insight into how other ligand-receptor systems of interest may be affected by fluorescent labeling, which in turn may provide rationalization for the selection of fluorescent labels in future fluorescence-based bioassays.

To analyze any biomolecule of interest, one must first be able to distinguish and quantify the amount of the target molecule in an often complex mixture. Thus, it is common practice to utilize easily detectable labels for identification and measurement purposes. These labels, which report on the behavior of the biomolecule of interest, can be radioactive isotopes (e.g., ³H or ³⁵S), spin probes (e.g., ¹³C), or fluorescent probes. Isotopic labeling of biomolecules has many advantages, including a high sensitivity of detection, typically in the picomolar-femtomolar range (10⁻¹²–10⁻¹⁵ M) (2). Despite the increased sensitivity and ease of radioassays, isotopic labeling requires very stringent safety regulations and practices, including specialized waste disposal. Furthermore, the introduction of heavier atoms can alter the equilibrium kinetics of sensitive ligand-receptor and enzyme-substrate reactions (3).

Target-directed fluorescent probes can be generated through the conjugation of fluorescent molecules such as rhodamine 6G or fluorescein to substrates, ligands, or proteins, resulting in a specific probe for the receptor/enzyme of interest. The widespread accessibility of commercially available fluorescent biomolecules and ease of labeling have resulted in a large number of absorbance and fluorescence-based assays. However, fluorescence-based measurements of K_d values below 10⁻⁸ M have proven to be difficult (4). Inconveniently, nonspecific interactions (association of the dye moiety with the lipid bilayer) may become significant at these concentrations, leading to high background and further complicating data analysis (5).

Additional issues surrounding the use of fluorophores as conjugates to small ligands/substrates include the potential to alter the natural equilibria and physiological effect of these biomolecules, often more substantially than that resulting from isotope labeling. AlexaFluor 488 (AF 488), a commercially available fluorophore, has a molecular weight of ∼885 g/mol; and a representative small drug, morphine, has a formula weight of ∼285 g/mol. In the above example, it is noted that the molecular mass of the fluorescent tag is ∼4 times larger than the ligand/drug which one may want to label. This substantial increase in molecular mass results in a reduced diffusion coefficient for the ligand in solution. Added bulk from the fluorophore also restricts the rotational motion of ligands in solution, which reduces the probability that the ligand will find the correct orientation for binding. The implications of reduced freedom of motion manifest in potential changes to the equilibrium binding rate constants and overall affinity of the ligands for the receptors.

Although various labeling and detection methods have allowed the explication of a myriad of biochemical information from molecules which otherwise would prove difficult to study, the effect of fluorescent labeling has been slow to arrive. Some effort has been made to quantify this effect both experimentally and theoretically. Experimental studies examining the effect of a covalently attached extrinsic fluorophore to proteins have returned conflicting results. Gajraj and Ofoli (7) noted that labeling bovine serum albumin (BSA) with fluorescein-isothiocynate molecules affected both the diffusion and adsorption behavior of the protein. Functional studies carried out by Zimmerman et al. (8) on labeled lysozymes report little to no change in the enzymatic activity when compared to unlabeled lysozymes. This suggests that fluorescent labels have little effect on their biological activity. Rosenthal and co-workers (9,10) have studied the effects of coupling membrane receptor proteins and ligands to quantum dots (QDs) and found that with long linker molecules, binding is largely unaffected. Importantly, many of these studies focused on quantifying the effect of labeling for proteins which are not expected to be affected to the same extent as small ligands or look at the effect of labeling only one of the components in the reaction. The study of ligand binding has been technically challenging.

Increasingly, correlation spectroscopy has been used to indirectly probe ligand binding by quantifying the loss of free fluorescently labeled ligand in the presence of the receptor, both in solution and in living cells (11–14). We have previously reported a facile method employing the correlation amplitudes (G(0)s and G_X(0)s) derived from fluorescence correlation spectroscopy (FCS) and fluorescence cross-correlation spectroscopy (FCCS), respectively (13,16). In both techniques the amplitudes are related to the concentrations of the labeled species in solution and, therefore, can be used to determine the concentration of bound species directly. FCCS has also been applied to protein-protein (7,17), DNA-DNA (18,19), and lipid-DNA (20) interactions and vesicle fusion (21). In two-photon excitation (TPE)-FCCS, both the ligand and the receptor are fluorescently labeled, thereby increasing any labeling effects which may be present. Conveniently, however, the decay curves obtained for individual autocorrelation and dually labeled cross-correlation decays can be fit to obtain information about the hydrodynamic radii of the two components (13,16). This information cannot be obtained from standard macroscopic fluorescence and radioligand assays; it provides additional means by which one can quantify the observed effects of labeling on both the small ligand and the larger receptor.

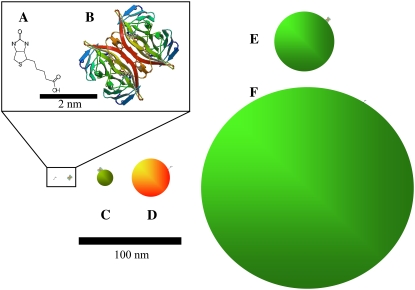
As mentioned above, we used the streptavidin-biotin system in this study of nanoparticle labeling. For this study of nanoparticle labeling, we chose to examine the well-characterized streptavidin-biotin system. FCCS was previously used in binding assays involving nanoparticle-labeled streptavidin-biotin interactions. Hwang and Wohland's (22) proof of principle used organic dye labeled streptavidin and biotin to demonstrate one-color single photon excitation FCCS for ligand-receptor binding. In their communication, Hwang and Wohland also presented evidence for binding between biotinylated fluorescein and a streptavidin-functionalized QD (655 nm). We recently used TPE-FCCS to probe streptavidin-biotin binding, each with QD labels (13), developing a method to directly measure the fractional occupancy, P_A, of the receptor and used this parameter to determine K_d and the ligand/receptor ratio. Semiconductor nanocrystals (i.e., QDs) (23) are increasingly being used as labels of biomolecules in fluorescence correlation spectroscopy (24,25), owing largely to their extreme brightness, which allows single molecule detection with relative ease. Our recent results describing the proof of principle to use QDs in streptavidin-biotin binding assays suggested that further study of the nanoparticle label effect on binding was warranted (13). Additionally, a biophysical understanding linking biomacromolecules using the streptavidin-biotin “bond” is of increasing importance. For comparative purposes, the relative structures and sizes of the systems studied here are shown in Fig. 1.

FIGURE 1.

Schematic diagram of relative sizes. (A) Biotin. (B) Streptavidin. (C) 525 streptavidin-QD (hydrodynamic radius, 4 nm). (D) 605 biotinylated-QD (hydrodynamic radius, 10 nm). (E) Green streptavidin-fluosphere (hydrodynamic radius, 20 nm). (F) Green biotinylated fluosphere (hydrodynamic radius, 100 nm).

The idea that biotin and streptavidin act as “molecular Velcro” and form a very strong bond (K_d ∼ 10⁻¹⁴ M) has led to their widespread use in many areas of science, including chemistry, biochemistry, physics, and even some medical/clinical applications (26). As such, the entire list of applications are too numerous to mention here, and a few examples will be presented to highlight the pervasive utilization of this ligand-receptor pair.

Tian et al. (27) have used the biotin-streptavidin linkage to create complex DNA templates for eventual use in DNA-based nanoelectronics. In a similar application, Lee et al. (28) employed the biotin-streptavidin pair in the construction of an ion channel biosensor switch. Recently, Rissin and Walt (29) demonstrated that it was possible to achieve attomolar detection limits using enzyme-amplified femtomolar arrays based on the biotin-streptavidin system. With respect to clinical applications, Hamblett et al. (26) discuss the possible use of biotin and streptavidin for specific tumor targeting and cancer therapeutics. They proposed injecting the patient with monoclonal antibodies, which are conjugated to streptavidin, for the tumor of interest. After an incubation period, the patient was injected with radiolabeled biotin to target radiation therapy (26). For this particular clinical application to be effective, it is imperative that the labeled biotin and streptavidin, ligand, and receptor retain their physiological binding activity.

Although the applications of biotin-streptavidin are diverse in nature, the rationale behind the use of this ligand-receptor pair typically is that it is the “strongest noncovalent interaction” (25). Indeed the strong noncovalent binding of the system is valid for an unlabeled biotin-streptavidin system. However, one can imagine that the conjugation of anything to either biotin or streptavidin may alter its native equilibrium. Our study investigates what effect the conjugation of bulky appendages (nanoparticle fluorophores in this case) has on the equilibrium binding and association/dissociation kinetics of this popular ligand-receptor pair.

MATERIALS AND METHODS

Commercial biotin and streptavidin conjugates

All materials were purchased from the suppliers and used without further purification. AF conjugates of streptavidin 488 and 594 (AF_S488 and AF_S594, respectively) were obtained as lyophilized powder (Molecular Probes, Eugene, OR). Stock solutions were prepared by dissolving 1 mg of the sample in 5 mL of 100 mM phosphate buffer (PB; pH 7.2, 0.1% BSA). Once dissolved, the sample vials were covered with aluminum foil and stored at 6°C. Using a molecular mass of ∼52 kDa for the streptavidin and ∼820 Da for the AF dye, the total mass of the labeled receptor was estimated to be ∼54,500 Da. This mass was used to determine the molarity of the stock solution (∼3.7 × 10⁻⁶ M). For all titration assays, the stock was diluted to ∼10 nM working solutions in the desired buffer for both the AF_S488 and AF_S594 conjugates. Typically, 1 nM streptavidin solutions were used for titration purposes.

FluoSphere conjugates of biotin (FS_B) and streptavidin (FS_S) were obtained and used as delivered (Invitrogen, Burlington, Ontario, Canada). Streptavidin-conjugated spheres (40 nm) as well as two samples of different sized biotinylated spheres (40 and 200 nm) were employed to dramatically alter the size of the ligand. All three conjugated FluoSphere beads had one-photon absorption and emission wavelength maxima in the yellow/green region of the spectrum (505/515, respectively). The concentration of the FluoSphere conjugates was determined using Eq. 1 (30):

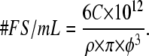(1)

In Eq. 1 the concentration of suspended beads measured in g/mL is denoted by C, the diameter of the spheres (in μm) is represented by φ, and ρ is the density of the polymer in g/mL.

For the polystyrene spheres used here, the density was equal to 1.05 g/mL. The number of microspheres per ml was converted to molar concentrations of spheres (mole/L) for each of the stock solutions. The concentrations for the 40 nm, 200 nm FS_B, and 40 nm FS_S solutions were 472 nM, 3.8 nM, and 236 nM, respectively. Dilutions of the 40 nm FS_B conjugate were made for titration purposes (5, 10, and 20 nM), whereas the 200 nm FS_B solution was used undiluted. Due to the intense brightness of the 200 nm FS_B ligands, titrations using this particular ligand were carried out with only 50% of the signal sent to the detectors. Studies were carried out to ensure that the G(0) and G_x(0) values were not affected by the reduced signal to the detectors. For titrations, FS_S receptors were used at the concentration of ∼1 nM to coincide with previously reported QD_S-QD_B titration conditions (13). QD biotin (QD_B605) and streptavidin conjugates (QD_S525 and QD_S605) were initially purchased from Quantum Dot (Hayward, CA) and later from Invitrogen. A number of buffer systems were utilized for the titration assays to quantify the effect of the total salt concentration on the equilibrium binding constants for the model system. The buffer systems were prepared from the 100 mM PB (pH 7.2, 0.1% BSA) by adding increased amounts of NaCl to examine the effect of ionic strength.

Optical setup

Samples were excited using 780 nm, 100 fs laser light from a Spectra Physics (Palo Alto, CA) Tsunami laser operating at 82 MHz. The laser power was attenuated to 20 mW with a neutral density filter to avoid photodamage. The QDot 605 and the organic fluorophores used all have appreciable TPE probability at 780 nm. The laser beam was expanded using a Galilean telescope to slightly overfill the back aperture of a 40×, 0.9 NA Zeiss objective lens (working distance = 2 mm) mounted on a Zeiss Axiovert 200 fluorescence microscope (Zeiss, Thornwood, NY). The long working distance objective lens available for this study produces a slightly larger excitation volume than typical high numerical aperture lenses. TPE fluorescence was collected by the same objective lens, passed through a broad band-pass filter to remove laser light (Omega Optical, XF3100, Brattleboro, VT), and reflected off a dichroic optic (Chroma, 700DCSPXR, Rockingham, VT) and through a tube lens in the side port of the microscope. A second dichroic optic (Chroma 565DCLP) was used to separate the red and green fluorescence. The spectrally separated light passes through band-pass filters (Chroma, E590LPv2 and D535/50× for the red and green emissions, respectively) and was coupled into optical fibers located at the focus of the tube lens. Using the optical fibers, the fluorescence was detected by two Si avalanche photodiodes (APDs; Perkin-Elmer, SPCQ-200, Fremont, CA). The output of the APDs was analyzed using a correlator card (ALV-5000; ALV, Langen, Germany).

FCS and FCCS data analysis

To measure the relative concentrations of species needed to determine the ligand-receptor equilibrium constants and off-rate kinetics, fluorescence correlation and cross-correlation analyses of the titration solutions were employed. Autocorrelation decays were modeled assuming a Gaussian TPE volume using the following equation (13,16):

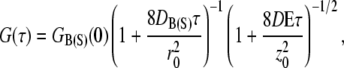(2)

where the subscripts B(S) indicate biotin (or streptavidin) associated fluorescent diffusers, τ is the lag time, D is the diffusion constant, r₀ is the laser beam radius at its focus, and z₀ is the 1/e² radius in the z direction. The TPE excitation volume was calibrated by measuring the autocorrelation decay for a 100 nM solution of Alexa 488 (D = 2.8 × 10⁻¹⁰ m²/s) in buffer (50 mM Tris-HCl pH 8.0). The excitation volume was found to be 3.3 fL (r₀ = 7.6 × 10⁻⁷ m and z₀ = 3.0 × 10⁻⁶ m). r₀ and z₀ were then held constant at these values. We have shown this method to be valid for calibrating the TPE volume (12). The meaning of the G(0)s will be presented shortly.

Cross-correlation decays were modeled as above using the following equation (13,16):

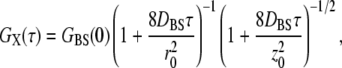(3)

where the subscript BS represents labeled ligands and receptors which are physically bound together and thus dual-color labeled. Nonlinear least-squares fitting to the data were accomplished using the software package Origin (OriginLab, Northampton, MA). The equations contain no terms to account for intersystem crossing or intermittent fluorescence, the effects of which were minimized here by keeping the excitation rates low (13,16,31). Also, we observed no fluorescence resonance energy transfer or fluorescence quenching in the case of bound systems. This was verified by the lack of relative changes in the brightness (count rate per particle) of either species when both were present in solution.

It was previously demonstrated that the fractional occupancy, P_A, could be calculated simply using G(0)s (13,16). Briefly, in the absence of cross talk between the two detection channels, the correlation and cross-correlation amplitudes are given by

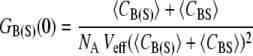(4)

and

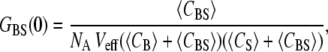(5)

where, N_A is Avogadro's number, V_eff is the effective TPE volume, 〈C_BS〉 is the time-averaged concentration of dually labeled species, and 〈C_B(S)〉 is the time-averaged concentration of biotin (or streptavidin). To use this equation, one assumes that the correlation amplitude is free of cross talk between the detection channels. We have previously shown this to be true for the QDs used in this study (13). Additionally, in the case of low concentrations, the autocorrelation G(0)s were corrected for the contribution of background noise as necessary (16).

For the equilibrium B + S ↔ BS, recall that fractional occupancy is

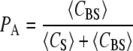(6)

This relation can be expressed in terms of G(0) values as follows:

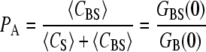(7)

Equation 7 shows that unlike the individual G(0)s, P_A is not dependent upon the TPE volume; however, where a precise calibration of this volume is available, more information about the system (such as the diffusion coefficients) can be gained.

Ligand-receptor binding data analysis

The binding data of ligand to receptor were analyzed in the following way. Since there may be multiple receptors per dot/sphere, one may need to consider a multiple-ligand equilibrium approach to binding. Thus for n ligands (L) associating with a nanoparticles/spheres (R) we have

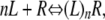(8)

where n can be a whole number or a fraction.

It can be shown that a standard analysis of this equilibrium produces the Hill equation for multiligand binding (30):

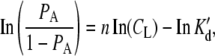(9)

where P_A is, again, the fractional occupancy of available binding sites on the dot/sphere, C_L is the concentration of ligand, and K′_d is the dissociation constant for the equilibrium presented in Eq. 8. Additionally, in the absence of cooperativity, taking the nth root of the dissociation constant, K′_d, gives the dissociation constant, K_d, for the formation of an individual ligand-receptor complex. Binding curve titrations were carried out as described previously (13,16).

Dissociation kinetics

For measuring the off-rate kinetics, equilibria were established such that 1:1 pairs of the streptavidin-biotin systems dominated. We can then give the following equilibrium equation considering a pair of QD labels:

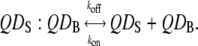(10)

Free d-biotin is added to measure the off-rate for the above reaction. This can be approximated as a perturbation that removes free QD_S, thus promoting more dissociation of QD_S:QD_B to restore equilibrium. Following our previously developed kinetic equations for the off-rate of the above equation, we use (13)

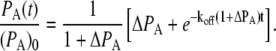(11)

Equation 11 has only one adjustable parameter, k_off, which represents the rate constant of QD_S:QD_B unbinding. ΔP_A = P_A(∞)/(P_A(0)–P_A(∞)). The derivation of this equation can be found in Briddon et al. (12).

RESULTS AND DISCUSSION

Fluorescent label size versus equilibrium binding constant

The streptavidin-biotin binding equilibrium was previously examined with respect to QD labels (13). In that study, we established that although the reduced association is not solely governed by increased ligand and receptor bulk, the added mass and dimension of the QD label reduced the binding constant by a relatively large factor (∼3600 times) and thus could not be neglected. To further quantify how the bulky nature of the fluorescent label affects the equilibrium binding kinetics of our model system, several different sized conjugated biotin and streptavidin species were studied. To establish which of the ligands was more affected by the bulky fluorescent label, the sizes of the streptavidin and biotin conjugates were systematically varied.

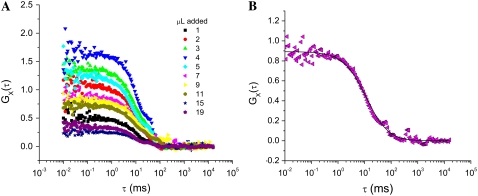
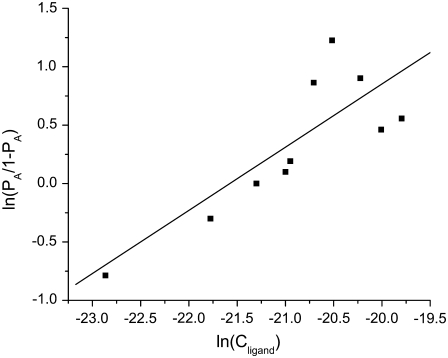
To understand and quantify the binding between various fluorophore-labeled streptavidin and biotin moieties, titrations were performed as described in Swift et al. (13). A series of FCCS decays for a titration of streptavidin-functionalized fluospheres (40 nm diameter, green emission) with biotinylated QDs (20 nm diameter, red emission) is presented in Fig. 2. The changes in correlation amplitude for this titration display the typical behavior of increasing slightly before decreasing (13). Using TPE-FCS and TPE-FCCS, G(0) values and diffusion coefficients red, green, and dually labeled species were determined. These G(0) values could then be used (Eq. 7) to calculate the fractional occupancy for each titration point. These data were plotted and analyzed using Eq. 9 to determine the equilibrium dissociation constant, K_d, for each combination of fluorescence label (see Fig. 3).

FIGURE 2.

(A) Cross-correlation decays for the titration of 1 nM green emitting streptavidin-coated fluospheres with increasing volumes of 605 nm emission biotinylated QDs (from a 10 nM stock QD solution). (B) Representative data set and fit using Eq. 4.

FIGURE 3.

Hill plot (Eq. 8 represents fitted line) of a titration of 1 nM green emitting streptavidin-coated fluospheres with increasing volumes of 605 nm emission biotinylated QDs (C_ligand). This plot gives a binding ratio of 1:1 and K_d of 2.3 × 10⁻⁹ M.

Due to the low quantum yield of organic fluorophores and the very low concentrations of biotin (ligand) required for accurate determination of the experimental K_d values, only QDs and fluorescent microspheres (FS) were suitable fluorescent labels for biotin. AF 488 and 594 commercially available organic fluorophores could be used as fluorescent tags for the streptavidin receptor. At concentrations of ∼10 nM, the AF_S samples could be detected with reliability and reproducibility. The AF-labeled streptavidin receptors are only slightly larger than the native streptavidin having radii of 3 and 2.5 nm, respectively (33). Thus, these conditions allowed us to examine the full effect of bulky labeling on the otherwise small ligand. Table 1 summarizes the experimental hydrodynamic radii of the ligands and receptors in each of the seven labeled systems examined. The values listed in Table 1 are the average values rounded to the nearest whole number. Importantly, these values agree within error to the manufacturer's specifications and were obtained from a minimum of 20 different autocorrelation decay curves.

TABLE 1.

Experimental hydrodynamic radius for biotin and streptavidin ligands and receptors examined in 100 mM phosphate buffer

System	Hydrodynamic radius of biotin (nm)	Hydrodynamic radius of streptavidin (nm)
AFS-QDB	10 ± 3	4 ± 2
FSS-QDB	10 ± 3	19 ± 2
QDS-QDB	10 ± 3	7 ± 1
QDS-(40 nm) FSB	27 ± 5	7 ± 1
AFS-(40 nm) FSB	27 ± 5	4 ± 2
QDS-(200 nm) FSB	104 ± 39	7 ± 1
AFS-(200 nm) FSB	104 ± 39	4 ± 2

The experimentally obtained dissociation constants, K_d, are presented in Table 2. One might imagine that the larger the total size of the bound complex, the weaker the interaction (as reflected by a larger K_d), but this is not the case. The strongest binding pair is the streptavidin QD (8 nm diameter) with the biotinylated fluospheres (40 nm diameter). From Table 2 it is apparent that the smaller streptavidin labels lead to stronger binding, but on the biotin side, the fluospheres dominate the stronger binding. This suggests that the nature of biotinylated surface is very important in determining binding strength, which could be related to the freedom of motion of the biotin and/or the environment the streptavidin encounters when in proximity to the fluosphere. To help decipher these streptavidin-biotin interactions, the contributions of on-rate kinetics were separated from the off-rate kinetics by measuring dissociation directly.

TABLE 2.

Experimental dissociation constants, off-rate constants, and calculated association rate constants in 100 mM phosphate buffer

System	Kd (M)	koff (s−1)	kon (M−1s−1)
AFS-QDB	4.3 × 10−10	4.0 × 10−5	9.3 × 104
FSS-QDB	2.3 × 10−9	3.4 × 10−5	1.5 × 104
QDS-QDB	4.0 × 10−10	4.0 × 10−5	1.0 × 105
QDS-(40 nm) FSB	1.3 × 10−10	3.4 × 10−4	2.6 × 106
AFS-(40 nm) FSB	2.8 × 10−10	1.4 × 10−4	5.0 × 105
QDS-(200 nm) FSB	1.9 × 10−10	4.0 × 10−4	2.1 × 106
AFS-(200 nm) FSB	1.4 × 10−10	1.1 × 10−4	7.9 × 105

Binding kinetics

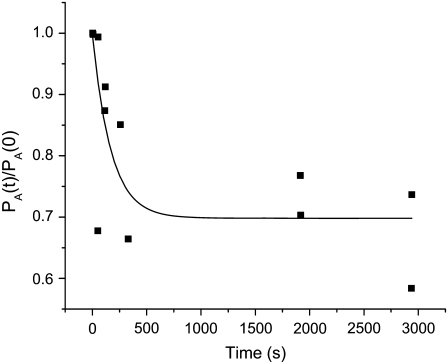
The off-rate kinetics for the series of binding pairs studied above was examined using the previous approach for the paired QD system (13). Briefly, equilibria were established such that a 1:1 binding ratio dominated for streptavidin-biotin pairs. Then a large excess of free d-biotin (∼1 μM) was added to the solution, and cross-correlation and autocorrelation decays were collected as a function of time after the d-biotin addition. The correlation amplitudes were then used to calculate the fractional occupancy, P_A, which was then normalized to time zero and plotted versus time (e.g., in Fig. 4). These plots were then fitted using Eq. 11 to determine k_off.

FIGURE 4.

Unbinding kinetics plot for a 1 nM QD_B-FS_S (1:1) solution into which 100 μM free biotin has been added. The time zero normalized fractional occupancy is plotted such that k_off can be determined directly from a fit using Eq. 12 (solid line).

The values of k_off were then used to calculate the on-rate constant for bind, k_on. Both of these quantities are also presented in Table 2. One might anticipate that the off-rate kinetics would not depend on the size of the fluorescent tags since this process is dictated more by the streptavidin binding pocket. This is reflected by the data. The on-rate kinetics may be more intimately related to the label size, since the collision kinetics is influenced by the diffusion coefficients of the colliding pair. However, as was earlier illustrated, the reaction rate also will depend on the densities of the labels on the nanoparticle surfaces (13).

It was demonstrated previously that the reduction of the on-rate coefficient compared with the native streptavidin-biotin binding can, in part, be accounted for by considering the changes in the number of collisions which result in binding and the relative diffusion of the conjugates (13). The most straightforward comparison between binding scenarios can be made by taking the relation of the frequency factors, A, for binding described by Arrhenius type kinetics (13):

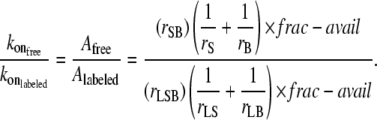(12)

The encounter distance is denoted by r_SB (which represents the radius of the colliding ligand), and receptor and r_S(B) is the hydrodynamic radius of the fluorescent species bearing the streptavidin (biotin). Subscript L is the fluorescent-labeled species measured. The values in the numerator are for literature values of free streptavidin and biotin. The fraction of the surface area of the labeled particle which is available for binding is denoted “frac-avail”. This factor represents the fraction of the collisions in which the alignment of the ligand and receptor are in the correct orientation for binding to occur. For the native system this value is close to 1 (suggesting every collision will have the correct orientation). However, the frac-avail can be very small (≪1) for the labeled systems, since the nanoparticle surfaces have a small fraction of streptavidin or biotin bound. Equation 13 is used to calculate the fraction available for binding:

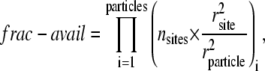(13)

where the number of binding sites/ligands per particle is given by n_sites, and r_site and r_particle are the radius of the binding site/ligand and label, respectively. It is important to note that for our model the frac-avail will be a product of both particles involved in the collision: either unlabeled or labeled biotin and streptavidin. Intuitively, the frac-avail for the labeled system will be substantially smaller than the native unlabeled system, as can be inferred from Fig. 1.

Using Eq. 13 it was possible to calculate the ratio of theoretical preexponential factors (A_free/A_label) for the systems assessed and compare them to native values. We found previously that this ratio did not entirely account for the differences observed in on-rate constants between the QD-labeled streptavidin and biotin and the native system. Therefore, we completed a more comprehensive study across fluorescent labels of a variety of sizes.

From Table 2, we directly observe that the decreased translational diffusion coefficients of the labeled particles do not completely account for the reduced association rate constant. This simplified model does not take into account rotational and orientational constraints for the large FS and QD labels. Intuitively, one would expect that the conjugation of the small ligand in particular could result in rotational limitations which would contribute to the reduced overall association rate for the labeled species.

Varying the size of fluorescent label on biotin and streptavidin biomolecules

From Table 2 it is evident that the bulky label on both the ligand and the receptor contribute to the altered rate constants, and upon initial inspection it is not evident whether a definitive trend is identifiable. It is interesting that the largest FS_B ligand (200 nm) does not always result in the lowest observed association rate constant. The origins of this are unclear; however, it may be due to the large number of biotin molecules conjugated to each of the spheres, which increase the probability of a binding interaction occurring upon collision. Again we are interested in determining if it is possible to account for the reduced association of the dually labeled systems using Eq. 12.

Table 3 summarizes the radii, number of binding sites, frac-avail, and calculated A_SB values for each of the labeled systems investigated. For the AF-labeled and QD streptavidin, the number of binding sites was estimated by carrying out a blocking assay that determined the concentration of unlabeled d-biotin necessary to completely block all binding with QD-labeled biotin. The number of biotin molecules per QD was based on manufacturers' specifications. For the FS_B and FS_S, values were calculated from binding data provided by the supplier.

TABLE 3.

Calculated theoretical frequency factors (A_SB) for native and labeled biotin-streptavidin binding systems in 100 mM phosphate buffer

System	nsites (strept)	nsites (biotin)	frac-avail	ASB	Afree/ Alabeled
Native (2)	4	1	0.16	1.67	-
AFS-QDB	3	6	2.5 × 10−4	1.2 × 10−3	1349
FSS-QDB	21	6	7.9 × 10−5	3.5 × 10−4	4812
QDS-QDB	10	6	8.4 × 10−4	4.1 × 10−3	405
QDS-(40 nm) FSB	10	148	9.3 × 10−4	5.7 × 10−3	293
AFS-(40 nm) FSB	3	148	8.6 × 10−4	7.6 × 10−3	220
QDS-(200 nm) FSB	10	18,540	7.8 × 10−3	1.3 × 10−1	13
AFS-(200 nm) FSB	3	18,540	7.2 × 10−2	2.0 × 10−1	8

Table 4 compares the theoretical ratios of the frequency factors to the experimentally derived ratio of rate constants. Once more we note that the ratios of the experimental association rate constants for the free and labeled species are much larger than the predicted values based on reduced translational diffusion of the bulky labels in solution. For all systems investigated the predicted ratio of A_free/A_labeled is much smaller than the experimental ratio of free and labeled association rate constants. From Table 4 it is evident that the association rate constants (k_on) are not purely governed by the frequency factors, and thus the reaction is not purely diffusion limited. Although this diffusion-based model may be an oversimplification of the reduced biotin-streptavidin interaction in the presence of bulky labels, the model serves to illustrate that the values we obtained for the association rate constants are not unrealistic.

TABLE 4.

Experimental association rate constants and theoretical frequency factors for native and labeled systems in 100 mM phosphate buffer

System	kon (M−1s−1)	kfree/klabeled (experimental)	Afree/Alabeled (theoretical)
Native (2)	2.0 × 109	-	-
AFS-QDB	9.3 × 104	21,505	1349
FSS-QDB	1.5 × 104	135,294	4812
QDS-QDB	1.0 × 105	20,000	405
QDS-(40 nm) FSB	2.6 × 106	765	293
AFS-(40 nm) FSB	5.0 × 105	4000	220
QDS-(200 nm)FSB	2.1 × 106	950	13
AFS-(200 nm)FSB	7.9 × 105	2532	8

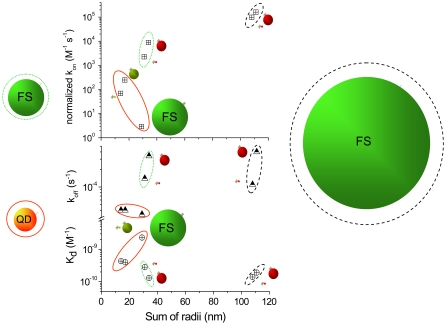
To reveal trends in the binding data, the constants presented in Tables 1 and 2 are plotted versus binding pair size in Fig. 5. In this plot, the on-rate constant, k_on, has been normalized to remove its dependence on the number of binding sites per particle pair. This was done by dividing by A_free/A_labeled from Table 3. Therefore, if the constants depend only on size, the k_ons should tend to decrease with size and the k_offs should be independent of size; and, therefore, the K_ds should increase with increasing particle size. A quick survey of Fig. 5 reveals that this is not the case.

FIGURE 5.

Plots of the streptavidin-biotin dissociation constant (K_d, crossed circles), off-rate constant (k_off, triangles), and normalized on-rate constants (k_on, crossed squares, normalized to remove dependence of the number of reactive sites per particle surface) versus sum of the radii of the interacting pair. Data are grouped according to the biotinylated species with a red QD (red oval around data), green 40-nm-diameter fluosphere (green oval around data) and green 200-nm-diameter fluosphere (black oval around data). Within the plots the streptavidin binding partners are given by a green 40 nm fluosphere or red or green QDs. The smallest binding partner is streptavidin labeled with AF dyes. The details of the data are found in Tables 1 and 2.

The k_offs (half-filled triangles) are considered first since these are measured directly. The constants are grouped into three categories based on the biotinylated species (40- and 200-nm-diameter fluospheres and 20-nm-diameter QDs). The fluosphere data have the largest off-rates, with the FS_B-QD_S pairs unbinding the fastest. This particular size effect may suggest that for fluosphere-biotin, the environment of the streptavidin dominates the unbinding process. This could relate to the ability of free biotin to enter the streptavidin pocket and/or to the energetic barrier to separation of the pair. The pairs that include QD_B are clustered together and have a rate constant slower by an order of magnitude. The nature of the streptavidin is less important, as all the k_offs are clustered close in value. For these combinations of smaller pairings, the biotinylated QD seems to be the important factor. All the pairings have rate constants larger than the value for the native streptavidin-biotin pair (5 × 10⁻⁶ s⁻¹), but the smaller pairs are closer to the native value.

Next we examine the equilibrium dissociation constants, K_d (circles with cross-hatches), which are also measured directly. In this case there is a slight trend of larger pairs possessing smaller K_ds, which means a thermodynamically stronger bond. Pairs containing the FS_B system have the smallest K_ds among the group. The least thermodynamically stable is the FS_S-QD_B pairing. All the pairs have K_ds that are considerably larger (10⁶–10⁴×) than the native system.

The K_ds and k_offs were used to calculate the on-rate constants for these combinations of labeled streptavidin and biotin. The values were then normalized as mentioned above. These are plotted in the topmost part of the graph and delineated as x-ed squares. The general trends are counterintuitive, from a size perspective, with the larger combinations possessing larger on-rate constants. This is particularly interesting for the large pairs with FS_B as one of the partners. The on-rate constants are one order of magnitude larger for the FS_B-QD_S pair than for the FS_B-AF_S pair. The latter of these has the streptavidin labeled with a small organic dye, which one might think is less of a perturbation than the larger QD. However, the organic dye perturbs the binding environment more for these pairs (circled by green and black lines in Fig. 5). The lowest k_ons come from the pairs with QD_B as one member of the binding pair—although in this data set (within the red oval), there is a trend of larger species being slower and thus reducing the rate constant. All told, it becomes clear from Fig. 5 that there is more than simply size effects responsible for the changes in nanoparticle-labeled streptavidin-biotin binding.

Schlosshauer and Baker have suggested that simply multiplying the diffusional component by the probability of a collision resulting in binding, as we have done, is overly naive (34). As an alternative, they presented a general expression for partially diffusion-controlled reactions which occur between two spherical molecules, accounting for the translation and rotation of the two particles. In the Schlosshauer and Baker model, the spherical molecules contain a single asymmetric reactive area, which can be thought of as a single receptor or ligand per sphere. Although their model is considerably more sophisticated than the simple diffusion-based model presented in Eq. 12, they report rate constants which are two orders of magnitude larger than expected from the simple geometric model presented here (34). From Table 4, we note that the ratio of observed rate constants (k_free/k_labeled) is much larger than the predicted ratio, except for the QD_S-FS_B (40 nm) binding pair.

A theoretical rate constant obtained using the Schlosshauer and Baker model would result in a larger denominator for the predicted ratio and thus serves to increase the discrepancy between the empirical and theoretical values. Furthermore, their model assumes only a single asymmetric reactive “patch” on each of the spheres. In our experimental systems both the streptavidin and biotinylated dots/spheres/fluorophores have more than one reactive ligand/receptor on their surface, making direct comparisons between the models difficult. We have estimated that for the systems under study here, rotation of the nanoparticles does not contribute significantly to the differences in binding kinetics. Rotational constraints become important when there is a single asymmetric binding site on the large molecule. For a spherical particle 10–100 nm in diameter with a larger number of conjugated biomolecules, rotational constraints are not significant. For the nanoparticle-labeled biotin-streptavidin interaction, the angular momentum of the particles is large enough that a number of potential ligands will encounter each other during a single collision event.

Other microscopic properties contributing to reduced association kinetics, including solvation and electrostatic effects, need to be considered. Indeed, there may be trends in activation energies for the on and/or off reactions that are connected with electrostatics and solvation in the surface region of the particles.

Effect of total salt concentration on equilibrium binding kinetics

Examining a series of nanoparticles joined by the streptavidin-biotin interaction as a function of solution ionic strength can provide insight into surface-related effects that influence association and dissociation kinetics. The systems which were used for this analysis were QD_S-QD_B, QD_S-FS_B (40 nm), and QD_S-FS_B (200 nm). Each of the ligand-receptor binding pairs were examined in 100 mM PB, 100 mM PB + 25 mM NaCl, and 100 mM PB + 50 mM NaCl, resulting in ionic strengths of 187.5, 212.5, and 262.5 mM, respectively. The average diffusion constants and subsequent hydrodynamic radius for each of the species were obtained for each buffer system to account for any changes in hydration shell with increased salt concentration. These experimentally determined values are presented in Table 5. The average hydrodynamic radii were the same to within error for all ligands/receptors examined in all the buffers used. Importantly, the consistency of the measured radii suggests also that the viscosity of the buffer is not affected significantly by the addition of increased salt.

TABLE 5.

Hydrodynamic radii (nm) for each of the species as a function of ionic strength

	187.5 mM	212.5 mM	262.5 mM
QDS (525)	4 ± 1	4 ± 1	4 ± 1
QDS (605)	7 ± 1	5 ± 1	5 ± 1
QDB	10 ± 3	8 ± 2	10 ± 2
FSB (40 nm)	27 ± 6	28 ± 6	28 ± 7
FSB (200 nm)	104 ± 39	106 ± 39	102 ± 33

Titration experiments were carried out as described previously for each of the systems (12). K_d and k_off-rate constants in addition to the calculated k_on-rate constraints for each of the systems are summarized in Tables 6–8. Results of Tables 6–8 were used to generate plots to compare the equilibrium binding constants (Fig. 5) and dissociation rate constants (Fig. 6) for each of the three systems.

TABLE 6.

Equilibrium dissociation constant, dissociation rate constant, and association rate constant for the QD_S-QD_B system

Ionic strength (mM)	Experimental Kd (M)	Experimental koff (s−1)	Calculated kon (M−1s−1)
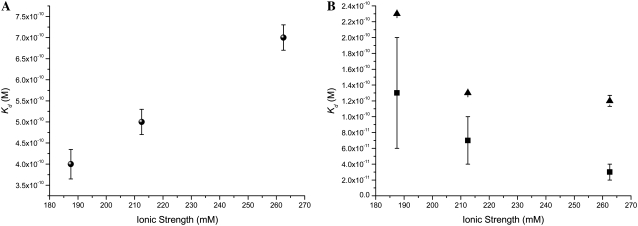
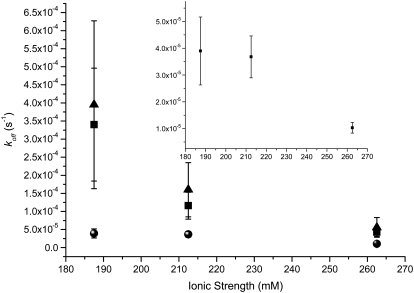
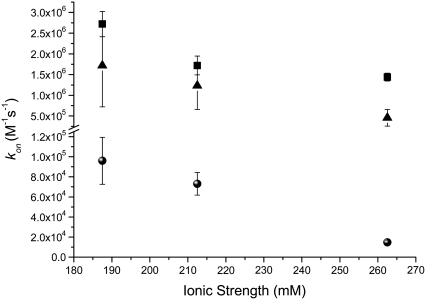
187.5	4.0 ± 0.4 × 10−10	4.0 ± 1.0 × 10−5	1.0 ± 0.2 × 105
212.5	5.0 ± 0.3 × 10−10	4.0 ± 0.8 × 10−5	8.0 ± 1.0 × 104
262.5	7.0 ± 0.3 × 10−10	1.0 ± 0.2 × 10−5	1.4 ± 0.2 × 104

TABLE 7.

Equilibrium dissociation constant, dissociation rate constant, and association rate constant for the QD_S-FS_B(40 nm) system

Ionic Strength (mM)	Experimental Kd (M)	Experimental koff (s−1)	Calculated kon (M−1s−1)
187.5	1.3 ± 0.7 × 10−10	3.4 ± 1.5 × 10−4	2.7 ± 0.3 × 106
212.5	7.0 ± 0.3 × 10−11	1.2 ± 0.7 × 10−4	1.7 ± 0.3 × 106
262.5	3.0 ± 1.0 × 10−11	4.3 ± 1.0 × 10−5	1.4 ± 0.1 × 106

TABLE 8.

Equilibrium dissociation constant, dissociation rate constant, and association rate constant for the QD_S-FS_B (200 nm) system

Ionic Strength (mM)	Experimental Kd (M)	Experimental koff (s−1)	Calculated kon (M−1s−1)
187.5	2.3 ± 0.06 × 10−10	4.0 ± 2.0 × 10−4	1.7 ± 1.0 × 106
212.5	1.3 ± 0.05 × 10−10	1.6 ± 0.7 × 10−4	1.2 ± 0.6 × 106
262.5	1.2 ± 0.7 × 10−10	5.6 ± 2.7 × 10−5	4.6 ± 2.0 × 105

FIGURE 6.

Comparison of the equilibrium unbinding constants (K_d) for (A) QD_S-QD_B (black), (B) QD_S-FS_B 40 nm (blue), and QD_S-FS_B 200 nm (red) at various ionic strengths.

In Fig. 6, we identify behavior for the QD_S-QD_B system that is contrary to the two QD_S-FS_B systems. An increased K_d for the QD_S-QD_B system is correlated to increased salt concentration, whereas both QD_S-FS_B systems result in smaller K_d values, which begin to approach the native unlabeled system. From the graph in Fig. 7, we note that for all three cases examined the dissociation rate decreases with increased ionic strength. Interestingly, Houen and Hansen (35) reported that various sugars were found to interfere with the binding of biotin and streptavidin. They attributed the reduced binding to the interaction of the sugar moieties with side-chain residues in the binding pocket. NaCl would not form hydrogen bonds with the tryptophan residues, which would be able to interact strongly with the both the biotin ligand and sugars molecules and thus should not affect the system in the same manner.

FIGURE 7.

Comparison of dissociation rate constants (k_off) for QD_S-QD_B (black), QD_S-FS_B 40 nm (blue), and QD_S-FS_B 200 nm (red) for different ionic strengths. Inset is an expanded version of the lowest plot.

From previous experiments done in our group, we know that the fluospheres can be highly charged (36), and thus the addition of salt to the solution would be expected to stabilize the system by balancing the excess surface charges. One would expect that if the dissolved salts were acting as counterions in a stabilizing manner then increased total salt concentrations should also result in an increase in the association rate for the FS_B-QD_S systems. A plot comparing the association rate for each of the three systems as a function of ionic strength is given in Fig. 8.

FIGURE 8.

Comparison of calculated association rate constants (k_on) for QD_S-QD_B (black), QD_S-FS_B 40 nm (blue), and QD_S-FS_B 200 nm (red) at various ionic strengths.

From Fig. 8 the calculated k_on for all three systems indicates that increased ionic strength is correlated with reduced association rates, which does not support the hypothesis presented above. As the salt readily dissolves in the buffer, it is unlikely that the small concentration of NaCl added altered the viscosity of the solution enough to account for the overall reduced k_on observed in Fig. 8. Moreover, there is no change in the diffusion coefficients for this range of ionic strength.

For all three systems examined, the addition of increased ionic strength lowers the k_off and the k_on at the same time. Since the association becomes slower in both the forward and reverse directions, it seems unlikely that the changes in ionic strength significantly change the Coulombic interactions between the particles, at least over the range of ionic strengths employed. Given that the apparent sizes of the particles were independent of ionic strength, it seems that significant changes in solution viscosity do not occur either. Additionally, since the streptavidin-biotin interaction can be considered the same in all cases, it seems unlikely that changes in this interaction will dominate the trends in binding kinetics and equilibria for the nanoparticle labels.

As the nanoparticles under investigation approach each other, water molecules must rearrange to accommodate the collisions. This can be thought of as a surface tension effect. It is well known that increasing salt concentration leads to increased surface tension for aqueous interfaces (37). Thus, the energetic barrier to collisions increases with increasing ionic strength, all other factors being essentially equal. This would result in a smaller k_on. A similar argument can be applied to unbinding, where the barrier to water rearrangement during nanoparticle-nanoparticle dissociation increases with ionic strength. Thus, the rate constants decrease in both the forward and reverse directions. This effect appears to be independent of the nanoparticle pair studied.

In contrast to the rate constants, the equilibrium dissociation constant, K_d, gets smaller for QD-FS binding (i.e., becomes a stronger bond) and larger for QD-QD binding (i.e., becomes a weaker bond) as a function of increasing ionic strength. The strengthening of the QD-FS interaction can be rationalized again in terms of surface tension. There is a net reduction in surface tension for the bound system, and this is enhanced in the presence of increasing salt concentration. The difference between the QD-FS and QD-QD interactions is that for the latter both nanoparticles are coated with polyethylene glycol (PEG). Thus, the PEG structure must also be taken into consideration for equilibrium binding. These PEG-PEG interactions seem less influential on the kinetics, as discussed above. It has been demonstrated that a PEG layer thins appreciably upon increasing ionic strength in the range 2–200 mM (38). Although our range is much smaller than this, it is possible that the increase in ionic strength also hinders the mobility of the biotin on the QD-PEG surface, reducing the binding probability and thus increasing K_d.

CONCLUSIONS

We have demonstrated that the conjugation of bulky fluorophores to both biotin and streptavidin has an effect on the equilibrium and kinetics of this model system. This effect is predominant in the association kinetics, or binding reactions, which were found to be on average six orders of magnitude slower than those of the native B-S system. The dissociation, or off-rate constants, for the labeled B-S systems were only ∼1 order of magnitude faster, at most, than the native system. Larger ligands were shown to increase the rate of dissociation for the B-S complex possibly through entropic surface mediated driving forces. Important corollaries of these results reflect the need to choose carefully the size and type of fluorescent label chosen to study small ligands and receptors. Countless examples exist in the literature where biotin and streptavidin are used as a “bridge” or “molecular Velcro” to link two different species of interest together.

When using this tight binding biotin and streptavidin system, it is important to remember that binding is a dynamic equilibrium while in solution. Conjugation of any species to either biotin or streptavidin will alter the equilibrium, reducing the association rate and/or increasing the dissociation rate of the complex. As such, this interaction may not be the molecular glue that is often quoted in the literature. Before using the B-S interaction it would be advisable to obtain the dissociation rate to understand the half-life of the complex. This would allow the design of experiments that avoid dissociation and allow increased time for association of the labeled/conjugated ligand-receptor complex.

In addition, we have shown that reduced association rates for this particular tight binding pair cannot be explained solely in terms of mesoscopic properties. Although the increased ligand bulk does contribute to the reduced frequency of binding events in solution, the reactions are not purely diffusion limited. The limited salt studies carried out suggest that there are surface tension effects at play for both binding and unbinding.

Taken together, the results from our study suggest that there are several effects of large fluorescent labels on the dynamics and equilibria of biomolecular binding interactions. These range from displacing equilibrium to altering the on- and off-rate kinetics. The changes are due in part to the sheer bulk of the labels and in part to the mesoscopic surface properties of the labels. However, much of the change in binding can be accounted for based on these two simple considerations; and thus it appears that for streptavidin-biotin binding, the integrity and function of the binding pair are not drastically altered when conjugated to these bulky labels. In effect, although the size of the nanoparticle does indeed matter, one must also consider its other properties to understand how a nanoparticle influences the chemistry of the species it labels.